Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis
Abstract
1. Introduction
2. Standard Process of the Methodology and Amenities
2.1. Brownian Motion
- ;
- is continuous for ;
- is independent for ;
- Anormal distribution is exhibited by with mean as well as variance .
2.2. Fractional Derivative and Its Feature
- ;
- ;
- ;
- ;
- .
2.3. Methodology
3. Application of the Method
4. Diverse Analyses Concerning to the Fractional Equation
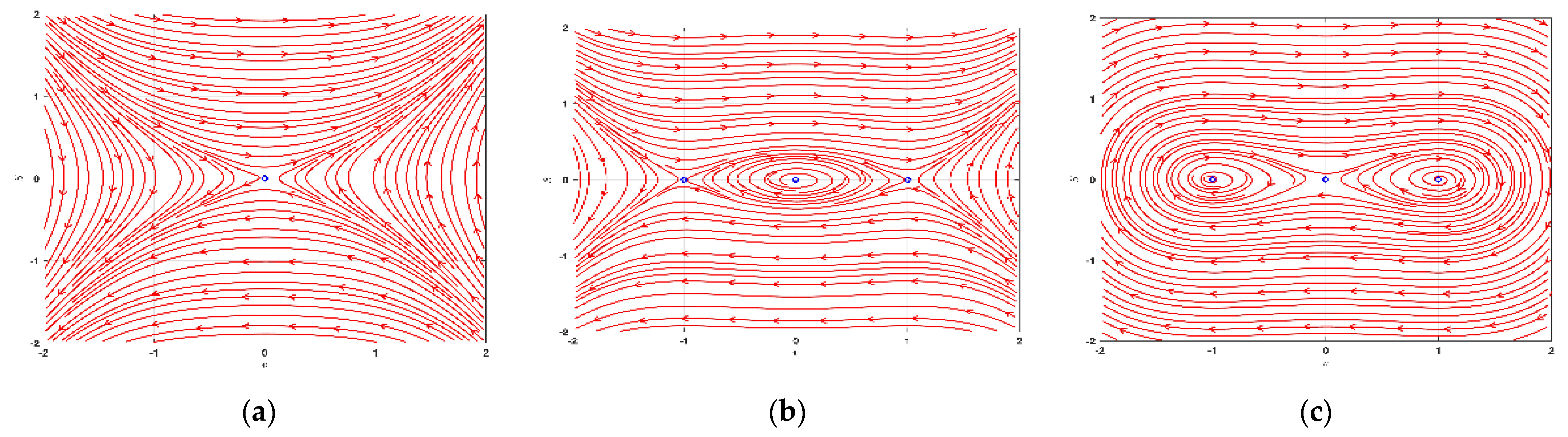
4.1. Bifurcation Analysis
- The equilibrium position represents a saddle point, when ;
- The equilibrium position denotes a center point, when ;
- The equilibrium position signifies a cuspid point, when .
- Instance 1: and .
- Instance 2: and .
- Instance 3: and .
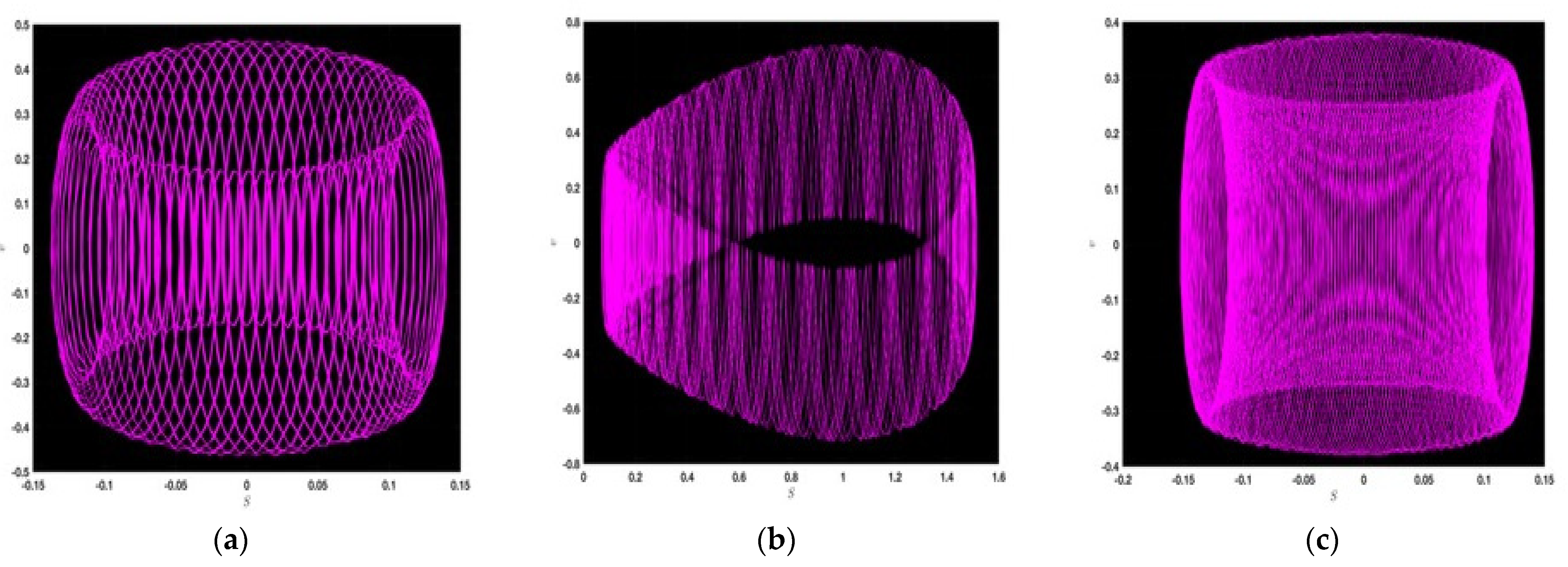
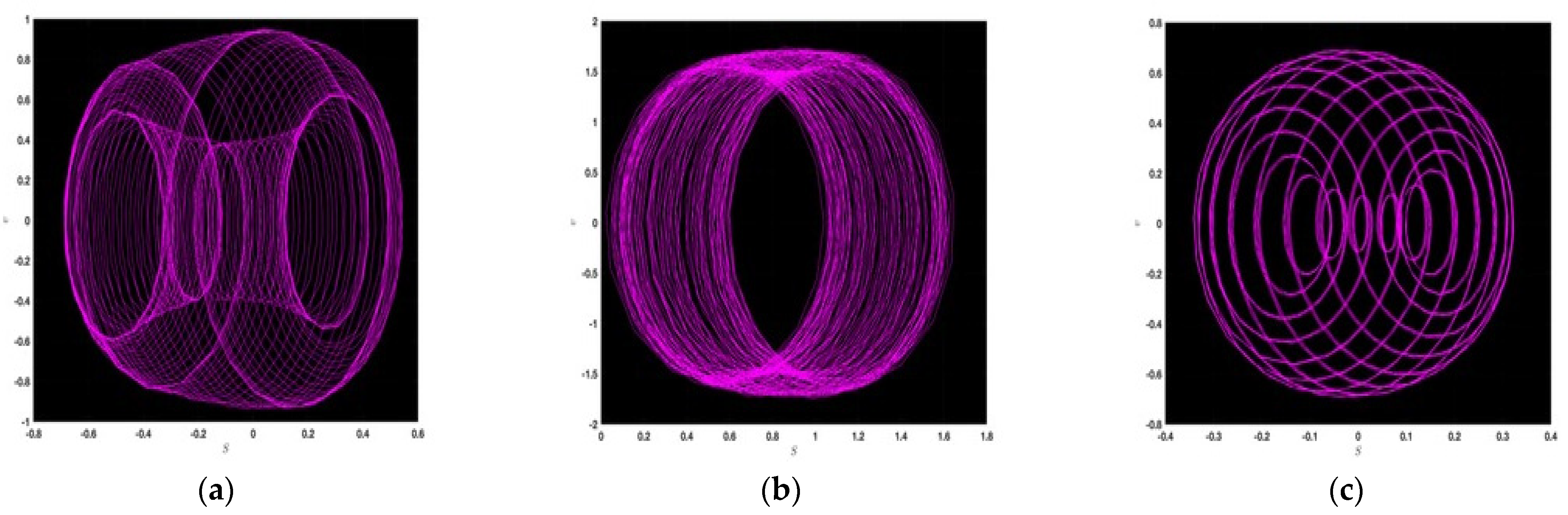
4.2. Chaotic Nature of the Dynamic System
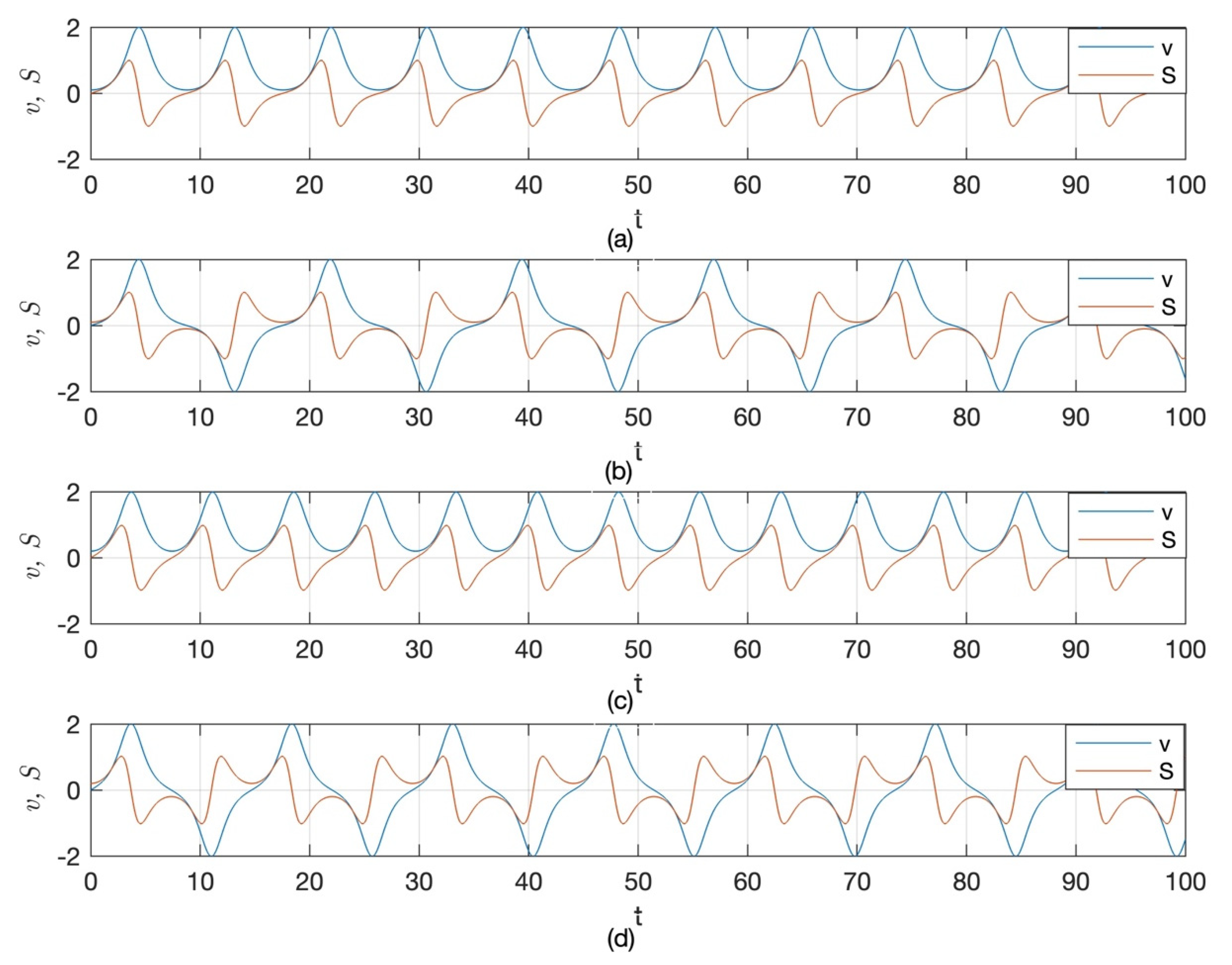
4.3. Sensitivity Analysis of the Dynamic System
4.4. Modulation Instability
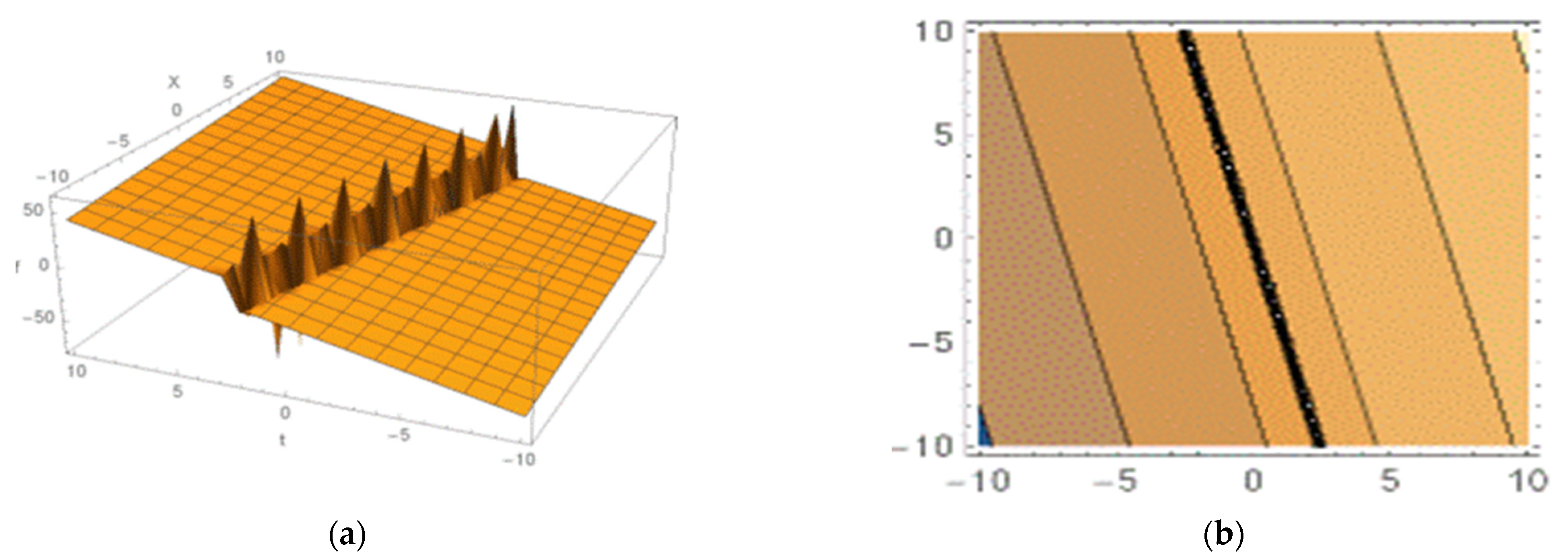
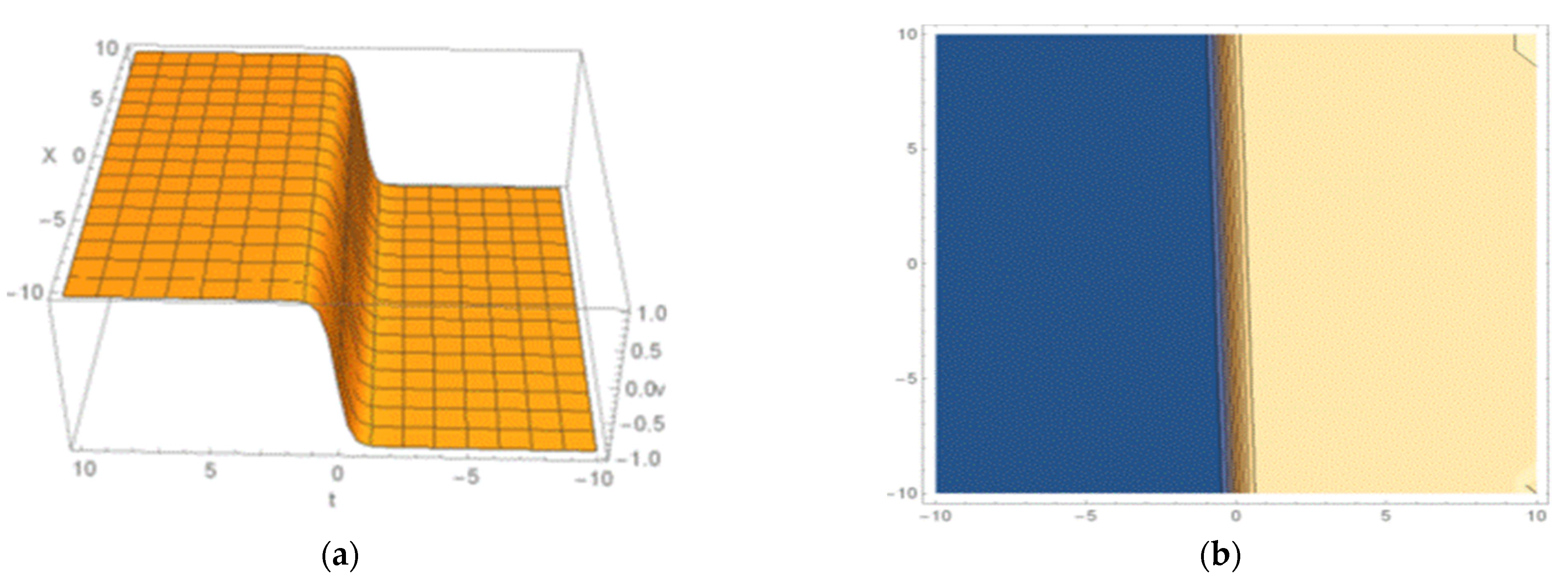
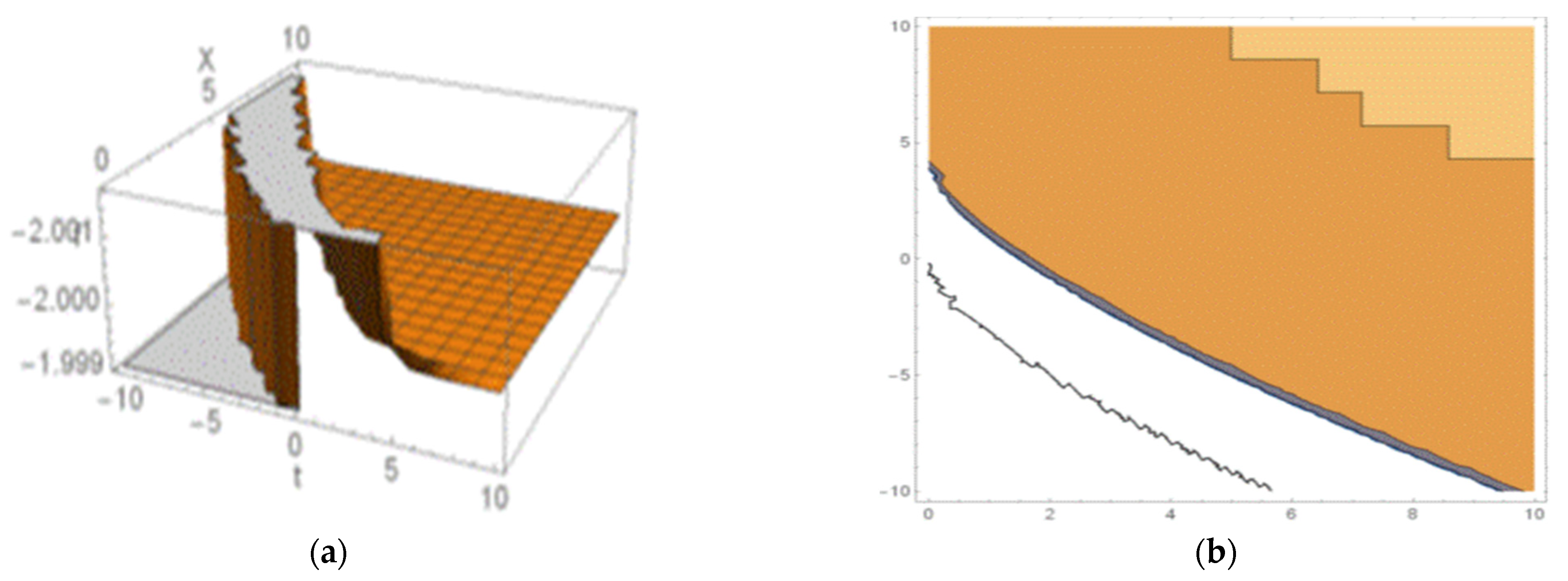
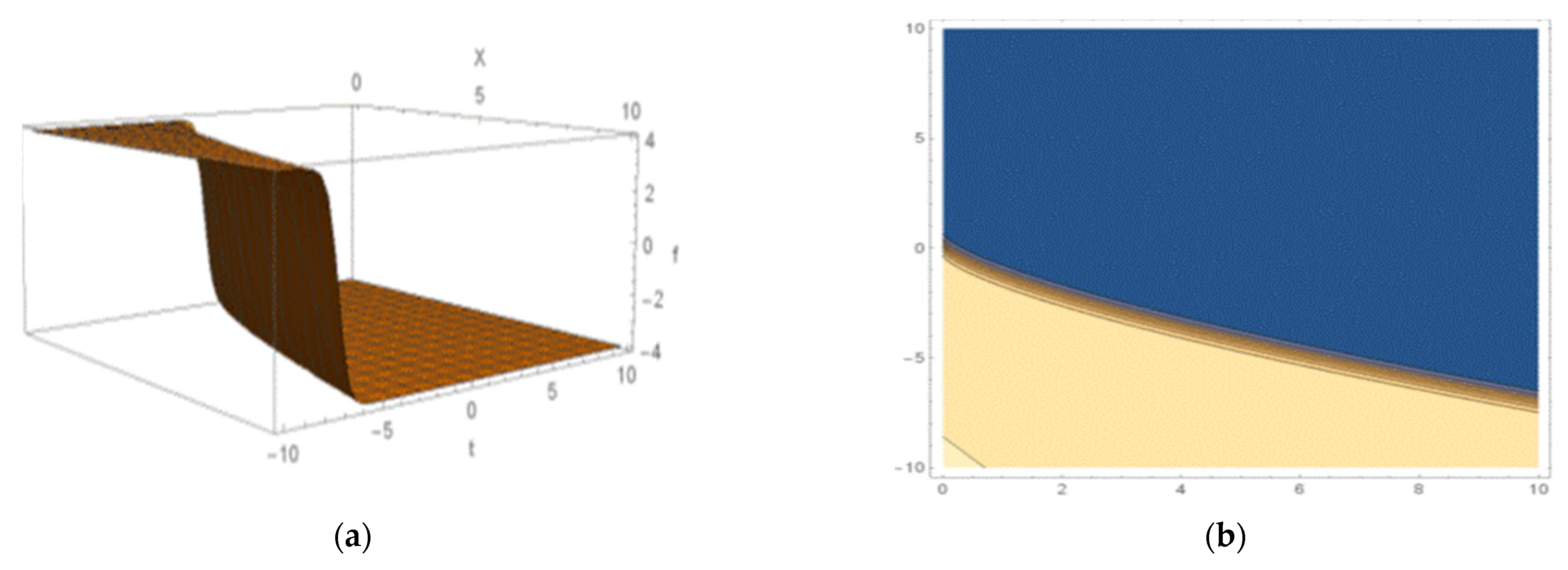
5. Graphical Explanation of Closed-Form Solutions
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Varol, D. Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation. Fractal Fract. 2023, 7, 539. [Google Scholar] [CrossRef]
- Gebril, E.; El-Azad, M.S.; Sameeh, M. Chebyshev collocation method for fractional Newell-Whitehead-Segel equation. Alex. Eng. J. 2024, 87, 39–46. [Google Scholar] [CrossRef]
- Guswanto, B.H.; Suroto; Istikaanah, N. Multi-order fractional nonlinear evolution equations system. Partial Differ. Equ. Appl. Math. 2024, 9, 100620. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Q.; Biswas, A.; Liu, W. Phase-shift controlling of three solitons in dispersion-decreasing fibers. Nonlinear Dyn. 2019, 98, 395–401. [Google Scholar] [CrossRef]
- Ma, W.X. Solitons by means of Hirota bilinear forms. Partial Differ. Equ. Appl. Math. 2022, 5, 100220. [Google Scholar] [CrossRef]
- Ali, K.K.; Yilmazer, R.; Baskonus, H.M.; Bult, H. Modulation instability analysis and analytical solutions to the system of equations for the ion sound and Langmuir waves. Phys. Scr. 2020, 95, 065602. [Google Scholar] [CrossRef]
- Dusunceli, F.; Celik, E.; Askin, M.; Bulut, H. New exact solutions for the doubly dispersive equation using improved Bernoulli sub-equation method. Indian J. Phys. 2021, 95, 309–314. [Google Scholar] [CrossRef]
- Ozkan, E.M. New Exact Solutions of Some Important Nonlinear Fractional Partial Differential Equations with Beta Derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Alyoubi, A.F.; Aloufi, R.G. New analytical solutions for two physical applications by the modified / expansion method. AIP Conf. Proc. 2022, 2472, 020001. [Google Scholar]
- Jordanov, I.P. Simple equations method applied to the equations of nonlinear Schrödinger kind. AIP Conf. Proc. 2022, 2459, 030016. [Google Scholar]
- Akram, G.; Sadaf, M.; Khan, M.A.U. Soliton solutions of Lakshmanan-Porsezian-Daniel model using modified auxiliary equation method with parabolic and anti-cubic law of nonlinearities. Opt.-Int. J. Light Electron Opt. 2022, 252, 168372. [Google Scholar] [CrossRef]
- Akram, G.; Zainab, I.; Sadaf, M.; Bucur, A. Solitons, one line rogue wave and breather wave solutions of a new extended KP-equation. Results Phys. 2023, 55, 107147. [Google Scholar] [CrossRef]
- Ali, H.M.S.; Habib, M.A.; Miah, M.M.; Miah, M.M.; Akbar, M.A. Diverse solitary wave solutions of fractional order Hirota-Satsuma coupled KdV system using two expansion methods. Alex. Eng. J. 2023, 66, 1001–1014. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Baleanu, D.; Miah, M.M.; Ali, H.M.S.; Alshehri, H.M.; Osman, M.S. New soliton solutions of the mZK equation and the Gerdjikov-Ivanov equation by employing the double (/, 1/)-expansion method. Results Phys. 2023, 47, 106391. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S. Stability, modulation instability, and analytical study of the confirmable time fractional Westervelt equation and the Wazwaz Kaur Boussinesq equation. Opt. Quantum Electron. 2024, 56, 948. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Ganie, A.H.; Osman, M.; Ma, W.X. Discovering new abundant optical solutions for the resonant nonlinear Schrödinger equation using an analytical technique. Opt. Quantum Electron. 2024, 56, 847. [Google Scholar] [CrossRef]
- Hussain, A.; Kara, A.H.; Zaman, F.D. An invariance analysis of the Vakhnenko-Parkes equation. Chaos Solitons Fractals 2023, 171, 113423. [Google Scholar] [CrossRef]
- Li, S. Nonlinear chirped optical solitons of the perturbation Fokas-Lenells equation in optical fibers. Opt.-Int. J. Light Electron Opt. 2023, 276, 170627. [Google Scholar] [CrossRef]
- Alam, B.E.; Javid, A. Optical dual-waves to a new dual-mode extension of a third order dispersive nonlinear Schrödinger’s equation. Phys. Lett. A 2023, 480, 128954. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Nifontov, D.R. Some specific optical wave solutions and combined other solitons to the advanced (3+1)-dimensional Schrödinger equation in nonlinear optical fibersy. Chaos Solitons Fractals 2023, 175, 114076. [Google Scholar] [CrossRef]
- Kumar, S.; Hamid, I.; Abdou, M.A. Some specific optical wave solutions and combined other solitons to the advanced (3+1)-dimensional Schrödinger equation in nonlinear optical fibers. Opt. Quantum Electron. 2023, 55, 728. [Google Scholar] [CrossRef]
- Niwas, M.; Kumar, S. New plenteous soliton solutions and other form solutions for a generalized dispersive long-wave system employing two methodological approaches. Opt. Quantum Electron. 2023, 55, 630. [Google Scholar] [CrossRef]
- Singh, S.; Ray, S.S. Newly exploring the Lax pair, bilinear form, bilinear Backlund transformation through binary Bell polynomials, and analytic solutions for the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation. Phys. Fluids 2023, 34, 087134. [Google Scholar] [CrossRef]
- Mohammed, W.W.; El-Morshedy, M.; Cesarano, C.; Al-Askar, F.M. Soliton solutions of fractional stochastic Kraenkel-Manna-Merle equations in ferromagnetic materials. Fractal Fract. 2023, 7, 328. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Khan, A.; Alqudah, M.A.; Abdeljawad, T. Adapted homotopy perturbation method with Shehu transform for solving conformable fractional nonlinear partial differential equations. Fractals 2023, 31, 2340027. [Google Scholar] [CrossRef]
- Du, H.; Yang, X.; Chen, Z. A new method of solving the best approximate solution for a nonlinear fractional equation. Int. J. Comput. Math. 2023, 100, 1702–1718. [Google Scholar] [CrossRef]
- Kumar, S.; Mohan, B. A novel analysis of Cole-Hopf transformations in different dimensions, solitons, and rogue wave for a (2+1)-dimensional shallow water wave equation of ion-acoustic waves in plasmas. Phys. Fluids 2023, 35, 127128. [Google Scholar] [CrossRef]
- Rong, F.; Li, Q.; Shi, B.; Chai, Z. A lattics Boltzmann model based on Cole-Hopf transformation for N-dimensional coupled Burgers’ equations. Comput. Math. Appl. 2023, 134, 101–111. [Google Scholar] [CrossRef]
- Ashraf, R.; Hussain, S.; Ashraf, F.; Akgul, A.; El Din, S.M. The extended Fan’s sub-equation method and its application to nonlinear Schrodinger equation with saturable nonlinearity. Results Phys. 2023, 52, 106755. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Dynamic nature of analytical soliton solutions of the (1+1)-dimensional Mikhailov-Novikov-Wang equation using the unified approach. Int. J. Math. Comput. Eng. 2023, 1, 217–228. [Google Scholar] [CrossRef]
- Mahmood, A.; Abbas, M.; Akram, G.; Sadaf, M.; Riaz, M.B.; Abdeljawad, T. Solitary wave solution of (2+1)-dimensional Chaffee–Infante equation using the modified Khater method. Results Phys. 2023, 48, 106416. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Shafee, A.; Shah, R. Noise effect on soliton phenomena in fractional stochastic Kraenkel-Manna-Merle system arising in ferromagnetic materials. Sci. Rep. 2024, 14, 1810. [Google Scholar] [CrossRef] [PubMed]
- Youssri, Y.H.; Zaky, M.A.; Hafez, R.M. Romanovski-Jacobi spectral schemes for higher-order differential equations. Appl. Numer. Math. 2024, 198, 148–159. [Google Scholar] [CrossRef]
- Tripathy, A.; Sahoo, S. A novel analytical method for solving (2+1)-dimensional extended Calogero-Bogoyavlenskii-Schiff equation in plasma physics. J. Ocean Eng. Sci. 2021, 6, 405–409. [Google Scholar] [CrossRef]
- Khalid, S.; Ahmad, S.; Ullah, A.; Ahmad, H.; Saifullah, S.; Nofal, T.A. New wave solutions of the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation using a novel expansion method. Results Phys. 2023, 50, 106450. [Google Scholar] [CrossRef]
- Mia, R.; Miah, M.M.; Osman, M.S. A new implementation for finding of analytical solutions in nonlinear PDEs. Heliyon 2023, 9, e15690. [Google Scholar] [CrossRef] [PubMed]
- Khalid, S.; Ullah, A.; Ahmad, S.; Akg, A.; Yusuf, A.; Sulaiman, T.A. Some novel analytic solutions of a new extended (2+1)-dimensional Boussinesq equation using a novel method. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar]
- Iqbal, M.A.; Miah, M.M.; Ali, H.M.S.T.; Shahen, N.H.M.; Deifalla, A. New applications of the fractional derivative to extract abundant soliton solutions of the fractional order PDEs in mathematics physics. Partial Differ. Equ. Appl. Math. 2024, 9, 100597. [Google Scholar] [CrossRef]
- Senol, M.; Akinyemi, L.; Nkansah, H.; Adel, W. New solutions for four novel generalized nonlinear fractional fifth-order equations. J. Ocean Eng. Sci. 2024, 9, 59–65. [Google Scholar]
- Zeid, S.S.; Alipour, M. A collocation method using generalized Laguerre polynomials for solving nonlinear optimal control problems governed by integro-differential equations. J. Comput. Appl. Math. 2024, 436, 115410. [Google Scholar] [CrossRef]
- Prathumwan, D.; Chaiya, I.; Trachoo, K. Three-dimensional simulation of the lumbar spine under lumbar spinal stenosis with different sizes of spinal canal. Partial Differ. Equ. Appl. Math. 2024, 9, 100614. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Ganie, A.H.; Miah, M.M.; Iqbal, M.A.; Seadawy, A.R.; Mishra, N.K. A highly effective analytical approach to innovate the novel closed form soliton solutions of the Kadomtsev-Petviashivili equations with applications. Opt. Quantum Electron. 2024, 56, 938. [Google Scholar] [CrossRef]
- Chen, J.; Pelinovsky, D.E. Periodic Travelling Waves of the Modified KdV Equation and Rogue Waves on the Periodic Background. J. Nonlinear Sci. 2019, 29, 2797–2843. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, S. Discontinuous initial value and Whitham modulation for the generalized Gerdjikov-Ivanov equation. Wave Motion 2024, 127, 103276. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Rasool, T.; Hussain, R.; Al Sharif, M.A.; Mahmoud, W.; Osman, M.S. A variety of optical soliton solutions for the M-truncated Paraxial wave equation using Sardar-subequation technique. Opt. Quantum Electron. 2023, 55, 396. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Kraenkel, R.A.; Manna, M.A.; Merle, V. Nonlinear short-wave propagation in ferrites. Phys. Rev. E 2000, 61, 976–979. [Google Scholar] [CrossRef]
- Hussain, Z.; Rehman, Z.U.; Abbas, T.; Smida, K.; Le, Q.H.; Abdelmalek, Z.; Tlili, I. Analysis of bifurcation and chaos in the traveling wave solution in optical fibers using the Radhakrishnan–Kundu–Lakshmanan equation. Results Phys. 2023, 55, 107145. [Google Scholar] [CrossRef]
- Biswas, A.; Bagchi, B.K.; Yildirim, Y.; Khan, S.; Asiri, A. Quasimonochromatic dynamical system and optical soliton cooling with triple-power law of self-phase modulation. Phys. Lett. A 2023, 480, 128985. [Google Scholar] [CrossRef]
- Shehzad, K.; Seadawy, A.R.; Wang, J.; Arshad, M. Multi peak solitons and breather types wave solutions of unstable NLSEs with stability and applications in optics. Opt. Quantum Electron. 2023, 55, 7. [Google Scholar] [CrossRef]
- Yang, Z. Voltammetry for quantitative determination of trace mercury ions in water via acetylene black modified carbon paste electrode. Alex. Eng. J. 2024, 87, 107–113. [Google Scholar] [CrossRef]
- Li, Z.; Hu, H. Chaotic pattern, bifurcation, sensitivity and traveling wave solution of the coupled Kundu-Mukherjee-Naskar equation. Results Phys. 2023, 48, 106441. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borhan, J.R.M.; Miah, M.M.; Alsharif, F.; Kanan, M. Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis. Fractal Fract. 2024, 8, 327. https://doi.org/10.3390/fractalfract8060327
Borhan JRM, Miah MM, Alsharif F, Kanan M. Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis. Fractal and Fractional. 2024; 8(6):327. https://doi.org/10.3390/fractalfract8060327
Chicago/Turabian StyleBorhan, J. R. M., M. Mamun Miah, Faisal Alsharif, and Mohammad Kanan. 2024. "Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis" Fractal and Fractional 8, no. 6: 327. https://doi.org/10.3390/fractalfract8060327
APA StyleBorhan, J. R. M., Miah, M. M., Alsharif, F., & Kanan, M. (2024). Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis. Fractal and Fractional, 8(6), 327. https://doi.org/10.3390/fractalfract8060327





