Exploring the Depths: Soliton Solutions, Chaotic Analysis, and Sensitivity Analysis in Nonlinear Optical Fibers

Abstract

This paper discusses the time-fractional nonlinear Schrödinger model with optical soliton solutions. We employ the $\left(f+\left(\frac{G^{\prime }}{G}\right)\right)$-expansion method to attain the optical solution solutions. An important tool for explaining the particular explosion of brief pulses in optical fibers is the nonlinear Schrödinger model. It can also be utilized in a telecommunications system. The suggested method yields trigonometric solutions such as dark, bright, kink, and anti-kink-type optical soliton solutions. Mathematica 11 software creates 2D and 3D graphs for many physically important parameters. The computational method is effective and generally appropriate for solving analytical problems related to complicated nonlinear issues that have emerged in the recent history of nonlinear optics and mathematical physics. Furthermore, we venture into uncharted territory by subjecting our model to chaotic and sensitivity analysis, shedding light on its robustness and responsiveness to perturbations. The proposed technique is being applied to this model for the first time.

1. Introduction

Solitons function similarly to Fourier modes in linear media and are now recognized as essential building blocks of modes in nonlinear dispersive media. Specifically, the particle (fermion) idea in the inverse scattering transform (IST) is supported by identifying a soliton as an eigenvalue. Concurrently, it was shown that self-focusing was possible in a Kerr medium [1], and it was shown that the balance between refraction and cubic nonlinearity led to the emergence of a spatially localized solution resembling a soliton. Due to its increasing importance, scientific research has concentrated heavily on studying nonlinear partial differential equations (PDEs). Various scientific domains use nonlinear PDEs, such as the earth sciences, physics, mathematics, engineering, and other technological sectors. Research has concentrated on understanding and solving these nonlinear PDEs for a long time, both analytically and numerically. For nonlinear PDEs and nonlinear optics in physics-related fields, including fluid mechanics, plasma theory, and nonlinear optics, numerous solitary wave solutions have been found in the domain of precise solutions. NLS equations have become vital instruments for discussing various physical events in many scientific domains.

Nonlinear partial differential equations (NPDEs) govern most physical phenomena and dynamical systems. The study of nonlinear wave propagation issues has promoted the development of NPDEs. The primary goal in nonlinear physics is to find solutions to NPDEs, predominantly solitary and soliton wave solutions. Solutions aid in the understanding of nonlinear physical and natural systems. In several basic sciences, including mathematics and engineering, non-partial differential equations (NPDEs) are used to approximate a variety of processes and dynamics [2,3,4,5,6].

Russell developed the key concept of the soliton in 1844 [7], based on a coincidental thought that happened on the Edinburgh–Glasgow Canal in 1834, referred to as “a great translation wave”. This phenomenon was eventually named “solitary waves” because of the shape of the single pulse. Therefore, two of the well-known researchers who have conducted a hypothetical examination on lone waves are Boussinesc and Rayleigh [7]. Since then, single-wave research has developed to become one of the main fields of study for single waves. Solitary waves that are self-contained, strong, steady, and persistent do not disperse and hold onto their identity as they move across the medium. They include high-speed media transmissions and the occurrence of controlled solitons in numerous crucial fields of physics and technology. Solitons are self-positioning wave units with their own Broglie wavelength equivalents due to Galilean symmetry. Conversely, the soliton, an extended particle-like object, has negative self-interaction energy (binding energy) and is bound by nonlinear self-interaction at the self-induced trapping potential. It provides details on the geometry and form of solitons [8].

Many researchers utilized diverse algorithms to find the analytical solution such as the Sine–Gordon expansion algorithm [9,10], the Jacobi-elliptic technique [11], the homogeneous balance technique [12], the modified simple equation approach [13,14,15], the auxiliary equation technique [16,17], the modified extended direct algebraic method [18], the extended tanh expansion method [19], $\left(\frac{G^{\prime }}{G}\right)$-expansion technique [20], the Auto-Bäcklund transformation [21], and Hirota’s bilinear technique [22]. A variety of fractional derivatives are essential to the physical phenomena of nonlinear partial differential equations, such as the Beta derivative [20], Jumarie’s modified Riemann–Liouville derivative [23], the Riemann–Liouville derivative [24], the fractal derivatives [25], Atangana’s conformable derivative [26], the Caputo derivative [27], and the Atangana–Baleanu fractional operator [28]. The coupled NLSE is utilized to search out the wave propagation in continuous mediums [29], which happens in the typical scenario arising slowly fluctuating waves of small amplitude, like the long-distance pulse propagation in fluid dynamics, optical fibers, nonlinear optics, quantum mechanics, and other physical nature [30,31], which reads

$$D_x{D}_t^{\beta }v=D_{xx}v+\frac{2}{1-{\delta }^2}\mid v^2\mid v+v(r-u),$$

(1)

$$D_t^{\beta }r=-\frac{D_t^{\beta }(\mid v{\mid }^2)}{1+\delta }+(1+\delta )D_{x}r,$$

(2)

$$D_t^{\beta }u=\frac{D_t^{\beta }(\mid v{\mid }^2)}{1+\delta }+(1-\delta )D_{x}u,$$

(3)

where $r(x,t)$ and $u(x,t)$ are the real functions, $v(x,t)$ is a complex function of time t and x. The parameters $\beta$ are the fractional order of derivatives having values $\beta \ge 0$. Moreover Equations (1)–(3) describe non-relativistic quantum mechanical behavior and nonlinear media. The main idea of this study is shown in Figure 1. The present study is distributed into different sections. In Section 2, we present the beta derivative and the description of the algorithm. Section 3 presents the optical solitary wave solution of the considered model. Section 4 presents the chaotic analysis and Section 5 presents the sensitivity analysis. The results attained through $\left(f+\left(\frac{G^{\prime }}{G}\right)\right)$-expansion algorithm will be analyzed graphically in Section 6. The conclusion is presented in Section 7.

2. Beta Derivative

Definition 1. 

Let $g\left(t\right)$ be a function defined for all non-negative ts. Then, the beta derivative of $g\left(t\right)$ of order β is given by [20]

$$T^{\beta }g\left(t\right)=\frac{d^{\beta }g\left(t\right)}{d{t}^{\beta }}=\underset{ϵ\to 0}{lim}\frac{g(t+ϵ{(t+\frac{1}{\Gamma \left(\beta \right)})}^{1-\beta })-g\left(t\right)}{ϵ},$$

where $0<\beta \le 1$.

Algorithm of the $\left(f+\left(\frac{G^{\prime }}{G}\right)\right)$-Expansion Method

Consider the NPDE as

$$P(v,v_x,v_y,v_z,v_t,v_{tt},v_{xx},v_{xt},...)=0.$$

(4)

In which P is a polynomial in v and its derivatives. The main steps are given as follows:

Step 1: Assume a wave transformation,

$$v(x,t)=V\left(\varphi \right),\varphi =x-ct.$$

(5)

Equation (5) is used in (4), then ODE is as follows:

$$H(V,V^{\prime },V^{″},V^{‴},...)=0,$$

(6)

where H is a function of $V\left(\varphi \right)$, and the prime represents its derivatives with respect to $\varphi$.

Step 2: The general form of (6) is defined as follows:

$$V\left(\varphi \right)=\sum _{i=-m}^M{\alpha }_i{(\Phi \left(\varphi \right))}^i,$$

(7)

where

$$\Phi \left(\varphi \right)=[f+\frac{G^{\prime }\left(\varphi \right)}{G\left(\varphi \right)}].$$

(8)

Here, f is constant, and its value can be found later; the values of ${\alpha }_{-m}$, or ${\alpha }_m$, may be zero, but all of them could not be zero at a time. The second order NODE satisfies for $G=G\left(\varphi \right)$, as follows:

$$G{G}^{″}=\omega G{G}^{\prime }+\xi G^2+\psi {\left(G^{\prime }\right)}^2.$$

(9)

Here, $\psi ,\xi$, and $\omega$ are real variables, and prime denotes the derivative of $\varphi$.

Equation (8) can be converted into the Riccati equation by utilizing the Col-Hopf transformation $\Psi \left(\varphi \right)={\left(\ln \left(G\right(\varphi )\right)}_{\varphi }=\frac{G^{\prime }\left(\varphi \right)}{G\left(\varphi \right)}$:

$${\Psi }^{\prime }\left(\varphi \right)=\xi +\omega \Psi \left(\varphi \right)+(\psi -1){\Psi }^2\left(\varphi \right).$$

(10)

There are twenty-five single solutions for Equation (10) [20].

Step 3: Put (7)–(9) in (6), then we will obtain polynomials in $[f+\frac{G^{\prime }(\varphi }{G\left(\varphi \right)}]$ and ${[f+\frac{G^{\prime }\left(\varphi \right)}{G\left(\varphi \right)}]}^{-1}$, $(m=0,1,2,\cdots ,M)$. Substituting each coefficient of polynomials equal to zero, we obtain a set of algebraic equations.

Step 4: We can solve all algebraic equations with MATHEMATICA 11 is used to obtain the constant values. In the end, the exact wave solutions of (4) can be attained by utilizing the values of the constant together with the solutions of (9).

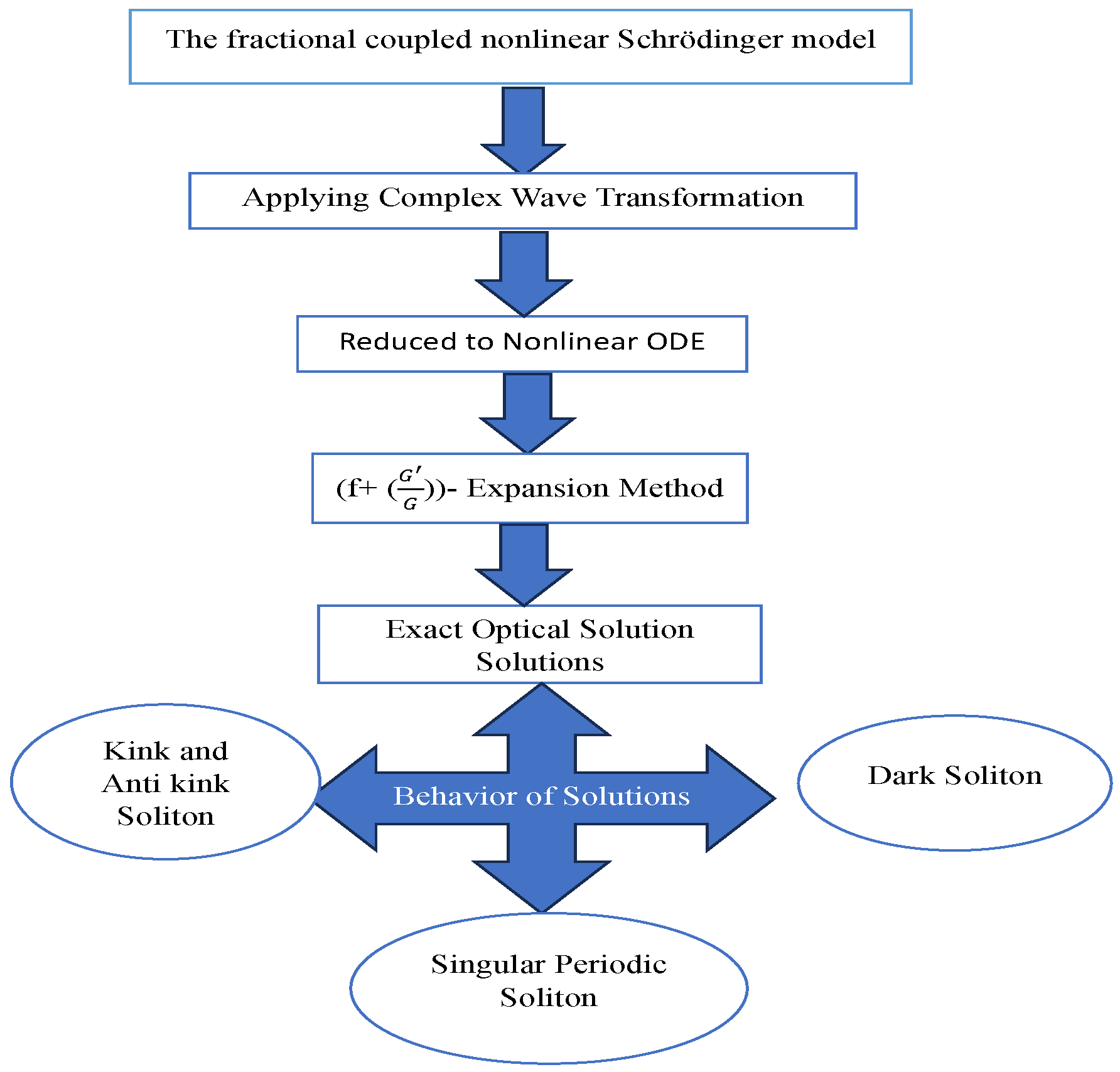
3. Optical Wave Solution to the Fractional NLSE

In this section, we change the fractional NLS equation into nonlinear ODEs with the help of the fractional complex transform, as follows:

$$v(x,t)=V\left(\varphi \right)e^{i\chi },r(x,t)=R\left(\varphi \right),u(x,t)=U\left(\varphi \right).$$

(11)

$$\varphi =\gamma x+\frac{\sigma }{\beta }{\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{\beta },\chi =\kappa x+\frac{\tau }{\beta }{\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{\beta },$$

(12)

where $\gamma ,\sigma ,\tau$, and $\kappa$ are the parameters. Inserting Equations (11) and (12) into (1), the real and imaginary parts are given as follows:

$$V^{″}\left(\varphi \right)+\left(\frac{\kappa (\kappa -\tau )}{\gamma (\sigma -\gamma )}\right)V\left(\varphi \right)-\left(\frac{2}{\gamma (\sigma -\gamma )(1-{\delta }^2)}\right)V^3\left(\varphi \right)+\left(\frac{u-r}{\gamma (\sigma -\gamma )}\right)V\left(\varphi \right)=0,$$

(13)

and

$$\tau \gamma +\sigma \kappa +2\gamma \kappa =0,$$

(14)

we can simplify (14),

$$\tau \gamma +\sigma \kappa +\gamma \kappa +\gamma \kappa =0.$$

$$(\tau +\kappa )\gamma +(\sigma +\gamma )\kappa =0.$$

$$(\tau +\kappa )\gamma =-(\sigma +\gamma )\kappa .$$

$$\frac{\kappa -\tau }{\sigma -\gamma }=\frac{\kappa }{\gamma }.$$

(15)

Substituting (15) into (13), we have the nonlinear ODE, as follows:

$$V^{″}\left(\varphi \right)+\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right)-\left(\frac{2}{\gamma (\sigma -\gamma )(1-{\delta }^2)}\right)V^3\left(\varphi \right)+\left(\frac{u-r}{\gamma (\sigma -\gamma )}\right)V\left(\varphi \right)=0.$$

(16)

Substituting (11) and (12) into (2) and (3), we then ingratiate the following:

$$R=\frac{-\sigma V^2}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}.$$

(17)

$$U=\frac{\sigma V^2}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}.$$

(18)

Substituting (17) and (18) into (16), we obtain the following:

$$V^{″}\left(\varphi \right)+\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right)-\left(\frac{2}{{\delta }^2{\gamma }^2-{(\sigma -\gamma )}^2}\right)V^3\left(\varphi \right)=0.$$

(19)

Next, we can apply the homogeneous balancing technique on (19); then we obtain $N=1$. So, Equation (6) is as follows:

$$V\left(\varphi \right)={\alpha }_{-1}{(\Phi \left(\varphi \right))}^{-1}+{\alpha }_0+{\alpha }_1\Phi \left(\varphi \right),$$

(20)

where ${\alpha }_{-1},{\alpha }_0$, and ${\alpha }_1$ are unknown parameters to be found. Substituting (20) into (16), we obtain the following set of solutions:

Set-1

$$\begin{array}{cc}\hfill & {\alpha }_{-1}=\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right),\hfill \\ & {\alpha }_0=\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega ),{\alpha }_1=0,\hfill \\ & \kappa =-\gamma \sqrt{2\xi (1-\psi )+\frac{{\omega }^2}{2}}.\hfill \end{array}$$

(21)

Set-2

$$\begin{array}{cc}\hfill & {\alpha }_{-1}=0,{\alpha }_0=\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(\pm 2f(\psi -1)-\omega ),\hfill \\ & {\alpha }_1=\pm \left(\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\right)(\psi -1),\kappa =-\gamma \sqrt{2\xi (1-\psi )+\frac{{\omega }^2}{2}}.\hfill \end{array}$$

(22)

Set-3

$$\begin{array}{cc}\hfill & {\alpha }_{-1}=0,{\alpha }_0=\pm \frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\sqrt{{\omega }^2-4\xi (\psi -1)},\hfill \\ & {\alpha }_1=\mp (\psi -1)\left(-\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\right),f=\frac{\sqrt{{\omega }^2-4\xi (\psi -1)}+\omega }{2(\psi -1)},\hfill \\ & \kappa =\gamma \sqrt{2\xi (1-\psi )+\frac{{\omega }^2}{2}}.\hfill \end{array}$$

(23)

Substituting (21) into (20), the solutions to (1)–(3) are as follows:

$$\begin{array}{cc}\hfill v_1(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right){(\Phi \left(\varphi \right))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill R_1(x,t)=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(\Phi \left(\varphi \right))}^{-1}+\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill U_1(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(\Phi \left(\varphi \right))}^{-1}+\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(26)

Furthermore, the solutions to (1)–(3) are given below.

Family 1

When $\Sigma ={\omega }^2-4\xi \psi +4\xi >0$ and $\omega (\psi -1)\ne 0$ (or $\xi (\psi -1)\ne 0$), we have

$$\begin{array}{cc}\hfill v_{1_1}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\tanh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill R_{1_1}(x,t)=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\tanh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill U_{1_1}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\tanh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill v_{1_2}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\coth \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill R_{1_2(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\coth \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill U_{1_2}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }\coth \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill v_{1_3}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & (f-\frac{1}{2(\psi -1)}\times {(\omega +\sqrt{\Sigma }(\tanh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{sech}\left(\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill R_{1_3(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & (f-\frac{1}{2(\psi -1)}\times {(\omega +\sqrt{\Sigma }(\tanh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{sech}\left(\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill U_{1_3}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & (f-\frac{1}{2(\psi -1)}\times {(\omega +\sqrt{\Sigma }(\tanh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{sech}\left(\sqrt{\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill v_{1_4}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }(\coth \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{csch}\left(\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill R_{1_4(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }(\coth \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{csch}\left(\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_4}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{\Sigma }(\coth \left(\sqrt{\Sigma }\varphi \right)\pm \iota \mathrm{csch}\left(\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_5}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{4(\psi -1)}\times (2\omega +\sqrt{\Sigma }(\tanh \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right)+\iota \coth \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_5(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{4(\psi -1)}\times (2\omega +\sqrt{\Sigma }(\tanh \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right)+\iota \coth \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_5}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{4(\psi -1)}\times (2\omega +\sqrt{\Sigma }(\tanh \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right)+\iota \coth \left(\frac{1}{4}\sqrt{\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_6}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}-D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_6(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}-D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_6}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}-D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_7}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}+D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_7(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}+D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_7}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{\Sigma (D^2+E^2)}+D\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)}{D\sinh \left(\sqrt{\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_8}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_8(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_8}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_9}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_9(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_9}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\frac{1}{2}\sqrt{\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{10}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{10}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{10}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \cosh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\sinh \left(\sqrt{\Sigma }\varphi \right)-\omega \cosh \left(\sqrt{\Sigma }\varphi \right)\pm \iota \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{11}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\sqrt{\Sigma }\varphi \right)\pm \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{11}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\sqrt{\Sigma }\varphi \right)\pm \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{11}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sinh \left(\sqrt{\Sigma }\varphi \right)}{\sqrt{\Sigma }\cosh \left(\sqrt{\Sigma }\varphi \right)-\omega \sinh \left(\sqrt{\Sigma }\varphi \right)\pm \sqrt{\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

Family 2

When $\Sigma ={\omega }^2-4\xi \psi +4\xi <0$ and $\omega (\psi -1)\ne 0$ (or $\xi (\psi -1)\ne 0)$, we have

$$\begin{array}{cc}\hfill v_{1_{12}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\sqrt{-\Sigma }\tan \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{12}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\sqrt{-\Sigma }\tan \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill U_{1_{12}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\sqrt{-\Sigma }\tan \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{13}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{13}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{13}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{14}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{14}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{14}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }\cot \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{15}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }(\cot \left(\sqrt{-\Sigma }\sigma \right)\pm \csc \left(\sqrt{-\Sigma }\sigma \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{15}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }(\cot \left(\sqrt{-\Sigma }\sigma \right)\pm \csc \left(\sqrt{-\Sigma }\sigma \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{15}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{2(\psi -1)}\times (\omega +\sqrt{-\Sigma }(\cot \left(\sqrt{-\Sigma }\sigma \right)\pm \csc \left(\sqrt{-\Sigma }\sigma \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{16}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{4(\psi -1)}\times (-2\omega +\sqrt{-\Sigma }(\tan \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right)-\cot \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{16}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{4(\psi -1)}\times (-2\omega +\sqrt{-\Sigma }(\tan \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right)-\cot \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{16}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{4(\psi -1)}\times (-2\omega +\sqrt{-\Sigma }(\tan \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right)-\cot \left(\frac{1}{4}\sqrt{-\Sigma }\varphi \right))))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{17}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}-D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{17}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}-D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{17}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}-D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{18}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}+D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{18}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}+D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{18}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{1}{2(\psi -1)}\times (-\omega +\frac{\pm \sqrt{-\Sigma (D^2-E^2)}+D\sqrt{-\Sigma }\cos \left(\sqrt{-\Sigma }\varphi \right)}{D\sin \left(\sqrt{-\Sigma }\varphi \right)+E}))}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{19}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{19}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{19}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{20}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{20}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{20}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{21}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{21}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{21}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{2\xi \cos \left(\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\sin \left(\sqrt{-\Sigma }\varphi \right)+\omega \cos \left(\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{22}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{22}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{22}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f+\frac{2\xi \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)}{\sqrt{-\Sigma }\cos \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)-\omega \sin \left(\frac{1}{2}\sqrt{-\Sigma }\varphi \right)\pm \sqrt{-\Sigma }})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

Family 3

When $\xi =0$ and $\omega (\psi -1)\ne 0$, we have

$$\begin{array}{cc}\hfill v_{1_{23}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega k}{(\psi -1)(k+\cosh (\omega \varphi )-\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{23}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega k}{(\psi -1)(k+\cosh (\omega \varphi )-\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{23}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega k}{(\psi -1)(k+\cosh (\omega \varphi )-\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_{1_{24}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega \cosh \left(\omega \varphi \right)+\sinh \left(\omega \varphi \right)}{(\psi -1)(k+\cosh (\omega \varphi )+\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{24}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega \cosh \left(\omega \varphi \right)+\sinh \left(\omega \varphi \right)}{(\psi -1)(k+\cosh (\omega \varphi )+\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{24}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{\omega \cosh \left(\omega \varphi \right)+\sinh \left(\omega \varphi \right)}{(\psi -1)(k+\cosh (\omega \varphi )+\sinh (\omega \varphi \left)\right)})}^{-1}\hfill \\ & +\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

where k is an arbitrary constant.

Family 4

When $(\psi -1)\ne 0$ and $\omega =\xi =0$, the solutions are

$$\begin{array}{cc}\hfill v_{1_{24}}(x,t)=& (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{(\psi -1)\varphi +c_1})}^{-1}+\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right))\times e^{i\chi }.\hfill \end{array}$$

$$\begin{array}{cc}\hfill R_{1_{24}(x,t)}=& \frac{1}{(1+\delta )(\sigma -(1+\delta \left)\gamma \right)}[-\sigma (\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{(\psi -1)\varphi +c_1})}^{-1}+\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

$$\begin{array}{cc}\hfill U_{1_{24}}(x,t)=& \frac{1}{(1-\delta )(\sigma -(1-\delta \left)\gamma \right)}\left[\sigma \right(\left(\pm \sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}\left(f^2(\psi -1)-f\omega +\xi \right)\right)\hfill \\ & {(f-\frac{1}{(\psi -1)\varphi +c_1})}^{-1}+\left(\frac{1}{2}\sqrt{{\gamma }^2\left({\delta }^2-1\right)+2\gamma \sigma -{\sigma }^2}(2f(\psi -1)\pm \omega )\right){)}^2].\hfill \end{array}$$

4. Chaotic Analysis

By adding a perturbation, we investigate the system’s possible chaotic tendencies in the analysis that follows, which is based on (19). We analyze the two-dimensional phase diagrams of the attained dynamical system. From (19) we have the following:

$$V^{″}\left(\varphi \right)=\left(\frac{2}{{\delta }^2{\gamma }^2-{(\sigma -\gamma )}^2}\right)V^3\left(\varphi \right)-\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right).$$

(38)

Let $V^{\prime }=\mathcal{M}$, then Equation (38) is converted into the dynamical system, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{dV}{d\varphi }=\mathcal{M},\hfill \\ \frac{d\mathcal{M}}{d\varphi }=\left(\frac{2}{{\delta }^2{\gamma }^2-{(\sigma -\gamma )}^2}\right)V^3\left(\varphi \right)-\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right).\hfill \end{array}\right.\end{array}$$

(39)

We will decompose system (39) into an autonomous conservative dynamical system (ACDS), as we have the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{dV}{d\varphi }=\mathcal{M},\hfill \\ \frac{d\mathcal{M}}{d\varphi }=\left(\frac{2}{{\delta }^2{\gamma }^2-{(\sigma -\gamma )}^2}\right)V^3\left(\varphi \right)-\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right)+m_0\cos \left(\epsilon \varphi \right),\hfill \end{array}\right.\end{array}$$

(40)

where $m_0$ represents the frequency and $\epsilon$ interprets the intensity of the perturbed factor. The two-dimensional phase graph of the dynamical system (40) utilizes different values of parameters $\gamma =0.02,\sigma =1,\delta =0.01,\kappa =0.01,m_0=3$, as shown in Figure 2 and Figure 3.

5. Sensitivity Analysis

Consider the following dynamical system to check the stability of the proposed model:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{dV}{d\varphi }=\mathcal{M},\hfill \\ \frac{d\mathcal{M}}{d\varphi }=\left(\frac{2}{{\delta }^2{\gamma }^2-{(\sigma -\gamma )}^2}\right)V^3\left(\varphi \right)-\left(\frac{{\kappa }^2}{{\gamma }^2}\right)V\left(\varphi \right).\hfill \end{array}\right.\end{array}$$

(41)

We will analyze the dynamical system (41) through the 2D plot with the help of different initial conditions and different values of parameters ($\gamma =0.02,\sigma =0.3,\delta =0.01,\kappa =0.08$). As we observe through Figure 4 and Figure 5 if we change a little bit, then there is no overlapping in the curve, so we can say that the proposed model is sensitive.

6. Results and Discussion

The graphical representation of the NLS model solutions is covered in this section. Using Mathematica 11 to help establish appropriate values for the arbitrary constants, the physical aspect of the nonlinear model is highlighted. In [32], Tariq et al. found dark, singular, bright, and periodic soliton solutions of the NLS equation using a unified method and the simple equation method. In [30], Rafiq et al. achieved period, kink, anti-kink, and dark solutions using the unified Riccati equation expansion method and the generalized Kudryashov method. In [31], Shakeel et al. discovered various optical soliton solutions employing the generalized exponential rational function method. In the current study, we are utilizing the $\left(f+\left(\frac{G^{\prime }}{G}\right)\right)$-expansion method to find out more generalized soliton solutions.

• Figure 6, Figure 7 and Figure 8 present the periodic behaviors of optical solitons. Periodic waves are repetitive disturbances that propagate through a medium at recurring intervals. These waves exhibit a consistent pattern of amplitude, frequency, and wavelength variations over time. The key aspect of periodic waves is that they regularly repeat their form after a certain interval.
• Figure 9 shows the dark behavior of the optical soliton. In the optics, “dark waves” might refer to regions in a wave pattern with significantly lower amplitude or intensity than surrounding areas. This could happen, for example, in interference patterns where formative and destructive interference outcomes are present in regions of light and darkness.
• Figure 10 and Figure 11 present the kink and anti-kink waves. Kinks are localized disturbances or “bumps” that occur within a medium. Anti-kinks are identical to kinks but illustrate transitions in the opposite approach. They also apply a sharp change in the field value (but in the opposite direction approximated to kinks). Anti-kink waves can be considered localized “dips” or “depressions” in the field profile.

In the 2D graph, there is a blue line for $t=1$, a black line for $t=1.5$, a red line for $t=2$, a blue line for $\beta =1$, a black line for $\beta =0.8$, and a red line for $\beta =0.6$. In the 2D graph, we observed that when the value of t increases, amplitude decreases, and amplitude increases when the value of t decreases. Similarly, by increasing the value of the beta amplitude, it decreases; otherwise, it increases. The fractional parameter $\beta =1$ value is the same in each 3D plot.

7. Conclusions

This article described the beta derivative-based time fractional nonlinear Schrödinger model. The generalized optical soliton solutions were achieved by utilizing the $\left(m+\left(\frac{G^{\prime }}{G}\right)\right)$-expansion method for a given model, and the results were successfully verified with chaotic and sensitivity analysis. Bright, kink, anti-kink, dark, exponential, trigonometric, and hyperbolic outcomes were attained. Additionally, applications for these analytical solitary wave solutions are evident in optical fibers and communication systems. The suggested approach is vital in solving nonlinear PDEs and mathematical physics. The results show that the nonlinearities and dispersive effects can be balanced to produce solutions for solitary waves that propagate while maintaining their speed and shape.