A Preconditioned Policy–Krylov Subspace Method for Fractional Partial Integro-Differential HJB Equations in Finance
Abstract
1. Introduction
2. Description of the Equation
3. Finite Difference Method with Theoretical Analysis
3.1. Finite Difference Method
3.2. Matrix Form
3.3. Stability and Convergence Analysis
4. Fast Policy–Krylov Subspace Iterative Method
4.1. Policy Iteration Method
| Algorithm 1 Policy iteration method |
Since is the k-th iteration of the policy iteration method for computing the solution . Let , and . Find such that
|
4.2. Fast Krylov Subspace Method
5. Preconditioning Technique
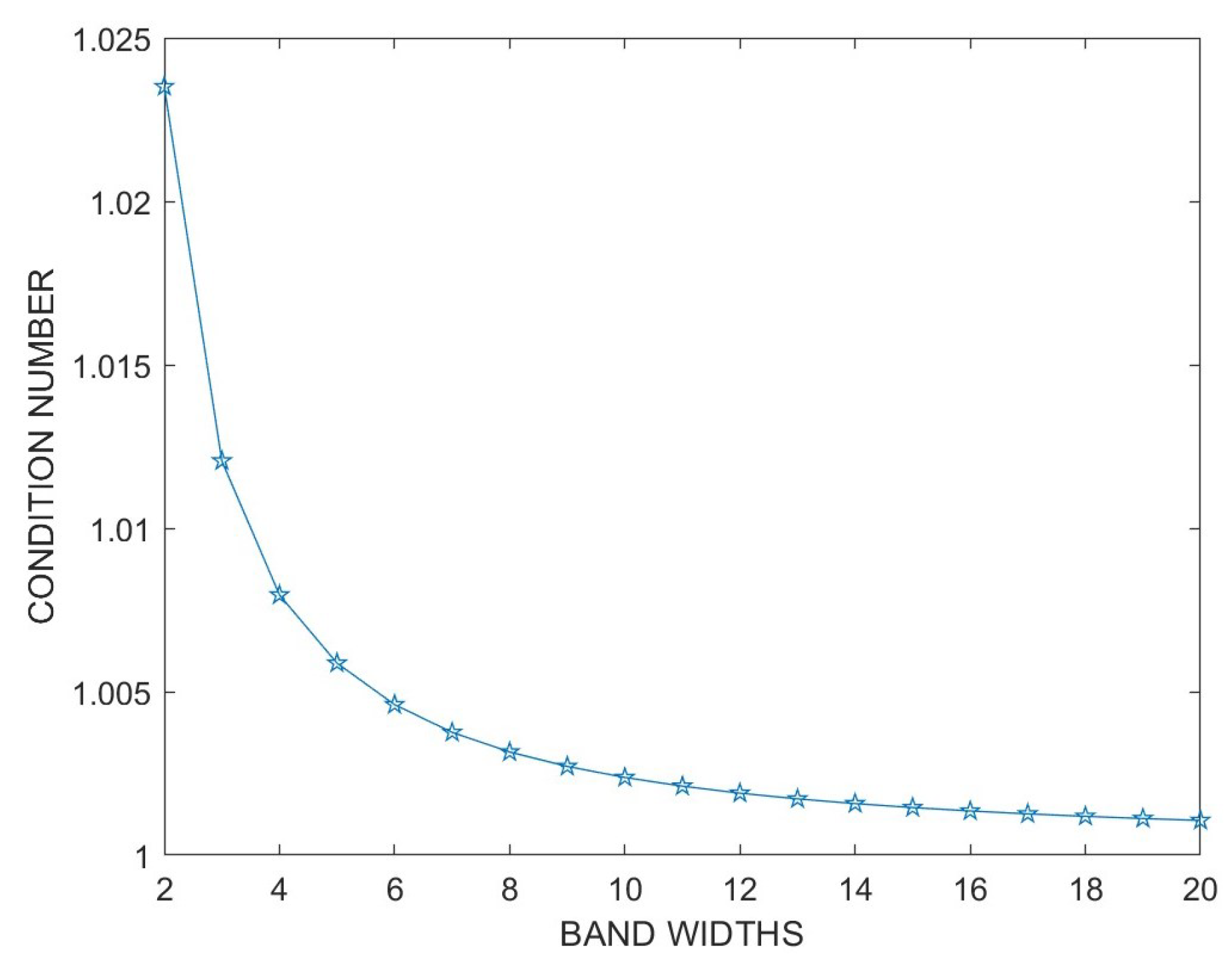
5.1. Banded Preconditioner
5.2. Properties of the Preconditioned Matrix
6. Numerical Experiments
6.1. American Call Option
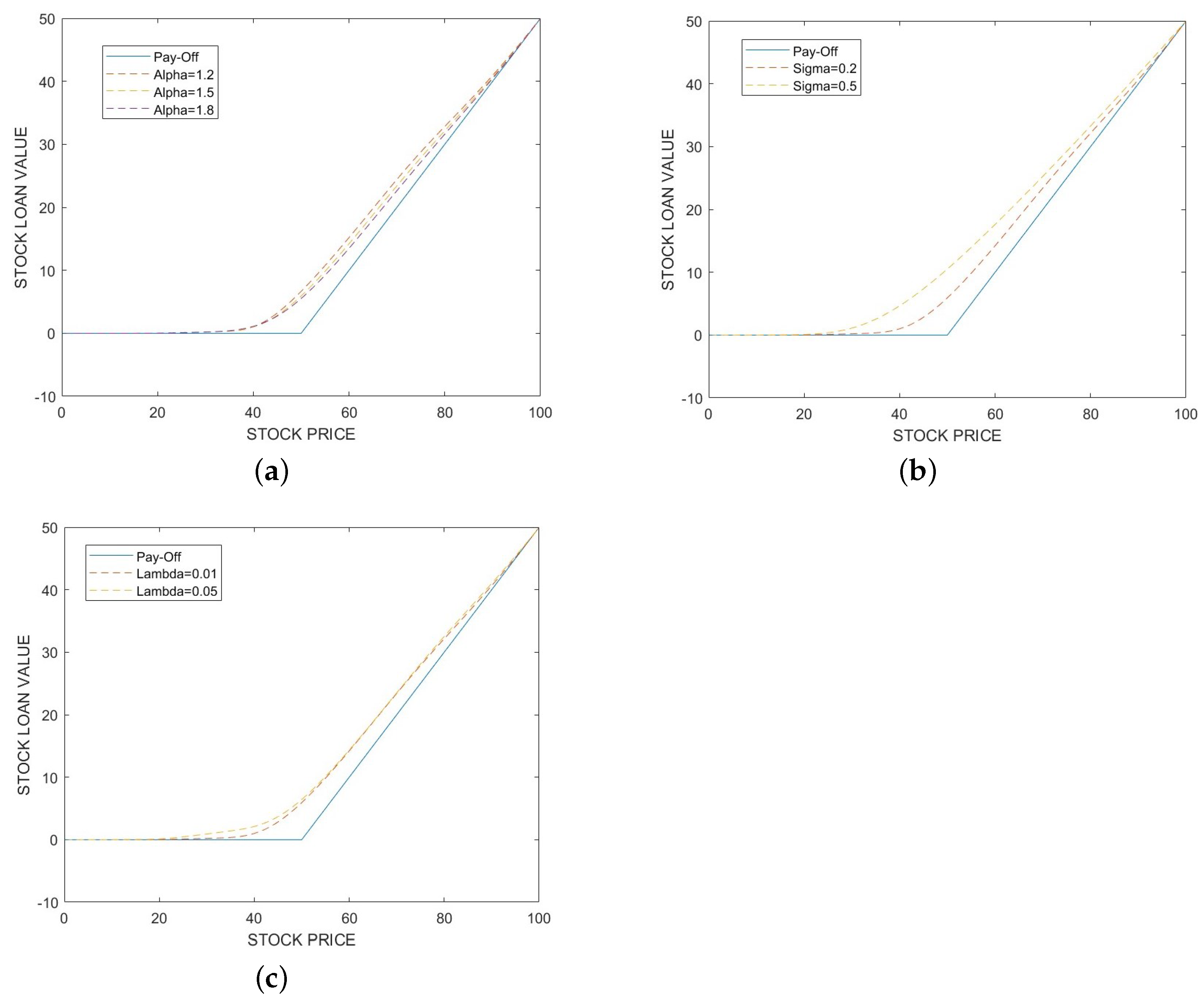
6.2. Stock Loan
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Stein, E.M.; Stein, J.C. Stock price distributions with stochastic volatility: An analytic approach. Rev. Financ. Stud. 1991, 4, 727–752. [Google Scholar] [CrossRef]
- Kou, S.G. A jump-diffusion model for option pricing. Manage. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef]
- Fulop, A.; Li, J.; Yu, J. Self-exciting jumps, learning, and asset pricing implications. Rev. Financ. Stud. 2015, 28, 876–912. [Google Scholar] [CrossRef]
- Hawkes, A.G. Hawkes jump-diffusions and finance: A brief history and review. Eur. J. Financ. 2022, 28, 627–641. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J. Pricing of American Carbon Emission Derivatives and Numerical Method under the Mixed Fractional Brownian Motion. Discrete Dyn. Nat. Soc. 2021, 2021, 6612284. [Google Scholar] [CrossRef]
- Huang, S.; He, X. Analytical approximation of European option prices under a new two-factor non-affine stochastic volatility model. AIMS. Math. 2022, 8, 4875–4891. [Google Scholar] [CrossRef]
- Bian, L.; Li, Z. Fuzzy simulation of European option pricing using sub-fractional Brownian motion. Chaos Solitons Fractals 2021, 153, 111442. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, Y.; Dai, L. European option pricing under sub-fractional Brownian motion regime in discrete time. Fractal Fract. 2024, 8, 13. [Google Scholar] [CrossRef]
- Cartea, A.; del Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Phys. A 2007, 374, 749–763. [Google Scholar] [CrossRef]
- Boyarchenko, S.; Levendorskii, S. Non-Gaussian Merton-Black–Scholes Theory; World Scientific: Singapore, 2002. [Google Scholar]
- Carr, P.; Geman, H.; Madan, D.B.; Yor, M. The fine structure of asset returns: An empirical investigation. J. Bus. 2002, 75, 305–333. [Google Scholar] [CrossRef]
- Carr, P.; Wu, L. The finite moment log stable process and option pricing. J. Financ. 2003, 58, 753–777. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, J.; Gao, X. Convergence of iterative laplace transform methods for a system of fractional PDEs amd PIDEs arising in option pricing. East Asian Appl. Math. 2018, 8, 782–808. [Google Scholar] [CrossRef]
- Fan, C.; Chen, W.; Feng, B. Pricing stock loans under the Lévy-α-stable process with jumps. Netw. Heterog. Media 2023, 18, 191–211. [Google Scholar] [CrossRef]
- Boyarchenko, S.; Levendorskii, S. American options in regime-switching models. SIAM J. Control Optim. 2009, 48, 1353–1376. [Google Scholar] [CrossRef]
- Yousuf, M.; Khaliq, A.; Liu, R. Pricing American options under multi-state regime switching with an efficient L-stable method. Int. J. Comput. Math. 2015, 92, 2530–2550. [Google Scholar] [CrossRef]
- Khaliq, A.; Voss, D.; Kazmi, S. A linearly implicit predictor–corrector scheme for pricing American options using a penalty method approach. J. Bank Financ. 2006, 30, 489–502. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Fang, H. On the variable two-step IMEX BDF method for parabolic integro-differential equations with nonsmooth initial data arising in finance. SIAM J. Numer. Anal. 2019, 57, 1289–1317. [Google Scholar] [CrossRef]
- Shi, X.; Yang, L.; Huang, Z. A fixed point method for the linear complementarity problem arising from American option pricing. Acta Math. Appl. Sin. Engl. Ser. 2016, 32, 921–932. [Google Scholar] [CrossRef]
- Lei, S.; Wang, W.; Chen, X.; Ding, D. A fast preconditioned penalty method for American options pricing under regime-switching tempered fractional diffusion models. J. Sci. Comput. 2018, 75, 1633–1655. [Google Scholar] [CrossRef]
- Bai, Z. Modulus-based matrix splitting iteration methods for linear complementarity problems. Numer. Linear Algebra Appl. 2010, 17, 917–933. [Google Scholar] [CrossRef]
- Saigal, R. On the Convergence Rate of Algorithms for Solving Equations That Are Based on Methods of Complementary Pivoting. Math. Oper. Res. 1977, 2, 108–124. [Google Scholar] [CrossRef]
- Toivanen, J.; Oosterlee, C.W. A projected algebraic multigrid method for linear complementarity problems. Numer. Math. Theor. Meth. Appl. 2012, 5, 85–98. [Google Scholar] [CrossRef]
- Chen, Y.; Wan, J.W.L. Deep neural network framework based on backward stochastic differential equations for pricing and hedging American options in high dimensions. Quant. Financ. 2021, 21, 45–67. [Google Scholar] [CrossRef]
- Gatta, F.; Cola, V.S.D.; Giampaolo, F.; Piccialli, F.; Cuomo, S. Meshless methods for American option pricing through Physics-Informed Neural Networks. Eng. Anal. Boundary Elem. 2023, 151, 68–82. [Google Scholar] [CrossRef]
- Reisinger, C.; Witte, J.H. On the use of policy iteration as an easy way of pricing American options. SIAM J. Financ. Math. 2012, 3, 459–478. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Pascucci, A.; Suarez-Taboada, M.; Vazquez, C. Mathematical analysis and numerical methods for a PDE model of a stock loan pricing problem. J. Math. Anal. Appl. 2013, 403, 38–53. [Google Scholar] [CrossRef]
- Pang, H.; Zhang, Y.; Vong, S.; Jin, X. Circulant preconditioners for pricing options. Linear Algebra Appl. 2011, 434, 2325–2342. [Google Scholar] [CrossRef]
- Lesmana, D.C.; Wang, S. An upwind finite difference method for a nonlinear Black–Scholes equation governing European option valuation under transaction costs. Appl. Math. Comput. 2013, 219, 8811–8828. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, J.; Sun, H. Fast Laplace transform methods for free-boundary problems of fractional diffusion equations. J. Sci. Comput. 2018, 74, 49–69. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Plemmons, R.J. M-matrix characterizations. I—nonsingular M-matrices. Linear Algebra Appl. 1977, 18, 175–188. [Google Scholar] [CrossRef]
- Huang, Y.; Forsyth, P.A.; Labahn, G. Methods for pricing American options under regime switching. SIAM J. Sci. Comput. 2011, 33, 2144–2168. [Google Scholar] [CrossRef]
- Varah, J.M. A lower bound for the smallest singular value of a matrix. Linear Algebra Appl. 1975, 11, 3–5. [Google Scholar] [CrossRef]
- Chen, X.; Wang, W.; Ding, D.; Lei, S. A fast preconditioned policy iteration method for solving the tempered fractional HJB equation governing American options valuation. Comput. Appl. Math. 2017, 73, 1932–1944. [Google Scholar] [CrossRef]
- Wang, Q.; She, Z.; Lao, C.; Lin, F. Fractional centered difference schemes and banded preconditioners for nonlinear Riesz space variable-order fractional diffusion equations. Numer. Algorithms 2024, 95, 859–895. [Google Scholar] [CrossRef]
- She, Z.; Lao, C.; Yang, H.; Lin, F. Banded Preconditioners for Riesz Space Fractional Diffusion Equations. J. Sci. Comput. 2021, 86, 31. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Aguilar, J.; Korbel, J. Simple formulas for pricing and hedging European options in the finite moment log-stable model. Risks 2019, 7, 36. [Google Scholar] [CrossRef]
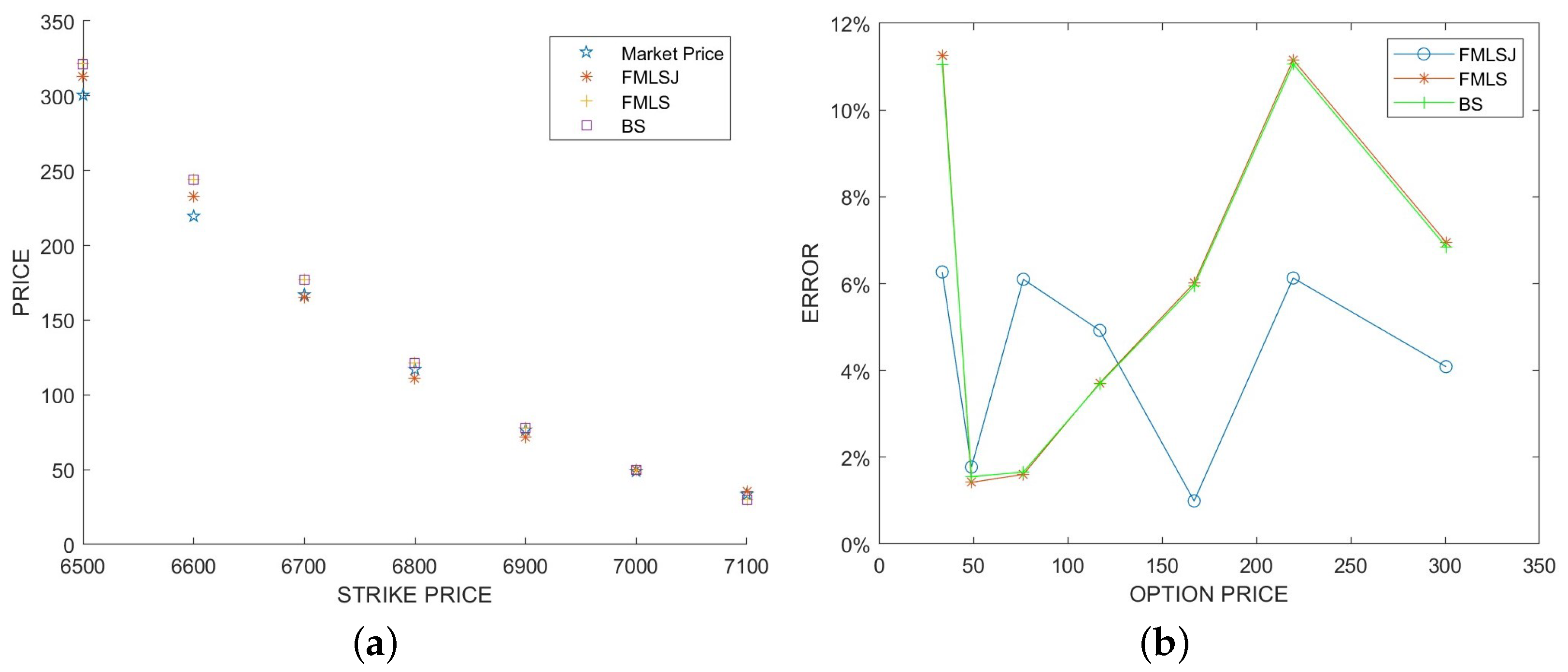
| MSE | ||||||
|---|---|---|---|---|---|---|
| BS | - | 0.0806 | - | - | - | 163.6608 |
| FMLS | 1.9990 | 0.0777 | - | - | - | 168.0140 |
| FMLSJ | 1.9990 | 0.0645 | 0.5523 | 0.2585 | 0.0132 | 56.4139 |
| GMRES | SGMRES | BGMRES (4) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Rate | Iter-Out | Error | Rate | Iter-Out | Error | Rate | Iter-Out | ||
| - | 2.0 | - | 2.0 | - | 2.0 | |||||
| 1.0138 | 2.0 | 1.0138 | 2.0 | 1.0138 | 2.0 | |||||
| 1.1026 | 2.0 | 1.1026 | 2.0 | 1.1026 | 2.0 | |||||
| 1.0876 | 2.0 | 1.0876 | 2.0 | 1.0876 | 2.0 | |||||
| 1.2163 | 2.0 | 1.2163 | 2.0 | 1.2163 | 2.0 | |||||
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Iter-In | Time (s) | Iter-In | Time (s) | Iter-In | Time (s) | Iter-In | Time (s) | |
| GMRES | 49.0 | 1.89 | 70.0 | 6.67 | 100.0 | 70.15 | 146.0 | 416.42 |
| SGMRES | 18.6 | 1.35 | 30.4 | 4.05 | 45.8 | 51.31 | 68.0 | 316.21 |
| BGMRES(2) | 4.0 | 0.32 | 4.0 | 0.58 | 4.0 | 4.12 | 4.0 | 17.29 |
| BGMRES(4) | 4.0 | 0.28 | 3.0 | 0.52 | 3.0 | 3.61 | 3.0 | 15.22 |
| BGMRES(7) | 4.0 | 0.30 | 3.0 | 0.64 | 3.0 | 4.18 | 3.0 | 18.10 |
| BGMRES(13) | 4.0 | 0.37 | 3.0 | 0.87 | 3.0 | 5.92 | 3.0 | 23.64 |
| M | Error | Rate | Iter-Out | Iter-In | Time (s) | ||
|---|---|---|---|---|---|---|---|
| GMRES | 0.9531 | 2.0 | 40.9 | 0.62 | |||
| 1.0049 | 2.0 | 45.0 | 3.51 | ||||
| 1.0786 | 2.0 | 49.0 | 9.54 | ||||
| 1.2104 | 2.0 | 54.0 | 69.94 | ||||
| SGMRES | 0.9531 | 2.0 | 13.8 | 0.29 | |||
| 1.0049 | 2.0 | 14.6 | 1.88 | ||||
| 1.0786 | 2.0 | 16.2 | 3.93 | ||||
| 1.2104 | 2.0 | 17.6 | 39.81 | ||||
| BGMRES (4) | 0.9531 | 2.0 | 7.0 | 0.15 | |||
| 1.0049 | 2.0 | 7.0 | 0.74 | ||||
| 1.0786 | 2.0 | 7.0 | 1.68 | ||||
| 1.2104 | 2.0 | 7.0 | 11.83 |
| M | Error | Rate | Iter-Out | Iter-In | Time (s) | ||
|---|---|---|---|---|---|---|---|
| GMRES | 1.0024 | 2.0 | 44.9 | 0.67 | |||
| 1.0320 | 2.0 | 55.0 | 4.25 | ||||
| 1.0983 | 2.0 | 68.0 | 13.29 | ||||
| 1.2176 | 2.0 | 84.0 | 119.81 | ||||
| SGMRES | 1.0024 | 2.0 | 14.7 | 0.32 | |||
| 1.0320 | 2.0 | 17.8 | 2.27 | ||||
| 1.0983 | 2.0 | 22.0 | 5.90 | ||||
| 1.2176 | 2.0 | 27.4 | 65.05 | ||||
| BGMRES (4) | 1.0024 | 2.0 | 7.2 | 0.16 | |||
| 1.0320 | 2.0 | 8.0 | 0.85 | ||||
| 1.0983 | 2.0 | 8.0 | 1.95 | ||||
| 1.2176 | 2.0 | 8.7 | 15.35 |
| M | Error | Rate | Iter-Out | Iter-In | Time (s) | ||
|---|---|---|---|---|---|---|---|
| GMRES | 1.0394 | 2.3 | 53.0 | 0.88 | |||
| 1.0459 | 2.2 | 68.8 | 5.98 | ||||
| 0.9830 | 2.2 | 89.5 | 19.49 | ||||
| 1.0802 | 2.2 | 117.8 | 165.29 | ||||
| SGMRES | 1.0394 | 2.3 | 21.2 | 0.64 | |||
| 1.0459 | 2.2 | 29.6 | 4.08 | ||||
| 0.9830 | 2.2 | 39.2 | 11.21 | ||||
| 1.0802 | 2.2 | 52.9 | 125.92 | ||||
| BGMRES (4) | 1.0394 | 2.3 | 7.0 | 0.18 | |||
| 1.0459 | 2.2 | 8.0 | 0.94 | ||||
| 0.9830 | 2.2 | 8.0 | 2.10 | ||||
| 1.0802 | 2.2 | 9.0 | 15.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Gong, X.-X.; Sun, Y.; Lei, S.-L. A Preconditioned Policy–Krylov Subspace Method for Fractional Partial Integro-Differential HJB Equations in Finance. Fractal Fract. 2024, 8, 316. https://doi.org/10.3390/fractalfract8060316
Chen X, Gong X-X, Sun Y, Lei S-L. A Preconditioned Policy–Krylov Subspace Method for Fractional Partial Integro-Differential HJB Equations in Finance. Fractal and Fractional. 2024; 8(6):316. https://doi.org/10.3390/fractalfract8060316
Chicago/Turabian StyleChen, Xu, Xin-Xin Gong, Youfa Sun, and Siu-Long Lei. 2024. "A Preconditioned Policy–Krylov Subspace Method for Fractional Partial Integro-Differential HJB Equations in Finance" Fractal and Fractional 8, no. 6: 316. https://doi.org/10.3390/fractalfract8060316
APA StyleChen, X., Gong, X.-X., Sun, Y., & Lei, S.-L. (2024). A Preconditioned Policy–Krylov Subspace Method for Fractional Partial Integro-Differential HJB Equations in Finance. Fractal and Fractional, 8(6), 316. https://doi.org/10.3390/fractalfract8060316







