Fractional Second-Grade Fluid Flow over a Semi-Infinite Plate by Constructing the Absorbing Boundary Condition
Abstract
1. Introduction
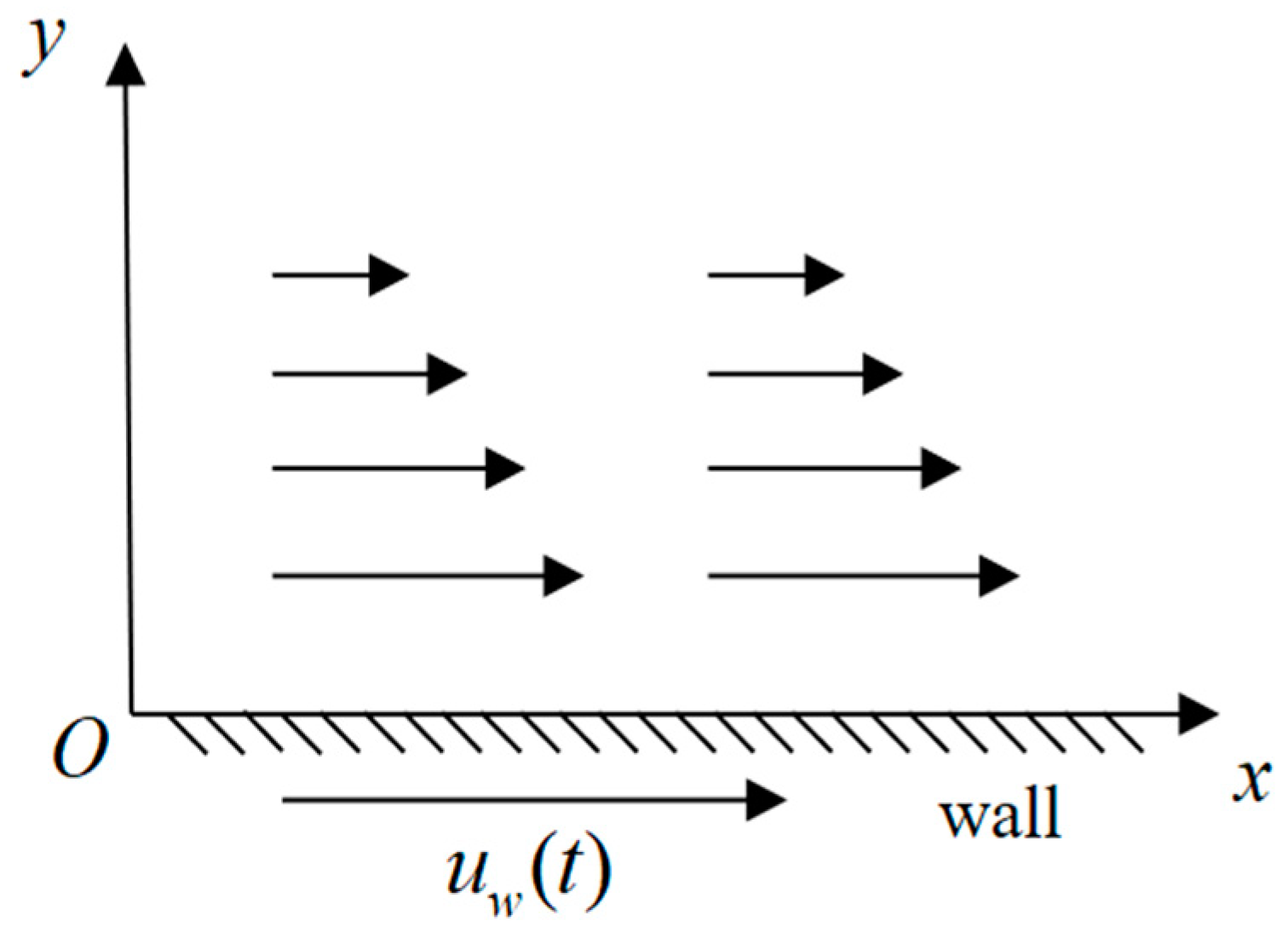
2. The Construction of the Governing Equation
3. The Establishment of the ABC
4. Construction of the FDM
5. Numerical Examples
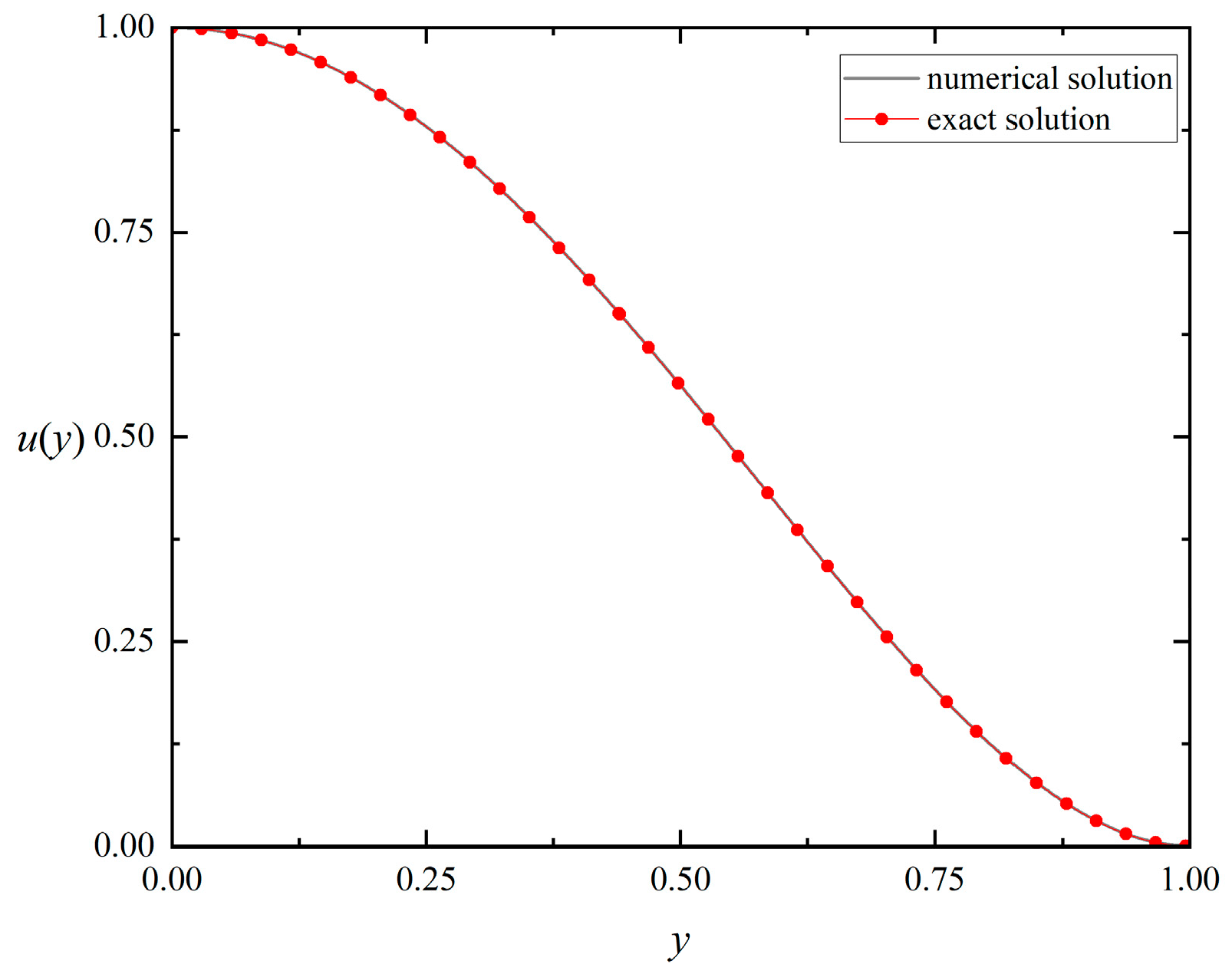
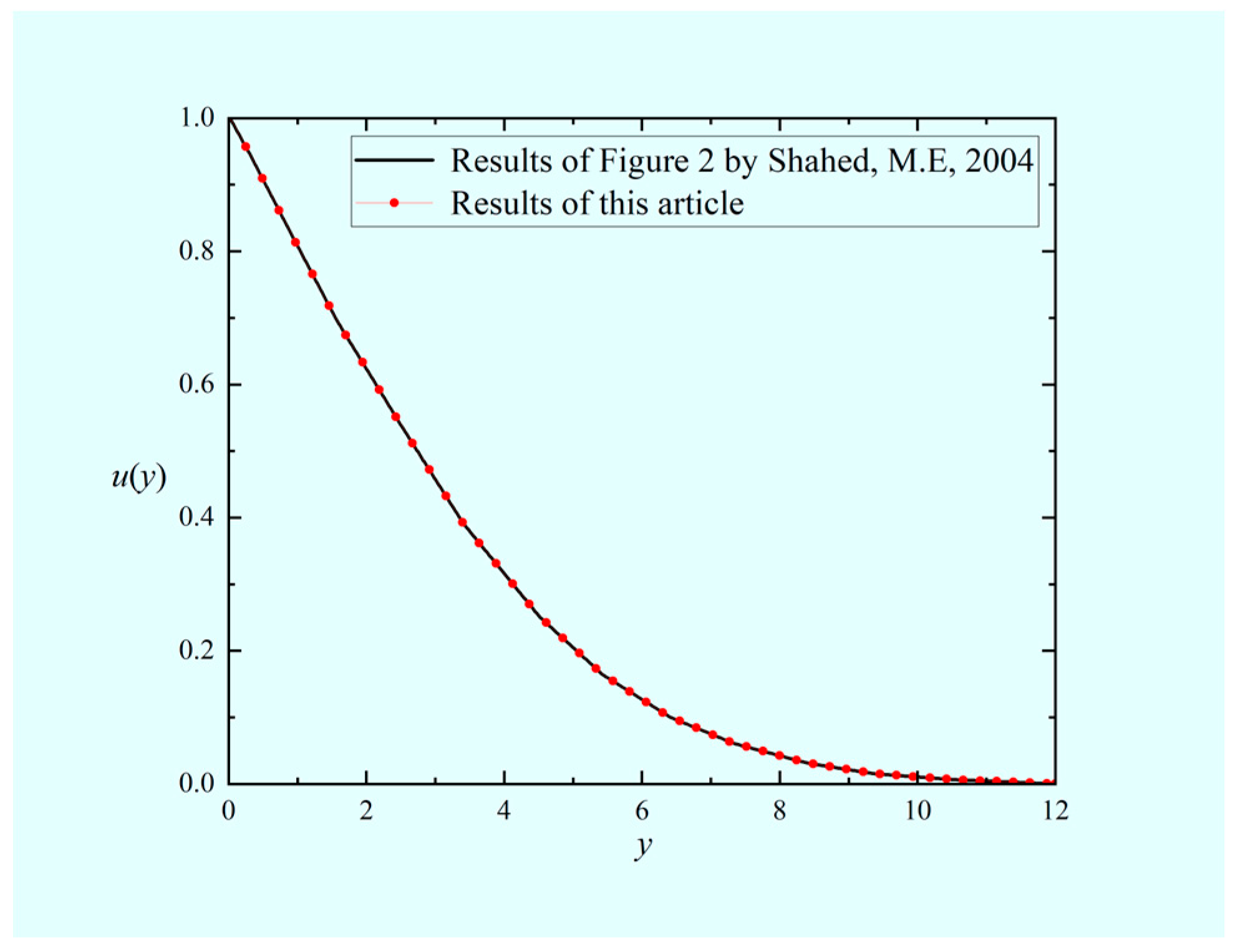
5.1. The Verification of the Solution and the ABC
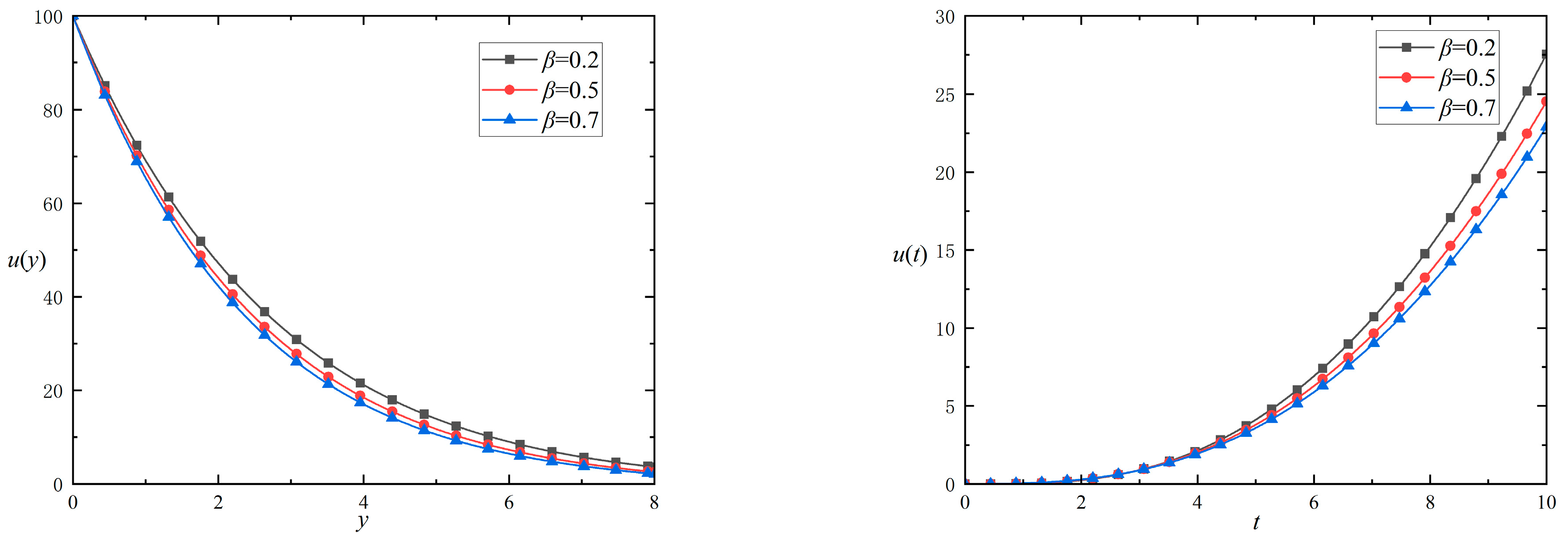
5.2. Impact of Parameter Variations on the Velocity Field Induced by a Moving Plate
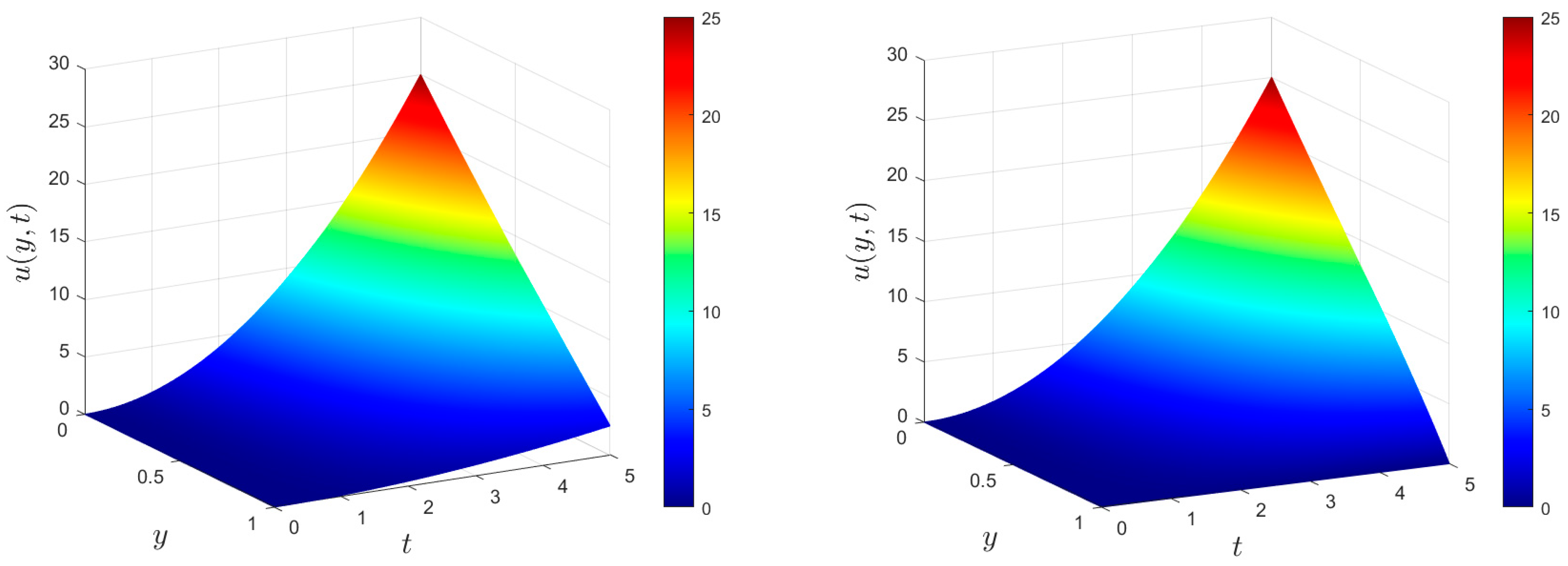
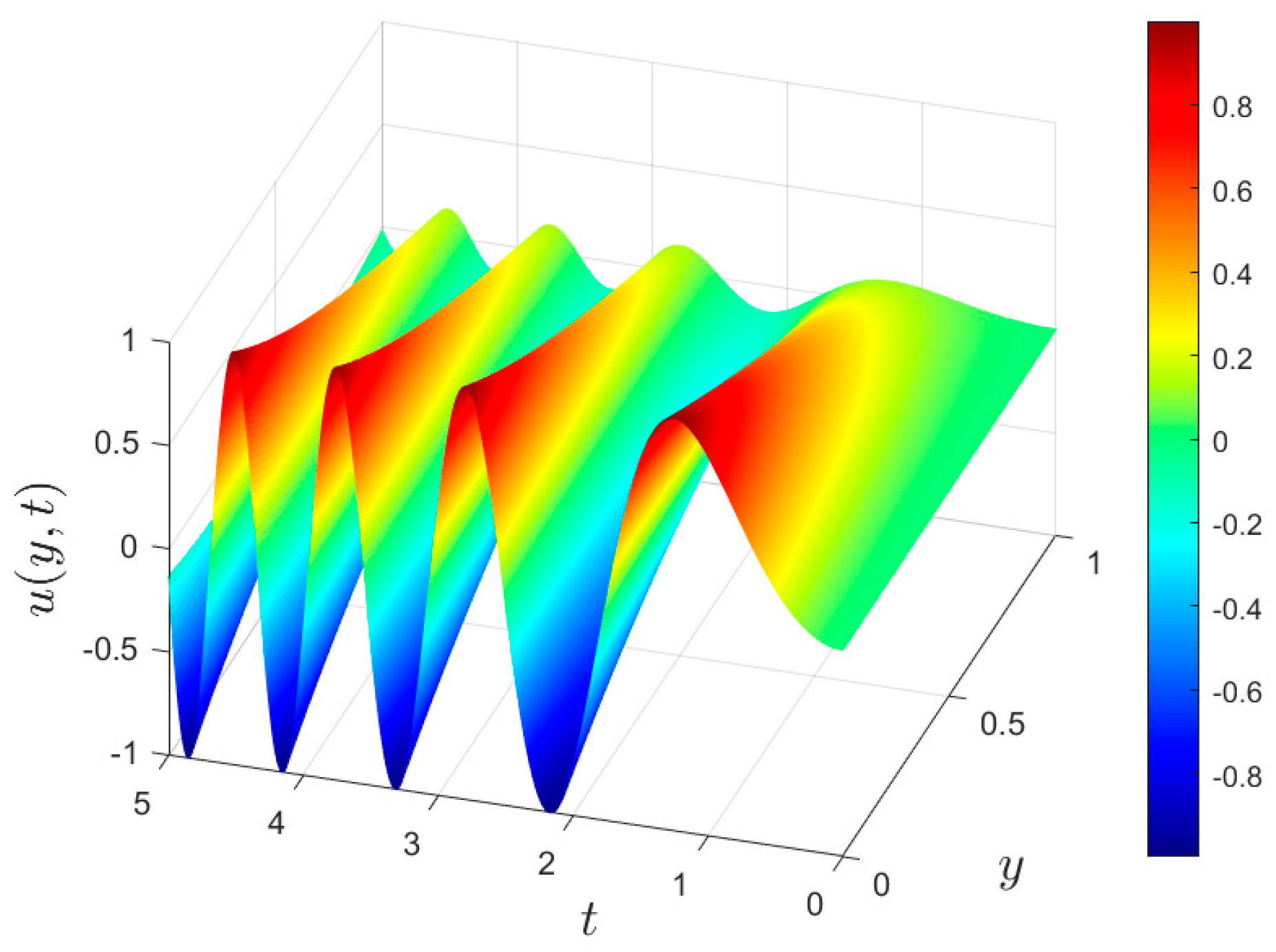
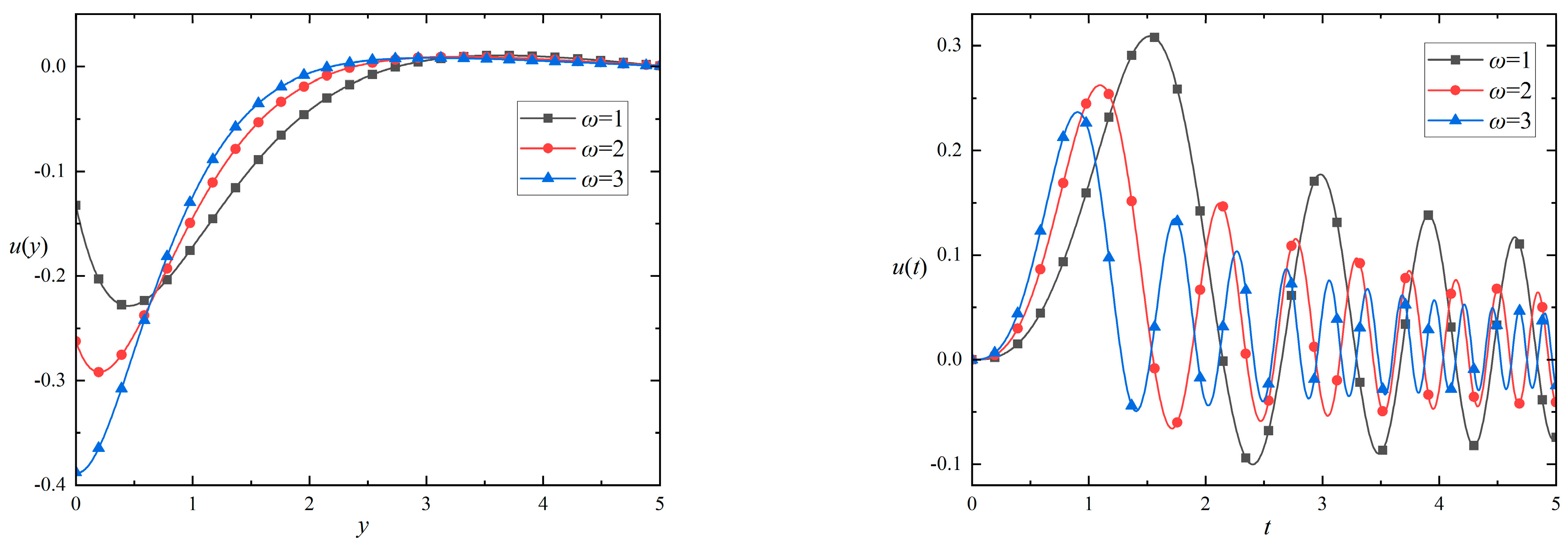
5.3. Various Velocities Induced by Vibrating Plates with Different Physical Parameters
5.4. Comparison of This Study with Other Methods in Ref. [58]
6. Conclusions
- (i)
- A higher fractional parameter leads to a slower rate of fluid flow;
- (ii)
- The delay effect increases with the decrease in relaxation parameters, and the fluid velocity rises as the relaxation parameter increases;
- (iii)
- The higher the oscillation frequency is, the faster the velocity will change, and the velocity distribution curve will exhibit a decreased period and amplitude;
- (iv)
- With a greater amplitude, the fluid velocity changes more rapidly and the amplitude of the velocity distribution curve also increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohamed, A.A.; Khishvand, M.; Piri, M. Entrapment and mobilization dynamics during the flow of viscoelastic fluids in natural porous media: A micro-scale experimental investigation. Phys. Fluids 2023, 35, 047119. [Google Scholar] [CrossRef]
- Steinhaus, B.; Shen, A.Q.; Sureshkumar, R. Dynamics of viscoelastic fluid filaments in microfluidic devices. Phys. Fluids 2007, 19, 073103. [Google Scholar] [CrossRef]
- Lauga, E. Propulsion in a viscoelastic fluid. Phys. Fluids 2007, 19, 083104. [Google Scholar] [CrossRef]
- VeeraKrishna, M.; Chamkha, A.J. Hall effects on unsteady MHD flow of second grade fluid through porous medium with ramped wall temperature and ramped surface concentration. Phys. Fluids 2018, 30, 053101. [Google Scholar] [CrossRef]
- Wang, S.; Tai, C.W.; Narsimhan, V. Dynamics of spheroids in an unbound quadratic flow of a general second-grade fluid. Phys. Fluids 2020, 32, 113106. [Google Scholar] [CrossRef]
- Ho, B.P.; Leal, L.G. Migration of rigid spheres in a two-dimensional unidirectional shear flow of a second-grade fluid. J. Fluid Mech. 1976, 76, 783–799. [Google Scholar] [CrossRef]
- Khan, M.; Wang, S. Flow of a generalized second-grade fluid between two side walls perpendicular to a plate with a fractional derivative model. Nonlinear Anal. Real World Appl. 2009, 10, 203–208. [Google Scholar] [CrossRef]
- Tassaddiq, A. MHD flow of a fractional second grade fluid over an inclined heated plate. Chaos Soliton. Fract. 2019, 123, 341–346. [Google Scholar] [CrossRef]
- Metzne, A.B.; Park, M.G. Turbulent flow characteristics of viscoelastic fluids. J. Fluid Mech. 1964, 20, 291–303. [Google Scholar] [CrossRef]
- Li, G.; McKinley, G.H.; Ardekani, A.M. Dynamics of particle migration in channel flow of viscoelastic fluids. J. Fluid Mech. 2015, 785, 486–505. [Google Scholar] [CrossRef]
- Billingham, J.; King, A.C. The interaction of a moving fluid/fluid interface with a flat plate. J. Fluid Mech. 1995, 296, 325–351. [Google Scholar] [CrossRef]
- Traugott, S.C. Impulsive Motion of an Infinite Plate in a Compressible Fluid with Non-Uniform External Flow. J. Fluid Mech. 1962, 13, 400–416. [Google Scholar] [CrossRef]
- Jaworski, J.W.; Peake, N. Aerodynamic noise from a poroelastic edge with implications for the silent flight of owls. J. Fluid Mech. 2013, 723, 456–479. [Google Scholar] [CrossRef]
- Sahoo, T.; Yip, T.L.; Chwang, A.T. Scattering of surface waves by a semi-infinite floating elastic plate. Phys. Fluids 2001, 13, 3215–3222. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Exact solutions for non-isothermal flows of second grade fluid between parallel plates. Nanomaterials 2023, 13, 1409. [Google Scholar] [CrossRef] [PubMed]
- Baranovskii, E.S. Analytical Solutions to the Unsteady Poiseuille Flow of a Second Grade Fluid with Slip Boundary Conditions. Polymers 2024, 16, 179. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the grade of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Carpinteri, A.; Francesco, M. Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 378. [Google Scholar]
- Uchaikin, V.; Renat, S. Fractional Kinetics in Space: Anomalous Transport Models; World Scientific: Singapore, 2018. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Shen, M.; Chen, L.; Zhang, M.; Liu, F. A renovated Buongiorno’s model for unsteady Sisko nanofluid with fractional Cattaneo heat flux. Int. J. Heat Mass Transf. 2018, 126, 277–286. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid model with Caputo-Liouville generalized fractional derivative. Chaos Soliton. Fract. 2020, 133, 109631. [Google Scholar] [CrossRef]
- Chan, P.C.H.; Leal, L.G. The motion of a deformable drop in a second-grade fluid. J. Fluid Mech. 1979, 92, 131–170. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, H.; Wang, S. Unsteady magnetohydrodynamic flow of generalized second grade fluid through porous medium with Hall effects on heat and mass transfer. Phys. Fluids 2020, 32, 113105. [Google Scholar] [CrossRef]
- Deswal, S.C.R.; Kalkal, K.K. Fractional grade heat conduction law in micropolar thermo-viscoelasticity with two temperatures. Int. J. Heat Mass Transf. 2013, 66, 451–460. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.; Qi, H. Transient magnetohydrodynamic flow and heat transfer of fractional Oldroyd-B fluids in a microchannel with slip boundary condition. Phys. Fluids 2020, 32, 103104. [Google Scholar] [CrossRef]
- Awad, E. Dual-phase-lag in the balance Sufficiency bounds for the class of Jeffreys’ equations to furnish physical solutions. Int. J. Heat Mass Transf. 2020, 158, 119742. [Google Scholar] [CrossRef]
- Coppola, G.; Veldman, A.E.P. Global and local conservation of mass, momentum and kinetic energy in the simulation of compressible flow. J. Comput. Phys. 2023, 475, 111879. [Google Scholar] [CrossRef]
- Tamim, S.; Bostwick, J.B. Spreading of a thin droplet on a soft substrate. J. Fluid Mech. 2023, 971, A32. [Google Scholar] [CrossRef]
- Mei, R.; Adrian, R.J. Flow past a sphere with an oscillation in the free-stream velocity and unsteady drag at finite Reynolds number. J. Fluid Mech. 1992, 237, 323–341. [Google Scholar] [CrossRef]
- Dennis, S.C.R. Calculation of the steady flow through a curved tube using a new finite-difference method. J. Fluid Mech. 1980, 99, 449–467. [Google Scholar] [CrossRef]
- Kim, T.Y.; Dolbow, J.; Fried, E. A numerical method for a second-gradient theory of incompressible fluid flow. J. Comput. Phys. 2007, 223, 551–570. [Google Scholar] [CrossRef]
- Gilmanov, A.; Sotiropoulos, F. A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies. J. Comput. Phys. 2005, 207, 457–492. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Zheng, C. Stability and error analysis for a second-grade fast approximation of the one-dimensional Schrödinger equation under absorbing boundary conditions. SIAM J. Sci. Comput. 2018, 40, A4083–A4104. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef]
- Özdemir, N.; Karadeniz, D.; İskender, B.B. Fractional optimal control problem of a distributed system in cylindrical coordinates. Phys. Lett. A 2009, 373, 221–226. [Google Scholar] [CrossRef]
- Yan, Y.; Khan, M.; Ford, N.J. An analysis of the modified L1 scheme for time-fractional partial differential equations with nonsmooth data. SIAM J. Numer. Anal. 2018, 56, 210–227. [Google Scholar] [CrossRef]
- Lyu, P.; Vong, S. A nonuniform L2 formula of Caputo derivative and its application to a fractional Benjamin-Bona-Mahony-type equation with nonsmooth solutions. Numer. Meth. Part Differ. Equ. 2020, 36, 579–600. [Google Scholar] [CrossRef]
- Xing, Z.; Wen, L. Numerical Analysis of the Nonuniform Fast L1 Formula for Nonlinear Time-Space Fractional Parabolic Equations. J. Sci. Comput. 2023, 95, 58. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W. Convergence of the uniaxial perfectly matched layer method for time-harmonic scattering problems in two-layered media. SIAM J. Numer. Anal. 2010, 48, 2158–2185. [Google Scholar] [CrossRef]
- Barucq, H.; Rouxelin, N.; Tordeux, S. Low-grade Prandtl-Glauert-Lorentz based Absorbing Boundary Conditions for solving the convected Helmholtz equation with Discontinuous Galerkin methods. J. Comput. Phys. 2022, 468, 111450. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Zheng, C. An efficient second-grade finite difference method for the one-dimensional Schrödinger equation with absorbing boundary conditions. SIAM J. Numer. Anal. 2018, 56, 766–791. [Google Scholar] [CrossRef]
- Muhr, M.; Nikolić, V.; Wohlmuth, B. Self-adaptive absorbing boundary conditions for quasilinear acoustic wave propagation. J. Comput. Phys. 2019, 388, 279–299. [Google Scholar] [CrossRef]
- Fu, W.; Wang, W.; Li, C.; Huang, S. An investigation of natural convection in parallel square plates with a heated bottom surface by an absorbing boundary condition. Int. J. Heat Mass Transf. 2013, 56, 35–44. [Google Scholar] [CrossRef]
- Baffet, D.; Grote, M.J. On wave splitting, source separation and echo removal with absorbing boundary conditions. J. Comput. Phys. 2019, 387, 589–596. [Google Scholar] [CrossRef]
- Hwang, J.; Jang, J.; Jung, J. The Fokker-Planck equation with absorbing boundary conditions in bounded domains. SIAM J. Math. Anal. 2018, 50, 2194–2232. [Google Scholar] [CrossRef]
- Tan, W.; Masuoka, T. Stokes’ first problem for a second grade fluid in a porous half-space with heated boundary. Int. J. Non-Linear Mech. 2005, 40, 515–522. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Ericksen, J.L.V. Stress-Deformation Relations for Isotropic Materials; Collected Papers of RS Rivlin Volume I and II; Springer: Berlin/Heidelberg, Germany, 1997; pp. 911–1013. [Google Scholar]
- Tan, W.; Xu, M. The impulsive motion of flat plate in a generalized second grade fluid. Mech. Res. Commun. 2002, 29, 3–9. [Google Scholar] [CrossRef]
- Khan, M.; Nadeem, S.; Hayat, T.; Siddiqui, A.M. Unsteady motions of a generalized second-grade fluid. Math. Comput. 2005, 41, 629–637. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Hristov, J. Linear viscoelastic responses and constitutive equations in terms of fractional operators with non-singular kernels-pragmatic approach, memory kernel correspondence requirement and analyses. Eur. Phys. J. Plus 2019, 134, 283. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo derivatives. Discrete. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Mahmood, A.; Fetecau, C.; Khan, N.A.; Jamil, M. Some exact solutions of the oscillatory motion of a generalized second grade fluid in an annular region of two cylinders. Acta Mech. Sin. 2010, 26, 541–550. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equation; Academic Press: San Diego, LA, USA, 1999. [Google Scholar]
- Alikhanov, A.A. A priori estimates for solutions of boundary value problems for fractional-grade equations. Differ. Equ. 2010, 46, 660–666. [Google Scholar] [CrossRef]
- Feng, L.; Liu, F.; Turner, I.; Zheng, L. Novel numerical analysis of multi-term time fractional viscoelastic non-Newtonian fluid models for simulating unsteady MHD Couette flow of a generalized Oldroyd-B fluid. Fract. Calc Appl. Anal. 2018, 21, 1073–1103. [Google Scholar] [CrossRef]
- Shahed, M.E. On the impulsive motion of flat plate in a generalized second grade fluid. Z. Naturfors. Sect. A-J. Phys. Sci. 2004, 59, 829–837. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Liu, L.; Chen, S.; Feng, L.; Xie, C. Fractional Second-Grade Fluid Flow over a Semi-Infinite Plate by Constructing the Absorbing Boundary Condition. Fractal Fract. 2024, 8, 309. https://doi.org/10.3390/fractalfract8060309
Yang J, Liu L, Chen S, Feng L, Xie C. Fractional Second-Grade Fluid Flow over a Semi-Infinite Plate by Constructing the Absorbing Boundary Condition. Fractal and Fractional. 2024; 8(6):309. https://doi.org/10.3390/fractalfract8060309
Chicago/Turabian StyleYang, Jingyu, Lin Liu, Siyu Chen, Libo Feng, and Chiyu Xie. 2024. "Fractional Second-Grade Fluid Flow over a Semi-Infinite Plate by Constructing the Absorbing Boundary Condition" Fractal and Fractional 8, no. 6: 309. https://doi.org/10.3390/fractalfract8060309
APA StyleYang, J., Liu, L., Chen, S., Feng, L., & Xie, C. (2024). Fractional Second-Grade Fluid Flow over a Semi-Infinite Plate by Constructing the Absorbing Boundary Condition. Fractal and Fractional, 8(6), 309. https://doi.org/10.3390/fractalfract8060309








