Time-Delay Effects on the Collective Resonant Behavior in Two Coupled Fractional Oscillators with Frequency Fluctuations
Abstract
1. Introduction
2. System Model
2.1. Complete Synchronization between the Average Behavior of the Two Oscillators
2.2. Output Amplitude Gain Of System
3. Collective Resonant Behavior
3.1. Collective Parameter-Induced SR based on System Parameters
3.2. Collective Conventional SR based on Noise Parameters
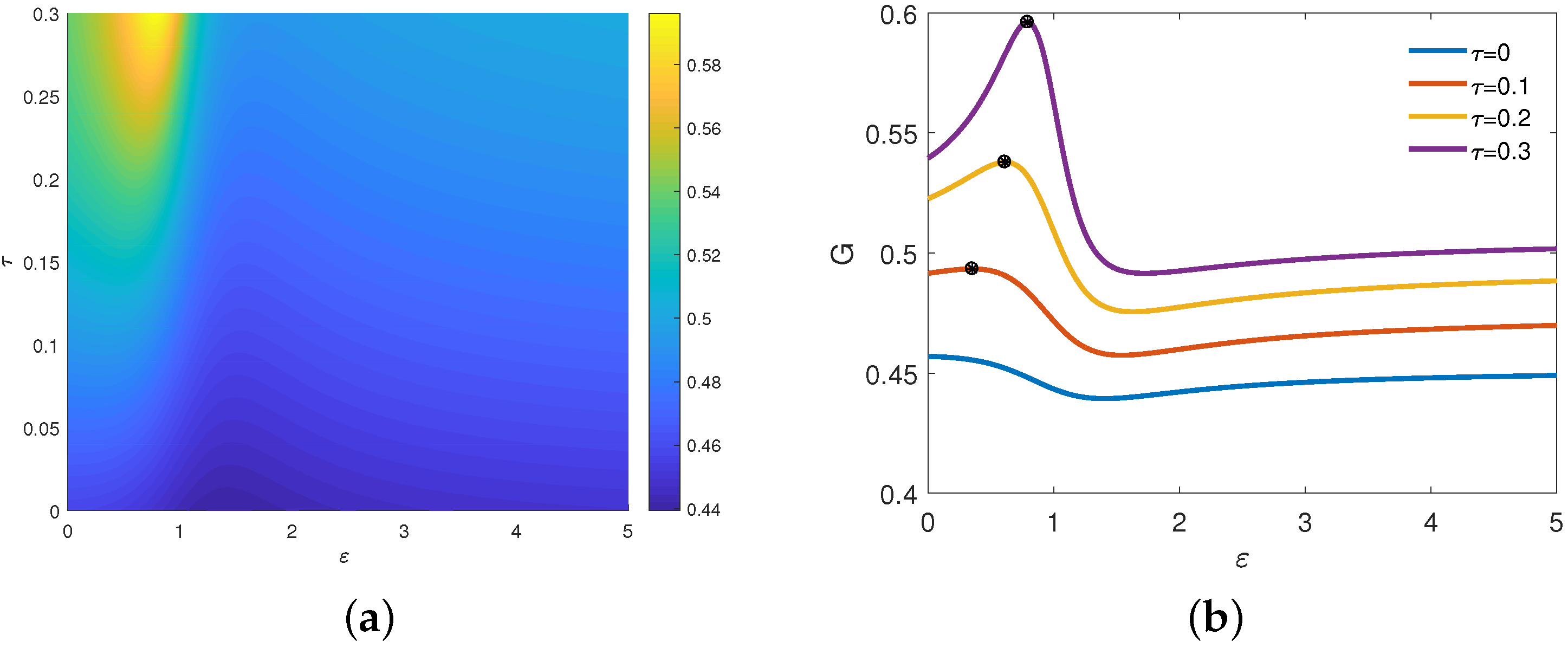
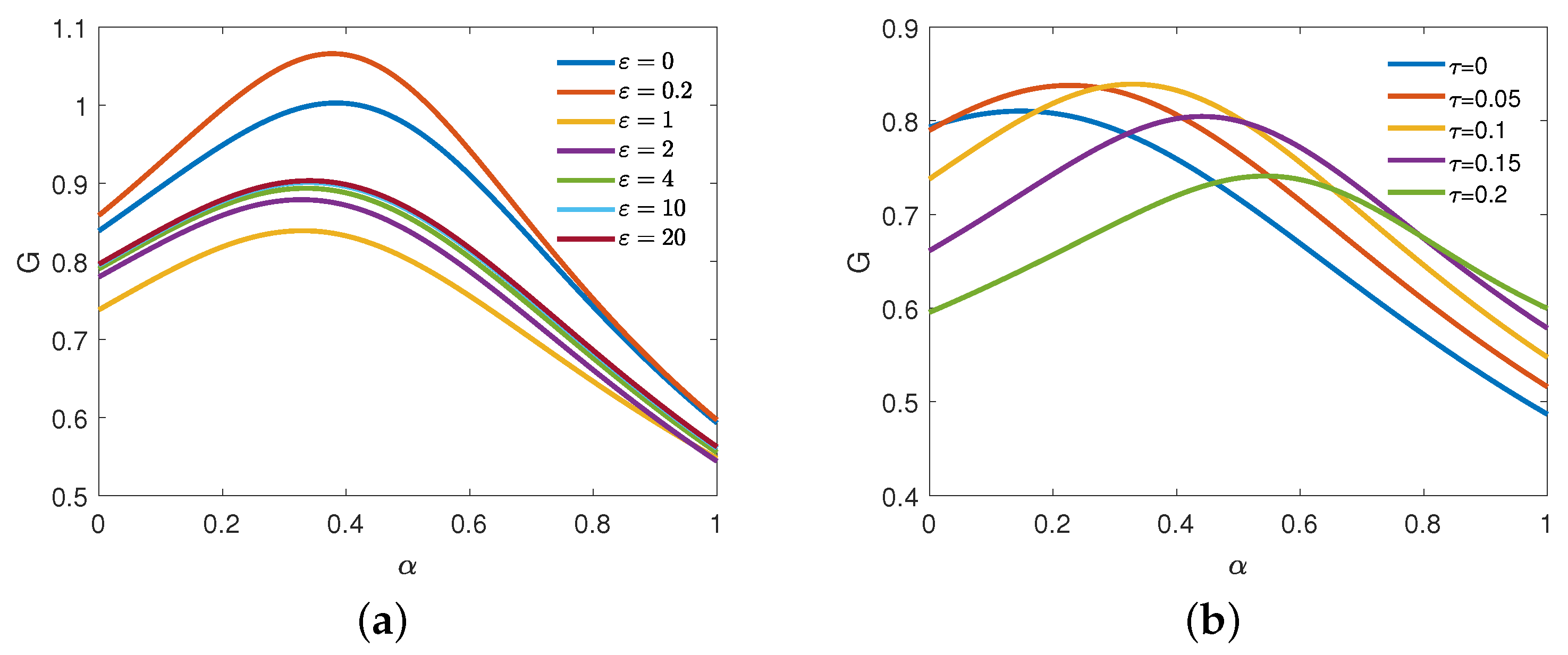
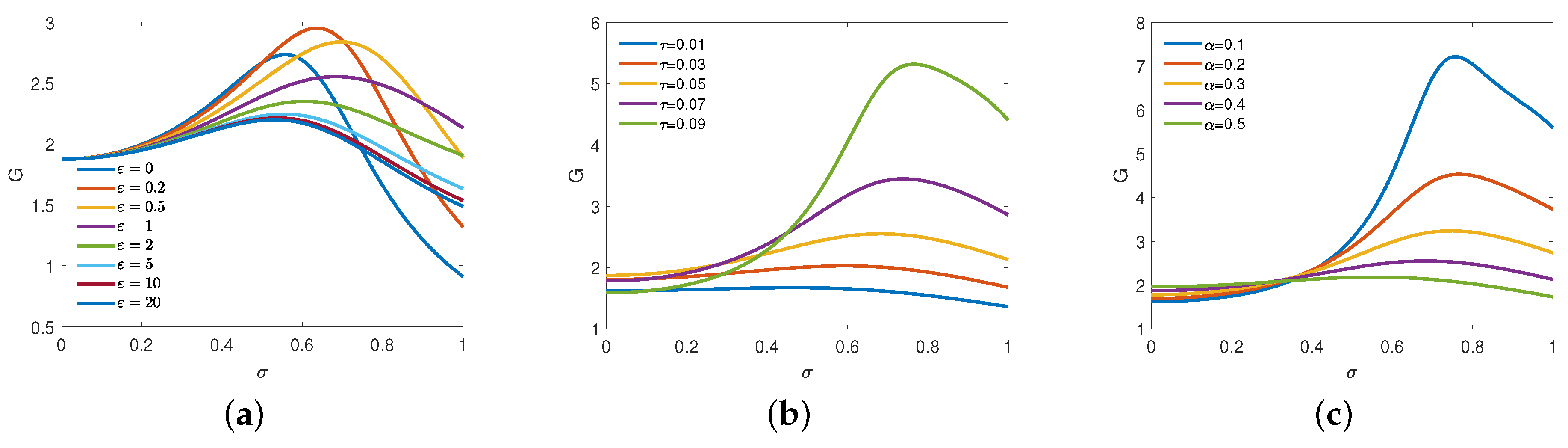
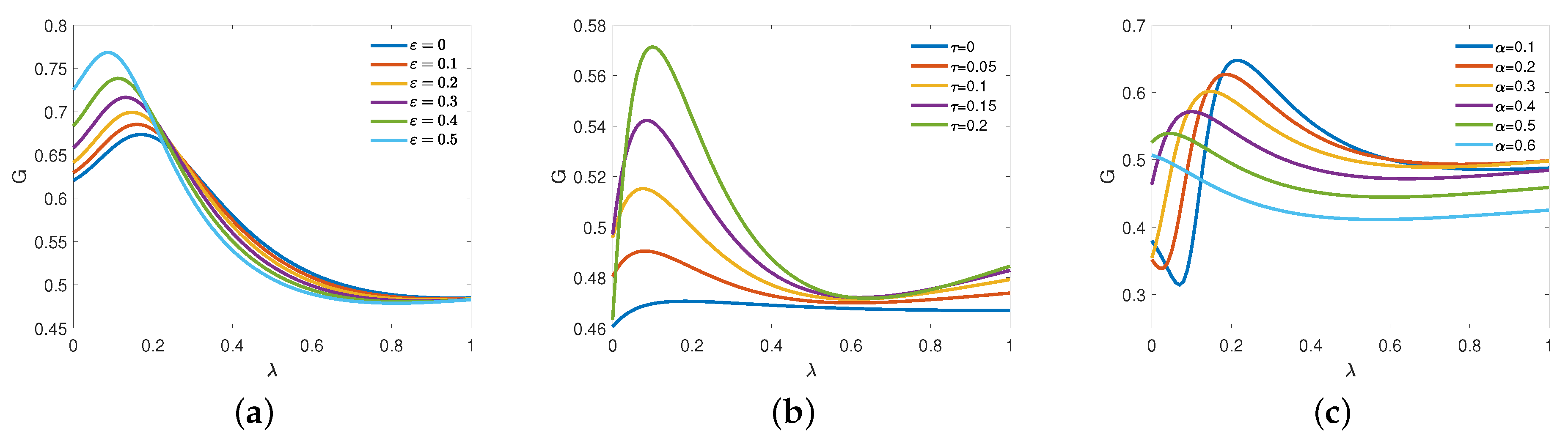
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Coefficients of Steady-State Output Amplitude
References
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A 1981, 14, L453–L457. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Spagnolo, B. Stochastic resonance in a tunnel diode in the presence of white or coloured noise. Nuovo Cimento D 1995, 17, 873–881. [Google Scholar] [CrossRef]
- Lanzara, E.; Mantegna, R.N.; Spagnolo, B.; Zangara, R. Experimental study of a nonlinear system in the presence of noise: The stochastic resonance. Am. J. Phys. 1997, 65, 341–349. [Google Scholar] [CrossRef]
- Chang, C.; Tsong, T. Stochastic resonance in a biological motor under complex fluctuations. Phys. Rev. E 2004, 69, 021914. [Google Scholar] [CrossRef] [PubMed]
- Dylov, D.V.; Fleischer, J.W. Nonlinear self-filtering of noisy images via dynamical stochastic resonance. Nat. Photonics 2010, 4, 323–328. [Google Scholar] [CrossRef]
- Bejarano, D.E.J.; Saeki, K. Stochastic resonance in a pulse-type cell body model. Nonlinear Theory Its Appl. IEICE 2017, 8, 279–288. [Google Scholar] [CrossRef][Green Version]
- Surazhevsky, I.A.; Demin, V.A.; Ilyasov, A.I.; Emelyanov, A.V.; Nikiruy, K.E.; Rylkov, V.V.; Shchanikov, S.A.; Bordanov, I.A.; Gerasimova, S.A.; Guseinov, D.V.; et al. Noise-assisted persistence and recovery of memory state in a memristive spiking neuromorphic network. Chaos Solitons Fractals 2021, 146, 110890. [Google Scholar] [CrossRef]
- Palabas, T.; Torres, J.J.; Perc, M.; Uzuntarla, M. Double stochastic resonance in neuronal dynamics due to astrocytes. Chaos Solitons Fractals 2023, 168, 113140. [Google Scholar] [CrossRef]
- Pikovsky, A.; Zaikin, A.; de la Casa, M.A. System size resonance in coupled noisy systems and in the Ising model. Phys. Rev. Lett. 2002, 88, 050601. [Google Scholar] [CrossRef]
- Casado-Pascual, J.; Gómez-Ordóñez, J.; Morillo, M.; Hänggi, P. Two-state theory of nonlinear stochastic resonance. Phys. Rev. Lett. 2003, 91, 210601. [Google Scholar] [CrossRef] [PubMed]
- Atsumi, Y.; Hata, S.; Nakao, H. Phase ordering in coupled noisy bistable systems on scale-free networks. Phys. Rev. E 2013, 88, 052806. [Google Scholar] [CrossRef] [PubMed]
- Gao, T.; Ai, B.; Zheng, Z.; Chen, J. The enhancement of current and efficiency in feedback coupled Brownian ratchets. J. Stat. Mech. 2016, 2016, 093204. [Google Scholar] [CrossRef]
- Berdichevsky, V.; Gitterman, M. Stochastic resonance in linear systems subject to multiplicative and additive noise. Phys. Rev. E 1999, 60, 1494. [Google Scholar] [CrossRef] [PubMed]
- Gitterman, M. Classical harmonic oscillator with multiplicative noise. Physica A 2005, 352, 309–334. [Google Scholar] [CrossRef]
- Li, J.; Han, Y. Phenomenon of stochastic resonance caused by multiplicative asymmetric dichotomous noise. Phys. Rev. E 2006, 74, 051115. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhong, S.C.; Peng, H.; Luo, M.K. Stochastic multi-resonance in a linear system driven by multiplicative polynomial dichotomous noise. Chin. Phys. Lett. 2011, 28, 090505. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, L. Noise effect on the signal transmission in an underdamped fractional coupled system. Nonlinear Dyn. 2020, 102, 2077–2102. [Google Scholar] [CrossRef]
- Vishwamittar; Batra, P.; Chopra, R. Stochastic resonance in two coupled fractional oscillators with potential and coupling parameters subjected to quadratic asymmetric dichotomous noise. Physica A 2021, 561, 125148. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, L.; Ji, Y.; Lai, L. Stochastic resonance of two coupled fractional harmonic oscillators with fluctuating mass. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 26–38. [Google Scholar] [CrossRef]
- Lin, L.; He, M.; Wang, H. Collective resonant behaviors in two coupled fluctuating-mass oscillators with tempered Mittag-Leffler memory kernel. Chaos Solitons Fractals 2022, 154, 111641. [Google Scholar] [CrossRef]
- Liu, H.; Hu, G.; Zhang, Y.; Xiao, J. Frequency-dependent stochastic resonance in globally coupled systems. Commun. Theor. Phys. 2000, 33, 197–204. [Google Scholar]
- Zhong, S.; Lv, W.; Ma, H.; Zhang, L. Collective stochastic resonance behavior in the globally coupled fractional oscillator. Nonlinear Dyn. 2018, 94, 905–923. [Google Scholar] [CrossRef]
- Gómez-Ordóñez, J.; Casado, J.M.; Morillo, M. Arrays of noisy bistable elements with nearest neighbor coupling: Equilibrium and stochastic resonance. Eur. Phys. J. B 2011, 82, 179–187. [Google Scholar]
- Nicolis, C.; Nocolis, G. Coupling-enhanced stochastic resonance. Phys. Rev. E 2017, 96, 042214. [Google Scholar] [CrossRef]
- Beuter, A.; Bélair, J.; Labrie, C. Feedback and delays in neurological diseases: A modeling study using dynamical systems. Bull. Math. Biol. 1993, 55, 525–541. [Google Scholar] [CrossRef]
- Guillouzic, S.; L’Heureux, I.; Longtin, A. Small delay approximation of stochastic delay differential equations. Phys. Rev. E 1999, 59, 3970–3982. [Google Scholar] [CrossRef]
- Guillouzic, S.; L’Heureux, I.; Longtin, A. Rate processes in a delayed, stochastically driven, and overdamped system. Phys. Rev. E 2000, 61, 4906–4914. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, L.; Wang, H.; Ma, H.; Luo, M. Nonlinear effect of time delay on the generalized stochastic resonance in a fractional oscillator with multiplicative polynomial noise. Nonlinear Dyn. 2017, 89, 1327–1340. [Google Scholar] [CrossRef]
- Li, Z.; Han, S.; Wang, J.; Ren, X.; Zhang, C. Time-delayed feedback tristable stochastic resonance weak fault diagnosis method and its application. Shock Vib. 2019, 2019, 2097164. [Google Scholar] [CrossRef]
- Jin, Y.; Hu, H. Coherence and stochastic resonance in a delayed bistable system. Physica A 2007, 382, 423–429. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Narahari Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Physica A 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Ryabov Ya, E.; Puzenko, A. Damped oscillations in view of the fractional oscillator equation. Phys. Rev. E 2002, 66, 184201. [Google Scholar] [CrossRef]
- Kojabad, E.A.; Rezapour, S. Approximate solutions of a sum-type fractional integro-differential equation by using Chebyshev and Legendre polynomials. Adv. Differ. Equ. 2017, 2017, 351. [Google Scholar]
- Jafari, H.; Tuan, N.A.; Ganji, R.M. A new numerical scheme for solving pantograph type nonlinear fractional integro-differential equations. J. King Saud Univ. Sci. 2021, 33, 101185. [Google Scholar] [CrossRef]
- Mennouni, A.; Bougoffa, L.; Wazwaz, A.M. A new recursive scheme for solving a fractional differential equation of ray tracing through the crystalline lens. Opt. Quantum Electron. 2022, 54, 373. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, T.; He, G.T.; Zhong, L.F.; Stanley, H.E. The resonance behavior in the fractional harmonic oscillator with time delay and fluctuating mass. Physica A 2020, 545, 123731. [Google Scholar] [CrossRef]
- You, P.; Lin, L.; Wang, H. Cooperative mechanism of generalized stochastic resonance in a time-delayed fractional oscillator with random fluctuations on both mass and damping. Chaos Solitons Fractals 2020, 135, 109789. [Google Scholar] [CrossRef]
- Tian, Y.; He, G.; Liu, Z.; Zhong, L.; Yang, X.; Stanley, H.E.; Tu, Z. The impact of memory effect on resonance behavior in a fractional oscillator with small time delay. Physica A 2021, 563, 125383. [Google Scholar] [CrossRef]
- Lin, L.; Lin, T.; Zhang, R.; Wang, H. Generalized stochastic resonance in a time-delay fractional oscillator with damping fluctuation and signal-modulated noise. Chaos Solitons Fractals 2023, 170, 113406. [Google Scholar] [CrossRef]
- He, M.Y.; Wang, H.Q.; Lin, L.F.; Zhong, S.C. Stochastic resonance of a time-delayed fractional oscillator with fluctuating frequency and signal-modulated noise. J. Sichuan Univ. (Nat. Sci. Ed.) 2024, 61, 011005. [Google Scholar]
- Kim, S.; Park, S.H.; Pyo, H.B. Stochastic resonance in coupled oscillator systems with time delay. Phys. Rev. Lett. 1999, 82, 1620–1623. [Google Scholar] [CrossRef]
- Banerjee, T.; Biswas, D. Synchronization in hyperchaotic time-delayed electronic oscillators coupled indirectly via a common environment. Nonlinear Dyn. 2013, 73, 2025–2048. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Zhang, T. Stochastic resonance of coupled time-delayed system with fluctuation of mass and frequency and its application in bearing fault diagnosis. J. Cent. South Univ. 2021, 28, 2931–2946. [Google Scholar] [CrossRef]
- Yu, H.; Guo, X.; Wang, J.; Li, K.; Deng, B.; Wei, X.; Liu, C. Multiple stochastic resonances and oscillation transitions in cortical networks with time delay. IEEE Trans. Fuzzy Syst. 2020, 28, 39–46. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Shapiro, V.E.; Loginov, V.M. “Formulae of differentiation” and their use for solving stochastic equations. Physica A 1978, 91, 563–574. [Google Scholar] [CrossRef]
- Li, J.L.; Xu, B.H. Parameter-induced stochastic resonance with a periodic signal. Chin. Phys. B 2006, 15, 2867–2871. [Google Scholar]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]



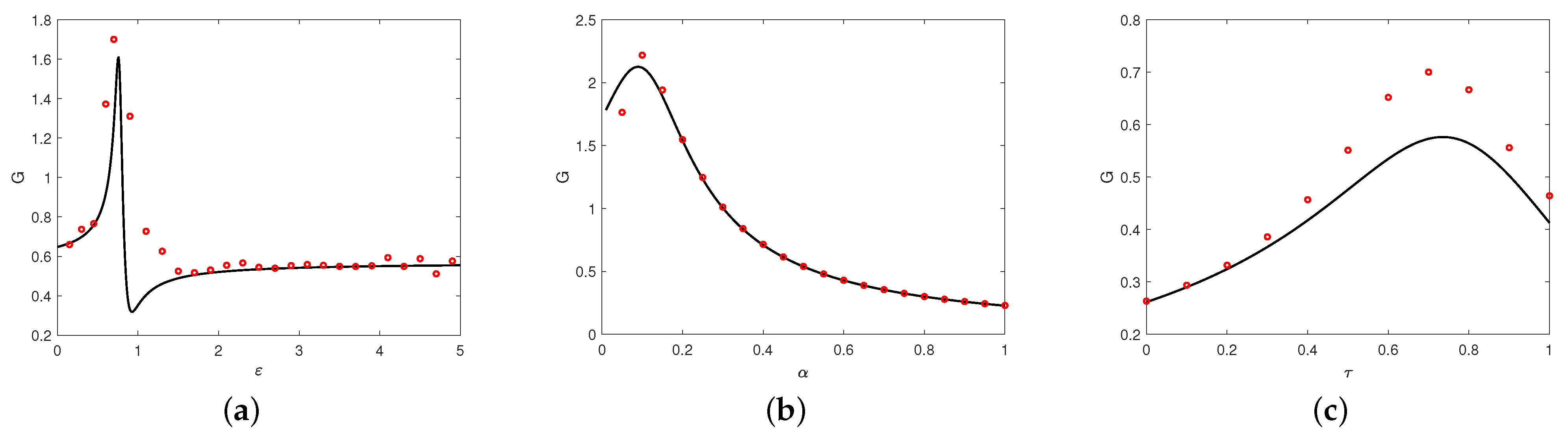
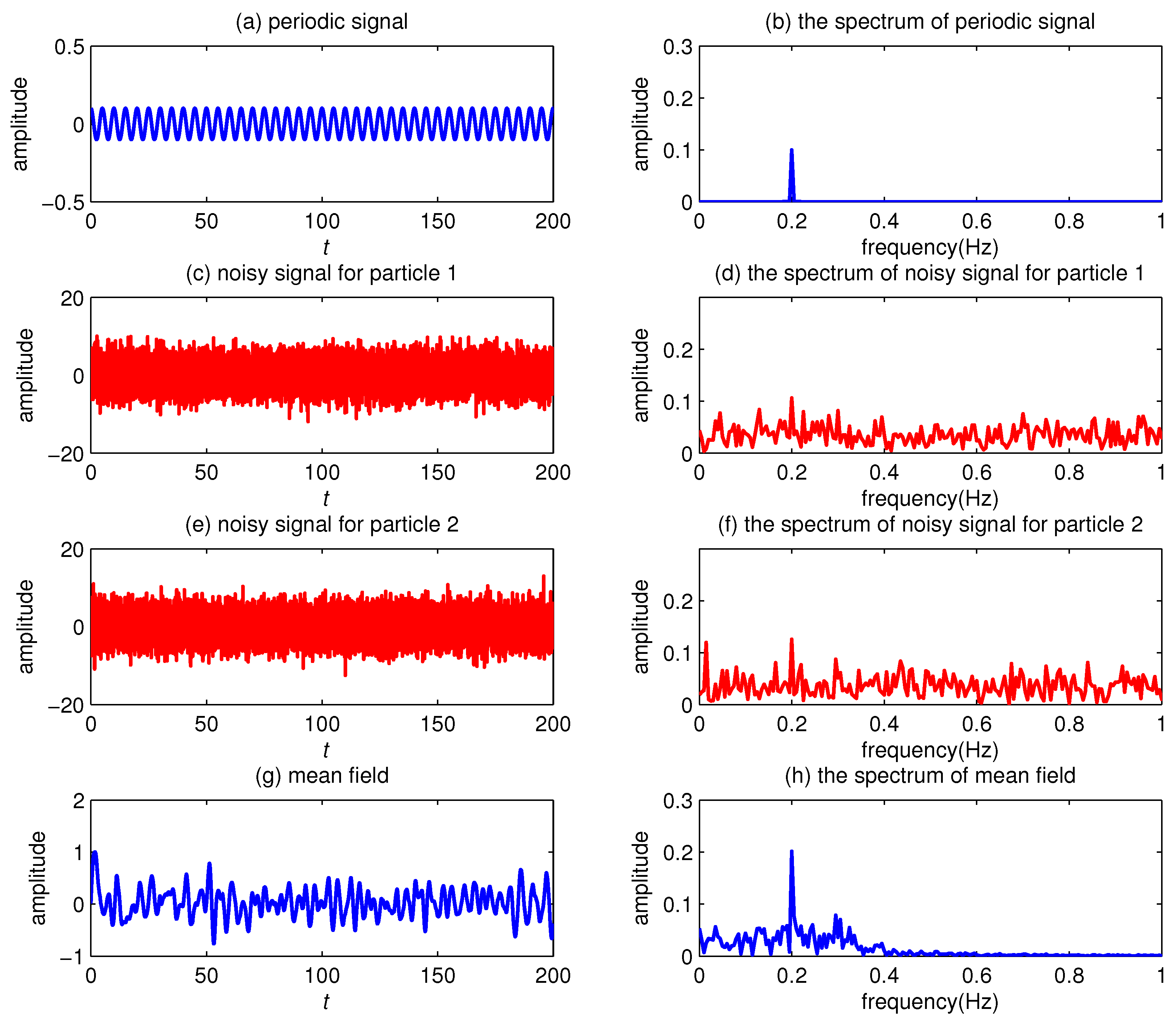
| m | 0.5 | 0.7 | 0.9 | 1.0 | 1.1 | 1.3 | 1.5 |
|---|---|---|---|---|---|---|---|
| 0.0062 | 0.0030 | 0.0006 | 0.0017 | 0.0025 | 0.0000 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, M.; Wang, H.; Lin, L. Time-Delay Effects on the Collective Resonant Behavior in Two Coupled Fractional Oscillators with Frequency Fluctuations. Fractal Fract. 2024, 8, 287. https://doi.org/10.3390/fractalfract8050287
He M, Wang H, Lin L. Time-Delay Effects on the Collective Resonant Behavior in Two Coupled Fractional Oscillators with Frequency Fluctuations. Fractal and Fractional. 2024; 8(5):287. https://doi.org/10.3390/fractalfract8050287
Chicago/Turabian StyleHe, Minyue, Huiqi Wang, and Lifeng Lin. 2024. "Time-Delay Effects on the Collective Resonant Behavior in Two Coupled Fractional Oscillators with Frequency Fluctuations" Fractal and Fractional 8, no. 5: 287. https://doi.org/10.3390/fractalfract8050287
APA StyleHe, M., Wang, H., & Lin, L. (2024). Time-Delay Effects on the Collective Resonant Behavior in Two Coupled Fractional Oscillators with Frequency Fluctuations. Fractal and Fractional, 8(5), 287. https://doi.org/10.3390/fractalfract8050287






