Fractal Features of Muscle to Quantify Fatty Infiltration in Aging and Pathology
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Dataset
2.1.1. Subjects
2.1.2. MRI Image Acquisition
2.2. Image Processing and Analysis
2.2.1. Analysis of MR Images
- -
- ρ: the ratio between lean (contractile) and fatty (non-contractile) portions of muscle tissue belonging to the lean muscle area (LeanCSA);
- -
- β: the lacunarity of lean muscle area, where fatty infiltration is assumed as lacunae;
- -
- µ: the succolarity of LeanCSA, where fatty infiltration is assumed as the empty space within the muscle tissue which is percolated by a hypothetical fluid crossing the set in four directions (down to up ↑; left to right →; up to down ↓; right to left ←).
2.2.2. Computation of Index ρ (Lean/Fat Ratio)
| Algorithm 1: (local threshold). Given the sub-image R, the histogram H of gray levels in R, and a tolerance T, compute the threshold τ by the following steps |
|
| Algorithm 2: (image segmentation). Let d be the diagonal of the rectangles in the partition of the ROI, and cj be the center of the j-th rectangle. Given the sub-images Rj, j = 0, 1, …, J, and the corresponding thresholds τj, j = 0, 1, …, J; compute nF and nL as the total number of pixels in the fat mass and in the lean mass, respectively, by the following steps |
|
|
2.2.3. Computation of Index β (Lacunarity)
2.2.4. Computation of Index µ (Succolarity)
3. Results
3.1. Mass Composition of Paraspinal Muscles
3.2. Fractal Features of Paraspinal Muscle
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Evans, W.J. Skeletal muscle loss: Cachexia, sarcopenia, and inactivity. Am. J. Clin. Nutr. 2010, 91, 1123S–1127S. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.J.; Paolisso, G.; Abbatecola, A.M.; Corsonello, A.; Bustacchini, S.; Strollo, F.; Lattanzio, F. Frailty and muscle metabolism dysregulation in the elderly. Biogerontology 2010, 11, 527–536. [Google Scholar] [CrossRef] [PubMed]
- Russ, D.W.; Grandy, J.S.; Toma, K.; Ward, C.W. Ageing, but not yet senescent, rats exhibit reduced muscle quality and sarcoplasmic reticulum function. Acta Physiol. 2011, 201, 391–403. [Google Scholar] [CrossRef] [PubMed]
- Seene, T.; Kaasik, P.; Riso, E.M. Review on aging, unloading and reloading: Changes in skeletal muscle quantity and quality. Arch. Gerontol. Geriatr. 2012, 54, 374–380. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, B.R.; Abdulla, J.; Andersen, H.E.; Schwarz, P.; Suetta, C. Sarcopenia and osteoporosis in older people: A systematic review and meta-analysis. Eur. Geriatr. Med. 2018, 9, 419–434. [Google Scholar] [CrossRef] [PubMed]
- Hida, T.; Shimokata, H.; Sakai, Y.; Ito, S.; Matsui, Y.; Takemura, M. Sarcopenia and sarcopenic leg as potential risk factors for acute osteoporotic vertebral fracture among older women. Eur. Spine J. 2016, 25, 3424–3431. [Google Scholar] [CrossRef]
- Iida, H.; Sakai, Y.; Watanabe, T.; Matsui, H.; Takemura, M.; Matsui, Y. Sarcopenia affects conservative treatment of osteoporotic vertebral fracture. Osteoporos Sarcopenia 2018, 4, 114–117. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, I.H. Summary comments: Epidemiological and methodological problems in determining nutritional status of older persons. Am. J. Clin. Nutr. 1989, 50, 1231–1233. [Google Scholar] [CrossRef]
- Rosenberg, I.H. Sarcopenia: Origins and clinical relevance. J. Nutr. 1997, 127, 990S–991S. [Google Scholar] [CrossRef]
- Delmonico, M.J.; Harris, T.B.; Lee, J.S.; Visser, M.; Nevitt, M.; Kritchevsky, S.B.; Tylavsky, F.A.; Newman, A.B.; Health, Aging and Body Composition Study. Alternative definitions of sarcopenia, lower extremity performance, and functional impairment with aging in older men and women. J. Am. Geriatr. Soc. 2007, 55, 769–774. [Google Scholar] [CrossRef]
- Goodpaster, B.H.; Park, S.W.; Harris, T.B.; Kritchevsky, S.B.; Nevitt, M.; Schwartz, A.V.; Simonsick, E.M.; Tylavsky, F.A.; Visser, M.; Newman, A.B. The loss of skeletal muscle strength, mass, and quality in older adults: The health, aging and body composition study. J. Gerontol. A Biol. Sci. Med. Sci. 2006, 61, 1059–1064. [Google Scholar] [CrossRef] [PubMed]
- Hiona, A.; Leeuwenburgh, C. The role of mitochondrial DNA mutations in aging and sarcopenia: Implications for the mitochondrial vicious cycle theory of aging. Exp. Gerontol. 2008, 43, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Marzetti, E.; Leeuwenburgh, C. Skeletal muscle apoptosis, sarcopenia and frailty at old age. Exp. Gerontol. 2006, 41, 1234–1238. [Google Scholar] [CrossRef] [PubMed]
- Fearon, K.; Evans, W.J.; Anker, S.D. Myopenia—A new universal term for muscle wasting. J. Cachexia Sarcopenia Muscle 2011, 2, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Clark, B.C.; Manini, T.M. Functional consequences of sarcopenia and dynapenia in the elderly. Curr. Opin. Clin. Nutr. Metab. Care 2010, 13, 271–276. [Google Scholar] [CrossRef] [PubMed]
- Gonzales, E.; Messi, M.L.; Delbono, O. The specific force of single intact extensor digitorum longus and soleus mouse muscle fibers declines with aging. J. Membr. Biol. 2000, 178, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Stackhouse, S.K.; Stevens, J.E.; Lee, S.C.; Pearce, K.M.; Snyder-Mackler, L.; Binder-Macleod, S.A. Maximum voluntary activation in nonfatigued and fatigued muscle of young and elderly individuals. Phys. Ther. 2001, 81, 1102–1109. [Google Scholar] [CrossRef]
- Weisleder, N.; Brotto, M.; Komazaki, S.; Pan, Z.; Zhao, X.; Nosek, T.; Parness, J.; Takeshima, H.; Ma, J. Muscle aging is associated with compromised Ca2+ spark signaling and segregated intracellular Ca2+ release. J. Cell. Biol. 2006, 174, 639–645. [Google Scholar] [CrossRef] [PubMed]
- Delmonico, M.J.; Harris, T.B.; Visser, M.; Park, S.W.; Conroy, M.B.; Velasquez-Mieyer, P.; Boudreau, R.; Manini, T.M.; Nevitt, M.; Newman, A.B.; et al. Longitudinal study of muscle strength, quality, and adipose tissue infiltration. Am. J. Clin. Nutr. 2009, 90, 1579–1585. [Google Scholar] [CrossRef]
- Heymsfield, S.B.; Adamek, M.; Gonzalez, M.C.; Gia, G.; Thomas, D.M. Assessing skeletal muscle mass: Historical overview and state of the art. J. Cachexia Sarcopenia Muscle 2014, 5, 9–18. [Google Scholar] [CrossRef]
- Cruz-Jentoft, A.J.; Baeyens, J.P.; Bauer, J.M.; Boirie, Y.; Cederholm, T.; Landi, F.; Martin, F.C.; Michel, J.P.; Rolland, Y.; Schneider, S.M.; et al. Sarcopenia: European consensus on definition and diagnosis: Report of the European Working Group on Sarcopenia in Older People. Age Ageing 2010, 39, 412–423. [Google Scholar] [CrossRef]
- Cruz-Jentoft, A.J.; Bahat, G.; Bauer, J.; Boirie, Y.; Bruyère, O.; Cederholm, T.; Cooper, C.; Landi, F.; Rolland, Y.; Sayer, A.A.; et al. Sarcopenia: Revised European consensus on definition and diagnosis. Age Ageing 2019, 48, 16–31. [Google Scholar] [CrossRef] [PubMed]
- Chianca, V.; Albano, D.; Messina, C.; Gitto, S.; Rufo, G.; Guarino, S.; Del Grande, F.; Sconfenza, L.M. Sarcopenia: Imaging assessment and clinical application. Abdom. Radiol. 2022, 47, 3205–3216. [Google Scholar] [CrossRef] [PubMed]
- Heskamp, L.; Okkersen, K.; van Nimwegen, M.; Ploegmakers, M.J.; Bassez, G.; Deux, J.-F.; van Engelen, B.G.; Heerschap, A.; For the OPTIMISTIC Consortium. Quantitative Muscle MRI Depicts Increased Muscle Mass after a Behavioral Change in Myotonic Dystrophy Type 1. Radiology 2020, 297, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Goutallier, D.; Postel, J.M.; Bernageau, J.; Lavau, L.; Voisin, M.C. Fatty muscle degeneration in cuff ruptures. Pre- and postoperative evaluation by CT scan. Clin. Orthop. Relat. Res. 1994, 304, 78–83. [Google Scholar] [CrossRef]
- Fortin, M.; Lazáry, À.; Varga, P.P.; Battié, M.C. Association between paraspinal muscle morphology, clinical symptoms and functional status in patients with lumbar spinal stenosis. Eur. Spine J. 2017, 26, 2543–2551. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, P.J.; Maeda, Y.; Welk, A.; Hough, B.; Kettner, N. Reliability of the Goutallier classification in quantifying muscle fatty degeneration in the lumbar multifidus using magnetic resonance imaging. J. Manip. Physiol. Ther. 2014, 37, 190–197. [Google Scholar] [CrossRef] [PubMed]
- Tamai, K.; Chen, J.; Stone, M.; Arakelyan, A.; Paholpak, P.; Nakamura, H.; Buser, Z.; Wang, J.C. The evaluation of lumbar paraspinal muscle quantity and quality using the Goutallier classification and lumbar indentation value. Eur. Spine J. 2018, 27, 1005–1012. [Google Scholar] [CrossRef] [PubMed]
- Fortin, M.; Battie, M.C. Quantitative paraspinal muscle measurements: Intersoftware reliability and agreement using OsiriX and ImageJ. Phys. Ther. 2012, 92, 853–864. [Google Scholar] [CrossRef]
- Armi, L.; Fekri-Ershad, S. Texture image analysis and texture classification methods—A review. arXiv 2019. [Google Scholar] [CrossRef]
- Zucker, S.W.; Terzopoulos, D. Finding structure in Co-occurrence matrices for texture analysis. Comput. Graph. Image Process. 1980, 12, 286–308. [Google Scholar] [CrossRef]
- Addison, O.; Marcus, R.L.; LaStayo, P.C.; Ryan, A.S. Intermuscular Fat: A Review of the Consequences and Causes. Int. J. Endocrinol. 2014, 2014, 309570. [Google Scholar] [CrossRef] [PubMed]
- Zaia, A.; Eleonori, R.; Maponi, P.; Rossi, R.; Murri, R. Medical imaging and osteoporosis: Fractal’s lacunarity analysis of trabecular bone in MR images. In Proceedings of the Eighteenth IEEE Symposium on Computer-Based Medical Systems (CBMS 2005), Dublin, Ireland, 23–24 June 2005; IEEE: New York, NY, USA, 2005; pp. 3–8. [Google Scholar] [CrossRef]
- Zaia, A.; Eleonori, R.; Maponi, P.; Rossi, R.; Murri, R. MR imaging and osteoporosis: Fractal lacunarity analysis of trabecular bone. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Zaia, A.; Rossi, R.; Egidi, N.; Maponi, P. Fractal’s lacunarity analysis of trabecular bone in MR images. In Computational Vision and Medical Image Processing; Tavares, J., Jorge, N., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 421–426. [Google Scholar]
- Zaia, A. Fractal lacunarity of trabecular bone and magnetic resonance imaging: New perspectives for osteoporotic fracture risk assessment. World. J. Orthop. 2015, 6, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. A Fractal’s Lacunarity, and how it can be Tuned and Measured. In Nonnenmacher TF, Losa GA, Weibel ER, editors. In Fractals in Biology and Medicine; Birkhauser Press: Basel, Switzerland, 1993; pp. 8–21. [Google Scholar]
- Plotnick, R.E.; Gardner, R.H.; Hargrove, W.W.; Prestegaard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis of spatial patterns. Phys. Rev. E 1996, 53, 5461–5468. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature. In Trees and the Diameter Exponent; WH Freeman: New York, NY, USA, 1977; pp. 156–165. [Google Scholar]
- Metze, K.; Adam, R.; Florindo, J.B. The fractal dimension of chromatin—A potential molecular marker for carcinogenesis, tumor progression and prognosis. Expert Rev. Mol. Diagn. 2019, 19, 299–312. [Google Scholar] [CrossRef] [PubMed]
- de Melo, R.H.C.; Conci, A. How Succolarity could be used as another fractal measure in image analysis. Telecommun. Syst. 2013, 52, 1643–1655. [Google Scholar] [CrossRef]
- de Melo, R.H.C.; Conci, A. Succolarity: Defining a method to calculate this fractal measure. In Proceedings of the 15th International Conference on Systems, Signals and Image Processing, Bratislava, Slovakia, 25–28 June 2008; pp. 291–294. [Google Scholar] [CrossRef]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552–3558. [Google Scholar] [CrossRef] [PubMed]
- Shur, N.F.; Creedon, L.; Skirrow, S.; Atherton, P.J.; MacDonald, I.A.; Lund, J.; Greenhaff, P.L. Age-related changes in muscle architecture and metabolism in humans: The likely contribution of physical inactivity to age-related functional decline. Ageing Res. Rev. 2021, 68, 101344. [Google Scholar] [CrossRef]
- Volpi, E.; Nazemi, R.; Fujita, S. Muscle tissue changes with aging. Curr. Opin. Clin. Nutr. Metab. Care 2004, 7, 405–410. [Google Scholar] [CrossRef]
- Pang, J.; Tu, F.; Han, Y.; Zhang, E.; Zhang, Y.; Zhang, T. Age-related change in muscle strength, muscle mass, and fat mass between the dominant and non-dominant upper limbs. Front. Public.Health 2023, 11, 1284959. [Google Scholar] [CrossRef] [PubMed]
- Rahemi, H.; Nigam, N.; Wakeling, J.M. The effect of intramuscular fat on skeletal muscle mechanics: Implications for the elderly and obese. J. R. Soc. Interface 2015, 12, 20150365. [Google Scholar] [CrossRef]
- Emanuelsson, E.B.; Berry, D.B.; Reitzner, S.M.; Arif, M.; Mardinoglu, A.; Gustafsson, T.; Ward, S.R.; Sundberg, C.J.; Chapman, M.A. MRI characterization of skeletal muscle size and fatty infiltration in long-term trained and untrained individuals. Physiol. Rep. 2022, 10, e15398. [Google Scholar] [CrossRef] [PubMed]
- Budui, S.L.; Rossi, A.P.; Zamboni, M. The pathogenetic bases of sarcopenia. Clin. Cases Miner. Bone Metab. 2015, 12, 22–26. [Google Scholar] [CrossRef] [PubMed]
- Scicchitano, B.M.; Pelosi, L.; Sica, G.; Musarò, A. The physiopathologic role of oxidative stress in skeletal muscle. Mech. Aging Dev. 2017, 170, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.E. Recent results: Biomarkers of aging. Exp. Gerontol. 2006, 41, 1243–1246. [Google Scholar] [CrossRef] [PubMed]
- Wagner, K.-H.; Cameron-Smith, D.; Wessner, B.; Franzke, B. Biomarkers of Aging: From Function to Molecular Biology. Nutrients 2016, 8, 338. [Google Scholar] [CrossRef] [PubMed]
- Burkle, A.; Moreno-Villanueva, M.; Bernhard, J.; Blasco, M.; Zondag, G.; Hoeijmakers, J.H.; Toussaint, O.; Grubeck-Loebenstein, B.; Mocchegiani, E.; Collino, S.; et al. Mark-age biomarkers of ageing. Mech. Ageing Dev. 2015, 151, 2–12. [Google Scholar] [CrossRef] [PubMed]
- Piantanelli, L.; Rossolini, G.; Basso, A.; Piantanelli, A.; Malavolta, M.; Zaia, A. Use of mathematical models of survivorship in the study of biomarkers of aging: The role of heterogeneity. Mech. Ageing Dev. 2001, 122, 1461–1475. [Google Scholar] [CrossRef]
- Zaia, A. Osteoporosis and fracture risk: New perspectives for early diagnosis and treatment assessment. In Osteoporosis: Etiology, Diagnosis and Treatment; Mattingly, B.E., Pillare, A.C., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 267–290. [Google Scholar]
- Pettersson, M. Complexity and Evolution; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Zaia, A.; Maponi, P. Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging. Fractal Fract. 2022, 6, 219. [Google Scholar] [CrossRef]
- Lipsitz, L.A.; Goldberger, A.L. Loss of ‘complexity’ and aging: Potential applications of fractals and chaos theory to senescence. JAMA 1992, 267, 1806–1809. [Google Scholar] [CrossRef]
- Grassberger, A.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Rigney, D.R.; West, B.J. Chaos and fractals in human physiology. Sci. Am. 1990, 262, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L. Non-linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Franceschi, C.; Garagnani, P.; Morsiani, C.; Conte, M.; Santoro, A.; Grignolio, A.; Monti, D.; Capri, M.; Salvioli, S. The Continuum of Aging and Age-Related Diseases: Common Mechanisms but Different Rates. Front. Med. 2018, 5, 61. [Google Scholar] [CrossRef] [PubMed]
- Mandelli, F.; Nüesch, C.; Zhang, Y.; Halbeisen, F.; Schären, S.; Mündermann, A.; Netzer, C. Assessing Fatty Infiltration of Paraspinal Muscles in Patients with Lumbar Spinal Stenosis: Goutallier Classification and Quantitative MRI Measurements. Front. Neurol. 2021, 12, 656487. [Google Scholar] [CrossRef] [PubMed]
- Coelho, A.L.V.; Lima, C.A.M. Assessing fractal dimension methods as feature extractors for EMG signal classification. Eng. Appl. Artif. Intell. 2014, 36, 81–98. [Google Scholar] [CrossRef]
- Zaia, A.; Rossi, R.; Galeazzi, R.; Sallei, M.; Maponi, P.; Scendoni, P. Fractal lacunarity of trabecular bone in vertebral MRI to predict osteoporotic fracture risk in over-fifties women. The LOTO study. BMC Musculoskelet. Disord. 2021, 22, 108. [Google Scholar] [CrossRef] [PubMed]
- Zaia, A.; Maponi, P.; Sallei, M.; Galeazzi, R.; Scendoni, P. Measuring Drug Therapy Effect on Osteoporotic Fracture Risk by Trabecular Bone Lacunarity: The LOTO Study. Biomedicines 2023, 11, 781. [Google Scholar] [CrossRef]
- Kjaer, P.; Bendix, T.; Sorensen, J.S.; Korsholm, L.; Leboeuf-Yde, C. Are MRI-defined fat infiltrations in the multifidus muscles associated with low back pain? BMC Med. 2007, 5, 2. [Google Scholar] [CrossRef]
- Lee, J.C.; Cha, J.G.; Kim, Y.; Kim, Y.I.; Shin, B.J. Quantitative analysis of back muscle degeneration in the patients with the degenerative lumbar flat back using a digital image analysis: Comparison with the normal controls. Spine 2008, 33, 318–325. [Google Scholar] [CrossRef] [PubMed]
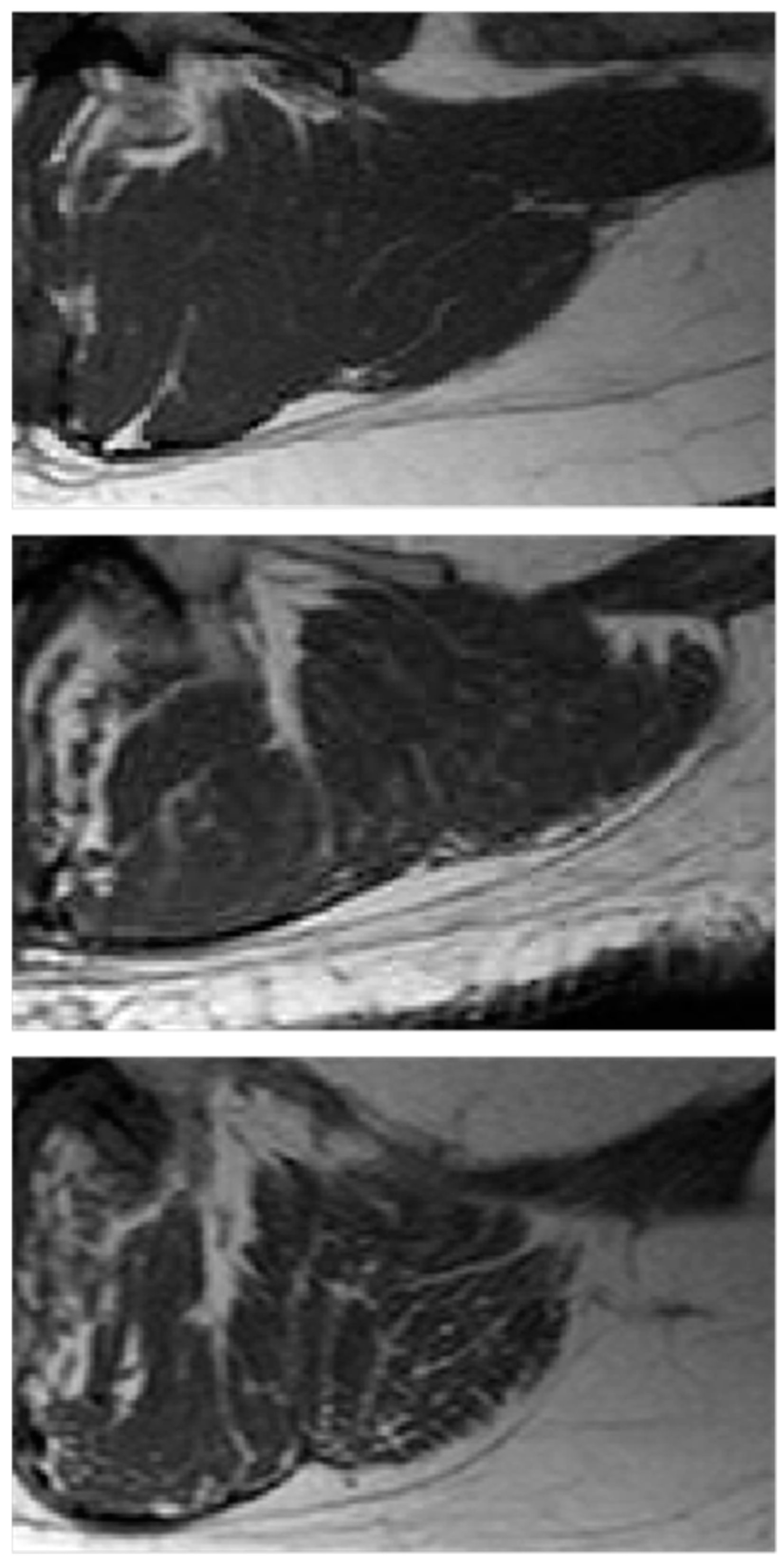
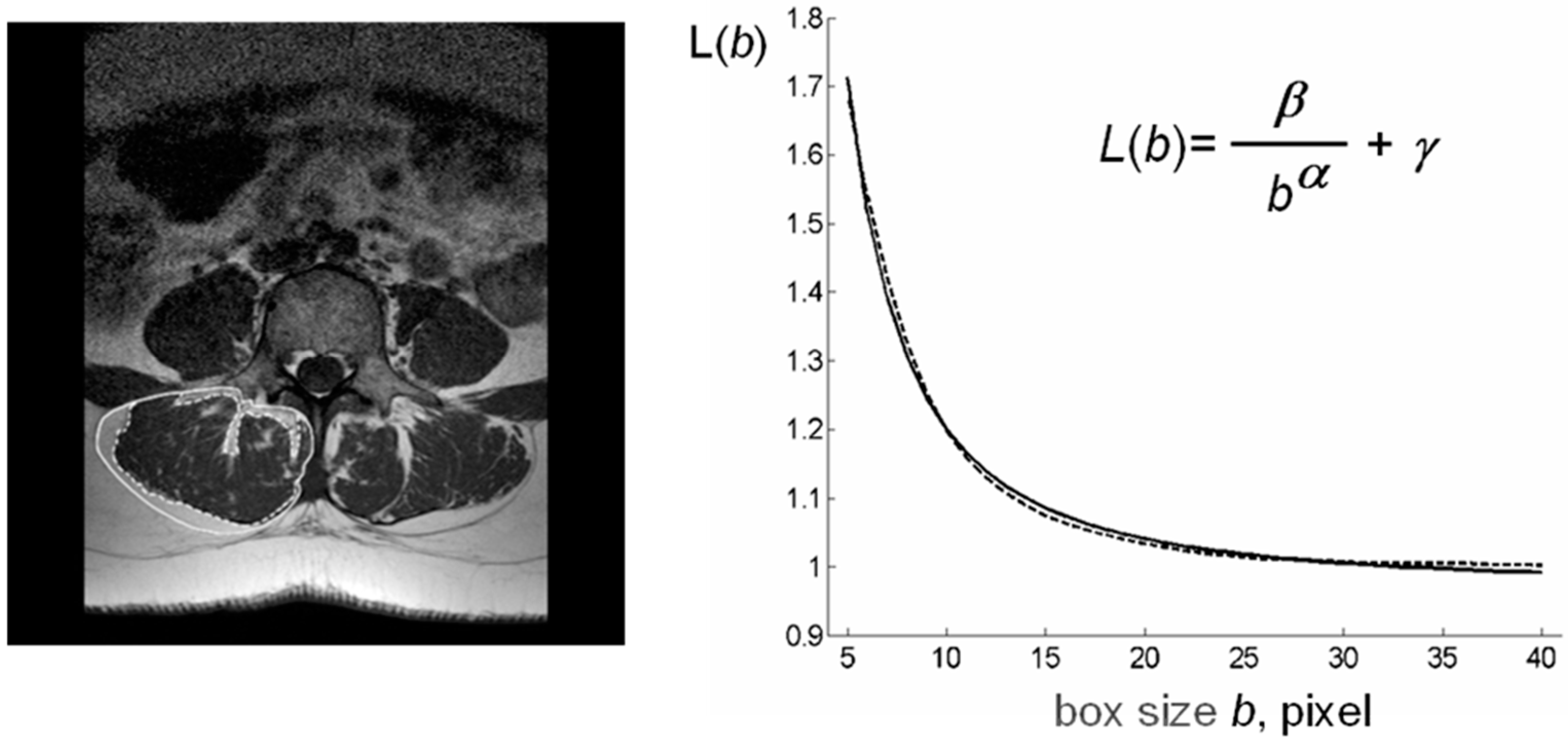
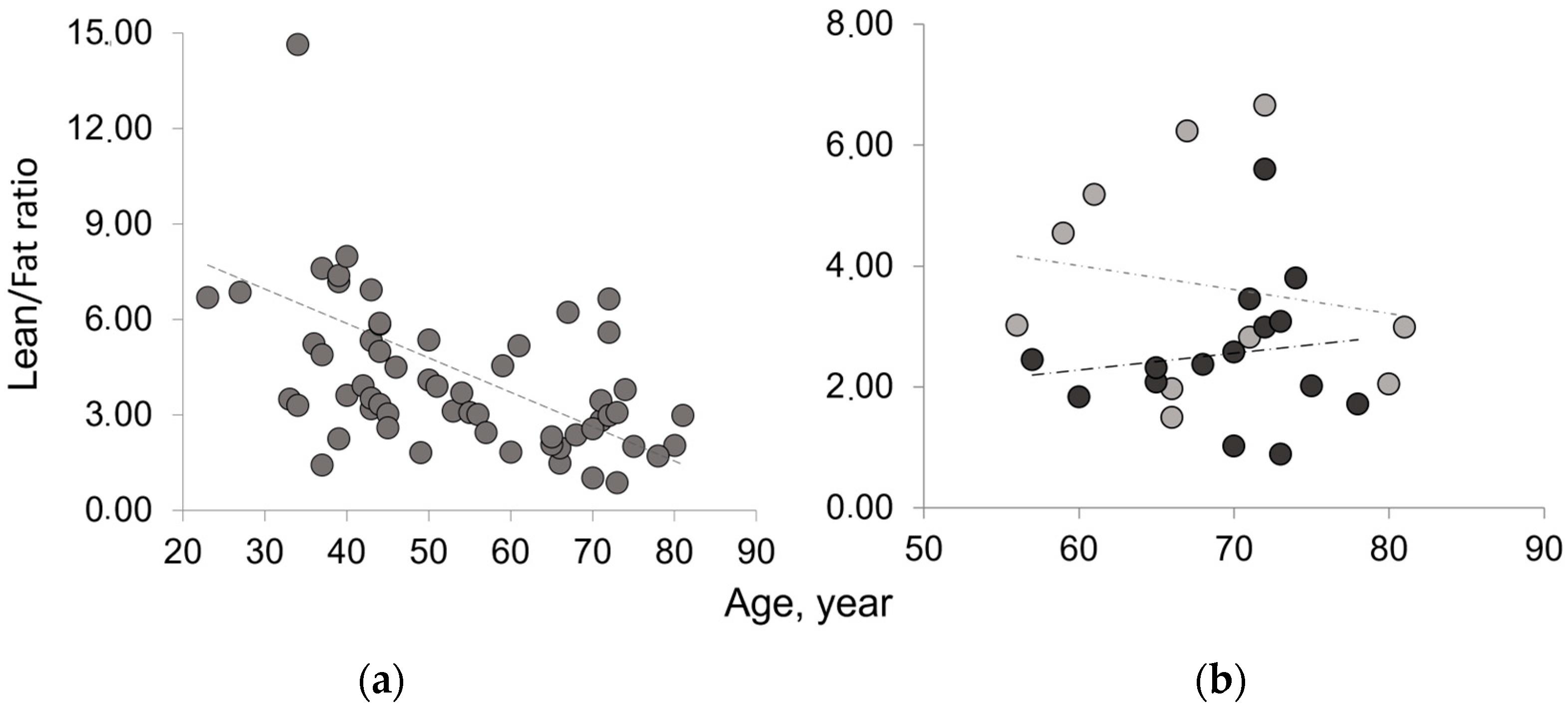
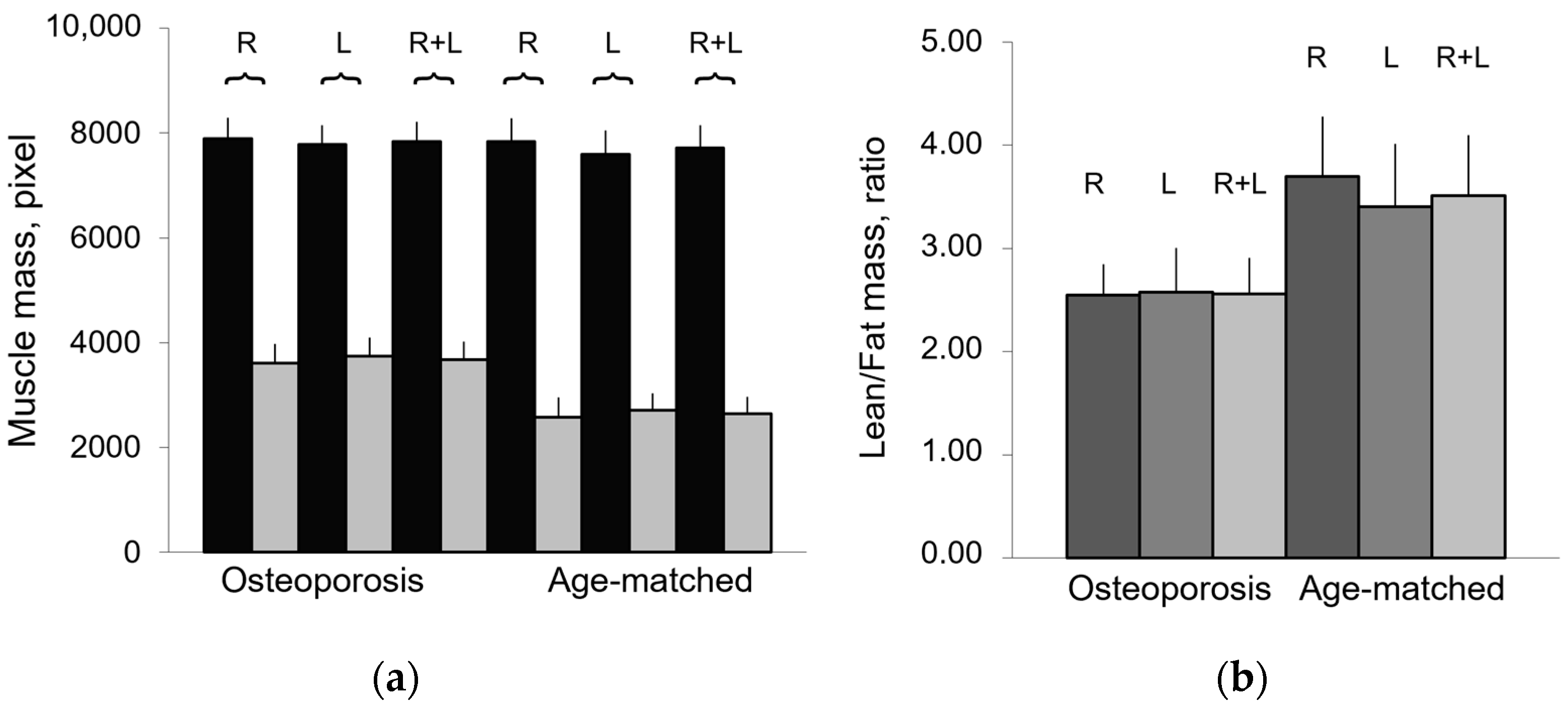
| Subjects | Number | Age Range | Mean Age 1 | Median Age |
|---|---|---|---|---|
| All | 59 | 23–81 | 53 ± 15 | 50 |
| Young | 15 | 23–40 | 35 ± 5 | 37 |
| Pre-menopause | 15 | 42–50 | 45 ± 3 | 44 |
| Menopause | 14 | 51–81 | 64 ± 10 | 64 |
| Osteoporosis 2 | 15 | 57–78 | 70 ± 6 | 71 |
| Age-matched 3 | 10 | 56–81 | 68 ± 8 | 67 |
| Subjects | TotCSA | LeanCSA * | FatCSA † | Lean/Fat Ratio |
|---|---|---|---|---|
| All | 11,114 ± 1858 | 8507 ± 2608 (77%) * | 1925 ± 1153 (23%) | 4.40 ± 3.53 |
| Young | 11,222 ± 1939 | 9364 ± 1929 (84%) | 1858 ± 1015 (16%) | 7.17 ± 5.73 |
| Pre-menopause | 10,652 ± 1686 | 8481 ± 1105 (80%) | 2171 ± 838 (20%) | 4.34 ± 1.35 |
| Menopause | 11,062 ± 2043 | 8332 ± 1609 (75%) | 2730 ± 1226 (25%) | 3.50 ± 1.54 |
| Age-matched 1 | 10,356 ± 1215 | 7714 ± 1364 (75%) | 2642 ± 1018 (25%) | 3.51 ± 1.87 |
| Osteoporosis 2 | 11,517 ± 1865 | 7837 ± 1449 (68%) | 3680 ± 1315 (32%) | 2.52 ± 1.34 |
| Subjects | Young | Pre-Menopause | Menopause | Age-Matched | Osteoporosis | p Value 1 |
|---|---|---|---|---|---|---|
| Lean mass 2 | 8586 ± 1778 | 7889 ± 1002 | 7277 ± 1638 | 6581 ± 1024 | 6890 ± 1402 | 0.286 |
| Fatty mass 2 | 2234 ± 756 | 2444 ± 732 | 2894 ± 936 | 2813 ± 1041 | 3627 ± 1114 | 0.046 |
| Lean/Fat ratio ρ | 4.21 ± 1.33 | 3.57 ± 0.68 | 2.70 ± 0.76 | 2.61 ± 0.89 | 2.08 ± 0.67 | 0.057 |
| Lacunarity α | 0.900 ± 0.403 | 0.572 ± 0.350 | 0.639 ± 0.303 | 0.672 ± 0.316 | 0.639 ± 0.420 | 0.420 |
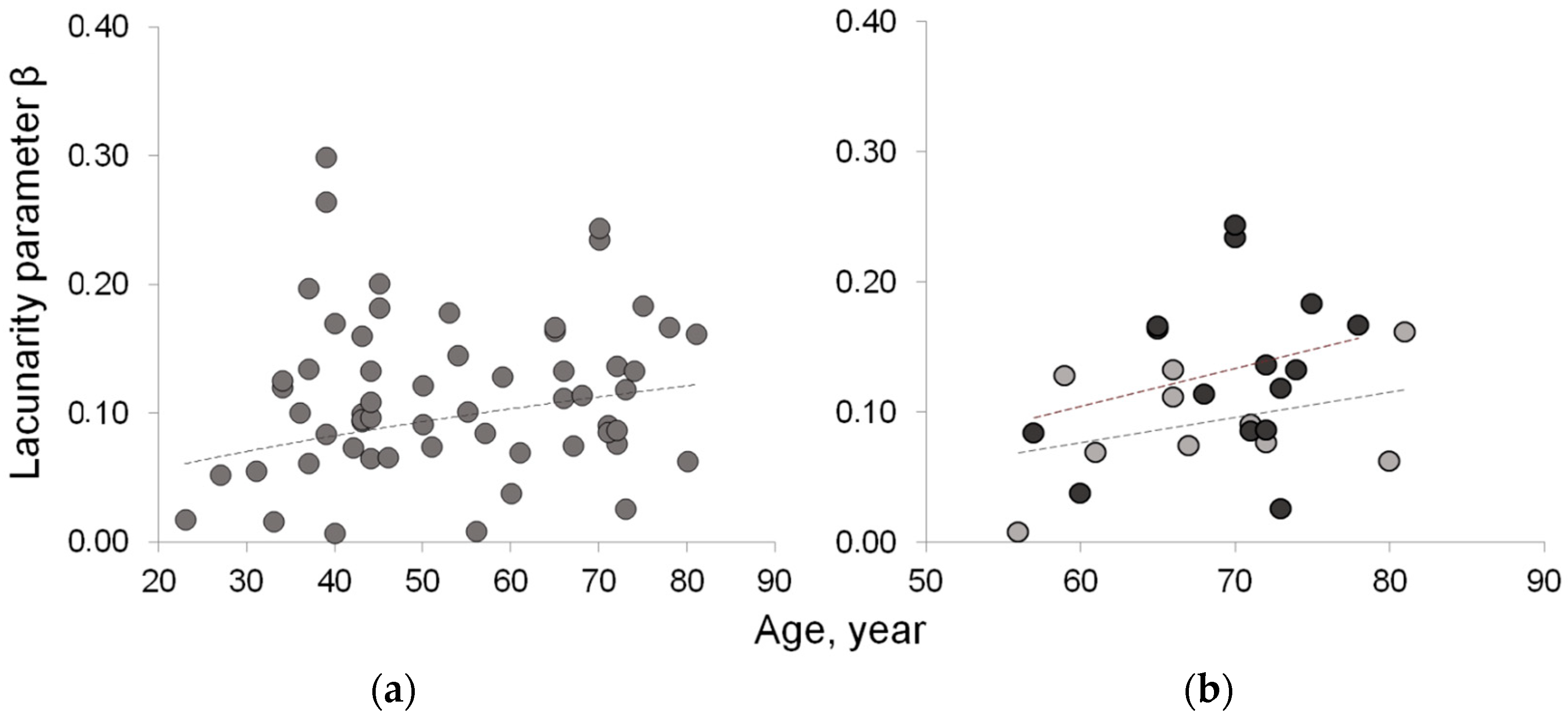
| Lacunarity β | 0.062 ± 0.039 | 0.113 ± 0.040 | 0.101 ± 0.044 | 0.092 ± 0.041 | 0.148 ± 0.062 | 0.012 |
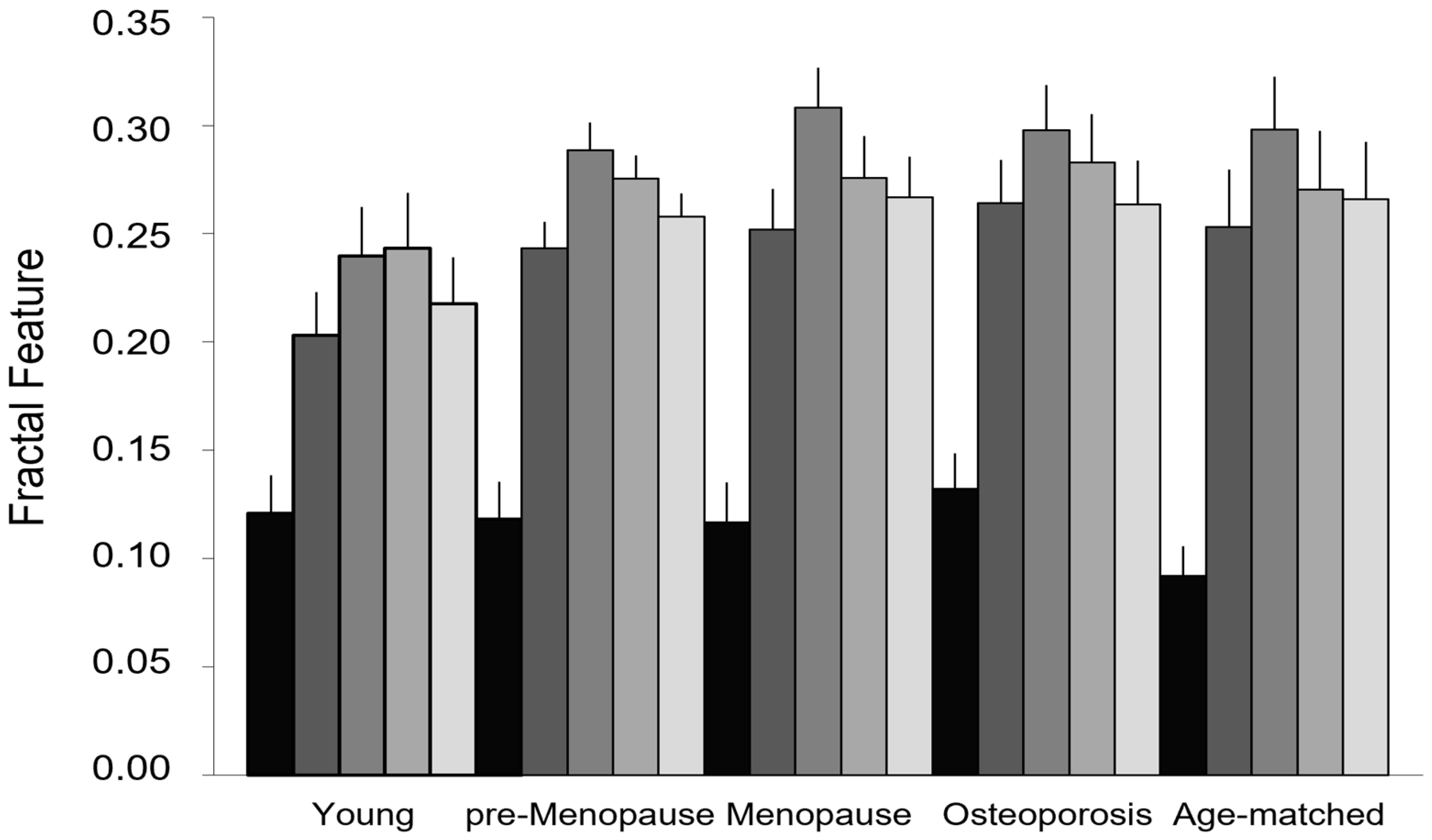
| Succolarity µ↑ | 0.203 ± 0.075 | 0.243 ± 0.047 | 0.252 ± 0.070 | 0.253 ± 0.084 | 0.264 ± 0.077 | 0.371 |
| Succolarity µ→ | 0.240 ± 0.085 | 0.288 ± 0.050 | 0.308 ± 0.070 | 0.298 ± 0.077 | 0.298 ± 0.080 | 0.499 |
| Succolarity µ↓ | 0.243 ± 0.096 | 0.275 ± 0.042 | 0.276 ± 0.072 | 0.270 ± 0.086 | 0.283 ± 0.086 | 0.361 |
| Succolarity µ← | 0.218 ± 0.080 | 0.258 ± 0.042 | 0.267 ± 0.071 | 0.266 ± 0.084 | 0.263 ± 0.079 | 0.470 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaia, A.; Zannotti, M.; Losa, L.; Maponi, P. Fractal Features of Muscle to Quantify Fatty Infiltration in Aging and Pathology. Fractal Fract. 2024, 8, 275. https://doi.org/10.3390/fractalfract8050275
Zaia A, Zannotti M, Losa L, Maponi P. Fractal Features of Muscle to Quantify Fatty Infiltration in Aging and Pathology. Fractal and Fractional. 2024; 8(5):275. https://doi.org/10.3390/fractalfract8050275
Chicago/Turabian StyleZaia, Annamaria, Martina Zannotti, Lucia Losa, and Pierluigi Maponi. 2024. "Fractal Features of Muscle to Quantify Fatty Infiltration in Aging and Pathology" Fractal and Fractional 8, no. 5: 275. https://doi.org/10.3390/fractalfract8050275
APA StyleZaia, A., Zannotti, M., Losa, L., & Maponi, P. (2024). Fractal Features of Muscle to Quantify Fatty Infiltration in Aging and Pathology. Fractal and Fractional, 8(5), 275. https://doi.org/10.3390/fractalfract8050275








