Dynamics and Complexity Analysis of Fractional-Order Inventory Management System Model

Abstract

To accurately depict inventory management over time, this paper introduces a fractional inventory management model that builds upon the existing classical inventory management framework. According to the definition of fractional difference equation, the numerical solution and phase diagram of an inventory management system are obtained by MATLAB simulation. The influence of parameters on the nonlinear behavior of the system is analyzed by a bifurcation diagram and largest Lyapunov exponent (LLE). Combined with the related indexes of time series, the complex characteristics of a quantization system are analyzed using spectral entropy and C0. This study concluded that the changing law of system complexity is consistent with the LLE of the system. By analyzing the influence of order on the system, it is found that the inventory changes will be periodic in some areas when the system is fractional, which is close to the actual conditions of the company’s inventory situation. The research results of this paper provide useful information for inventory managers to implement inventory and facility management strategies.

1. Introduction

In management operations, queuing, inventory, planning and scheduling systems produce chaos under different management decision rules. Inventory shows strong chaotic characteristics with time; that is, inventory is neither periodic nor random [1]. Chaotic behavior makes forecasting more difficult, leading to new tools development, to investigate whether the time series data are chaotic [2,3,4].

As an important part of the supply chain, inventory is directly related to the interests of enterprises. The ultimate goal of logistics is to minimize costs such as inventory expenses. Lei et al. [5] simplified a three-dimensional discrete system into a two-dimensional discrete system for the discrete inventory management model and analyzed the nonlinear characteristics of the inventory management model using fractional complexity. Many professional scholars have studied this model [6,7,8,9].

In 2001, Yao et al. [6] adopted the stability theory of differential equations and implemented feedback control with a variable parameter structure to manage multi-parameter inventory. They successfully controlled the chaotic model of inventory management. In 2003, Yao et al. [6] and Chen et al. [7] analyzed the chaotic and periodic characteristics of the inventory management system using a phase diagram. They improved the adaptive control method based on the Lyapunov approach and used it to effectively control the chaotic inventory management system. Hua et al. [8] conducted a study on a specific inventory management model and proved that the system produces Neimark–Sacker bifurcation and the asymptotic expression of the invariant ring at the fixed point, using discrete-time dynamic system theory. Concerning the inventory management model, Lei et al. [9] used LSTM, CNN–LSTM, DLSTM, and other deep learning algorithms to predict the time series data generated by the discrete inventory management model and found that LSTM was better for inventory prediction.

Inventory management could be considered as a three-dimensional discrete chaotic model [9]. Scholars have made fruitful achievements in discrete chaotic model [10,11,12]. Previous research [13,14,15,16] studied the classical tent discrete system from numerical analysis, system model change, and application. According to the characteristics of the parameter range of the tent map and the logistic map, Hua et al. proposed an interactive two-dimensional chaotic map [17]. Hua et al. used one chaotic map to control the parameters of another map dynamically, and they proposed a dynamic parameter modulation model. The new map generated by this model was more sensitive to the initial value, and it had a wider chaotic range [18]. After that, they built a variety of discrete chaotic systems [19,20,21], such as the sin discrete system [21]. At present, the application of image encryption and discrete memristor have become hot topics in the field of discrete nonlinear systems [22,23,24,25,26], and the research on these two topics is based on the analysis of dynamics and complexity.

Research on the inventory management dynamics system has utilized the aforementioned discrete system. This raises questions as to whether the inventory management system conforms to the characteristics of the integer-order discrete system and whether other factors influence the system. Since integer order is a special fractional order case, it is more accurate than integer order [27]. In other words, the fractional-order system model includes integer order [28,29], making the fractional-order warehouse management model a more comprehensive framework capable of capturing specific phenomena. Furthermore, the fractional order system has short-term memory [27,30,31]. The fractional-order inventory management model is related to the inventory resources in previous periods, which is more consistent with the characteristics of inventory management resources. The fractional model has been applied in many fields, such as a fractional-order COVID-19 model [32], fractional-order DC motor system [33], fractional-order laser system [34], infectious disease model, and many more.

In this study, we investigate the dynamics and complexity of a kind of fractional inventory management system. The  structure of the paper is as follows: Section 1 reviews the discrete models of economy and inventory management, and  it analyzes the recent development of discrete chaotic models; then, according to the classical inventory management model, Section 2 constructs the fractional-order discrete inventory management model, and numerical simulation illustrates the fractional-order discrete inventory management model’s phase diagram. Section 3 displays the dynamic characteristics of the system when the parameters $q_1$, q, and r change, using a bifurcation diagram and the Lyapunov exponent; Section 4 showcases the SE and C0 complexity algorithms results of system complexity when the parameters change; finally, Section 5 gives the relevant conclusions of this research work.

2. Fractional-Order Inventory Management System Model

2.1. Definition of Fractional-Order Discrete System

Definition 1 ([35]). 

  There is a relationship g: $N_a\to R$ and $v>0$. We define fractional sums as

$${\Delta }_a^{-v}g\left(t\right)=\frac{1}{\Gamma \left(v\right)}\sum _{s=g_0}^{t-v}{(t-\xi \left(s\right))}^{(v-1)}g\left(s\right)$$

(1)

$g_0$ is the initial time, and $\xi \left(s\right)=s+1, N_{g}0=\{g_0,g_0+1,g_0+2\cdots \}$. The descending factorial function is $t^{\left(v\right)}$, which is defined as follows:

$$t^{\left(v\right)}=\frac{\Gamma (t+1)}{\Gamma (t+1-v)}.$$

(2)

Definition 2. 

For $f\left(t\right)$ defined as $N_a$, when $v>0$ and $v\notin N$, the difference of its Caputo type is defined as

$$\begin{array}{cc}\hfill {}^C\Delta _a^{v}x\left(t\right)& ={\Delta }_a^{-(m-v)}{\Delta }^{m}x\left(t\right)\hfill \\ \hfill & =\frac{1}{\Gamma (m-v)}\sum _{s=a}^{t-(m-v)}{(t-\sigma \left(s\right))}^{(m-v-1)}{\Delta }_s^{m}x\left(s\right).\hfill \end{array}$$

(3)

Among these, $t\in N_{a+m-v}, m=\left[v\right]+1, and{\Delta }^m, where{\Delta }_a^m$ represents integer-order difference with starting times of 0 and a.

Theorem 1. 

The fractional-order difference formula is [36]

$${}^c\Delta _a^{v}x\left(t\right)=f(t+v-1,x(t+v-1)),$$

(4)

where ${\Delta }^{k}x\left(a\right)=c_k, k=0,1,\dots ,m-1$. Equation (4) continues to be equivalent to

$$x\left(t\right)=x_0\left(t\right)+\frac{1}{\Gamma \left(v\right)}\sum _{s=a+m-v}^{t-v}{(t-\sigma \left(s\right))}^{(v-1)}f(s+v-1,x(s+v-1)),$$

(5)

where $t\in {\mathbb{N}}_{a+m}$, and the initial value $x_0\left(t\right)$ is defined as

$$x_0\left(t\right)=\sum _{k=0}^{m-1}\frac{{(t-a)}^{\left(k\right)}}{k!}{\Delta }^{k}x\left(a\right).$$

(6)

2.2. Numerical Solution of Fractional-Order Inventory Management System

According to Definitions 1 and 2 and the nonlinear discrete inventory management dynamics model [2,6,7,8,9], the expression of the fractional inventory management system is as follows:

$$\begin{array}{cc}\hfill & {}^c\Delta _a^{q_1}x\left(t\right)=s+p·z(t+q_1-1)\hfill \\ \hfill & {}^c\Delta _a^{q_1}y\left(t\right)=q·x(t+q_1-1)+r·y(t+q_1-1)·z(t+q_1-1)\hfill \\ \hfill & {}^c\Delta _a^{q_1}z\left(t\right)=1-x(t+q_1-1)-y(t+q_1-1)+z(t+q_1-1).\hfill \end{array}$$

(7)

Let the variable x represent the resources used for sales in stage t, and let y represent the resources in stage t. A customer quantity z represents the enterprise’s inventory capital in stage t, the parameter item s represents the base initially used for sales, p represents the transfer rate of inventory capital, q is the ratio of product resources, and r is the efficiency of inventory.

According to the definition of a fractional order of Caputo type, it is converted into a fractional difference equation as follows:

$$\begin{array}{cc}\hfill & x\left(t\right)=x\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{s=1-q_1}^{t-q_1}{(t-s-1)}^{q_1-1}[(s+p·z(s+q_1-1))-x(s+q_1-1)]\hfill \\ \hfill & y\left(t\right)=y\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{s=1-q_1}^{t-q_1}{(t-s-1)}^{q_1-1}\left[\right(q·x(s+q_1-1)\hfill \\ \hfill & +r·y(s+q_1-1)·z(s+q_1-1))-y(s+q_1-1)]\hfill \\ \hfill & z\left(t\right)=z\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{s=1-q_1}^{t-q_1}{(t-s-1)}^{q_1-1}\left[\right(1-x(s+q_1-1)-y(s+q_1-1)\hfill \\ \hfill & +z(s+q_1-1))-z(s+q_1-1)].\hfill \end{array}$$

(8)

For convenience, when $s+q_1\in N$, let $s+q_1=j$ and let kernel function ${(t-\sigma \left(s\right))}^{q_1-1}/\Gamma \left(q_1\right)=\Gamma (t-s)/(\Gamma \left(q_1\right)\Gamma (t-s-q_1+a))$. Here, if the initial value point $a=0$ and the fractional order $0<q_1<1$, Formula (9) can be rewritten as

$$\begin{array}{cc}\hfill & x\left(t\right)=x\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{j=1}^t\frac{\Gamma \left(t-j+q_1\right)}{\Gamma (t-j+1)}·[s+p·z(j-1)-x(j-1)]\hfill \\ \hfill & y\left(t\right)=y\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{j=1}^t\frac{\Gamma \left(t-j+q_1\right)}{\Gamma (t-j+1)}[q·x(j-1)+r·y(j-1)·z(j-1)-y(j-1)]\hfill \\ \hfill & z\left(t\right)=z\left(0\right)+\frac{1}{\Gamma \left(q_1\right)}\sum _{j=1}^t\frac{\Gamma \left(t-j+q_1\right)}{\Gamma (t-j+1)}[1-x(j-1)-y(j-1)+z(j-1)-z(j-1)].\hfill \end{array}$$

(9)

Let $q_1=0.9$, $p=0.43$, $q=0.38$, $s=0.11$, and $r=0.625$ in Equation (10). This study uses MATLAB software to write a program to solve Equation (9), and obtain the trajectory phase of the fractional-order inventory management system model, as shown in Figure 1. It can be seen from the trajectory phase diagram that the system is a periodic trajectory.

Let $q_1=0.99$, $p=0.43$, $q=0.38$, $s=0.11$, and $r=0.625$ in Equation (9). This study uses MATLAB software to write a program, and solve Equation (9), to obtain the trajectory phase of the fractional-order inventory management system model, as shown in Figure 2. It can be seen from the trajectory phase diagram that the system is a chaos trajectory.

The source code of Equation (10) is in Appendix A.

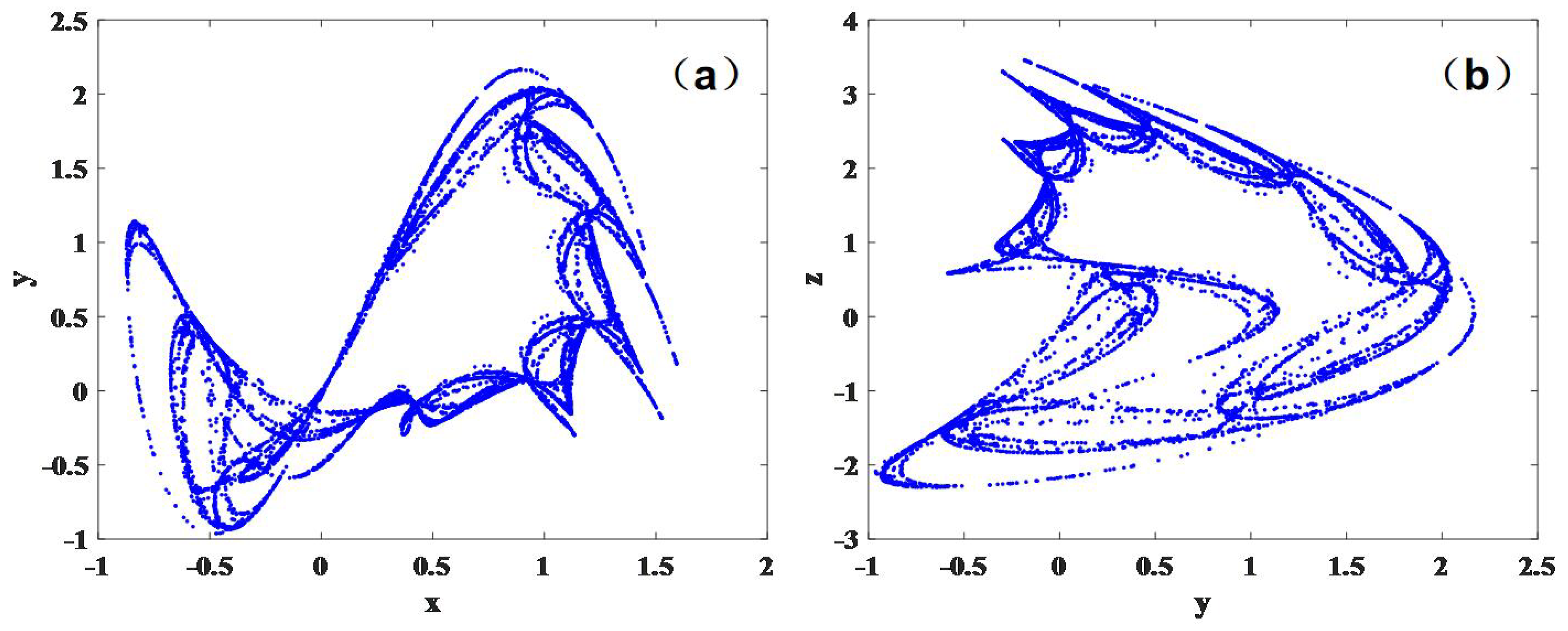
3. Dynamics Analysis

In this section, the influence of parameters on discrete inventory system will be given by a bifurcation diagram and largest Lyapunov exponent (LLE) spectrum. A bifurcation diagram is obtained by capturing the maximum point of mapping, and LLE is obtained by calculating a discrete sequence by the wolf method. Using the control variable method means changing one parameter and fixing other parameters.

3.1. Fractional-Order $q_1$ Change

First, change the fractional-order $q_1$, the range of change is 0.9–1, and the other parameters of the inventory management system are fixed. MATLAB draws the bifurcation diagram and LLE diagram of the system, and the results are shown in Figure 3. As can be seen from Figure 3, $q_1\in [0.9,0.97]$ is a periodic state, and $q_1\in [0.97,1]$ is a chaos state. The fractional-order $q_1$ affects the state of the system. When the fractional-order $q_1$ is low, the system is prone to cycle, which is consistent with the actual inventory system in special circumstances. In most fractional-order regions, the system is in a periodic state. It can also be seen from the figure that the LLE of the system is greater than zero when it is in a chaos state; when the system is in a non-chaos state, the LLE is zero. Under the condition that the inherent parameters of the system are fixed, the fractional order $q_1$ can affect the state of the inventory management model, and it can appear to cycle or chaos, which is in line with the real inventory model.

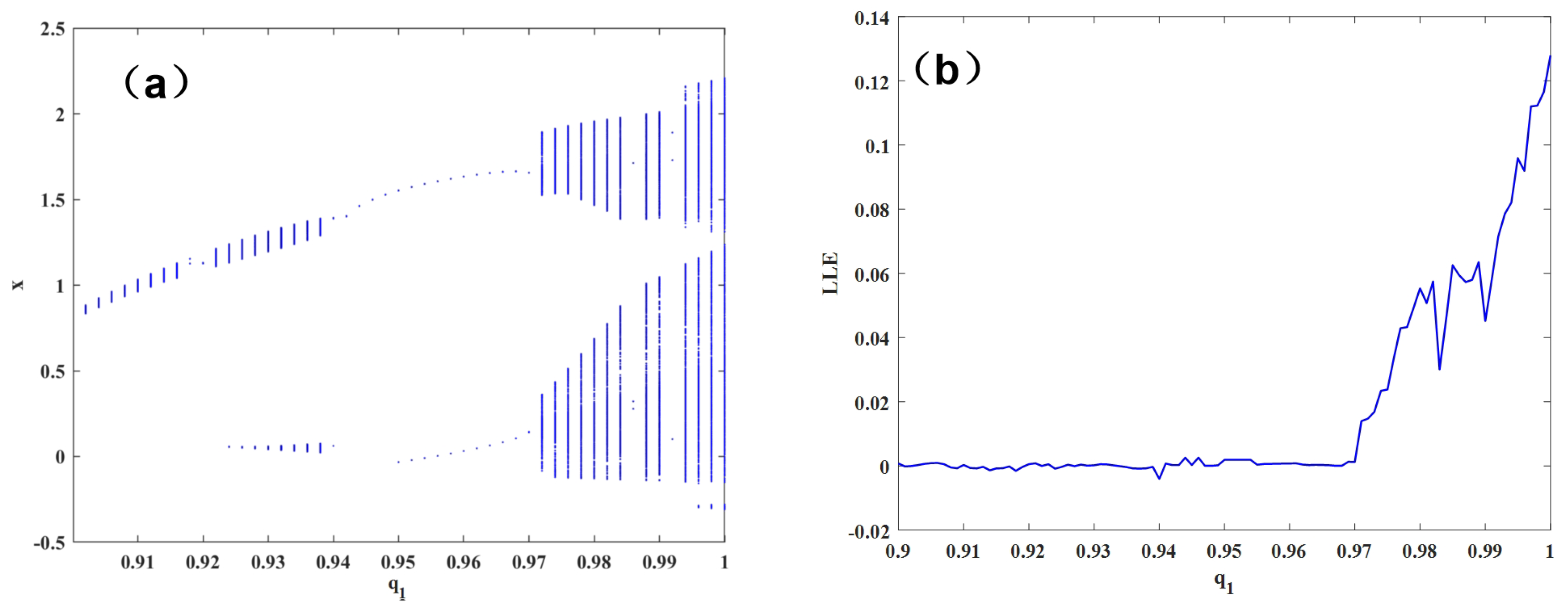
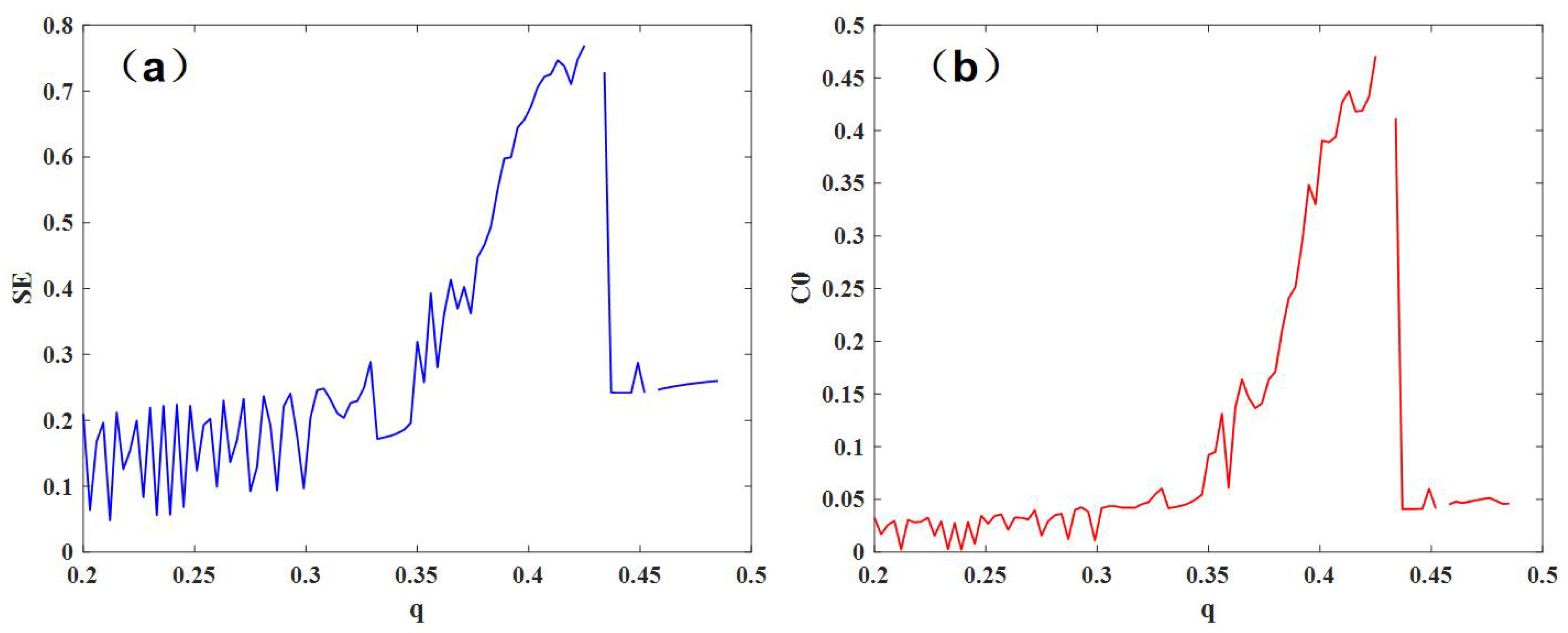
3.2. Parameter q Change

The fractional order $q_1$ = 0.99, changing the product resource rate $q\in [0.2,0.5]$, keeping the other parameters of the inventory management system model unchanged, and drawing the bifurcation diagram and the LLE of the system is shown in Figure 4. It can be seen from Figure 4a that the $q\in [0,2,0.35]$ system is periodic and that the LLE corresponding to Figure 4b is equal to zero. When $q\in (0.35,0.44]$, the system is chaos, and the corresponding LLE is greater than zero. However, when $q\in (0.44,0.49]$, the bifurcation diagram shows that the system is periodic but that the LLE does not exist. When the bifurcation diagram is drawn, the range of the coordinate axis Y axis is limited to [−0.5, 2.5]. The maximum value of the y series of the system has reached ${10}^{36}$, and the system is a divergent system; therefore, the LLE does not exist. At this time, the system appears to be in a divergent state. Because the maximum value of the divergence is relatively large, we cannot obtain it; therefore, the bifurcation diagram cannot be drawn by the variable maximum method. This kind of phenomenon is common in continuous systems, especially when some parameters are near zero.

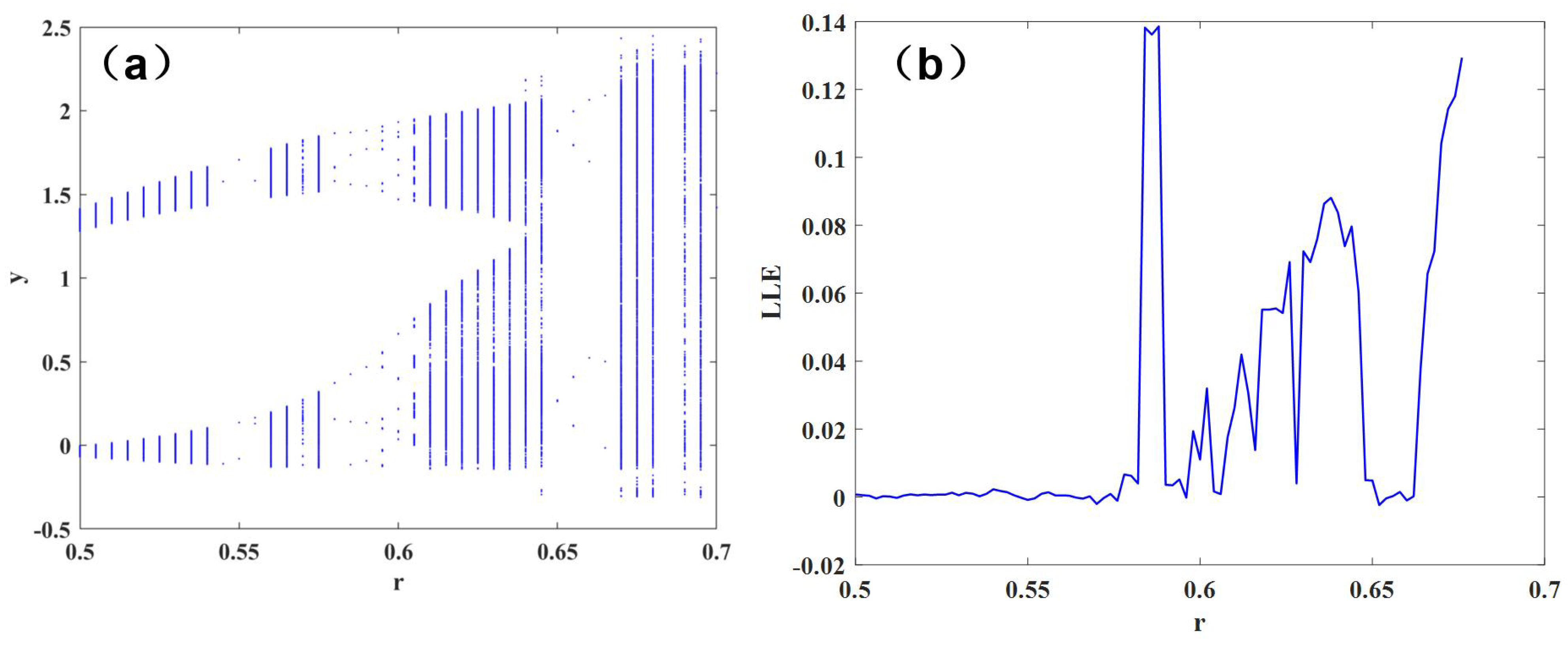
3.3. Parameter r Change

The fixed fractional order $q_1$ = 0.99, q = 0.38, the changing inventory efficiency $r\in [0.5,0.7]$, and the other parameters of the inventory management system remain unchanged. The bifurcation diagram and the LLE of the system are drawn by MATLAB software, as shown in Figure 5. With the change of parameter r, the system presents complex changes. It can be seen from the bifurcation diagram that when $r=0.5\sim 0.6$, the system is in a periodic state and the largest Lyapunov exponent is equal to zero. When $r=0.6\sim 0.65$ is in chaos, the largest Lyapunov exponent is greater than zero, and when $r=0.65\sim 0.67$ is in a periodic state, the LLE of the system is less than zero. When $r=0.67\sim 0.7$, it can be seen from the bifurcation diagram that the system is in a periodic and chaos region, the LLE of the system does not exist for the same reason that the region of the LLE does not exist when the parameter q changes: that is, the actual state of the system at this time is a divergent system rather than in the LLE.

4. Complexity Analysis

4.1. SE Complexity Algorithm

In the spectral entropy (SE) method [28,37], a discrete Fourier transform is performed, combined with the Shannon entropy algorithm, and the related results are obtained. The detailed design process is as follows:

(1) Delete the average part of the system, this paper processes the sequence, and the formula is as follows:

$$x\left(n\right)=x\left(n\right)-\overline{x},$$

(10)

where $\overline{x}=\frac{1}{N}{\sum }_{n=0}^{N-1}x\left(n\right)$.

(2) Fourier transform: Using the basic definition of Fourier transform, Equation (11) is transformed. The formula is as follows:

$$X\left(l\right)=\sum _{n=0}^{N-1}x\left(n\right){\mathrm{e}}^{-j\frac{2\pi }{N}nl}=\sum _{n=0}^{N-1}x\left(n\right)W_N^{nl}.$$

(11)

Among these, $l=0,1,2,\cdots ,N-1.$

(3) Relative power spectrum: Take the first part of the sequence after the dispersion processing, and use the Paserval algorithm to obtain the power spectrum of one of the specific frequencies, as follows:

$$p\left(k\right)=\frac{1}{N}{\left|X\left(k\right)\right|}^2.$$

(12)

Among these, $k=0,1,2,\cdots ,(N-1)/2.$ The total power of x(k) is defined as

$$p_{\mathrm{tot}}=\frac{1}{N}\sum _{k=0}^{N/2-1}{\left|X\left(k\right)\right|}^2.$$

(13)

The probability of the relative power spectrum can be expressed as

$$P_k=\frac{p\left(k\right)}{p_{\mathrm{tot}}}=\frac{\frac{1}{N}{\left|X\left(k\right)\right|}^2}{\frac{1}{N}{\sum }_{k=0}^{N/2-1}{\left|X\left(k\right)\right|}^2}=\frac{{\left|X\left(k\right)\right|}^2}{{\sum }_{k=0}^{N/2-1}{\left|X\left(k\right)\right|}^2}.$$

(14)

(4) Combining the Shannon entropy concept, the signal spectrum entropy expression is

$$se=-\sum _{k=0}^{N/2-1}{P}_{k}ln{P}_k.$$

(15)

In order to compare the complexity of signals conveniently, the results of spectral entropy are normalized as follows:

$$SE\left(N\right)=\frac{se}{ln(N/2)}.$$

(16)

It can be seen from the above transformation that the more unstable the power spectrum of the sequence changes, the less prominent the signal amplitude and the smaller the complexity measurement value.

4.2. C0 Algorithm

The algorithm of the C0 complexity mainly calculates the regular signal and the irregular signal in the sequence signal separately [28,38]. The specific calculation process is as follows [28]:

(1) The signal is Fourier-transformed as follows:

$$X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right){\mathrm{e}}^{-j\frac{2\pi }{N}nk}=\sum _{n=0}^{N-1}x\left(n\right)W_N^{nk}.$$

(17)

Among these, $k=0,1,2,\cdots ,N-1.$

(2) Remove the irregular part of the sequence $x\left(k\right)$, the square mean of $x\left(k\right)$, as in Equation (12).

Add a parameter r to Formula (18), leaving the part that exceeds the mean square value R times, and assume that the value of the remaining part is zero, such that

$$\tilde{X}\left(k\right)=\left\{\begin{array}{cc}X\left(k\right),\hfill & {\left|X\left(k\right)\right|}^2>r{G}_N\hfill \\ 0,\hfill & {\left|X\left(k\right)\right|}^2<r{G}_N\hfill \end{array}\right..$$

(18)

(3) Carry out an inverse Fourier transform to obtain

$$\tilde{X}\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}\tilde{X}\left(k\right){\mathrm{e}}^{\frac{2\pi }{N}nk}=\frac{1}{N}\sum _{k=0}^{N-1}\tilde{X}\left(k\right)W_N^{-nk}.$$

(19)

(4) The formula for defining the C0 complexity is as follows:

$$C0(r,N)=\sum _{n=0}^{N-1}|x\left(n\right)-\tilde{x}{\left(n\right)|}^2/\sum _{n=0}^{N-1}{\left|x\left(n\right)\right|}^2.$$

(20)

The algorithm of the C0 complexity is based on the fast Fourier transform (FFT). The main idea is to keep the irregular sequence, so that the more irregular parts there are in the sequence, the greater the C0 complexity.

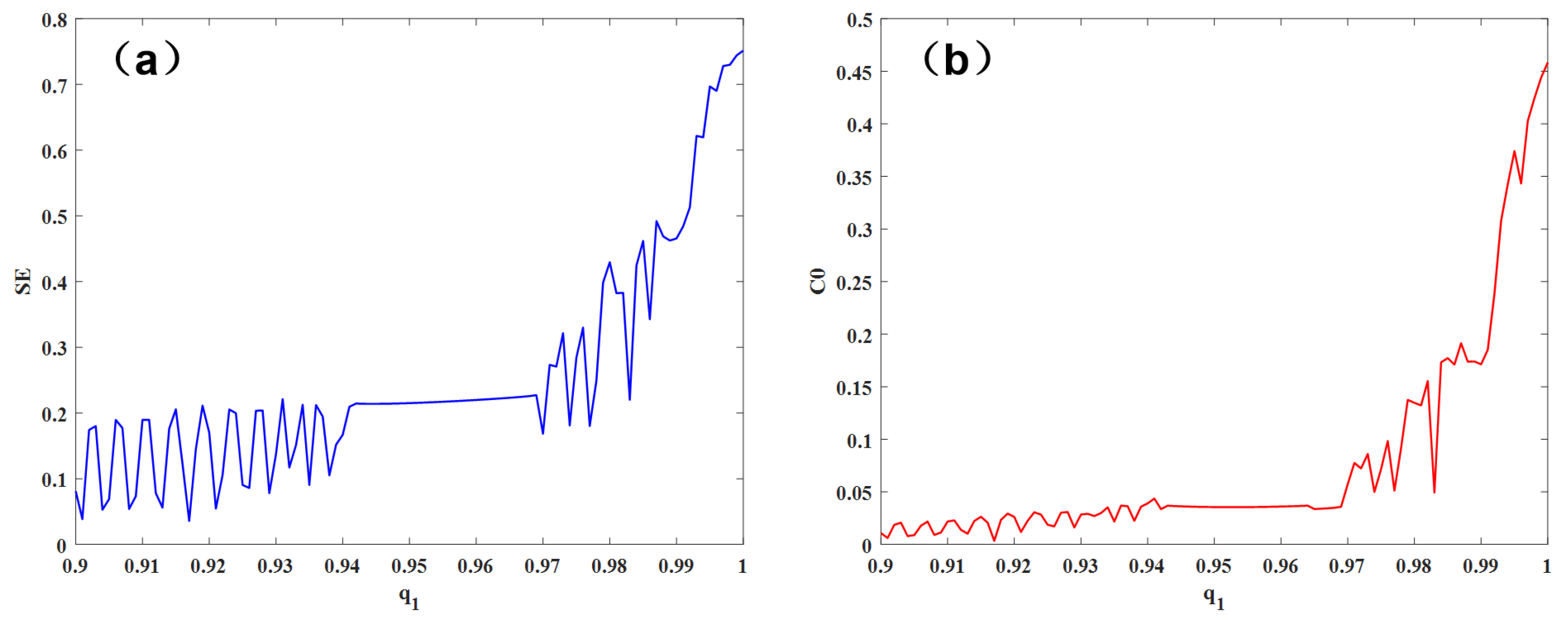
4.3. C0 and SE Complexity of the Model

The definition of complexity is introduced above. In a chaotic system, we mainly describe the complexity of the system sequence but not the complexity of the system structure equation. From the application of a discrete chaotic system, the complexity of the system output value is more important, and the complexity of the equation does not affect the output complexity.

In the same way as in the previous section, we change the fractional order of the system to the same range, observe the complexity transformation of the system, and compare the relationship between complexity and LLE. The complexity of the SE and the C0 is shown in Figure 6. When the system is in the periodic state, the complexity of the SE and of the C0 is at its smallest, and the periodic state is obvious when $q_1$ = 0.9–0.97, which should be expected by our inventory management system but rarely happens in practice. After $q_1>0.97$, with the increase of q, the complexity of the SE and of the C0 shows an overall upward trend, which is consistent with the corresponding verification results, such as the Lyapunov index spectrum and the bifurcation diagram (Figure 3). It is also consistent with the complexity change of the SE and of the C0, but the complexity of the SE is relatively high and that of the C0 is relatively low.

The fractional order $q_1$= 0.99, changing the product resource rate $q\in [0.2,0.5]$, keeping other parameters of the inventory management system model unchanged, and drawing the complexity of the system, as shown in Figure 7. When q = 0.2$,\sim$0.35, the system’s complexity is unchanged and relatively small. At this time, the system is in a non-chaotic state. When q = 0.35∼0.44, the complexity of the system is higher, it is increasing, and the system presents a chaos state. At q = 0.44∼0.5, the system complexity appears blank, indicating that this interval complexity does not exist and that the system is divergent; therefore, the system complexity cannot be obtained. The change of the system complexity in Figure 7 is consistent with the LLE change of the system in Figure 4.

The fixed fractional order $q_1$ = 0.99, q = 0.38, the changing inventory efficiency $r\in [0.5,0.7]$, and the other parameters of the inventory management system remain unchanged. The SE and C0 complexity of the system is drawn by MATLAB software, as shown in Figure 8. When the system is in chaos, the complexity is high; the complexity is less when the system is in cycle. The change of system complexity is consistent with the change of the LLE of the system in Figure 5. In some intervals, the system is in a divergent state; therefore, there is no LLE, and the corresponding complexity does not exist. Compared with Lei et al. [5], this model is more similar to the actual inventory situation. For example, during the inventory efficiency r = 0.6–0.65, the system is in a periodic state, which does not conform to the basic inventory convention. In this paper, the inventory efficiency r = 0.6–0.65, which is in a chaotic state and accords with the basic inventory dynamics.

4.4. C0 and SE Complexity Space of Model

The above research is based on the system complexity given a single parameter change. When two parameters change at the same time, it is important to study the state of the system so that we can easily find the chaotic region and the periodic region of the system.

A complex space diagram with two parameters, the x axis and the y axis, represent the two parameters, and color is used to represent complexity. Different colors have different complexity. The complexity diagram is shown in Figure 9. The colors in the diagram are dark blue, sky blue, light green, yellow, orange, red, and black, indicating the complexity from low to high. The areas with high complexity are in the upper right of the two graphs—that is, the areas with larger fractional order $q_1$ and larger parameter r—and the complex space graphs of the SE and of the C0 are the same. A complexity diagram can offer useful information to warehouse managers to control inventory efficiency within a certain range in inventory management.

5. Conclusions

In this work, we studied and analyzed the complex behavior of an inventory management system. Based on the integer-order discrete inventory management system model, a fractional-order inventory management system is constructed. Combined with the related algorithms of the fractional-order difference equation, the phase diagram of the system is simulated and verified by MATLAB. At the same time, bifurcation and the largest Lyapunov exponent of the system are used to analyze the chaos dynamic characteristics when the related parameters change. In order to further study the nonlinear characteristics of the system, we use SE and C0 measurements to analyze the system’s complexity and construct the complexity space diagram. The simulation results show that when the area of fractional-order chaos is reduced, the quantity of the goods inventory in the warehouse can be easily controlled. Practically speaking, when the fractional order can be reduced by a more frequent record of goods in the warehouses, coupled with control by sales record management, all these can raise the accuracy of inventory prediction. This study provides theoretical support for inventory and facility managers to calculate and adjust inventory plans. Thus, the results can provide practical information to stakeholders when they design facility management strategies and the area a company needs to rent for inventory purposes in the future.