A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays
Abstract
1. Introduction
1.1. Inspiration and Motivation
1.2. Literature Review
1.3. Contribution and Paper Structure
- •
- The mathematical model of MFO may be enhanced by including the concept of FC and FD integration. This integration aims to improve the optimization feature of MFO, namely its convergence rate.
- •
- To validate the performance of the proposed FODMFO, a total of 11 benchmark functions including unimodal and multimodal function have been solved in terms of mean fitness value among 100 independent runs.
- •
- The novel application of a fractional memetic computing approach, FODMFO, is used to minimize and optimize the operating time of DOCRs in a standard test system, by adjusting the values of TDS and PS.
- •
- The suggested scheme of a FODMFO aims to decrease the overall running duration of DOCRs in conventional networks. This is recognized by restricting the TDS and PS within acceptable ranges, considering varied topological and operational conditions.
- •
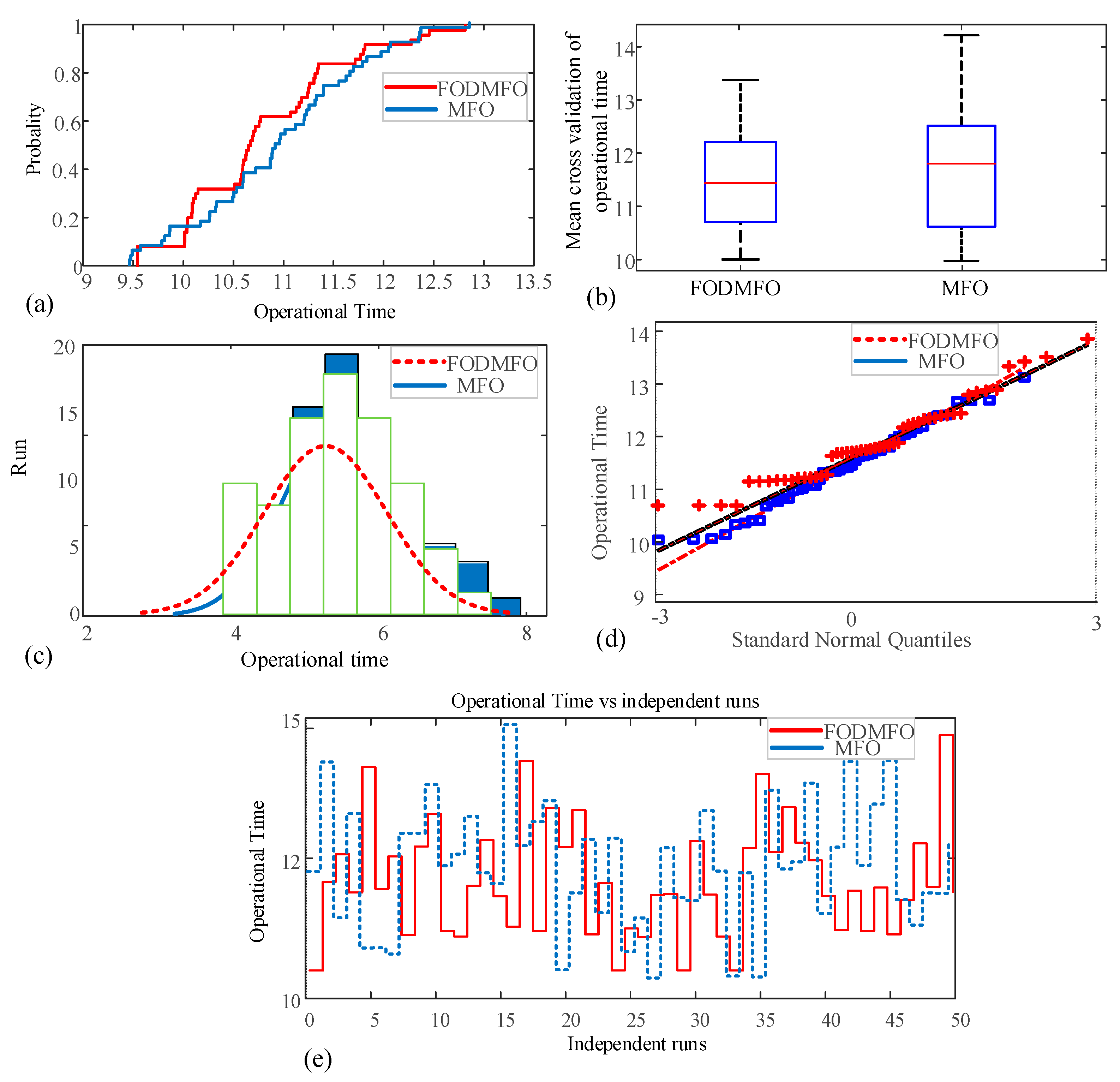
- The statistical illustrations, such as cumulative distribution function plots, box-plots, histogram illustrations, standard normal quantile plots, and minimum fitness value plots, are developed to assess the stability, accuracy, and robustness of the proposed FODMFO algorithm in independent runs.
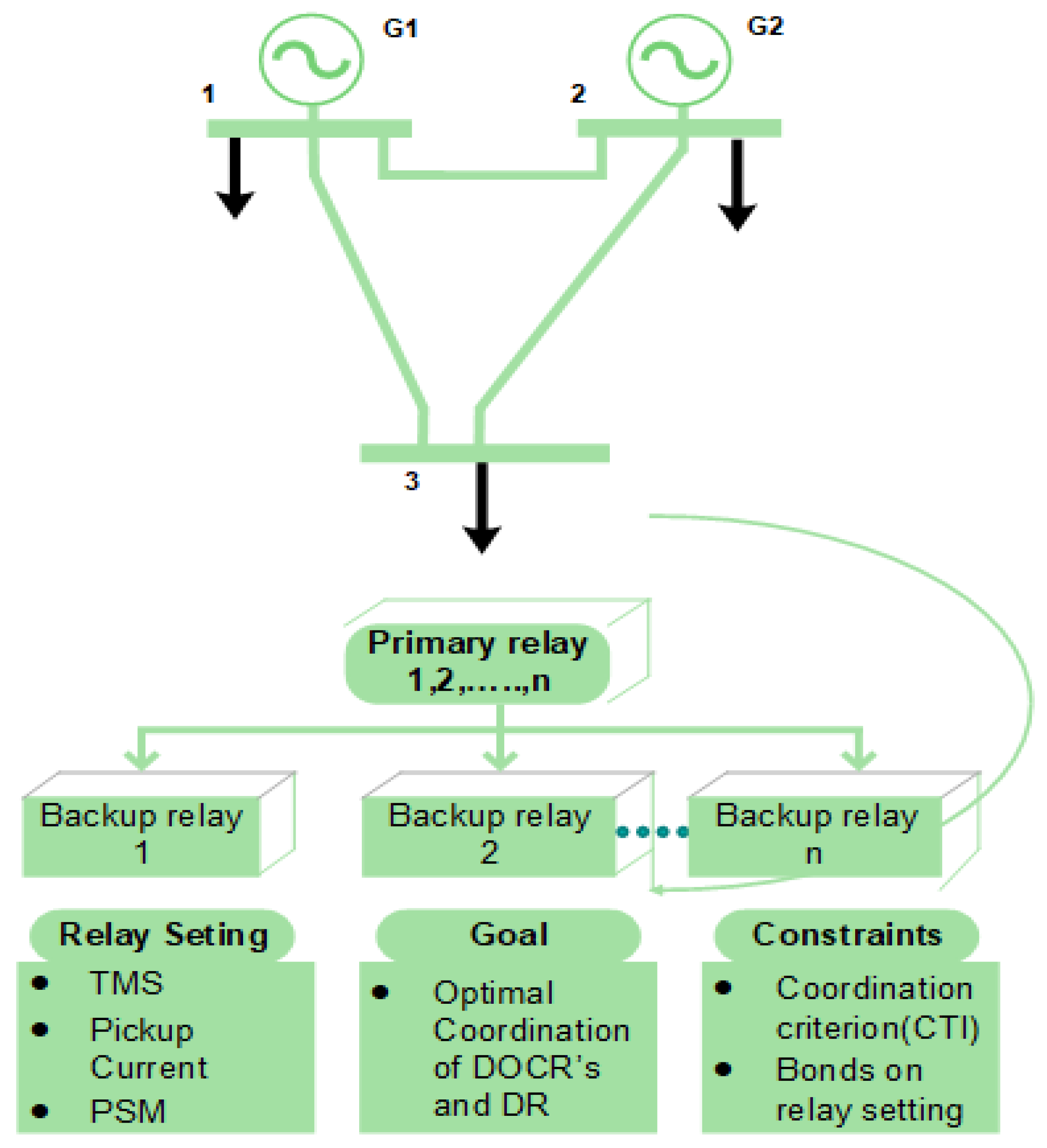
2. DOCR Problem Formulation
2.1. Coordination Criterion
- the primary (or main) relay operating time;
- the backup relay operating time.
2.2. Relay Setting Bounds
3. Design Methodology
3.1. Moth Flame Optimization (MFO)
3.2. Fractional-Order Derivative Moth Flame Optimization (FODMFO)
- Step 1: Random initialization of search agent’s (moths) population. Introduce a set of n search agents with dimensions corresponding to the controllable factors of the dimension into the population of moths, denoted as “M”.
- Step 2: Fitness evaluation. The fitness value of each search agent is determined by submitting it to the necessary objective function related to the entire operational time.
- Step 3: Sorting initial search agent population. The search agents are ranked based on their unique fitness function scores and then assigned to the flame population “F” according to their individual fitness function values “OF”.
- Step 3: Updating position of search agents. A logarithmic spiral function is used to precisely modify the location of a moth in relation to the optimum flame.
- Step 4: Velocity calculation of each search agent based on fractional-order strategy. The velocity for each nth month is determined using fractional order.
- Step 5: Fractional-order velocity strategy adopted to further update position. The location of each moth is updated using the following equation, which takes into account the moth’s fractional velocity relative to its previous position: Mnp(t) = Mnp(t − 1) + Mnv(t).
- Step 6: Stopping criteria. The stopping criteria of the FODMFO algorithm rely on a set number of iterations.
- Step 7: Storage of results. The control variables of the DOCR issue are determined by the minimum active total operational time, which is based on the best result achieved by the moths or search agent.
- Step 8: Statistical analysis. Statistical analysis is conducted on one hundred independent trials utilizing histogram, box-plot, and CDF-based analysis.
| Algorithm 1: FODMFO |
| 1: Randomly initialize each individual in moths using (8); 2: Initialize the iteration count t = 1; 3: while t < t + 1; 4: Update fno using (17); 5: OM= Fitness Function (M); 6: If t=1; 7: F = sort(M); 8: OF = sort(OM); 9: else 10: F = sort ((Mtl, Mt); 11: OF = sort (Mt1, Mt); 12: end if 13: for i in range(n): # loop through moths 14: for j in range(d): # loop through dimensions 15: Update r and t; (These parameters might be predefined or updated based on a schedule) Calculate D using Equations (11) and (13) with respect to the corresponding moth; 16: Calculate the fractional-order velocity using Equations (27) and (22) with respect to the corresponding moth 17: end for 18: if r < 0.5: vel_ij = F[i][j] − r × D 19: else: 20: vel_ij = F[i][j] + r × D Update the position of the moth using the fractional-order velocity Assuming M[i][j] represents the position and vel_ij represents the velocity in dimension j for moth i 21: End if 22: M[i][j] = M[i][j] + t × vel_ij 23: OFM= Fitness Function (FM); 24: Update the best solution; 25: t = t + 1; 26: end while |
4. Results and Discussion
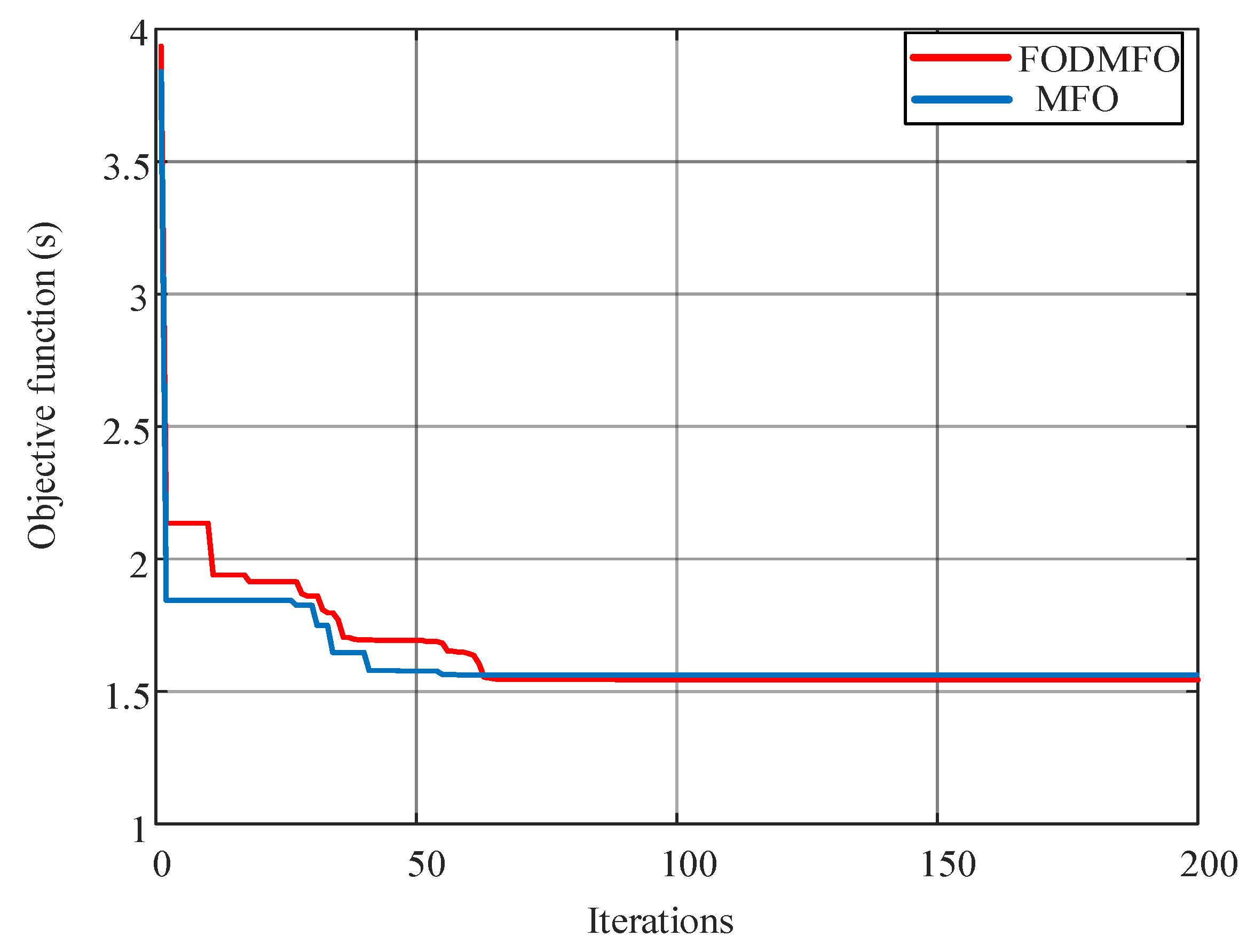
4.1. Case Study 1: IEEE 3-Bus System
4.2. IEEE 8-Bus System for DOCRs
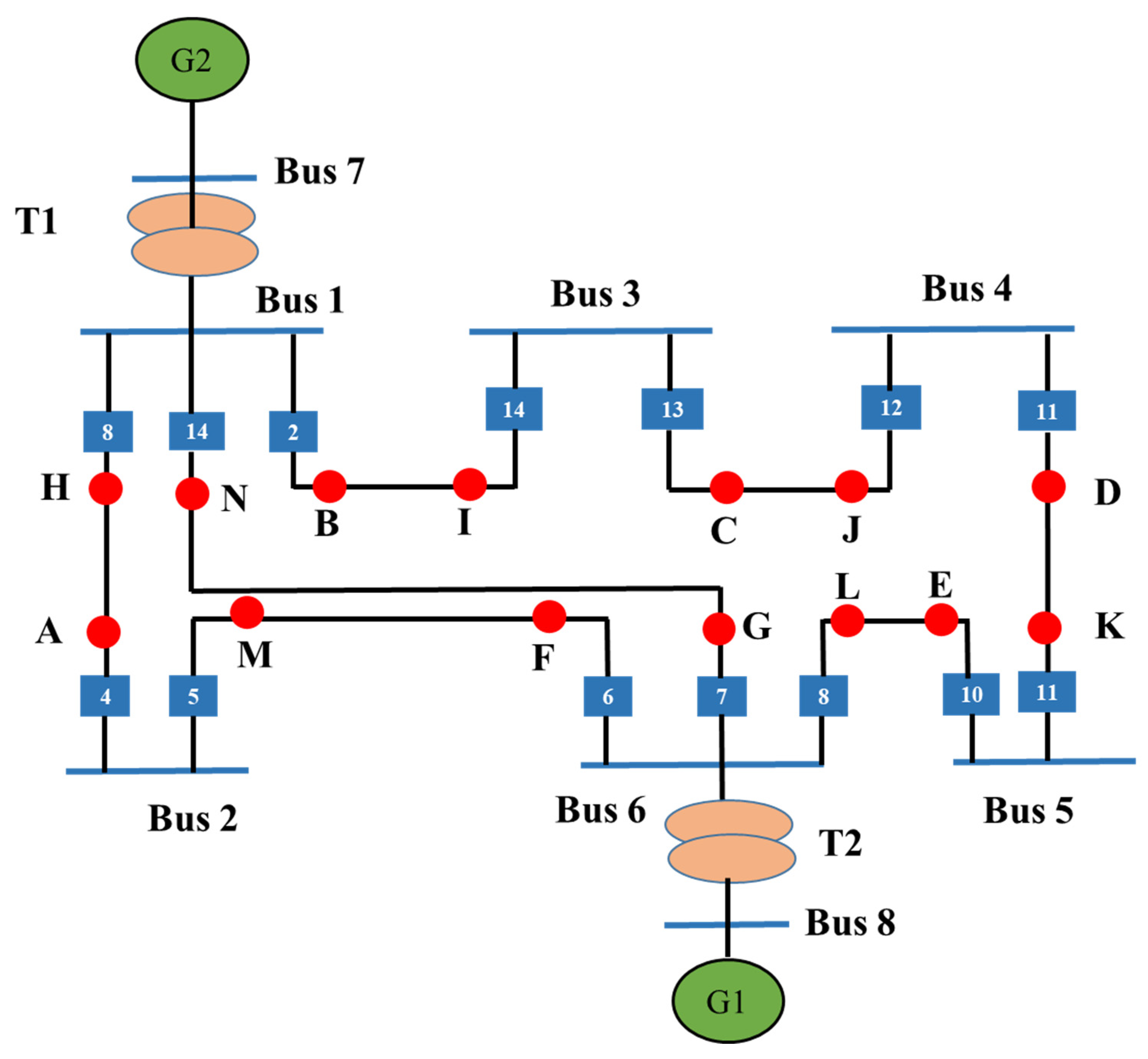
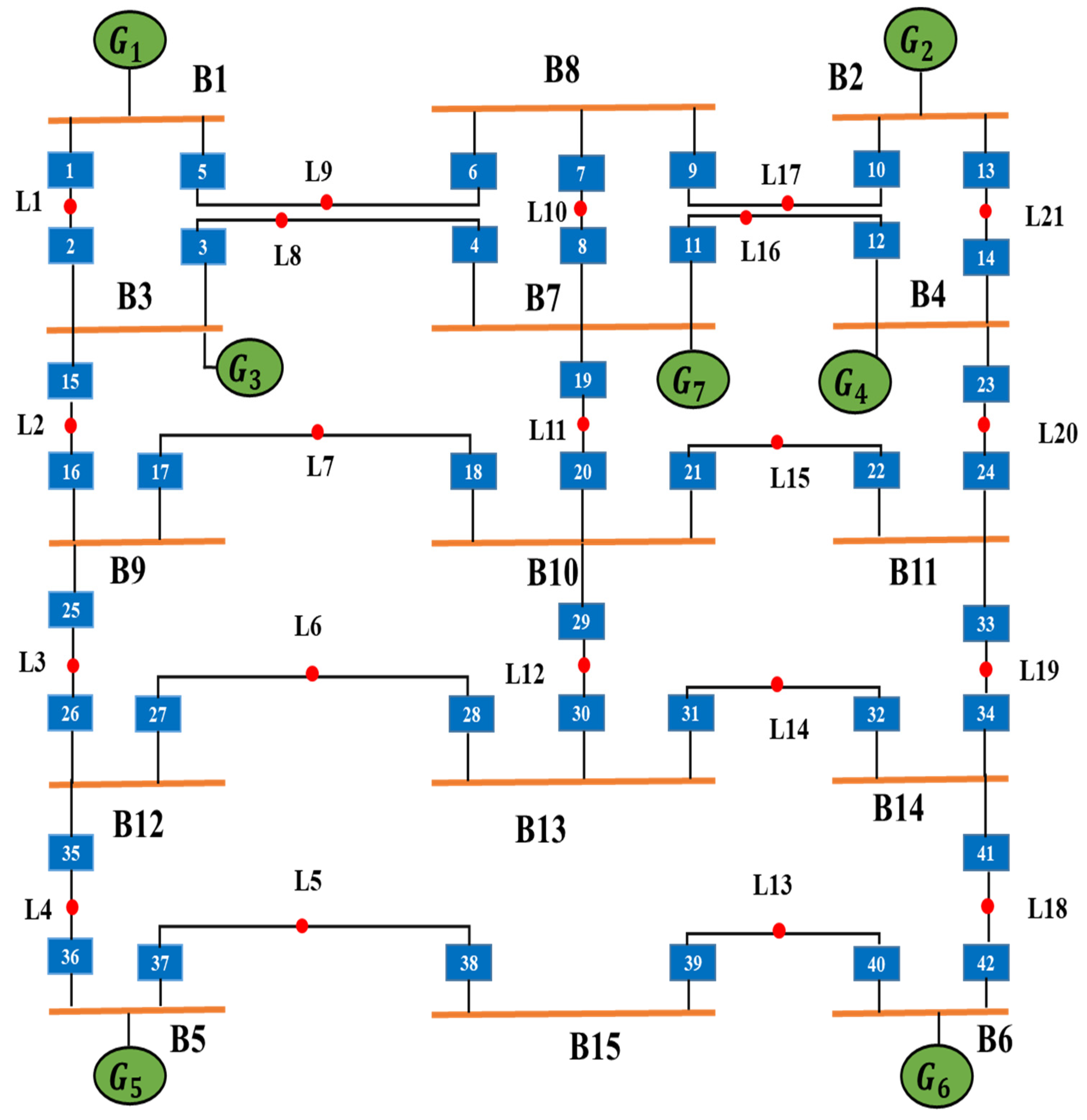
4.3. IEEE 15-Bus System for DOCRs
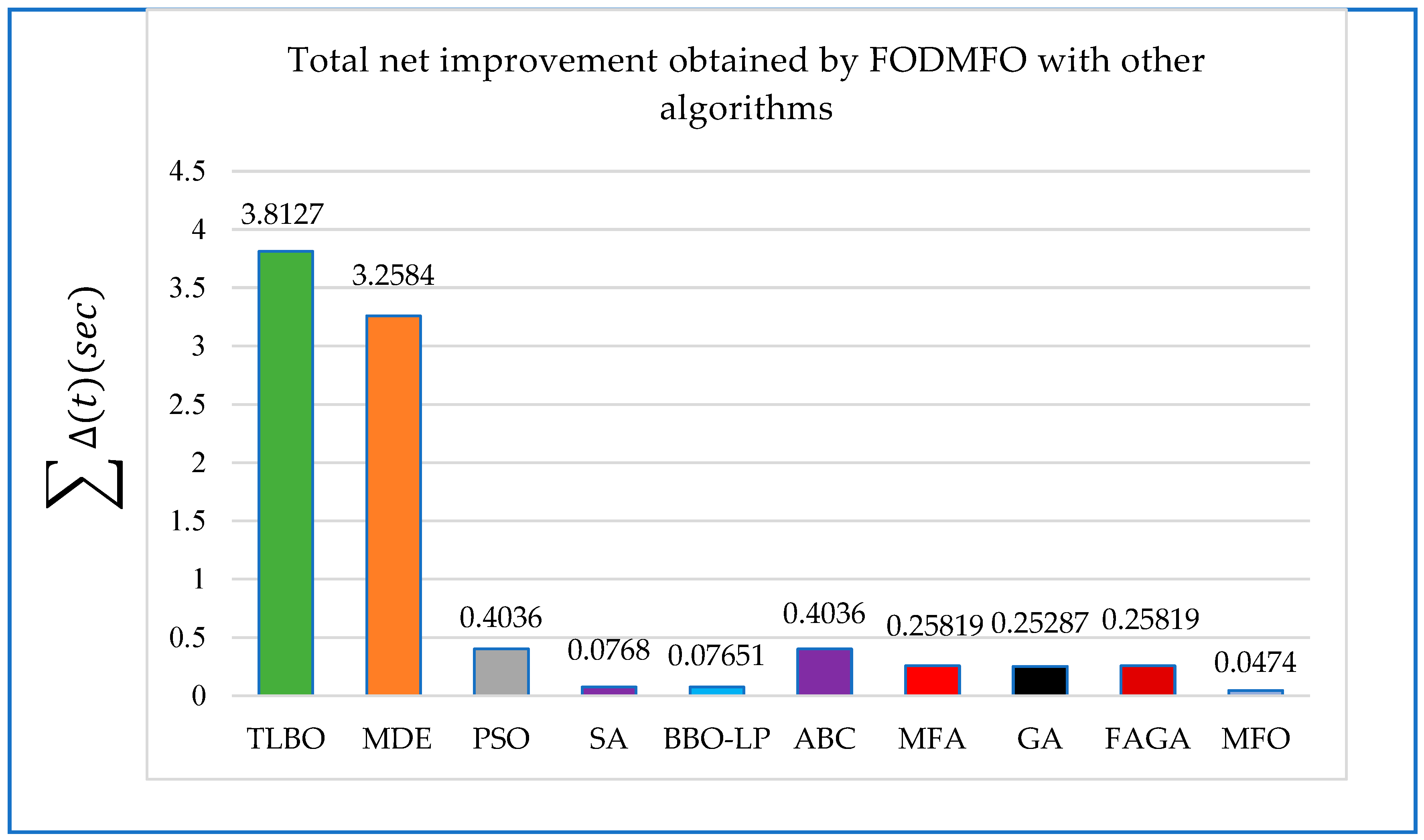
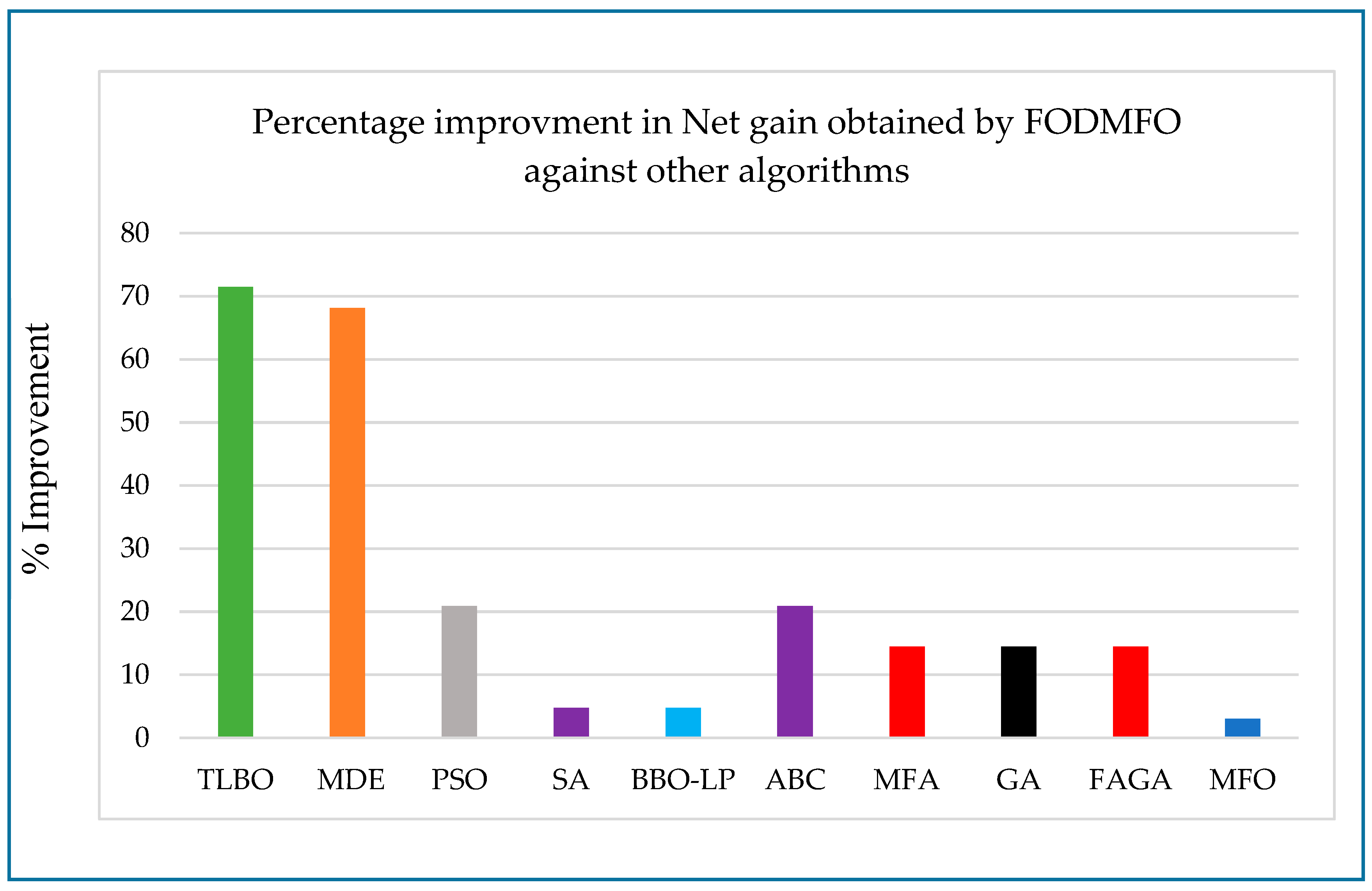
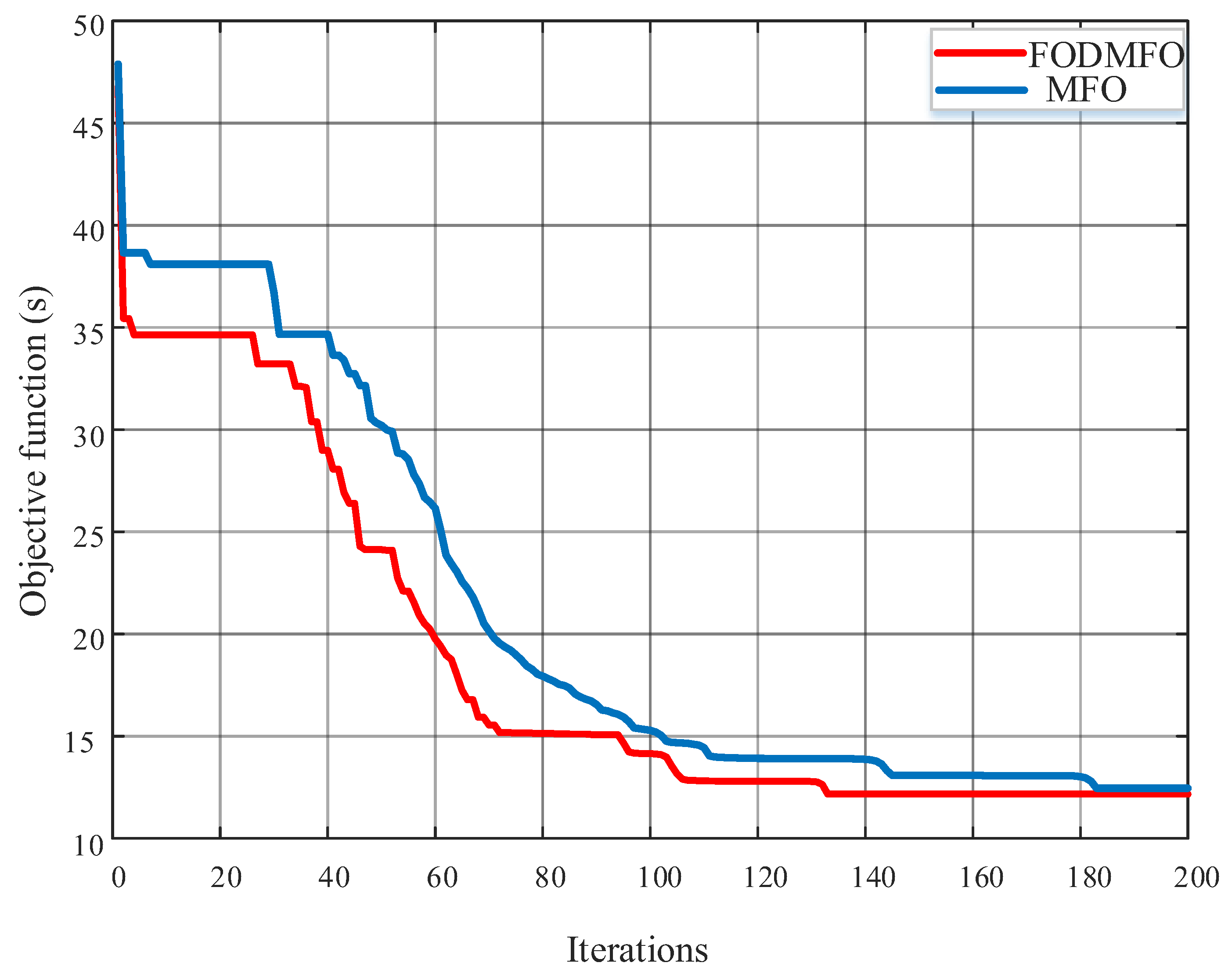
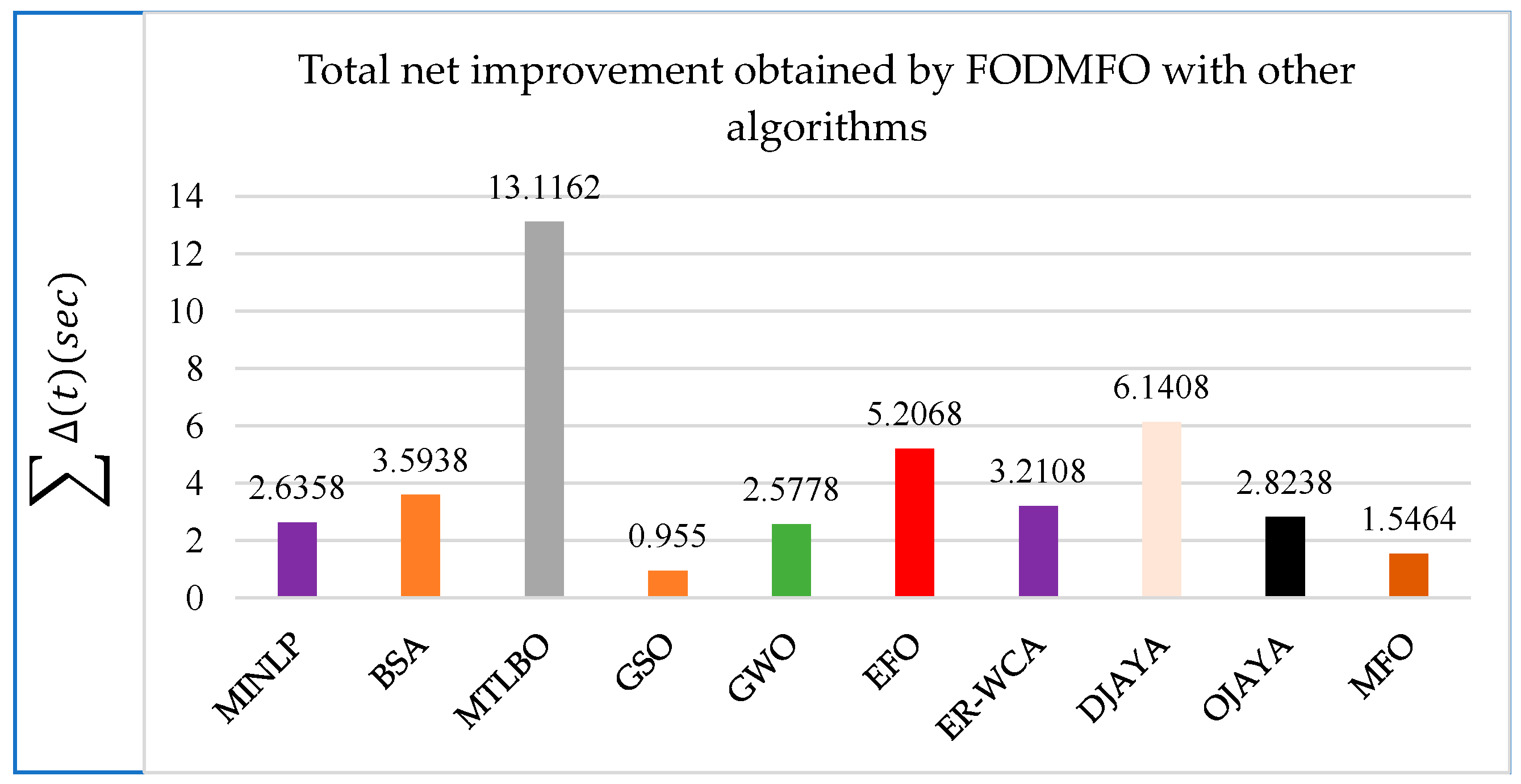
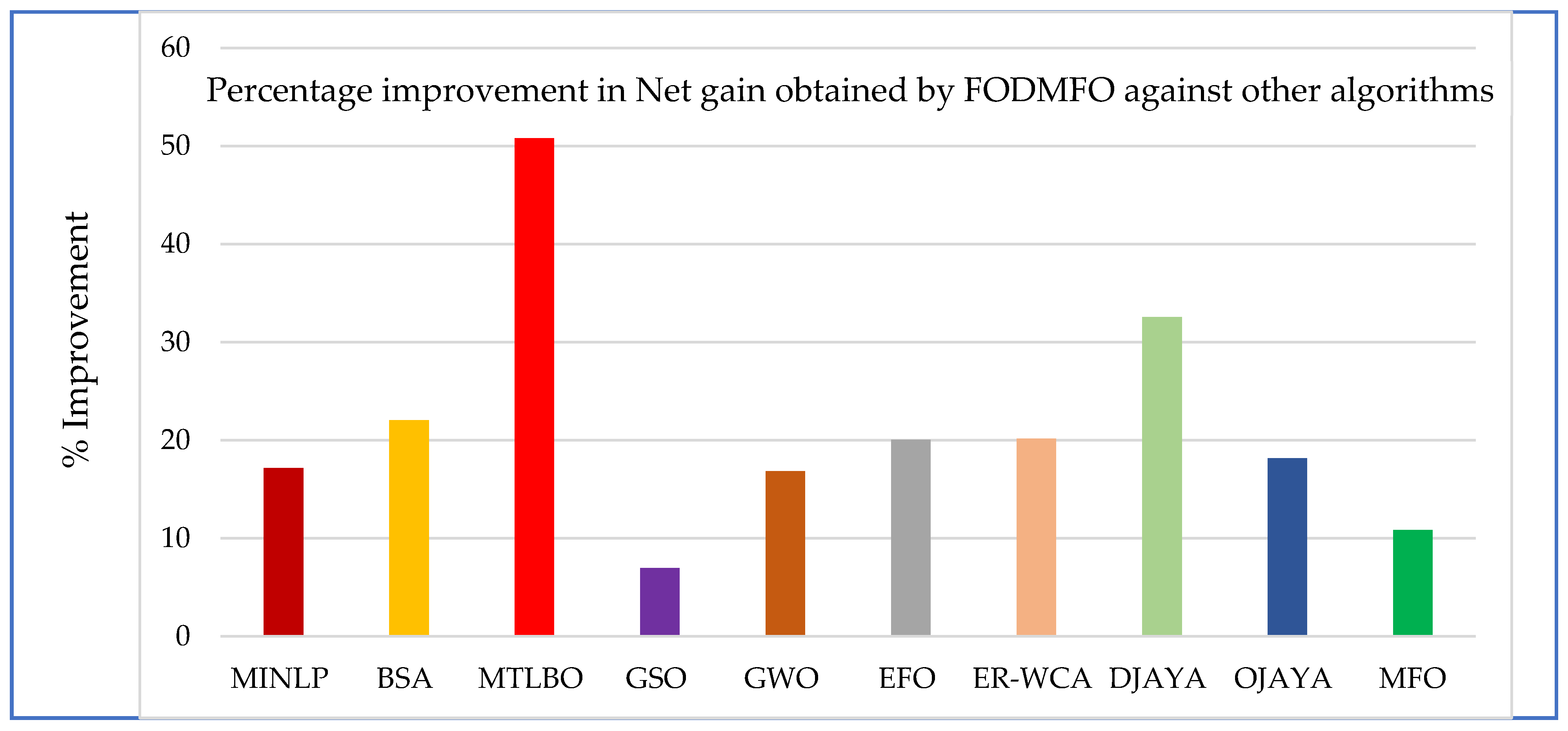
5. Comparative and Statistical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Damborg, M.; Ramaswami, R.; Venkata, S.; Postforoosh, J. Computer aided transmission protection system design part I: Alcorithms. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 51–59. [Google Scholar]
- Birla, D.; Maheshwari, R.; Gupta, H. A New nonlinear directional overcurrent relay coordination technique, and banes and boons of near-end faults based approach. IEEE Trans. Power Deliv. 2006, 21, 1176–1182. [Google Scholar] [CrossRef]
- Sharifian, H.; Abyaneh, H.A.; Salman, S.K.; Mohammadi, R.; Razavi, F. Determination of the minimum break point set using expert system and genetic algorithm. IEEE Trans. Power Deliv. 2010, 25, 1284–1295. [Google Scholar] [CrossRef]
- Lu, Y.; Chung, J.-L. Detecting and solving the coordination curve intersection problem of overcurrent relays in subtransmission systems with a new method. Electr. Power Syst. Res. 2013, 95, 19–27. [Google Scholar] [CrossRef]
- Ezzeddine, M.; Kaczmarek, R.; Iftikhar, M. Coordination of directional overcurrent relays using a novel method to select their settings. IET Gener. Transm. Distrib. 2011, 5, 743–750. [Google Scholar] [CrossRef]
- Yu, J.; Kim, C.H.; Rhee, S.B. Oppositional Jaya algorithm with distance-adaptive coefficient in solving directional over current relays coordination problem. IEEE Access 2019, 7, 150729–150742. [Google Scholar] [CrossRef]
- Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Yu, J.; Kim, C.H.; Rhee, S.B. An improved optimal solution for the directional overcurrent relays coordination using hybridized whale optimization algorithm in complex power systems. IEEE Access 2019, 7, 90418–90435. [Google Scholar] [CrossRef]
- Wadood, A.; Khurshaid, T.; Farkoush, S.G.; Yu, J.; Kim, C.H.; Rhee, S.B. Nature-inspired whale optimization algorithm for optimal coordination of directional overcurrent relays in power systems. Energies 2019, 12, 2297. [Google Scholar] [CrossRef]
- Wadood, A.; Farkoush, S.G.; Khurshaid, T.; Yu, J.T.; Kim, C.H.; Rhee, S.B. Application of the JAYA Algorithm in Solving the Problem of the Optimal Coordination of Overcurrent Relays in Single-and Multi-Loop Distribution Systems. Complexity 2019, 2019, 5876318. [Google Scholar] [CrossRef]
- Bhattacharya, S.K.; Goswami, S.K. Distribution network reconfiguration considering protection coordination constraints. Electr. Power Compon. Syst. 2008, 36, 1150–1165. [Google Scholar] [CrossRef]
- Abyaneh, H.; Al-Dabbagh, M.; Karegar, H.; Sadeghi, S.; Khan, R. A new optimal approach for coordination of overcurrent relays in interconnected power systems. IEEE Trans. Power Deliv. 2003, 18, 430–435. [Google Scholar] [CrossRef]
- Bedekar, P.P.; Bhide, S.R. Optimum coordination of directional overcurrent relays using the hybrid GA-NLP approach. IEEE Trans. Power Deliv. 2010, 26, 109–119. [Google Scholar] [CrossRef]
- Noghabi, A.S.; Sadeh, J.; Mashhadi, H.R. Considering different network topologies in optimal overcurrent relay coordination using a hybrid GA. IEEE Trans. Power Deliv. 2009, 24, 1857–1863. [Google Scholar] [CrossRef]
- Urdaneta, A.; Perez, L.; Restrepo, H. Optimal coordination of directional overcurrent relays considering dynamic changes in the network topology. IEEE Trans. Power Deliv. 1997, 12, 1458–1464. [Google Scholar] [CrossRef]
- Noghabi, A.S.; Mashhadi, H.R.; Sadeh, J. Optimal coordination of directional overcurrent relays considering different network topologies using interval linear programming. IEEE Trans. Power Deliv. 2010, 25, 1348–1354. [Google Scholar] [CrossRef]
- Najy, W.K.; Zeineldin, H.H.; Woon, W.L. Optimal protection coordination for microgrids with grid-connected and islanded capability. IEEE Trans. Ind. Electron. 2012, 60, 1668–1677. [Google Scholar] [CrossRef]
- Saleh, K.A.; Zeineldin, H.H.; El-Saadany, E.F. Optimal protection coordination for microgrids considering N-1 contingency. IEEE Trans. Ind. Inform. 2017, 13, 2270–2278. [Google Scholar] [CrossRef]
- Saleh, K.A.; Zeineldin, H.H.; Al-Hinai, A.; El-Saadany, E.F. Optimal coordination of directional overcurrent relays using a new time-current-voltage characteristic. IEEE Trans. Power Syst. 2014, 30, 537–544. [Google Scholar] [CrossRef]
- Saleh, K.A.; El-Saadany, E.F.; Al-Hinai, A.; Zeineldin, H.H. Dual-setting characteristic for directional overcurrent relays considering multiple fault locations. IET Gener. Transm. Distrib. 2015, 9, 1332–1340. [Google Scholar] [CrossRef]
- Korashy, A.; Kamel, S.; Alquthami, T.; Jurado, F. Optimal coordination of standard and non-standard direction overcurrent relays using an improved moth-flame optimization. IEEE Access 2020, 8, 87378–87392. [Google Scholar] [CrossRef]
- Irfan, M.; Wadood, A.; Khurshaid, T.; Khan, B.M.; Kim, K.C.; Oh, S.R.; Rhee, S.B. An optimized adaptive protection scheme for numerical and directional overcurrent relay coordination using Harris hawk optimization. Energies 2021, 14, 5603. [Google Scholar] [CrossRef]
- Amraee, T. Coordination of directional overcurrent relays using seeker algorithm. IEEE Trans. Power Deliv. 2012, 27, 1415–1422. [Google Scholar] [CrossRef]
- Urdaneta, A.; Nadira, R.; Jimenez, L.P. Optimal coordination of directional overcurrent relays in interconnected power systems. IEEE Trans. Power Deliv. 1988, 3, 903–911. [Google Scholar] [CrossRef]
- Wadood, A.; Farkoush, S.G.; Khurshaid, T.; Kim, C.-H.; Yu, J.; Geem, Z.W.; Rhee, S.-B. An optimized protection coordination scheme for the optimal coordination of overcurrent relays using a nature-inspired root tree algorithm. Appl. Sci. 2018, 8, 1664. [Google Scholar] [CrossRef]
- Wadood, A.; Khurshaid, T.; Farkoush, S.G.; Kim, C.H.; Rhee, S.B. A bio-inspired rooted tree algorithm for optimal coordination of overcurrent relays. In International Conference on Intelligent Technologies and Applications; Springer: Singapore, 2018; pp. 188–201. [Google Scholar]
- Wadood, A.; Kim, C.-H.; Khurshiad, T.; Farkoush, S.G.; Rhee, S.-B. Application of a continuous particle swarm optimization (CPSO) for the optimal coordination of overcurrent relays considering a penalty method. Energies 2018, 11, 869. [Google Scholar] [CrossRef]
- Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Kim, C.-H.; Cho, N.; Rhee, S.-B. Modified particle swarm optimizer as optimization of time dial settings for coordination of directional overcurrent relay. J. Electr. Eng. Technol. 2019, 14, 55–68. [Google Scholar] [CrossRef]
- Habib, K.; Lai, X.; Wadood, A.; Khan, S.; Wang, Y.; Xu, S. Hybridization of PSO for the Optimal Coordination of Directional Overcurrent Protection Relays. Electronics 2022, 11, 180. [Google Scholar] [CrossRef]
- Habib, K.; Lai, X.; Wadood, A.; Khan, S.; Wang, Y.; Xu, S. An improved technique of Hybridization of PSO for the Optimal Coordination of Directional Overcurrent Protection Relays of IEEE bus system. Energies 2022, 15, 3076. [Google Scholar] [CrossRef]
- Mansour, M.M.; Mekhamer, S.F.; El-Kharbawe, N. A modified particle swarm optimizer for the coordination of directional overcurrent relays. IEEE Trans. Power Deliv. 2007, 22, 1400–1410. [Google Scholar] [CrossRef]
- Thangaraj, R.; Pant, M.; Deep, K. Optimal coordination of over-current relays using modified differential evolution algorithms. Eng. Appl. Artif. Intell. 2010, 23, 820–829. [Google Scholar] [CrossRef]
- Bouchekara, H.; Zellagui, M.; Abido, M.; Bouchekara, H.R.E.-H. Optimal coordination of directional overcurrent relays using a modified electromagnetic field optimization algorithm. Appl. Soft Comput. 2017, 54, 267–283. [Google Scholar] [CrossRef]
- Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Kim, C.H.; Yu, J.; Rhee, S.B. Improved firefly algorithm for the optimal coordination of directional overcurrent relays. IEEE Access 2019, 7, 78503–78514. [Google Scholar] [CrossRef]
- Damchi, Y.; Dolatabadi, M.; Mashhadi, H.R.; Sadeh, J. MILP approach for optimal coordination of directional overcurrent relays in interconnected power systems. Electr. Power Syst. Res. 2018, 158, 267–274. [Google Scholar] [CrossRef]
- Kim, C.H.; Khurshaid, T.; Wadood, A.; Farkoush, S.G.; Rhee, S.B. Gray wolf optimizer for the optimal coordination of directional overcurrent relay. J. Electr. Eng. Technol. 2018, 13, 1043–1051. [Google Scholar]
- Albasri, F.A.; Alroomi, A.R.; Talaq, J.H. Optimal Coordination of directional overcurrent relays using biogeography-based optimization algorithm. IEEE Trans. Power Deliv. 2015, 30, 1810–1820. [Google Scholar] [CrossRef]
- Singh, M.; Panigrahi, B.; Abhyankar, A. Optimal coordination of directional over-current relays using teaching learning-based optimization (TLBO) algorithm. Int. J. Electr. Power Energy Syst. 2013, 50, 33–41. [Google Scholar] [CrossRef]
- El-Hana Bouchekara, H.R.; Zellagui, M.; Abido, M.A. Coordination of directional overcurret relays using the backtracking search algorithm. J. Electr. Syst. 2016, 12, 387–405. [Google Scholar]
- Kalage, A.A.; Ghawghawe, N.D. Optimum coordination of directional overcurrent relays using modified adaptive teaching learning based optimization algorithm. Intell. Ind. Syst. 2016, 2, 55–71. [Google Scholar] [CrossRef]
- Mahari, A.; Seyedi, H. An analytic approach for optimal coordination of overcurrent relays. IET Gener. Transm. Distrib. 2013, 7, 674–680. [Google Scholar] [CrossRef]
- Alipour, M.; Teimourzadeh, S.; Seyedi, H. Improved group search optimization algorithm for coordination of directional overcurrent relays. Swarm Evol. Comput. 2015, 23, 40–49. [Google Scholar] [CrossRef]
- Foqha, T.; Khammash, M.; Alsadi, S.; Omari, O.; Refaat, S.S.; Al-Qawasmi, K.; Elrashidi, A. Optimal coordination of directional overcurrent relays using hybrid firefly–genetic algorithm. Energies 2023, 16, 5328. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. A novel feature selection approach based on FODPSO and SVM. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2935–2947. [Google Scholar] [CrossRef]
- Ates, A.; Alagoz, B.B.; Kavuran, G.; Yeroglu, C. Implementation of fractional order filters discretized by modified fractional order darwinian particle swarm optimization. Measurement 2017, 107, 153–164. [Google Scholar] [CrossRef]
- Couceiro, M.S.; Rocha, R.P.; Ferreira, N.F.; Machado, J.T. Introducing the fractional-order Darwinian PSO. Signal Image Video Process. 2012, 6, 343–350. [Google Scholar] [CrossRef]
- Shahri, E.S.A.; Alfi, A.; Machado, J.T. Fractional fixed-structure H∞ controller design using augmented Lagrangian particle swarm optimization with fractional order velocity. Appl. Soft Comput. 2019, 77, 688–695. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V. The chronicles of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 307–336. [Google Scholar] [CrossRef]
- Fan, Q.; Ma, Y.; Wang, P.; Bai, F. Otsu Image Segmentation Based on a Fractional Order Moth–Flame Optimization Algorithm. Fractal Fract. 2024, 8, 87. [Google Scholar] [CrossRef]
- Zhu, Q.; Yuan, M.; Liu, Y.L.; Chen, W.D.; Chen, Y.; Wang, H.R. Research and application on fractional-order Darwinian PSO based adaptive extended Kalman filtering algorithm. IAES Int. J. Robot. Autom. 2014, 3, 245. [Google Scholar] [CrossRef]
- Kuttomparambil Abdulkhader, H.; Jacob, J.; Mathew, A.T. Fractional-order lead-lag compensator-based multi-band power system stabiliser design using a hybrid dynamic GA-PSO algorithm. IET Gener. Transm. Distrib. 2018, 12, 3248–3260. [Google Scholar] [CrossRef]
- Kosari, M.; Teshnehlab, M. Non-linear fractional-order chaotic systems identification with approximated fractional-order derivative based on a hybrid particle swarm optimization-genetic algorithm method. J. AI Data Min. 2018, 6, 365–373. [Google Scholar]
- Khan, B.S.; Qamar, A.; Wadood, A.; Almuhanna, K.; Al-Shamma, A.A. Integrating economic load dispatch information into the blockchain smart contracts based on the fractional-order swarming optimizer. Front. Energy Res. 2024, 12, 1350076. [Google Scholar] [CrossRef]
- Muhammad, Y.; Raja, M.A.Z.; Shah, M.A.A.; Awan, S.E.; Ullah, F.; Chaudhary, N.I.; Cheema, K.M.; Milyani, A.H.; Shu, C.M. Optimal coordination of directional overcurrent relays using hybrid fractional computing with gravitational search strategy. Energy Rep. 2021, 7, 7504–7519. [Google Scholar] [CrossRef]
- Muhammad, Y.; Akhtar, R.; Khan, R.; Ullah, F.; Raja, M.A.Z.; Machado, J.T. Design of fractional evolutionary processing for reactive power planning with FACTS devices. Sci. Rep. 2021, 11, 593. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Sabatier, J.A.T.M.J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; No. 9; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Razmjooei, H.; Shafiei, M.H.; Palli, G.; Arefi, M.M. Non-linear finite-time tracking control of uncertain robotic manipulators using time-varying disturbance observer-based sliding mode method. J. Intell. Robot. Syst. 2022, 104, 36. [Google Scholar] [CrossRef]
- Abido, M.A. Power system stability enhancement using FACTS controllers: A review. Arab. J. Sci. Eng. 2009, 34, 153–172. [Google Scholar]




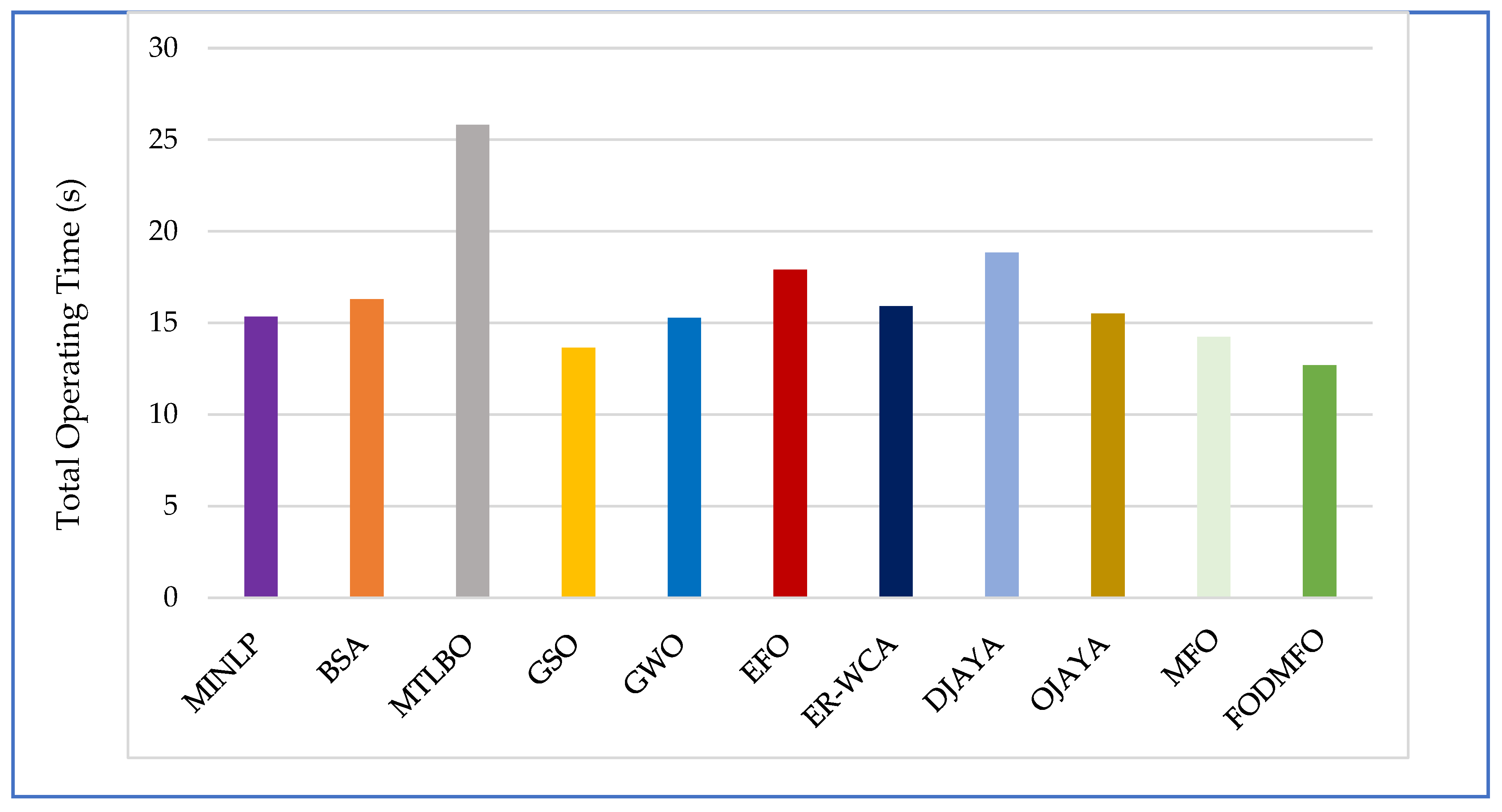
| Functions | Dim | MFO [55] | PSO [55] | GSA [55] | BA [55] | FODMFO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| 100 | 0.000117 | 0.00015 | 1.32115 | 1.15388 | 608.232 | 464.654 | 20,792.4 | 5892.40 | 4.23 × 10−34 | 4.20 × 10−34 | |
| 100 | 0.000639 | 0.000877 | 7.71556 | 4.13212 | 22.7526 | 3.36513 | 89.785 | 41.9577 | 4.02 × 10−17 | 1.80 × 10−17 | |
| 100 | 696.730 | 188.527 | 736.393 | 361.781 | 135,760. | 48,652.6 | 62,481.3 | 29,769.1 | 3.64 × 10−33 | 4.64 × 10−33 | |
| 100 | 70.6864 | 5.27505 | 12.9728 | 2.63443 | 78.7819 | 2.81410 | 49.7432 | 10.14363 | 1.77 × 10−17 | 6.40 × 10−18 | |
| 100 | 139.148 | 120.260 | 77,360.83 | 51,156.15 | 741.003 | 781.2393 | 199,512 | 125,238 | 7.3340 | 0.1542 | |
| 100 | 0.00011 | 9.87 × 10−5 | 286.651 | 107.079 | 3080.96 | 898.635 | 17,053.4 | 4917.56 | 0.1210 | 0.0821 | |
| 100 | 0.091155 | 0.04642 | 1.037316 | 0.310315 | 0.112975 | 0.037607 | 6.045055 | 3.045277 | 2.34 × 10−4 | 1.73 × 10−4 | |
| 100 | 8496.78 | 725.8737 | −3571 | 430.7989 | −2352.32 | 382.167 | 65,535 | 0 | −2.51 × 103 | 317.3344 | |
| 100 | 84.600 | 16.1665 | 124.29 | 14.2509 | 31.0001 | 13.6605 | 96.2152 | 19.5875 | 0.2530 | 1.9868 | |
| 100 | 1.2603 | 0.72956 | 9.1679 | 1.56898 | 3.74098 | 0.17126 | 15.9460 | 0.77495 | 3.98 × 10−15 | 1.20 × 10−15 | |
| 100 | 0.0190 | 0.02173 | 12.418 | 4.16583 | 0.04978 | 0.04978 | 220.281 | 54.7066 | 0.0055 | 0.0291 | |
| Functions | Dim | FPA [55] | SMS [55] | FA [55] | GA [55] | FODMFO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| 100 | 203.638 | 78.3984 | 120 | 0 | 7480.74 | 894.849 | 21,886.0 | 2879.58 | 4.23 × 10−34 | 4.20 × 10−34 | |
| 100 | 11.1687 | 2.91959 | 0.0205 | 0.00471 | 39.3253 | 2.46586 | 56.5175 | 5.66085 | 4.02 × 10−17 | 1.80 × 10−17 | |
| 100 | 237.56 | 136.6463 | 37,820 | 0 | 17,357.3 | 1740.11 | 37,010.2 | 5572.21 | 3.64 × 10−33 | 4.64 × 10−33 | |
| 100 | 12.5728 | 4 2.29 | 69.1700 | 3.87666 | 33.9535 | 1.86966 | 59.14331 | 4.648526 | 1.77 × 10−17 | 6.40 × 10−18 | |
| 100 | 10,974. | 12,057.2 | 638,224 | 729,967 | 3,795,009 | 759,030. | 3,132,141 | 5,264,496 | 7.3340 | 0.1542 | |
| 100 | 175.38 | 63.4525 | 41,439. | 3295.23 | 7828.72 | 975.210 | 20,964.8 | 3868.10 | 0.1210 | 0.0821 | |
| 100 | 0.13594 | 0.061212 | 0.04952 | 0.024015 | 1.906313 | 0.460056 | 13.37504 | 3.08149 | 2.34 × 10−4 | 1.73 × 10−4 | |
| 100 | −8086.74 | 155.346 | −3942.82 | 404.160 | −3662.05 | 214.163 | −6331.19 | 332.566 | −2.51 × 103 | 317.3 | |
| 100 | 92.6917 | 14.2239 | 152.844 | 18.5535 | 214.895 | 17.2191 | 236.82 | 19.03359 | 0.2530 | 1.9868 | |
| 100 | 6.84483 | 1.24998 | 19.1325 | 0.23852 | 14.5676 | 0.46751 | 17.8461 | 0.53114 | 3.98 × 10−15 | 1.20 × 10−15 | |
| 100 | 2.7160 | 0.72771 | 420.525 | 25.25612 | 69.65755 | 12.11393 | 179.9046 | 32.43956 | 0.0055 | 0.0291 | |
| Primary Relay | Fault Current (A) | Backup Relay | Fault Current (A) | ||
|---|---|---|---|---|---|
| Relay No | CTR | PTS | |||
| 1 | 300/5 | 5 | 1978.90 | 5 | 175.00 |
| 2 | 200/5 | 1.5 | 1525.70 | 4 | 545.00 |
| 3 | 200/5 | 5 | 1683.90 | 1 | 617.22 |
| 4 | 300/5 | 4 | 1815.40 | 6 | 466.17 |
| 5 | 200/5 | 2 | 1499.66 | 3 | 384.00 |
| 6 | 400/5 | 2.5 | 1766.30 | 2 | 145.34 |
| Relay No | MFO | Relay No | FODMFO | ||
|---|---|---|---|---|---|
| TDS | PTS | TDS | PTS | ||
| 1 | 0.1021 | 1.500 | 1 | 0.1001 | 1.500 |
| 2 | 0.1000 | 3.000 | 2 | 0.1000 | 3.000 |
| 3 | 0.1000 | 3.000 | 3 | 0.1000 | 3.500 |
| 4 | 0.1120 | 3.000 | 4 | 0.1000 | 2.500 |
| 5 | 0.1000 | 2.000 | 5 | 0.1000 | 2.000 |
| 6 | 0.1009 | 1.500 | 6 | 0.1002 | 1.500 |
| Objective function (s) | 1.5696 | 1.5222 | |||
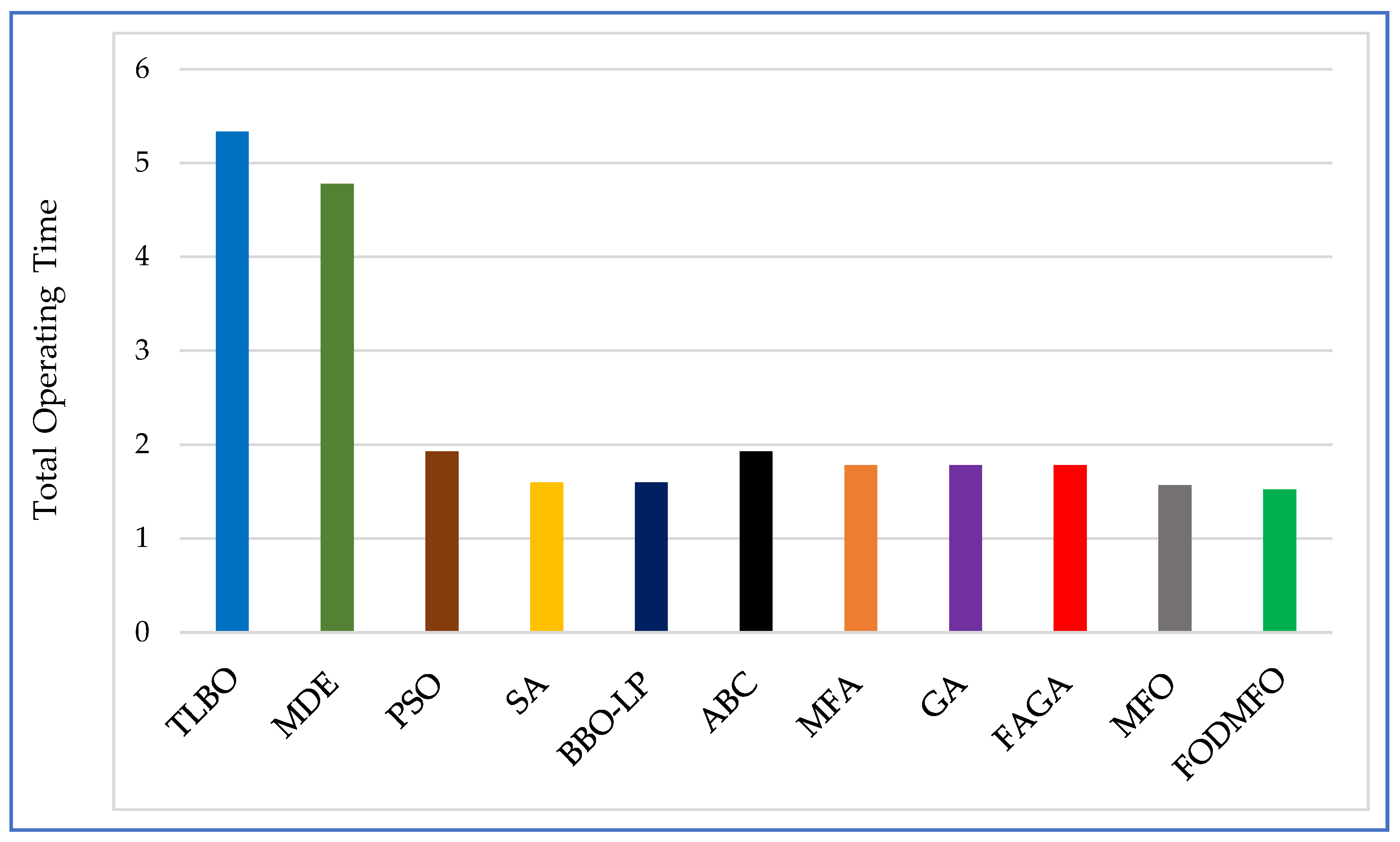
| Algorithm | Objective Function (s) |
|---|---|
| TLBO [37] | 5.3349 |
| MDE [31] | 4.7806 |
| PSO [30] | 1.9258 |
| SA [22] | 1.599 |
| BBO-LP [36] | 1.59871 |
| ABC [42] | 1.9258 |
| MFA [42] | 1.78039 |
| GA [42] | 1.78047 |
| FAGA [42] | 1.78039 |
| MFO | 1.5696 |
| FODMFO | 1.5222 |
| Relay No | CTR | Relay No | CTR |
|---|---|---|---|
| 1 | 1200/5 | 8 | 1200/5 |
| 2 | 1200/5 | 9 | 800/5 |
| 3 | 800/5 | 10 | 1200/5 |
| 4 | 1200/5 | 11 | 1200/5 |
| 5 | 1200/5 | 12 | 1200/5 |
| 6 | 1200/5 | 13 | 1200/5 |
| 7 | 800/5 | 14 | 800/5 |
| Primary Relay | Fault Current (A) | Backup Relay | Fault Current (A) |
|---|---|---|---|
| 1 | 3232 | 6 | 3232 |
| 2 | 5924 | 1 | 996 |
| 2 | 5924 | 7 | 1890 |
| 3 | 3556 | 2 | 3556 |
| 4 | 3783 | 3 | 2244 |
| 5 | 2401 | 4 | 2401 |
| 6 | 6109 | 5 | 1197 |
| 6 | 6109 | 14 | 1874 |
| 7 | 5223 | 5 | 1197 |
| 7 | 5223 | 13 | 987 |
| 8 | 6093 | 7 | 1890 |
| 8 | 6093 | 9 | 1165 |
| 9 | 2484 | 10 | 2484 |
| 10 | 3883 | 11 | 2344 |
| 11 | 3707 | 12 | 3707 |
| 12 | 5899 | 13 | 987 |
| 12 | 5899 | 14 | 1874 |
| 13 | 2991 | 8 | 2991 |
| 14 | 5199 | 1 | 996 |
| 14 | 5199 | 9 | 1165 |
| Relay No | MFO | Relay No | FODMFO | ||
|---|---|---|---|---|---|
| TDS | PTS | TDS | PTS | ||
| 1 | 0.1000 | 2.5000 | 1 | 0.1001 | 2.5000 |
| 2 | 0.3600 | 1.5000 | 2 | 0.2300 | 2.5000 |
| 3 | 0.3010 | 2.0000 | 3 | 0.2021 | 2.5000 |
| 4 | 0.1700 | 2.0000 | 4 | 0.1523 | 2.5000 |
| 5 | 0.1031 | 2.5000 | 5 | 0.1030 | 2.5000 |
| 6 | 0.2000 | 1.5000 | 6 | 0.2209 | 2.0000 |
| 7 | 0.2601 | 2.5000 | 7 | 0.3000 | 1.5000 |
| 8 | 0.2501 | 2.0000 | 8 | 0.2000 | 2.5000 |
| 9 | 0.2201 | 1.5000 | 9 | 0.1700 | 2.5000 |
| 10 | 0.3106 | 1.0000 | 10 | 0.2110 | 2.0000 |
| 11 | 0.2300 | 2.0000 | 11 | 0.1744 | 2.5000 |
| 12 | 0.3100 | 2.5000 | 12 | 0.3500 | 1.0000 |
| 13 | 0.2405 | 1.0000 | 13 | 0.1999 | 1.0000 |
| 14 | 0.3005 | 2.0000 | 14 | 0.3700 | 1.0000 |
| Objective function (s) | 9.5455 | 8.6567 | |||
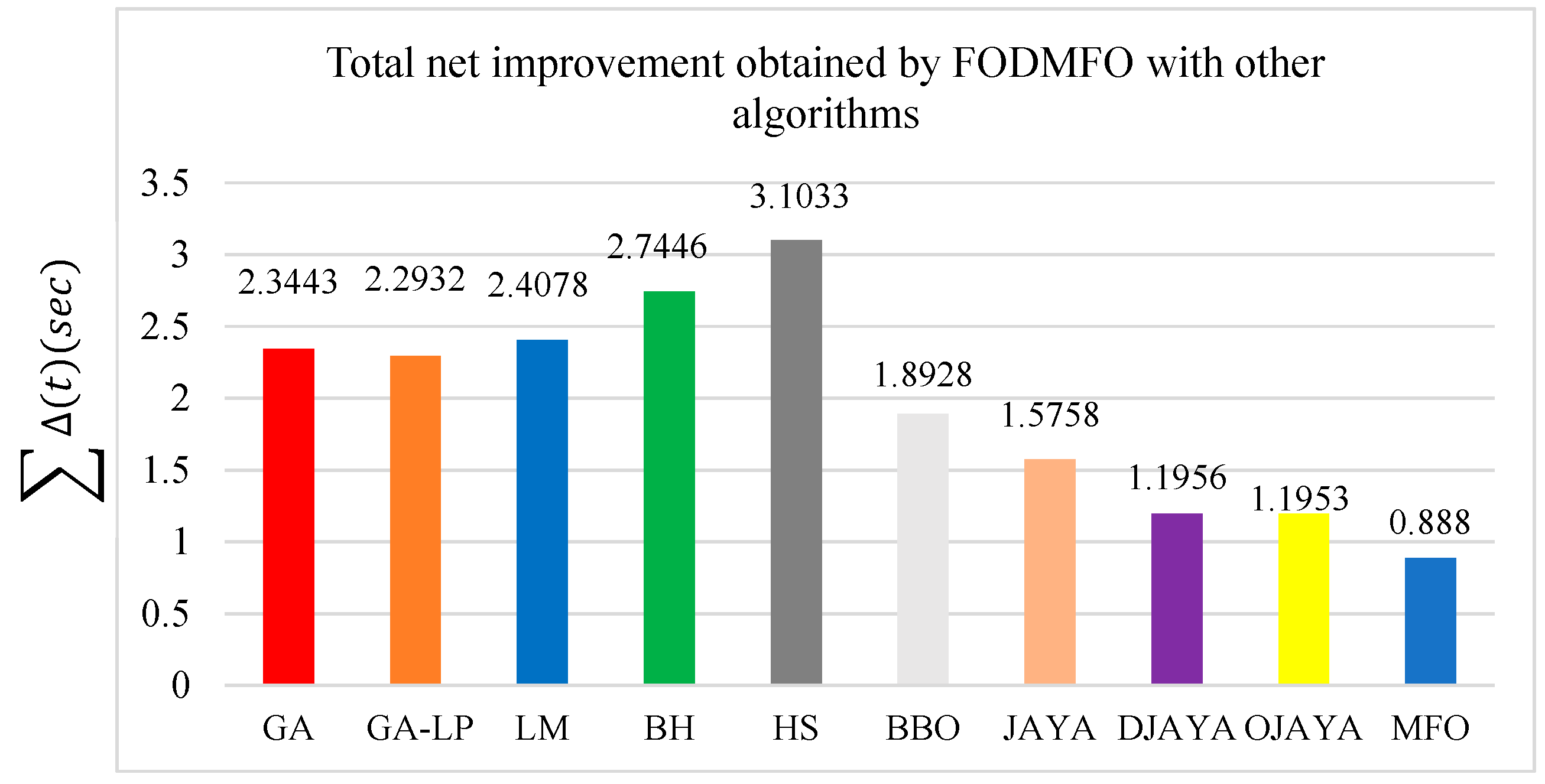
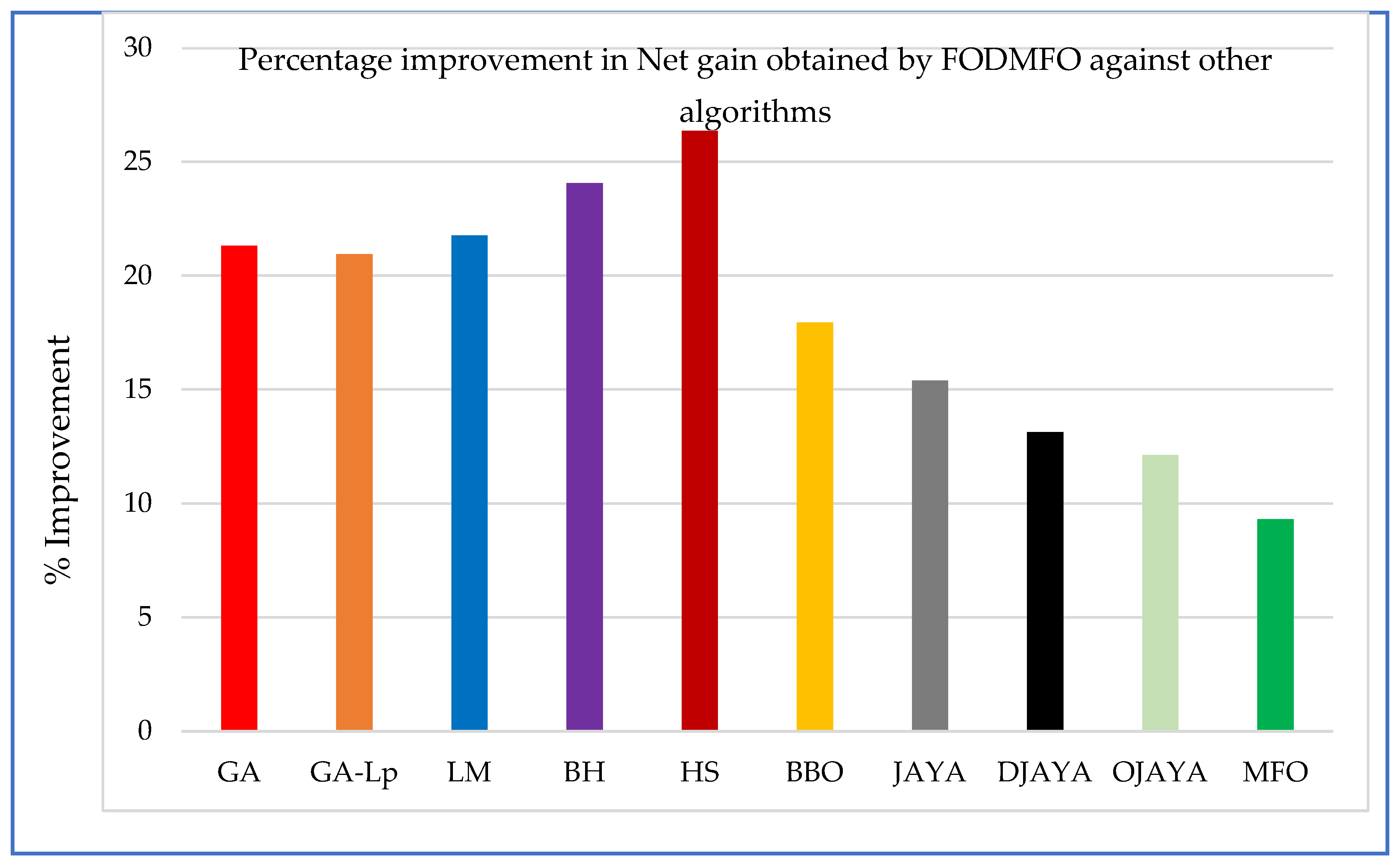
| Method | Objective Function (s) |
|---|---|
| GA [13] | 11.001 |
| GA-LP [13] | 10.9499 |
| LM [5] | 11.0645 |
| BH [20] | 11.401 |
| HS [20] | 11.760 |
| BBO [36] | 10.5495 |
| JAYA [6] | 10.2325 |
| DJAYA [6] | 9.9661 |
| OJAYA [6] | 9.8520 |
| MFO | 9.5455 |
| FODMFO | 8.6567 |
| Relay No | CT Ratio |
|---|---|
| 18-20-21-29 | 1600/5 |
| 2-4-8-11-12-14-15-23 | 1200/5 |
| 1-3-5-10-13-19-36-37-40-42 | 800/5 |
| 6-7-9-16-24-25-26-27-28-31-32-33-35 | 600/5 |
| 17-22-30-34-38-39-41 | 400/5 |
| Primary Relay | Fault Current (A) | Backup Relay | Fault Current (A) | Primary Relay | Fault Current (A) | Backup Relay | Fault Current (A) |
|---|---|---|---|---|---|---|---|
| 1 | 3621 | 6 | 1233 | 20 | 7662 | 30 | 681 |
| 2 | 4597 | 4 | 1477 | 21 | 8384 | 17 | 599 |
| 2 | 4597 | 16 | 743 | 21 | 8384 | 19 | 1372 |
| 3 | 3984 | 1 | 853 | 21 | 8384 | 30 | 681 |
| 3 | 3984 | 16 | 743 | 22 | 1950 | 23 | 979 |
| 4 | 4382 | 7 | 1111 | 22 | 1950 | 34 | 970 |
| 4 | 4382 | 12 | 1463 | 23 | 4910 | 11 | 1475 |
| 4 | 4382 | 20 | 1808 | 23 | 4910 | 13 | 1053 |
| 5 | 3319 | 2 | 922 | 24 | 2296 | 21 | 175 |
| 6 | 2647 | 8 | 1548 | 24 | 2296 | 34 | 970 |
| 6 | 2647 | 10 | 1100 | 25 | 2289 | 15 | 969 |
| 7 | 2497 | 5 | 1397 | 25 | 2289 | 18 | 1320 |
| 7 | 2497 | 10 | 1100 | 26 | 2300 | 28 | 1192 |
| 8 | 4695 | 3 | 1424 | 26 | 2300 | 36 | 1109 |
| 8 | 4695 | 12 | 1463 | 27 | 2011 | 25 | 903 |
| 8 | 4695 | 20 | 1808 | 27 | 2011 | 36 | 1109 |
| 9 | 2943 | 5 | 1397 | 28 | 2525 | 29 | 1828 |
| 9 | 2943 | 8 | 1548 | 28 | 2525 | 32 | 697 |
| 10 | 3568 | 14 | 1175 | 29 | 8346 | 17 | 599 |
| 11 | 4342 | 3 | 1424 | 29 | 8346 | 19 | 1372 |
| 11 | 4342 | 7 | 1111 | 29 | 8346 | 22 | 642 |
| 11 | 4342 | 20 | 1808 | 30 | 1736 | 27 | 1039 |
| 12 | 4195 | 13 | 1503 | 30 | 1736 | 32 | 697 |
| 12 | 4195 | 24 | 753 | 31 | 2867 | 27 | 697 |
| 13 | 3402 | 9 | 1009 | 31 | 2867 | 29 | 1828 |
| 14 | 4606 | 11 | 1475 | 32 | 2069 | 33 | 1162 |
| 14 | 4606 | 24 | 753 | 32 | 2069 | 42 | 907 |
| 15 | 4712 | 1 | 853 | 33 | 2305 | 21 | 1326 |
| 15 | 4712 | 4 | 1477 | 33 | 2305 | 23 | 979 |
| 16 | 2225 | 18 | 1320 | 34 | 1715 | 31 | 809 |
| 16 | 2225 | 26 | 905 | 34 | 1715 | 42 | 907 |
| 17 | 1875 | 15 | 969 | 35 | 2095 | 25 | 903 |
| 17 | 1875 | 26 | 905 | 35 | 2095 | 28 | 1192 |
| 18 | 8426 | 19 | 1372 | 36 | 3283 | 38 | 882 |
| 18 | 8426 | 22 | 642 | 37 | 3301 | 35 | 910 |
| 18 | 8426 | 30 | 681 | 38 | 1403 | 40 | 1403 |
| 19 | 3998 | 3 | 1424 | 39 | 1434 | 37 | 1434 |
| 19 | 3998 | 7 | 1111 | 40 | 3140 | 41 | 745 |
| 19 | 3998 | 12 | 1463 | 41 | 1971 | 31 | 809 |
| 20 | 7662 | 17 | 599 | 41 | 1971 | 33 | 1162 |
| 20 | 7662 | 22 | 642 | 42 | 3295 | 39 | 896 |
| Relay No | MFO | Relay No | FODMFO | ||
|---|---|---|---|---|---|
| TDS | PTS | TDS | PTS | ||
| 1 | 0.1000 | 1.9800 | 1 | 0.1000 | 2.5000 |
| 2 | 0.1024 | 0.5120 | 2 | 0.1000 | 0.5000 |
| 3 | 0.1793 | 1.0011 | 3 | 0.1532 | 1.4999 |
| 4 | 0.1000 | 1.9810 | 4 | 0.1000 | 2.0000 |
| 5 | 0.1800 | 1.2100 | 5 | 0.1100 | 1.3120 |
| 6 | 0.1246 | 1.8000 | 6 | 0.1300 | 1.7990 |
| 7 | 0.1117 | 2.5000 | 7 | 0.1018 | 1.9998 |
| 8 | 0.1140 | 1.5900 | 8 | 0.1200 | 0.6000 |
| 9 | 0.1016 | 0.5011 | 9 | 0.1021 | 0.5000 |
| 10 | 0.1213 | 0.5000 | 10 | 0.1021 | 0.5000 |
| 11 | 0.1730 | 0.5000 | 11 | 0.1800 | 0.5000 |
| 12 | 0.1067 | 1.3010 | 12 | 0.1080 | 1.2990 |
| 13 | 0.1006 | 1.9000 | 13 | 0.1000 | 2.0000 |
| 14 | 0.1000 | 1.8000 | 14 | 0.1000 | 1.7990 |
| 15 | 0.1000 | 2.5000 | 15 | 0.1000 | 2.5000 |
| 16 | 0.1073 | 0.8423 | 16 | 0.1090 | 0.5999 |
| 17 | 0.1855 | 0.5002 | 17 | 0.1900 | 0.5000 |
| 18 | 0.1000 | 1.5670 | 18 | 0.1000 | 1.6999 |
| 19 | 0.1054 | 0.5001 | 19 | 0.1060 | 0.5000 |
| 20 | 0.1000 | 1.7000 | 20 | 0.1001 | 1.6988 |
| 21 | 0.1000 | 1.7001 | 21 | 0.1000 | 1.6988 |
| 22 | 0.1000 | 2.5000 | 22 | 0.1000 | 2.5000 |
| 23 | 0.1011 | 1.2000 | 23 | 0.1000 | 1.3120 |
| 24 | 0.1045 | 2.5000 | 24 | 0.1001 | 2.4999 |
| 25 | 0.1447 | 1.7740 | 25 | 0.1500 | 1.8000 |
| 26 | 0.1630 | 1.3010 | 26 | 0.1500 | 1.4100 |
| 27 | 0.1633 | 0.5000 | 27 | 0.1701 | 0.5000 |
| 28 | 0.2000 | 1.8000 | 28 | 0.1990 | 1.9800 |
| 29 | 0.1000 | 2.5000 | 29 | 0.1002 | 1.7532 |
| 30 | 0.1000 | 2.5000 | 30 | 0.1000 | 2.5000 |
| 31 | 0.1000 | 2.5000 | 31 | 0.1001 | 2.5000 |
| 32 | 0.1000 | 2.5000 | 32 | 0.1111 | 2.5000 |
| 33 | 0.3000 | 0.5000 | 33 | 0.2901 | 0.5000 |
| 34 | 0.1762 | 1.4000 | 34 | 0.1800 | 1.5000 |
| 35 | 0.3007 | 0.5000 | 35 | 0.1000 | 0.5000 |
| 36 | 0.1015 | 2.5000 | 36 | 0.1001 | 2.5000 |
| 37 | 0.3000 | 0.5000 | 37 | 0.1000 | 0.5000 |
| 38 | 0.2007 | 0.5000 | 38 | 0.1910 | 0.5000 |
| 39 | 0.1410 | 1.3990 | 39 | 0.1000 | 1.5000 |
| 40 | 0.2000 | 1.2000 | 40 | 0.1000 | 0.5000 |
| 41 | 0.1444 | 1.8010 | 41 | 0.1003 | 1.9000 |
| 42 | 0.1000 | 2.5000 | 42 | 0.1000 | 2.5000 |
| Objective function (s) 14.2456 | 12.6992 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wadood, A.; Park, H. A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays. Fractal Fract. 2024, 8, 251. https://doi.org/10.3390/fractalfract8050251
Wadood A, Park H. A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays. Fractal and Fractional. 2024; 8(5):251. https://doi.org/10.3390/fractalfract8050251
Chicago/Turabian StyleWadood, Abdul, and Herie Park. 2024. "A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays" Fractal and Fractional 8, no. 5: 251. https://doi.org/10.3390/fractalfract8050251
APA StyleWadood, A., & Park, H. (2024). A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays. Fractal and Fractional, 8(5), 251. https://doi.org/10.3390/fractalfract8050251







