Abstract
Fractional-order differential equations have been proved to have great practical application value in characterizing the dynamical peculiarity in biology. In this article, relying on earlier work, we formulate a new fractional oxygen–plankton model with delay. First of all, the features of the solutions of the fractional delayed oxygen–plankton model are explored. The judgment rules on non-negativeness, existence and uniqueness and the boundedness of the solution are established. Subsequently, the generation of bifurcation and stability of the model are dealt with. Delay-independent parameter criteria on bifurcation and stability are presented. Thirdly, a hybrid controller and an extended hybrid controller are designed to control the time of onset of bifurcation and stability domain of this model. The critical delay value is provided to display the bifurcation point. Last, software experiments are offered to support the acquired key outcomes. The established outcomes of this article are perfectly innovative and provide tremendous theoretical significance in balancing the oxygen density and the phytoplankton density in biology.
Keywords:
fractional oxygen–plankton model; well-posedness; Hopf bifurcation; stability; hybrid controller; delay MSC:
34C23; 34K18; 37GK15; 39A11; 92B20
1. Introduction
Phytoplankton are special plant forms in communities and can be regarded as the foremost producers in marine ecosystems [1]. They are the crucial foundation of the food chain for various aquatic life and have important effects on the chemical balance of life in the natural world because of their consumption of CO2 and release of O2, owing to their chlorophyll [1]. Zooplankton are special animal forms in communities and live on phytoplankton. The relationship between zooplankton and phytoplankton is that of predator and prey. Predator–prey models have attracted great interest from various scholars due to their great value in ocean ecology.
During the past decades, delayed dynamical models have attracted great interest from numerous mathematicians and biologists. In particular, delay often occur in biological and ecological models since some conversion processes between two different biological states do not take place immediately in these systems. In many cases, a delay will result in the alteration of the dynamical behavior of these dynamical models. For example, a delay will lead to the loss of stability, onset of periodic vibration phenomenon, generation of chaos and so on. In biology, delays also play a vital role in interactions between prey populations and predator populations. A great deal of studies show that delayed predator–prey models display more plentiful dynamical behavior than general predator–prey models. A lot of ordinary differential predator–prey models ignore the delay of the functional response in system elements, especially in the consumption of oxygen [2,3,4,5,6]. In reality, it is generally recognized that the dynamical behavior of phytoplankton is affected by delays, owing to various factors such as temperature, light, nutrients, salinity and so on [1]. For a long time, many valuable works on delayed oxygen–plankton models have been carried out and many excellent results have been reported. For example, Sekerci and Ozarslan [7] dealt with a fractional-order oxygen–plankton model involving a climate factor by applying Caputo–Fabrizio and Atangana-Baleanu nonsingular fractional operators. The study shows that global warming plays a vital role in the depletion of oxygen and extinction of plankton. Gökçe et al. [8] explored the stability and the emergence of bifurcation of an oxygen–plankton system involving delay. The derived results provided important theoretical value in climate variation and global warming. Guo et al. [9] investigated a stochastic plankton–nutrient system. The derived findings showed that plankton mortality is beneficial to plankton survival in aquatic environments. For more detailed aspects, one can see [10,11,12,13].
In 2020, Gökçe et al. [1] formulated the following oxygen–plankton model with delay:
where stands for the oxygen density at time t and stands for the phytoplankton density at time t. stands for the environmental factor, the parameters are half saturation constants, stands for the growth rate of phytoplankton, is the maximum per capita phytoplankton respiration rate, r stands for the intraspecific competition coefficient of phytoplankton, stands for natural death coefficient of phytoplankton, stands for the strength of delayed feedback, stands for feedback time of the population growth of phytoplankton. All the parameters are non-negative. For detailed implications of the parameters in model (1), one may consult [1].
Here we must point out that all studies mentioned above are merely concerned with integer-order dynamical equations. In the past decades, fractional-order dynamical equations have been found to be a more suitable tool in portraying the object phenomena in real life, since they have the ability to characterize the memory and genetic impact of populations in the entire life of many ecosystems [14]. Recently, many works on various fractional-order dynamical models have been carried out and very rich results on this topic have been reported. For instance, Shi et al. [15] focused on the chaotic behavior and bifurcation phenomenon of a fractional delayed financial dynamical model. Ramesh et al. [16] discussed the well-posedness and bifurcation of a fractional prey–predator model with delay and Holling type-II functional response. Ali et al. [17] explored the stability of a fractional prey–predator model involving immigration. Ou et al. [18] carried out a mathematical analysis of the bifurcation phenomenon and controller design of a class of delayed BAM neural networks. For more detailed publications, one can consult [19,20,21,22,23,24].
In order to investigate the relationship of the oxygen density and the phytoplankton density, it is important for us to formulate a fractional delayed oxygen–plankton model to describe the hereditary peculiarity and memory function of the oxygen density and phytoplankton density. In model (1), we cannot find the hereditary peculiarity and memory function of the oxygen density and phytoplankton density. Through exploring the dynamical property of the fractional oxygen–plankton model, we can master its intrinsic interaction law of the oxygen density and the phytoplankton density and then effectively serve human beings. Keeping in mind this fact, we can modify model (1) as the following fractional-order form:
where . Since the left-hand dimensions of two equations of model (2) are and the right-hand dimensions of the two equations of model (2) are time−1, based on the idea of Mandal et al. [25], we modify the dimension of model (2) and obtain the following expression:
For simplicity, we let Then system (3) can be rewritten as
This study will explore the following topics:
- Discuss the well-posedness of system (4)
- Acquire a delay-independent parameter criterion for bifurcation and stability of system (4).
- Design a hybrid controller to explore the bifurcation control issue and stability domain of system (4).
- Design an extended hybrid controller to explore the bifurcation control issue and stability domain of system (4).
The prime contributions of this study are provided as follows:
- ⋄
- Relying on the foregone results, we formulate a novel fractional oxygen–plankton model with delay.
- ⋄
- ⋄
- A hybrid controller is effectually formulated to control the generation of bifurcation and stability domain of system (4).
- ⋄
- An extended hybrid controller is availably constructed to control the generation of bifurcation and stability domain of system (4).
- ⋄
- The exploration approach can be put to use to treat the bifurcation control issue for plentiful differential dynamical models in vast fields.
The fundamental frame of this study is provided as follows. The “Fundamental principle” section provides the indispensable lemmas and definitions for the fractional-order differential system. The “Well-posedness” section explores the existence, uniqueness, non-negativeness and boundedness to the solutions of system (4). The “Discussion of bifurcation” section probes the Hopf bifurcation and stability issue of system (4). The “Hybrid controller design for Hopf bifurcation” section handles the control problem of bifurcation of system (4) by a hybrid controller. The “ Extended hybrid controller design for Hopf bifurcation” section focuses on the control problem of bifurcation of system (4) by an extended hybrid controller. The “Two illustrated examples” section carries out Matlab (7.0) simulations to check the acquired conclusions. The “Conclusions” section ends this study.
2. Fundamental Principle
In this part, we provide several essential lemmas and definitions concerning the fractional differential system.
Definition 1
([26]). The fractional integral of order ϱ of the function is provided as follows:
where and .
Definition 2
([26]). The Caputo fractional-order derivative of order ϱ of a function is provided as follows:
where and ι represents a positive integer (. Moreover, when , then
Lemma 1
([27]). Let and . Assume that ; then, is a non-decreasing function regarding . Assume that ; then, is a non-increasing function regarding .
Lemma 2
([28]). Consider the fractional model where Label the root of the characteristic equation of . Then system is locally asymptotically stable if and system is stable if and the evert critical eigenvalue satisfying admits geometric multiplicity one.
Lemma 3
([28]). If and obeys
where , then
3. Well-Posedness
This part will deal with the well-posedness, including the existence, uniqueness, non-negativeness and boundedness, of the solutions of system (4). We use fixed point theorem to explore the existence and uniqueness of the solution, use the inequality technique to explore the non-negativeness of the solution and use a suitable function to explore the boundedness of the solution.
Theorem 1.
Label , where stands for a positive constant. For each , system (4) under the initial value admits a unique solution
Proof.
Set
where
∀, one gains
where
Then obeys the Lipschitz condition regarding U (see [29]). Therefore, Theorem 1 is correct.□
Remark 1.
From the biological viewpoint, the existence and uniqueness of the solution of model (4) imply that the oxygen density and the phytoplankton density exist and are unique.
Theorem 2.
All solutions of system (4) beginning with remain non-negative.
Proof.
Let be the initial value of system (4). Suppose that ∃ a constant ( such that
Based on model (4), we gain
In view of Lemma 1, we can find that , which is a contradiction according to system (9). Then ∀ Applying a similar approach, we can lightly conclude that ∀ .□
Remark 2.
From the biological viewpoint, the non-negativeness of the solution of model (4) implies that the oxygen density and the phytoplankton density remain at levels greater than zero. This shows that the oxygen density and the phytoplankton density continue to exist and keep the balance of the biological population.
Theorem 3.
If , then all solutions of system (4) beginning with are uniformly bounded.
Proof.
Let
Then
which produces
Taking advantage of Lemma 3, one finds
then
which completes the proof of Theorem 3.□
Remark 3.
From the biological viewpoint, the boundedness of the solution of model (4) implies that the oxygen density and the phytoplankton density lie in a limited range. This shows that the oxygen density and the phytoplankton density cannot come to infinite growth.
4. Discussion of Bifurcation
In this part, we are going to explore the stability and bifurcation phenomenon of system (4). Let be the equilibrium point of system (4), where satisfy
The characteristic equation of (17) can be expressed as
Then
where
Let ; then (20) becomes
where If
holds, then both roots of (22) conform to . Utilizing Lemma 2, we can lightly conclude that the equilibrium point of system (4) under the condition maintains locally asymptotically stable status.
By (23), one gains
Define
If
is true, because , then Equation (28) admits at least one positive real root. Hence, Equation (20) admits at least a pair of pure roots. In view of Sun et al. [30], the following outcome is acquired.
Lemma 4.
Set . Now we give the following assumption:
where
Lemma 5.
Let be a root of (20) at satisfying . Then
Relying on Lemma 2, we acquire the following outcome.
Theorem 4.
Remark 4.
Applying the Hurwitz theorem and bifurcation theory of fractional-order differential equations, we discuss the stability and onset of bifurcation for model (4). By this analysis, we know that when the parameters obey a suitable condition, the oxygen density and the phytoplankton density will tend to a fixed value and when under a suitable parameter, if the delay crosses a critical value, the oxygen density and the phytoplankton density will maintain a periodic movement.
Remark 5.
Delay-independent parameter criteria on bifurcation and stability are important. Based on these criteria, we can effectively control the stability domain and bifurcation onset under arbitrary delay.
Remark 6.
By analyzing the distribution of roots of the characteristic equation, we can seek the critical delay value. When the delay is less than the critical delay value, then the system is stable. When the delay crosses the the critical delay value, the system loses stability and Hopf bifurcation appears.
5. Hybrid Controller Design for Hopf Bifurcation
During the past several decades, numerous controllers to control the bifurcation of fractional-order differential systems have been developed. In this section, we adopt a hybrid controller relying on the viewpoint of [31]. This controller includes state feedback and parameter perturbation concerning delay. Inspired by this viewpoint, we set up the following controlled system:
where is the control parameter. Clearly, system (36) has the same equilibrium point as that in system (4). The linear part of system (5.1) at takes the expression
where
It follows from (40) that
If then (42) takes
where If
is true, then the two roots of (43) conform to . Using Lemma 2, we can lightly conclude that the equilibrium point of system (36) under the condition keeps a locally asymptotically stable level.
By (44), one gains
Define
If
holds and one considers that , then Equation (49) admits at least one positive real root. Hence, Equation (42) admits at least a pair of pure roots. In view of Sun et al. [30], we can obtain the following outcome.
Lemma 6
Label . Now we present the following assumption:
where
Lemma 7.
Let be a root of (5.5) at obeying . Then
Proof.
Then
In view of , we gain
□
Relying on Lemma 2, the following outcome is lightly acquired.
6. Extended Hybrid Controller Design for Hopf Bifurcation
In this section, we will apply two controllers to achieve the bifurcation control objective. Relying on the viewpoint of Gao [32], we design the following controller:
where and represent the derivative control coefficient and the proportional control coefficient, respectively. We add a hybrid controller to the first equation of system (4) and add a controller to the second equation of model (4). Then
where is the control parameter. System (58) can be written as
Clearly, system (59) has the same equilibrium point as that in system (4). The linear part of system (59) at takes the expression
where
It follows from (63) that
If then (65) takes
where If
is true, then the two roots of (6.10) conform to . Using Lemma 2, we can lightly conclude that the equilibrium point of system (65) under the condition keeps a locally asymptotically stable level.
By (67), one gains
Define
If
holds and one considers that , then Equation (72) admits at least one positive real root. Hence, Equation (63) admits at least a pair of pure roots. In view of Sun et al. [30], we can acquire the following outcome.
Lemma 8.
Label . Now we present the following assumption:
where
Lemma 9.
Let be a root of (63) at obeying . Then
Proof.
Relying on Lemma 2, the following outcome is lightly acquired.
Theorem 6.
Remark 7.
In [21], Xu et al. dealt with the bifurcation control for a 3D delayed plankton–oxygen model via two extended hybrid controllers. In this paper, we deal with bifurcation control for a 2D delayed plankton–oxygen model via two other extended hybrid controllers. Based on this viewpoint, our work is different from that in [21].
Remark 8.
We can effectively adjust the control parameter to adjust the stability domain and bifurcation onset via these extended hybrid controllers.
Remark 9.
By analyzing the stability and onset of Hopf bifurcation, we can adjust the delay to realize control of the stability region. By designing the extended hybrid controllers, we can narrow and enlarge the stability region and the time of bifurcation onset in biology.
7. Two Illustrated Examples
In this paper, we use Matlab software to carry out numerical simulation.
Example 1.
Consider the following fractional delayed oxygen–plankton model:
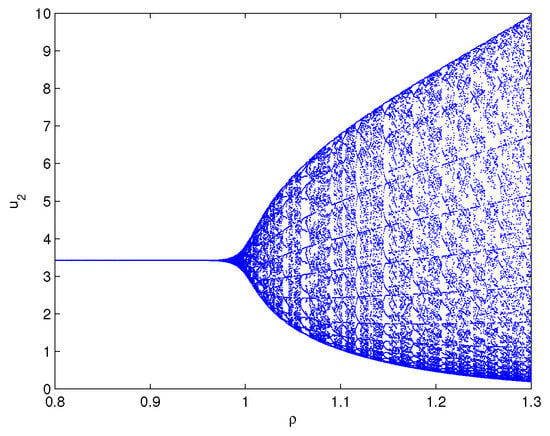
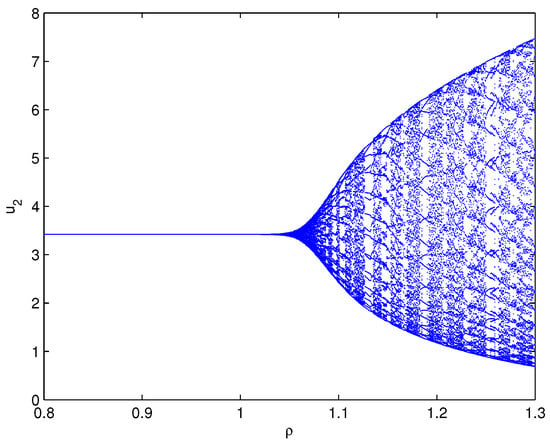
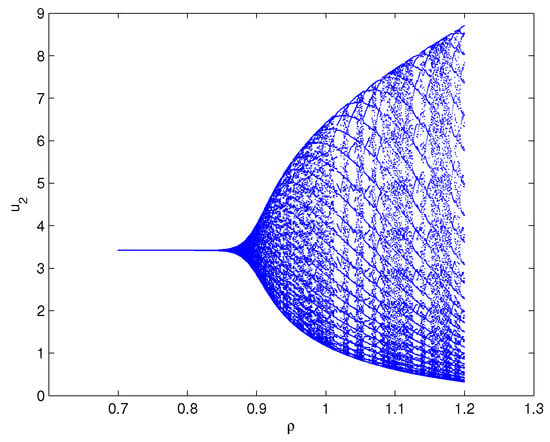
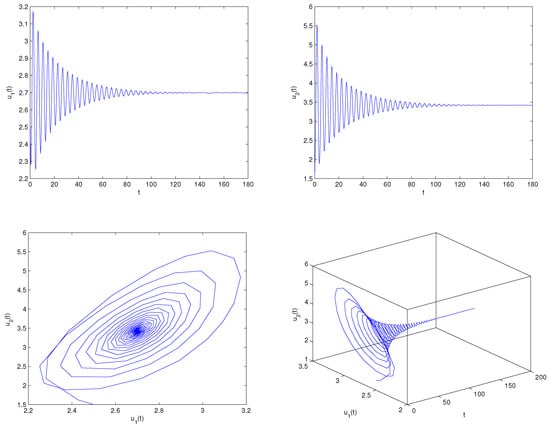
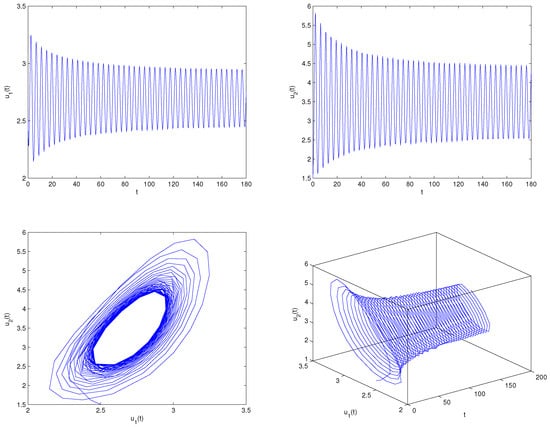
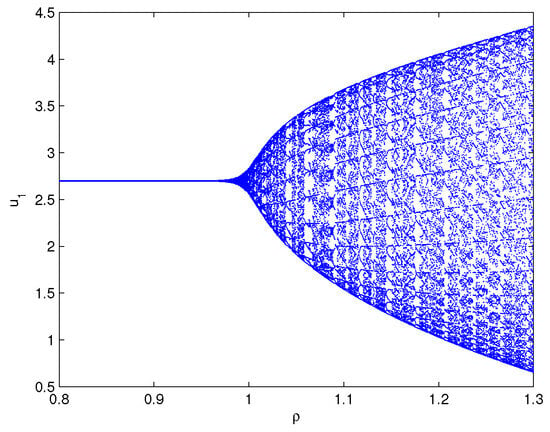
where By operation, one can lightly know that the equilibrium point of system (80) equals . Furthermore, we can find and the three assumptions in Theorem 4 are fulfilled. Select , which shows . For the delay value , the software simulation outcomes are provided in Figure 1. Figure 1 reveals perspicuously that the two variables will eventually run to , respectively, when The practical implication shows that the oxygen density will go to and the phytoplankton density will go to . Select , which shows that ρ exceeds the critical delay . For the delay value , the software simulation outcomes are provided in Figure 2. Figure 2 reveals perspicuously that the two variables will eventually remain a periodic oscillation around the values , respectively, when The practical implication shows that the oxygen density will keep cyclical movement around and the phytoplankton density will keep cyclical movement around . In addition, in order to display visually the bifurcation value of system (80), we also draw the corresponding bifurcation diagrams with regard to the delay ρ (see Figure 3 and Figure 4). One can clearly see that the bifurcation value of system (80) is .

Figure 1.
Matlab experiment results of system (80) with delay The equilibrium point maintains a locally asymptotically stable status.

Figure 2.
Matlab experiment results of system (80) with delay A family of limit cycles (i.e., Hopf bifurcations) arises near the equilibrium point .

Example 2.
Consider the following fractional controlled delayed oxygen–plankton model:
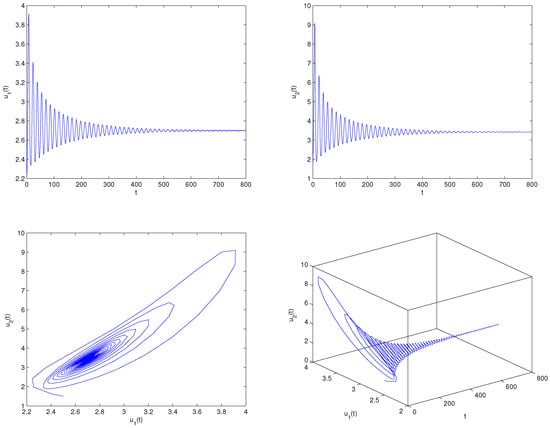
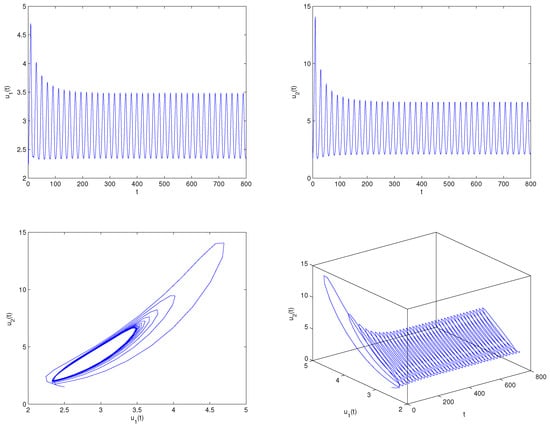
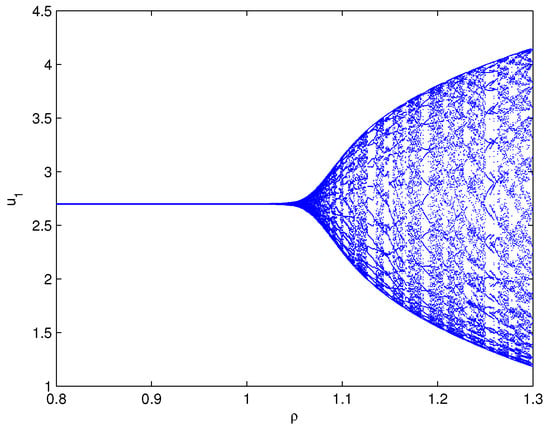
where Let By operation, one can lightly know that the equilibrium point of system (81) equals . Furthermore, we can find and the three assumptions in Theorem 5 are fulfilled. Select , which shows . For the delay value , the software simulation outcomes are provided in Figure 5. Figure 5 reveals perspicuously that the two variables will eventually run to , respectively, when The practical implication shows that the oxygen density will go to and the phytoplankton density will go to . Select , which shows that ρ exceeds the critical delay . For the delay value , the software simulation outcomes are provided in Figure 6. Figure 6 reveals perspicuously that the two variables will eventually remain a periodic oscillation around the values , respectively, when The practical implication shows that the oxygen density will keep cyclical movement around and the phytoplankton density will keep cyclical movement around . In addition, in order to display visually the bifurcation value of system (81), we also draw the corresponding bifurcation diagrams with regard to the delay ρ (see Figure 7 and Figure 8). One can clearly see that the bifurcation value of system (81) is .

Figure 5.
Matlab experiment results of system (81) with delay The equilibrium point maintains a locally asymptotically stable status.

Figure 6.
Matlab experiment results of system (81) with delay A family of limit cycles (i.e., Hopf bifurcations) arises near the equilibrium point .

Example 3.
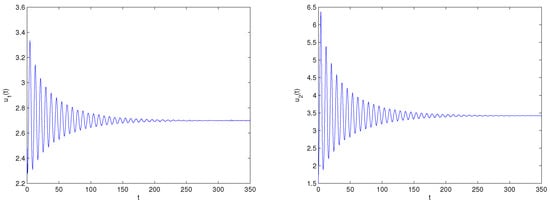
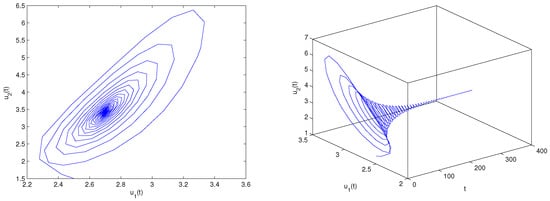
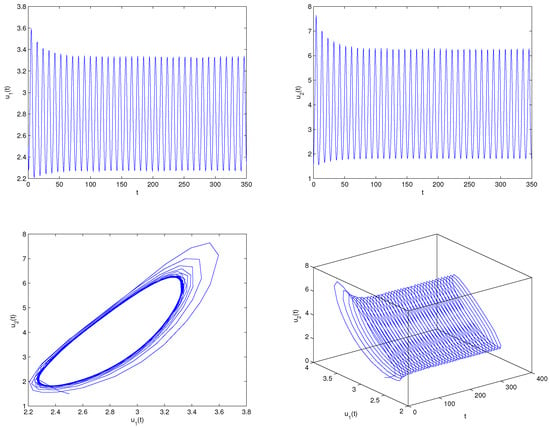
Consider the following fractional controlled delayed oxygen–plankton model:
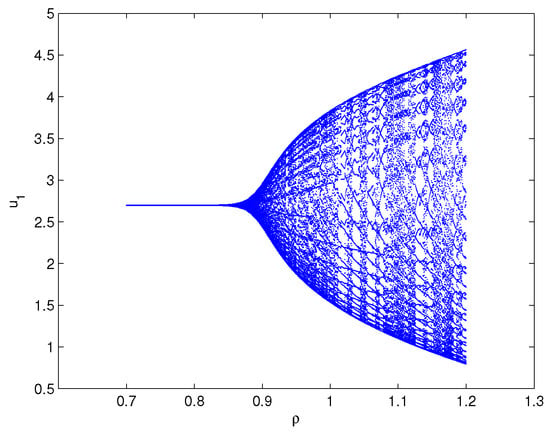
where Let By operation, one can lightly know that the equilibrium point of system (82) equals . Furthermore, we can find and the three assumptions in Theorem 6 are fulfilled. Select , which shows . For the delay value , the software simulation outcomes are provided in Figure 9. Figure 9 reveals perspicuously that the two variables will eventually run to , respectively, when The practical implication shows that the oxygen density will go to and the phytoplankton density will go to . Select , which shows that ρ exceeds the critical delay . For the delay value , the software simulation outcomes are provided in Figure 10. Figure 10 reveals perspicuously that the two variables will eventually remain a periodic oscillation around the values , respectively, when The practical implication shows that the oxygen density will keep cyclical movement around and the phytoplankton density will keep cyclical movement around . In addition, in order to display visually the bifurcation value of system (82), we also draw the corresponding bifurcation diagrams with regard to the delay ρ (see Figure 11 and Figure 12). One can clearly see that the bifurcation value of system (82) is .


Figure 9.
Matlab experiment results of system (82) with delay The equilibrium point maintains a locally asymptotically stable status.

Figure 10.
Matlab experiment results of system (82) with delay A family of limit cycles (i.e., Hopf bifurcations) arises near the equilibrium point .

Remark 10.
Based on the simulation results of Examples 1–3, one can easily know that the bifurcation points of Examples 1–3 are respectively. It is not difficult to conclude that the time of onset of bifurcation of system (80) is postponed and the stability region of system (80) is enlarged by virtue of our constructed hybrid controller and extended hybrid controller.
8. Conclusions
As is known to us, fractional-order dynamical systems have displayed great application value in describing the dynamical behavior of various differential models in biology. Based on the previous studies, in this exploration, we set up a novel fractional oxygen–plankton model with delay. Applying fixed point theorem, inequality skills and a suitable formation of the function, we explore the nature of the solutions (non-negativeness, existence, uniqueness, boundedness) to the fractional delayed oxygen–plankton model. A set of sufficient parameter conditions on non-negativeness, existence, uniqueness and boundedness are derived. Taking advantage of stability and bifurcation theory of fractional differential systems, we have found the critical delay value for stabilizing the system and controlling the onset of Hopf bifurcation of the model. By virtue of a suitable hybrid controller that involves state feedback and parameter perturbation concerning delay, we have successfully controlled the time of onset of bifurcation and stability domain of the fractional oxygen–plankton model. By using a proper extended hybrid controller that involves a hybrid controller and controller, we have effectively adjusted the time of onset of bifurcation and stability domain of the fractional oxygen–plankton model. This exploration shows that delay and control parameters are important factors that affect the stability domain and the time of onset of Hopf bifurcation of the fractional oxygen–plankton model. The obtained outcomes of this study are completely novel and display great theoretical significance in controlling and stabilizing the phytoplankton density and the oxygen density in biology. Also, this exploration approach can be applied to deal with the bifurcation and chaos for various other differential dynamical models, including integer-order and fractional-order cases. Of course, there are other bifurcation control techniques for model (4). We leave this topic for future research.
Author Contributions
Methodology, Y.Z. and C.X.; Software, C.X.; Formal analysis, Y.Z. and C.X.; Investigation, Y.Z. and C.X.; Data curation, Y.Z.; Writing—original draft, Y.Z. and C.X.; Writing—review & editing, Y.Z. and C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 12261015, No. 62062018) and the Project of High-level Innovative Talents of Guizhou Province ([2016]5651).
Data Availability Statement
No data were used in the research described in this article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Gökçe, A.; Yazar, S.; Sekerci, Y. Delay induced nonlinear dynamics of oxygen-plankton interactions. Chaos Solitons Fractals 2020, 141, 110327. [Google Scholar] [CrossRef]
- Petrovskii, S.; Sekerci, Y.; Venturino, E. Venturino, Regime shifts and ecological catastrophes in a model of plankton-oxygen dynamics under the climate change. J. Theor. Biol. 2017, 424, 91–109. [Google Scholar] [CrossRef] [PubMed]
- Shukla, J.; Misra, A.; Chandra, P. Mathematical modeling and analysis of the depletion of dissolved oxygen in eutrophied water bodies affected by organic pollutants. Nonlinear Anal. Real World Appl. 2008, 9, 1851–1865. [Google Scholar] [CrossRef]
- Sekerci, Y.; Petrovskii, S. Mathematical modelling of plankton-oxygen dynamics under the climate change. Bull. Math. Biol. 2015, 77, 2325–2353. [Google Scholar] [CrossRef] [PubMed]
- Geng, D.X.; Wang, H.; Jiang, W.H.; Wang, H.B. Double-Hopf bifurcation and Pattern Formation of a Gause-Kolmogorov-Type system with indirect prey-taxis and direct predator-taxis. Commun. Nonlinear Sci. Numer. Simul. 2024, 128, 107647. [Google Scholar] [CrossRef]
- Qi, H.K.; Liu, B. Stationary distribution of a stochastic reaction-diffusion predator-prey model with additional food and fear effect. Appl. Math. Lett. 2024, 150, 108978. [Google Scholar] [CrossRef]
- Sekerci, Y.; Ozarslan, R. Oxygen-plankton model under the effect of global warming with nonsingular fractional order. Chaos Solitons Fractals 2020, 132, 109532. [Google Scholar] [CrossRef]
- Gökçe, A.; Yazar, S.; Sekerci, Y. Sekerci, Stability of spatial patterns in a diffusive oxygen-plankton model with time lag effect. Math. Comput. Simul. 2022, 194, 109–123. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Y.; Dai, C.; Wang, L.; Liu, H.; Li, J.; Tiwari, P.K.; Zhao, M. Dynamics of a stochastic nutrient-plankton model with regime switching. Ecol. Model. 2023, 477, 110249. [Google Scholar] [CrossRef]
- McEwan, N.; Pawlowicz, R.; Pakhomov, E.; Maldonado, M.T. Seasonality of modelled planktonic food web structure in the Strait of Georgia, Canada. Ecol. Model. 2023, 482, 110402. [Google Scholar] [CrossRef]
- Saha, T.K.; Jany, Z.R.; Yeasmine, S.; Mahmud, Y.; Moniruzzaman, M.; Hossain, Z. Yeasmine, Y. Mahmud, M. Moniruzzaman, Z. Hossain, Impacts of freshwater mussels on planktonic communities and water quality. Heliyon 2023, 9, e15372. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhao, Y.; Du, P.; Ma, X.; Li, S.; Li, H.; Zhang, W.; Xiao, T. Planktonic ciliate community structure and its distribution in the oxygen minimum zones in the Bay of Bengal (eastern Indian Ocean). J. Sea Res. 2022, 190, 102311. [Google Scholar] [CrossRef]
- Lakhani, K.; Lynch-Stieglitz, J.; Monteagudo, M. Monteagudo, Constraining calcification habitat using oxygen isotope measurements in tropical planktonic foraminiferal tests from surface sediments. Mar. Micropaleontol. 2022, 170, 102074. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, Z. Impact of allee and fear effects in a fractional order prey-predator system incorporating prey refuge. Chaos 2023, 33, 013131. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.P.; He, K.; Fang, H. Chaos, Hopf bifurcation and control of a fractional-order delay financial system. Math. Comput. Simul. 2022, 194, 348–364. [Google Scholar] [CrossRef]
- Ramesh, K.; Kumar, G.R.; Nisar, K.S. A nonlinear mathematical model on the dynamical study of a fractional-order delayed predator-prey scheme that incorporates harvesting together and Holling type-II functional response. Results Appl. Math. 2023, 19, 100390. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Hosseini, K. A fractal Cfractional—order modified predator-prey mathematical model with immigrations. Math. Comput. Simul. 2023, 207, 466–481. [Google Scholar] [CrossRef]
- Ou, W.; Xu, C.J.; Cui, Q.Y.; Pang, Y.C.; Liu, Z.X.; Shen, J.W.; Baber, M.Z.; Farman, M.; Ahmad, S. Hopf bifurcation exploration and control technique in a predator-prey system incorporating delay. AIMS Math. 2023, 9, 1622–1651. [Google Scholar] [CrossRef]
- Li, P.; Gao, R.; Xu, C.; Shen, J.; Ahmad, S.; Li, Y. Exploring the impact of delay on Hopf bifurcation of a type of BAM neural network models concerning three nonidentical delays. Neural Process. Lett. 2023, 55, 5905–5921. [Google Scholar] [CrossRef]
- Xu, C.; Ou, W.; Pang, Y.; Cui, Q.; Rahman, M.U.; Farman, M.; Ahmad, S.; Zeb, A. Hopf bifurcation control of a fractional-order delayed turbidostat model via a novel extended hybrid controller. MATCH Commun. Math. Comput. Chem. 2024, 91, 367–413. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J.; Qin, Y.; Farman, M.; Ahmad, S. Mathematical exploration on control of bifurcation for a plankton-oxygen dynamical model owning delay. J. Math. Chem. 2023, 1–31. [Google Scholar] [CrossRef]
- Chinnamuniyandi, M.; Chandran, S.; Xu, C. Fractional order uncertain BAM neural networks with mixed time delays: An existence and Quasi-uniform stability analysis. J. Intell. Fuzzy Syst. 2024, 46, 4291–4313. [Google Scholar] [CrossRef]
- Uddin, M.J.; Rana, S.M.S.; Işık, S.; Kangalgil, F. On the qualitative study of a discrete fractional order prey—Cpredator model with the effects of harvesting on predator population. Chaos Solitons Fractals 2023, 175, 113932. [Google Scholar] [CrossRef]
- Balci, E. Predation fear and its carry-over effect in a fractional order prey-predator model with prey refuge. Chaos Solitons Fractals 2023, 175, 114016. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.K.; Kar, T.K. Modeling and analysis of a fractional-order prey-predator system incorporating harvesting. Model. Earth Syst. Environ. 2021, 7, 1159–1176. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Naik, M.K.; Baishya, C.; Veeresha, P. A chaos control strategy for the fractional 3D Lotka-Volterra like attractor. Math. Comput. Simul. 2023, 211, 1–22. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational engineering in systems and application multi-conference, Lille, France, 9–12 July 1996; IEEE-SMC Proceedings, Lille, 2. IMACS: Plantation, FL, USA, 1996; pp. 963–968. [Google Scholar]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z.D. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Sun, Q.S.; Xiao, M.; Tao, B.B. Local bifurcation analysis of a fractional-order dynamic model of genetic regulatory networks with delays. Neural Process. Lett. 2018, 47, 1285–1296. [Google Scholar] [CrossRef]
- Du, W.T.; Xiao, M.; Ding, J.; Yao, Y.; Wang, Z.X.; Yang, X.S. Fractional-order PD control at Hopf bifurcation in a delayed predator-prey system with trans-species infectious diseases. Math. Comput. Simul. 2023, 205, 414–438. [Google Scholar] [CrossRef]
- Gao, Z. Analytical criterion on stabilization of fractional-order plants with interval uncertainties using fractional-order PDμ controllers with a filter. ISA Trans. 2018, 83, 25–34. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).