Asymptotic and Mittag–Leffler Synchronization of Fractional-Order Octonion-Valued Neural Networks with Neutral-Type and Mixed Delays
Abstract
:1. Introduction
- For the first time in the literature, to our knowledge, an FOOVNN with time-varying, distributed, and neutral-type delays is put forward, combining fractional calculus with octonion algebra.
- The asymptotic and Mittag–Leffler synchronization properties are studied for the proposed model, and sufficient criteria are given both in terms of LMIs and of algebraic inequalities by decomposing the OVNN system of equations into a real-valued one, in order to avoid the non-associativity problem of octonion algebra.
- To accomplish synchronization, we use two different types of state feedback controllers, two different types of Lyapunov-type functionals in conjunction with two Halanay-type lemmas specific to FONNs, as well as the free weighting matrix method, a classical lemma, and Young’s inequality.
- Each of the four theorems formulated in the paper is illustrated by one numerical example.
- The model is general, and can be particularized for fractional-order CVNNs (FOCVNNs) and fractional-order QVNNs (FOQVNNs), for which the corresponding results do not exist in the literature, to our knowledge, for such general models.
2. Preliminaries
| × | ||||||||
3. Main Results
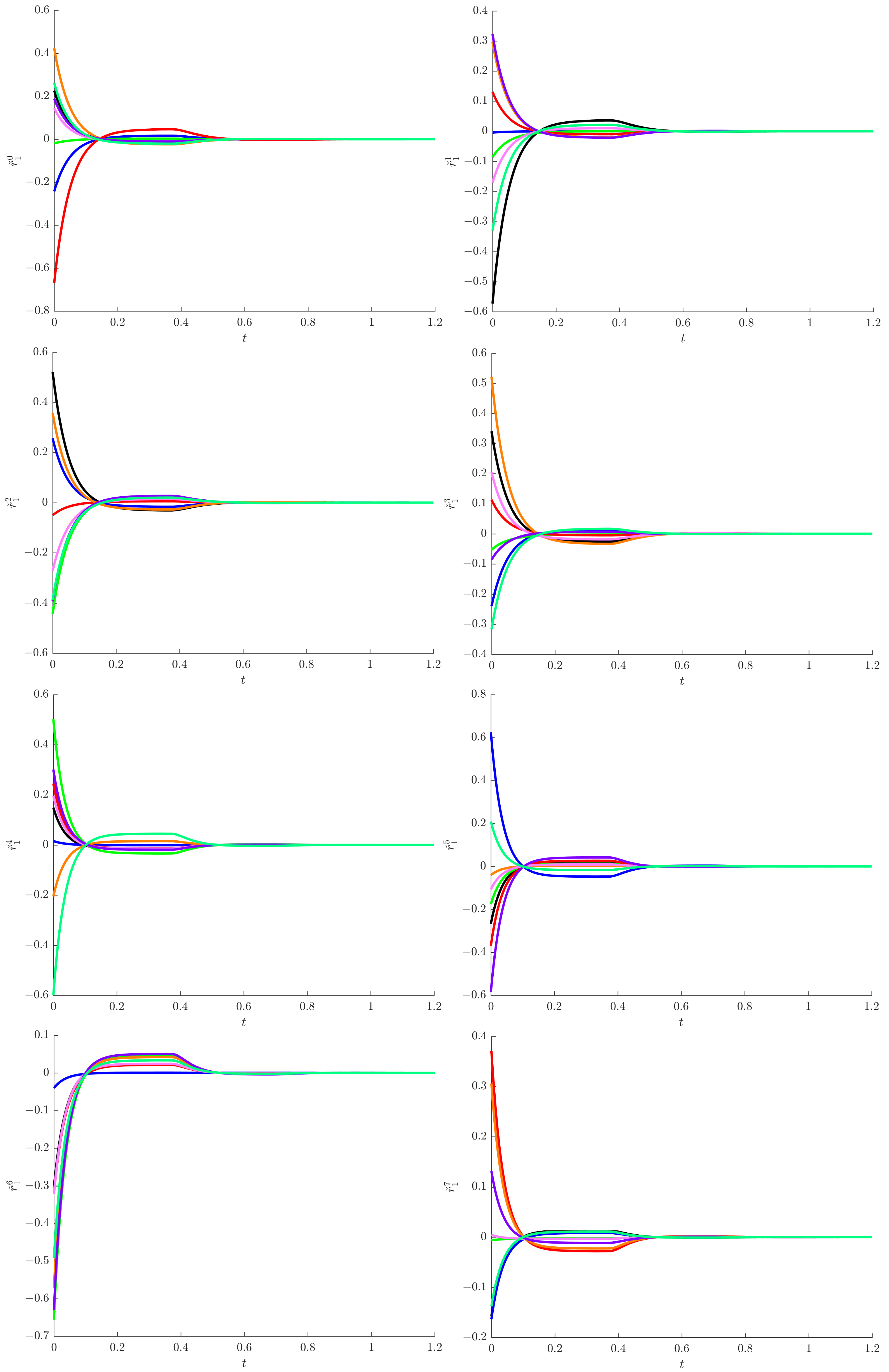
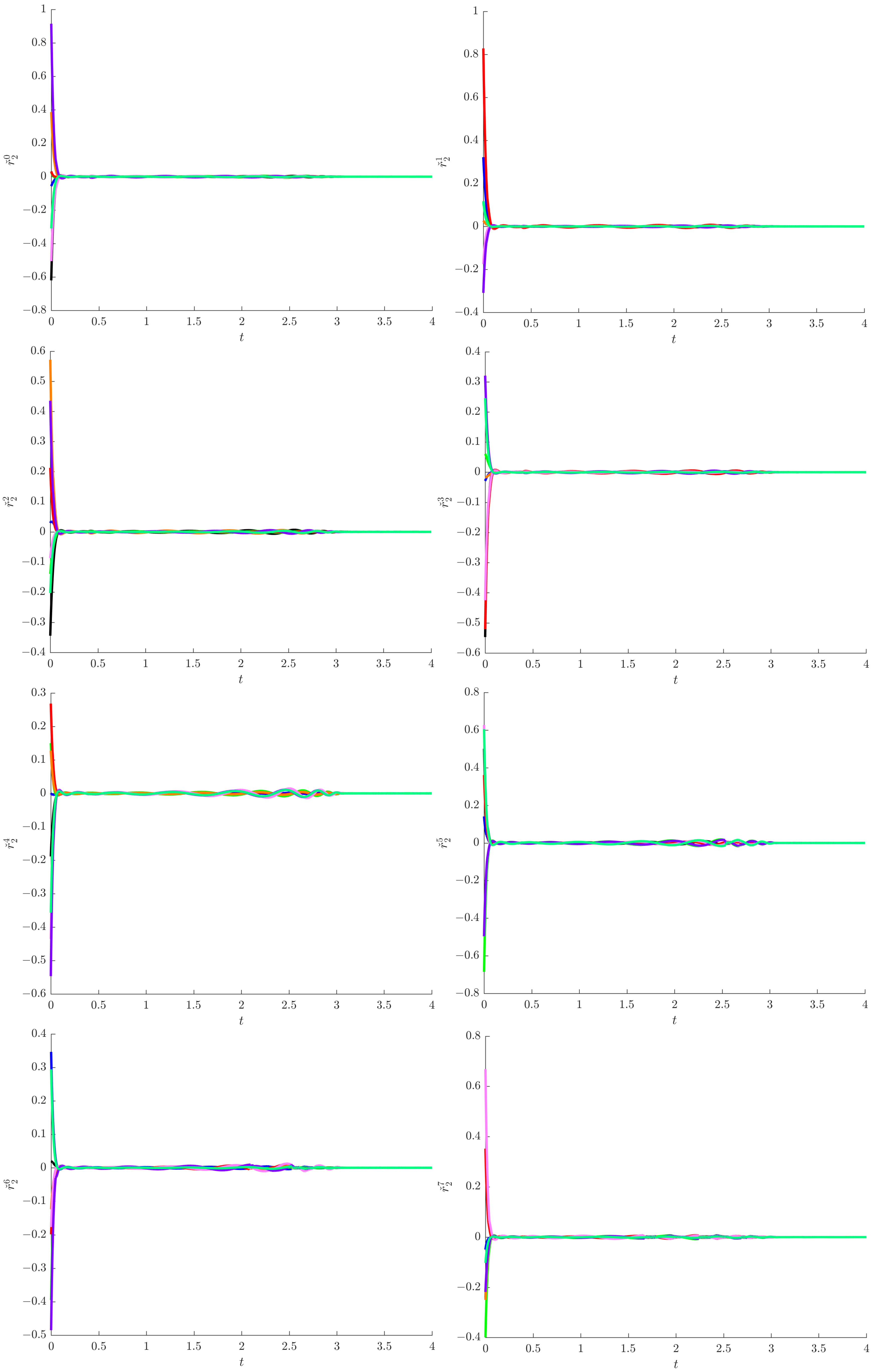
4. Numerical Examples
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popa, C.A. Octonion-Valued Neural Networks. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2016, Barcelona, Spain, 6–9 September 2016; pp. 435–443. [Google Scholar] [CrossRef]
- Snopek, K.M. Quaternions and Octonions in Signal Processing—Fundamentals and Some New Results. Prz. Telekomun.+Wiad. Telekomun. 2015, 6, 618–622. [Google Scholar] [CrossRef]
- Wang, R.; Xiang, G.; Zhang, F. L1-norm minimization for octonion signals. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016. [Google Scholar] [CrossRef]
- Błaszczyk, L.; Snopek, K.M. Octonion Fourier Transform of real-valued functions of three variables—Selected properties and examples. Signal Process. 2017, 136, 29–37. [Google Scholar] [CrossRef]
- Gao, H.Y.; Lam, K.M. From quaternion to octonion: Feature-based image saliency detection. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014. [Google Scholar] [CrossRef]
- Gao, H.Y.; Lam, K.M. Salient object detection using octonion with Bayesian inference. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014. [Google Scholar] [CrossRef]
- Bauer, S.; Leon, F.P. Hyperspectral fluorescence data fusion using quaternion and octonion phase. In Proceedings of the 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden-Baden, Germany, 19–21 September 2016. [Google Scholar] [CrossRef]
- Chanyal, B.C. Octonion massive electrodynamics. Gen. Relativ. Gravit. 2013, 46, 1646. [Google Scholar] [CrossRef]
- Demir, S.; Tanişli, M. Hyperbolic octonion formulation of the fluid Maxwell equations. J. Korean Phys. Soc. 2016, 68, 616–623. [Google Scholar] [CrossRef]
- Demir, S. Hyperbolic Octonion Formulation of Gravitational Field Equations. Int. J. Theor. Phys. 2012, 52, 105–116. [Google Scholar] [CrossRef]
- Popa, C.A. Global exponential stability of neutral-type octonion-valued neural networks with time-varying delays. Neurocomputing 2018, 309, 117–133. [Google Scholar] [CrossRef]
- Popa, C.A. Global exponential stability of octonion-valued neural networks withleakage delay and mixed delays. Neural Netw. 2018, 105, 277–293. [Google Scholar] [CrossRef]
- Chouhan, S.S.; Kumar, R.; Sarkar, S.; Das, S. Multistability analysis of octonion-valued neural networks with time-varying delays. Inf. Sci. 2022, 609, 1412–1434. [Google Scholar] [CrossRef]
- Chouhan, S.S.; Kumar, U.; Das, S.; Cao, J. Fixed time synchronization of octonion valued neural networks with time varying delays. Eng. Appl. Artif. Intell. 2023, 118, 105684. [Google Scholar] [CrossRef]
- Gao, J.; Dai, L. Weighted pseudo almost periodic solutions of octonion-valued neural networks with mixed time-varying delays and leakage delays. AIMS Math. 2023, 8, 14867–14893. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y. Weyl almost periodic solutions of octonion-valued high-order fuzzy neural networks with delays. Comput. Appl. Math. 2023, 42, 155. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhang, Y.F.; Wang, J.J. Investigation of the Time Fractional Generalized (2+1)-Dimensional Zakharov–Kuznetsov Equation with Single-Power Law Nonlinearity. Fractals 2023, 31, 2350033. [Google Scholar] [CrossRef]
- Wang, K.J.; Xu, P.; Shi, F. Nonlinear Dynamic Behaviors Of The Fractional (3+1)-Dimensional Modified Zakharov–Kuznetsov Equation. Fractals 2023, 31, 23500883. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Korkmaz, E.; Ozdemir, A.; Yildirim, K. Asymptotical Stability of Riemann-Liouville Nonlinear Fractional Neutral Neural Networks with Time-Varying Delays. J. Math. 2022, 2022, 6832472. [Google Scholar] [CrossRef]
- Popa, C.A. Neutral-Type and Mixed Delays in Fractional-Order Neural Networks: Asymptotic Stability Analysis. Fractal Fract. 2022, 7, 36. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Huang, C.; Alzabut, J.; Bagdasar, O. O(t-β)-Synchronization and Asymptotic Synchronization of Delayed Fractional Order Neural Networks. Acta Math. Sci. 2022, 42, 1273–1292. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H. Asymptotic stability and synchronization of fractional delayed memristive neural networks with algebraic constraints. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106694. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zhu, S.; Wang, H. Asymptotical stability and synchronization of Riemann–Liouville fractional delayed neural networks. Comput. Appl. Math. 2022, 42, 20. [Google Scholar] [CrossRef]
- Ci, J.; Guo, Z.; Long, H.; Wen, S.; Huang, T. Multiple asymptotical ω-periodicity of fractional-order delayed neural networks under state-dependent switching. Neural Netw. 2023, 157, 11–25. [Google Scholar] [CrossRef]
- Popa, C.A. Neutral-type, leakage, and mixed delays in fractional-order neural networks: Asymptotic synchronization analysis. AIMS Math. 2023, 8, 15969–15992. [Google Scholar] [CrossRef]
- Yang, D.; Yu, Y.; Hu, W.; Yuan, X.; Ren, G. Mean Square Asymptotic Stability of Discrete-Time Fractional Order Stochastic Neural Networks with Multiple Time-Varying Delays. Neural Process. Lett. 2023, 55, 9247–9268. [Google Scholar] [CrossRef]
- Zhang, F.; Zeng, Z. Multiple Mittag-Leffler Stability of Delayed Fractional-Order Cohen–Grossberg Neural Networks via Mixed Monotone Operator Pair. IEEE Trans. Cybern. 2021, 51, 6333–6344. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.L.; Bao, H.; Zhang, L.; Jiang, H.; Li, Z. Global Mittag–Leffler stability and synchronization of discrete-time fractional-order delayed quaternion-valued neural networks. Neurocomputing 2022, 511, 290–298. [Google Scholar] [CrossRef]
- Zhang, X.L.; Li, H.L.; Kao, Y.; Zhang, L.; Jiang, H. Global Mittag-Leffler synchronization of discrete-time fractional-order neural networks with time delays. Appl. Math. Comput. 2022, 433, 127417. [Google Scholar] [CrossRef]
- Zheng, B.; Wang, Z. Mittag-Leffler synchronization of fractional-order coupled neural networks with mixed delays. Appl. Math. Comput. 2022, 430, 127303. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, S.; Liu, X.; Wen, S. Multiple Mittag-Leffler Stability of Fractional-Order Complex-Valued Memristive Neural Networks with Delays. IEEE Trans. Cybern. 2023, 53, 5815–5825. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.N.; Li, Z.Y. Mittag-Leffler stabilization of anti-periodic solutions for fractional-order neural networks with time-varying delays. AIMS Math. 2023, 8, 1610–1619. [Google Scholar] [CrossRef]
- Popa, C.A.; Kaslik, E. Finite-Time Mittag–Leffler Synchronization of Neutral-Type Fractional-Order Neural Networks with Leakage Delay and Time-Varying Delays. Mathematics 2020, 8, 1146. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Alam, M.I.; Rajchakit, G.; Boonsatit, N.; Kumar, P.; Hammachukiattikul, P. Adaptive Fuzzy Feedback Controller Design for Finite-Time Mittag-Leffler Synchronization of Fractional-Order Quaternion-Valued Reaction-Diffusion Fuzzy Molecular Modeling of Delayed Neural Networks. IEEE Access 2021, 9, 130862–130883. [Google Scholar] [CrossRef]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H. Finite-Time Synchronization of Memristive Neural Networks with Fractional-Order. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3739–3750. [Google Scholar] [CrossRef]
- Li, X.; Cao, Y.; Zheng, C.; Feng, Z.; Xu, G. Finite-Time Synchronization of Fractional-Order Complex-Valued Cohen-Grossberg Neural Networks with Mixed Time Delays and State-Dependent Switching. Adv. Math. Phys. 2022, 2022, 4227067. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Liu, L. Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay. Fractal Fract. 2022, 6, 350. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y. Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays. Fractal Fract. 2023, 7, 294. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Vembarasan, V.; Cao, J.; Alsaedi, A. Dissipativity and stability analysis of fractional-order complex-valued neural networks with time delay. Neural Netw. 2017, 86, 42–53. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, M.; Fei, K. Dissipativity Analysis of Memristor-Based Fractional-Order Hybrid BAM Neural Networks with Time Delays. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 773–785. [Google Scholar] [CrossRef]
- Ali, M.S.; Narayanan, G.; Nahavandi, S.; Wang, J.L.; Cao, J. Global Dissipativity Analysis and Stability Analysis for Fractional-Order Quaternion-Valued Neural Networks with Time Delays. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4046–4056. [Google Scholar] [CrossRef]
- Aouiti, C.; Touati, F. Global Dissipativity of Quaternion-Valued Fuzzy Cellular Fractional-Order Neural Networks with Time Delays. Neural Process. Lett. 2022, 55, 481–503. [Google Scholar] [CrossRef]
- Xiao, J.; Zhong, S.; Wen, S. Unified Analysis on the Global Dissipativity and Stability of Fractional-Order Multidimension-Valued Memristive Neural Networks with Time Delay. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 5656–5665. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, C.; Li, M. Quasi-Synchronization and Dissipativity Analysis for Fractional-Order Neural Networks with Time Delay. Fractal Fract. 2023, 7, 364. [Google Scholar] [CrossRef]
- Aravind, R.V.; Balasubramaniam, P. Global asymptotic stability of delayed fractional-order complex-valued fuzzy cellular neural networks with impulsive disturbances. J. Appl. Math. Comput. 2022, 68, 4713–4731. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, H.; Zhang, W.; Zhang, H. Quasi-projective Synchronization for Caputo Type Fractional-order Complex-valued Neural Networks with Mixed Delays. Int. J. Control. Autom. Syst. 2022, 20, 1723–1734. [Google Scholar] [CrossRef]
- Hymavathi, M.; Muhiuddin, G.; Ali, M.S.; Al-Amri, J.F.; Gunasekaran, N.; Vadivel, R. Global Exponential Stability of Fractional Order Complex-Valued Neural Networks with Leakage Delay and Mixed Time Varying Delays. Fractal Fract. 2022, 6, 140. [Google Scholar] [CrossRef]
- Chen, S.; Song, Q.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Global asymptotic stability of fractional-order complex-valued neural networks with probabilistic time-varying delays. Neurocomputing 2021, 450, 311–318. [Google Scholar] [CrossRef]
- Song, Q.; Chen, Y.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Robust stability of fractional-order quaternion-valued neural networks with neutral delays and parameter uncertainties. Neurocomputing 2021, 420, 70–81. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, M. Stability of Memristor-based Fractional-order Neural Networks with Mixed Time-delay and Impulsive. Neural Process. Lett. 2022, 55, 4697–4718. [Google Scholar] [CrossRef]
- Han, X.; Hymavathi, M.; Sanober, S.; Dhupia, B.; Ali, M.S. Robust Stability of Fractional Order Memristive BAM Neural Networks with Mixed and Additive Time Varying Delays. Fractal Fract. 2022, 6, 62. [Google Scholar] [CrossRef]
- Liu, P.; Kong, M.; Zeng, Z. Projective Synchronization Analysis of Fractional-Order Neural Networks with Mixed Time Delays. IEEE Trans. Cybern. 2022, 52, 6798–6808. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Huang, C. Exploration of bifurcation for a fractional-order BAM neural network with n+2 neurons and mixed time delays. Chaos Solitons Fractals 2022, 159, 112117. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Liu, Z.; Yao, L. Delay-induced periodic oscillation for fractional-order neural networks with mixed delays. Neurocomputing 2022, 488, 681–693. [Google Scholar] [CrossRef]
- Yan, H.; Qiao, Y.; Ren, Z.; Duan, L.; Miao, J. Master–slave synchronization of fractional-order memristive MAM neural networks with parameter disturbances and mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107152. [Google Scholar] [CrossRef]
- Ali, M.S.; Hymavathi, M.; Alsulami, H.; Saeed, T.; Ahmad, B. Passivity Analysis of Fractional-Order Neutral-Type Fuzzy Cellular BAM Neural Networks with Time-Varying Delays. Math. Probl. Eng. 2022, 2022, 9035736. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H.; Sun, J.; Qiao, W. Stability analysis of fractional reaction-diffusion memristor-based neural networks with neutral delays via Lyapunov functions. Neurocomputing 2023, 550, 126497. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H. Pinning synchronization of fractional memristor-based neural networks with neutral delays and reaction–diffusion terms. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107039. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Cao, J.; Ho, D.W.; Huang, X. LMI-based criteria for global robust stability of bidirectional associative memory networks with time delay. Nonlinear Anal. Theory Methods Appl. 2007, 66, 1558–1572. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Hou, Y.; Dai, L. S-Asymptotically ω-Periodic Solutions of Fractional-Order Complex-Valued Recurrent Neural Networks with Delays. IEEE Access 2021, 9, 37883–37893. [Google Scholar] [CrossRef]
- Zeng, J.; Yang, X.; Wang, L.; Chen, X. Robust Asymptotical Stability and Stabilization of Fractional-Order Complex-Valued Neural Networks with Delay. Discret. Dyn. Nat. Soc. 2021, 2021, 5653791. [Google Scholar] [CrossRef]
- Pahnehkolaei, S.M.A.; Alfi, A.; Machado, J.T. Delay-dependent stability analysis of the QUAD vector field fractional order quaternion-valued memristive uncertain neutral type leaky integrator echo state neural networks. Neural Netw. 2019, 117, 307–327. [Google Scholar] [CrossRef]
- Ali, M.S.; Narayanan, G.; Shekher, V.; Alsaedi, A.; Ahmad, B. Global Mittag-Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105088. [Google Scholar] [CrossRef]
- Yan, H.; Qiao, Y.; Duan, L.; Miao, J. Novel methods to global Mittag-Leffler stability of delayed fractional-order quaternion-valued neural networks. Neural Netw. 2021, 142, 500–508. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, C.-A. Asymptotic and Mittag–Leffler Synchronization of Fractional-Order Octonion-Valued Neural Networks with Neutral-Type and Mixed Delays. Fractal Fract. 2023, 7, 830. https://doi.org/10.3390/fractalfract7110830
Popa C-A. Asymptotic and Mittag–Leffler Synchronization of Fractional-Order Octonion-Valued Neural Networks with Neutral-Type and Mixed Delays. Fractal and Fractional. 2023; 7(11):830. https://doi.org/10.3390/fractalfract7110830
Chicago/Turabian StylePopa, Călin-Adrian. 2023. "Asymptotic and Mittag–Leffler Synchronization of Fractional-Order Octonion-Valued Neural Networks with Neutral-Type and Mixed Delays" Fractal and Fractional 7, no. 11: 830. https://doi.org/10.3390/fractalfract7110830
APA StylePopa, C.-A. (2023). Asymptotic and Mittag–Leffler Synchronization of Fractional-Order Octonion-Valued Neural Networks with Neutral-Type and Mixed Delays. Fractal and Fractional, 7(11), 830. https://doi.org/10.3390/fractalfract7110830






