High-Frequency Fractional Predictions and Spatial Distribution of the Magnetic Loss in a Grain-Oriented Magnetic Steel Lamination
Abstract
1. Introduction
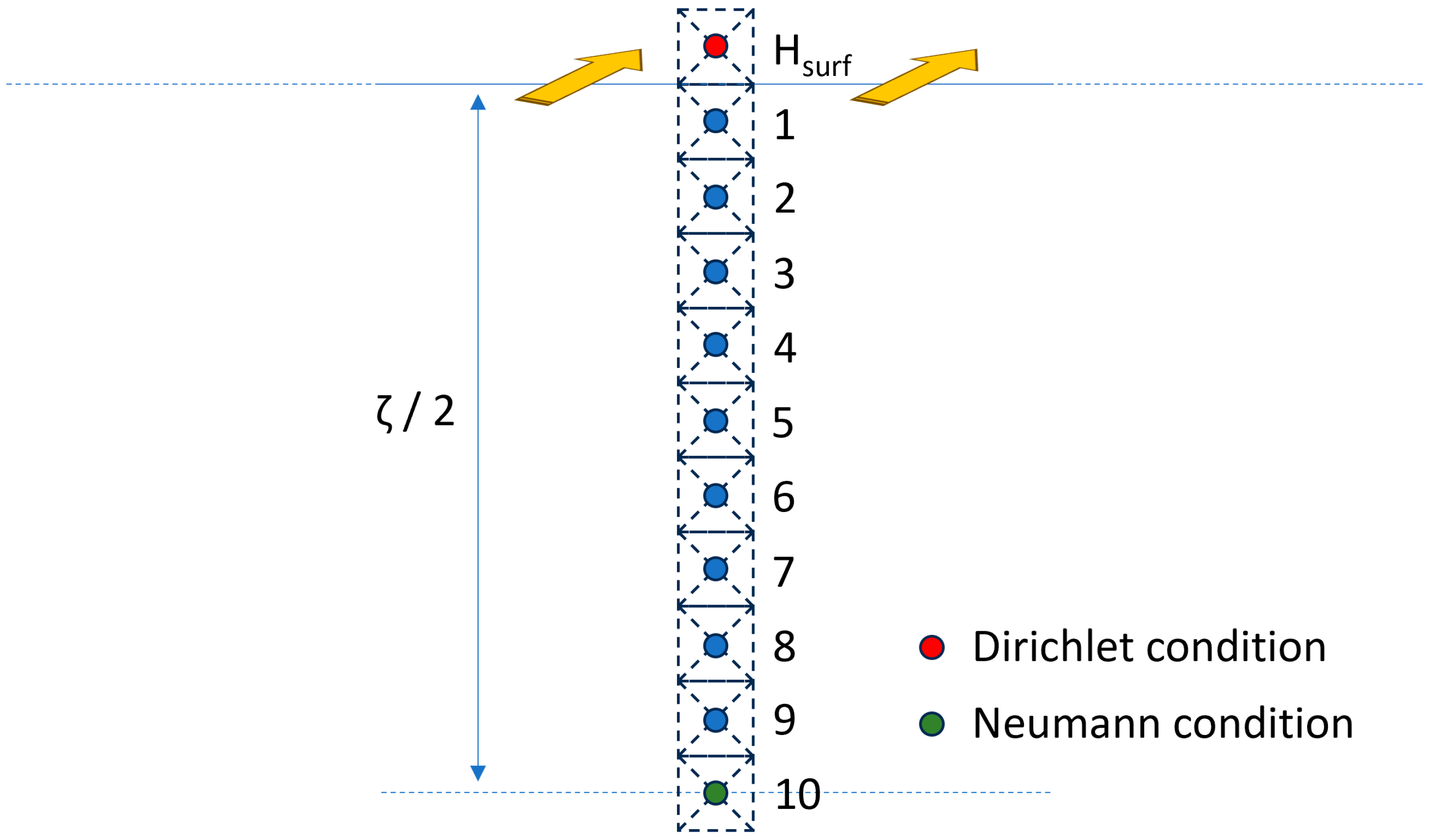
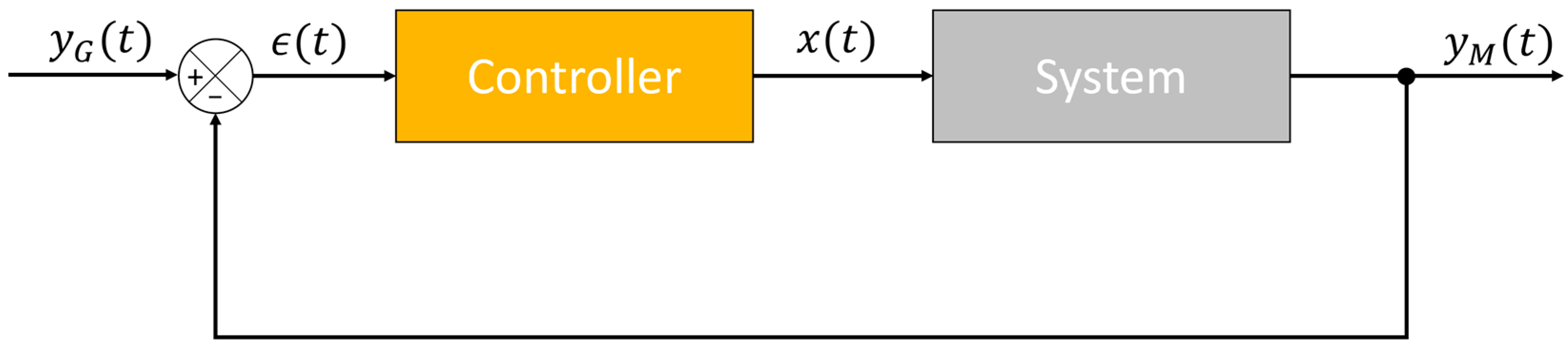
2. Simulation Method Description
2.1. Fractional Differential Equation: Physical Interpretation and Resolution
2.2. Combining Equation (8) and Equation (2) for a Simultaneous Resolution
3. Experimental Setup Description
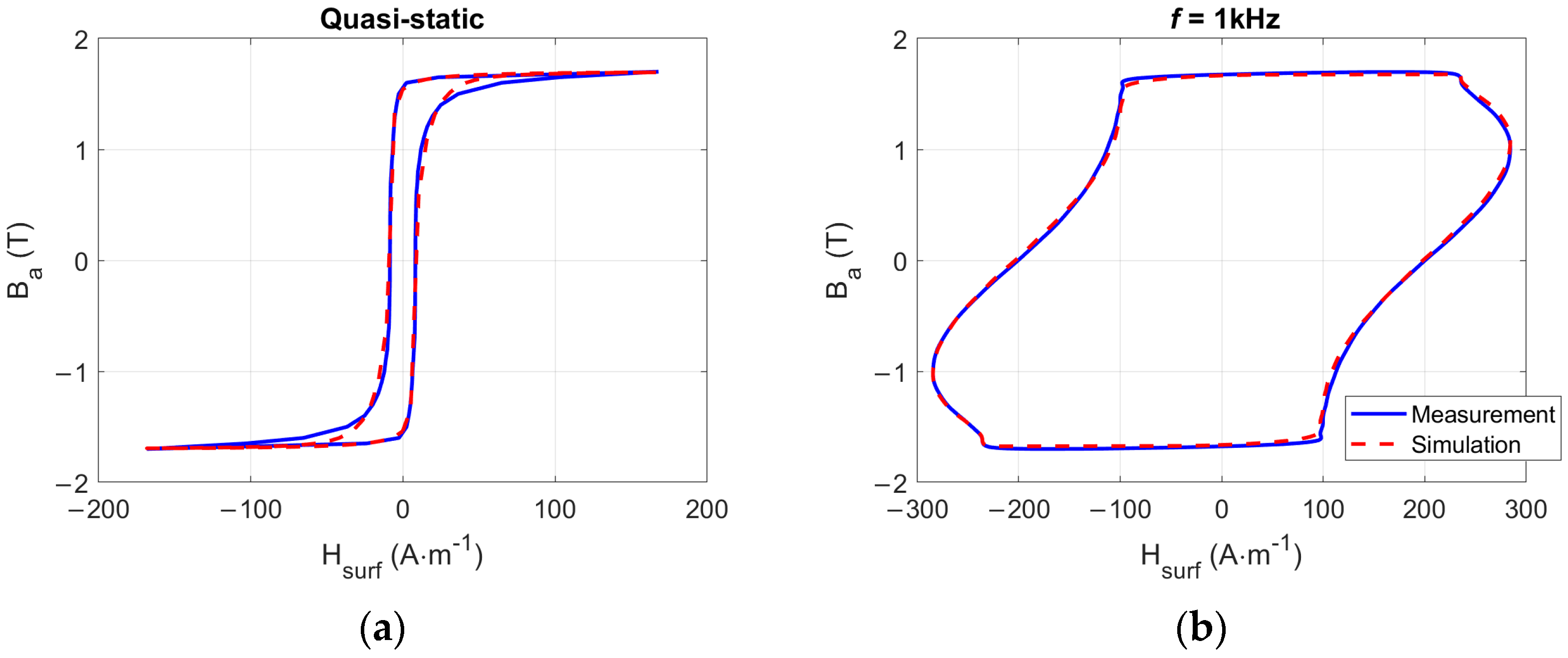
4. Simulation Method Settings and Validation up to 1 kHz and 1.7 T
4.1. Comparisons Simulation/Measurement, Model Validation
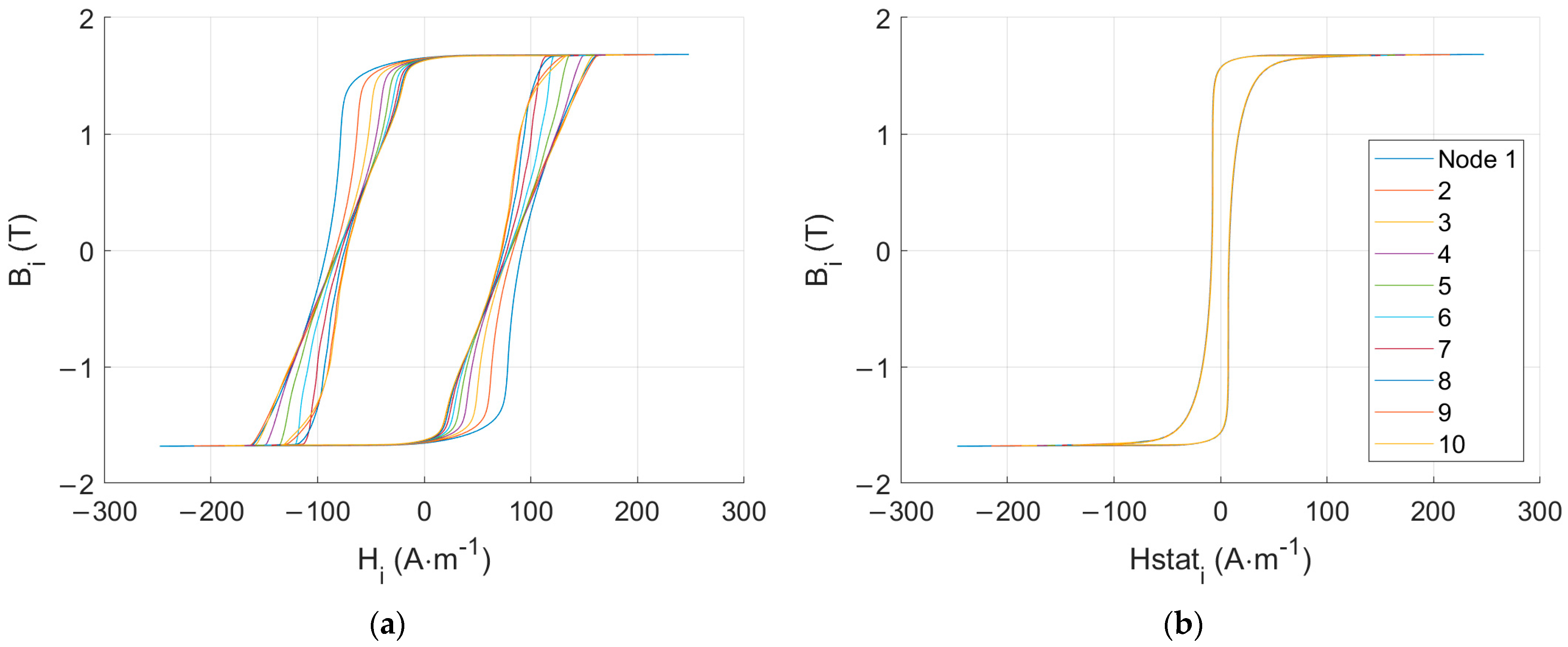
4.2. Model Exploitation, Spatial Losses Distribution
5. Model Predictions
5.1. Sinus B-Imposed Simulation
5.2. From 2 to 10 kHz Predictions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Silveyra, J.M.; Ferrara, E.; Huber, D.L.; Monson, T.C. Soft magnetic materials for a sustainable and electrified world. Science 2018, 362, eaao0195. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers; Gulf Professional Publishing: Houston, TX, USA, 1998. [Google Scholar]
- Krings, A.; Boglietti, A.; Cavagnino, A.; Sprague, S. Soft magnetic material status and trends in electric machines. IEEE Trans. Ind. Electron. 2016, 64, 2405–2414. [Google Scholar] [CrossRef]
- Zhao, H.; Ragusa, C.; Appino, C.; de la Barrière, O.; Wang, Y.; Fiorillo, F. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms. IEEE Trans. Power Electron. 2018, 34, 2655–2665. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- Xia, Z.; Kang, Y.; Wang, Q. Developments in the production of grain-oriented electrical steel. J. Magn. Magn. Mater. 2008, 320, 3229–3233. [Google Scholar] [CrossRef]
- Fiorillo, F.; Bertotti, G.; Appino, C.; Pasquale, M. Soft magnetic materials. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 1–42. [Google Scholar]
- Hayakawa, Y. Mechanism of secondary recrystallization of Goss grains in grain-oriented electrical steel. Sci. Technol. Adv. Mater. 2017, 18, 480–497. [Google Scholar] [CrossRef]
- Bertotti, G. Physical interpretation of eddy current losses in ferromagnetic materials. I. Theoretical considerations. J. Appl. Phys. 1985, 57, 2110–2117. [Google Scholar] [CrossRef]
- Shilyashki, G.; Pfützner, H.; Bengtsson, C.; Huber, E. Time-averaged and instantaneous magnetic loss characteristics of different products of electrical steel for frequencies of 16 2/3 Hz up to 500 Hz. IET Electr. Power Appl. 2022, 16, 525–535. [Google Scholar] [CrossRef]
- Chwastek, K.R. The effects of sheet thickness and excitation frequency on hysteresis loops of non-oriented electrical steel. Sensors 2022, 22, 7873. [Google Scholar] [CrossRef]
- Ducharne, B.; Zhang, S.; Sebald, G.; Takeda, S.; Uchimoto, T. Electrical steel dynamic behavior quantitated by inductance spectroscopy: Toward prediction of magnetic losses. J. Magn. Magn. Mater. 2022, 560, 169672. [Google Scholar] [CrossRef]
- Pfützner, H.; Shilyashki, G.; Huber, E. Calculated versus measured iron losses and instantaneous magnetization power functions of electrical steel. Electr. Eng. 2022, 104, 2449–2455. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Kim, J.S.; Koh, C.S. An Improved Model for Anomalous Loss Utilizing Loss Separation and Comparison with ANN Model in Electrical Steel Sheet. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Ducharne, B.; Sebald, G. Combining a fractional diffusion equation and a fractional viscosity-based magneto dynamic model to simulate the ferromagnetic hysteresis losses. AIP Adv. 2022, 12, 035029. [Google Scholar] [CrossRef]
- Moses, A.J. Energy efficient electrical steels: Magnetic performance prediction and optimization. Scr. Mater. 2012, 67, 560–565. [Google Scholar] [CrossRef]
- De la Barriere, O.; Ragusa, C.; Appino, C.; Fiorillo, F. Prediction of energy losses in soft magnetic materials under arbitrary induction waveforms and DC bias. IEEE Trans. Ind. Electron. 2016, 64, 2522–2529. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Steentjes, S.; Hameyer, K.; Chwastek, K.; Zurek, S.; Harrison, R.G. Dynamic magnetization models for soft ferromagnetic materials with coarse and fine domain structures. J. Magn. Magn. Mater. 2015, 394, 229–236. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Viscosity-based magnetodynamic model of soft magnetic materials. IEEE Trans. Magn. 2006, 42, 2121–2132. [Google Scholar] [CrossRef]
- Petrun, M.; Steentjes, S. Iron-loss and magnetization dynamics in non-oriented electrical steel: 1-D excitations up to high frequencies. IEEE Access 2020, 8, 4568–4593. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J.; Jiles, D.C.; Matsuo, T. Generalization of the classical method for calculating dynamic hysteresis loops in grain-oriented electrical steels. IEEE Trans. Magn. 2008, 44, 2113–2126. [Google Scholar] [CrossRef]
- Sadowski, N.; Batistela, N.J.; Bastos, J.P.A.; Lajoie-Mazenc, M. An inverse Jiles-Atherton model to take into account hysteresis in time-stepping finite-element calculations. IEEE Trans. Magn. 2002, 38, 797–800. [Google Scholar] [CrossRef]
- Davino, D.; Giustiniani, A.; Visone, C. Fast inverse Preisach models in algorithms for static and quasi-static magnetic-field computations. IEEE Trans. Magn. 2008, 44, 862–865. [Google Scholar] [CrossRef]
- Cardelli, E.; Torre, E.D.; Tellini, B. Direct and inverse Preisach modeling of soft materials. IEEE Trans. Magn. 2000, 36, 1267–1271. [Google Scholar] [CrossRef]
- Ducharne, B.; Sebald, G. Fractional derivatives for the core losses prediction: State of the art and beyond. J. Magn. Magn. Mater. 2022, 563, 169961. [Google Scholar] [CrossRef]
- Liu, R.; Li, L. Analytical prediction model of energy losses in soft magnetic materials over broadband frequency range. IEEE Trans. Power Electron. 2020, 36, 2009–2017. [Google Scholar] [CrossRef]
- Raulet, M.A.; Ducharne, B.; Masson, J.P.; Bayada, G. The magnetic field diffusion equation including dynamic hysteresis: A linear formulation of the problem. IEEE Trans. Magn. 2004, 40, 872–875. [Google Scholar] [CrossRef]
- Samko, S.G. Fractional integrals and derivatives. In Theory Applications; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasticity: An experimental study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J. Which derivative? Fractal Fract. 2017, 1, 3. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J. Fractional definite integral. Fractal Fract. 2017, 1, 2. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar] [CrossRef]
- Scorretti, R.; Sabariego, R.V.; Sixdenier, F.; Ducharne, B.; Raulet, M.A. Integration of a New Hysteresis Model in the Finite Elements Method. Compumag 2011. 2011, p. n-334. Available online: https://hal.science/hal-00582555/ (accessed on 8 December 2023).
- Fagan, P.; Ducharne, B.; Skarlatos, A. Optimized magnetic hysteresis management in numerical electromagnetic field simulations. In Proceedings of the 2021 IEEE International Magnetic Conference (INTERMAG), Lyon, France, 26–30 April 2021; pp. 1–5. [Google Scholar]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Jiles, D. Introduction to Magnetism and Magnetic Materials; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Chen, N.; Zaefferer, S.; Lahn, L.; Günther, K.; Raabe, D. Effects of topology on abnormal grain growth in silicon steel. Acta Mater. 2003, 51, 1755–1765. [Google Scholar] [CrossRef]
- BS EN 10280:2001 + A1:2007; Magnetic Materials-Methods of Measurement of the Magnetic Properties of Electrical Sheet and Strip by Means of a Single Sheet Tester. BSI: Alameda, CA, USA, 2001.
- UKAS. M3003-The Expression of Uncertainty and Confidence in Measurement, 4th ed.; United Kingdom Accreditation Service: Staines, UK, 2019. [Google Scholar]
- Hamzehbahmani, H.; Anderson, P.; Jenkins, K. Interlaminar insulation faults detection and quality assessment of magnetic cores using flux injection probe. IEEE Trans. Power Deliv. 2015, 30, 2205–2214. [Google Scholar] [CrossRef]
- Fagan, P.; Ducharne, B.; Zurek, S.; Domenjoud, M.; Skarlatos, A.; Daniel, L.; Reboud, C. Iterative methods for waveform control in magnetic measurement systems. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Gruebler, H.; Krall, F.; Leitner, S.; Muetze, A. Loss-surface-based iron loss prediction for fractional horsepower electric motor design. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; p. P-1. [Google Scholar]
- Magni, A.; Sola, A.; de La Barriere, O.; Ferrara, E.; Martino, L.; Ragusa, C.; Appino, C.; Fiorillo, F. Domain structure and energy losses up to 10 kHz in grain-oriented Fe-Si sheets. AIP Adv. 2021, 11, 015220. [Google Scholar] [CrossRef]
- Ducharne, B.; Zurek, S.; Sebald, G. A universal method based on fractional derivatives for modeling magnetic losses under alternating and rotational magnetization conditions. J. Magn. Magn. Mater. 2022, 550, 169071. [Google Scholar] [CrossRef]
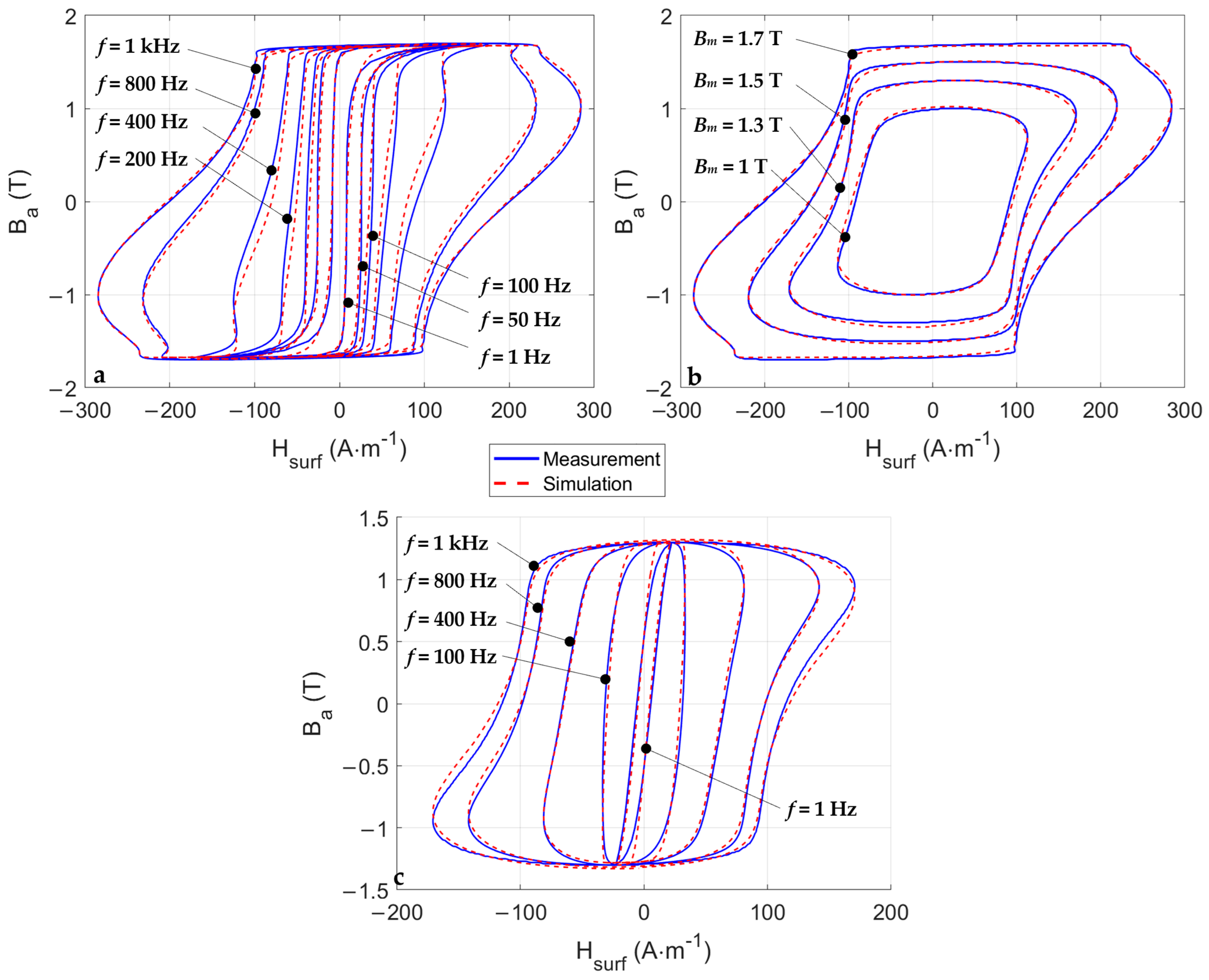
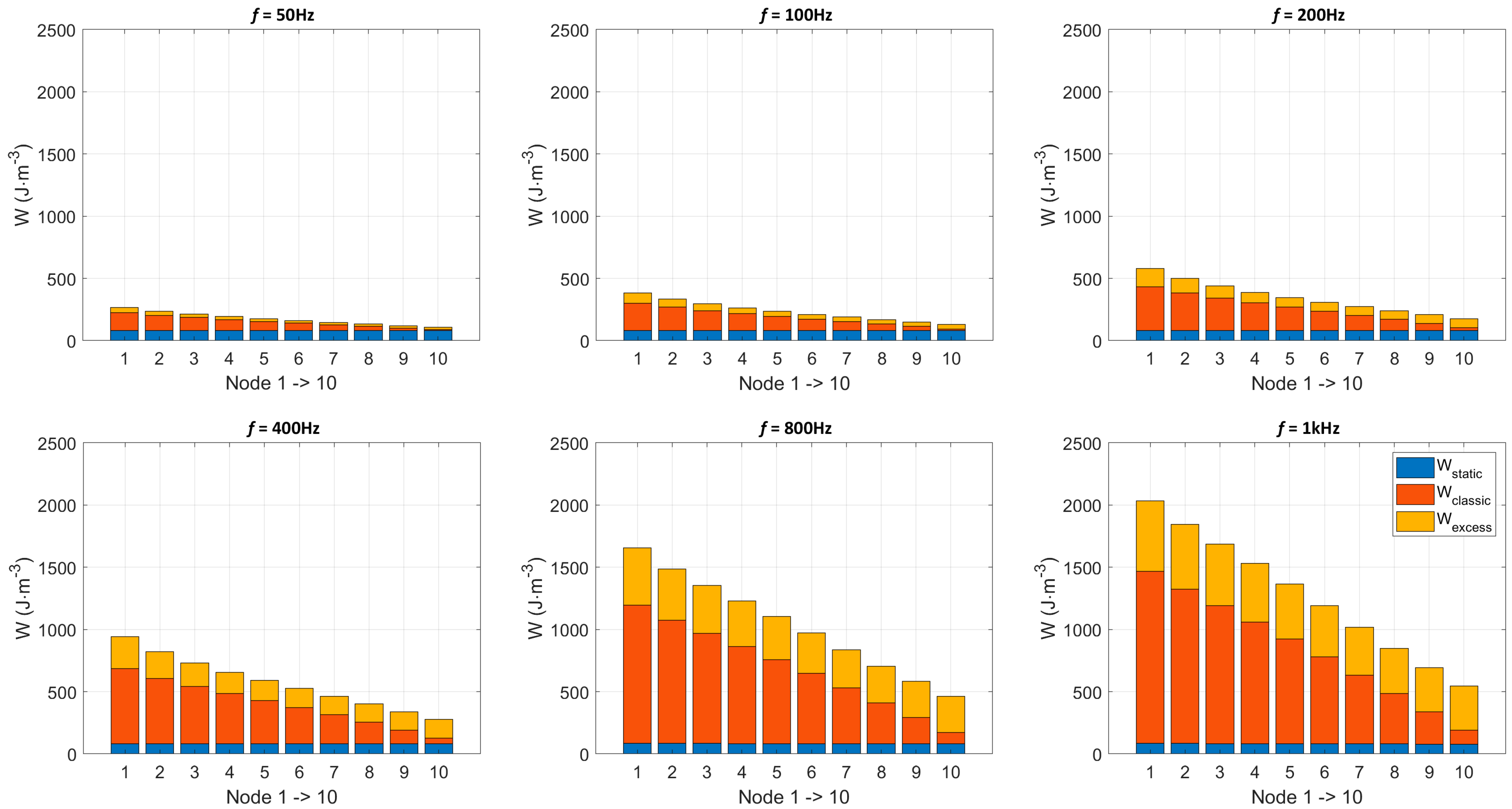

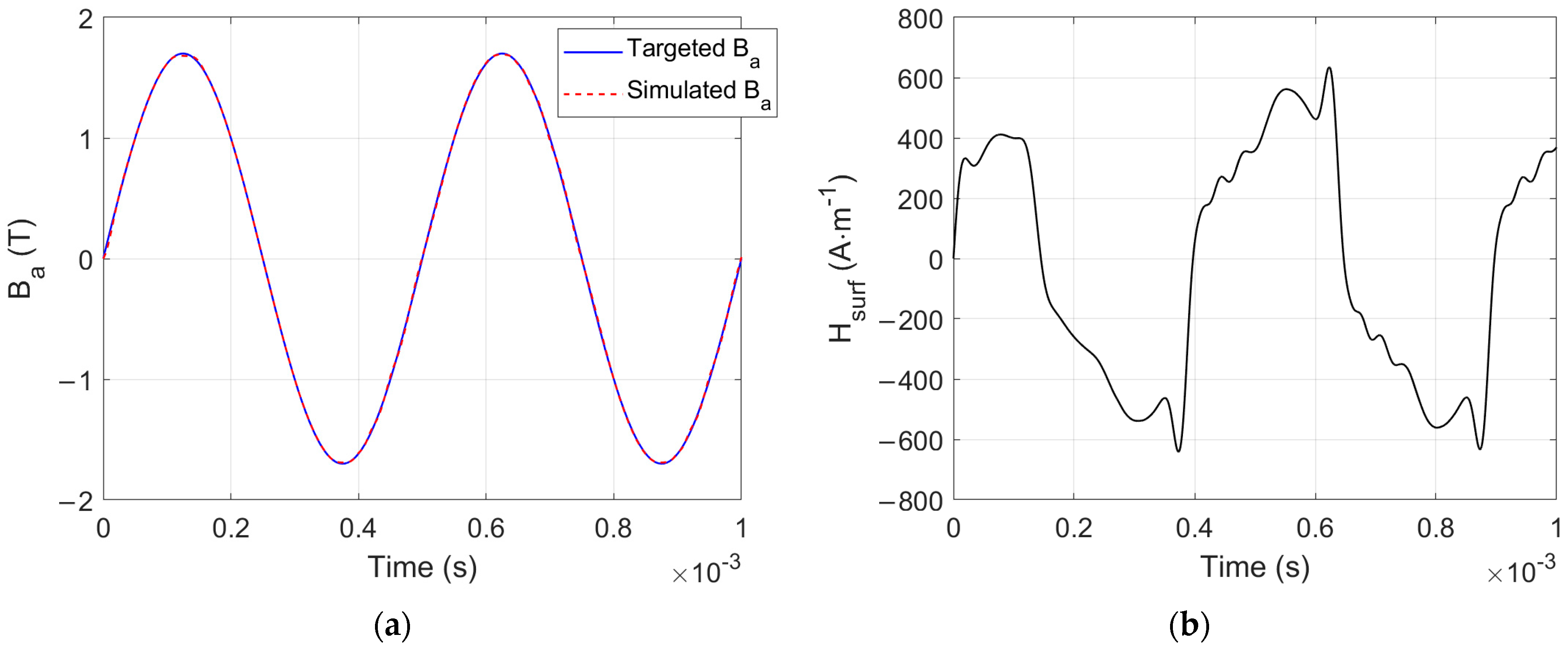
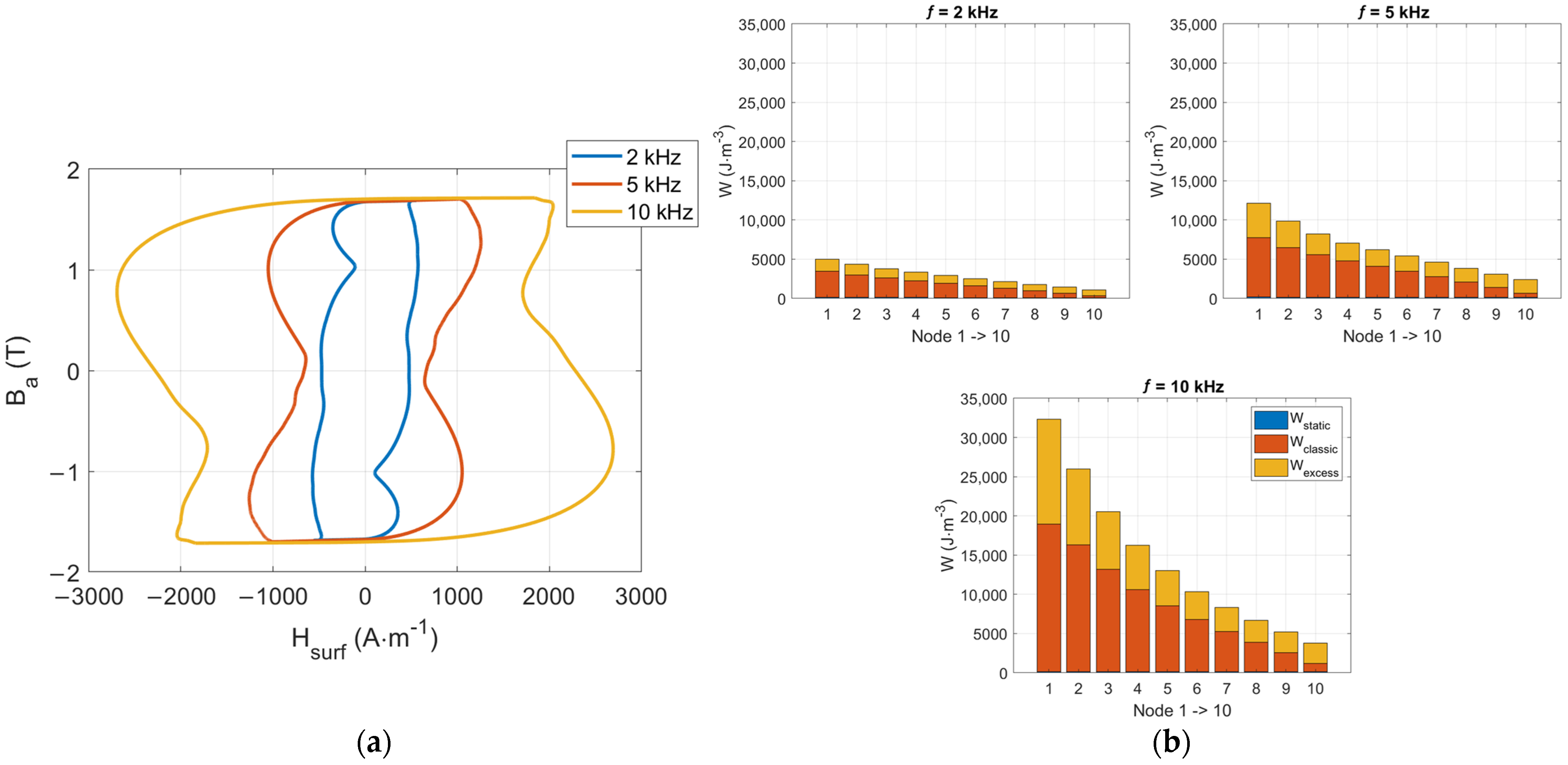
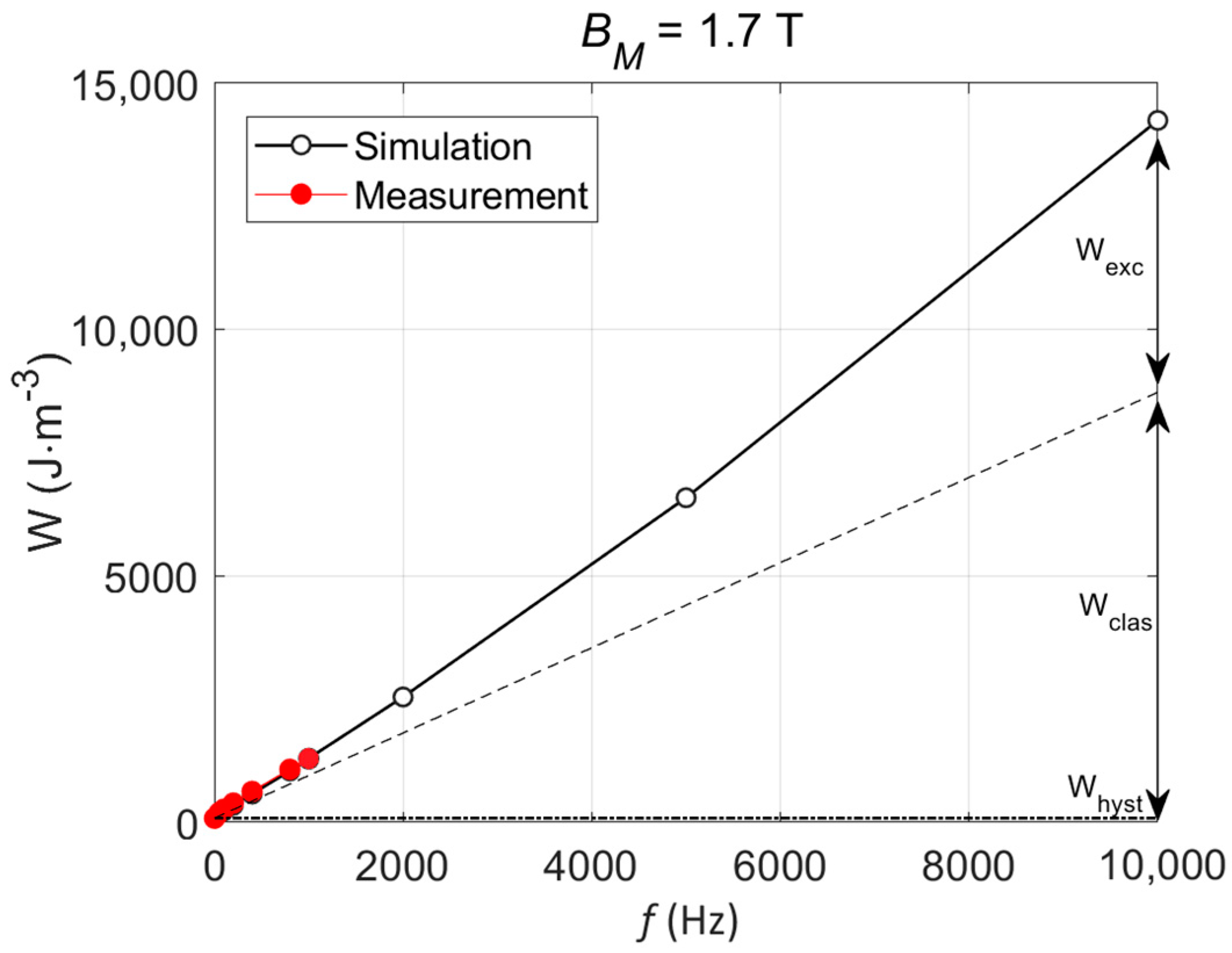
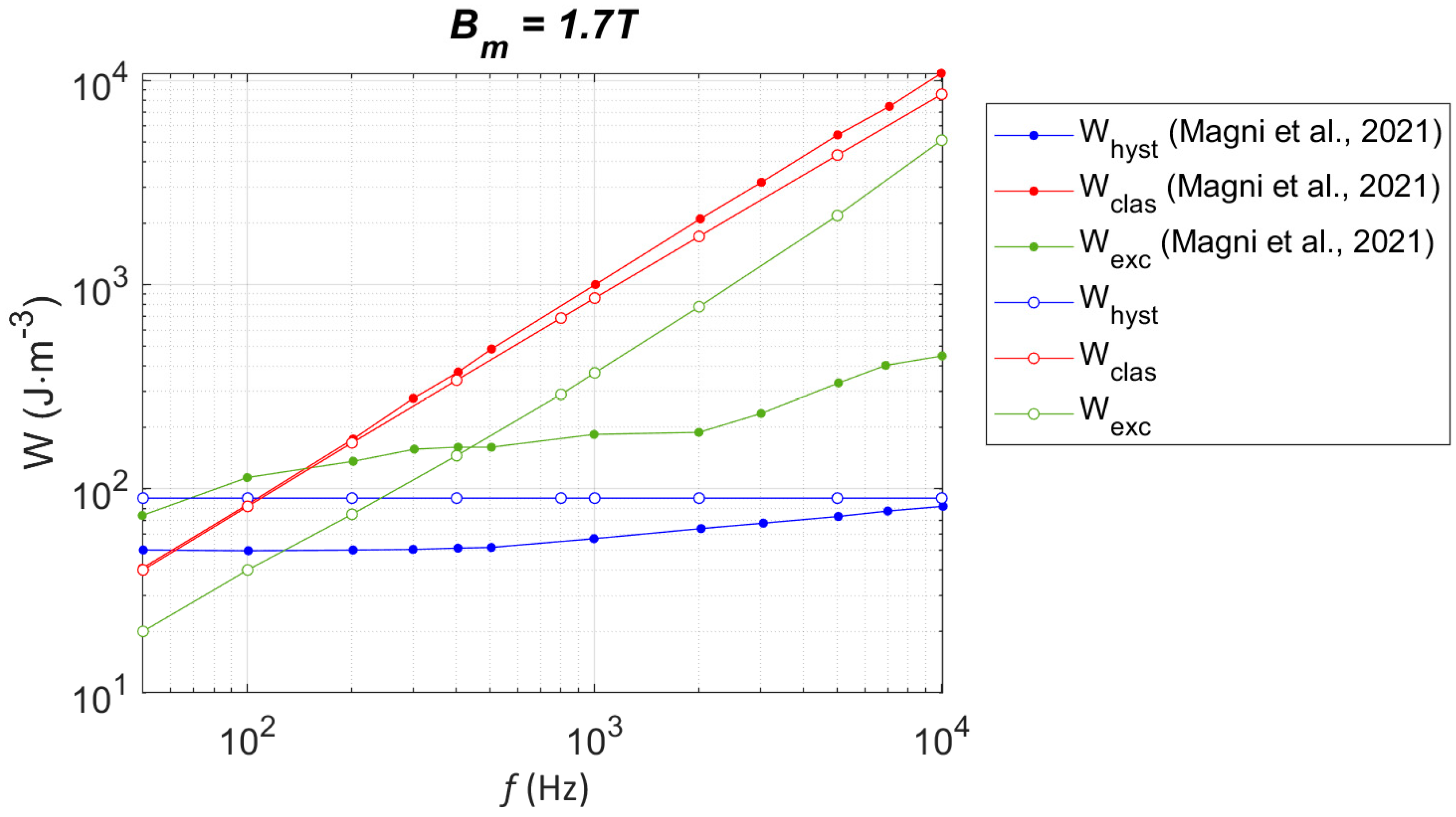
| Quasi-Static | f = 50 Hz | f = 100 Hz | f = 200 Hz | f = 400 Hz | f = 800 Hz | f = 1000 Hz | Av. | |
| red(%) | 13.1 | 7.3 | 10.1 | 9.6 | 8 | 2.7 | 1 | 7.4 |
| red(%)—dyn. cont. | - | 2.4 | 8.6 | 8.6 | 7.2 | 1.8 | 0.2 | 4.8 |
| FF(%) | 0.22 | 0.118 | 0.111 | 0.068 | 0.028 | 0.003 | 0.005 | 0.0875 |
| Bm = 1 T | Bm = 1.3 T | Bm = 1.5 T | Bm = 1.7 T | Av. | ||||
| red (%) | 2.4 | 6 | 5 | 1 | 3.6 | |||
| FF(%) | 0.002 | 0.002 | 0.004 | 0.005 | 0.0033 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ducharne, B.; Hamzehbahmani, H.; Gao, Y.; Fagan, P.; Sebald, G. High-Frequency Fractional Predictions and Spatial Distribution of the Magnetic Loss in a Grain-Oriented Magnetic Steel Lamination. Fractal Fract. 2024, 8, 176. https://doi.org/10.3390/fractalfract8030176
Ducharne B, Hamzehbahmani H, Gao Y, Fagan P, Sebald G. High-Frequency Fractional Predictions and Spatial Distribution of the Magnetic Loss in a Grain-Oriented Magnetic Steel Lamination. Fractal and Fractional. 2024; 8(3):176. https://doi.org/10.3390/fractalfract8030176
Chicago/Turabian StyleDucharne, Benjamin, Hamed Hamzehbahmani, Yanhui Gao, Patrick Fagan, and Gael Sebald. 2024. "High-Frequency Fractional Predictions and Spatial Distribution of the Magnetic Loss in a Grain-Oriented Magnetic Steel Lamination" Fractal and Fractional 8, no. 3: 176. https://doi.org/10.3390/fractalfract8030176
APA StyleDucharne, B., Hamzehbahmani, H., Gao, Y., Fagan, P., & Sebald, G. (2024). High-Frequency Fractional Predictions and Spatial Distribution of the Magnetic Loss in a Grain-Oriented Magnetic Steel Lamination. Fractal and Fractional, 8(3), 176. https://doi.org/10.3390/fractalfract8030176






