The Soliton Solutions for Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation via Riemann–Hilbert Problem
Abstract
1. Introduction
2. Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation
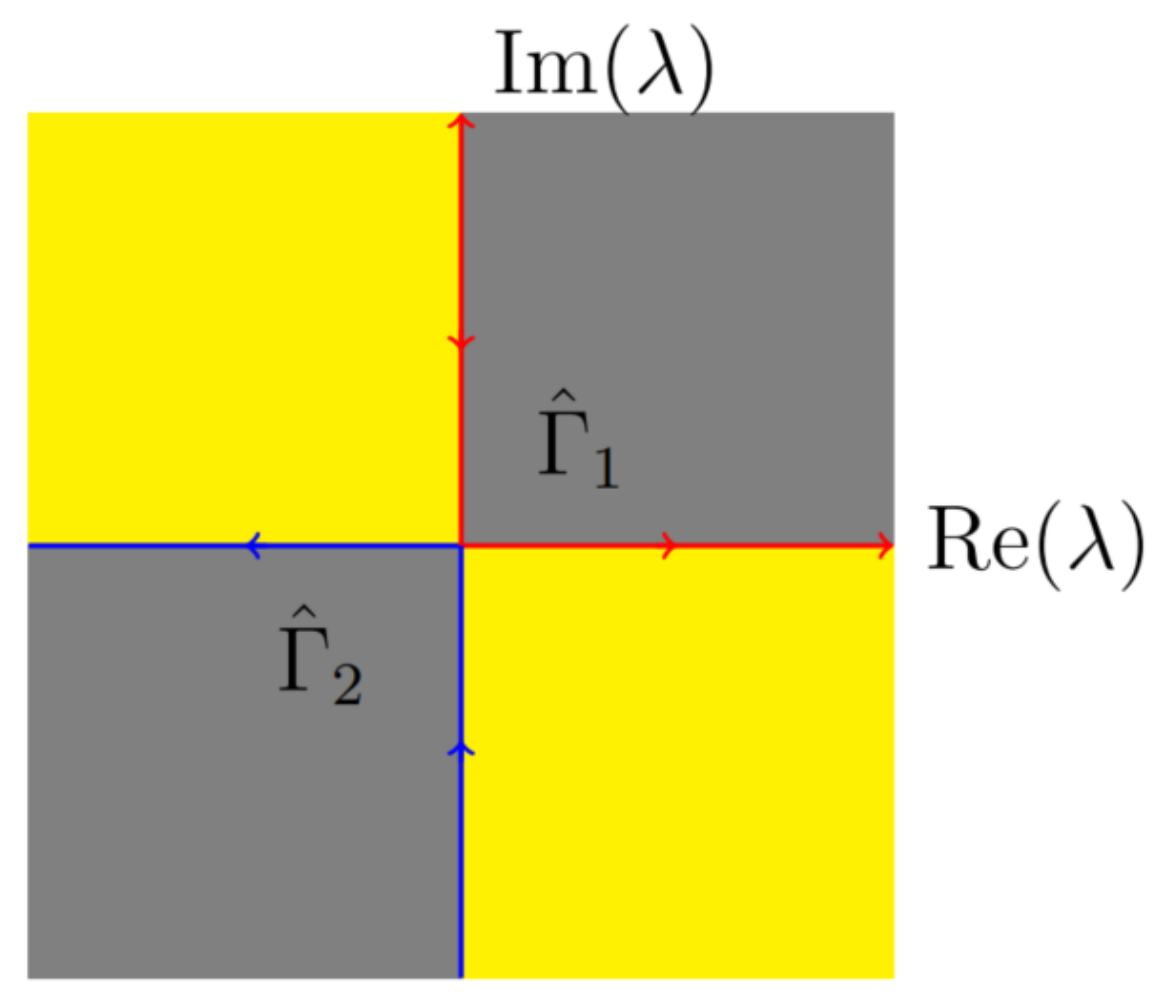
3. Riemann–Hilbert Problem of the Reverse-Spacetime mHOGI Equation
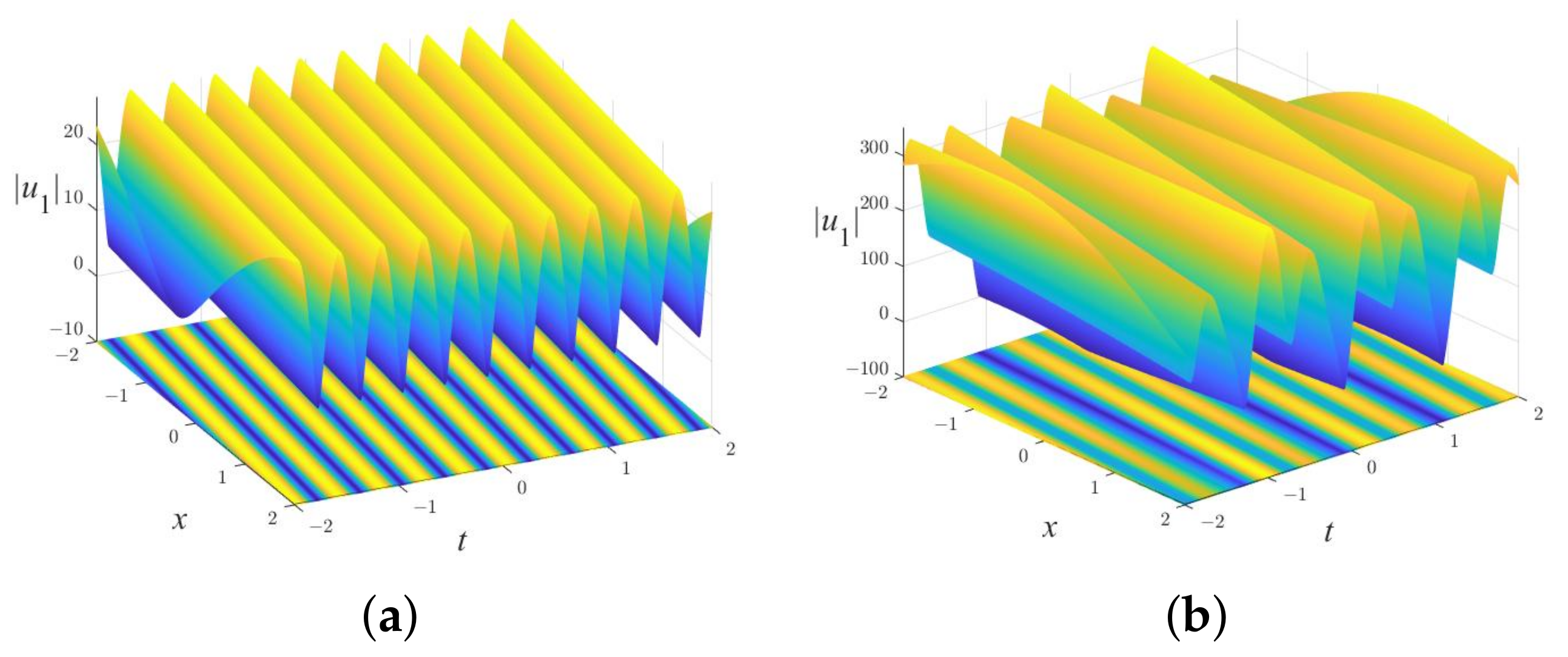
4. Solutions by the Riemann–Hilbert Method
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gardner, C.S.; Greene, M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 1967, 19, 1095–1149. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Date, E.; Jimbo, M.; Kashiwara, M.; Miwa, T. KP hierarchies of orthogonal and symplectic typetransformation groups for soliton equations VI. J. Phys. Soc. Jpn. 1981, 50, 3813–3818. [Google Scholar] [CrossRef]
- Thomas, R.; Kharif, C.; Manna, M. A nonlinear Schrödinger equation for water waves on finite depth with constant vorticity. Phys. Fluids 2012, 24, 66–84. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Wang, M.M.; Chen, Y. Dynamic behaviors of general n-solitons for the nonlocal generalized nonlinear Schrödinger equation. Nonlinear Dyn. 2021, 104, 2621–2638. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Tuszynski, J.A. Exact solutions of the multidimensional derivative nonlinear Schrödinger equation for many-body systems of criticality. J. Phys. A 1990, 23, 1171–1196. [Google Scholar] [CrossRef]
- Mio, K.; Ogino, T.; Minami, K.; Takeda, S. Modulational, Instability and Envelope-Solitons for Nonlinear Alfve’n Waves Propagating along the Magnetic Field in Plasmas. J. Phys. Soc. Jpn. 1976, 41, 667–673. [Google Scholar] [CrossRef]
- Zhou, H.J.; Chen, Y. Breathers and rogue waves on the double-periodic background for the reverse-space-time derivative nonlinear Schrödinger equation. Nonlinear Dyn. 2021, 6, 3437–3451. [Google Scholar] [CrossRef]
- Hisakado, M.; Wadati, M. Integrable Multi-Component Hybrid Nonlinear Schrödinger Equations. J. Phys. Soc. Jpn. 1995, 64, 408–413. [Google Scholar] [CrossRef]
- Kaup, D.J.; Newell, A.C. An exact solution for a derivative nonlinear Schrödinger equation. J. Math. Phys. 1978, 19, 798–801. [Google Scholar] [CrossRef]
- Chen, H.H.; Lee, Y.C.; Liu, C.S. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Phys. Scr. 1979, 20, 3–4. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Ivanov, M.I. The quadratic bundle of general form and the nonlinear evolution equations. Bulg. J. Phys. 1938, 10, 16. [Google Scholar]
- Wadati, M.; Sogo, K. Gauge transformations in soliton theory. Phys. Soc. Jpn. 1983, 52, 394–398. [Google Scholar] [CrossRef]
- Kakei, S.; Sasa, N.; Satsuma, J. Bilinearization of a generalized derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 1995, 64, 1519–1523. [Google Scholar] [CrossRef]
- Fan, E.G. Darboux transformation and soliton-like solutions for the Gerdjikov-Ivanov equation. J. Phys. A Math. Gen. 2000, 33, 6925–6964. [Google Scholar] [CrossRef]
- Zhang, J.S.; Guo, L.J.; He, J.S.; Zhou, Z.X. Darboux transformation of the second-type derivative nonlinear Schrödinger equation. Lett. Math. Phys. 2015, 105, 853–891. [Google Scholar] [CrossRef]
- Xu, S.W.; He, J.S. The rogue wave and breather solution of the Gerdjikov-Ivanov equation. J. Math. Phys. 2012, 53, 063507. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable Nonlocal Nonlinear Schrödinger Equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef]
- Yan, Z.Y. Integrable PT-symmetric local and nonlocal vector nonlinear Schrödinger equations: A unified two-parameter model. Appl. Math. Lett. 2015, 47, 61–68. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear equations. Appl. Math. Lett. 2017, 139, 7–59. [Google Scholar] [CrossRef]
- Lou, S.Y. Alice-Bob systems, symmetry invariant and symmetry breaking soliton solutions. J. Math. Phys. 2018, 59, 083507. [Google Scholar] [CrossRef]
- Xu, Z.X.; Chow, K.W. Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl. Math. Lett. 2016, 56, 72–77. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Saxena, A. Complete integrability of nonlocal nonlinear Schrödinger equation. J. Math. Phys. 2017, 58, 013502. [Google Scholar] [CrossRef]
- Rao, J.G.; Cheng, Y.; Porsezian, K.; Mihalache, D.; He, J.S. PT-symmetric nonlocal Davey-Stewartson I equation: Soliton solutions with nonzero background. Phys. D Nonlinear Phenom. 2020, 401, 132180. [Google Scholar] [CrossRef]
- Ma, W.X.; Huang, Y.H.; Wang, F.D. Inverse scattering transforms and soliton solutions of nonlocal reverse-space nonlinear Schrödinger hierarchies. Stud. Appl. Math. 2020, 145, 563–585. [Google Scholar] [CrossRef]
- Ma, W.X. Riemann-Hilbert problems and inverse scattering of nonlocal real reverse-spacetime matrix AKNS hierarchies. Phys. D 2020, 430, 563–585. [Google Scholar] [CrossRef]
- Yu, J.; He, J.S.; Han, J.W. Two kinds of new integrable decompositions of the Gerdjikov-Ivanov equation. J. Math. Phys. 2012, 53, 033510. [Google Scholar] [CrossRef]
- Kakei, S.; Kikuchi, T. Solutions of a derivative nonlinear Schrödinger hierarchy and its similarity reduction. Glasg. Math. J. 2005, 47, 99–107. [Google Scholar] [CrossRef]
- Kakei, S.; Kikuchi, T. Affine Lie group approach to a derivative nonlinear Schrödinger equation and its similarity reduction. Int. Math. Res. Not. 2004, 2004, 4181–4209. [Google Scholar] [CrossRef]
- Kundu, A. Exact solutions to higher-order nonlinear equations through gauge transformation. Phys. D Nonlinear Phenom. 1987, 25, 399–406. [Google Scholar] [CrossRef]
- Ma, W.X.; Yong, X.L.; Qin, Z.Y.; Gu, X.; Zhou, Y. A generalized Liouville’s formula. Appl. Math. J. Chin. Univ. 2016, 37, 470–474. [Google Scholar] [CrossRef]
- Novikov, S.P.; Manakov, S.V.; Pitaevskii, L.P.; Zakharov, V.E. Theory of Solitons: The Inverse Scattering Method, 1st ed.; Consultants Bureau: New York, NY, USA, 1984; pp. 52–86. [Google Scholar]
- Lenells, J. Dressing for a Novel Integrable Generalization of the Nonlinear Schrödinger Equation. J. Nonlinear Sci. 2010, 20, 709–722. [Google Scholar] [CrossRef]
- Guo, B.L.; Ling, L.M. Riemann-Hilbert approach and N-soliton formula for coupled derivative Schrödinger equation. J. Math. Phys. 2012, 53, 073506. [Google Scholar] [CrossRef]
- Kawata, T. Riemann Spectral Method for the Nonlinear Evolution Equations, 1st ed.; Cambridge University Press: Cambridge, UK, 1984; pp. 102–143. [Google Scholar]
- Zhou, X.; Fan, E.G. Long time asymptotics for the nonlocal mKdV equation with finite density initial data. Phys. D Nonlinear Phenom. 2022, 440, 133458. [Google Scholar] [CrossRef]
- Zhou, X.; Fan, E.G. Long time asymptotic behavior for the nonlocal mKdV Equation in solitonic space-time regions. Math. Phys. Anal. Geom. 2023, 26, 3. [Google Scholar] [CrossRef]
- Peng, W.Q.; Chen, Y. Long-time asymptotics for the integrable nonlocal Lakshmanan-Porsezian-Daniel equation with decaying initial value data. Appl. Math. Lett. 2024, 152, 109030. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Dong, H.; Fang, Y.; Zhang, Y. The Soliton Solutions for Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation via Riemann–Hilbert Problem. Fractal Fract. 2024, 8, 177. https://doi.org/10.3390/fractalfract8030177
Liu J, Dong H, Fang Y, Zhang Y. The Soliton Solutions for Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation via Riemann–Hilbert Problem. Fractal and Fractional. 2024; 8(3):177. https://doi.org/10.3390/fractalfract8030177
Chicago/Turabian StyleLiu, Jinshan, Huanhe Dong, Yong Fang, and Yong Zhang. 2024. "The Soliton Solutions for Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation via Riemann–Hilbert Problem" Fractal and Fractional 8, no. 3: 177. https://doi.org/10.3390/fractalfract8030177
APA StyleLiu, J., Dong, H., Fang, Y., & Zhang, Y. (2024). The Soliton Solutions for Nonlocal Multi-Component Higher-Order Gerdjikov–Ivanov Equation via Riemann–Hilbert Problem. Fractal and Fractional, 8(3), 177. https://doi.org/10.3390/fractalfract8030177






