Hybrid LSTM-Based Fractional-Order Neural Network for Jeju Island’s Wind Farm Power Forecasting

Abstract

Efficient integration of wind energy requires accurate wind power forecasting. This prediction is critical in optimising grid operation, energy trading, and effectively harnessing renewable resources. However, the wind’s complex and variable nature poses considerable challenges to achieving accurate forecasts. In this context, the accuracy of wind parameter forecasts, including wind speed and direction, is essential to enhancing the precision of wind power predictions. The presence of missing data in these parameters further complicates the forecasting process. These missing values could result from sensor malfunctions, communication issues, or other technical constraints. Addressing this issue is essential to ensuring the reliability of wind power predictions and the stability of the power grid. This paper proposes a long short-term memory (LSTM) model to forecast missing wind speed and direction data to tackle these issues. A fractional-order neural network (FONN) with a fractional arctan activation function is also developed to enhance generated wind power prediction. The predictive efficacy of the FONN model is demonstrated through two comprehensive case studies. In the first case, wind direction and forecast wind speed data are used, while in the second case, wind speed and forecast wind direction data are used for predicting power. The proposed hybrid neural network model improves wind power forecasting accuracy and addresses data gaps. The model’s performance is measured using mean errors and R² values.

1. Introduction

Optimising the integration of wind energy into the power grid and ensuring grid stability relies heavily on accurate wind power prediction. Over the years, researchers have explored various techniques, including neural networks, machine learning, and deep learning methods, to enhance the precision and reliability of wind power predictions. Machine learning creates a generalised model from previous input data and output results, then predicts outcomes in the future using multiple learning methods. In machine learning approaches, artificial neural networks (ANNs) [1] and support vector machines (SVMs) [2] are commonly used. ANNs can predict non-linear data and analyse the correlation between impact data and wind power. Training ANNs requires a lot of data and time, while high-dimensional data limits computational speed, leading to local optimum solutions. SVM avoids these issues and generalises them effectively. In [3], the integration of least squares and SVM (LS-SVM) was used to estimate the wind power load, enhancing computation efficiency and predicting accuracy. Incorporating LS-SVM principles, Zhang et al. introduced modifications to the model that effectively minimised prediction errors [4]. In [5], the researchers developed a fuzzy neural network for wind power forecasting coupled with online risk assessment and, in addition, investigated the effectiveness and potential improvements in enhancing wind energy forecasting models. Jie Shi et al. combined the Hilbert–Huang transform with artificial intelligence (AI) for power forecasting and further explored the effectiveness of this integrated model in improving prediction accuracy and enhancing renewable energy integration [6]. In [7], the authors developed the application of radial basis function neural networks in wind power forecasting, incorporating probabilistic methods to enhance forecasting accuracy and uncertainty assessment. The researchers employed the empirical mode decomposition (EMD) model with a neural network to forecast wind power and speed [8]. Further, they investigated the effectiveness of EMD-based models in improving short-term wind forecasting accuracy. The authors in [9] created an emotional neural network technique for predicting weather patterns and wind power generation. Additionally, they emphasised that this method can be applied to real-world scenarios. The authors proposed Gaussian processes integrated with numerical weather prediction (NWP) and complex-valued ANN for day-ahead wind power forecasting and examined their effectiveness in optimising wind energy generation and improving prediction accuracy [10,11].

Jyotirmayee et al. presented a variational mode decomposition technique in combination with a multi-kernel regularised pseudo-inverse ANN for wind power forecasting [12]. The authors developed 3D convolutional neural networks (CNNs) for extracting numerical weather prediction data in wind power forecasting, investigated similar methods to enhance prediction accuracy, and considered the potential benefits of utilising 3D CNNs in this context [13]. In [14], the structured neural network model for predicting short-term wind power emphasises the developed model’s effectiveness and potential in achieving accurate short-term predictions. The researchers in [15,16] implemented an ANN for predicting wind power’s discrete wavelet-transform-based wind speed and highlighted the network’s effectiveness and potential in improving renewable energy integration. Additionally, the researchers emphasised the need for further investigation into model enhancements to address uncertainties and improve forecasting precision. In addition, the authors of [17] explored the current machine learning techniques for power forecasting, identifying emerging trends, and highlighted the key challenges faced in this domain. AI has shown promise in enhancing wind power generation forecasting through hybrid approaches, but significant challenges still need to be addressed for practical implementation and improved accuracy [18]. Despite these obstacles, the prospects for AI-based forecasting in the renewable energy sector remain encouraging. The authors of [19] employed an ANN model to forecast the wind power generation of the Pawan Danawi wind farm in Sri Lanka and highlighted that the model could also be applied to the environmental and climatic conditions to identify the wind power potential of the area. Machine learning methods are more effective than statistical approaches in predicting non-linear wind power data due to their adaptability and self-learning capabilities. However, these models have limitations in expressing complex data. This is because of the advancement of big data technology. Deep learning algorithms can overcome these challenges by extracting higher-level abstract features from the original samples. This enables the discovery of complex rules in high-dimensional data.

Deep learning models have advanced significantly in recent years, and deep neural network (DNN) algorithms have been introduced [20,21,22]. Recurrent neural networks (RNNs) and LSTM networks are robust architectures for sequence data, demonstrating advantages in non-linear feature learning [23]. Thus, RNN and LSTM are the most often used deep learning models in wind power prediction research. The authors of [24] conducted wind power generation prediction using multivariate LSTM time series. The researchers of [21] implemented deep feature extraction and LSTM techniques for data-driven wind speed forecasting and explored the effectiveness of these techniques in improving wind speed predictions. In [25], the authors used data cleaning and feature extraction techniques for power prediction. In [26], the authors used machine learning algorithms such as light gradient boosting machines (GBMs) and LSTM networks for short-term wind forecasting of weather stations in India and also aimed to enhance wind energy prediction accuracy, contributing to efficient renewable energy integration and management. The authors of [27] implemented an ensemble approach combining algorithms, namely, deep learning and gradient descent, for wind power forecasting and explored the model’s effectiveness in improving forecasting accuracy and reliability. The deep-learning-based methods in [28] were developed to generate accurate and reliable prediction intervals for wind power forecasting, addressing the multi-objective nature of the problem. The researchers in [29] employed a Seq2Seq wind power output prediction method developed using deep learning and a clustering algorithm to forecast wind power with NWP data and real-time historical wind data. Adam Kisvari et al. [30] applied a deep learning approach using a data-driven and a gated recurrent unit (GRU) to forecast wind power. Further, the researchers in [31] implemented a temporal convolution network (TCN)-based approach for day-ahead wind power forecasting and compared the implemented method with the LSTM and GRU models. In [32], the authors developed LSTM-based RNNs for wind power forecasting, focusing on variable selection techniques. The authors in [33] implemented the GRU neural network method for wind power prediction, utilising evolutionary network architecture search for optimisation. The researchers in [34,35] constructed multi-modal spatio-temporal neural networks and optimised deep autoregressive RNNs for multi-horizontal wind power forecasting.

The use of attention-based models has become more popular for predicting long-term series. In [36,37], the authors demonstrated self-attention’s effectiveness in capturing complex patterns and dynamics, particularly in capturing long-distance dependencies within time-series data. Juan Ren et al. [38] developed the CNN-LSTM-LightGBM framework with an attention mechanism for short-term wind power forecasting, which aimed to enhance forecasting accuracy by efficiently capturing temporal dependencies and extracting relevant features from wind power data. In [39], the authors proposed wind power forecasting methods using variational mode decomposition, and LSTM attention networks showed the encoder–decoder structure’s superiority over a dual attention–LSTM neural network in enhancing prediction performance. Lei Wang et al. constructed an advanced transformer model for ultra-short-term wind power prediction [40]. Nevertheless, challenges such as space–time complexity and input and output sequence limitations remain. Furthermore, Ref. [41] developed a novel method for ultra-short-term wind power prediction, addressing previous limitations through feature extractions. The approach shows promising results, improving prediction accuracy and addressing space–time complexity issues.

A fractional-order activation function is a specific activation function used in artificial neural networks. It allows the use of non-integer exponents to calculate the output of a neuron, which can improve the performance of specific neural networks. These activation functions possess unique properties that make them suitable for specific modelling tasks and data. They are beneficial for capturing long-range dependencies and non-linear relationships in data, which cannot be effectively handled by conventional activation functions such as arctan. The fractal nature of these activation functions is attributed to their self-similarity property, which enables them to capture complex patterns in data at multiple scales. Hence, they benefit time-series forecasting applications where the data may exhibit fractal-like behaviour [42]. Using fractional-order activation functions can enhance the performance of FONN model-based forecasting by allowing for more accurate and efficient modelling of complex non-linear relationships in the data. Additionally, these functions can help to reduce overfitting, a common problem in traditional neural networks. The use of fractional-order activation functions may increase the computational load during training. However, this can be offset by the improved performance and accuracy of the model, leading to faster and more efficient forecasting [43]. Therefore, it is justified to use fractional-order activation functions because of their ability to capture complex non-linear relationships in data, which can improve the efficiency and accuracy of FONN model-based forecasting.

Motivated by the above literature, this paper presents a new hybrid model that uses LSTM to forecast missing input data and FONN to predict generated wind power. The performance of the proposed approach is evaluated based on the wind data collected from Jeju Island’s wind farm in three different island sites. The key contributions of this research are outlined below:

• The LSTM model is designed to predict missing input parameters, including wind speed and direction. Its performance is evaluated through root mean squared error (RMSE) assessment.
• The FONN model predicts wind power using the LSTM’s forecast data and evaluates performance with a coefficient of determination (R²) and mean squared error (MSE).
• The models developed were evaluated in two case studies involving missing data scenarios for specific parameters.

The subsequent sections of the manuscript are organised to explore the research comprehensively. Section 2 describes the dataset from Jeju Island in three different sites and presents the data visualisation and correlation analysis in various scenarios. Section 3 describes the proposed hybrid LSTM-based fractional-order neural network model for wind power forecasting. Section 4 shows the results and discussion of the proposed models’ performance evaluation to handle the missing parameter data. Section 5 concludes the proposed work.

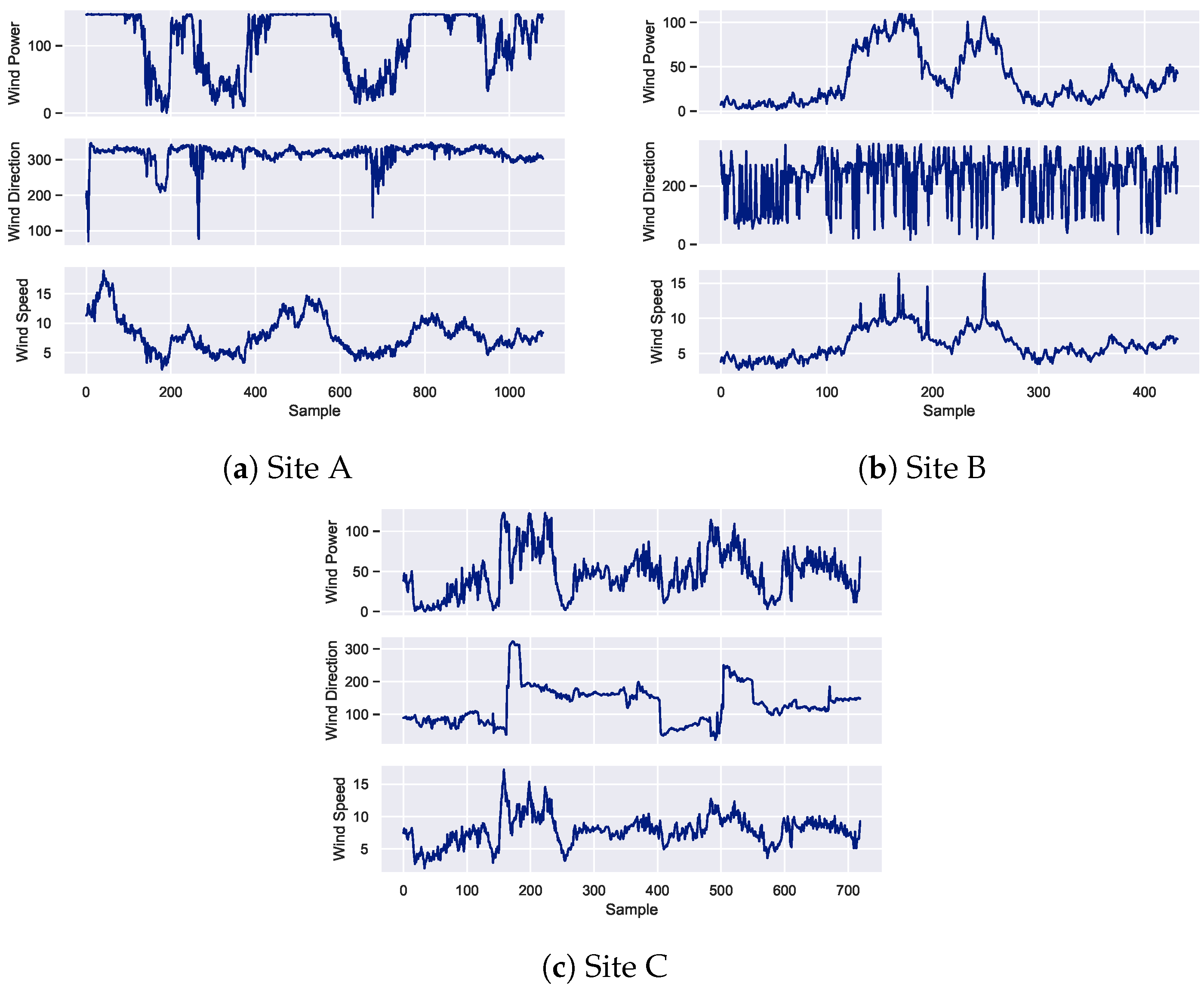
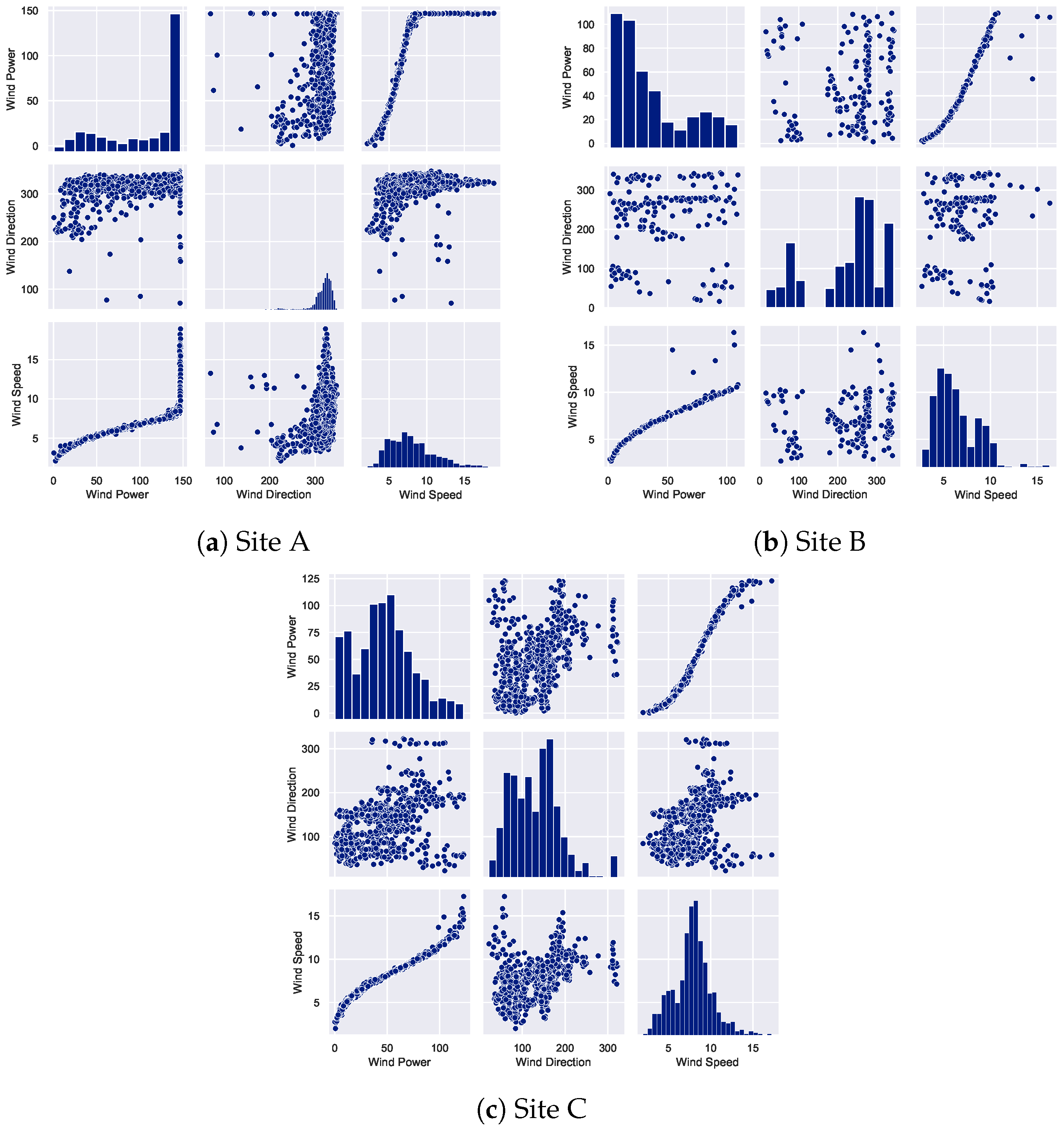
2. Dataset Description

In South Korea, Jeju Island has a prosperous wind energy landscape with advanced wind farms strategically placed throughout scenic terrain. These wind farms take advantage of the island’s plentiful wind resources, significantly contributing to its renewable energy portfolio. Sites A, B, and C are among the top wind farms on Jeju Island, each with unique specifications and characteristics.

Table 1. Jeju Island’s wind farm data and specifications.

Data Aspect	Site A	Site B	Site C
Data Collection Period	11 January 2014–25 January 2014	11 January 2014–20 January 2014	11 January 2014–25 January 2014
Collection Time Interval	10 min	10 min	10 min
Wind Turbine Specifications
Model	U88	U50	U50
Output	2000 kW	750 kW	750 kW
Wind Speed	Up to 12 m/s	Up to 12.5 m/s	Up to 12.5 m/s
Rotor Speed Range	6–17.5 rpm	9–28 rpm	9–28 rpm
Voltage and Frequency	690 V/60 Hz	690 V/60 Hz	690 V/60 Hz
Rotor Diameter	88 m	50 m	50 m
Hub Height	80 m	50 m	50 m
Power Control	Pitch Regulation	Pitch Regulation	Pitch Regulation

provides an overview of the data collection period, collection time interval, and detailed wind turbine specifications for Sites A, B, and C [44].

The wind turbine specifications presented in the table highlight each site’s customised design and engineering considerations. These specifications, which include the model, output, wind speed capacity, rotor dynamics, voltage, and power control, showcase Jeju Island’s commitment to harnessing wind energy efficiently and sustainably. The island’s wind farms are characterised by their meticulous data collection and cutting-edge turbine specifications, which testify to their dedication to renewable energy and their aspiration to create a cleaner and greener future.

As shown in Figure 1, the data from sites A, B, and C include wind power, direction, and speed, indicating the chaotic behaviour. There were 1080, 432, and 720 samples from sites A, B, and C, respectively. These samples’ pair plots are shown in Figure 2 and Figure 3. Figure 1 shows the pairwise relationships in a dataset, while Figure 3 shows correlation coefficients between wind direction, speed, and power at the three sites. As shown in the figure, the diagonal elements are one, indicating a perfect correlation with each variable. The off-diagonal elements in the figure show the correlation between the two parameters.

Utilising the Pearson correlation coefficient, a numerical measure ranging from −1 to 1, the correlation analysis shown in Figure 3 can quantify the strength and direction of relationships. This method is invaluable in providing essential insights into how changes in one parameter might correspond to changes in another. Upon examination of the wind farms at each site, it was discovered that a positive linear relationship exists between wind direction, speed, and power. The correlation coefficient between wind direction and speed at Site A is 0.25, at Site B it is 0.22, and at Site C it is 0.36, indicating a weak correlation. Similarly, the correlation coefficient between wind direction and power at Site A is 0.34, at Site B it is 0.17, and at Site C it is 0.38, indicating a weak correlation. Lastly, the correlation coefficient between wind speed and wind power at Site A is 0.82, at Site B it is 0.95, and at Site C it is 0.98, indicating a robust correlation. It is important to note that all correlation coefficients fall within the range of −1 to 1, demonstrating that the relationships are positive and linear. Additionally, it should be noted that the correlations observed at Site C are stronger than those at Site A, and the correlations at Site A are the most robust of the three sites.

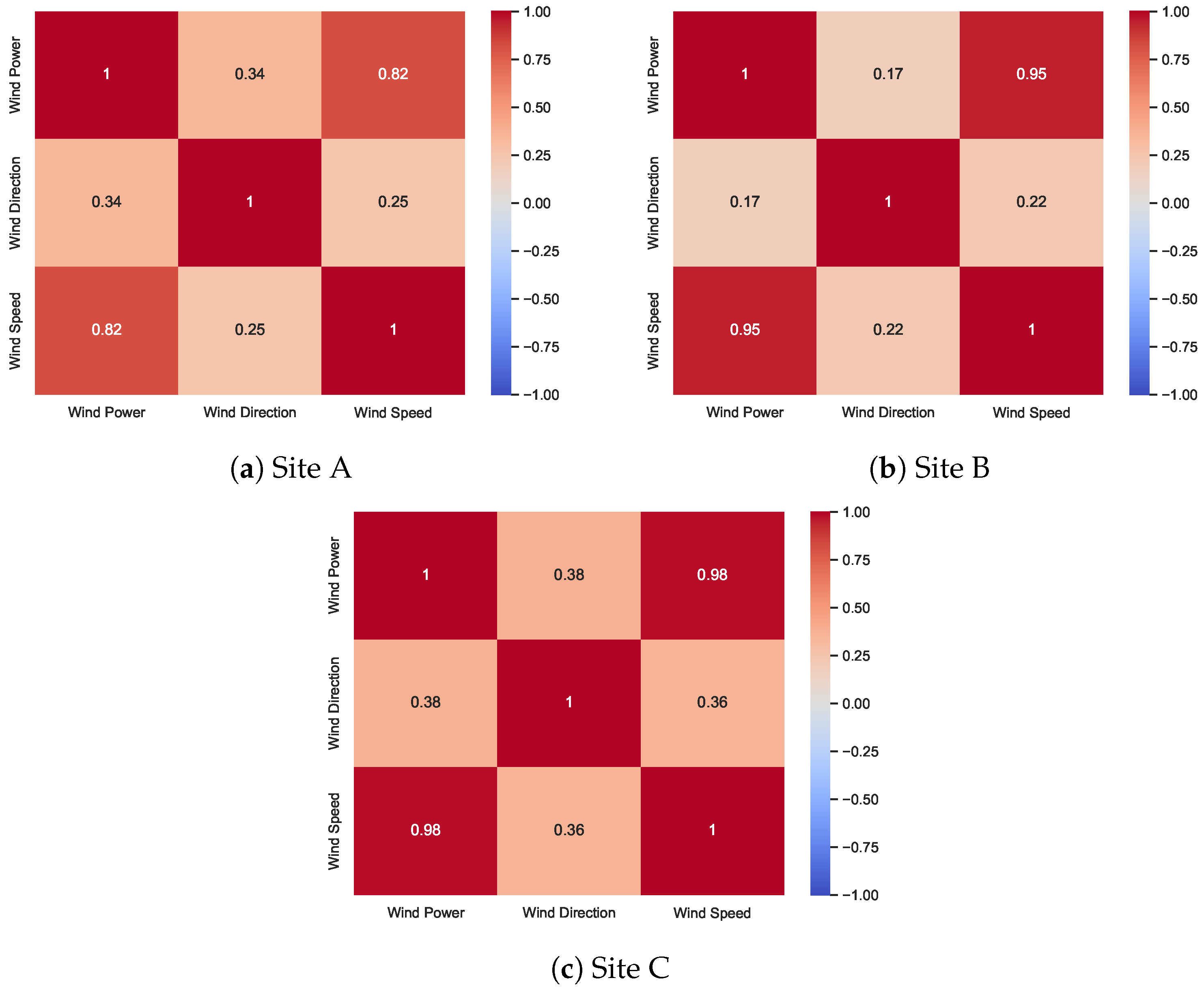
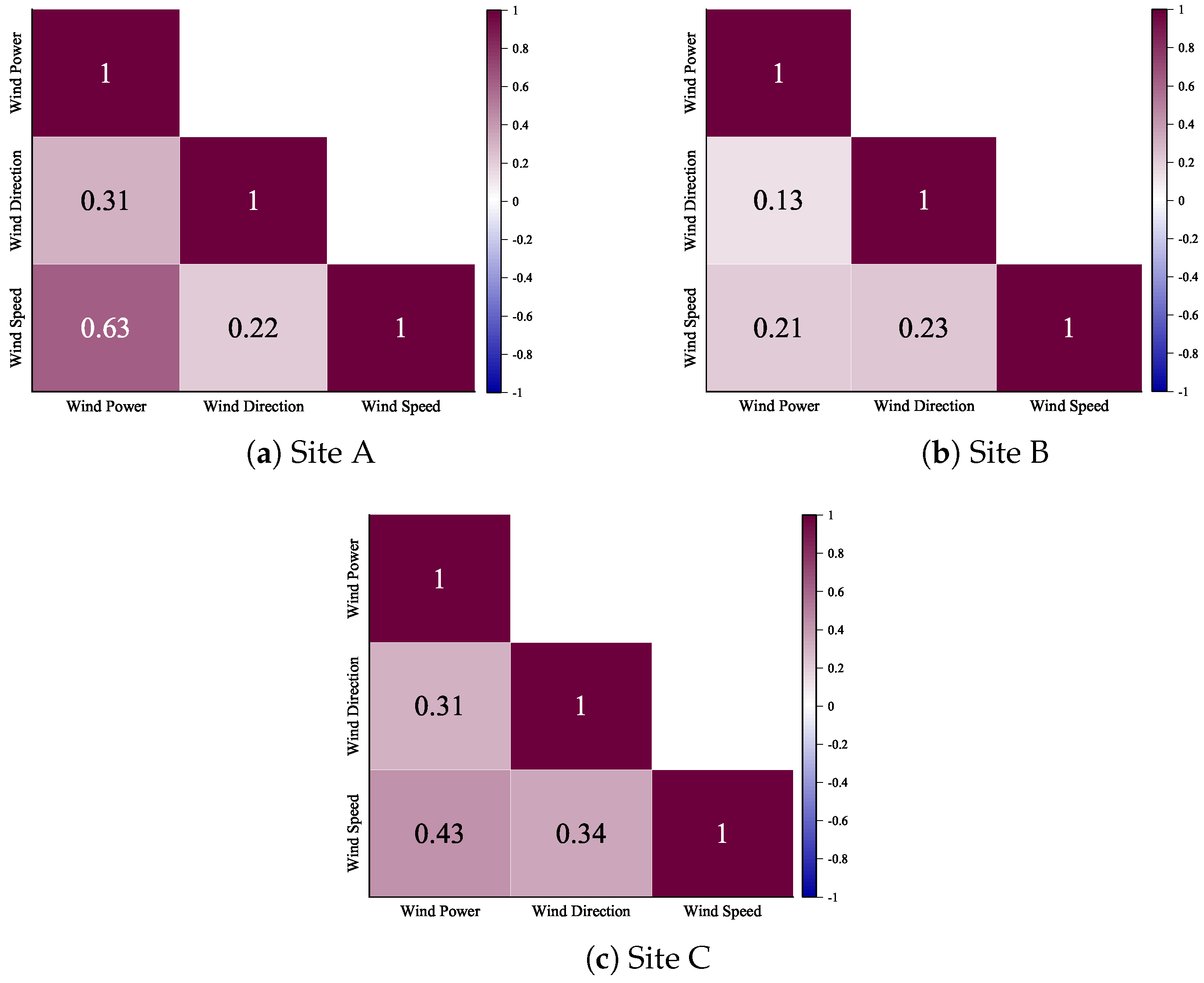
2.1. Correlation Analysis of Wind Speed Parameter with Missing Data

The first case examines the correlation between wind direction, speed, and power across Sites A, B, and C, where the wind speed parameter has missing data. The correlation matrix for Site A, shown in Figure 4, presents a comprehensive view of these relationships. Notable correlations emerge, with wind power and direction exhibiting a moderate positive correlation of 0.31, indicating a tendency for increased wind direction to coincide with heightened wind power. Additionally, wind power and speed show a stronger positive correlation of 0.63, suggesting that higher wind power values correspond to elevated wind speed values. Conversely, wind direction and speed demonstrate a more modest positive correlation of 0.22. The correlation matrix for Site B mirrors these trends, showing modest positive correlations of 0.13, 0.21, and 0.23 between wind power and direction, wind power and speed, and wind direction and speed, respectively. At Site C, wind power and wind direction exhibit a moderately positive correlation of 0.31. In contrast, the correlation between wind power and speed is characterised by a relatively moderate positive correlation of 0.43. Similarly, wind direction and speed display a moderately positive correlation of 0.34. Together, these correlation matrices provide a comprehensive understanding of the relationships between wind power, direction, and speed, shedding light on the nature and strength of these associations and emphasising the need for thorough analysis, particularly in instances of missing data.

2.2. Correlation Analysis of Wind Direction Parameter with Missing Data

The second case examines the correlation between wind direction, speed, and power across Sites A, B, and C, where the wind direction parameter has missing data. As shown in Figure 5, the correlation matrices for these sites reveal insightful connections. At Site A, wind power displays a moderate positive correlation with wind direction of 0.22 and a strong positive correlation with wind speed of 0.82. Additionally, a moderately positive correlation of 0.3 between wind direction and wind speed becomes evident. Site B’s matrix unveils distinctive relationships. Wind power and wind direction exhibit a moderate negative correlation of −1.19, while wind power and wind speed share a robust positive correlation of 0.92. In contrast, wind direction and speed show a weak negative correlation of −1.084. Similarly, Site C’s matrix reveals meaningful correlations. Wind power positively correlates with wind direction, with a correlation value of 0.19, and strongly correlates with wind speed, with a correlation value of 0.93. Further, wind direction and speed demonstrate a weak positive correlation of 0.081. In both scenarios, the correlation coefficients provide essential insights into the strength and nature of these relationships. Such understanding holds substantial implications for informed decision making and predictive analyses, particularly within renewable energy and meteorology.

3. Proposed Methodology

The proposed methodology outlines a step-by-step framework for predicting missing wind parameters and power generation within the Jeju Island wind farm context across different sites, as shown in Figure 6. This approach incorporates well-defined techniques to offer unique insights into predictive modelling and performance assessment. The initial step involves data collection and pre-processing. Specifically, the wind power, speed, and direction datasets from the Jeju Island wind farm at Sites A, B, and C are collected. This dataset provides the implementation for subsequent analysis and predictive modelling. Next, the correlation analysis is conducted with missing input data. This step considers two scenarios: missing wind speed data and missing wind direction data. The correlation analysis examines the complex relationships between wind speed, direction, and power under both scenarios. This analysis provides insights into how these parameters influence wind power generation. The detailed outcomes of this analysis are depicted in Figure 4 and Figure 5.

In the third step of the process, an LSTM model is used to forecast the missing wind speed and direction data. The process begins with data normalisation within the range of −1 to +1, followed by the compilation of time-series data. The dataset is then partitioned into distinct subsets for training and testing. This step involves building and training the LSTM model, progressively improving its predictive capabilities by learning from the data. Continuous evaluation ensures that the model reaches the desired level of accuracy within the allocated number of training iterations. If this level is not achieved, adjustments are made through loss calculations and model updates. Once the desired level of proficiency is attained, the model is used to forecast missing wind speed and direction data. These predicted data are then compared against actual data for comprehensive analysis. The model’s accuracy is evaluated through performance metrics such as the RMSE and visualisation of original and forecast waveforms.

The final stages of the methodology focus on predicting wind power using the FONN model. The process begins with developing a fractional-order arctan activation function using fractional derivatives. This newly developed function enhances the predictive capabilities of the FONN model. Subsequently, the FONN model is designed by integrating the developed fractional-order arctan function, rendering it adept at accurate wind power prediction. A precise parametrization of the model follows, encompassing the determination of the number of hidden layers and neurons. The FONN model is then iteratively trained to enhance its predictive performance. If necessary, model parameters are adjusted and retrained, ensuring continuous optimisation. A main evaluation criterion is whether the model achieves improved accuracy. Finally, the trained model is tested using a test dataset, and its performance is evaluated in terms of the coefficient of determination (R²) and MSE, with comparisons made against a conventional neural network model. This comprehensive methodology offers a structured approach to predicting wind power and leveraging predictive modelling techniques for renewable energy applications. As shown in Figure 6 and as explained earlier, the first part of the methodology is the LSTM model’s development for forecasting missing input data of wind speed and direction. The next part presents the FONN model that is used to make predictions of the generated wind power.

3.1. LSTM Model

The LSTM model’s architecture for forecasting 20% of missing input data of wind speed and direction is demonstrated in Figure 7. The input to the LSTM consists of three time-steps $x_{t-1}, x_t$, and $x_{t+1}$. The architecture includes memory blocks comprising each memory cell, input, forget, and output dates, which will be explained below.

In the forget gate, $f_t$ is computed using the sigmoid function; $\sigma (·)$ determines the past information to forget:

$$f_t=\sigma (w_f·\left[h_{t-1},x_t\right]+b_f),$$

(1)

In the above equation, $h_{t-1}$, $w_f$, and $b_f$ represent the previous cell’s output, and the gate’s weight and bias, respectively. The sigmoid function $\sigma (·)$ output varies between 0 and 1, representing complete forgetting at 0 and full retention at 1.

As for the input gate $i_t$, it is also calculated based on the information to be stored in the cell state:

$$i_t=\sigma (w_i·\left[h_{t-1},x_t\right]+b_i).$$

(2)

This gate’s “tanh” layer adds weight to the cell state. The update equation for the memory cell, represented as ${\tilde{C}}_t$, is

$${\tilde{C}}_t=tanh(w_C·\left[h_{t-1},x_t\right]+b_C),$$

(3)

Here, $w_C$ and $b_C$ denote the memory cell’s weight and bias.

Using the output gate $O_t$ to determine the output information from the current cell, it can be calculated as

$$O_t=\sigma (w_O·\left[h_{t-1},x_t\right]+b_O).$$

(4)

The current cell’s output ($h_t$) will be calculated as

$$h_t=O_t\times tanh\left(C_t\right).$$

(5)

where $C_t$ is the cell state and $O_t$ is the output gate.

Two critical factors that influence the performance of an LSTM model are input delays and the number of hidden units. An LSTM network with 10 hidden units was trained to achieve adequate performance using a trial-and-error approach. Incomplete learning, limited generalisation, and underfitting can occur if the LSTM model is not sufficiently trained. Incomplete learning can cause suboptimal performance because the model fails to capture all underlying patterns. Limited generalisation means that the model needs to extend its predictions beyond the training data, leading to poor performance on missing data. On the other hand, underfitting causes poor performance on both training and test datasets. However, overtraining is unlikely due to the need for more learning from the data. Therefore, adequate training is crucial for accurate predictions. To achieve this, the Adam solver was introduced with variable learning and dropout rates of 0.005 and 0.2, respectively, over 1000 epochs.

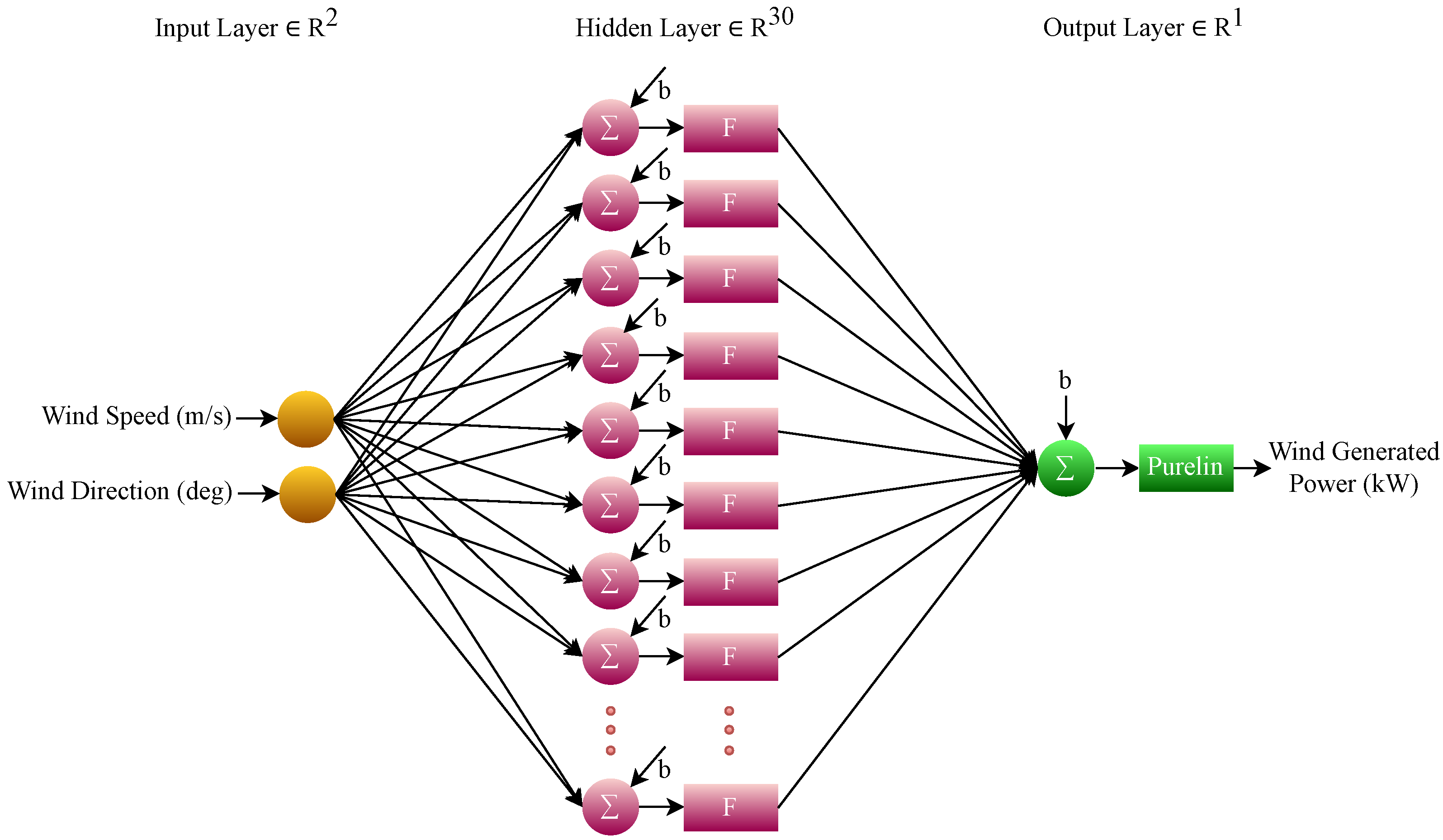
3.2. FONN Model

The FONN model’s architecture, designed to predict generated wind power using forecast missing wind direction and speed data with an LSTM model, is illustrated in Figure 8 [42]. In this configuration, there are 2 input nodes, 30 hidden nodes, and 1 output node, and their ratios are 2:30:1. The number of nodes in a hidden layer plays a significant role in determining the predictive capabilities of a neural network. Too few nodes may result in underfitting, while too many can lead to overfitting. In this case, a trial-and-error approach was used to determine that a hidden layer with 30 nodes would achieve satisfactory results. Within the architecture, bias values at the hidden and output layers were represented as “b”, with values [30, 1]. For the output layer, the activation function selected was “Purelin”. In contrast, the hidden layers’ activation function “F” employed can vary between developed and standard tangential functions. This variation was assessed to determine the model’s performance. For the training algorithm, the Levenberg–Marquardt algorithm was selected. This neural network training algorithm helps to fine-tune the model’s parameters effectively. The model’s performance evaluation was conducted using the performance measures outlined in the subsequent section, ensuring a comprehensive assessment of its predictive capabilities.

3.3. Fractional-Order Tangential Activation Functions

The tansig activation function, also known as the hyperbolic tangent sigmoid, is commonly used in hidden layers for classification tasks [45]. This function maps input values from the range of $(-\infty ,+\infty )$ to $(-1,1)$. Its mathematical expression is given below [42]:

$$f\left(x\right)=\frac{2}{1+e^{-2x}}-1.$$

(6)

The tansig function is known to have a higher derivative compared to the sigmoid function. Additionally, its output mean is 0 when the average input values approach 0. These properties make the tansig function a valuable tool for training neural networks, as it can significantly improve convergence rates and expedite the training process. However, similar to the sigmoid function, tansig is also prone to the vanishing gradient problem [46]. Incorporating fractional-order derivatives into the tansig function to introduce a non-linear component can address the gradient problem. The fractional ordering of tansig can be derived by expressing Equation (6) using the MacLaurin series expansion as follows:

$$f\left(x\right)=\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}}{\left(2n\right)!}{x}^{2n-1}.$$

(7)

The fractional ordering of the tansig activation function can be computed for an order $\alpha \in (0,0.9)$ as follows [42]:

$$\begin{array}{cc}\hfill D^{\alpha }f\left(x\right)=g\left(x\right)& =D^{\alpha }\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}}{\left(2n\right)!}{x}^{2n-1},\hfill \\ \hfill g\left(x\right)& =\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}(2n-1)!}{\left(2n\right)!\mathsf{\Gamma }(2n-\alpha )}{x}^{2n-1-\alpha }.\hfill \end{array}$$

(8)

Figure 9a shows the response of the fractional-order derivative of the tansig activation function for various values of $\alpha$, as compared to the behaviour of the regular tansig function. The conventional tansig function has an S-shaped curve, similar to the sigmoid function and its variations. On the other hand, the fractional-order derivative of tansig has an S-shaped curve for lower values of $\alpha$. However, for higher values of $\alpha$, the function becomes non-linear due to the fractional ordering, which can help solve the vanishing gradient problem.

The hard tansig function is a commonly used version of the tansig activation function in deep learning applications. Unlike the tansig function, the hard tansig function is more efficient and computationally cheaper. It has a range of $[-1,1]$ and is defined as follows [45,47]:

$$f\left(x\right)=\left\{\begin{array}{cc}-1\hfill & \mathrm{if}x<-1,\hfill \\ x\hfill & \mathrm{if}-1\le x\le 1,\hfill \\ 1\hfill & \mathrm{if}x>1.\hfill \end{array}\right.$$

(9)

The fractional-order derivative of the hard tansig function can be computed for an order $\alpha \in (0,0.9)$ as follows [42]:

$$\begin{array}{cc}\hfill D^{\alpha }f\left(x\right)=g\left(x\right)& =D^{\alpha }\left\{\begin{array}{cc}-1\hfill & \mathrm{if}x<-1\hfill \\ x\hfill & \mathrm{if}-1\le x\le 1\hfill \\ 1\hfill & \mathrm{if}x>1\hfill \end{array}\right.,\hfill \\ \hfill g\left(x\right)& =\left\{\begin{array}{cc}\frac{-1}{\mathsf{\Gamma }(1-\alpha )}{x}^{-\alpha }\hfill & \mathrm{if}x<-1\hfill \\ \frac{1}{\mathsf{\Gamma }(2-\alpha )}{x}^{1-\alpha }\hfill & \mathrm{if}-1\le x\le 1\hfill \\ \frac{1}{\mathsf{\Gamma }(1-\alpha )}{x}^{-\alpha }\hfill & \mathrm{if}x>1\hfill \end{array}\right..\hfill \end{array}$$

(10)

The comparison shown in Figure 9b highlights the response of the fractional-order derivative of the hard tansig activation function for different values of $\alpha$ orders compared to the conventional derivative. The analysis reveals that the functions take the $\alpha$ value derivative in specific intervals while exhibiting zero gradients in others. This aspect indicates that the vanishing gradient problem is less likely to occur in the fractional-order derivative of the hard tansig function as long as most of these units operate within the periods when the gradient is 1. Moreover, the analysis suggests that the fractional ordering has introduced non-linearity into the function, which will help resolve the vanishing gradient problem.

The LiSHT (linearly scaled hyperbolic tangent) is a popular activation function used in deep learning to address the “dead ReLU” issue. When the ReLU function is given negative input, it can become inactive, resulting in a zero gradient that prevents weight updates during backpropagation. As a result, to solve this problem, the LiSHT function multiplies the input with the element-wise hyperbolic tangent output. Additionally, since the hyperbolic tangent function has a range of [−1, 1], negative gradients are not eliminated like with ReLU functions, which helps maintain the optimal learning for training deep neural networks. The LiSHT function can be computed by multiplying the tansig function with its input, as shown in [47].

$$f\left(x\right)=x·\delta \left(x\right),$$

(11)

The following expression defines the tansig function $\delta \left(x\right)$, which can be found in Equation (6):

$$\delta \left(x\right)=\frac{2}{1+e^{-2x}}-1.$$

(12)

The LiSHT function in Equation (11) can be expressed using a MacLaurin series expansion as follows:

$$f\left(x\right)=\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}}{\left(2n\right)!}{x}^{2n}.$$

(13)

The equation above enables computation of the fractional ordering of the LiSHT activation function for an order $\alpha \in (0,0.9)$ as follows [42]:

$$\begin{array}{cc}\hfill D^{\alpha }f\left(x\right)=g\left(x\right)& =D^{\alpha }\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}}{\left(2n\right)!}{x}^{2n},\hfill \\ \hfill g\left(x\right)& =\sum _{n=0}^{\infty }\frac{4^n(4^n-1)B_{2n}\mathsf{\Gamma }(2n+1)}{\left(2n\right)!\mathsf{\Gamma }(2n-\alpha +1)}{x}^{2n-\alpha }.\hfill \end{array}$$

(14)

The response of the fractional-order derivative of the LiSHT activation function for various $\alpha$ orders, compared with the conventional one, is shown in Figure 9c. The response indicates that the conventional LiSHT produces a positive output response. For lower $\alpha$ values, the fractional ordering of LiSHT achieves similar behaviour. However, the response shows fractional ordering introduces more significant non-linearity than other activation functions for higher $\alpha$ values.

Additionally, the conventional arctan activation function is employed at the hidden layer in neural networks. However, its non-monotonic nature can pose optimisation challenges. Mathematically, the arctan function is expressed as [48]

$$f\left(x\right)={tan}^{-1}\left(x\right).$$

(15)

This equation can be expanded using the MacLaurin series as follows:

$$f\left(x\right)=\sum _{n=0}^{\infty }\frac{{(-1)}^n}{2n+1}{x}^{2n+1}.$$

(16)

The arctan function is enhanced by introducing fractional-order derivatives to tackle these challenges, improving its smoothness and optimisation potential within the FONN model. The fractional-order derivative of the arctan activation function for an order $\alpha \in (0,0.9)$ can be computed as [49]

$$\begin{array}{cc}\hfill D^{\alpha }f\left(x\right)=g\left(x\right)& =D^{\alpha }\sum _{n=0}^{\infty }\frac{{(-1)}^n}{2n+1}{x}^{2n+1},\hfill \\ \hfill g\left(x\right)& =\sum _{n=0}^{\infty }\frac{{(-1)}^n\mathsf{\Gamma }(2n+3)}{(2n+1)\mathsf{\Gamma }(2n+2-\alpha )}{x}^{2n+1-\alpha }.\hfill \end{array}$$

(17)

This enhancement results in smoother derivatives for the fractional-order arctan function, facilitating more effective gradient-based optimisation, which makes it better at capturing complex dynamics and long-range dependencies in wind power data, and its response at different $\alpha$ values is shown in Figure 9d. Compared to conventional functions, fractal activation functions like fractional-order arctan provide more flexibility in modelling non-linear systems. They are better at adapting to intricate patterns in renewable energy data.

Furthermore, the Purelin activation function is employed at the networks’ output layer. It is a linear function that directly relates output to input, giving a response of $kx$ for an input of x. The response of Purelin is shown in Figure 10. For $k=1$, it functions as an identity. This function, with a hyperparameter k, is described as [50]

$$f\left(x\right)=kx.$$

(18)

3.4. Performance Metrics

The MSE and RMSE are widely recognised performance metrics that assess the difference between predicted and actual values. Extensive studies have demonstrated their effectiveness as error measures in numerical prediction tasks [51,52]. The MSE is computed between actual ($Y_i$) and predicted ($\widehat{Y_i}$) as follows:

$$\mathrm{MSE}={\displaystyle \frac{1}{\mathrm{N}}}\sum _{i=1}^{\mathrm{N}}{(Y_i-\widehat{Y_i})}^2.$$

(19)

The RMSE provides an interpretable measure of the average forecasting error, which is computed as follows:

$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}.$$

(20)

Additionally, the coefficient of determination, denoted as R², is frequently used to show the predictive capability of forecasting methods in fitting actual data ($Y_i$), calculated as [52]

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{i=1}^{\mathrm{N}}{(Y_i-\widehat{Y_i})}^2}{{\sum }_{i=1}^{\mathrm{N}}{(Y_i-\overline{Y_i})}^2}}.$$

(21)

where $\overline{Y}$ signifies the average of the predicted values. R² yields values ranging from 0 (indicating a poor match) to 1 (representing a perfect fit).

In all the above equations, ‘N’ represents the sample size and ${\widehat{Y}}_i$ denotes predicted values. These metrics provide valuable insights into numerical forecasting approaches’ accuracy and predictive performance.

4. Results and Discussion

This section evaluates the LSTM model’s accuracy in forecasting missing wind speed and direction data and the FONN model’s performance in predicting wind power using the forecast data of missing wind speed and direction data in the Jeju Island wind farm for all sites under different cases.

4.1. Performance of LSTM Model

In Jeju Island’s wind farm, 20% of wind speed and direction data are missing at three sites (A, B, and C). This missing data can negatively impact the accuracy of power predictions, operational planning, efficiency, safety, and overall system reliability. An LSTM model has been developed to forecast missing wind speed and direction data to address the issue, as mentioned in Section 3 and compared with non-linear autoregressive (NAR) [53], and autoregressive integrated moving average (ARIMA) [54] models. The LSTM model has one input, 200 hidden units, and one output. The model uses learning and dropout rates of 0.005 and 0.2, respectively, for 1000 iterations.

Table 2. Performance comparison of various forecasting models for missing data of wind speed and direction at different sites.

Model	Site	Wind Speed (m/s)	Wind Direction (deg)
		RMSE	RMSE
LSTM	Site A	0.18	0.16
	Site B	0.425	0.185
	Site C	0.112	0.126
NAR	Site A	0.353	0.442
	Site B	0.297	0.185
	Site C	0.457	0.395
ARIMA	Site A	0.583	0.386
	Site B	0.458	0.572
	Site C	0.387	0.454

displays RMSE values for various models used in forecasting missing wind speed and direction data at three sites. The table compares the performance of three different forecasting models: LSTM, NAR, and ARIMA. Based on Table 2, the performance analysis of various forecasting models is as follows:

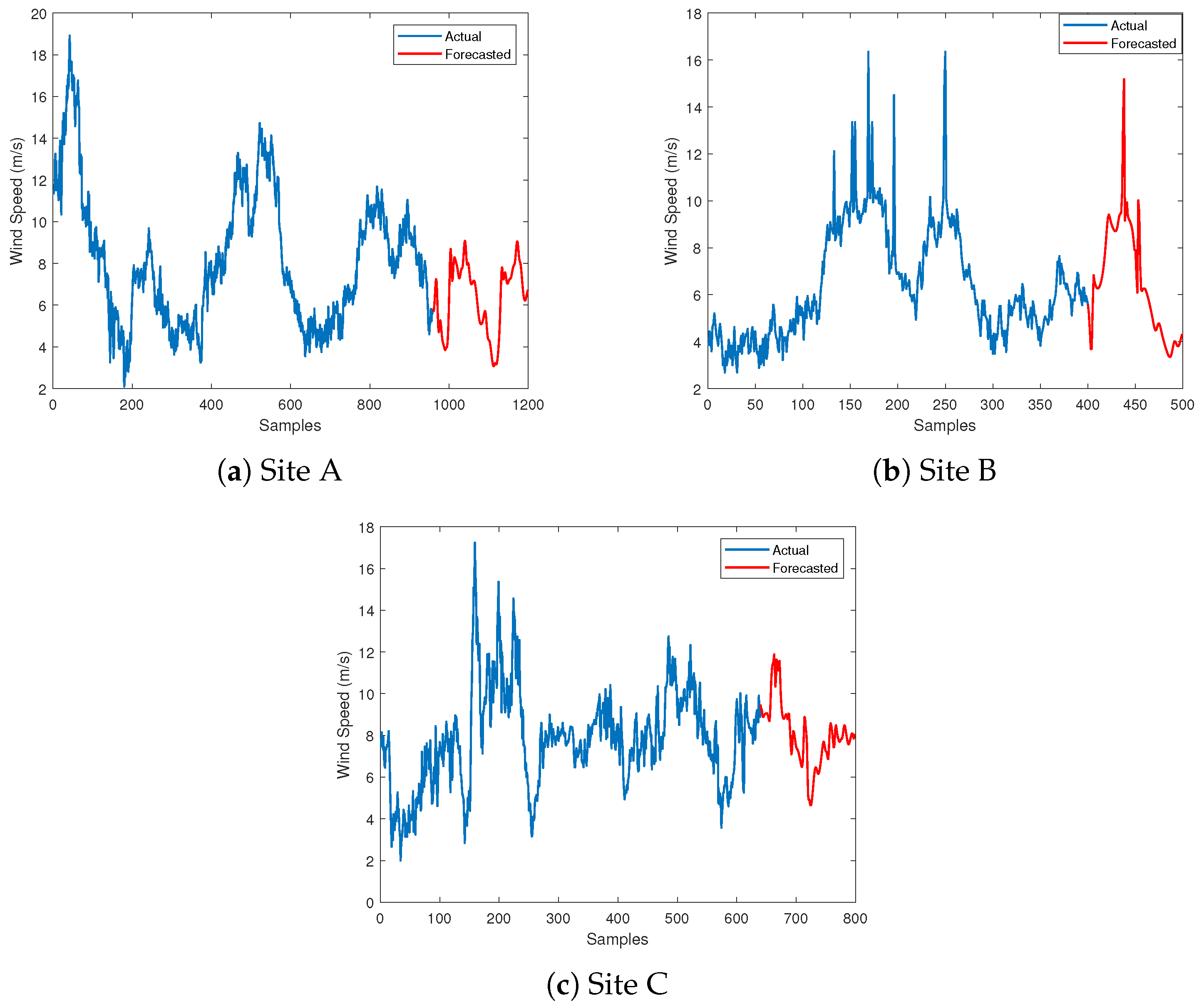
• The LSTM model exhibits the lowest RMSE values compared to the NAR and ARIMA models for forecasting missing wind speed data across all sites.
• At Site A, the LSTM model achieved the lowest RMSE value of 0.16, followed by NAR with an RMSE of 0.353 and ARIMA with an RMSE of 0.583.
• Similarly, the LSTM model at Site B outperformed the other models with an RMSE of 0.185, while the NAR and ARIMA models showed higher RMSE values of 0.297 and 0.458, respectively.
• Finally, at Site C, the LSTM model exhibited the lowest RMSE of 0.112, followed by ARIMA with an RMSE of 0.387 and NAR with the highest RMSE of 0.457.
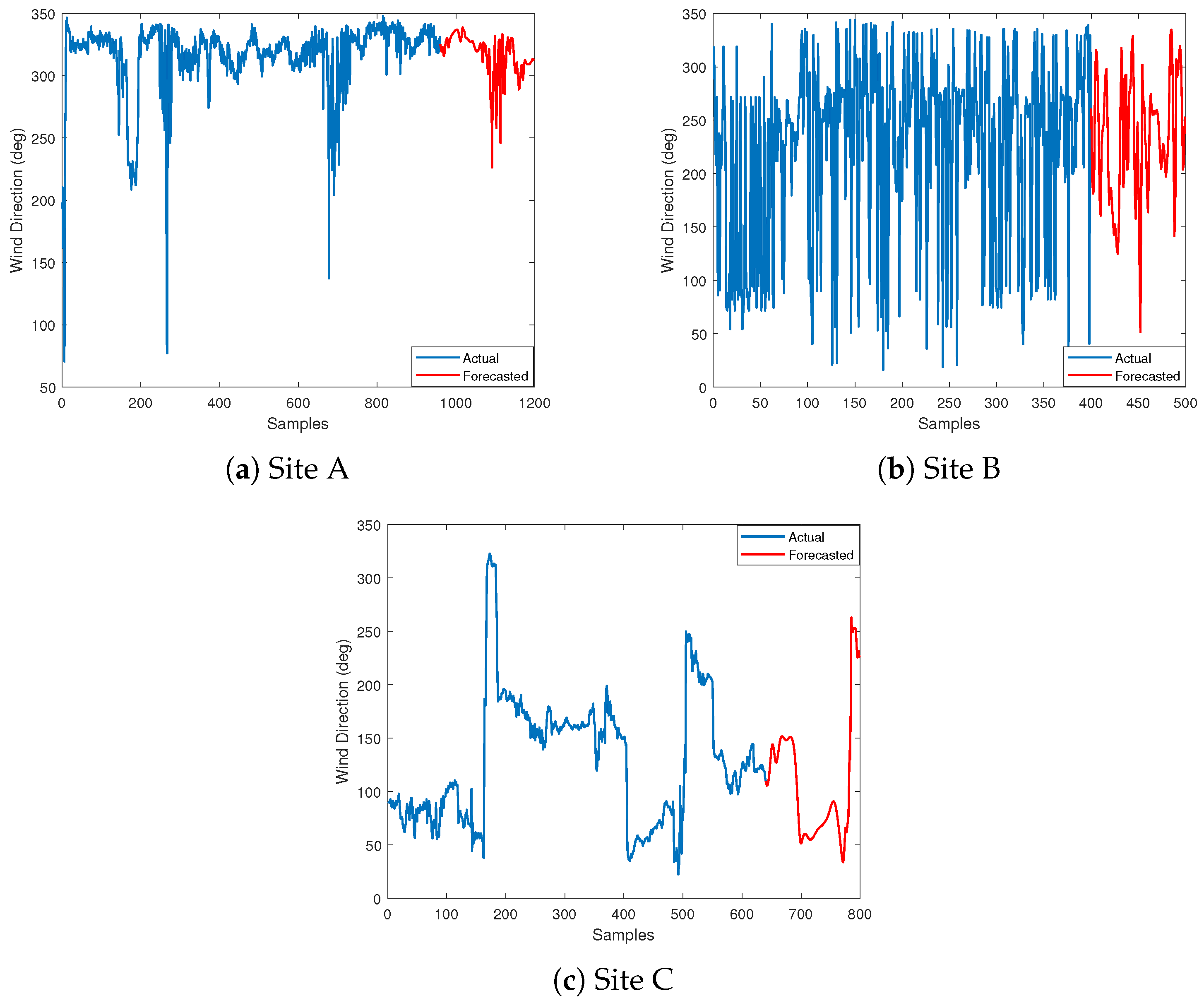
• The following analysis is related to missing wind direction data forecasting, where the performance of the models varies across different sites.
• At Site A, the LSTM model had the lowest RMSE of 0.18, followed by ARIMA with an RMSE of 0.386 and NAR with the highest RMSE of 0.442.
• Similarly, at Site B, the LSTM model performed best with an RMSE of 0.425, followed by NAR with an RMSE of 0.185, and ARIMA with the highest RMSE of 0.572.
• Finally, at Site C, the NAR model had the lowest RMSE of 0.395, followed by LSTM with an RMSE of 0.126, and ARIMA with the highest RMSE of 0.454.

The results show that the LSTM model performs better than the NAR and ARIMA models in forecasting wind speed and wind direction missing data across different sites. However, the performance may vary depending on the specific site and the nature of the wind data. Figure 11 and Figure 12 depict the actual wind speed and direction and those forecast by the LSTM model. Further, the numerical values in Table 2 indicate the model’s best performance, with RMSEs of around 0.11 and 0.12, respectively.

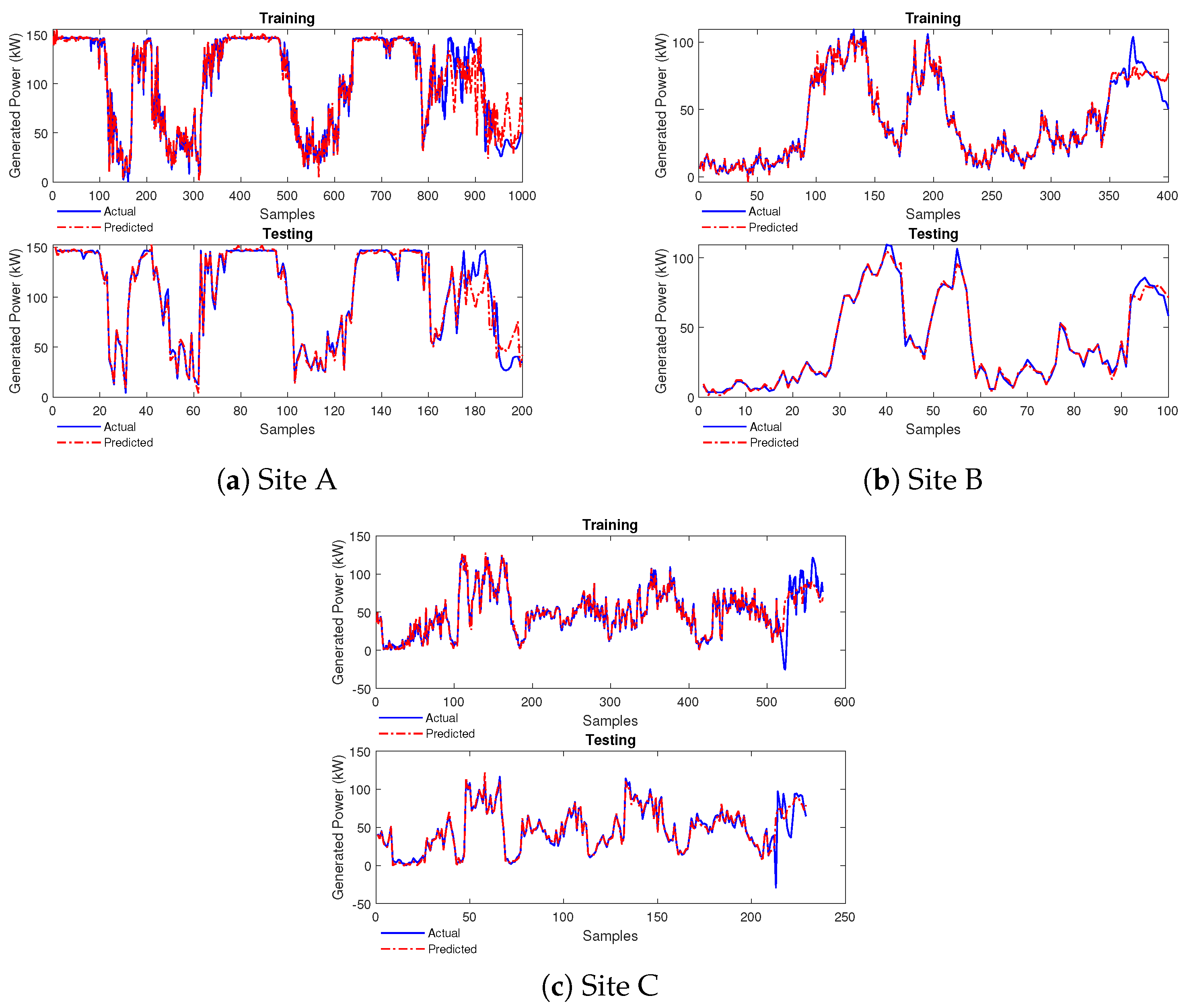
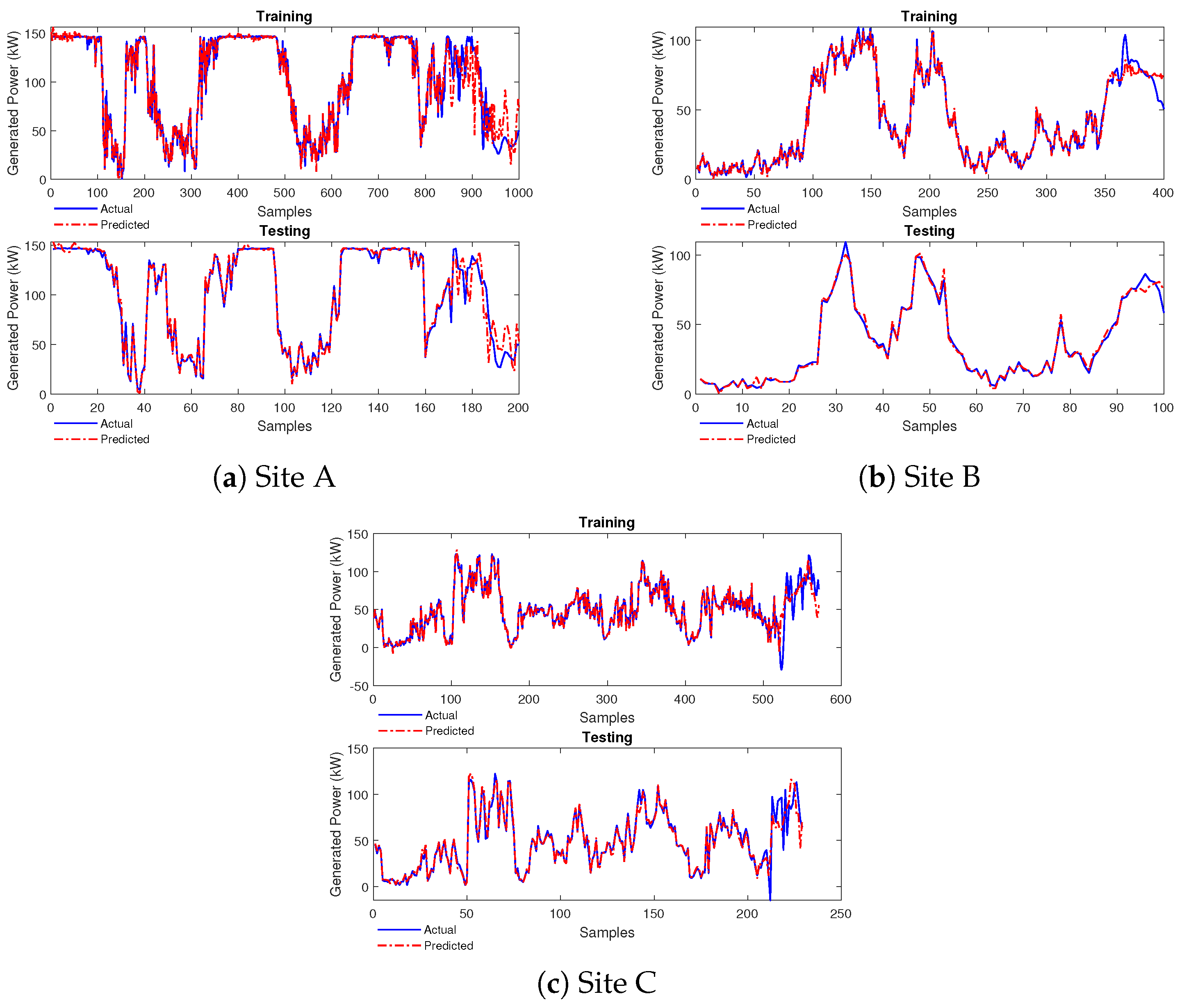
4.2. Performance of FONN Model

This section presents the FONN model’s performance in predicting wind power using the forecast missing wind speed and direction data with the LSTM model at different sites. As per the previous section, the LSTM model showed the best performance among the forecasting models. There are two case studies considered for predicting wind power. The first case study involves predicting generated wind power using wind direction data and forecast missing wind speed data. The second case study presents generated wind power using wind speed data and forecast missing wind direction data.

4.2.1. Case Study 1

As mentioned, a FONN model with a single hidden layer was used in the first case study, as depicted in Figure 8. This neural network predicts wind power using wind direction data and forecasts missing wind speed data. The architecture comprises 2 nodes in the input layer, 30 in the hidden layer, and 1 in the output layer. The activation function “Purelin” was chosen for the network’s output layer. In contrast, the hidden layer’s activation function “F” varied between conventional and developed tangential functions to evaluate the performance of the FONN model in terms of R² and MSE. The analysis of the performance of the activation function is given in

Table 3. Performance comparison of different functions in training and testing phases for various sites under case study 1.

Site	Conventional Function	Training		Testing		Fractional Function	Training		Testing
		R2	MSE	R2	MSE		R2	MSE	R2	MSE
Site A	Tansig	0.8578	0.0753	0.8642	0.0764	Tansig	0.8739	0.0628	0.8864	0.0612
	Hard tansig	0.8954	0.0521	0.9075	0.0516	Hard tansig	0.9263	0.0424	0.9369	0.0397
	LiSHT	0.8749	0.0683	0.8873	0.0621	LiSHT	0.9025	0.0612	0.9173	0.0598
	Arctan	0.9727	0.0227	0.9733	0.0207	Arctan	0.9749	0.0205	0.9831	0.0142
Site B	Tansig	0.9328	0.0662	0.9436	0.0652	Tansig	0.9428	0.0534	0.9497	0.0529
	Hard tansig	0.9489	0.0583	0.9517	0.0578	Hard tansig	0.9543	0.0464	0.9609	0.0432
	LiSHT	0.9532	0.0428	0.9584	0.0414	LiSHT	0.9572	0.0399	0.9621	0.0386
	Arctan	0.9901	0.0063	0.9948	0.0035	Arctan	0.9929	0.0046	0.9952	0.0032
Site C	Tansig	0.8216	0.0853	0.8362	0.0817	Tansig	0.8931	0.0742	0.9026	0.0629
	Hard tansig	0.8453	0.0732	0.8564	0.0695	Hard tansig	0.9035	0.0598	0.9163	0.0586
	LiSHT	0.8762	0.0789	0.8758	0.0778	LiSHT	0.8864	0.0752	0.8973	0.0745
	Arctan	0.9469	0.0158	0.9529	0.0134	Arctan	0.9573	0.0123	0.9635	0.0115

, based on the results obtained, as follows.

The following analysis was conducted to determine the accuracy of different activation functions on Site A during the training and testing phases. The results indicate that the fractional arctan function had the highest accuracy, with R² values of 0.9749 and 0.9831 during the training and testing phases, respectively, with MSE values of 0.0205 and 0.0142. Similarly, the fractional hard tansig function performed the best, with R² values of 0.9263 and 0.9369 and MSE values of 0.0424 and 0.0397 during the training and testing phases, respectively. The hard tansig function also performed well, with R² values of 0.8954 and 0.9075 in the training and testing phases, respectively, and an MSE value of 0.0521 in both phases. On the other hand, the conventional tansig function had the lowest accuracy, with R² values of 0.8578 and 0.8642 during the training and testing phases, respectively, and MSE values of 0.0753 and 0.0764, respectively.

At Site B, the fractional tansig function performed the best, with R² values of 0.9428 and 0.9497 during training and testing phases, respectively, and MSE values of 0.0534 and 0.0529. The hard tansig function also performed well, with R² values of 0.9489 and 0.9517 during the training and testing phases, respectively, and MSE values of 0.0583 and 0.0578, respectively. On the other hand, the worst-performing function for Site B was the conventional tansig function, with R² values of 0.9328 and 0.9436 in the training and testing phases, respectively, and MSE values of 0.0662 and 0.0652, respectively. Moreover, the fractional hard tansig function performed better during the training and testing phases, with R² values of 0.9543 and 0.9609 and MSE values of 0.0464 and 0.0432, respectively. The conventional LiSHT function had R² values of 0.9532 and 0.9584 and MSE values of 0.0428 and 0.0414 during the training and testing phases, respectively. The fractional LiSHT function performed better, with R² values of 0.9572 and 0.9621 and MSE values of 0.0399 and 0.0386 during the training and testing phases, respectively. For the highest accuracy, the fractional arctan function proved to be the best option, with R² values of 0.9929 and 0.9952 in the training and testing phases, respectively, and MSE values of 0.0046 and 0.0032, respectively. Similarly, the conventional arctan function also performed well, with R² values of 0.9901 and 0.9948 during the training and testing phases, respectively, and MSE values of 0.0063 and 0.0035, respectively.

For Site C, the fractional tansig function performed better than the conventional tansig function, with R² values of 0.8931 and 0.9026 and MSE values of 0.0742 and 0.0629 during the training and testing phases, respectively. Similarly, the fractional hard tansig function performed better than the conventional hard tansig function, with R² values of 0.9035 and 0.9163 and MSE values of 0.0598 and 0.0586 during the training and testing phases, respectively. For the LiSHT function, the fractional LiSHT function performed slightly better than the conventional LiSHT function, with R² values of 0.8864 and 0.8973, and MSE values of 0.0752 and 0.0745 during the training and testing phases, respectively. The highest accuracy was achieved using the fractional arctan function, with R² values of 0.9573 and 0.9635 and MSE values of 0.0123 and 0.0115 during the training and testing phases, respectively. The conventional arctan function also performed well, with R² values of 0.9469 and 0.9529 and MSE values of 0.0158 and 0.0134 during the training and testing phases, respectively.

Therefore, from the results across all the sites shown in Table 3, the FONN model’s best performance with the conventional arctan function is depicted in Figure 13 and the fractional arctan function is shown in Figure 14 at the hidden layer. The neural network’s performance varied across sites and activation functions. The developed arctan arctan function provided improved results compared to other functions, reflected in higher R² values and lower MSE values for training and testing across different sites.

4.2.2. Case Study 2

The following analysis presents the second case study, which uses the same network as the previous case, with an identical node count and activation functions. However, this network uses wind speed data and forecast wind direction data as inputs to predict the generated wind power. The obtained results are shown in

Table 4. Performance comparison of different functions in training and testing phases for various sites under case study 2.

Site	Conventional Function	Training		Testing		Fractional Function	Training		Testing
		R2	MSE	R2	MSE		R2	MSE	R2	MSE
Site A	Tansig	0.8973	0.0621	0.9043	0.0594	Tansig	0.9264	0.0519	0.9329	0.0497
	Hard tansig	0.9264	0.0372	0.9378	0.0346	Hard tansig	0.9726	0.0218	0.9832	0.0169
	LiSHT	0.9163	0.0583	0.9289	0.0542	LiSHT	0.9517	0.0487	0.9619	0.0453
	Arctan	0.9898	0.0081	0.9931	0.0059	Arctan	0.9899	0.0081	0.9946	0.0048
Site B	Tansig	0.8245	0.0982	0.8463	0.0968	Tansig	0.8562	0.0841	0.8678	0.0832
	Hard tansig	0.8674	0.0721	0.8689	0.0708	Hard tansig	0.8864	0.0682	0.8949	0.0617
	LiSHT	0.8462	0.0819	0.8573	0.0798	LiSHT	0.8693	0.0739	0.8715	0.0716
	Arctan	0.9826	0.0129	0.9875	0.0094	Arctan	0.9835	0.0124	0.9867	0.0094
Site C	Tansig	0.9041	0.0528	0.9146	0.0512	Tansig	0.9317	0.0425	0.9462	0.0419
	Hard tansig	0.9089	0.0481	0.9163	0.0479	Hard tansig	0.9273	0.0341	0.9526	0.0252
	LiSHT	0.8932	0.0514	0.9023	0.0506	LiSHT	0.9172	0.0459	0.9251	0.0445
	Arctan	0.9793	0.0085	0.9866	0.0054	Arctan	0.9816	0.0076	0.9865	0.0052

, and the analysis of the performance of the activation functions at the three sites is as follows.

Table 4 shows that conventional and fractional functions performed well across all the sites during the training and testing phases. Among the conventional functions, hard tansig and arctan outperformed the others in terms of R² and MSE values during both training and testing phases. On the other hand, the fractional function performed better overall, with higher R² values and lower MSE values than the corresponding conventional functions. For instance, for Site A, arctan had the highest R² value of 0.9898 and the lowest MSE value of 0.0081 for training, while for testing, it had the highest R² value of 0.9931 and the lowest MSE value of 0.0059. Similarly, the fractional arctan function had the highest R² value of 0.9899 and the lowest MSE value of 0.0081 for training, while for testing, it had the highest R² value of 0.9946 and the lowest MSE value of 0.0048. These values indicate that arctan and its corresponding fractional function were the best-performing functions for Site A. The second-best performing function for Site A was hard tansig and its corresponding fractional function. For training, hard tansig had the highest R² value of 0.9264 and the lowest MSE value of 0.0372, while for testing, it had the highest R² value of 0.9378 and the lowest MSE value of 0.0346. Similarly, the fractional hard tansig function had the highest R² value of 0.9726 and the lowest MSE value of 0.0218 for training, while for testing, it had the highest R² value of 0.9832 and the lowest MSE value of 0.0169. On the other hand, the tansig function had the lowest R² value of 0.8973 and the highest MSE value of 0.0621 during training. Similarly, during testing, it had the lowest R² value of 0.9043 and the highest MSE value of 0.0594. Similarly, the fractional tansig function had the lowest R² value of 0.9264 and the highest MSE value of 0.0519 during training, while it had the lowest R² value of 0.9329 and the highest MSE value of 0.0497 when tested. These values indicate that tansig and its corresponding fractional function were the worst-performing functions at Site A.

At Site B, the activation function arctan performed the best in both training and testing phases, with R² values of 0.9826 and 0.9875, respectively, and MSE values of 0.0129 and 0.0094, respectively. The arctan arctan function also performed well, with R² values of 0.9835 and 0.9867 and MSE values of 0.0124 and 0.0094, respectively. The best-performing activation function was arctan hard tansig, with R² values of 0.8864 and 0.8949 in the training and testing phases, respectively, and MSE values of 0.0682 and 0.0617, respectively. The tansig and LiSHT activation functions performed well but not as well as the arctan and arctan hard tansig functions. In conclusion, the arctan and arctan hard tansig activation functions performed the best for Site B, with arctan being slightly better regarding the R² value. Similarly, for Site C, the activation function arctan performed the best in both training and testing phases, with R² values of 0.9793 and 0.9866, respectively, and MSE values of 0.0085 and 0.0054, respectively. The arctan arctan function also performed well, with R² values of 0.9816 and 0.9865 and MSE values of 0.0076 and 0.0052, respectively. The second-best-performing activation function was arctan hard tansig, with R² values of 0.9273 and 0.9526 in the training and testing phases, respectively, and MSE values of 0.0341 and 0.0252, respectively. The tansig and LiSHT activation functions also performed well but not as well as the arctan and arctan hard tansig functions. Thus, the arctan and arctan hard tansig activation functions performed the best for Site C, with arctan being slightly better regarding the R² value. The worst-performing activation function was tansig for both conventional and fractional functions.

Therefore, the results presented in Table 4, the best performance of the FONN model with the conventional arctan function, is shown in Figure 15, and the developed arctan arctan activation function is depicted in Figure 16 at the hidden layer during training and testing at all three sites. The conventional arctan and the developed arctan arctan functions exhibit strong predictive abilities compared to other functions at all three sites. Minor variations in the R² and MSE values demonstrate the consistent and dependable performance of both functions for predicting generated wind power using the provided input data.

The results in both case studies compared the performance of the arctan tangential functions and the conventional tangential functions in predicting wind power across various sites. The arctan arctan function consistently achieved higher R² values and lower MSE values than the other functions, indicating better predictive capabilities of the FONN model. These findings have important implications for fields that rely on predictive modelling, such as finance, economics, and engineering.

5. Conclusions

A hybrid approach combining LSTMs and FONNs has been presented in this paper to forecast data missing from wind parameters and predict generated wind power across all the sites in the Jeju Island wind farm. An LSTM model was employed to forecast missing wind speed and direction data, obtaining RMSE values of approximately 0.11 and 0.12, respectively. In addition, the FONN model was used to predict wind power with forecast missing wind parameters data through two case studies. In the first case, using wind direction and forecast wind speed data, the developed arctan arctan activation function outperformed the conventional arctan function in the neural network, with high R² and low MSE values, around 0.97 and 0.003, respectively, during training and testing. Similarly, both activation functions exhibited strong predictive capabilities in predicting wind power using wind speed. During training and testing, the forecast wind direction in the second case achieved high R² and low MSE values, around 0.98 and 0.004, respectively. The results highlight the potential of the developed arctan arctan function, which consistently proved its effectiveness in enhancing predictive capabilities compared to the conventional arctan function and among all the tangential functions in both case studies. The study provides valuable insights into predicting generated wind power and fills gaps in missing data, demonstrating the potential of advanced neural networks in renewable energy applications. The developed arctan tangential activation functions have improved predictive capabilities compared to the conventional tangential functions, but their increased complexity may limit their practical implementation. In future work, there is a possibility of expanding the analysis carried out on fractional activation functions at $\alpha$ = 0.1 to determine the optimal $\alpha$ value. This extension of $\alpha$ could potentially increase the predictive accuracy of power in wind farms.