Otsu Image Segmentation Based on a Fractional Order Moth–Flame Optimization Algorithm

Abstract

To solve the shortcomings of the Otsu image segmentation algorithm based on traditional Moth–Flame Optimization (MFO), such as its poor segmentation accuracy, slow convergence, and tendency to fall into local optimum, this paper proposes fractional order moth–flame optimization with the Otsu image segmentation algorithm. Utilizing the advantages of memorability and heritability in fractional order differentiation, the position updating of moths is controlled by fractional order. Using the adaptive fractional order, the positions of moths are used to adjust the fractional order adaptively to improve the convergence speed. Combining the improved MFO algorithm with the two-dimensional Otsu algorithm, the optimization objective function is achieved by using its dispersion matrix. The experimental results indicate that, compared with traditional MFO, the convergence rate of the proposed algorithm is improved by about 74.62%. Furthermore, it has better segmentation accuracy and a higher fitness value than traditional MFO.

1. Introduction

Image segmentation is a crucial part of image processing that aims to divide an image into meaningful parts and extract the target of interest [1]. One of the most commonly used segmentation methods is threshold image segmentation, which is both simple and effective. The maximum inter-class variance method (Otsu) is a classical algorithm for threshold segmentation. On the basis of the image grayscale histogram, it maximizes the inter-class variance of the target and the background as the basis for automatically determining the segmentation threshold. The two-dimensional Otsu algorithm has better segmentation and higher operational efficiency than the traditional Otsu algorithm. Xiong et al. [2] presented an interleaved Otsu algorithm to segment MR images with biased fields. In most cases, the method excluded MR images that were severely corrupted by noise and achieved the desired classification of MR images with intensity inhomogeneities. Kumar et al. [3] introduced a context energy curve-based three-dimensional Otsu algorithm that considers both pixel intensity values and spatial information with the same histogram properties. In terms of performance metrics, the energy curve-based three-dimensional Otsu algorithm is superior to the histogram-based Otsu algorithm, which has better segmentation results.

Moth–flame optimization (MFO) is a novel population intelligence algorithm proposed by Seyedali Mirjalili in 2015. It based on the lateral navigation mechanism of moths in flight when simulating their spiral flight paths [4], which has received widespread attention in recent years. The et al. [5] provided a method to enhance the MFO algorithm by employing a combination of Levy flight functions and logarithmic functions in the flame update formulation. This method was also evaluated using a set of benchmark functions and multi-threshold image segmentation from CEC2013. The experimental results show that the improved algorithm is more effective. Khairuzzaman et al. [6] improved the MFO algorithm and applied it to multi-threshold image segmentation. Cross-entropy was used as an objective function to select the optimal threshold. Their algorithm was compared with the original MFO, Particle Swarm Optimization (PSO), Bacterial Foraging Optimization (BFO), and the Whale Optimization Algorithm (WOA); it performed better in terms of image segmentation quality, stability, and time.

In recent years, fractional order calculus has become increasingly common in modern signal analysis and processing. For example, it has been a hot topic in research for a long time because of its significant advantages in enhancing signal strength and stabilizing the signal [7]. With images being one of the important fields of signal analysis and processing, fractional order calculus is applied to the research directions of image enhancement, segmentation, and edge detection, and there has been a significant amount of research on this. In order to reach the optimal threshold, it is common for optimization algorithms to be combined. Yang et al. [8] proposed an algorithm that is adaptive for fractional order wolf packs. The algorithm’s convergence speed is enhanced by adaptively adjusting the fractional order based on the position information of wolves. Yousri et al. [9] employed fractional order calculus and a cuckoo search algorithm to identify the parameters of fractional order-chaotic, noisy-chaotic, and hyper-chaotic financial systems and it operated with a greater efficiency. However, there are a few researchers that have combined fractional order and population intelligence algorithms for image segmentation [10].

In response to the low segmentation accuracy of the Otsu algorithm, the MFO algorithm still suffers from the problems of having a slow convergence and easily falling into local optimality. Considering the superiority of fractional order calculus in the fields of signal analysis and image processing, this paper proposed an Otsu image segmentation algorithm based on fractional order MFO to solve the above problems. Taking the advantages of fractional order differentiation, which has memory for past states, the position updating of moths is controlled by fractional order. Using the adaptive fractional order, the position of moths is used to adjust the fractional order adaptively to improve the convergence speed. Aiming towards obtaining the optimal threshold, we combined the improved MFO algorithm with the two-dimensional Otsu algorithm to enhance the segmentation accuracy and convergence speed of the image.

2. Materials

2.1. Two-Dimensional Otsu Threshold Segmentation Algorithm

In 1979, the Otsu algorithm, an efficient adaptive threshold segmentation algorithm, was proposed by a Japanese scholar named OTSU [11]. Using the gray scale properties of the image, the idea is to divide the image into two parts: the target and the background. The binary image can be obtained by utilizing the different and large differences in the grayscale histograms and background changes in the target image by calculating the interclass variance, as the higher the interclass variance is, the greater the pixel difference between the background and the target of the image. The effectiveness of image segmentation is determined by the threshold value selection.

The segmentation results are poor because the Otsu algorithm does not fully utilize the correlation information between pixel points. It is affected by noise and other disturbing factors [12]. A two-dimensional Otsu algorithm can solve the above problems [13]. Both the distribution of the gray values of pixels and the differences between them and the average gray levels of their neighboring pixels are considered in the two-dimensional Otsu algorithm. The result is a two-dimensional vector threshold that enhances segmentation accuracy. A two-dimensional histogram of the gray scale gradient is formed if the horizontal coordinate is regarded as the gray scale, and the vertical coordinate is regarded as the gradient.

In the following discussion, assuming the size of an image is $M\times N$, $i$ and $j$ are grayscale and gradient, respectively. The probability that a pixel $n_{ij}$occurs is:

$$p_{ij}=\frac{n_{ij}}{M\times N}.$$

(1)

The grayscale image is divided into two classes by threshold: the background class (B) and the target class (T).

The probability distributions of these can be expressed as follows:

$$P_B\left(s,t\right)=\sum _{i=1}^s\sum _{j=1}^t{p}_{ij},$$

(2)

$$P_T\left(s,t\right)=\sum _{i=s+1}^L\sum _{j=t+1}^L{p}_{ij},$$

(3)

where, $L$, $s,$ and $t$ are, respectively, the gray level, average gray level of the segmentation threshold, and the gradient value.

We define the mean vector $u$, $u_B,$ and $u_T$, respectively, with the following:

$$u\left(s,t\right)={\left(u_i,u_j\right)}^T={\left(\sum _{i=1}^s\sum _{j=1}^t{ip}_{ij},\sum _{i=1}^s\sum _{j=1}^t{jp}_{ij}\right)}^T,$$

(4)

$$u_B\left(s,t\right)={\left(u_{Bi},u_{Bj}\right)}^T={\left(\sum _{i=1}^s\sum _{j=1}^t\frac{{ip}_{ij}}{p_B},\sum _{i=1}^s\sum _{j=1}^t\frac{{jp}_{ij}}{p_B}\right)}^T,$$

(5)

$$u_T\left(s,t\right)={\left(u_{Ti},u_{Tj}\right)}^T={\left(\sum _{i=1}^s\sum _{j=1}^t\frac{{ip}_{ij}}{p_T},\sum _{i=1}^s\sum _{j=1}^t\frac{{jp}_{ij}}{p_T}\right)}^T,$$

(6)

where $u$, $u_B,$ and $u_T$, respectively, are the total mean vector of pixels, the mean vector of background classes, and the target classes.

The function of the inter-class dispersion matrix between the pixels in the background and the target class is:

$$S_{(s,t)}=P_B\times \left(u_B-u\right){\times \left(u_B-u\right)}^T+P_T\times \left(u_T-u\right){\times \left(u_T-u\right)}^T.$$

(7)

A higher value of the dispersion measure indicates a larger contrast between the background and the target, which leads to greater segmentation accuracy. Therefore, the optimal segmentation threshold $\left(s^{\ast },t^{\ast }\right)$ for the image is determined by the maximum value of the discretization measure function. This can be expressed as:

$$\begin{gathered} tr\left(S_{\left(s^{\ast },t^{\ast }\right)}\right)=max\left(tr\left(S_{\left(s,t\right)}\right)\right)=P_B\left(s,t\right)\times \left[{\left(u_{Bi}-u_i\right)}^2+{\left(u_{Bj}-u_j\right)}^2\right]+ \\ {P}_T\left(s,t\right)\times \left[{\left(u_{Ti}-u_i\right)}^2+{\left(u_{Tj}-u_j\right)}^2\right]. \end{gathered}$$

(8)

Although the two-dimensional Otsu algorithm can improve image segmentation accuracy, its performance improvement is dependent on increasing the computation time. It cannot overcome the slow segmentation speed of the traditional Otsu algorithm [14]. Consequently, optimization is performed with the help of group intelligence algorithms. This paper combined the MFO algorithm with the two-dimensional Otsu algorithm to enhance the segmentation effect and convergence speed.

2.2. The MFO Algorithm

2.2.1. Principles of MFO

The MFO algorithm is a new type of heuristic algorithm that takes inspiration from the lateral navigation mechanism of moths during flight. A moth has a unique way of navigating at night. To fly in a straight line, it relies on moonlight by using a transverse orientation mechanism that keeps a fixed angle relative to the moon. However, moths frequently mistake artificial light for the light emitted by the moon in real life. Moths spiral around the artificial light to avoid eventually converging on the light source, which also demonstrates the ineffectiveness of lateral localization. Chen et al. [15] indicates that the position of the moth is a variable in solving the optimization problem in the MFO algorithm, and the flame is the best position currently. Moths approach the global optimal position by changing position vectors in the search space through spiral flight. In the traditional MFO algorithm, the matrix $M$ is used to represent the moth’s position as follows:

$$M=\left[\begin{array}{cc}{m}_{1, 1}& \begin{array}{ccc}{m}_{\mathrm{1,2}}& \cdots & m_{1,d}\end{array}\\ \begin{array}{c}{m}_{\mathrm{2,1}}\\ ⋮\\ m_{n,1}\end{array}& \begin{array}{ccc}\begin{array}{c}{m}_{\mathrm{2,2}}\\ ⋮\\ m_{n,2}\end{array}& \begin{array}{c}\cdots \\ \\ \cdots \end{array}& \begin{array}{c}{m}_{2,d}\\ ⋮\\ m_{n,d}\end{array}\end{array}\end{array}\right],$$

(9)

where $n$ and $d$, respectively, are the number of moths and the dimension of the control variable. The fitness values of the moths are stored in the matrix $OM$, which is denoted as follows:

$$OM=\left[\begin{array}{c}{OM}_1\\ \begin{array}{c}{OM}_2\\ ⋮\\ {OM}_n\end{array}\end{array}\right],$$

(10)

where $n$ is the number of moths.

The MFO algorithm requires each moth to update its position using the unique flame corresponding to it, which effectively avoids it from falling into a local optimum. Therefore, the moth population in the search space was consistent with the number of flames in the initial iteration. The position of the flame is represented by the matrix $F$ as follows:

$$F=\left[\begin{array}{cc}{F}_{1, 1}& \begin{array}{ccc}{F}_{\mathrm{1,2}}& \cdots & F_{1,d}\end{array}\\ \begin{array}{c}{F}_{\mathrm{2,1}}\\ ⋮\\ F_{n,1}\end{array}& \begin{array}{ccc}\begin{array}{c}{F}_{\mathrm{2,2}}\\ ⋮\\ F_{n,2}\end{array}& \begin{array}{c}\cdots \\ \\ \cdots \end{array}& \begin{array}{c}{F}_{2,d}\\ ⋮\\ F_{n,d}\end{array}\end{array}\end{array}\right],$$

(11)

where $n$ and $d$, respectively, are the number of moths and the dimension of the control variable. The matrix $OF$ stores the fitness values of the flame, denoted as follows:

$$OF=\left[\begin{array}{c}{OF}_1\\ \begin{array}{c}{OF}_2\\ ⋮\\ {OF}_n\end{array}\end{array}\right],$$

(12)

where $n$ is the number of moths.

The search space is populated by moths, and each moth searches a flame by tagging and updating it as it finds a better solution. The MFO algorithm is described as a globally optimal ternary as follows:

$$MFO=\left(I,P,T\right).$$

(13)

The function $I$ generates a population of moths and their fitness values randomly. The model is as follows:

$$I:\phi \to \left\{M,OM\right\}.$$

(14)

$P$ is the principal function that moves the moth through the search space. $\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x} M$ is accepted by $P$, and returns the updated value.

$$P:M\to M.$$

(15)

The function $T$ will return true if the termination criterion is fulfilled; otherwise, it will return false.

$$T:M\to \left\{true,false\right\}.$$

(16)

Function $P$ is used to change the moth’s position in the search space after initializing function $I$. Until the function $T$ returns true, the iteration will be executed.

2.2.2. Location Update and Spiral Search Mechanism

Moths flying around a flame follow a spiral search mechanism. Three conditions are met by this mechanism, i.e., the starting point of the spiral function is the position of the moth, the end point of the moth’s flight is the flame position, and the fluctuation of the spiral function adopts a logarithmic spiral structure. Meanwhile, it is also required that the fluctuation range does not exceed the search space. The spiral equation allows the moth to fly “around” the flame, rather than just in the space between the flames. Moths can obtain new positions by flying around the flame through a spiral search mechanism, which ensures exploration and utilization of the search space. According to Ma et al. [16], the spiral flight equation for a moth is:

$$X_i\left(t+1\right)=\left|X_i\left(t\right)-F_i\left(t\right)\right|e^{bl}\cos \left(2\pi l\right)+F_i\left(t\right),$$

(17)

where $X$ and $F$, respectively, represent the moth populations and flame populations. $i$ is the selected problem dimension, $t$ represents the current iteration number, and $b$ denotes the constant that defines the shape of the logarithmic spiral. $l$ is a random number between $\left[-1, 1\right]$; when nearest to the flame, $l$ is −1, and when farthest from the flame, $l$ is 1.

An adaptive reduction mechanism is proposed for the flames in order to improve the efficiency of the optimization search [4]. The global optimal solution was the only flame that remained in the last iteration. The flame reduction process is shown in Equation (18):

$${Flame}_{no}=round\left(N-t\times \frac{N-1}{T}\right),$$

(18)

where$t$ and $T$, respectively, are the current and maximum number of iterations. $N$ is defined as the initial number of flames. The number of iterative flames decreases linearly from $N$ to 1.

The MFO algorithm has advantages over other group intelligence algorithms such as fewer parameters, a simpler algorithmic model, and a stronger parallel optimization ability, but it still has some shortcomings. The moth position updating mechanism in the algorithm is achieved by using the logarithmic spiral function. The optimal solution of the moth is saved as the flame position for the next generation in the iterative process, and by matching the moth to the sorted flame one by one, the MFO algorithm’s local development capability can be improved. If the moth’s new position is superior to the flame’s during multiple iterations, the flame must be updated in its entirety at this point. But, if the flame before updating is closer to the global optimal position, the moth misses the opportunity to continue to find the optimal position when the flame is updated in the global optimal position. The algorithm tends to fall into local extremes due to this.

3. Methods

3.1. Fractional Order Calculus

According to Bolat [17], Leibniz introduced fractional order calculus at the same time as his theory of calculus, which encompasses fractional order differentiation and fractional order integration. It has better memorization and hereditary properties [18] and it is a step forward in the field of integer order calculus. Fractional order calculus has different definitions, and the common expression for the G–L (Grumwald–Letniko) definition is [19]:

$$D^v\left[x\left(t\right)\right]=\underset{h\to 0}{\lim }\left[\frac{1}{h^v}\sum _{k=0}^{+\infty }\frac{{\left(-1\right)}^k\mathsf{\Gamma }\left(v+1\right)x\left(t-kh\right)}{\mathsf{\Gamma }\left(k+1\right)\mathsf{\Gamma }\left(v-k+1\right)}\right].$$

(19)

Its discrete expression is:

$$D^v\left[x\left(t\right)\right]=\frac{1}{T^v}\sum _{k=0}^r\frac{{\left(-1\right)}^k\mathsf{\Gamma }\left(v+1\right)x\left(t-kh\right)}{k!\mathsf{\Gamma }\left(v-k+1\right)},$$

(20)

where: $vϵ\left[0, 1\right]$ stands for order; $r$ and $T$, respectively, are the cut-off order and cycle; and $\mathsf{\Gamma }\left(N\right)={\int }_0^{\infty }{e}^{-t}{t}^{n-1}dt=\left(n-1\right)!$ is a Gamma function.

3.2. MFO Algorithms for Fractional Order Optimization

This paper proposed a fractional order moth–flame optimization (FMFO) algorithm to prevent the traditional MFO algorithm from reaching local optimality and enhance the algorithm’s convergence speed. It takes advantage of the memory and genetic properties of fractional order differentiation to combine the MFO algorithm with fractional order differentiation. During spiral flight, the algorithm controls the moth’s position update with fractional order and introduces adaptive fractional order. Its convergence speed can be improved by adaptively adjusting the fractional order based on the moth’s position information. Equation (17) can be replaced by:

$$X_i\left(t+1\right)-X_i\left(t\right)=\left|X_i\left(t\right)-F_i\left(t\right)\right|e^{bl}\cos \left(2\pi l\right)+F_i\left(t\right)-X_i\left(t\right),$$

(21)

where the left side of Equation (21) shows the discrete form of the fractional order G–L, which defines the order as 1. In Equation (20), let $T=1,$ and $r=4$ can be obtained:

$$\begin{gathered} D^v\left[x\left(t+1\right)\right]\approx x\left(t+1\right)-vx\left(t\right)+\frac{1}{2}v\left(v-1\right)x\left(t-1\right)- \\ \frac{1}{6}v\left(v-1\right)\left(v-2\right)x\left(t-2\right)+\frac{1}{24}v\left(v-1\right)\left(v-2\right)\left(v-3\right)x\left(t-3\right). \end{gathered}$$

(22)

From Equation (22), it can be seen that the fractional order differentiation results are connected to the past state values, and the influence of these past state values on the current state diminishes as time goes by. Its unique past memory allows it to describe processes that have time spans, changes in spatial location, and changes in velocity more accurately. Thus, fractional order differentiation is added to the spiral flight of the MFO algorithm and the moth’s spiral flight behavior of Equation (22) can be described as:

$$\begin{gathered} x\left(t+1\right)=vx\left(t\right)-\frac{1}{2}v\left(v-1\right)x\left(t-1\right)+\frac{1}{6}v\left(v-1\right)\left(v-2\right)x\left(t-2\right)- \\ \frac{1}{24}v\left(v-1\right)\left(v-2\right)\left(v-3\right)x\left(t-3\right)+\left|X_i\left(t\right)-F_i\left(t\right)\right|e^{bl}\cos \left(2\pi l\right)+F_i\left(t\right). \end{gathered}$$

(23)

As shown in the equation above, the fractional order can affect the moth position update. Wei et al. [20] showed an evolutionary factor to make the fractional order adaptively. Moth position information is used to adaptively adjust the fractional order. The specific steps for this are as follows:

The average distance between one moth $i$ and other moths is:

$$d_{ix}=\frac{1}{N}\sum _{j=1,j\equiv i}^N\sqrt{\sum _{k=1}^D{\left(x_{ik}-x_{jk}\right)}^2},$$

(24)

where $N$ and $D$ are, respectively, the number and dimension of moths.

The moth’s current state is determined by the evolution factor $f$, which can be expressed as:

$$f=\frac{d_g-d_{min}}{d_{max}-d_{min}}ϵ\left[0, 1\right],$$

(25)

where $d_g$ is the global optimal position, i.e., the average distance from the flame position to the other moths, and $d_{max}$ and $d_{min}$, respectively, are the maximum and minimum values of $d_{ix}$.

According to Wei et al. [20], the astringent effect is best when the fractional order and the dynamic regulation mechanism of order $v$ is:

$$v\left(f\right)=\frac{1}{2}{e}^{-0.47f}ϵ\left[0.5, 0.8\right].$$

(26)

3.3. FMFO Algorithms for Two-Dimensional Otsu Image Segmentation

The original MFO algorithm with the optimized two-dimensional Otsu image segmentation algorithm (MFO-Otsu) can solve the traditional Otsu algorithm’s problem of low segmentation accuracy. However, the algorithm continues to converge slowly and tends to fall into extremes. Aiming to alleviate these problems, this paper applies the fractional order differential algorithm and the MFO algorithm to the Otsu segmentation algorithm, and introduces the adaptive fractional order. Then, the two-dimensional Otsu image threshold segmentation algorithm based on the fractional order MFO algorithm (FMFO-Otsu) is proposed. The steps of this algorithm are as follows:

1.

Initialize the parameters. Let the number of populations $N=20$, maximum number of iterations $T=100$, individual moth locations be $x_i$, logarithmic spiral shape constant be $b$, current number of iterations be $t$, and flight factor $lϵ\left[-1, 1\right]$.

2.

Input the image to be segmented and generate the objective function based on the two-dimensional Otsu segmentation algorithm.

3.

Use the moth’s current position as a two-dimensional threshold vector to optimize, using Equation (7) as the objective function. The value of the objective function is used to generate moth locations as the initial populations. Then, the flame is assigned the moth’s spatial position after sorting it in the order of increasing value of the objective function. The flame’s initial position is determined by the optimal value, and the positions of the moth and the flame are saved and sorted.

4.

Determine whether the termination condition is fulfilled. If it is fulfilled, the optimal position is obtained as the segmentation threshold. If it is not fulfilled, the algorithm continues to be executed.

5.

Update the moth position of the current generation in accordance with Equation (23), the fractional order spiral flight formula.

6.

Reorder the updated moth and flame locations according to the objective function values, and the location of the next generation flame will be selected based on the spatial location update with a better objective function value.

7.

According to Equation (18), the adaptive mechanism decreases the number of flames from N linear to 1 through iterations.

8.

Identify whether the maximum number of iterations has been reached, exit the iteration if it has been reached, or go back to step 3 if it has not been reached.

9.

The optimal position of the output $\left(s,t\right)$ is used as the best threshold for two-dimensional Otsu image segmentation.

The flow of the FMFO-Otsu algorithm is shown in Figure 1.

4. Results and Discussion

4.1. Benchmark Function

4.1.1. Test Function

To verify the effect of improvement on the traditional MFO algorithm, this paper used six benchmark test functions that are commonly used in group intelligence algorithms to conduct simulation experiments on the MFO and FMFO. The specific descriptions of all functions are shown in

Table 1. The details of the benchmark functions.

Functions	Formulas	Range	${\mathit{f}}_{\mathit{o}\mathit{p}\mathit{t}}$
Schwefel 2.21	$f_1\left(x\right)={max}_i\left\{\left|x_i\right|1\le i\le n\right\}$	$[-\mathrm{100,\; 100}]$	0
Rosenbrock	$f_2\left(x\right)={\displaystyle \sum _{i=1}^{n-1}}\left[{100\left(x_i-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]$	$[-\mathrm{30,\; 30}]$	0
Quartic	$f_3\left(x\right)={\displaystyle \sum _{i=1}^n}i{x}_i^4+random\left[0,\left.1\right)\right.$	$[-\mathrm{1.28,\; 1.28}]$	0
Ackley	$f_4\left(x\right)=-20exp\left(-0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{x}_i^2}\right)-exp\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n}cos\left(2\pi x_i\right)\right)+20+e$	$[-\mathrm{32,\; 32}]$	0
Griewank	$f_5\left(x\right)=\frac{1}{4000}{\displaystyle \sum _{i=1}^n}{x}_i^2-{\displaystyle \prod _{i=1}^n}cos\left(\frac{x_i}{\sqrt{i}}\right)+1$	$[-\mathrm{600,\; 600}]$	0
Kowalik	$f_6\left(x\right)=$${{\displaystyle {\sum }_{i=1}^{11}\left[a_i-\frac{x_1\left(b_i^2+b_1{x}_2\right)}{b_i^2+b_1{x}_3+x_4}\right]}}^2$	$[-5, 5]$	0.0003075

. Here, $f_{opt}$ is the theoretical optimum, and $x_i$ denotes the position of the ith moth. The function dimension $d$ is set to 10, the population size $N$ of the two algorithms is 20, and the number of iterations is 1000. Among these, $f_1$, $f_2$, and $f_3$ are single-modal functions. They have only one globally optimal solution in the domain of definition but no local extremes, and they are more suitable to test the convergence speed of the algorithm. $f_4$ and $f_5$ are multi-modal functions where the number of local minima increases exponentially with the problem dimension, and they can measure the optimization accuracy and capability of the algorithm. $f_6$ is multi-modal function with many local minima, for which the number of local minima for each function and the dimension of the function are small. These benchmark test functions are useful for us to judge the performance of algorithms.

4.1.2. Test Results

The convergence curves of the Schwefel 2.21 Function, Rosenbrock Function, Quartic Function, Ackley Function, Griewank Function, and Kowalik Function are shown in Figure 2. According to Figure 2a, the MFO algorithm tends to converge after 1000 iterations, while the FMFO algorithm converges at around 190 iterations. Figure 2b shows that the MFO algorithm converges slowly in the early stage and only starts to converge after 1000 iterations. Its ability to seek optimization is weak and the accuracy of its convergence is poor. In Figure 2c, it can be seen that the FMFO algorithm is closer to the theoretical optimum, but the MFO algorithm performs poorly in terms of both convergence accuracy and speed. In Figure 2d,e, the fitness curves of the MFO algorithm become parallel to the x-axis after 600 and 500 times, respectively. This indicates that the MFO algorithm is stuck in a local optimality and it is difficult for the algorithm to jump out of the local optimality at a later stage. The MFO algorithm’s optimization seeking performance is limited, it suffers from local convergence defects and performs poorly overall. From Figure 2f, it can be seen that FMFO converges earlier than MFO and is closer to the optimal value.

Compared to the MFO algorithm, the FMFO algorithm introduces adaptive fractional order differentiation in the global optimization. As we can be seen from Figure 2, the FMFO algorithm has more folds. This illustrates that the algorithm has a strong ability to jump out of the local optimum. The results show that the FMFO algorithm is closer to the theoretical optimum than the MFO algorithm, and that the convergence speed of the FMFO algorithm is significantly superior to the MFO algorithm, which shows a better optimization-seeking effect.

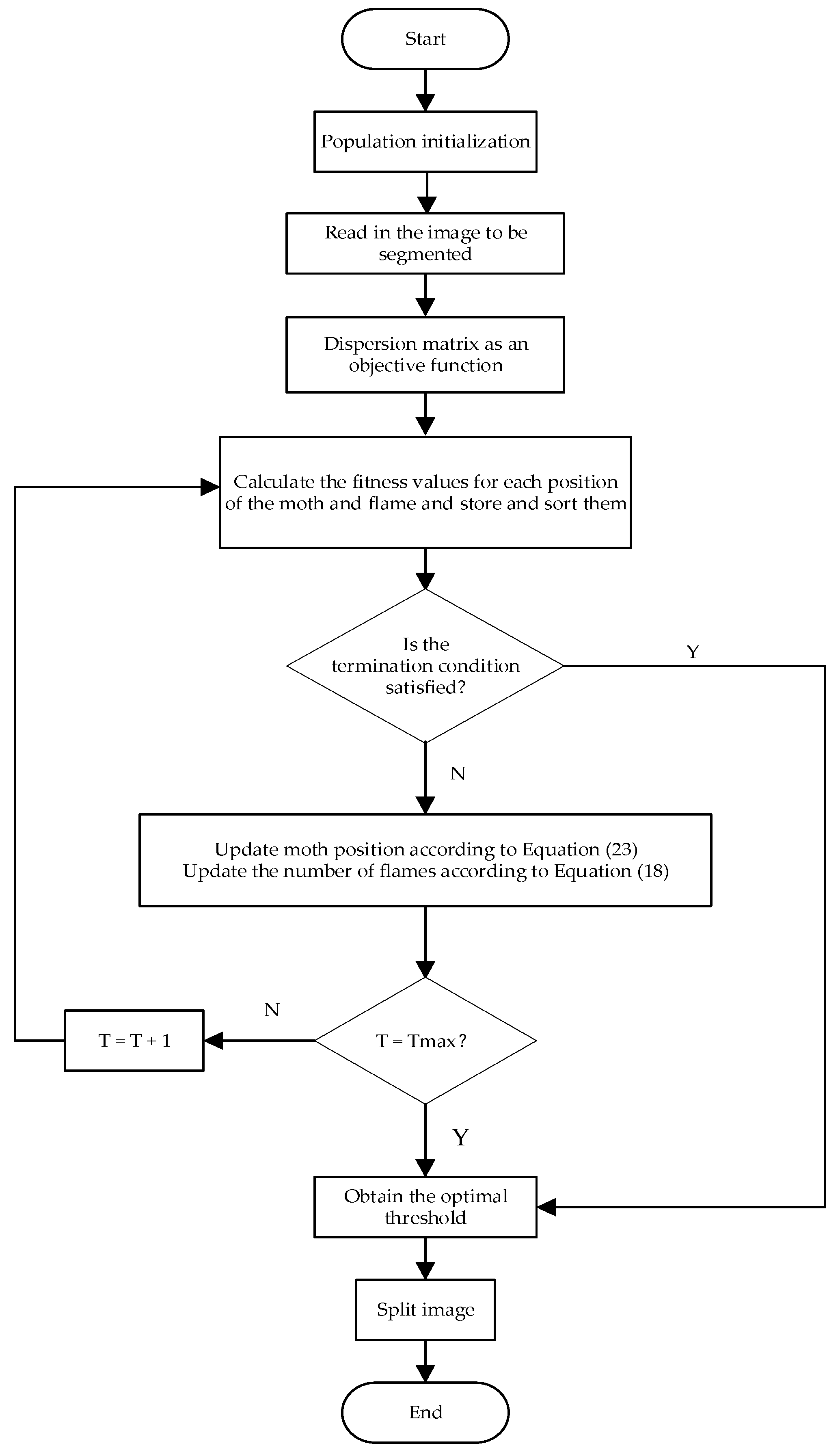
4.2. Image Segmentation Results and Analysis

This paper tested the convergence speed and segmentation accuracy of the improved algorithm by using different types of images from the Standardized Test Image Dataset, Berkeley Segmentation Dataset, and UCI Dataset for the experiments. Firstly, the algorithm proposed in this paper (FMFO-Otsu) was compared with the original MFO optimized two-dimensional Otsu image segmentation algorithm (MFO-Otsu), Fractional Order Cuckoo Search Otsu algorithm (FCS-Otsu) [21], Fractional Order Particle Swarm Otsu algorithm (FPSO-Otsu) [20], and Fractional Order Firefly Otsu algorithm (FFA-Otsu) [22]. Then, in order to further verify the performance of the improved algorithm and the superiority of fractional order, the FMFO-Otsu algorithm was compared with the two-dimensional Otsu image segmentation algorithm based on Other group intelligence algorithms, including the two-dimensional Otsu based on the Cuckoo Search algorithm (CS-Otsu) [21], the two-dimensional Otsu based on the Particle Swarm algorithm (PSO-Otsu) [20], the two-dimensional Otsu based on the Wolf Pack algorithm (WPA-Otsu) [8], and the two-dimensional Otsu based on the Sparrow Search algorithm (SSA-Otsu) [23].

In this paper, the algorithm’s convergence speed is evaluated according to the number of iterations required to reach convergence in the fitness curve. Evaluation metrics for image segmentation accuracy include the fitness value, peak signal-to-noise ratio (PSNR), structural similarity (SSIM), and mean square error (MSE). The larger the fitness value, the greater the spacing between the background class and the target class, which indicates a more pronounced segmentation effect. The larger the PSNR value, the less noise information is required and the more the algorithm’s noise immunity is improved. The greater the SSIM value, the smaller the difference between the image before and after segmentation, and the better the image segmentation quality. And the MSE reflects the error of image segmentation that the accuracy of image segmentation increases with the smaller the MSE.

There were different types of images selected for the segmentation experiment. Some of these images were analyzed in detail, such as showing the image segmentation effect, the fitness curve, and the evaluation metrics. Some other images were averaged for each metric in addition to showing the image segmentation effect. Six types of images were used for image segmentation: character images, architectural images, animal images, plant images, scenery images, and object images.

In the first part, the following four images were presented: the Couple image, the Cablecar image, the Boats image, and the Building image. The image segmentation results are shown in Figure 3. In subjective vision, for the segmentation of the Couple image, FCS-Otsu, FPSO-Otsu, and FFA-Otsu over-segmented some regions like the face of a person and part of the background. The edges of the image were not segmented precisely enough with MFO-Otsu. In comparison, FMFO-Otsu generated more detailed segmentation results in the corner and character. In the Cablecar image segmentation results, FMFO-Otsu was better able to preserve the Cablecar details and segments, such as the detailed parts around the lawn in the red frame area, than other algorithms. For the segmentation of the Boats image, the other four algorithms did not segment the vessel contour completely. For example, there is a slight lack of details in the MFO-Otsu algorithm. But FMFO-Otsu retained more details and accurately segmented the edges of the image. In the Building image segmentation results, FMFO-Otsu generated more detailed segmentation results in the bridge and lake areas. Therefore, the FMFO-Otsu algorithm performed better in the segmentation of these images.

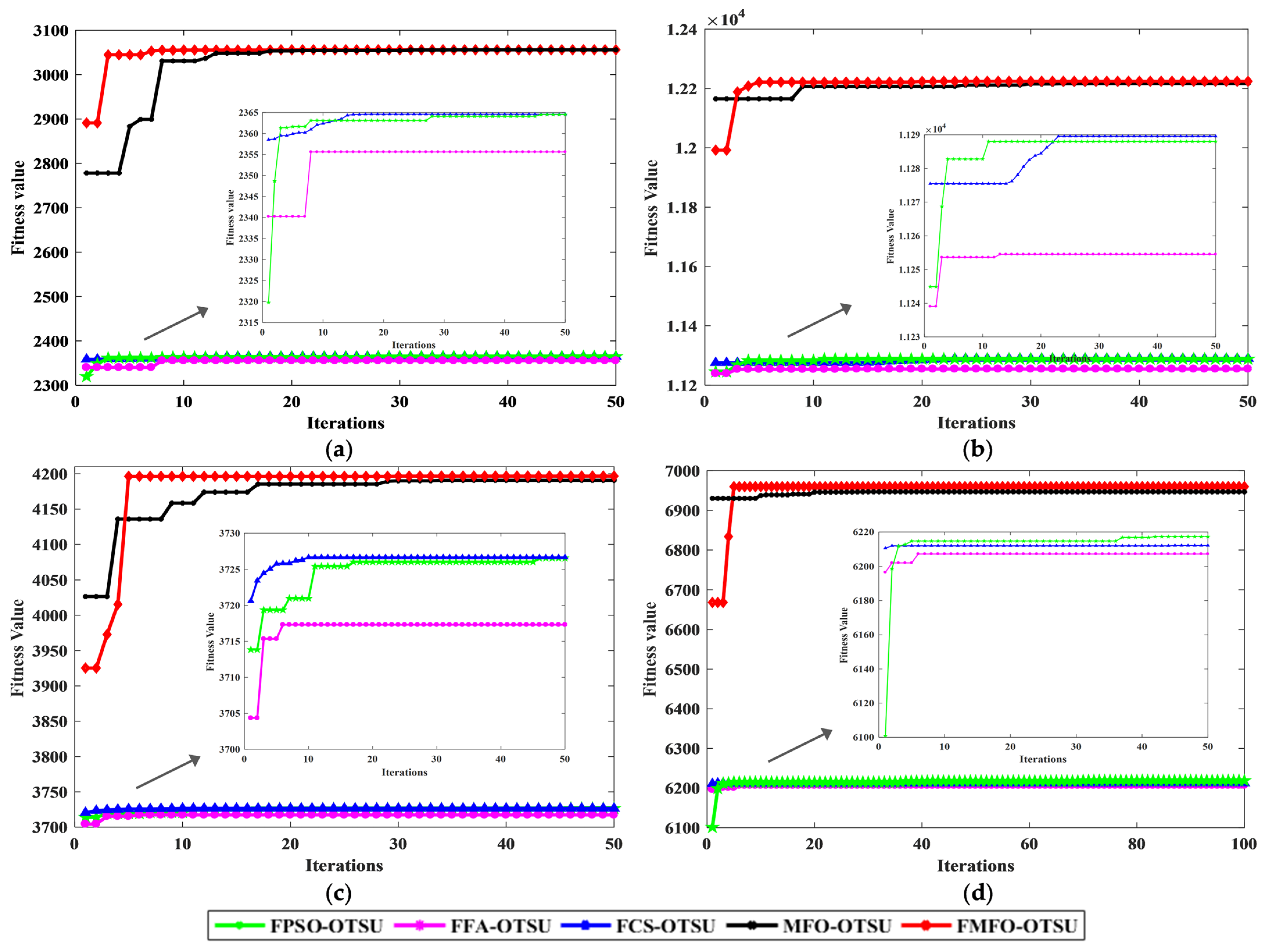
The objective evaluation index of the Couple image, the Cablecar image, the Boats image, and the Building image segmentation results are shown in

Table 2. The objective evaluation index of the Couple image, Cablecar image, Boats image, and Building image segmentation results, respectively.

Image	Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
	MFO-Otsu	7.9419	0.3041	10,444.5119	3055.9567	31
	FCS-Otsu	7.9094	0.3176	10,522.8627	2357.3554	14
Couple	FPSO-Otsu	7.8543	0.3124	10,657.3305	2364.5947	9
	FFA-Otsu	5.9230	0.0051	16,625.5484	2360.0738	9
	FMFO-Otsu	8.0389	0.3031	10,213.8782	3056.0320	7
	MFO-Otsu	12.4328	0.3201	3713.6514	12,216.6315	30
	FCS-Otsu	12.5088	0.3295	3649.2116	11,289.6663	22
Cablecar	FPSO-Otsu	12.5144	0.3234	3644.5075	11,289.5662	11
	FFA-Otsu	4.9616	0.0031	20,745.1735	11,254.5329	13
	FMFO-Otsu	12.5854	0.3326	3585.3844	12,224.2937	6
	MFO-Otsu	7.9073	0.4571	10,528.1484	4190.7102	29
	FCS-Otsu	7.9010	0.4712	10,543.2814	3726.5026	11
Boats	FPSO-Otsu	7.8297	0.4617	10,717.6902	3726.3861	17
	FFA-Otsu	6.1178	0.0081	15,896.2779	3709.3913	6
	FMFO-Otsu	8.0037	0.4619	10,296.9341	4196.6738	4
	MFO-Otsu	10.7400	0.4671	5483.8436	6946.7614	30
	FCS-Otsu	10.7344	0.4691	5490.7597	6212.1730	78
Building	FPSO-Otsu	10.7558	0.4714	5463.7552	6218.5972	70
	FFA-Otsu	3.9221	0.0048	26,355.0664	6207.1261	7
	FMFO-Otsu	10.8063	0.4798	5400.6767	6959.9531	5

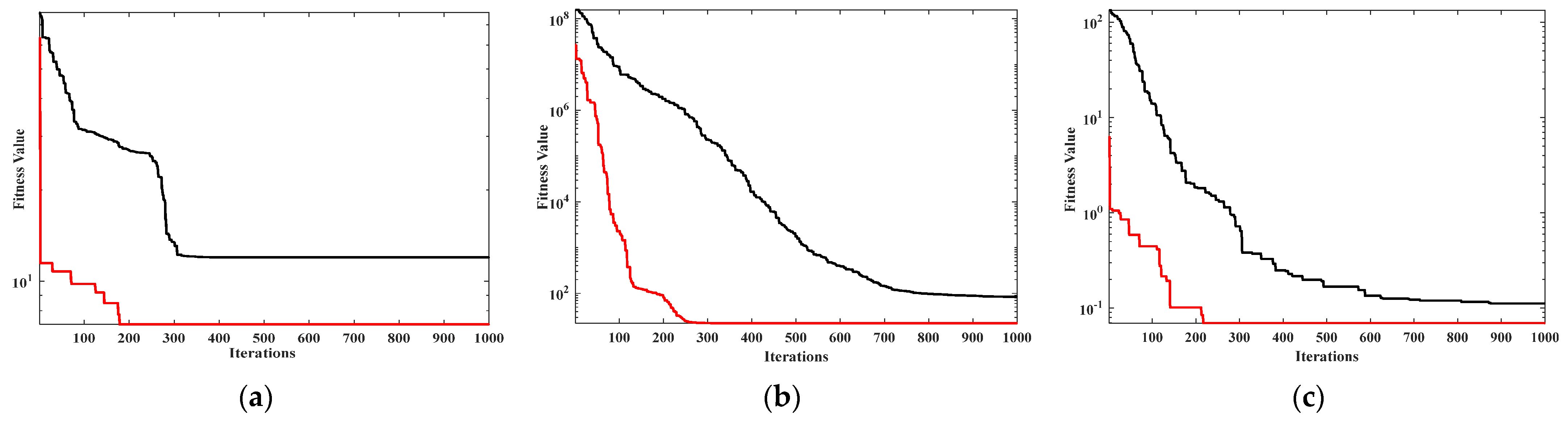
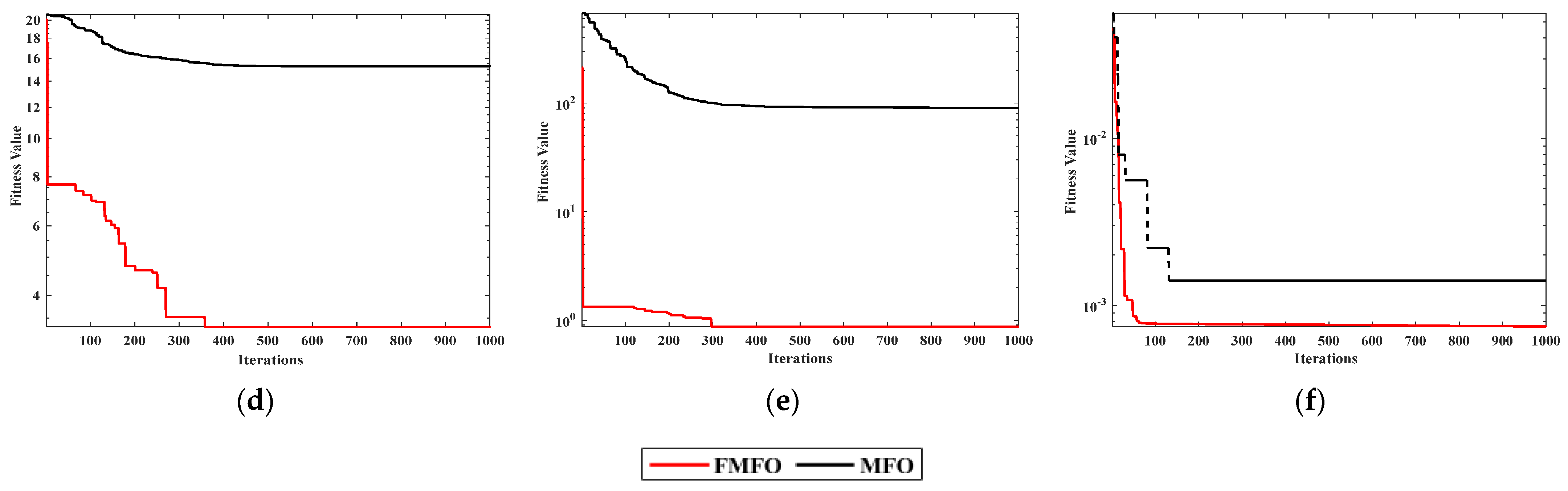
, and Figure 4 indicates the fitness curve of them. For the segmentation results of the Couple image, MFO-Otsu finds the segmentation threshold in 31 iterations, FCS-Otsu reaches convergence at 14 iterations, FPSO-Otsu and FFA-Otsu both converge after 9 iterations, and FMFO-Otsu converges at 7 times. Therefore, FMFO-Otsu achieves maximum class spacing first, which means that FMFO-Otsu converges faster than other algorithms. In addition, FMFO-Otsu had the highest fitness value. The PSNR of FMFO-Otsu is higher than the other four algorithms. This shows that FMFO-Otsu is capable of enhancing the segmentation details of the image and ensuring noise immunity. Furthermore, FMFO-Otsu has a lower MSE than the other four algorithms, which suggests that its accuracy is more advantageous compared to the other algorithms.

For the Cablecar image, MFO-Otsu falls into local optimum after about 30 iterations, FCS-Otsu converges around 22, FPSO-Otsu finishes converging around 11, FFA-Otsu converges after 13 iterations, and FMFO-Otsu discovers the best segmentation threshold in 6 iterations. And the PSNR, SSIM, and fitness values of FMFO-Otsu are improved when compared to the other four algorithms. As the value of fitness increases, the value of the discretization matrix in the Otsu segmentation algorithm increases, i.e., the target and background class segmentation becomes more pronounced. It is evident that FMFO-Otsu not only improves the convergence speed but also enhances the accuracy of the image segmentation results. The MSE of FMFO-Otsu is lower than the other four algorithms, which indicates that FMFO-Otsu has a lower error rate before and after segmentation.

For the Boats image, MFO-Otsu reaches convergence after 29 iterations, FCS-Otsu converges around 11 times, FPSO-Otsu converges at 17 times, FFA-Otsu converges after 6 iterations, and FMFO-Otsu has the fastest speed that finishes converging around 4 times. Furthermore, the PSNR of FMFO-Otsu is greater than the other four algorithms, while the SSIM is slightly inferior. And there was a significant increase in the fitness value of FMFO-Otsu. Despite this, FMFO-Otsu is more noise-resistant and has superior segmentation details overall. The MSE of FMFO-Otsu is lower than others, which means that the segmentation effect of FMFO-Otsu is superior to that of the other algorithms.

For the Building image, the convergence of the FMFO-Otsu algorithm, compared with MFO-Otsu, FCS-Otsu, FPSO-Otsu, and FFA-Otsu, is accelerated by 83.33%, 93.58%, 92.85%, and 28.57%, respectively. As for other objective evaluation indicators, FMFO-Otsu performs better than the other algorithms. This indicates that the performance of the FMFO-Otsu algorithm has been significantly improved compared to the original algorithm.

To confirm the segmentation effect of FMFO-Otsu on various images in this paper, 28 images of characters, 32 images of architectures, 24 images of animals, and 15 images of plants were selected from other datasets and segmented using MFO-Otsu, FCS-Otsu, FPSO-Otsu, FFA-Otsu, and FMFO-Otsu. Then, we calculated the average value of objective evaluation indexes. The average experimental values are presented in

Table 3. The average objective evaluation index value for the character images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
MFO-Otsu	9.3449	0.2615	7644.6091	5143.2640	28
FCS-Otsu	9.1011	0.2451	8144.2055	4334.7567	26
FPSO-Otsu	9.1289	0.2412	8083.4398	4334.5049	25
FFA-Otsu	4.6828	0.0020	22,382.2149	4323.4212	13
FMFO-Otsu	9.3834	0.2682	7580.0448	5147.5313	7

,

Table 4. The average objective evaluation index value for the architectural images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
MFO-Otsu	8.9533	0.3780	8990.6142	4434.7999	30.5
FCS-Otsu	8.6274	0.3918	9741.1110	5400.6262	49
FPSO-Otsu	8.6174	0.3832	9791.6460	5400.5245	48.5
FFA-Otsu	5.3720	0.0016	19,301.0372	5388.5668	16
FMFO-Otsu	9.0966	0.3665	8640.7660	6255.0526	8

,

Table 5. The average objective evaluation index value for the animal images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
MFO-Otsu	8.4688	0.3041	9800.5075	3686.4759	21
FCS-Otsu	8.3323	0.3148	10,153.887	3194.5167	39
FPSO-Otsu	8.3379	0.3003	10,144.5902	3171.7427	52
FFA-Otsu	5.4481	0.0045	19,026.0643	3162.8722	12
FMFO-Otsu	8.5021	0.3189	9727.0375	3689.7578	8

and

Table 6. The average objective evaluation index value for the plant images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
MFO-Otsu	8.9756	0.2578	8272.3216	4955.3890	33
FCS-Otsu	8.8020	0.2142	8604.4498	4199.0134	48
FPSO-Otsu	8.8881	0.2144	8418.5829	4197.4762	41
FFA-Otsu	6.3909	0.0018	15,298.5110	4181.4200	17
FMFO-Otsu	9.2111	0.2614	7824.8220	4982.5595	9

, and some corresponding experimental segmentation images can be found in Figure 5, Figure 6, Figure 7 and Figure 8. The disparities in image segmentation outcomes among the various algorithms are emphasized by the red squares.

Figure 5 shows the original character images and the segmented images, and the average objective evaluation index values for the character images are indicated in Table 3. Based on the resultant segmentation, it can be seen that FMFO-Otsu not only preserves the image contours better, but also segments the edge parts better. For example, in the first row of images, FMFO-Otsu preserves the details well in the wall part. For the second image, FMFO-Otsu generates more details in the grass and construction areas. Based on objective metrics, the iterations of FMFO-Otsu were decreased by 75%, 73%, 72%, and 46% compared to MFO-Otsu, FCS-Otsu, FPSO-Otsu, and FFA-Otsu, respectively. PSNR values improved by 0.4%, 3%, 2.7%, and 50%, respectively. SSIM values improved by 2.4%, 8.6%, 10%, and 99%, respectively. MSE values declined by 0.84%, 6.9%, 6.2%, and 66.1%, respectively. The fitness values improved by 0.08%, 15.8%, 15.7%, and 16%, respectively. These experimental results demonstrate that FMFO-Otsu yields superior segmentation outcomes.

Figure 6 shows the original building image and the image segmented by the five algorithms. The evaluations after calculating the averages of the architectural images are shown in Table 4. In the first row of images, FMFO-Otsu is more detailed in the yard and roof sections. In the second row of images, all five algorithms roughly retained the outline of the original image, but FMFO-Otsu divided the first floor more clearly. For the third image, FMFO-Otsu better preserved the details of the top of the building and the bridge. For the fourth image, FMFO-Otsu produced a more complete outline. On the basis of objective data, FMFO-Otsu achieves higher accuracy in segmenting architectural images, especially in terms of the PSNR value, MSE value, and fitness value, showing significant improvements.

Figure 7 shows the original animal images and the segmented results. Table 5 lists the average values for the animal images after segmentation. In the image of the first line, the segmentation effect of FCS-Otsu, FPSO-Otsu, and FFA-Otsu is poor, while the segmentation effect of FMFO-Otsu is more accurate. Image 2 preserves the outline of the original image completely. In the third image, FMFO-Otsu’s division of the stone is much clearer. In the fourth image segmentation result, compared with the other algorithms, FMFO-Otsu can segment the edge of the image better on the basis of preserving the image contour. In the objective data on the animal images, FMFO-Otsu performed better overall. Compared with MFO-Otsu, the PSNR, SSIM, fitness value, and convergence speed increased by 0.39%, 4.87%, 0.09%, and 61.9%, respectively, and the MSE decreased by 0.75%.

Figure 8 shows the original images of the plants and the segmented details. The average indicators after the segmentation of plant images are shown in Table 6. Due to the nature of the plant image in the first row of these images, FMFO-Otsu segmented out more details in the leaf section. In the second image, FMFO-Otsu not only better preserved the details of the middle flowers, but also better divided the flowers at the edges. In Figure 3 and Figure 4, the segmentation effect of FMFO-Otsu is more obvious. From the objective data, compared with MFO-Otsu and FPSO-Otsu, the PSNR value increased by 2.62% and 3.63%; the SSIM value increased by 1.4% and 21.92%; the MSE value decreased by 5.41% and 7.05%; and the fitness value increased by 0.55% and 19.16%. The convergence rate was improved by 72.73% and 78.05%. Therefore, compared with the other four algorithms, FMFO-Otsu has a faster segmentation rate and higher accuracy.

In the second part, to more effectively illustrate the segmentation effect of the proposed algorithm and the advantages of fractional order, the FMFO-Otsu algorithm was compared with the CS-Otsu algorithm, the PSO-Otsu algorithm, the WPA-Otsu algorithm, and the SSA-Otsu algorithm.

The four images that were presented are as follows: the Cat image, the Girl image, the Cemetery image, and the Lawn image. The segmentation results for these images are shown in Figure 9. In the subjective visual perspective, for the segmentation of the Cat image, the segmentation results of the other algorithms were comparatively rough, whereas FMFO-Otsu exhibited clearer segmentation in the cat’s ears and forehead area. In the case of the Girl image, although all five algorithms successfully segmented the silhouette of the girl, FMFO-Otsu outperformed others in terms of capturing the finer details. Regarding the Cemetery image, PSO-Otsu, CS-Otsu, and SSA-Otsu demonstrated imprecise segmentation. However, FMFO-Otsu preserved better delineation in the road area. Unlike other algorithms that failed to fully segment the Lawn image, FMFO-Otsu generated more comprehensive contours. Consequently, it can be concluded that FMFO-Otsu achieves the superior segmentation performance.

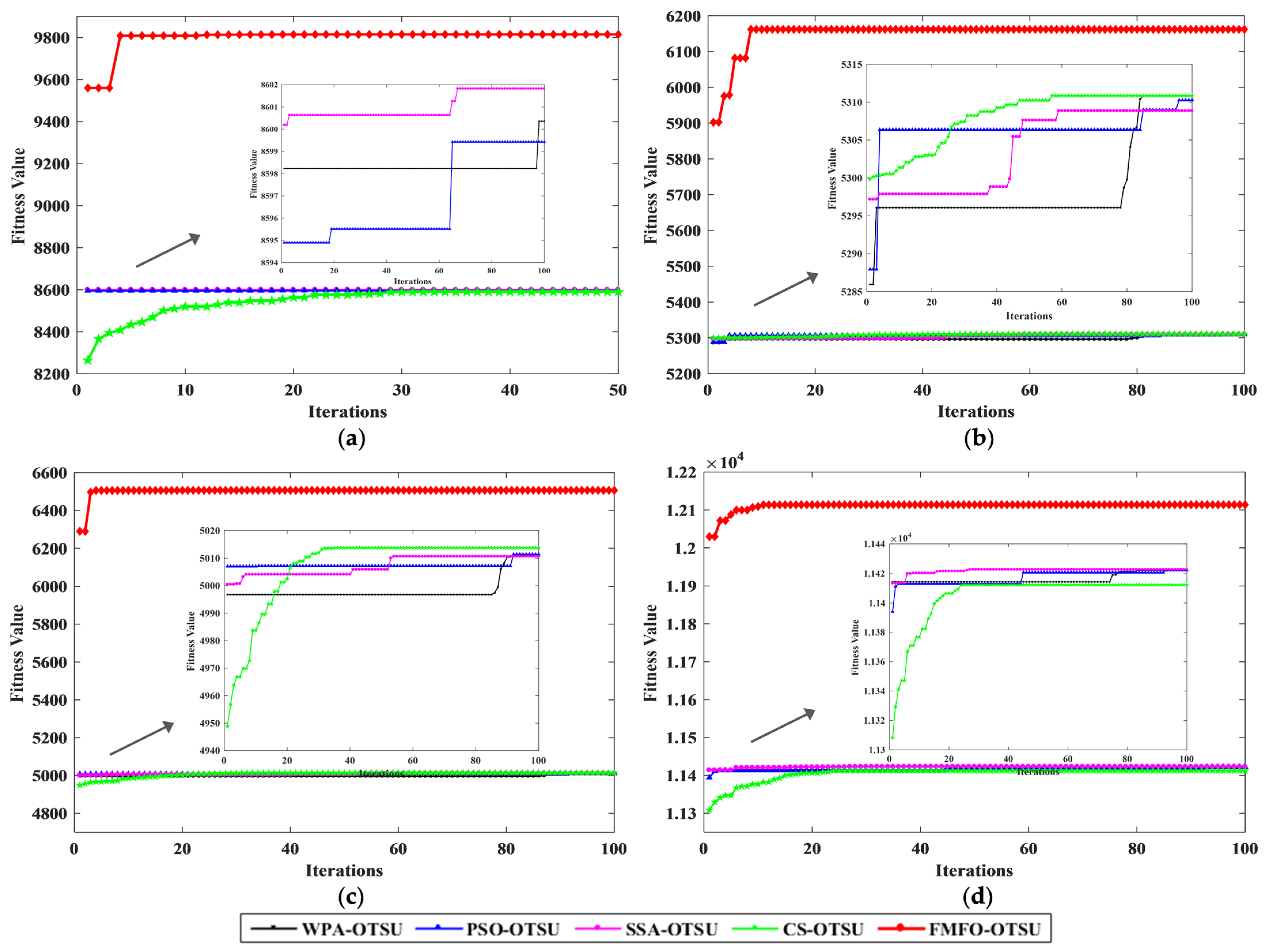
The objective evaluation indexes of the Cat image, the Girl image, the Cemetery image, and the Lawn image segmentation results are shown in

Table 7. The objective evaluation indexes for the Cat image, Girl image, Cemetery image, and Lawn image segmentation results, respectively.

Image	Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
	CS-Otsu	11.0341	0.2852	5124.6981	8589.6211	29
	SSA-Otsu	10.9977	0.2826	5167.7788	8601.8191	68
Cat	PSO-Otsu	5.0099	0.0027	20,515.4963	8599.4286	66
	WPA-Otsu	11.0166	0.2837	5145.3388	8600.3541	99
	FMFO-Otsu	11.1375	0.3074	5004.1539	9814.8055	11
	CS-Otsu	9.8971	0.2493	6658.3851	5310.8523	58
	SSA-Otsu	9.8692	0.2458	6701.2761	5308.8572	59
Girl	PSO-Otsu	5.1411	0.0018	19,905.8071	5310.2630	95
	WPA-Otsu	9.7574	0.2332	6875.9284	5311.0877	83
	FMFO-Otsu	9.9248	0.2507	6616.1373	6162.1129	8
	CS-Otsu	9.1102	0.1521	7981.0352	5013.7171	33
	SSA-Otsu	9.1422	0.1542	7922.4465	5010.6722	54
Cemetery	PSO-Otsu	5.4909	0.0013	18,364.5613	5011.4071	91
	WPA-Otsu	9.1102	0.1521	7981.0315	5010.9636	90
	FMFO-Otsu	9.5582	0.2103	7198.8538	6506.3032	4
	CS-Otsu	11.1043	0.2389	5042.5267	11,412.2544	24
	SSA-Otsu	11.0810	0.2378	5069.6361	11,422.7414	26
Lawn	PSO-Otsu	5.0046	0.0026	20,540.8931	11,422.1047	92
	WPA-Otsu	11.1043	0.2393	5033.3751	11,422.3525	92
	FMFO-Otsu	11.3284	0.2509	4788.9094	12,113.91760	11

, and Figure 10 indicates the fitness curves of these results. For the segmentation results of the Cat image, the CS-Otsu algorithm converges after 29 iterations, and the SSA-Otsu and PSO-Otsu algorithms converge after 68 and 66 iterations, respectively. The WPA algorithm achieves convergence at approximately 99 iterations, whereas the FMFO-Otsu algorithm converges much faster, at around 11 iterations. Hence, it can be concluded that the FMFO-Otsu algorithm exhibits a superior convergence rate compared to the other algorithms. Based on objective data from the Cat images, compared to CS-Otsu, SSA-Otsu, PSO-Otsu, and WPA-Otsu, FMFO-Otsu improved the PSNR by 0.94%, 1.27%, 122.31%, and 1.10%, respectively. The SSIM increased by 7.78%, 8.78%, 11285.19%, and 8.35%, respectively. The fitness value added by 14.26%, 14.10%, 14.13%, and 14.12%, respectively. The MSE decreased by 2.35%, 3.17%, 75.61%, and 2.74%, respectively. The iteration rate was accelerated by 62.07%, 83.82%, 83.33%, and 88.89%, respectively.

For the segmentation of the Girl image, CS-Otsu and PSO-Otsu converge after 58 and 59 iterations, respectively. PSO-Otsu falls into local optimality after 95 iterations, WPA-Otsu converges after 83 iterations, and FMFO-Otsu converges around 8 iterations. Compared to the other four algorithms, the iteration rate of FMFO-Otsu is improved by 86.21%, 86.44%, 91.58%, and 90.36%, respectively. From the objective evaluation index of the Girl image, it can be seen that the PSNR value, SSIM value, and adaptation value of FMFO-Otsu are higher than the other four algorithms, which indicates that the image details of FMFO-Otsu’s segmentation are better and the noise resistance is stronger. The MSE values of FMFO-Otsu are all lower than those of the other four algorithms, indicating that the accuracy of FMFO-Otsu’s segmentation is more favorable than the other algorithms.

In the Cemetery image segmentation, CS-Otsu converges at about 33 iterations, SSA-Otsu converges at about 54 iterations, PSO-Otsu and WPA-Otsu converge after 91 and 90 iterations, respectively, and FMFO-Otsu approximately converges at 4 iterations. In addition, the objective metrics of FMFO-Otsu are dramatically enhanced compared to all four methods, demonstrating that the fractional order enhances the performance of the original MFO algorithm significantly.

The fitness curve of the Lawn image shows that FMFO-Otsu has a faster iteration speed than other algorithms. Consequently, FMFO-Otsu increases the algorithm’s rate of convergence and fixes the issue with the previous algorithm’s susceptibility to local optimization. Furthermore, a higher degree of resemblance is indicated by FMFO-Otsu’s highest SSIM value. The MSE values of FMFO-Otsu are all lower than those of the other algorithms, indicating that the errors before and after image segmentation are smaller and the segmentation accuracy is improved. Therefore, FMFO-Otsu has a greater segmentation accuracy as a result.

There are 12 scenery images and 9 object images that were selected and segmented using the above five algorithms, and the results are averaged. The partial segmentation results are shown in Figure 11 and Figure 12, and the average segmentation results are shown in

Table 8. The average objective evaluation index values for the scenery images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
CS-Otsu	11.0642	0.3728	5289.9163	9392.9112	41
SSA-Otsu	11.0198	0.3713	5347.0236	9392.9322	70
PSO-Otsu	4.8496	0.0055	21,575.4078	9394.9889	79
WPA-Otsu	11.0491	0.3722	5305.7256	9396.8863	73
FMFO-Otsu	11.2914	0.3768	4988.5007	10,268.6839	7

and

Table 9. The average objective evaluation index values for the object images.

Algorithms	PSNR	SSIM	MSE	Fitness Value	Iterations
CS-Otsu	10.2217	0.4095	7484.4221	8271.8263	65
SSA-Otsu	10.2257	0.4081	7470.3681	8271.0888	52
PSO-Otsu	5.0965	0.0061	20,648.1657	8270.4589	70
WPA-Otsu	10.2365	0.4088	7462.1392	8266.8044	62
FMFO-Otsu	10.3795	0.4088	7314.2260	9187.4568	9

.

The original and segmented scenery images are shown in Figure 11. Table 8 describes the average data for the plant image segmentation. Subjectively, for the images in the first and second rows, FMFO-Otsu can segment some details more clearly than other algorithms. In the images on the third and fourth rows, some edge regions of the CS-Otsu, PSO-Otsu, and SSA-Otsu results were not clearly divided, but FMFO-Otsu’s result was better divided in the window and branch areas. According to the objective index, the performance of the FMFO-Otsu algorithm is better. For example, compared with CS-Otsu, SSA-Otsu, and WPA-Otsu, the iterations of FMFO-Otsu were decreased by 82.93%, 90%, and 90.41%, respectively; the PSNR values improved by 2.05%, 2.46%, and 2.19%, respectively; the SSIM values improved by 1.07%, 1.48%, and 1.24%, respectively; the MSE values declined by 5.7%, 6.71%, and 5.98%, respectively; and the fitness values improved by 9.32%, 9.32%, and 9.28%, respectively.

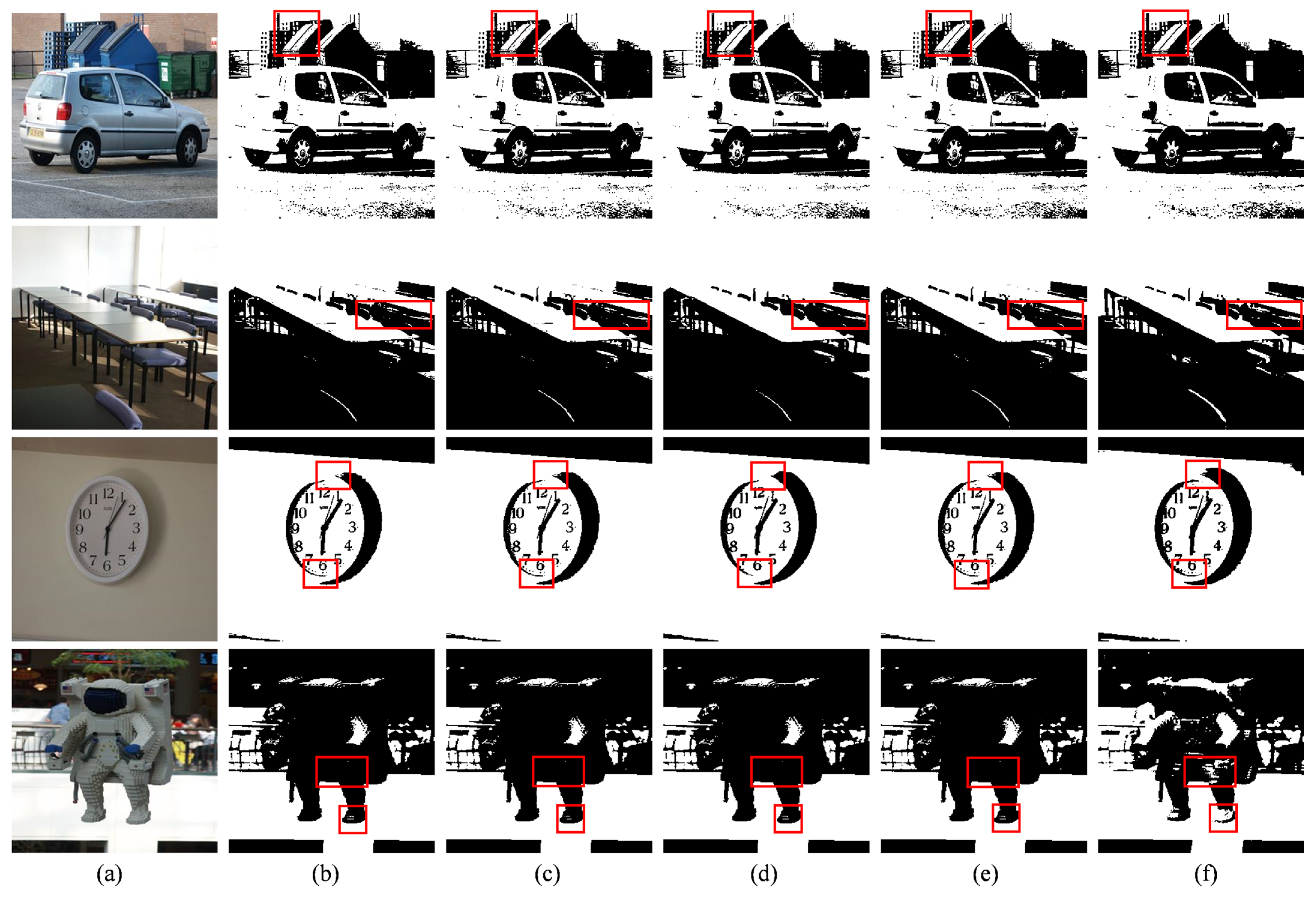
Figure 12 shows the original object images and the segmented images after five algorithms. The evaluation indicators after the object image averaging are shown in Table 9. In Figure 1, FMFO-Otsu splits a clear outline of the car. In the second row of images, CS-Otsu, SSA-Otsu, and PSO-Otsu exhibit the phenomenon of over-segmentation. For the third and fourth lines of images, the contours after FMFO-Otsu segmentation are clearer. According to the objective data, the SSIM value is slightly poor, but other indicators are effectively improved. FMFO-Otsu has a higher PSNR value and fitness value, and a lower MSE value and number of iterations. Through the above experimental results of different types of image segmentation, it can be seen that FMFO-Otsu performs better in subjective vision and several objective evaluation indexes. The algorithm convergence speed has also been improved.

5. Conclusions

The MFO algorithm has some drawbacks, including its low optimization accuracy, slow convergence rate, and its being prone to fall into local optimality. To avoid the disadvantages of the MFO algorithm, this paper proposes the FMFO algorithm based on adaptive parameters and fractional order differentiation. With the help of fractional order differentiation’s ability to memorize historical states, the position update of moths during flight is controlled with adaptive fractional order. The FMFO algorithm was tested on six benchmark functions and compared with the MFO algorithm. The results display that the FMFO algorithm’s local exploitation is improved and the speed of convergence was enhanced. The FMFO-Otsu algorithm is proposed in order to be used for image segmentation by combining the FMFO algorithm with the two-dimensional Otsu algorithm. To validate the segmentation effect of this FMFO-Otsu algorithm, this paper uses several types of images to demonstrate it, such as scenery images, character images, animal images, and so on. According to the results from this experiment, although the improvement of individual metrics is small, the convergence speed and segmentation accuracy of FMFO-Otsu are better than those of other algorithms, generally. Compared with the MFO-Otsu algorithm, the convergence rate of the FMFO-Otsu algorithm is improved by about 74.62%, and the PSNR, SSIM and the fitness value are increased by around 0.37%, 2.45%, and 0.12%, respectively. The MSE is decreased by about 0.82%, and the FMFO-Otsu algorithm has more substantial enhancements and advantages over other algorithms. Therefore, the FMFO-Otsu algorithm realizes effective improvement in segmentation accuracy and convergence rate compared to the MFO-Otsu algorithm and other algorithms.

In the future, we will try to modify the FMFO algorithm using other methods of fractional order, like R-L and Caputo. Additionally, we are going to apply the FMFO algorithm and newer algorithms to other images, resulting in better segmentation results and greater operational efficiency via comparison and enhancement.