Modeling and Analysis of Caputo–Fabrizio Definition-Based Fractional-Order Boost Converter with Inductive Loads
Abstract
1. Introduction
- (1)
- A large signal model of a fractional-order Boost converter with a fractional-order inductive load based on the C-F definition is constructed by using the state space averaging method. The accurate analytical solutions of the quiescent operating point and the ripple parameters of three state variables are derived. Moreover, simulation experiments are conducted where the results are consistent with the calculation results, verifying the correctness of the proposed model.
- (2)
- The transfer functions of the fractional-order circuit with three state variables are derived by performing the small-signal linearization method. Simulation experiments are conducted where the results from frequency sweep analysis verify the correctness of the transfer function.
- (3)
- According to the aforementioned results, the effect of the DC component of the state variables and ripple parameters on the order of energy storage components is analyzed.
2. Preliminaries
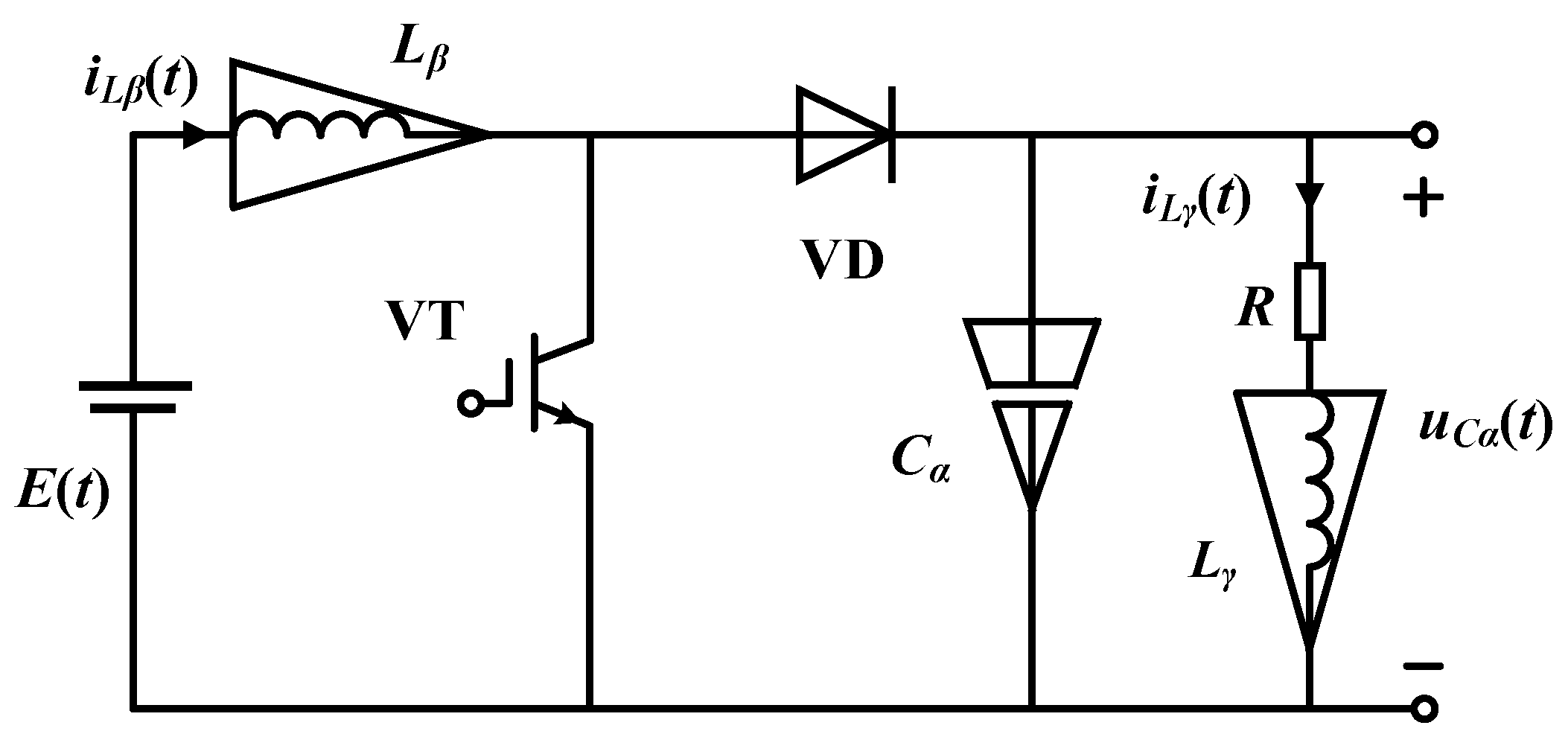
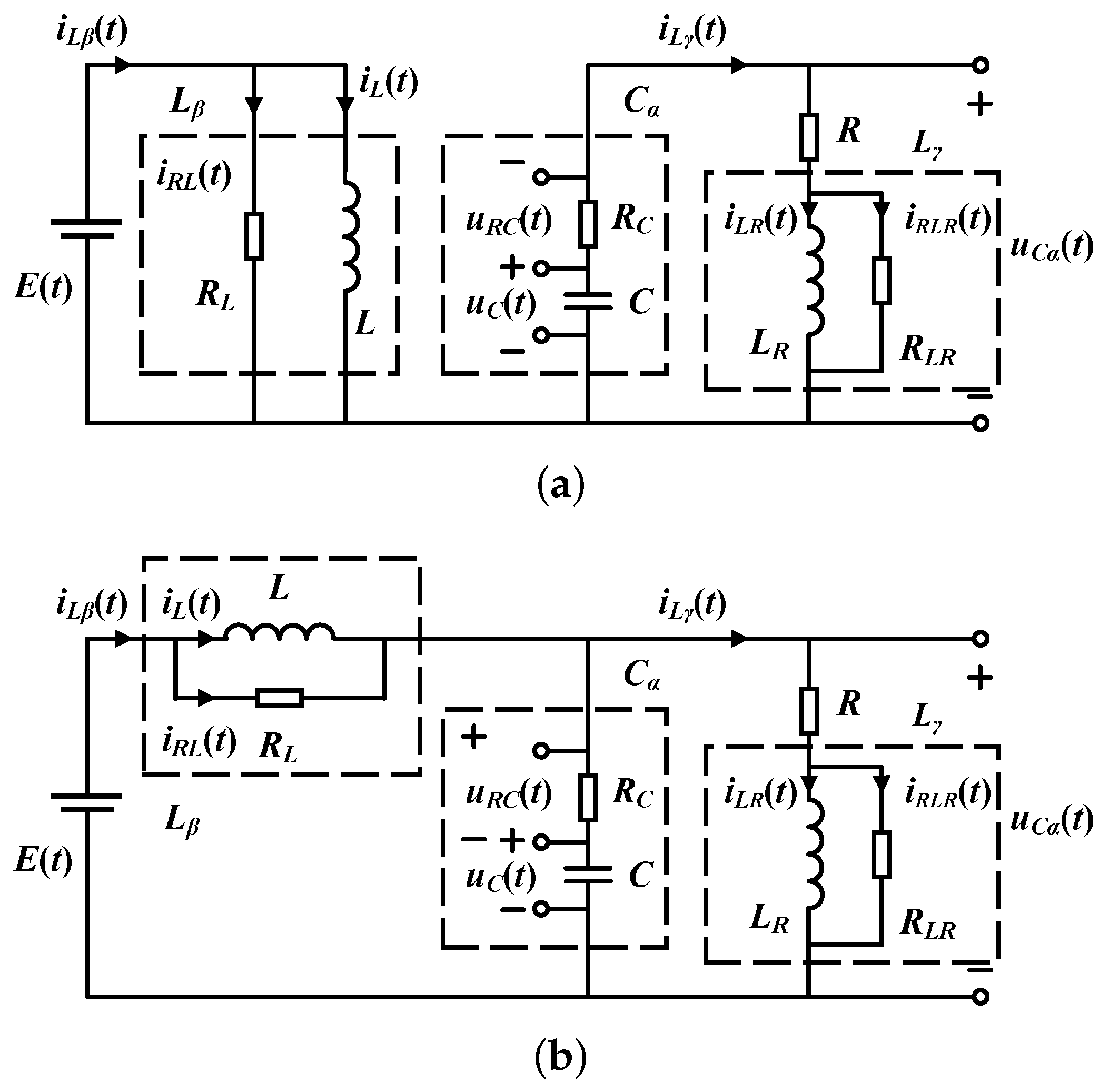
3. Modeling of the C-F Definition-Based Fractional-Order Boost Converter with Inductive Load
3.1. Quiescent Operating Point
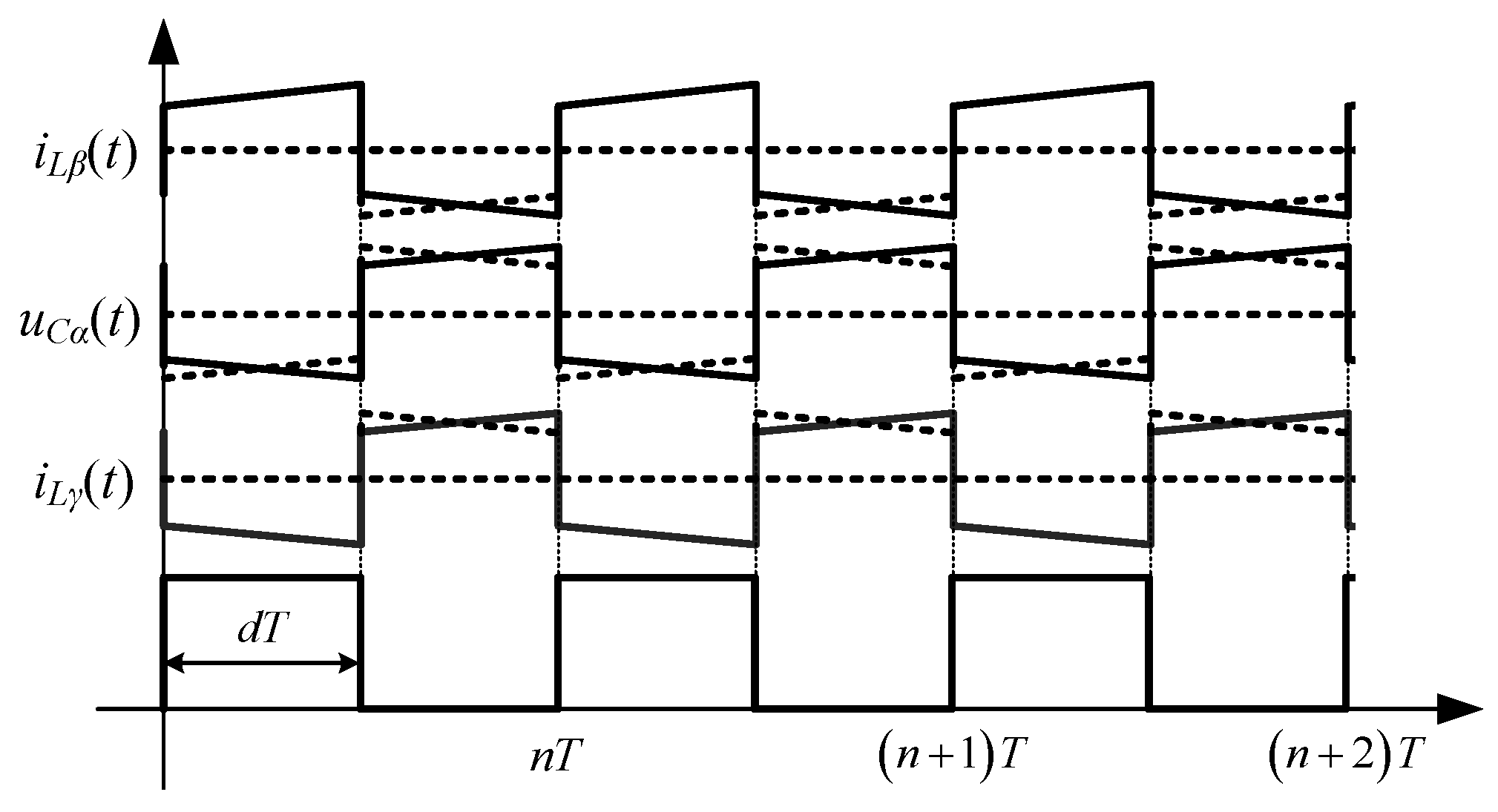
3.2. Ripple Parameters
3.3. Small-Signal Model
4. Simulation Experiment Results
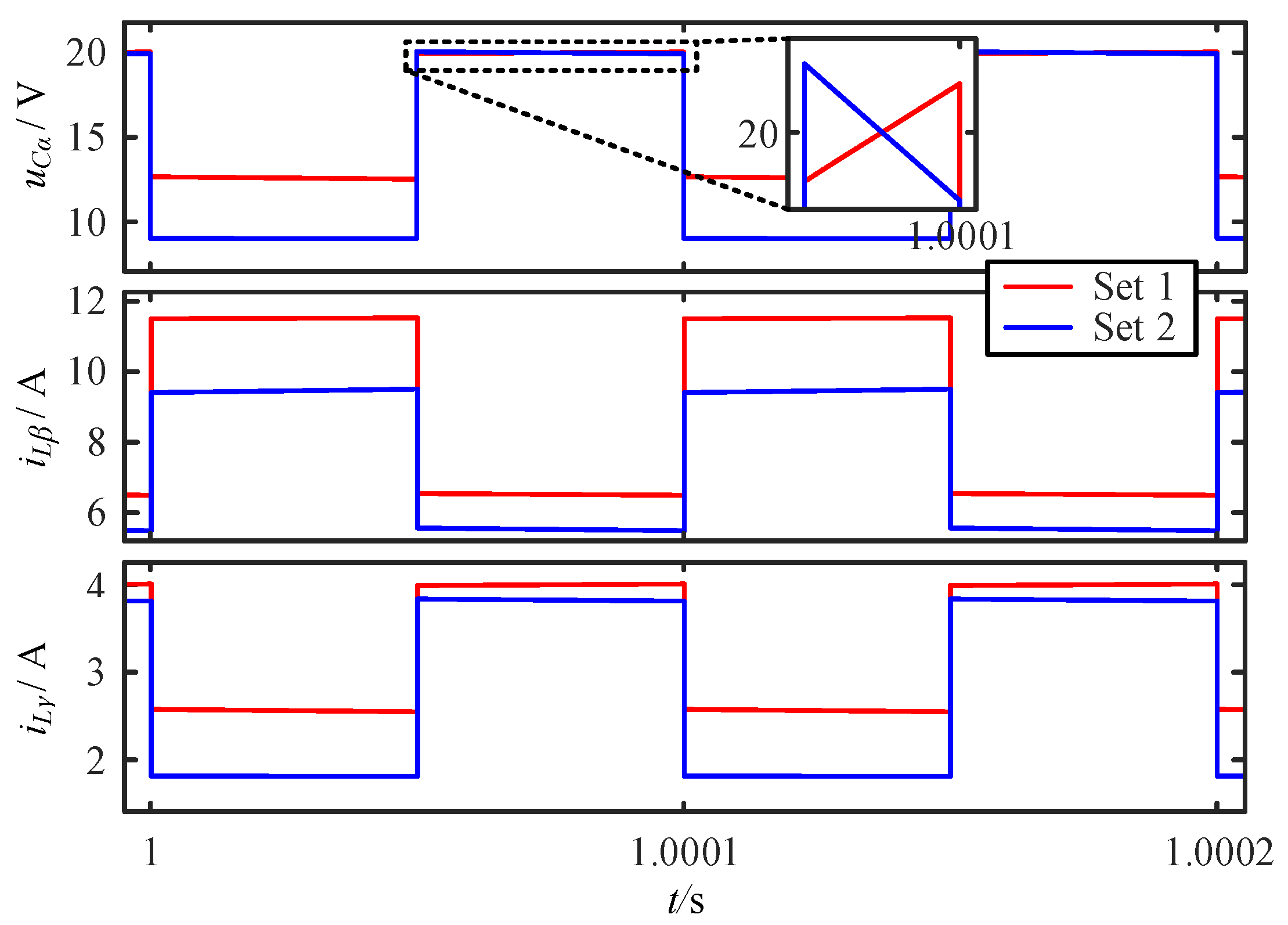
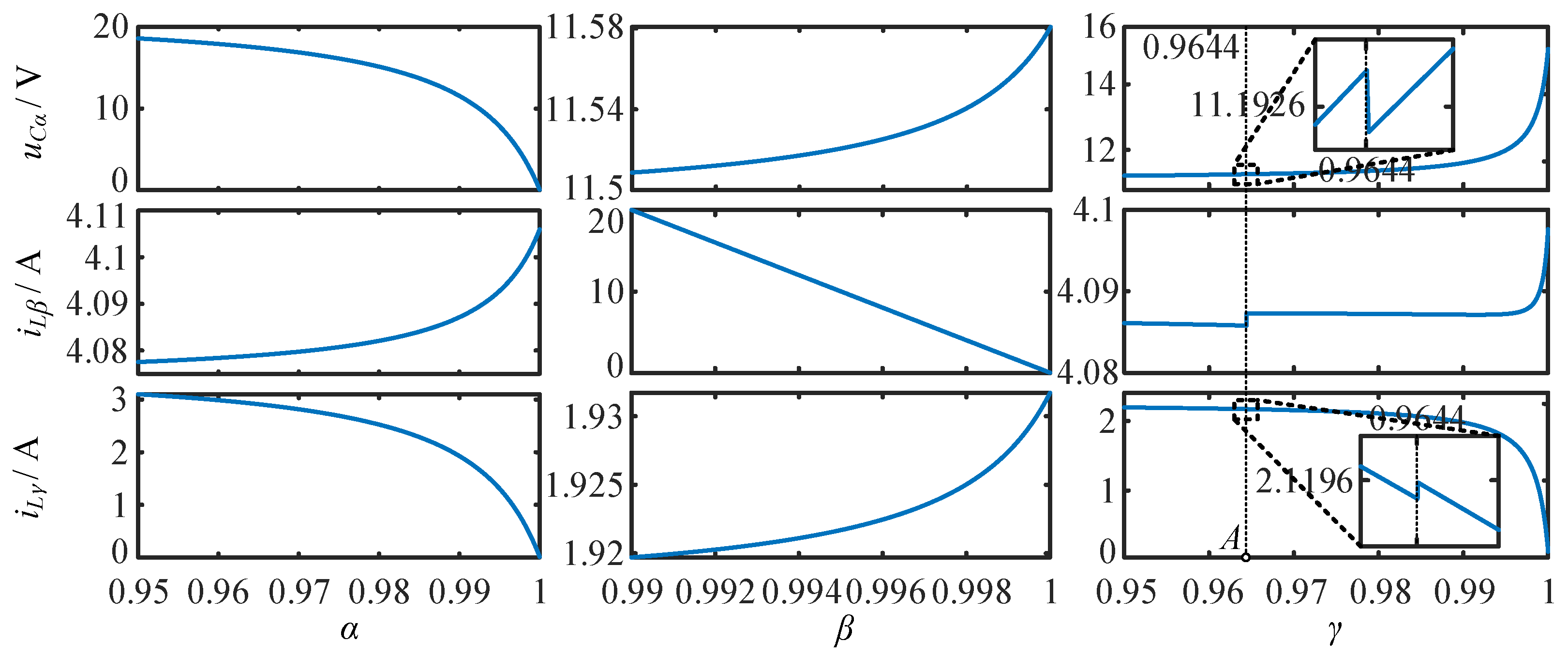
4.1. Analysis of Circuit Parameters at the Quiescent Operating Point
- Set 1: , , , , , , , , .
- Set 2: , , , , , , , , .
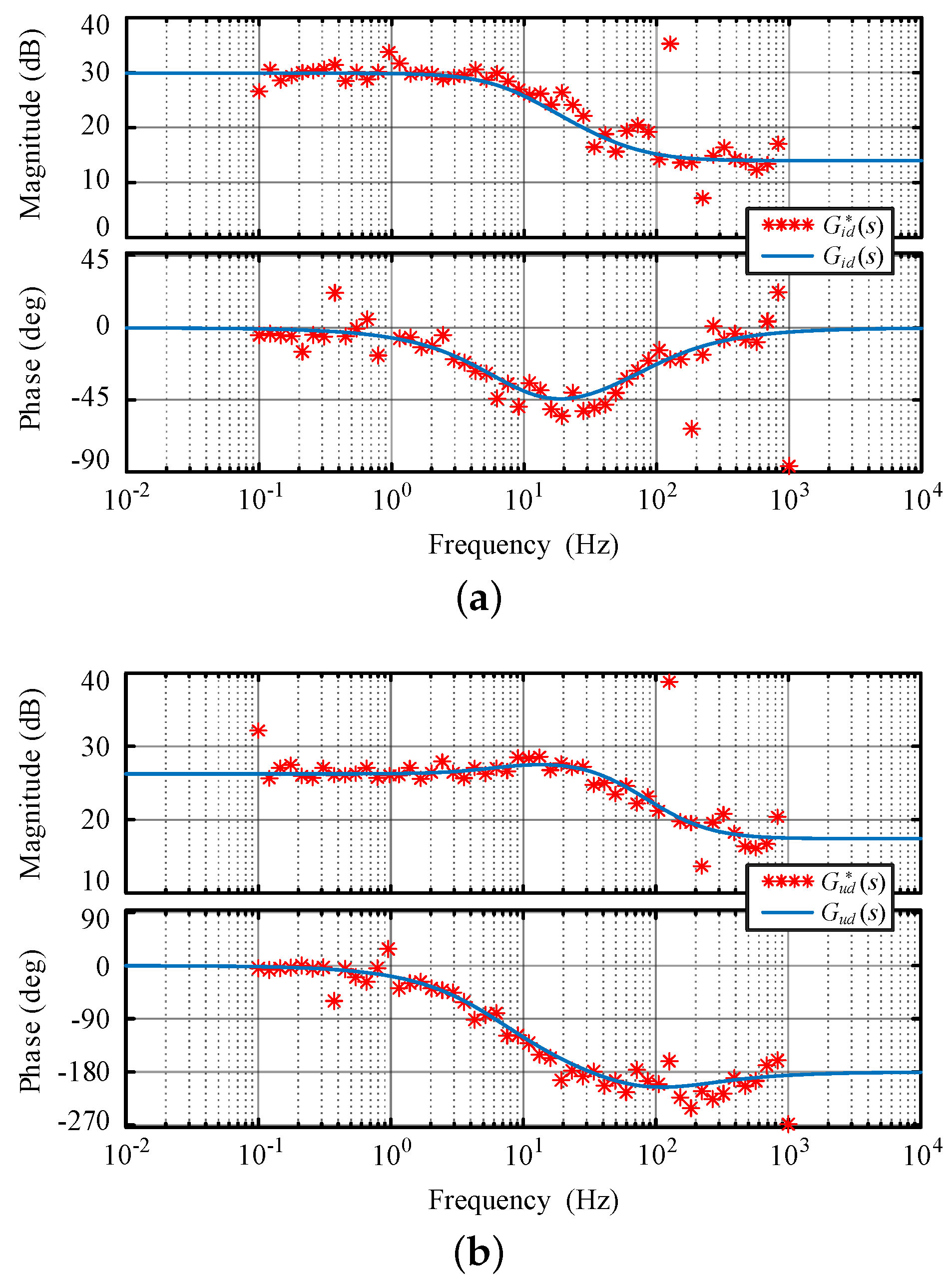
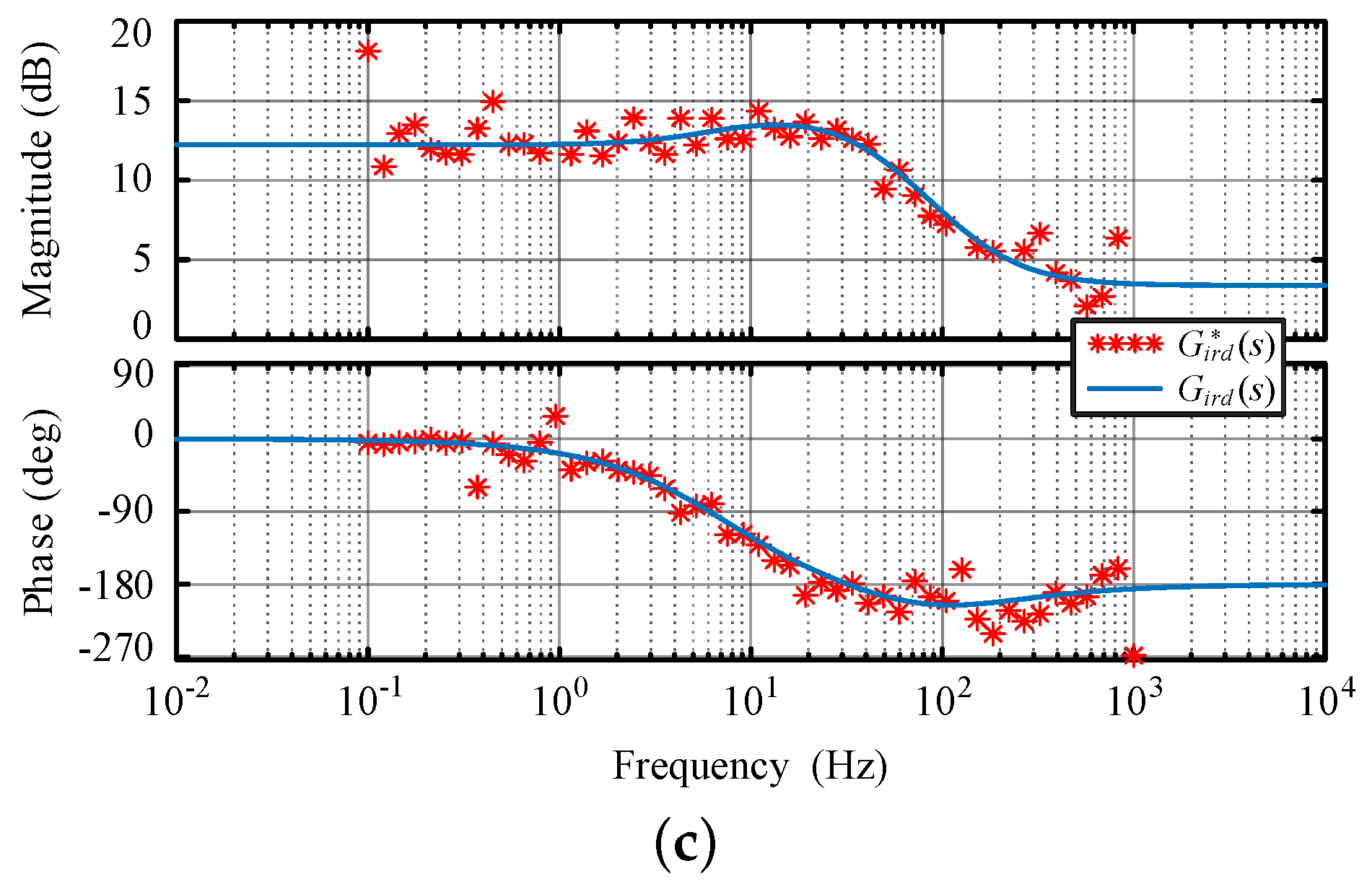
4.2. Verification of Small Signal Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Petráš, I. Fractional calculus. In Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; pp. 7–42. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Chen, Y.; Petras, I.; Xue, D. Fractional order control-a tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1397–1411. [Google Scholar]
- Koseoglu, M.; Deniz, F.N.; Alagoz, B.B.; Alisoy, H. An effective analog circuit design of approximate fractional-order derivative models of M-SBL fitting method. Eng. Sci. Technol. Int. J. 2022, 33, 101069. [Google Scholar] [CrossRef]
- Suzuki, J.L.; Gulian, M.; Zayernouri, M.; D’Elia, M. Fractional modeling in action: A survey of nonlocal models for subsurface transport, turbulent flows, and anomalous materials. J. Peridyn. Nonlocal Model. 2023, 5, 392–459. [Google Scholar] [CrossRef]
- Swaminathan, N.; Cao, Y. An overview of high-conversion high-voltage DC–DC converters for electrified aviation power distribution system. IEEE Trans. Transp. Electrif. 2020, 6, 1740–1754. [Google Scholar] [CrossRef]
- Al-Greer, M.; Armstrong, M.; Ahmeid, M.; Giaouris, D. Advances on system identification techniques for DC–DC switch mode power converter applications. IEEE Trans. Power Electron. 2018, 34, 6973–6990. [Google Scholar] [CrossRef]
- Song, S.; Zhang, X.; An, Y.; Ma, Y. Advanced fractional-order lithium-ion capacitor model with time-domain parameter identification method. IEEE Trans. Ind. Electron. 2021, 69, 13808–13817. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B. Comparative study of Riemann–Liouville and Caputo derivative definitions in time-domain analysis of fractional-order capacitor. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2184–2188. [Google Scholar] [CrossRef]
- Al-Daloo, M.; Soltan, A.; Yakovlev, A. Advance interconnect circuit modeling design using fractional-order elements. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 39, 2722–2734. [Google Scholar] [CrossRef]
- Koton, J.; Dvorak, J.; Kubanek, D.; Herencsar, N. Designing series of fractional-order elements. Analog. Integr. Circuits Signal Process. 2021, 106, 553–563. [Google Scholar] [CrossRef]
- Koton, J.; Kubanek, D.; Herencsar, N.; Dvorak, J.; Psychalinos, C. Designing constant phase elements of complement order. Analog. Integr. Circuits Signal Process. 2018, 97, 107–114. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.I. Improved Performance in the Control of DC–DC Three-Phase Power Electronic Converter Using Fractional-Order SMC and Synergetic Controllers and RL-TD3 Agent. Fractal Fract. 2022, 6, 729. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.; Zhang, B.; Qiu, D. A modeling and analysis method for fractional-order DC–DC converters. IEEE Trans. Power Electron. 2016, 32, 7034–7044. [Google Scholar] [CrossRef]
- Atangana, A.; Hammouch, Z. Fractional calculus with power law: The cradle of our ancestors. Eur. Phys. J. Plus 2019, 134, 429. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Gabrick, E.C.; Protachevicz, P.R.; Lenzi, E.K.; Sayari, E.; Trobia, J.; Lenzi, M.K.; Borges, F.S.; Caldas, I.L.; Batista, A.M. Fractional Diffusion Equation under Singular and Non-Singular Kernel and Its Stability. Fractal Fract. 2023, 7, 792. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Javed, F.; Riaz, M.B.; Iftikhar, N.; Awrejcewicz, J.; Akgül, A. Heat and mass transfer impact on differential type nanofluid with carbon nanotubes: A study of fractional order system. Fractal Fract. 2021, 5, 231. [Google Scholar] [CrossRef]
- Sitthiwirattham, T.; Arfan, M.; Shah, K.; Zeb, A.; Djilali, S.; Chasreechai, S. Semi-analytical solutions for fuzzy Caputo–Fabrizio fractional-order two-dimensional heat equation. Fractal Fract. 2021, 5, 139. [Google Scholar] [CrossRef]
- Idrees, M.; Alnahdi, A.S.; Jeelani, M.B. Mathematical Modeling of Breast Cancer Based on the Caputo–Fabrizio Fractal-Fractional Derivative. Fractal Fract. 2023, 7, 805. [Google Scholar] [CrossRef]
- Cramer, E.Y.; Ray, E.L.; Lopez, V.K.; Bracher, J.; Brennen, A.; Castro Rivadeneira, A.J.; Gerding, A.; Gneiting, T.; House, K.H.; Huang, Y.; et al. Evaluation of individual and ensemble probabilistic forecasts of COVID-19 mortality in the United States. Proc. Natl. Acad. Sci. USA 2022, 119, e2113561119. [Google Scholar] [CrossRef] [PubMed]
- Anjam, Y.N.; Shafqat, R.; Sarris, I.E.; Ur Rahman, M.; Touseef, S.; Arshad, M. A fractional order investigation of smoking model using Caputo–Fabrizio differential operator. Fractal Fract. 2022, 6, 623. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Liao, X. State-of-art survey of fractional order modeling and estimation methods for lithium-ion batteries. Fract. Calc. Appl. Anal. 2019, 22, 1449–1479. [Google Scholar] [CrossRef]
- Yang, N.; Xu, C.; Wu, C.; Jia, R.; Liu, C. Fractional-order cubic nonlinear flux-controlled memristor: Theoretical analysis, numerical calculation and circuit simulation. Nonlinear Dyn. 2019, 97, 33–44. [Google Scholar] [CrossRef]
- Alilou, M.; Azami, H.; Oshnoei, A.; Mohammadi-Ivatloo, B.; Teodorescu, R. Fractional-Order Control Techniques for Renewable Energy and Energy-Storage-Integrated Power Systems: A Review. Fractal Fract. 2023, 7, 391. [Google Scholar] [CrossRef]
- Lin, D.; Liao, X.; Dong, L.; Yang, R.; Samson, S.Y.; Iu, H.H.C.; Fernando, T.; Li, Z. Experimental study of fractional-order RC circuit model using the Caputo and Caputo–Fabrizio derivatives. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1034–1044. [Google Scholar] [CrossRef]
- Mahdavi, J.; Emaadi, A.; Bellar, M.; Ehsani, M. Analysis of power electronic converters using the generalized state-space averaging approach. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 767–770. [Google Scholar] [CrossRef]
- Yang, C.; Xie, F.; Chen, Y.; Xiao, W.; Zhang, B. Modeling and analysis of the fractional-order flyback converter in continuous conduction mode by caputo fractional calculus. Electronics 2020, 9, 1544. [Google Scholar] [CrossRef]
- Xie, L.; Liu, Z.; Zhang, B. A modeling and analysis method for CCM fractional order Buck-Boost converter by using R–L fractional definition. J. Electr. Eng. Technol. 2020, 15, 1651–1661. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, B.; Jiang, Y. Analysis and modeling of fractional-order buck converter based on Riemann-Liouville derivative. IEEE Access 2019, 7, 162768–162777. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Hu, J.; Zhang, B.; Qiu, D. A symbolic analysis method for fractional-order boost converter in discontinuous conduction mode. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 8738–8743. [Google Scholar]
- Jia, Z.; Liu, C. Fractional-order modeling and simulation of magnetic coupled boost converter in continuous conduction mode. Int. J. Bifurc. Chaos 2018, 28, 1850061. [Google Scholar] [CrossRef]
- Fang, S.; Wang, X. Modeling and analysis method of fractional-order buck–boost converter. Int. J. Circuit Theory Appl. 2020, 48, 1493–1510. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching, D.L.C.; Ullah, S.; Khan, I. Mathematical and statistical analysis of RL and RC fractional-order circuits. Fractals 2020, 28, 2040030. [Google Scholar] [CrossRef]
- Kianpoor, N.; Yousefi, M.; Bayati, N.; Hajizadeh, A.; Soltani, M. Fractional order modelling of DC–DC boost converters. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 864–869. [Google Scholar]
- Sharma, M.; Rajpurohit, B.S.; Agnihotri, S.; Rathore, A.K. Development of fractional order modeling of voltage source converters. IEEE Access 2020, 8, 131750–131759. [Google Scholar] [CrossRef]
- Leng, M.; Zhou, G.; Tian, Q.; Xu, G.; Blaabjerg, F. Small signal modeling and design analysis for boost converter with valley V 2 control. IEEE Trans. Power Electron. 2020, 35, 13475–13487. [Google Scholar] [CrossRef]
- Siddhartha, V.; Hote, Y.V.; Saxena, S. Non-ideal modelling and IMC based PID Controller Design of PWM DC–DC Buck Converter. IFAC-PapersOnLine 2018, 51, 639–644. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Baleanu, D.; Escobar-Jiménez, R.F.; Mohamed Al Qurashi, M. Analytical solutions of the electrical RLC circuit via Liouville–Caputo operators with local and non-local kernels. Entropy 2016, 18, 402. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Rosales, J.; Filoteo, J.D.; González, A. A comparative analysis of the RC circuit with local and non-local fractional derivatives. Rev. Mex. Fís. 2018, 64, 647–654. [Google Scholar] [CrossRef]
- Montesinos-García, J.J.; Barahona-Avalos, J.L.; Linares-Flores, J.; Juárez-Abad, J.A. Uncertainty Observer-Based Control for a Class of Fractional-Order Non-Linear Systems with Non-Linear Control Inputs. Fractal Fract. 2023, 7, 836. [Google Scholar] [CrossRef]
- Liao, X.; Ran, M.; Yu, D.; Lin, D.; Yang, R. Chaos analysis of Buck converter with non-singular fractional derivative. Chaos Solitons Fractals 2022, 156, 111794. [Google Scholar] [CrossRef]
- Liao, X.; Wang, Y.; Yu, D.; Lin, D.; Ran, M.; Ruan, P. Modeling and analysis of Buck-Boost converter with non-singular fractional derivatives. Chaos Solitons Fractals 2023, 169, 113336. [Google Scholar] [CrossRef]
- Xie, L.; Shi, J.; Yao, J.; Wan, D. Research on the Period-Doubling Bifurcation of Fractional-Order DCM Buck–Boost Converter Based on Predictor-Corrector Algorithm. Mathematics 2022, 10, 1993. [Google Scholar] [CrossRef]
- Abuaisha, T.; Kertzscher, J. Fractional-order modelling and parameter identification of electrical coils. Fract. Calc. Appl. Anal. 2019, 22, 193–216. [Google Scholar] [CrossRef]
- Raorane, A.A.; Patil, M.D.; Vyawahare, V.A. Analysis of full-wave controlled rectifier with lossy inductive load using fractional-order models. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 750–755. [Google Scholar]
- Zhu, J.; Chen, D.; Zhao, H.; Ma, R. Nonlinear dynamic analysis and modeling of fractional permanent magnet synchronous motors. J. Vib. Control 2016, 22, 1855–1875. [Google Scholar] [CrossRef]
- Khubalkar, S.; Junghare, A.; Aware, M.; Das, S. Modeling and control of a permanent-magnet brushless DC motor drive using a fractional order proportional-integral-derivative controller. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 4223–4241. [Google Scholar] [CrossRef]
- Tripathy, M.C.; Mondal, D.; Biswas, K.; Sen, S. Experimental studies on realization of fractional inductors and fractional-order bandpass filters. Int. J. Circuit Theory Appl. 2015, 43, 1183–1196. [Google Scholar] [CrossRef]
- Zhang, L.; Kartci, A.; Elwakil, A.; Bagci, H.; Salama, K.N. Fractional-order inductor: Design, simulation, and implementation. IEEE Access 2021, 9, 73695–73702. [Google Scholar] [CrossRef]
- Said, L.A.; Ismail, S.M.; Radwan, A.G.; Madian, A.H.; Abu El-Yazeed, M.F.; Soliman, A.M. On the optimization of fractional order low-pass filters. Circuits Syst. Signal Process. 2016, 35, 2017–2039. [Google Scholar] [CrossRef]
- Yu, D.; Liao, X.; Wang, Y.; Ran, M.; Dalin; Xia, J. Modeling and Characteristic Analysis of Fractional-Order Boost Converter based on the Caputo–Fabrizio Fractional Derivatives. Fractals 2023, 31, 2350082. [Google Scholar] [CrossRef]
- Liao, X.; Yu, D.; Lin, D.; Ran, M.; Xia, J. Characteristic Analysis of Fractional-Order RLC Circuit based on the Caputo–Fabrizio Definition. Fractals 2022, 30, 2250078. [Google Scholar] [CrossRef]



| Simulation | Calculation | Simulation | Calculation | ||||
|---|---|---|---|---|---|---|---|
| Set1 | Set1 | ||||||
| Set2 | Set2 | ||||||
| Set1 | Set1 | ||||||
| Set2 | Set2 | ||||||
| Set1 | Set1 | ||||||
| Set2 | Set2 | ||||||
| Set1 | Set1 | ||||||
| Set2 | Set2 | ||||||
| Set1 | |||||||
| Set2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Liao, X.; Wang, Y. Modeling and Analysis of Caputo–Fabrizio Definition-Based Fractional-Order Boost Converter with Inductive Loads. Fractal Fract. 2024, 8, 81. https://doi.org/10.3390/fractalfract8020081
Yu D, Liao X, Wang Y. Modeling and Analysis of Caputo–Fabrizio Definition-Based Fractional-Order Boost Converter with Inductive Loads. Fractal and Fractional. 2024; 8(2):81. https://doi.org/10.3390/fractalfract8020081
Chicago/Turabian StyleYu, Donghui, Xiaozhong Liao, and Yong Wang. 2024. "Modeling and Analysis of Caputo–Fabrizio Definition-Based Fractional-Order Boost Converter with Inductive Loads" Fractal and Fractional 8, no. 2: 81. https://doi.org/10.3390/fractalfract8020081
APA StyleYu, D., Liao, X., & Wang, Y. (2024). Modeling and Analysis of Caputo–Fabrizio Definition-Based Fractional-Order Boost Converter with Inductive Loads. Fractal and Fractional, 8(2), 81. https://doi.org/10.3390/fractalfract8020081








