Generalized Sampling Theory in the Quaternion Domain: A Fractional Fourier Approach

Abstract

The field of quaternions has made a substantial impact on signal processing research, with numerous studies exploring their applications. Building on this foundation, this article extends the study of sampling theory using the quaternion fractional Fourier Transform (QFRFT). We first propose a generalized sampling expansion (GSE) for fractional bandlimited signals via the QFRFT, extending the classical Papoulis expansion. Next, we design fractional quaternion Fourier filters to reconstruct both the signals and their derivatives, based on the GSE and QFRFT properties. We illustrate the practical utility of the QFRFT-based GSE framework with a case study on signal denoising, demonstrating its effectiveness in noise reduction with the Mean Squared Error (MSE), highlighting the improvement in signal restoration.

1. Introduction

In signal processing, the Fourier Transform (FT) serves as a fundamental tool for representing a signal in the frequency domain and analyzing its frequency components. However, because of the more complex and diverse applications in signal processing, more powerful transforms have been developed to meet specific demands and problems. The fractional Fourier Transform (FRFT) is one of those transforms which has garnered significant interest because of its capacity to give a more flexible time-frequency representation. Quite a lot of research has been performed on the FRFT; see [1,2,3,4,5,6,7,8,9,10].

The QFRFT is an extension of the FRFT into the quaternion domain, offering a powerful framework for processing quaternion-valued signals. This extension is particularly helpful in applications involving multi-dimensional data such as color image processing, vector fields, and other complex-valued signal analyses. The QFRFT inherits the properties of the FRFT while introducing new capabilities afforded by quaternion algebra, making it a versatile tool in modern signal processing. This groundbreaking advancement in signal processing within the quaternion domain has ushered in a new era of research, as evidenced by the work in [11,12,13,14,15,16,17,18].

Related Work on Generalized Sampling Expansion

In digital signal processing (DSP), the sampling theory is considered as a cornerstone. It provides the theoretical underpinning for transforming continuous signals into discrete signals without loss of information. Traditional sampling theorems, such as the Nyquist–Shannon sampling theorem [19], are well-known for the FT, and have been applied to the FRFT. The formulation of the Shannon sampling theorem provided essential principles that catalyzed significant advancements in DSP, leading to its widespread adoption and growth across various applications. This Shannon sampling theorem [19] served as a bridge between analog and digital signals, facilitating their seamless integration and transformation. With the help of this theorem, the researchers were able to reconstruct the bandlimited signals from its samples. After the advent of sampling theorem, the classical sampling theory gained popularity [20,21,22,23]. This leads to the GSE, commonly known as the multi-channel sampling expansion. The FT and its generalizations have revolutionized sampling theory in the field of signal processing, catalyzing transformative breakthroughs and advances. However, extending these theorems to the quaternion domain is still a relatively new field of research. Many researchers have focused on this domain, significantly contributing to its development and application. Cheng et al. [24] used the relationship between the quaternion linear canonical transform (QLCT) and the quaternion Fourier Transform (QFT) for deriving the GSE of the quaternionic signals. Siddiqui et al. [25,26] employed the derivative technique for signal reconstruction. Xiaoxiao Hu and Kit Ian Kou discussed the sampling techniques of quaternionic signals, which are non-bandlimited, in [27]. In [21], the authors have discussed the sampling formulas in the 2D QFT and 2D QLCT domains in detail. Despite significant advancements, the field of the GSE for quaternion-valued signals remains rich with unanswered questions. Researchers have the potential to delve into new avenues within this discipline, discovering a wealth of opportunities, and expanding the boundaries of current knowledge.

This article aims to explore the GSE in the context of the one-dimensional quaternion fractional Fourier Transform (1DQFRFT) defined by [11]. We investigate how the QFRFT framework can be employed to develop new sampling theorems that are applicable to quaternion-valued signals. Our focus is on deriving conditions under which these signals can be perfectly reconstructed from their samples in the QFRFT domain, considering the additional degrees of freedom introduced by quaternion algebra.

The contributions of this paper are twofold. Firstly, we provide a comprehensive formulation of the GSE for 1DQFRFT, detailing the mathematical foundations and derivations of the sampling conditions. Secondly, we investigated how a signal can be reconstructed using a signal and its derivative.

By advancing the theory of sampling in the QFRFT domain, this work not only broadens the scope of quaternion signal processing, but also opens up new avenues for research and application in areas where multi-dimensional and quaternion-valued data are prevalent. The results presented here are expected to have significant implications for fields such as communications and beyond, where the need for efficient and accurate signal representation and reconstruction is paramount.

The highlights of the article are as follows:

• We derived the GSE for the 1DQFRFT domain, providing a robust framework for quaternion signal processing.
• We employed quaternion Fourier filters in the derivation of the GSE, showcasing their effectiveness in managing the additional complexity and degrees of freedom inherent in quaternion signals.
• We implemented the derivative technique of the 1DQFRFT to achieve accurate signal reconstruction, highlighting its precision and reliability within the quaternion framework.
• We suggested future research directions, including the exploration of other transforms in the quaternion domain, and the extension of the GSE framework to higher dimensions.
• We identified open questions in the GSE for quaternionic signals, encouraging further exploration and discovery in this emerging area of study.
• We have discussed a detailed case study for the use of the QFRFT-based GSE in analyzing its performance in reducing stationary Gaussian noise versus non-stationary, chirped noise.

The rest of the article is structured as follows. Section 2 covers the foundational concepts and mathematical preliminaries essential for understanding the subsequent discussions. Section 3 revolves around the derivation and presentation of the GSE specifically for the 1DQFRFT domain. In Section 4, a case study highlights the effectiveness of the proposed scheme. We offer a detailed discussion and analysis of the results, highlighting the advantages and implications of the GSE method compared to traditional techniques in Section 5. The article concludes with a summary of key findings and insights, along with suggestions for future research directions in Section 6.

2. Preliminaries

Quaternions are an extension of complex numbers, exhibiting associativity but lacking commutativity over the real numbers $\mathbb{R}$. Each quaternion, $\mathbb{H}$, can be expressed as follows [16]:

$$q=x_1+x_{2}i+x_{3}j+x_{4}k,x_1,x_2,x_3,x_4\in \mathbb{R},$$

(1)

where

$$ij=k,ji=-k,jk=i,kj=-i,ki=j,ik=-j,$$

$$i^2=j^2=k^2=ijk=-1.$$

(2)

In a quaternion $q=x_1+x_{2}i+x_{3}j+x_{4}k\in \mathbb{H}$, $x_1$ is the scalar part of q, as denoted by

$$\mathrm{Sc}\left(q\right)=x_1,$$

where

$$\mathrm{V}\left(q\right)=x_{2}i+x_{3}j+x_{4}k$$

represents the vector part.

From (2), quaternion multiplications can be defined as

$$qz=(x_1+x_{2}i+x_{3}j+x_{4}k)(y_1+y_{2}i+y_{3}j+y_{4}k),$$

(3)

resulting in

$$\begin{array}{cc}\hfill qz=& (x_1{y}_1-x_2{y}_2-x_3{y}_3-x_4{y}_4)+(x_1{y}_2+x_2{y}_1+x_3{y}_4-x_4{y}_3)i\hfill \\ \hfill & +(x_1{y}_3-x_2{y}_4+x_3{y}_1+x_4{y}_2)j+(x_1{y}_4+x_2{y}_3-x_3{y}_2+x_4{y}_1)k,\hfill \end{array}$$

(4)

where

$$\mathrm{Sc}\left(qz\right)=x_1{y}_1-x_2{y}_2-x_3{y}_3-x_4{y}_4,$$

(5)

and

$$\begin{array}{cc}\hfill \mathrm{V}\left(qz\right)=& (x_1{y}_2+x_2{y}_1+x_3{y}_4-x_4{y}_3)i+(x_1{y}_3-x_2{y}_4+x_3{y}_1+x_4{y}_2)j\hfill \\ \hfill & +(x_1{y}_4+x_2{y}_3-x_3{y}_2+x_4{y}_1)k.\hfill \end{array}$$

(6)

Quaternions exhibit a cyclic multiplication symmetry,

$$\mathrm{Sc}\left(qrs\right)=\mathrm{Sc}\left(rqs\right)=\mathrm{Sc}\left(srq\right),q,r,s\in \mathbb{H}.$$

(7)

The quaternion conjugate of any quaternion q is defined as

$$\overline{q}=x_1-x_{2}i-x_{3}j-x_{4}k,$$

(8)

which satisfies

$$\overline{qz}=\overline{zq}q,z\in \mathbb{H}.$$

(9)

The order of multiplication is changed by the quaternion conjugate. The norm of $q\in \mathbb{H}$ is

$$\left|q\right|=\sqrt{x_1^2+x_2^2+x_3^2+x_4^2}.$$

(10)

It can be checked whether

$${\left|q\right|}^2=q\overline{q},qz=q\overline{z},\mathrm{and}q+z=q+z,q,z\in \mathbb{H}.$$

(11)

The inverse of $q\in \mathbb{H}$ is given by

$$q^{-1}={\displaystyle \frac{\overline{q}}{{\left|q\right|}^2}}.$$

(12)

This demonstrates that $\mathbb{H}$ is a normed division algebra. A quaternion q is called a unit quaternion if $\left|q\right|=1$, and a pure quaternion if $a=0$. Analogous to the complex numbers, the inner product of $f,g:\mathbb{R}\to \mathbb{H}$ is defined as

$$(f,g)L^2(\mathbb{R};\mathbb{H})={\int }_{\mathbb{R}}f\left(x\right)\overline{g\left(x\right)},dx.$$

(13)

For $f=g$, the $L^2(\mathbb{R};\mathbb{H})$-norm is given by

$${\left|f\right|}_{L^2(\mathbb{R};\mathbb{H})}={\left({\int }_{\mathbb{R}}{\left|f\left(x\right)\right|}^2,dx\right)}^{{\displaystyle \frac{1}{2}}}.$$

(14)

3. Quaternion Fractional Fourier Transform Domain

The 1DQFRFT with angle $\beta$ of a signal $f\left(t\right)$, denoted as $F_{\beta }\left(u\right)$, is defined as [11]

$$\begin{array}{cc}\hfill F_{\beta }\left(u\right)& =F^{\beta }\left[f\left(t\right)\right]\left(u\right)={\int }_{-\infty }^{\infty }f\left(t\right)K_{\beta }(u,t)dt\hfill \end{array}$$

(15)

where

$$\begin{array}{cc}\hfill f\left(t\right)& ={\int }_{-\infty }^{\infty }{F}_{\beta }\left(u\right)K_{\beta }^{*}(u,t)du\hfill \end{array}$$

(16)

The transforming kernel of the QFRFT is defined as

$$\begin{array}{cc}\hfill K_{\beta }(u,t)& =\left\{\begin{array}{cc}{A}_{\beta }{e}^{j\left({\displaystyle \frac{t^2+u^2}{2}}\right)}\cot (\beta )-jtu\csc (\beta ),\hfill & \mathrm{if}\beta \ne k\pi \hfill \\ \delta (t-u),\hfill & \mathrm{if}\beta =2k\pi \hfill \\ \delta (t+u),\hfill & \mathrm{if}\beta =(2k+1)\pi \hfill \end{array}\right.\hfill \end{array}$$

(17)

Here, $\beta$ represents the rotation angle, and ∗ denotes complex conjugation. The term $A_{\beta }=\sqrt{{\displaystyle \frac{1-j\cot \left(\beta \right)}{2\pi }}}$ is a scaling factor, and $F^{\beta }$ denotes the corresponding QFRFT with angle $\beta$. For $\beta ={\displaystyle \frac{\pi }{2}}$, the QFRFT simplifies to the QFT. From (15), we can see that, for $f\left(t\right)\in \mathbb{R}$, the position of the kernel can be interchanged as

$$\begin{array}{cc}\hfill F_{\beta }\left(u\right)& ={\int }_{-\infty }^{\infty }f\left(t\right)K_{\beta }(u,t)dt\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{K}_{\beta }(u,t)f\left(t\right)dt\hfill \end{array}$$

(18)

The following is the differential property for the QFRFT:

$$\begin{array}{cc}\hfill F^{\beta }\left[f^{\prime }\left(t\right)\right]\left(u\right)& =\left(\cos \beta {\displaystyle \frac{d}{du}}+\sin \beta ju\right)F_{\beta }\left(u\right)\hfill \end{array}$$

(19)

$$\begin{array}{c}\hfill F^{\beta }\left[{\displaystyle \frac{d^{k}f\left(t\right)}{d{t}^k}}\right]\left(u\right)={\left(\cos \beta {\displaystyle \frac{d}{du}}+\sin \beta ju\right)}^k{F}_{\beta }\left(u\right)\end{array}$$

(20)

Here, $f\left(t\right)$ is bandlimited to a frequency range of ${\Omega }_{\beta }$ in the QFRFT domain.

3.1. QFRFT Based GSE

Let us consider M linear systems. The quaternion fractional Fourier filters are denoted as

$$\begin{array}{c}\hfill H_1^{\beta }\left(u\right),H_2^{\beta }\left(u\right),\dots ,H_M^{\beta }\left(u\right)\end{array}$$

(21)

For these systems, we consider a signal $f\left(t\right)$, bandlimited to a frequency range of ${\Omega }_{\beta }$ in the QFRFT domain. The outputs are then given by

$$\begin{array}{cc}\hfill g_k\left(t\right)& =A_{-\beta }{\int }_{-{\Omega }_{\beta }}^{{\Omega }_{\beta }}{F}_{\beta }\left(u\right)H_k^{\beta }\left(u\right)e^{-j\left({\displaystyle \frac{t^2+u^2}{2}}\cot \left(\beta \right)\right)+jtu \csc \left(\beta \right)}du\hfill \end{array}$$

(22)

Then, we will see that $f\left(t\right)$ can be retrieved from the output $g_k\left(n{T}_0\right),k=1,2,\dots ,M,-\infty \le n\le \infty$. The sampling rate for these outputs is ${\displaystyle \frac{1}{M}}$. Here, the sampling period is $T_0$, and satisfies $T_0=MT={\displaystyle \frac{M\pi }{{\Omega }_{\beta }\csc \left(\beta \right)}}$. Then, we obtain the system of equations as follows:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{H}_1^{\beta }\left(u\right)e^{-jtu \csc \left(\beta \right)}{Y}_1(u,t)+\dots +H_M^{\beta }\left(u\right)e^{-jtu \csc \left(\beta \right)}{Y}_M(u,t)=1,\hfill \\ H_1^{\beta }(u+c)e^{-jtu \csc \left(\beta \right)}{Y}_1(u,t)+\dots +H_M^{\beta }(u+c)e^{-jtu \csc \left(\beta \right)}{Y}_M(u,t)=e^{jct \csc \left(\beta \right)},\hfill \\ \dots \hfill \\ H_1^{\beta }[u+(M-1)c]e^{-jtu \csc \left(\beta \right)}{Y}_1(u,t)+\dots +H_M^{\beta }[u+(M-1)c]e^{-jtu \csc \left(\beta \right)}{Y}_M(u,t)\hfill \\ =e^{j(M-1)ct \csc \left(\beta \right)}.\hfill \end{array}\right.\hfill \end{array}$$

(23)

where $t\in \mathbb{R}$, $u\in [-{\Omega }_{\beta },-{\Omega }_{\beta }+c]$, and $c={\displaystyle \frac{{\Omega }_{\beta }}{M}}$ is the sub-bandwidth in the QFRFT domain. This setup generates a collection of unknown functions $Y_1(u,t),Y_2(u,t),\dots ,Y_M(u,t)$. For this system to possess solutions, a necessary condition is that the determinant must be zero for all $u\in [-{\Omega }_{\beta },-{\Omega }_{\beta }+c]$. This condition indicates that $H_{\beta }^k\left(u\right)$ are not arbitrary; they must satisfy the system’s constraints.

Theorem 1.

Let $f\left(t\right)$ be a signal whose bandwidth is ${\Omega }_{\beta }$. This signal passes via M filters $H_1^{\beta }\left(u\right),H_2^{\beta }\left(u\right),\dots ,H_M^{\beta }\left(u\right)$. Then, we have

$$\begin{array}{cc}\hfill f\left(t\right)=e^{-j{\displaystyle \frac{t^2\cot \left(\beta \right)}{2}}}{\displaystyle \sum _{n=-\infty }^{\infty }}& \left[g_1\left(n{T}_0\right)e^{j{\displaystyle \frac{{\left(n{T}_0\right)}^2\cot \left(\beta \right)}{2}}}{y}_1(t-n{T}_0)\right.\hfill \\ \hfill & +\dots +\left.g_M\left(n{T}_0\right)e^{j{\displaystyle \frac{{\left(n{T}_0\right)}^2\cot \left(\beta \right)}{2}}}{y}_M(t-n{T}_0)\right]\hfill \end{array}$$

(24)

With $g_k\left(t\right)$ as outputs of filters,

$$y_k\left(t\right)={\displaystyle \frac{1}{c}}{\int }_{-{\Omega }_{\beta }}^{-{\Omega }_{\beta }+c}{e}^{-jtu \csc \left(\beta \right)}{Y}_k(u,t)e^{jtu \csc \left(\beta \right)}du,k=1,2,\dots ,M$$

(25)

and

$$T_0={\displaystyle \frac{2\pi }{\csc \left(\beta \right)}}={\displaystyle \frac{M\pi }{{\Omega }_{\beta }\csc \left(\beta \right)}}$$

Proof. 

We can see that

$$\begin{array}{c}\hfill c(t+T_0)\csc \left(\beta \right)=ct\csc \left(\beta \right)+c{T}_0\csc \left(\beta \right)=ct\csc \left(\beta \right)+2\pi \end{array}$$

(26)

because the coefficients $H_k^{\beta }\left(u\right)$ of the system of equations do not depend on t, and the R.H.S of system of equations constitutes periodic functions with period T. Consequently, we can write from (25) that

$$\begin{array}{cc}\hfill y_k(t-n{T}_0)& ={\displaystyle \frac{1}{c}}{\int }_{-{\Omega }_{\beta }}^{{\Omega }_{\beta }+c}{e}^{-jtu \csc \left(\beta \right)}{Y}_k(u,t)e^{jtu \csc \left(\beta \right)}{e}^{-jn{T}_{0}u \csc \left(\beta \right)}du,k=1,2,\dots ,M\hfill \\ \hfill & ={\displaystyle \frac{1}{c}}{\int }_{-{\Omega }_{\beta }}^{-{\Omega }_{\beta }+c}{Y}_k(u,t)e^{-jn{T}_{0}u \csc \left(\beta \right)}du\hfill \end{array}$$

(27)

Which demonstrates that, in the interval $(-{\Omega }_{\beta },{\Omega }_{\beta }+c)$, $y(t-n{T}_0)$ is $nth$ coefficient of Fourier series expansion for $Y_k(u,t)$. Therefore,

$$Y_k(u,t)=\sum _{n=-\infty }^{\infty }{y}_k(t-n{T}_0)e^{jun{T}_0\csc \left(\beta \right)}$$

(28)

Substituting (28) in (27) yields

$$\begin{array}{cc}\hfill H_1^{\beta }\left(u\right)e^{-jtu \csc \left(\beta \right)}{Y}_1(u,t)+\dots +H_M^{\beta }\left(u\right)e^{-jtu \csc \left(\beta \right)}{Y}_M(u,t)& =1\hfill \end{array}$$

(29)

and using the inversion formula from (30),

$$\begin{array}{cc}\hfill f\left(t\right)& =A_{-\beta }{\int }_{-{\Omega }_{\beta }}^{{\Omega }_{\beta }}{F}_{\beta }\left(u\right)e^{-j(t^2+u^2)\cot \left(\beta \right)/2+jtu \csc \left(\beta \right)}du\hfill \end{array}$$

(30)

we obtain

$$\begin{array}{cc}\hfill f\left(t\right)& =e^{-j{\displaystyle \frac{t^2\cot \left(\beta \right)}{2}}}{A}_{-\beta }{\int }_{-{\Omega }_{\beta }}^{{\Omega }_{\beta }}{F}_{\beta }\left(u\right)e^{-j{\displaystyle \frac{u^2\cot \left(\beta \right)}{2}}}\times [H_1^{\beta }\left(u\right)Y_1(u,t)+\dots +H_M^{\beta }\left(u\right)Y_M(u,t)]du\hfill \end{array}$$

(31)

Alternatively,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f\left(t\right)& =e^{-j{\displaystyle \frac{t^2\cot \left(\beta \right)}{2}}}{\displaystyle \sum _{n=-\infty }^{\infty }}\left[g_1\left(n{T}_0\right)e^{j{\displaystyle \frac{{\left(n{T}_0\right)}^2\cot \left(\beta \right)}{2}}}{y}_1(t-n{T}_0)\right.\hfill \\ \hfill & +\dots +\left.g_M\left(n{T}_0\right)e^{j{\displaystyle \frac{{\left(n{T}_0\right)}^2\cot \left(\beta \right)}{2}}}{y}_M(t-n{T}_0)\right]\hfill \end{array}\end{array}$$

(32)

with

$$\begin{array}{cc}\hfill g_k\left(n{T}_0\right)& =A_{-\beta }{\int }_{-{\Omega }_{\beta }}^{{\Omega }_{\beta }}{F}_{\beta }\left(u\right)H_k^{\beta }\left(u\right)e^{-j\left({\left(n{T}_0\right)}^2+u^2\right)\cot \left(\beta \right)/2+jun{T}_0\csc \left(\beta \right)}du\hfill \end{array}$$

(33)

which completes the proof. □

From the above discussion, we can conclude that M filters can be used to reconstruct the original signal, i.e., a filtered version of a signal is helpful in reconstructing the signal.

3.2. Sampling Reconstruction Method Using Signal and Its Derivative

Here, we have used the derivative of the QFRFT, and designed the QFRFT filters for sampling purposes.

The derivative of the QFRFT, taken from Equation (20), is given as

$$\begin{array}{c}\hfill F^{\beta }\left[{\displaystyle \frac{d^{k}f\left(t\right)}{d{t}^k}}\right]\left(u\right)={\left(\cos \beta {\displaystyle \frac{d}{du}}+\sin \beta ju\right)}^k{F}_{\beta }\left(u\right)\end{array}$$

We set

$$\begin{array}{c}\hfill H_k^{\beta }\left(u\right)={\left(\cos \beta {\displaystyle \frac{d}{du}}+\sin \beta ju\right)}^{k-1}\end{array}$$

(34)

So that

$$\begin{array}{c}\hfill g_k\left(t\right)=f^{(k-1)}\left(t\right)\end{array}$$

(35)

Corollary 1.

Let $f\left(t\right)$ be a continuous and bandlimited signal with bandwidth ${\Omega }_{\beta }$. If $f^{\prime }\left(t\right)$ is also continuous, then $f\left(t\right)$ has the following representation:

$$\begin{array}{c}\hfill f\left(t\right)=e^{-j{\displaystyle \frac{t^2\cot \left(\beta \right)}{2}}}{\displaystyle \sum _{n=-\infty }^{\infty }}{e}^{{\displaystyle \frac{j{\left(n{T}_0\right)}^2\cot \left(\beta \right)}{2}}}\left[{\displaystyle \frac{f\left(n{T}_0\right)}{{({\Omega }_{\beta }t\csc \left(\beta \right)-2n\pi )}^2}}+{\displaystyle \frac{f^{\prime }\left(n{T}_0\right)}{{\Omega }_{\beta }({\Omega }_{\beta }t-2n\pi \sin \left(\beta \right))}}\right]\\ \hfill \times 4{\sin }^2\left({\displaystyle \frac{{\Omega }_{\beta }t}{2\sin \left(\beta \right)}}\right)\end{array}$$

(36)

where

$$\begin{array}{c}{T}_0={\displaystyle \frac{2\pi }{{\Omega }_{\beta }\csc \left(\beta \right)}}\end{array}$$

Proof. 

For simplicity, we take $M=2$; then,

$$T_0={\displaystyle \frac{2\pi }{{\Omega }_{\beta }\csc \left(\beta \right)}},c={\Omega }_{\beta },g_1\left(t\right)=f\left(t\right),g_2\left(t\right)=f^{\prime }\left(t\right)$$

Let ${\overline{Y}}_i(u,t)=e^{-jtu \csc \left(\beta \right)}{Y}_i(u,t),i=1,2$; then, System (23) yields

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\overline{Y}}_1(u,t)+(\cos \left(\beta \right){\displaystyle \frac{d}{du}}+\sin \left(\beta \right)ju){\overline{Y}}_2(u,t)& =1\hfill \\ \hfill {\overline{Y}}_1(u,t)+(\cos \left(\beta \right){\displaystyle \frac{d}{du}}+\sin \left(\beta \right)j(u+{\Omega }_{\beta })){\overline{Y}}_2(u,t)& =e^{j{\Omega }_{\beta }t \csc \left(\beta \right)}\hfill \end{array}\hfill \end{array}\right.$$

(37)

Solving the above equations yields

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\overline{Y}}_1(u,t)& =1-{\displaystyle \frac{u}{{\Omega }_{\beta }}}(e^{j{\Omega }_{\beta }t \csc \left(\beta \right)}-1)\hfill \\ \hfill {\overline{Y}}_2(u,t)& ={\displaystyle \frac{1}{j \sin \left(\beta \right){\Omega }_{\beta }}}(e^{j{\Omega }_{\beta }t \csc \left(\beta \right)}-1)\hfill \end{array}\hfill \end{array}\right.$$

(38)

By inserting (38) into (25), we obtain

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill y_1\left(t\right)& ={\displaystyle \frac{4{\sin }^2\left(\frac{{\Omega }_{\beta }t \csc \left(\beta \right)}{2}\right)}{{({\Omega }_{\beta }t \csc \left(\beta \right))}^2}}\hfill \\ \hfill y_2\left(t\right)& ={\displaystyle \frac{4{\sin }^2\left(\frac{{\Omega }_{\beta }t \csc \left(\beta \right)}{2}\right)}{{\Omega }_{\beta }^{2}t}}\hfill \end{array}\hfill \end{array}\right.$$

(39)

Using (24), we can derive (36). □

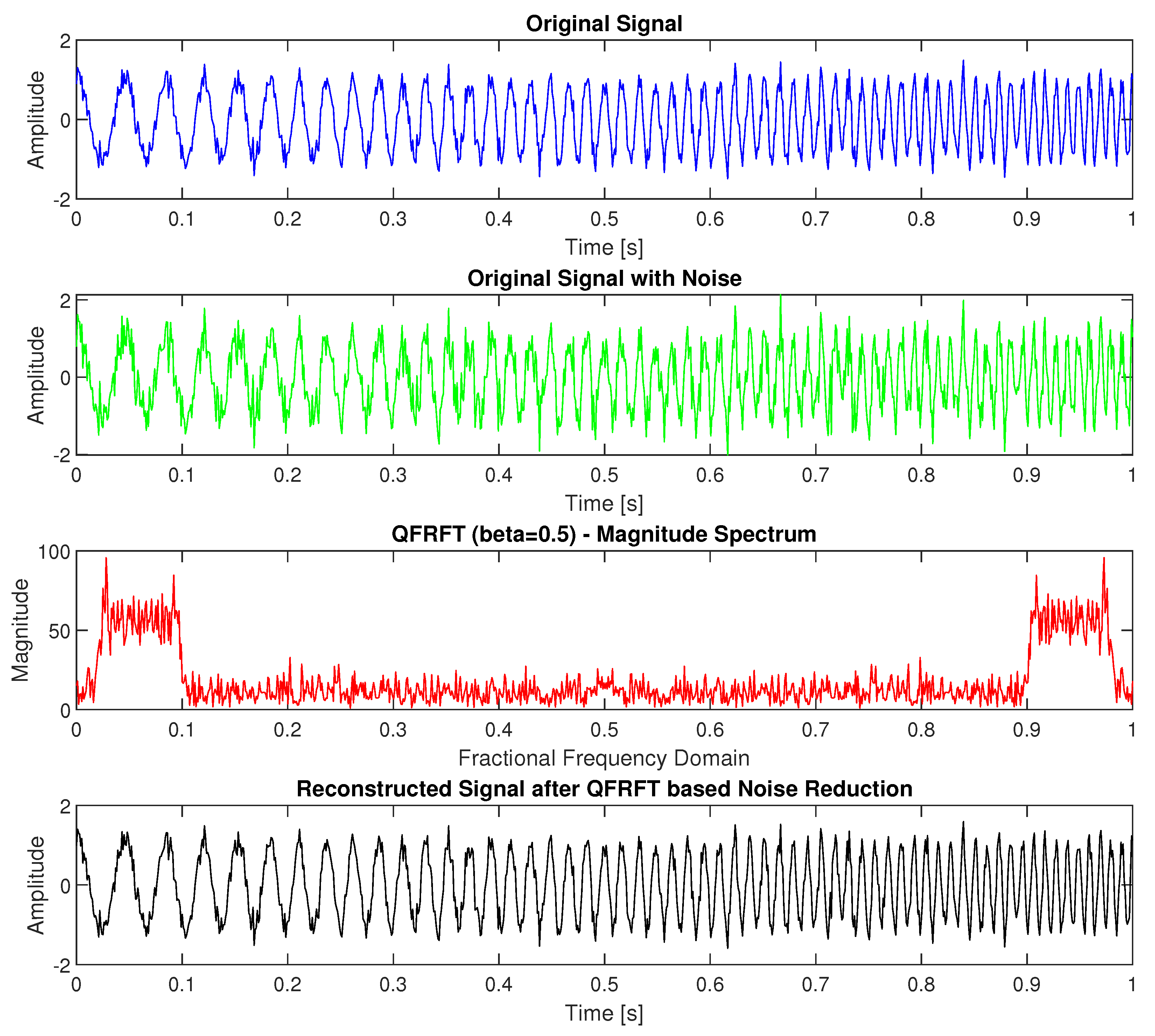
4. Case Study

This section explores the efficacy of the GSE of the QFRFT in denoising applications. Specifically, we analyze its performance in reducing stationary Gaussian noise versus non-stationary chirped noise, while also highlighting the unique advantages and limitations of the QFRFT-based approach.

The QFRFT enables a fractional rotation of the signal in the frequency domain, controlled by a rotation angle $\beta$. It is particularly suited for handling stationary noise components due to its ability to focus on specific frequency bands. For a quaternion-valued stationary Gaussian noise signal $\mathbf{x}\left(t\right)$, where the noise is represented as a quaternion with real and imaginary components, the QFRFT retains the Gaussian form in fractional domains,

$${\mathbf{x}}_{\mathrm{Gaussian}}\left(t\right)=\left[{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}{e}^{-{\displaystyle \frac{t^2}{2{\sigma }^2}}}\right]+j·\left[{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}{e}^{-{\displaystyle \frac{t^2}{2{\sigma }^2}}}\right],$$

(40)

where $\mathbf{x}\left(t\right)$ is a quaternion signal with real and imaginary components representing the stationary Gaussian noise.

For the chirped noise signals, represented by a time-dependent frequency component ${\mathbf{x}}_{\mathrm{chirp}}\left(t\right)=e^{j\pi k{t}^2}$, the QFRFT does not adapt as well. The non-stationary characteristics of chirped signals lead to incomplete suppression, as the QFRFT alone cannot capture the time-frequency variations inherent in chirped signals. The quaternion representation of this signal would be

$${\mathbf{x}}_{\mathrm{chirp}}\left(t\right)=e^{j\pi k{t}^2}+j·e^{j\pi k{t}^2}.$$

(41)

To illustrate these effects, we create a quaternion-valued signal composed of stationary Gaussian noise and non-stationary chirped noise. The combined quaternion signal is defined as

$$\mathbf{s}\left(t\right)={\mathbf{x}}_{\mathrm{Gaussian}}\left(t\right)+{\mathbf{x}}_{\mathrm{chirp}}\left(t\right),$$

(42)

where both components are quaternion-valued signals.

We apply the QFRFT to this signal at a fractional order of $\beta =0.5$, $f_s=1000$ Hz, $\Delta \left(t\right)=0.001$ s, and a signal duration of 1 s. The simulation consists of the following steps:

• Generating the original signal.
• Adding noise to the original signal.
• Applying the QFRFT-based GSE at $\beta =0.5$.
• Reconstructing the signal using the inverse IQFRFT.

The results, as shown in Figure 1, illustrate the effectiveness of the QFRFT-based GSE in filtering the noise from the signal. Additionally, the Gaussian noise was effectively attenuated, showing reduced magnitude peaks, highlighting the QFRFT’s strength in stationary noise reduction.

To quantify the effectiveness of the QFRFT-based denoising, we introduce an MSE metric. The MSE between the original signal (with noise) and the reconstructed signal is computed to measure the error reduction,

$$\mathrm{MSE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(\mathbf{s}\left(t_i\right)-{\mathbf{X}}_{\mathrm{reconstructed}}\left(t_i\right)\right)}^2$$

(43)

where N is the number of time samples, and the error term is the difference between the original and reconstructed signals at each time instant as shown in Figure 2.

The figure shows the stabilization of the MSE values over time. This indicates that the proposed method effectively reduces restoration inaccuracies as the reconstruction progresses.

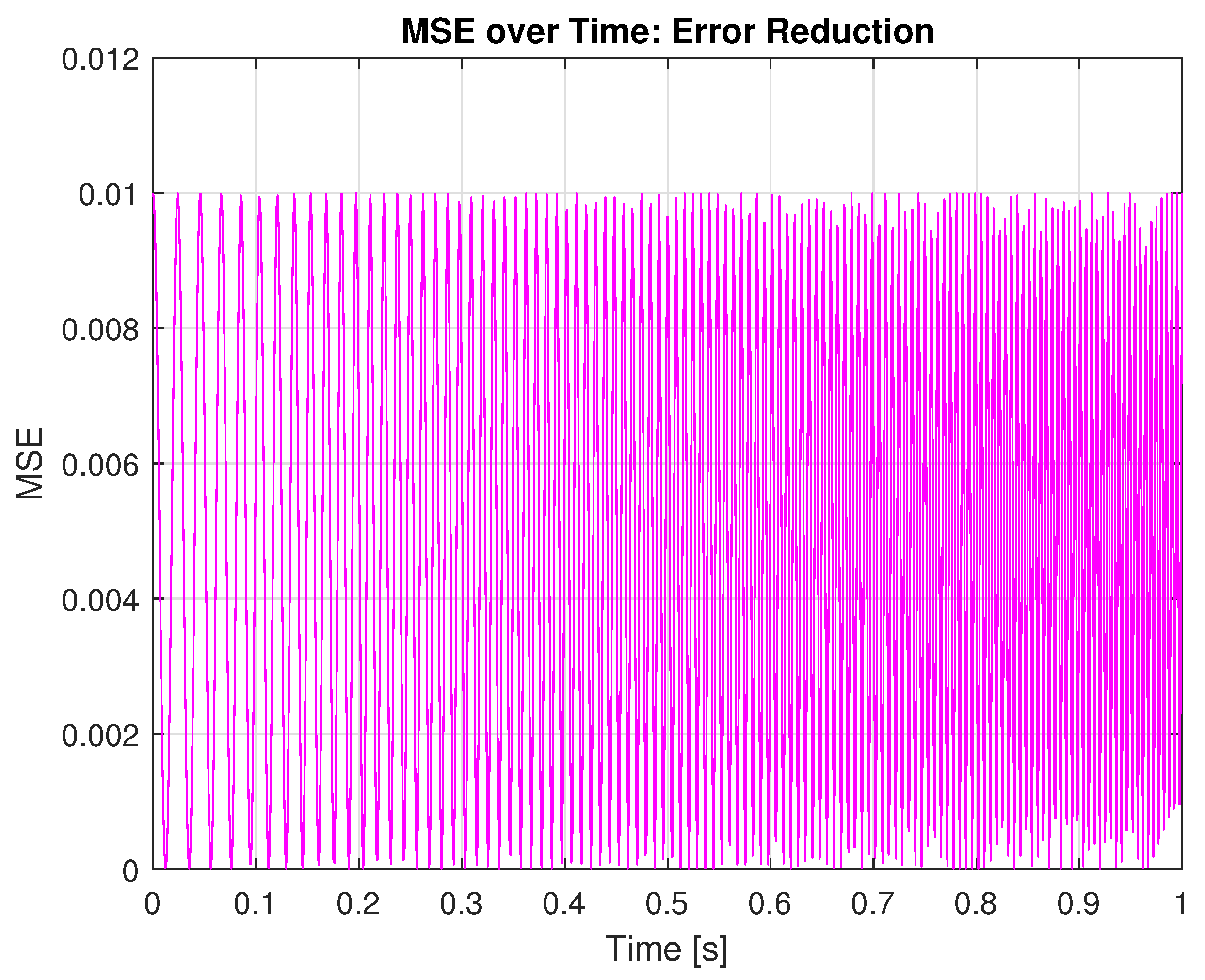
5. Discussion and Analysis

The proposed GSE builds upon the existing framework of the FRFT, extending it to the quaternion domain through the QFRFT. This extension enables the processing of multi-channel, quaternion-valued signals, offering a more comprehensive and richer representation compared to the traditional FRFT. The QFRFT’s ability to handle quaternion signals provides additional degrees of freedom, enhancing its applicability in advanced signal and image processing tasks.

The choice between FRFT and QFRFT depends on the nature of the signal and the specific application requirements. While FRFT offers flexibility in time-frequency trade-offs for single-channel signals, QFRFT extends these capabilities, accommodating multi-dimensional signals, and enabling more intricate analysis and reconstruction. This makes QFRFT particularly suited for applications that demand a balance between computational efficiency and the richness of information representation. This work underscores the potential of the QFRFT in advancing state-of-the-art methodologies for signal and image processing, providing a robust framework for future research and applications.

6. Conclusions and Future Insights

Our study introduces a robust framework for reconstructing signals from generalized sampling points, including both the signal and its derivatives, achieving efficient sub-Nyquist sampling through the GSE in the QFRFT domain. This approach not only enhances signal recovery, but also broadens the applicability of quaternion-based processing for complex, multi-dimensional data. Moreover, a denoising case study demonstrates its effectiveness in signal clarity, with the inclusion of MSE highlighting the significant improvement in signal restoration. Future work could enhance non-stationary signal handling by integrating the QFRFT with time-frequency techniques like wavelet or STFT to better capture time-varying features.