Abstract
The goal of this paper is to study the existence of a mild solution and controllability for a class of neutral stochastic differential equations (SDEs) involving the -Hilfer fractional derivatives, a generalization of the well-known Riemann–Liouville fractional derivative using almost sectorial operators. Sufficient conditions for controllability are established using the notion of measure of noncompactness (MNC) and the Mönch fixed-point theorem. An example is given to illustrate the abstract findings.
1. Introduction
Over the years, fractional differential equations (FDEs) have been extensively studied by researchers, significantly advancing the mathematical analysis of these equations. FDEs accurately represent certain natural phenomena more accurately than integer-order differential equations. This ability has increased interest and research in the field, as fractional derivatives allow for varying the order of the differential equation, which is closely linked to solving FDEs. Lately, Sousa et al. [1] introduced a fractional mathematical model based on the diffusion equation of time-fractions, which more effectively describes nutrient concentration in the blood compared with the integer-order model. Additional studies and analyses of mathematical models using FDEs can be found in [2,3,4].
Utilizing broader classes of fractional derivatives, which encompass a broad range of fractional derivatives, including the Riemann–Liouville and Caputo derivatives, offers significant advantages. Sousa et al. [5] presented the -Hilfer derivatives, which include several well-known derivatives, such as the Caputo and Riemann–Liouville derivatives. The benefit of analyzing nonlinear FDEs involving the -Hilfer derivative lies in its ability to preserve the properties investigated in FDEs with other fractional derivative operators, as detailed in [5]. Foundational studies on the existence, stability, and uniqueness properties of solutions to FDEs involving the -Hilfer (FDEs) can be found in [6,7,8].
Control theory is a crucial discipline for engineers, mathematicians, and researchers, providing the framework for developing and managing processes and systems. The range of control problems varies from straightforward scenarios like heat conduction through a rod to complex ones such as landing an aircraft on a carrier, managing a nation’s economy, or controlling epidemics. Controllability is a well-known attribute of a control system that is significant in multiple control problems in finite and infinite dimensional space. A great deal of emphasis has been focused on controllability issues for diverse, dynamic systems that are deterministic, stochastic, linear, and nonlinear.
Controllability is typically sufficient in many applications in modern science and technology. Many researchers are concerned with studying the controllability results for various dynamical systems, for instance, [9,10,11,12]. Recently, the controllability result of FDEs involving Caputo derivatives has been extensively studied. However, exploring the controllability concerning the Hilfer FDEs is still in the initial stage. In papers [13,14], researchers examined the approximate controllability of FDEs employing a fixed-point approach. Additionally, in [15,16,17], authors investigated the existence of Hilfer FDEs utilizing almost sectorial operators.
In [18], Bose and Udhayakumar focused on the controllability of the following Hilfer fractional integrodifferential equation of order and type , shown as follows,
and they proved the controllability results for the considered system via MNC.
Stochastic models should be explored instead of deterministic ones since noise and fluctuations can occur in manufactured and natural systems. Unpredictability exists in the theoretical representation of a particular occurrence in differential equations with stochastic components. For a broad introduction to stochastic differential equations and its uses, see [19,20]. In [21], Sivasankar et al. studied the existence result of the following Hilfer neutral stochastic FDEs,
where order , and type .
To the best of our knowledge, the controllability of neutral SDEs utilizing the MNC, particularly incorporating the -Hilfer FDEs with infinite delay, has yet to be addressed in the existing literature. This is the motivation of our work.
In this paper, we consider the following neutral -Hilfer stochastic FDEs in a separable Hilbert space
where , denotes the -Hilfer fractional derivatives with order and type , denotes the -Riemann–Liouville integral of order . is the state function, A represents the almost sectorial operator that produces an analytic semigroup on H. The history function defined by takes values in some phase space . Let K and U be another separable Hilbert spaces. denotes the K-valued Wiener process. The control function is a set of admissible control functions on a separable Hilbert space U, and the operator B is bounded. , and are given functions to be specified later.
2. Preliminaries and Assumptions
Let be a complete probability space, denotes a normal filtration satisfying the usual condition (i.e., right continuity and contains all -null sets of ). A stochastic process is a set of random variables . An H-valued random variable is a -measurable function .
Let be an orthonormal basis of K and be a K-valued Wiener process with finite trace nuclear covariance operator . Then there exists a bounded sequence of non-negative real numbers such that satisfying . We define where are a mutually independent one-dimensional standard Wiener process. For every we define
The term refers to a Q-Hilbert–Schmidt operator if We denote the space containing all Q-Hilbert–Schmidt operators by , where is a completion of which is a Hilbert space with respect to the norm defined by
The set of all H-valued, square integrable, strongly measurable random variables is represented by the equipped with the norm
where represents the expectation given by
Assume that , and let denotes the Banach space of all continuous functions from to with the condition .
We denote and and define
with the norm
Clearly, is a Banach space.
We discuss the abstract phase space (defined in [22]). Let be a continuous function with . The Banach space induced by the function h is described as follows:
with the norm
We define the space
with the norm
Lemma 1
([22]). Suppose then for , and ,
where .
Definition 1
([5]). Let be a positive function on such that is continuous and for all . Then, the left Ψ-Hilfer fractional derivative of order δ and type γ, is defined by
where .
Definition 2
([23]). If then a stochastic process is called a mild solution of (1), if x satisfies the following integral equation
where
and is the Wright function defined by
which satisfies the following
Definition 3
([24]). Consider and , A ∈ where is the family of closed linear operators, and A is called an almost sectorial operator on H.
- (i)
- There exists a constant such that for any
Lemma 2
([25]). The operators and have the following characteristics:
- (i)
- For fixed and are linear and bounded operators withandfor all , where and .
- (ii)
- The operators and are strongly continuous for , that is, for all and , we have
Definition 4.
Here, we discuss some of the definitions and properties of the measure of noncompactness (MNC).
Definition 5.
Suppose ℧ is the bounded set in H; then, the Hausdorff MNC χ is defined by
Lemma 3
([26]). Let H be a Hilbert space and are bounded subsets of H. Then, the following statements hold.
- is relatively compact .
- if .
- .
- For every , .
- , where .
- , where and denote the closure and convex hull of , respectively.
- If the operator is Lipschitz continuous with constant k, then for any bounded subset , where represents the Hausdorff MNC in the Banach space .
Lemma 4
([26]). If is equicontinuous and bounded, then is continuous for , and
where .
Theorem 1
([26,27]). If is a sequence of Bochner integrable functions from J→H such that for almost every and for all , where ξ, then the function , and satisfies
Lemma 5
([28]). Let ℧ be a convex and closed subset of a Banach space X and 0 . If a continuous mapping of satisfies Mönch’s condition, (i.e., is countable, and implies that is compact), then f has a fixed point in ℧.
To deal with the measure of stochastic integral terms, we need the following lemma:
Lemma 6
([29]). If for all , then the Hausdorff MNC χ satisfies
where
and is a Q-Wiener process.
Remark 1.
For in Lemma 6, we have
3. Results
To establish the main result, we need the following assumptions:
Hypothesis 1
(H1). For all bounded subsets and x,
for each fixed w.
Hypothesis 2
(H2). The function satisfies the following properties:
- (i)
- For all x and for any ν, the function is continuous and there exists s.t. and ∀ satisfies
- (ii)
- is completely continuous and for any bounded set , the set is equicontinuous in H.
Hypothesis 3
(H3). The function satisfies the following conditions:
- (i)
- is strongly measurable for every y and x. is continuous for a.e. , and is strongly measurable function.
- (ii)
- There exist integrable function ∈∈ and non-decreasing real-valued continuous function s.t.where satisfies
- (iii)
- There exists a function ∈∈ such that for each bounded subset ,for a.e. .
Hypothesis 4
(H4). The function satisfies the following conditions:
- (i)
- is strongly measurable for every is continuous for a.e. ν belong to J, and is strongly measurable function.
- (ii)
- There exists integrable function ∈∈, and non-decreasing real-valued continuous function such thatwhere satisfies
- (iii)
- There exists a function such that for each bounded subset ,for a.e. ν.
Hypothesis 5
(H5). The operator B is bounded, i.e., , where is a positive constant.
Hypothesis 6
(H6). The operator : , defined by
satisfies the following:
- (i)
- It has an inverse operator , which take the values in Ker , and there exists a positive constant such that .
- (ii)
- For and for any bounded subset , there exists s.t.
Take and .
Theorem 2.
Suppose assumptions (H1)–(H6) are satisfied, then the system (1) is controllable on J if
Proof.
Using the assumption (H6), we define the control function as
By using this control function, we show that the operator , defined by
possesses a fixed point, which is a mild solution of (1). It is trivial that . So, the system (1) is controllable on .
For , we define by
then . Set . It is trivial that x satisfies (2) if, and only if, satisfies and
where is obtained from (3) by replacing .
Let . For any , we have
and forms a Banach space.
For , define the set
The set is a convex, closed, and bounded set. For all and for all , by Lemma 1, we obtain
Similarly, Let us take .
Consider the operator defined by
Clearly, the existence of a fixed point of the operator is equivalent to the existence of a fixed point of the operator . We prove that has a fixed point. We divide the proof into several steps:
Step 1. There exists such that . Suppose that the condition is not true; then, for all , there exists such that , i.e., . From (7), we have
where
By dividing Equation (8) from both sides with and applying the limit , we obtain , which is a contradiction. Therefore, .
Step 2. The operator is continuous on .
For any with , we have
Using assumption (H2), we obtain
Take
Then, by the dominated convergence theorem with assumption (H2), we get
Using (H3), we obtain
We assume that
Using the dominated convergence theorem together with (H3), we obtain
Using (H5), we obtain
Define
Using the dominated convergence theorem together with (H3), we obtain
and
From (3), we obtain
Using (10)–(12), the above inequality converges to zero as .
Step 3. To prove is equicontinuous, we take and , then we have
By the strong continuity of the operators and and the dominated convergence theorem, we find that
Hence, is equicontinuous on .
Step 4. The Mönch’s statement is true.
Let , where
Let be countable and We show that .
Suppose . We have to show that is relatively compact in H for all . Using Theorem 1, we obtain
where
Using Theorem 1 and the assumptions (H2)–(H4), we obtain
Also, we have
where
Using Lemma 4, we have
Therefore, from Mönch’s condition we have
which implies that . Hence, is relatively compact.
4. Applications
4.1. Application 1
Consider the following -Hilfer fractional differential equation given by
where denotes the -Hilfer fractional derivative with order and type . denotes the -Riemann–Liouville integral of order . and are continuous functions. In addition, is continuous and satisfies specific smoothness criteria, and , and are the appropriate functions. The filtered probability space represents the one-dimensional Brownian motion in K, which is denoted as . is the control function in Hilbert space U.
To change the system into an abstract form, let be endowed with the norm, and is defined as with
and
where is the orthogonal set of eigen vectors of A.
Here, A is the infinitesimal generator of analytic semigroup on H. is not a compact semigroup on H with , where denotes the Hausdorff measure of noncompactness and ∃ s.t. . Also, is equicontinuous, , and .
4.2. Application 2
The -Hilfer stochastic fractional differential equation is a useful tool for systems affected by stochastic noise since it expands the traditional -Hilfer fractional differential equations to incorporate random effects. In addition to modeling uncertainties and random perturbations, which are inherent in digital signal processing, these equations incorporate the memory and heredity features of fractional calculus.
Stochastic fractional differential equations are used in digital filter systems to create sophisticated filtering mechanisms for signals impacted by stochastic noise. This is especially helpful in communication systems, control systems, and biomedical signal processing, where noise and unpredictability have a big impact on signal quality. When a signal is distorted or corrupted by noise, signal restoration techniques can be employed to recover the original signal. For instance, sound recordings produced by certain equipment may contain noise and one common approach to restoring the signal is to apply filters, often using convolution. When it comes to stochastic systems, the distortion can be explained by the existence of a random noise term, which is usually modeled as white noise or a Wiener process. Thus, a stochastic differential equation can be used to model the signal restoration process.
Motivated by the filter system presented in [30,31,32], we describe the digital filter system corresponding to the mild solution in (1).
The -Hilfer stochastic fractional differential equation governing the filter can be expressed as defined in (1), where x is the output signal (filtered signal), the function represents the stochastic effect of noise, and is the controller. The mild solution of differential Equation (1) is given as
In this solution (14), the deterministic integral component captures the low-frequency signal, while the stochastic integral term represents the effect of random noise, allowing for adaptive filtering.
Figure 1 describes the following:
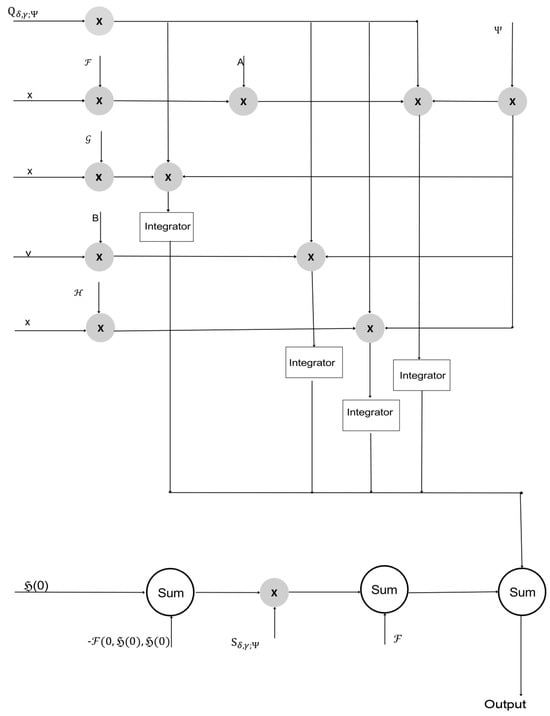
Figure 1.
Filter system model.
- Product modulator 1 accepts the input and produces the output .
- Product modulator 2 accepts the input and A, and produces the output .
- Product modulator 3 accepts the input and and produces the output .
- Product modulator 4 accepts the input and -function and obtains the output .
- Product modulator 5 accepts the input and produces the output .
- Product modulator 6 accepts the input and and produces the output .
- Product modulator 7 accepts the input and -function, and obtains the output .
- Product modulator 8 accepts the input and B, and produces the output .
- Product modulator 9 accepts the input and and produces the output .
- Product modulator 10 accepts the input and -function and obtains the output .
- Product modulator 11 accepts the input and produces the output .
- Product modulator 12 accepts the input and and produces the output .
- Product modulator 13 accepts the input and -function and obtains the output .
- Product modulator 14 accepts and at time and produces .
- The integrators execute the following value,and produce the integral value over the period .
Finally, all outputs from the integrators are directed to the summer network, resulting in the output , which is bounded and approximately controllable.
5. Conclusions
In this article, we studied the controllability results of fractional stochastic neutral differential equations involving -Hilfer FDEs with infinite delay using the measure of noncompactness. Sufficient conditions for the controllability of -Hilfer fractional stochastic differential equations were obtained by using weak compactness criteria, appropriate assumptions, the theory of semigroups of bounded linear operators, and Mönch’s fixed-point theorem via a measure of noncompactness.
Further, these results can be extended to study the approximate controllability of the Hilfer fractional differential equation in an infinite dimensional state space. We plan to examine the controllability of -Hilfer FDEs with infinite delay using the concept of the measure of noncompactness.
Author Contributions
A.R., J.A. and F.A.K. conceptualized the study; A.R. and A.K. supervised the study; E.A. and F.M.A. were responsible for formal analysis; A.R. and J.A. wrote the original draft; F.M.A. Khan, A.A., E.A. and F.M.A. were responsible for the funding acquisition of the study; A.R., J.A. and A.K. conducted the writing—review and editing; A.R., F.A.K., E.A. and A.A. performed the investigation of study; A.A. and F.M.A. were responsible for project administration. All authors have read and agreed to the published version of the manuscript.
Funding
The first author acknowledges the Science and Engineering Research Board (SERB), India, for providing financial support through MATRICS research project with reference no. MTR/2023/000060.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sousa, J.V.D.C.; De Oliveira, E.C.; Magna, L.A. Fractional calculus and the ESR test. arXiv 2016, arXiv:1701.07379. [Google Scholar]
- Kumar, S.; Kumar, A.; Odibat, Z.M. A nonlinear fractional model to describe the population dynamics of two interacting species. J. Am. Math. Soc. 2017, 40, 4134–4148. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P.K. A mathematical model on fractional Lotka-Volterra equations. J. Theoret. Biol. 2011, 277, 1–6. [Google Scholar] [CrossRef]
- Dipierro, S.; Valdinoci, E. A simple mathematical model inspired by the Purkinje cells: From delayed travelling waves to fractional diffusion. Bull. Math. Biol. 2018, 80, 1849–1870. [Google Scholar] [CrossRef] [PubMed]
- Sousa, J.V.D.C.; De Oliveira, E.C. On the ψ-Hilfer fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; De Oliveira, E.C. A Gronwall inequality and the Cauchy-type problem by means of Ψ-Hilfer operator. arXiv 2017, arXiv:1709.03634. [Google Scholar]
- Kucche, D.K.; Mali, D.A.; Sousa, J.V.D.C. On the nonlinear Ψ-Hilfer fractional differential equations. Comput. Appl. Math. 2019, 38, 73. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; Kucche, K.D.; De Oliveira, E.C. Stability of ψ-Hilfer impulsive fractional differential equations. Appl. Math. Lett. 2019, 88, 73–80. [Google Scholar] [CrossRef]
- Mahmudov, N.I. Approximate controllability of semilinear deterministic and stochastic evolution equations in abstract spaces. SIAM J. Control Optim. 2003, 42, 1604–1622. [Google Scholar] [CrossRef]
- Mahmudov, N.I. Finite-approximate controllability of fractional evolution equations: Variational approach. Fract. Calc. Appl. Anal. 2018, 21, 919–936. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Zorlu, S. Approximate controllability of fractional integro-differential equations involving nonlocal initial conditions. Bound. Value Probl. 2013, 2013, 118. [Google Scholar] [CrossRef][Green Version]
- Chang, Y.K.; Pereira, A.; Ponce, R. Approximate controllability for fractional differential equations of Sobolev type via properties on resolvent operators. Fract. Calc. Appl. Anal. 2017, 20, 963–987. [Google Scholar] [CrossRef]
- Dineshkumar, C.; Udhayakumar, R.; Vijayakumar, V.; Shukla, A.; Nisar, K.S. Results on approximate controllability of neutral integro-differential stochastic system with state-dependent delay. Numer. Methods Partial Differ. Equ. 2024, 40, e22698. [Google Scholar] [CrossRef]
- Dineshkumar, C.; Udhayakumar, R. New results concerning to approximate controllability of Hilfer fractional neutral stochastic delay integro-differential systems. Numer. Methods Partial Differ. Equ. 2021, 37, 1072–1090. [Google Scholar] [CrossRef]
- Kavitha, K.; Vijayakumar, V.; Udhayakumar, R. Results on controllability of Hilfer fractional neutral differential equations with infinite delay via measures of noncompactness. Chaos Solitons Fractals 2020, 139, 110035. [Google Scholar] [CrossRef]
- Zhou, M.; Li, C.; Zhou, Y. Existence of mild solutions for Hilfer fractional evolution equations with almost sectorial operators. Axioms 2022, 11, 144. [Google Scholar] [CrossRef]
- Bedi, P.; Kumar, A.; Abdeljawad, T.; Khan, Z.A.; Khan, A. Existence and approximate controllability of Hilfer fractional evolution equations with almost sectorial operators. Adv. Differ. Equ. 2020, 2020, 615. [Google Scholar] [CrossRef]
- Bose, C.V.; Udhayakumar, R. Analysis on the controllability of Hilfer fractional neutral differential equations with almost sectorial operators and infinite delay via measure of noncompactness. Qual. Theory Dyn. Syst. 2023, 22, 22. [Google Scholar] [CrossRef]
- Sivasankar, S.; Udhayakumar, R. A note on approximate controllability of second-order neutral stochastic delay integro-differential evolution inclusions with impulses. Math. Methods Appl. Sci. 2022, 45, 6650–6676. [Google Scholar] [CrossRef]
- Boudaoui, A.; Slama, A. Approximate controllability of nonlinear fractional impulsive stochastic differential equations with nonlocal conditions and infinite delay. Nonlinear Dyn. Syst. Theory. 2016, 16, 35–48. [Google Scholar]
- Sivasankar, S.; Udhayakumar, R.; Muthukumaran, V.; Gokul, G.; Al-Omari, S. Existence of Hilfer fractional neutral stochastic differential systems with infinite delay. Bull. Karaganda Univ. Math. Ser. 2024, 113, 174–193. [Google Scholar] [CrossRef]
- Chang, Y.K. Controllability of impulsive functional differential systems with infinite delay in Banach spaces. Chaos Solitons Fractals 2007, 22, 22. [Google Scholar] [CrossRef]
- Gu, H.; Trujillo, J.J. Existence of mild solution for evolution equation with Hilfer fractional derivative. Appl. Math. Comput. 2015, 257, 344–354. [Google Scholar] [CrossRef]
- Periago, F.; Straub, B. A functional calculus for almost sectorial operators andapplications to abstract evolution equations. J. Evol. Equ. 2002, 2, 41–68. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiao, F. Existence of mild solutions for fractional neutral evolution equations. Comput. Math. Appl. 2010, 59, 1063–1077. [Google Scholar] [CrossRef]
- Banaś, J. On measures of noncompactness in Banach spaces. Comment. Math. Univ. Carolin. 1980, 21, 131–143. [Google Scholar]
- Wang, J.; Fan, Z.; Zhou, Y. Nonlocal controllability of semi linear dynamic systems with fractional derivative in Banach spaces. J. Optim. Theory Appl. 2012, 154, 292–302. [Google Scholar] [CrossRef]
- Mönch, H. Boundary value problems for nonlinear ordinary differential equations of second order in Banach spaces. Nonlinear Anal. 1980, 4, 985–999. [Google Scholar] [CrossRef]
- Shu, L.; Shu, X.B.; Mao, J. Approximate controllability and existence of mild solutions for Riemann-Liouville fractional stochastic evolution equations with nonlocal conditions of order 1< α < 2. Fract. Calc. Appl. Anal. 2019, 22, 1086–1112. [Google Scholar]
- Chandra, A.; Chattopadhyay, S. Design of hardware efficient FIR filter: A review of the state-of-the-art approaches. Eng. Sci. Technol. Int. J. 2016, 19, 212–226. [Google Scholar] [CrossRef]
- Dineshkumar, C.; Udhayakumar, R.; Vijayakumar, V.; Nisar, K.S. A discussion on the approximate controllability of Hilfer fractional neutral stochastic integro-differential systems. Chaos Solitons Fractals 2020, 142, 110472. [Google Scholar] [CrossRef]
- Zahoor, S.; Naseem, S.; Meng, W. Design and implementation of an efficient FIR digital filter. Cogent Eng. 2017, 4, 1323373. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).