Discovery of Intrinsic Ferromagnetism Induced by Memory Effects in Low-Dimensional System
Abstract
1. Introduction
2. Theory of Magnetic Respond Induced by Fractional Temporal Derivatives
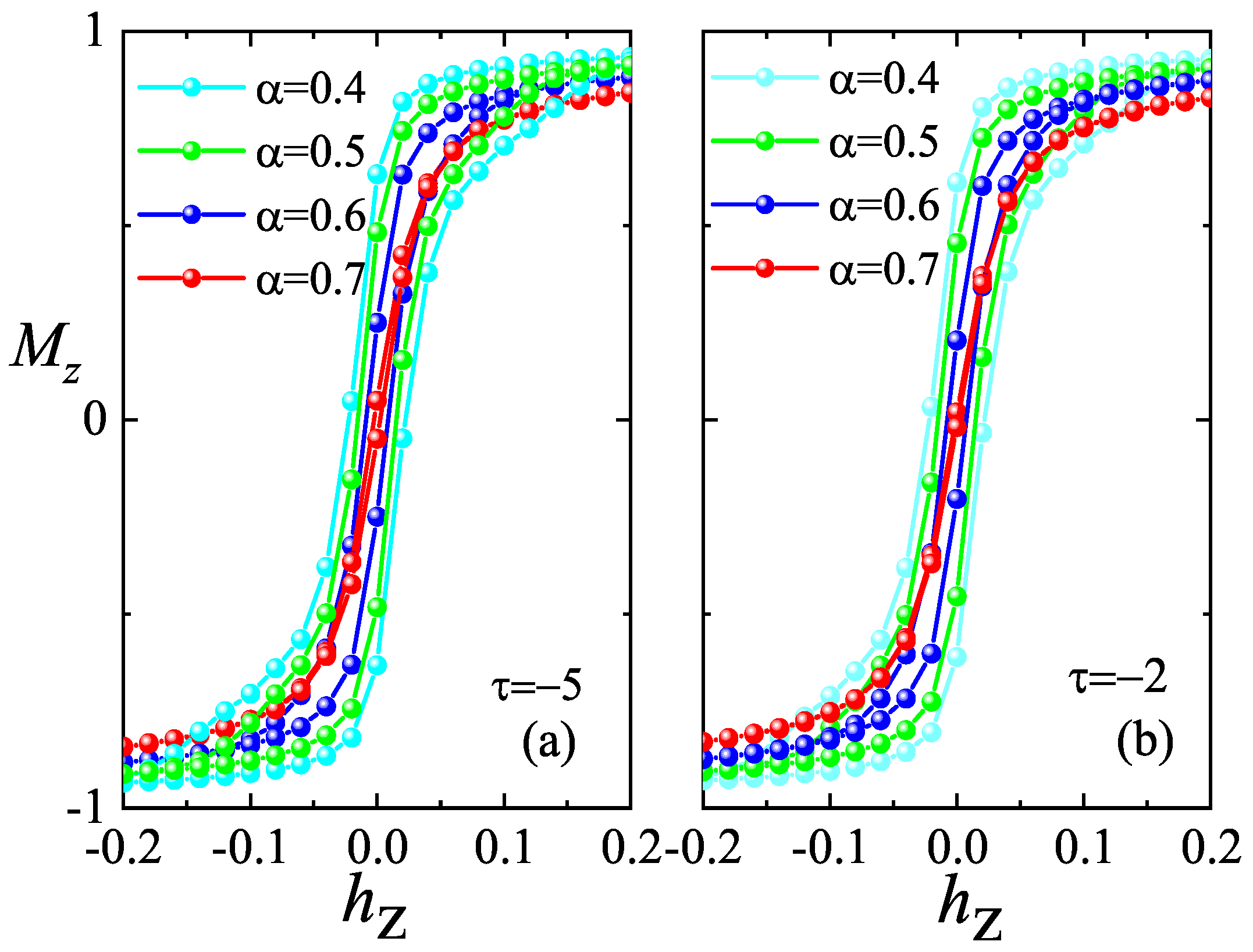
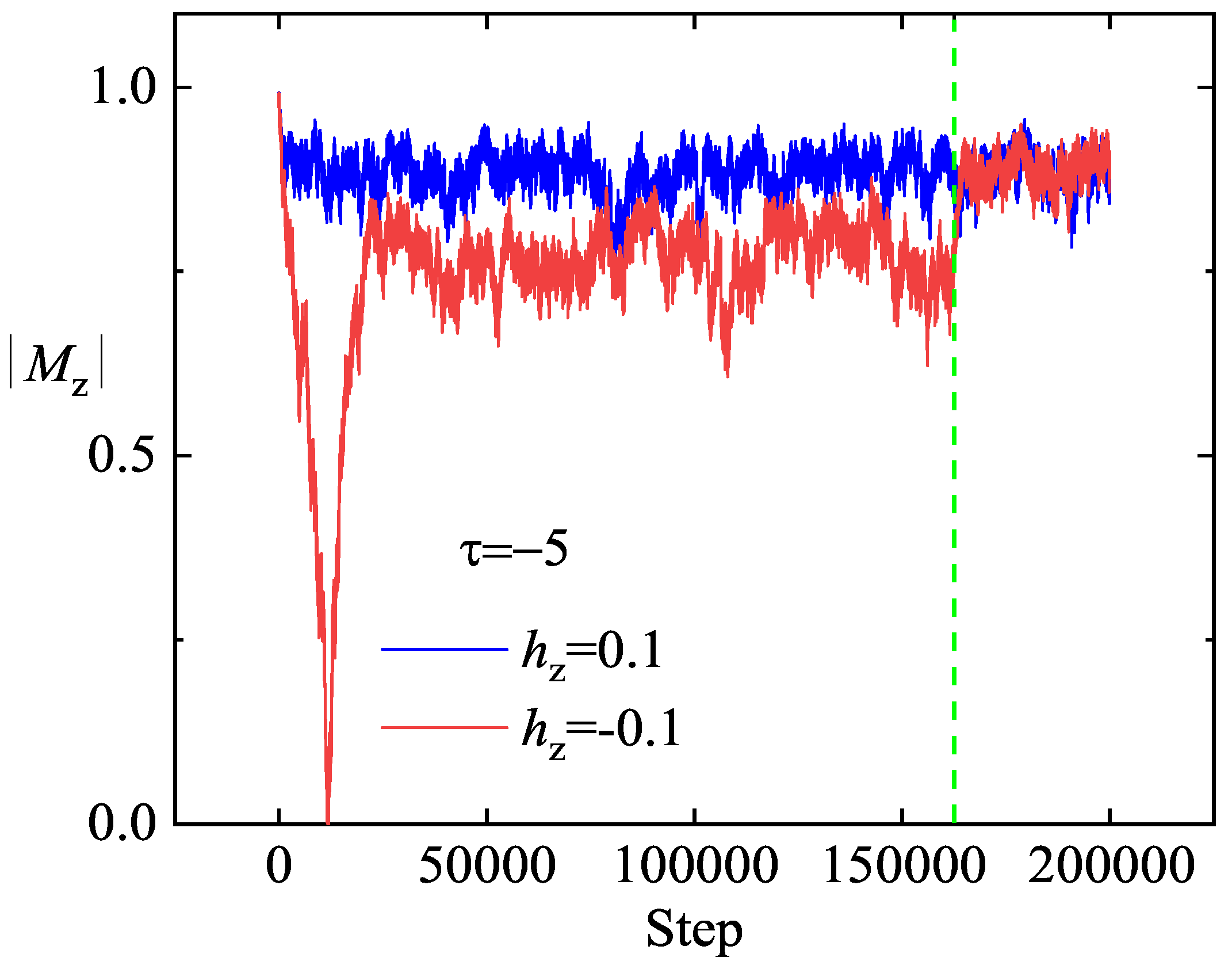
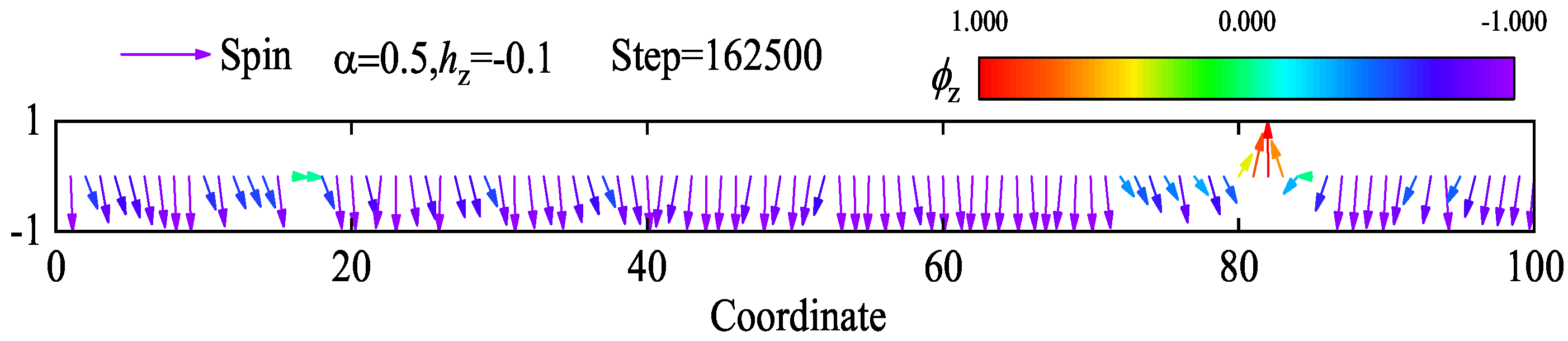
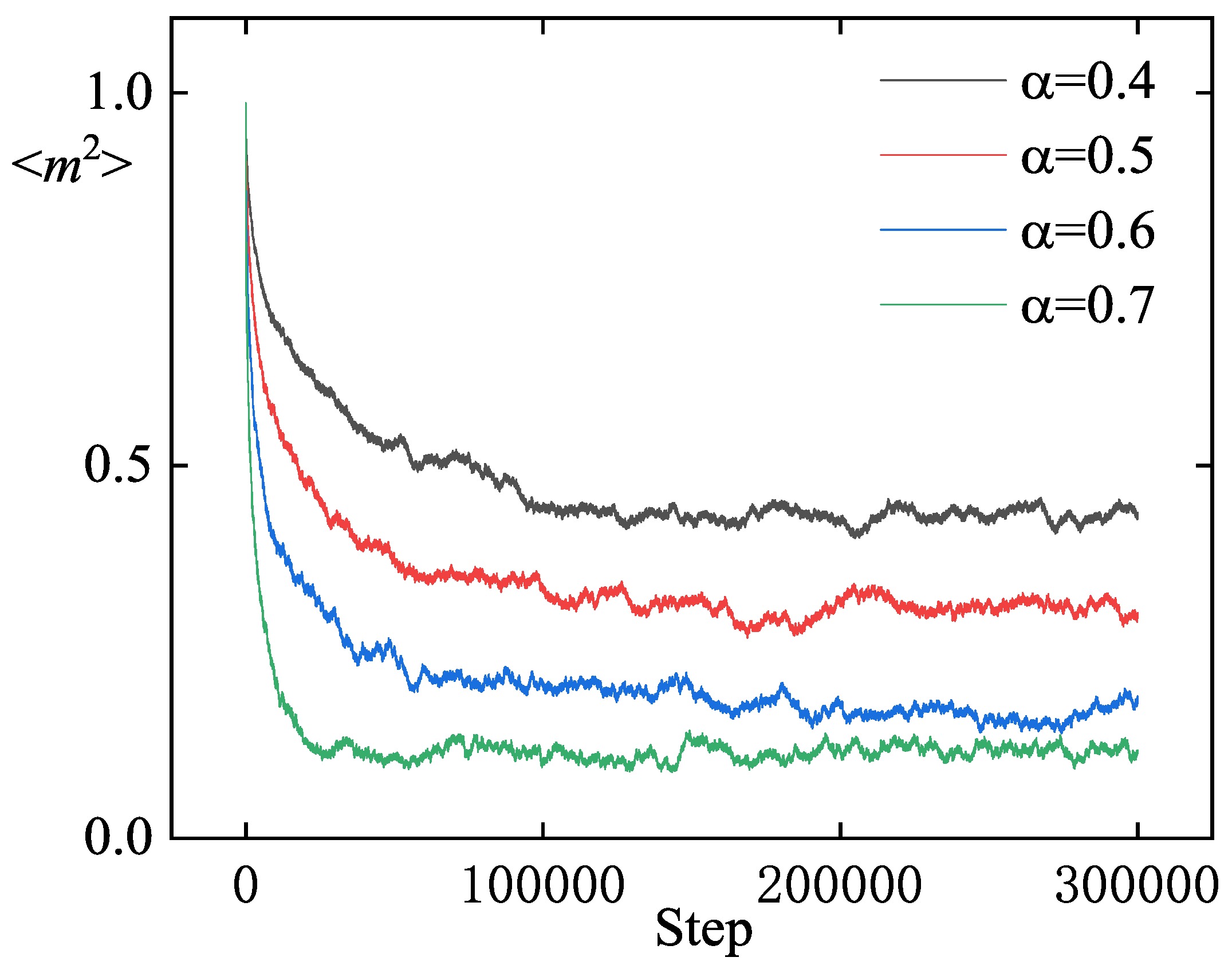
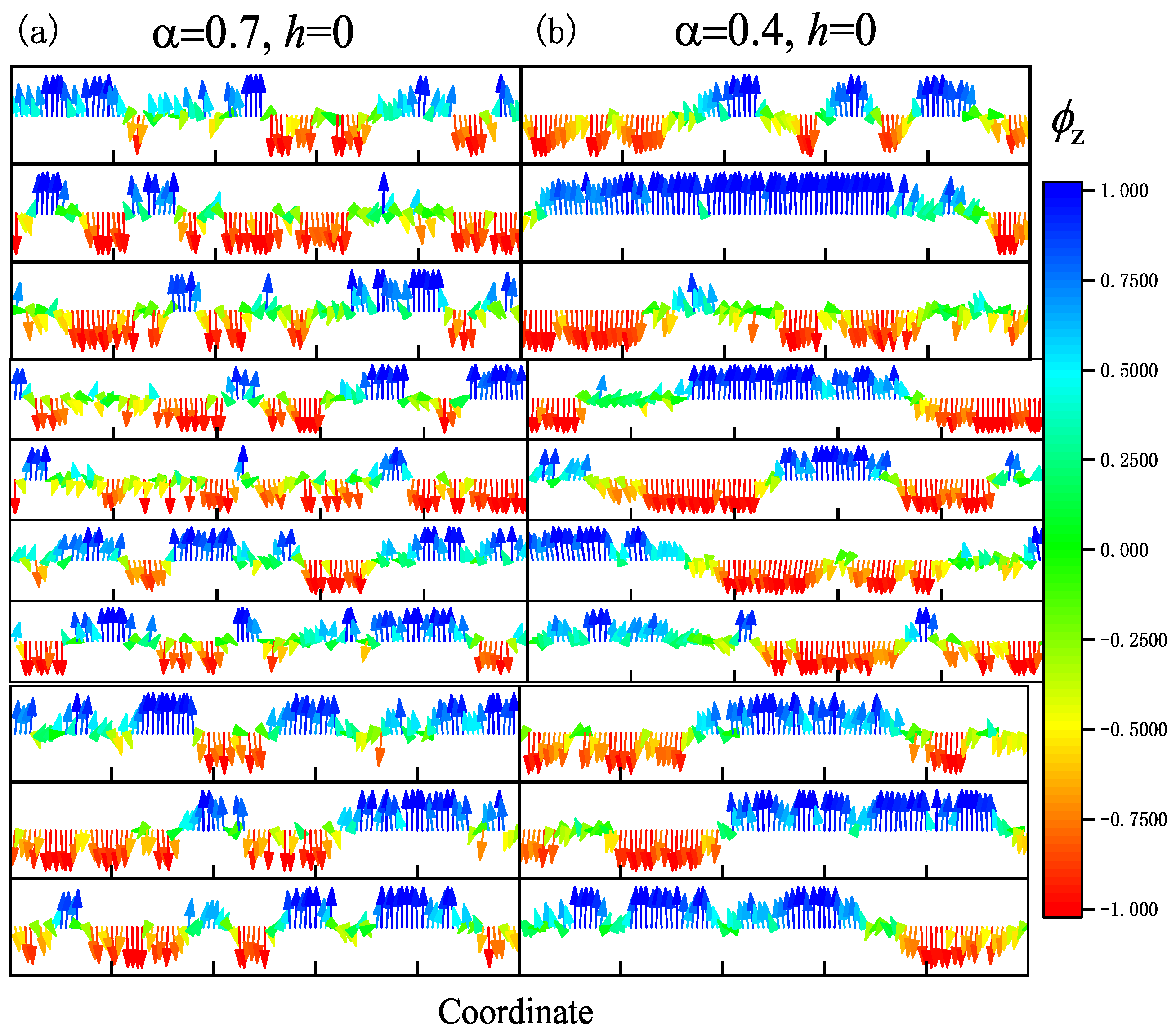
3. Simulation of Continuous Symmetry Landau–Ginzburg Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, K. Introduction to Statistical Physics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar] [CrossRef]
- Lemme, M.C.; Li, L.J.; Palacios, T.; Schwierz, F. Two-dimensional materials for electronic applications. Mrs Bull. 2014, 39, 711–718. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Perkins, D.H. Introduction to High Energy Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hinrichsen, H. Non-equilibrium phase transitions. Phys. A Stat. Mech. Its Appl. 2006, 369, 1–28. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Cugliandolo, L.F.; Kurchan, J.; Mézard, M. Out of equilibrium dynamics in spin-glasses and other glassy systems. Spin Glas. Random Fields 1998, 12, 161. [Google Scholar]
- Bouchaud, J.P.; Dupuis, V.; Hammann, J.; Vincent, E. Separation of time and length scales in spin glasses: Temperature as a microscope. Phys. Rev. B 2001, 65, 024439. [Google Scholar] [CrossRef]
- Zeng, S.; Zhong, F. Theory of critical phenomena with long-range temporal interaction. Phys. Scr. 2023, 98, 075017. [Google Scholar] [CrossRef]
- Sperstad, I.B.; Stiansen, E.B.; Sudbø, A. Quantum criticality in spin chains with non-Ohmic dissipation. Phys. Rev. B 2012, 85, 214302. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Keim, N.C.; Paulsen, J.D.; Zeravcic, Z.; Sastry, S.; Nagel, S.R. Memory formation in matter. Rev. Mod. Phys. 2019, 91, 035002. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Preface. In Theory and Applications of Fractional Differential Equations; Kilbas, A.A., Srivastava, H.M., Trujillo, J.J., Eds.; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, pp. vii–x. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Adelman, S.A. Fokker–Planck equations for simple non-Markovian systems. J. Chem. Phys. 1976, 64, 124–130. [Google Scholar] [CrossRef]
- Jeon, J.H.; Metzler, R. Fractional Brownian motion and motion governed by the fractional Langevin equation in confined geometries. Phys. Rev. E 2010, 81, 021103. [Google Scholar] [CrossRef]
- González-Herrero, H.; Gómez-Rodríguez, J.M.; Mallet, P.; Moaied, M.; Palacios, J.J.; Salgado, C.; Ugeda, M.M.; Veuillen, J.Y.; Yndurain, F.; Brihuega, I. Atomic-scale control of graphene magnetism by using hydrogen atoms. Science 2016, 352, 437–441. [Google Scholar] [CrossRef]
- Telford, E.J.; Chica, D.G.; Ziebel, M.E.; Xie, K.; Manganaro, N.S.; Huang, C.Y.; Cox, J.; Dismukes, A.H.; Zhu, X.; Walsh, J.P.S.; et al. Designing Magnetic Properties in CrSBr through Hydrostatic Pressure and Ligand Substitution. Adv. Phys. Res. 2023, 2, 2300036. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, J.; Wu, H.; Yang, L.; Jin, W.; Zhang, W.; Chang, H. Field-free room-temperature modulation of magnetic bubble and stripe domains in 2D van der Waals ferromagnetic Fe3GaTe2. Appl. Phys. Lett. 2023, 123, 101901. [Google Scholar] [CrossRef]
- Yao, Y.; Zhivulin, V.; Zykova, A.; Cherkasova, N.; Vinnik, D.; Trofimov, E.; Gudkova, S.; Zaitseva, O.; Taskaev, S.; Alyabyeva, L.; et al. High entropy BaFe12-x(Ti/Mn/Ga/In)xO19 (x = 1–7) oxides: Correlation of the composition, entropy state, magnetic characteristics, and terahertz properties. Ceram. Int. 2023, 49, 31549–31558. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Vinnik, D.A.; Starikov, A.Y.; Zhivulin, V.E.; Astapovich, K.A.; Turchenko, V.A.; Zubar, T.I.; Trukhanov, S.V.; Kohout, J.; Kmječ, T.; Yakovenko, O.; et al. Changes in the Structure, Magnetization, and Resistivity of BaFe12–xTixO19. ACS Appl. Electron. Mater. 2021, 3, 1583–1593. [Google Scholar] [CrossRef]
- Gambardella, P.; Dallmeyer, A.; Maiti, K.; Malagoli, M.; Eberhardt, W.; Kern, K.; Carbone, C. Ferromagnetism in one-dimensional monatomic metal chains. Nature 2002, 416, 301–304. [Google Scholar] [CrossRef]
- Fisher, M.E.; Ma, S.k.; Nickel, B.G. Critical Exponents for Long-Range Interactions. Phys. Rev. Lett. 1972, 29, 917–920. [Google Scholar] [CrossRef]
- Nair, R.; Sepioni, M.; Tsai, I.L.; Lehtinen, O.; Keinonen, J.; Krasheninnikov, A.V.; Thomson, T.; Geim, A.; Grigorieva, I. Spin-half paramagnetism in graphene induced by point defects. Nat. Phys. 2012, 8, 199–202. [Google Scholar] [CrossRef]
- Červenka, J.; Katsnelson, M.; Flipse, C. Room-temperature ferromagnetism in graphite driven by two-dimensional networks of point defects. Nat. Phys. 2009, 5, 840–844. [Google Scholar] [CrossRef]
- Taroni, A.; Bramwell, S.T.; Holdsworth, P.C.W. Universal window for two-dimensional critical exponents. J. Phys. Condens. Matter 2008, 20, 275233. [Google Scholar] [CrossRef]
- Wang, Q.H.; Bedoya-Pinto, A.; Blei, M.; Dismukes, A.H.; Hamo, A.; Jenkins, S.; Koperski, M.; Liu, Y.; Sun, Q.C.; Telford, E.J.; et al. The Magnetic Genome of Two-Dimensional van der Waals Materials. ACS Nano 2022, 16, 6960–7079. [Google Scholar] [CrossRef]
- Jin, B. Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Hoffmann, K.; Tang, Q. Ginzburg-Landau Phase Transition Theory and Superconductivity; International Series of Numerical Mathematics; Birkhäuser Basel: Basel, Switzerland, 2012. [Google Scholar]
- Cardy, J. Scaling and Renormalization in Statistical Physics; Cambridge University Press: Cambridge, UK, 1996; Volume 5. [Google Scholar]
- Diethelm, K.; Ford, N. The analysis of fractional differential equations. In Lecture Notes in Mathematics; Springer Nature: Berlin, Germany, 2010; Volume 2004. [Google Scholar]
- Samraiz, M.; Mehmood, A.; Iqbal, S.; Naheed, S.; Rahman, G.; Chu, Y.M. Generalized fractional operator with applications in mathematical physics. Chaos Solitons Fractals 2022, 165, 112830. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Milici, C.; Drăgănescu, G.; Machado, J.T. Introduction to Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2018; Volume 25. [Google Scholar]
- Thiel, L.; Wang, Z.; Tschudin, M.A.; Rohner, D.; Gutiérrez-Lezama, I.; Ubrig, N.; Gibertini, M.; Giannini, E.; Morpurgo, A.F.; Maletinsky, P. Probing magnetism in 2D materials at the nanoscale with single-spin microscopy. Science 2019, 364, 973–976. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, S.; Wan, X.; Hu, Y.; Tan, S.; Wang, B. Discovery of Intrinsic Ferromagnetism Induced by Memory Effects in Low-Dimensional System. Fractal Fract. 2024, 8, 668. https://doi.org/10.3390/fractalfract8110668
Zeng S, Wan X, Hu Y, Tan S, Wang B. Discovery of Intrinsic Ferromagnetism Induced by Memory Effects in Low-Dimensional System. Fractal and Fractional. 2024; 8(11):668. https://doi.org/10.3390/fractalfract8110668
Chicago/Turabian StyleZeng, Shaolong, Xuejin Wan, Yangfan Hu, Shijing Tan, and Biao Wang. 2024. "Discovery of Intrinsic Ferromagnetism Induced by Memory Effects in Low-Dimensional System" Fractal and Fractional 8, no. 11: 668. https://doi.org/10.3390/fractalfract8110668
APA StyleZeng, S., Wan, X., Hu, Y., Tan, S., & Wang, B. (2024). Discovery of Intrinsic Ferromagnetism Induced by Memory Effects in Low-Dimensional System. Fractal and Fractional, 8(11), 668. https://doi.org/10.3390/fractalfract8110668




