The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise
Abstract
1. Introduction
2. Preliminaries
3. Averaging Principle
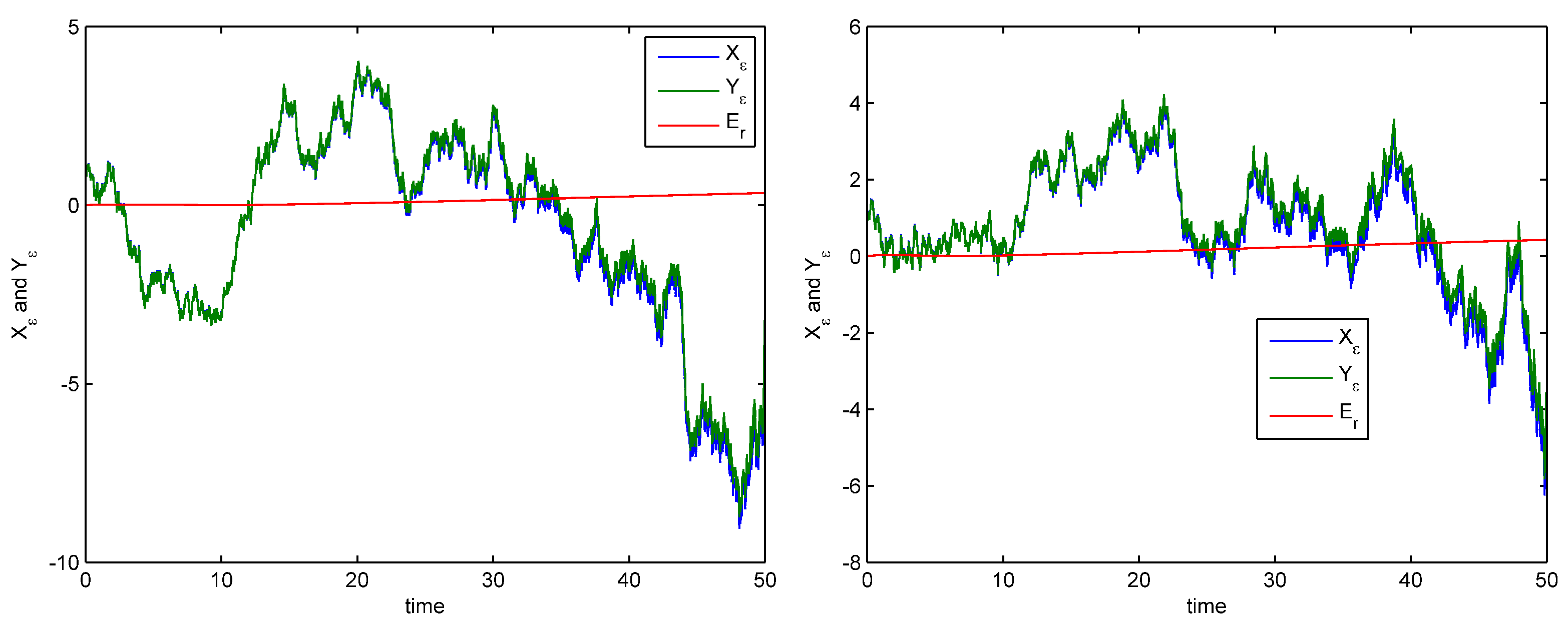
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, W.; Xu, W.; Zhang, S. The averaging principle for stochastic differential equations with Caputo fractional derivative. Appl. Math. Lett. 2019, 93, 79–84. [Google Scholar] [CrossRef]
- Guo, Z.; Hu, J.; Yuan, C. Averaging principle for a type of Caputo fractional stochastic differential equations. Chaos 2021, 31, 053123. [Google Scholar] [CrossRef] [PubMed]
- Gao, P. Averaging principle for multiscale stochastic reaction-diffusion-advection equations. Math. Methods Appl. Sci. 2019, 42, 1122–1150. [Google Scholar] [CrossRef]
- Luo, D.; Zhu, Q.; Zhang, Z. An averaging principle for stochastic fractional differential equations with time-delays. Appl. Math. Lett. 2020, 105, 106290. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Zhu, Q. The averaging principle of Hilfer fractional stochastic delay differential equations with Poisson jumps. Appl. Math. Lett. 2021, 112, 106755. [Google Scholar] [CrossRef]
- Xu, W.; Xu, W. An effective averaging theory for fractional neutral stochastic equations of order 0<α<1 with Poisson jumps. Appl. Math. Lett. 2020, 106, 106344. [Google Scholar]
- Xu, W.; Xu, W.; Lu, K. An averaging principle for stochastic differential equations of fractional order 0<α<1. Fract. Calc. Appl. Anal. 2020, 23, 908–919. [Google Scholar]
- Li, M.; Wang, J. The existence and averaging principle for Caputo fractional stochastic delay differential systems. Fract. Calc. Appl. Anal. 2023, 26, 893–912. [Google Scholar] [CrossRef]
- Wang, Q.; Han, Z.; Zhang, X.; Yang, Y. Dynamics of the delay-coupled bubble system combined with the stochastic term. Chaos Solitons Fractals 2021, 148, 111053. [Google Scholar] [CrossRef]
- Xiao, G.; Fečkan, M.; Wang, J. On the averaging principle for stochastic differential equations involving Caputo fractional derivative. Chaos 2022, 32, 101105. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q. Stability of stochastic differential equations with Lévy noise. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 5211–5216. [Google Scholar]
- Xu, Y.; Duan, J.; Xu, W. An averaging principle for stochastic dynamical systems with Lévy noise. Physica D 2011, 240, 1395–1401. [Google Scholar] [CrossRef]
- Shen, G.; Xu, W.; Wu, J. An averaging principle for stochastic differential delay equations driven by time-changed Lévy noise. Acta Math. Sci. 2022, 42, 540–550. [Google Scholar] [CrossRef]
- Shen, G.; Xiao, R.; Yin, X. Averaging principle and stability of hybrid stochastic fractional differential equations driven by Lévy noise. Int. J. Syst. Sci. 2020, 51, 2115–2133. [Google Scholar] [CrossRef]
- Xu, W.; Duan, J.; Xu, W. An averaging principle for fractional stochastic differential equations with Lévy noise. Chaos 2020, 30, 083126. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Fu, H.; Wang, W. An averaging principle for caputo fractional stochastic differential equations with compensated Poisson random measure. J. Partial. Differ. Equ. 2022, 35, 1–10. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Umamaheswari, P.; Balachandran, K.; Annapoorani, N. Existence and stability results for Caputo fractional stochastic differential equations with Lévy noise. Filomat 2020, 34, 1739–1751. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Application, 2nd ed.; Horwood Publishing Limited: Chichester, UK, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, L.; Xiao, G. The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal Fract. 2024, 8, 595. https://doi.org/10.3390/fractalfract8100595
Ren L, Xiao G. The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal and Fractional. 2024; 8(10):595. https://doi.org/10.3390/fractalfract8100595
Chicago/Turabian StyleRen, Lulu, and Guanli Xiao. 2024. "The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise" Fractal and Fractional 8, no. 10: 595. https://doi.org/10.3390/fractalfract8100595
APA StyleRen, L., & Xiao, G. (2024). The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal and Fractional, 8(10), 595. https://doi.org/10.3390/fractalfract8100595




