Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis
Abstract
1. Introduction
2. Samples and Methodology
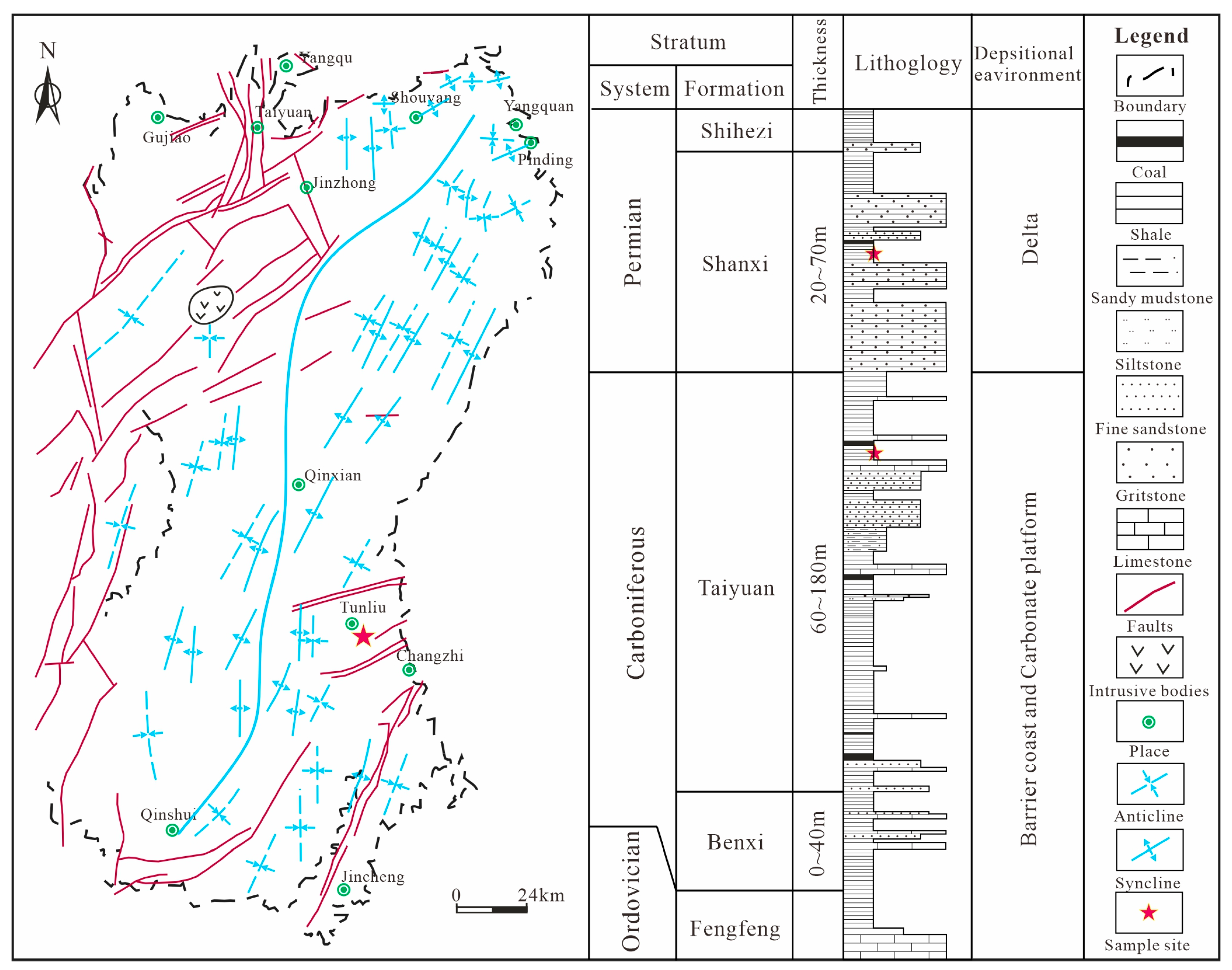
2.1. Geological Setting and Sample Collection
2.2. Experiments
2.3. Methods
2.3.1. Matrix Compression and MIP-Corrected Method
2.3.2. Multifractal Model
3. Results
3.1. TOC and Mineral Compositions
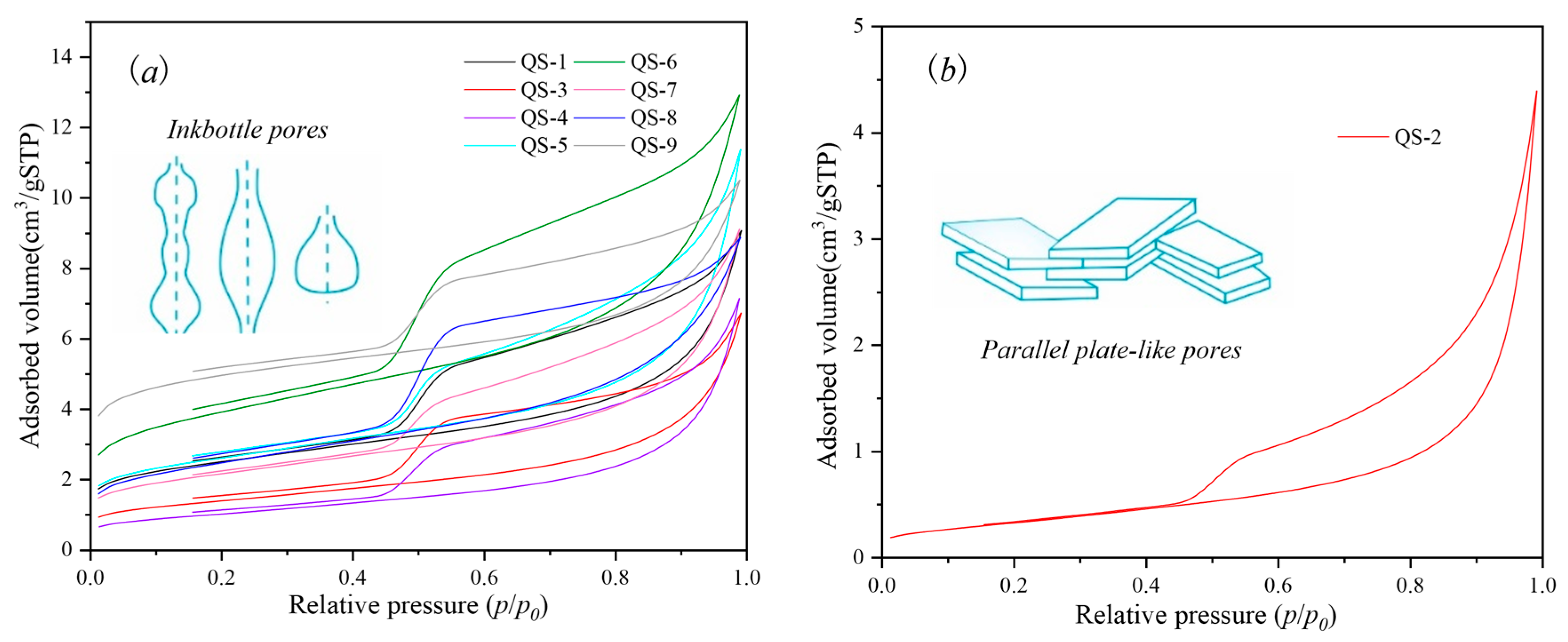
3.2. Nanopore Type Characteristics
3.3. Matrix Compressibility Coefficients
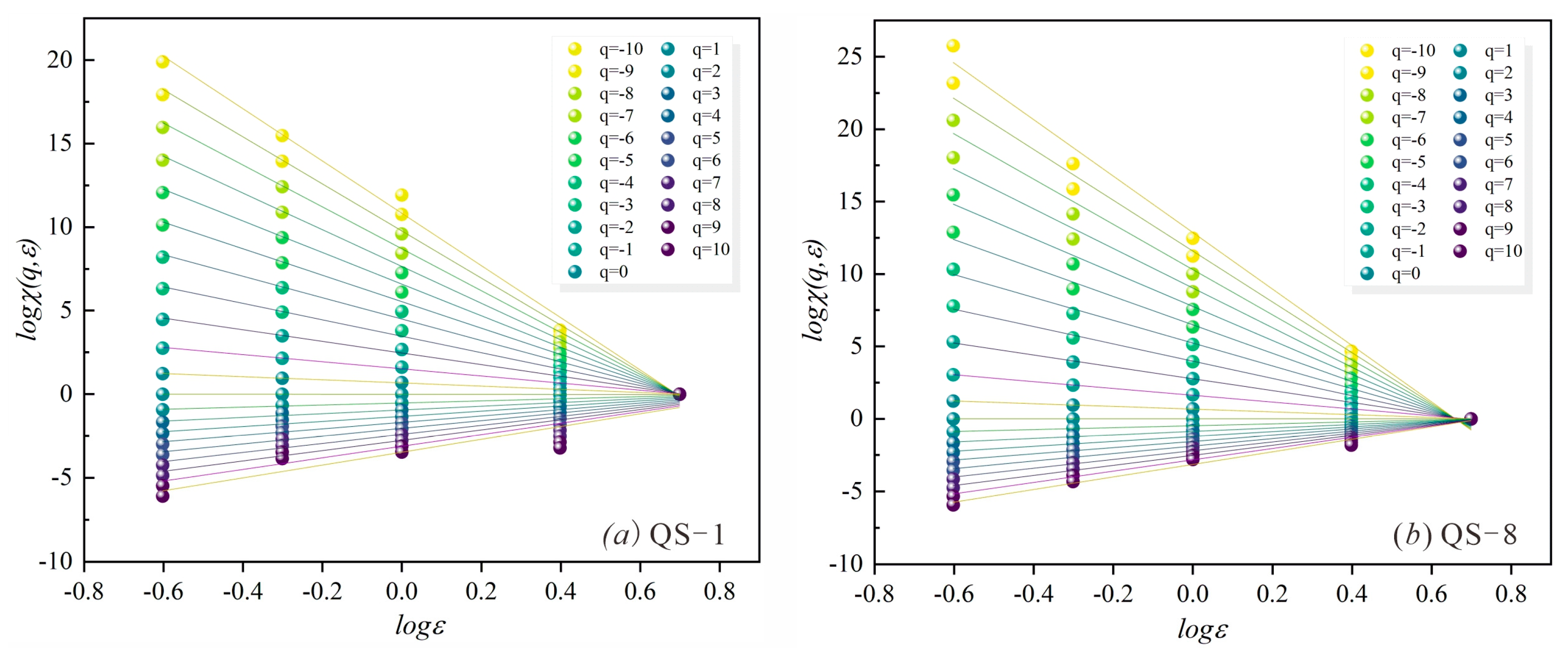
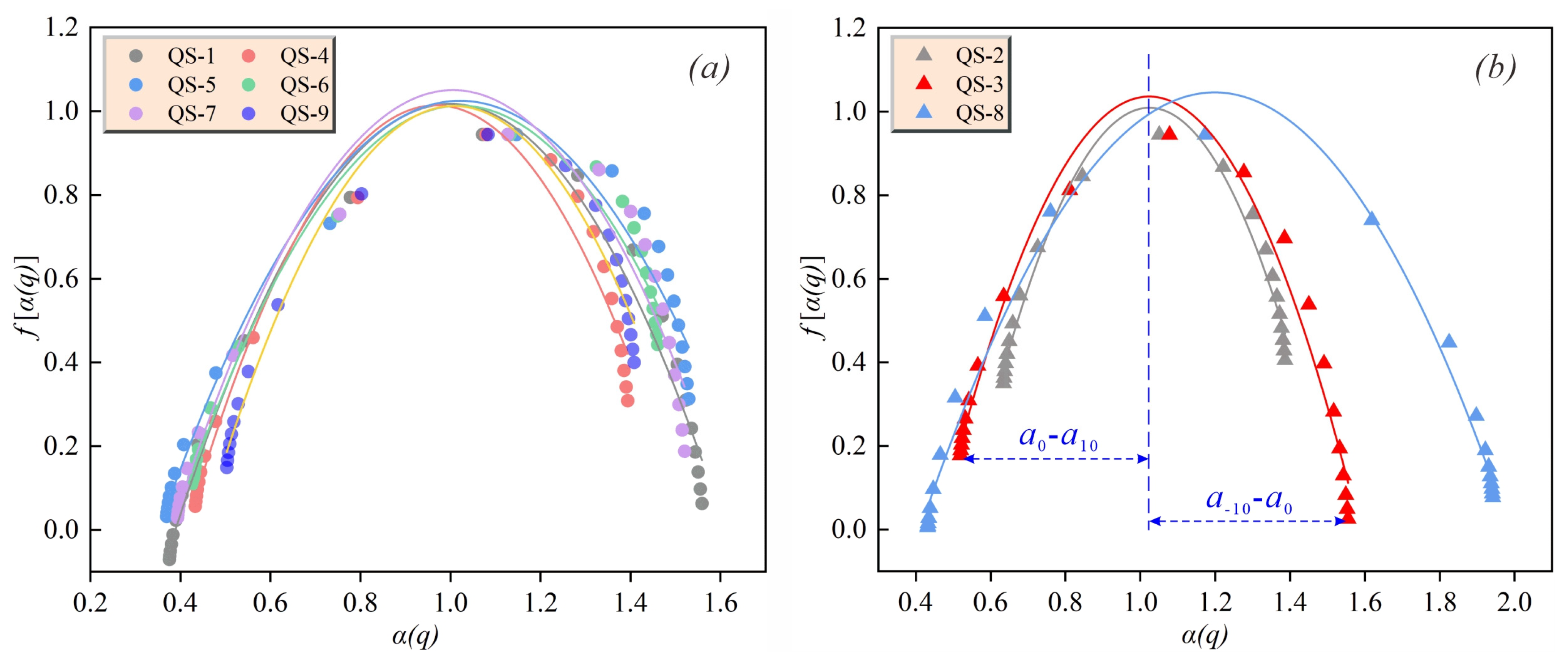
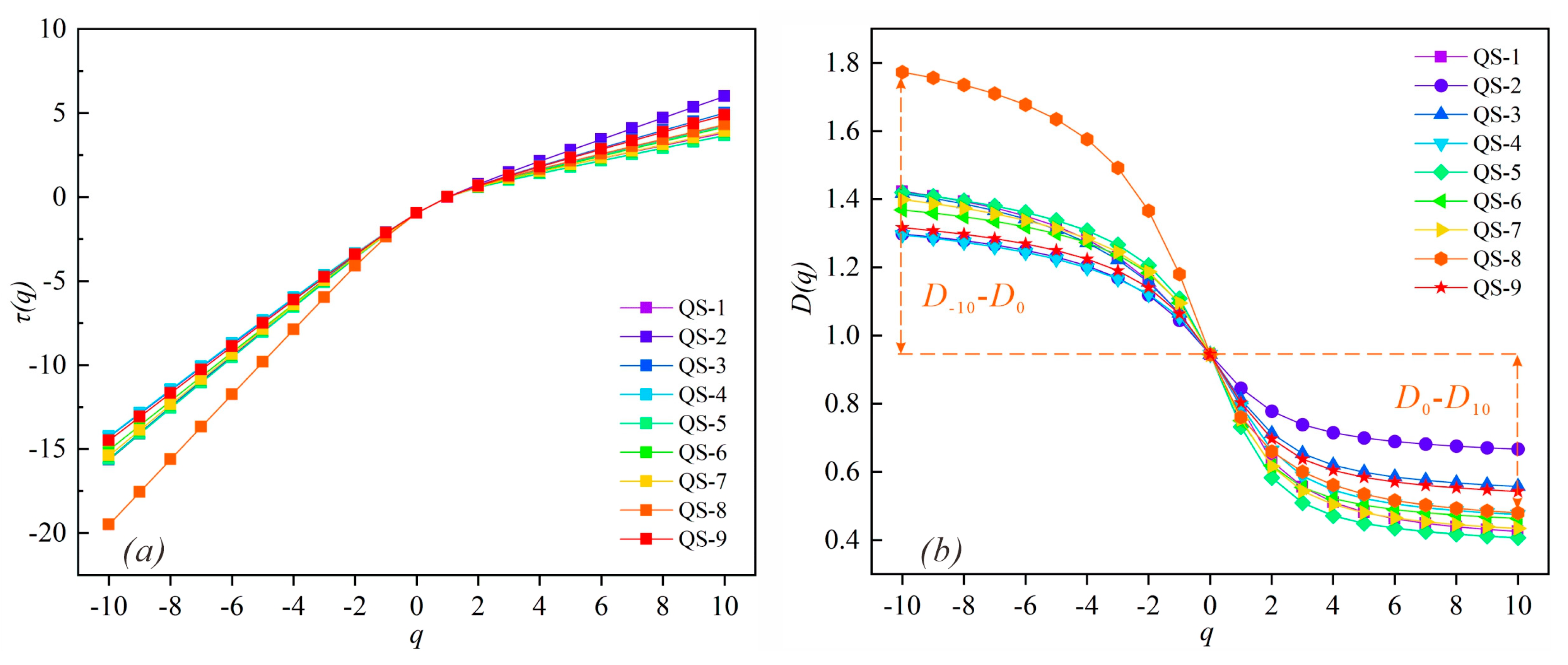
3.4. Multifractal Parameter Calculations
4. Discussions
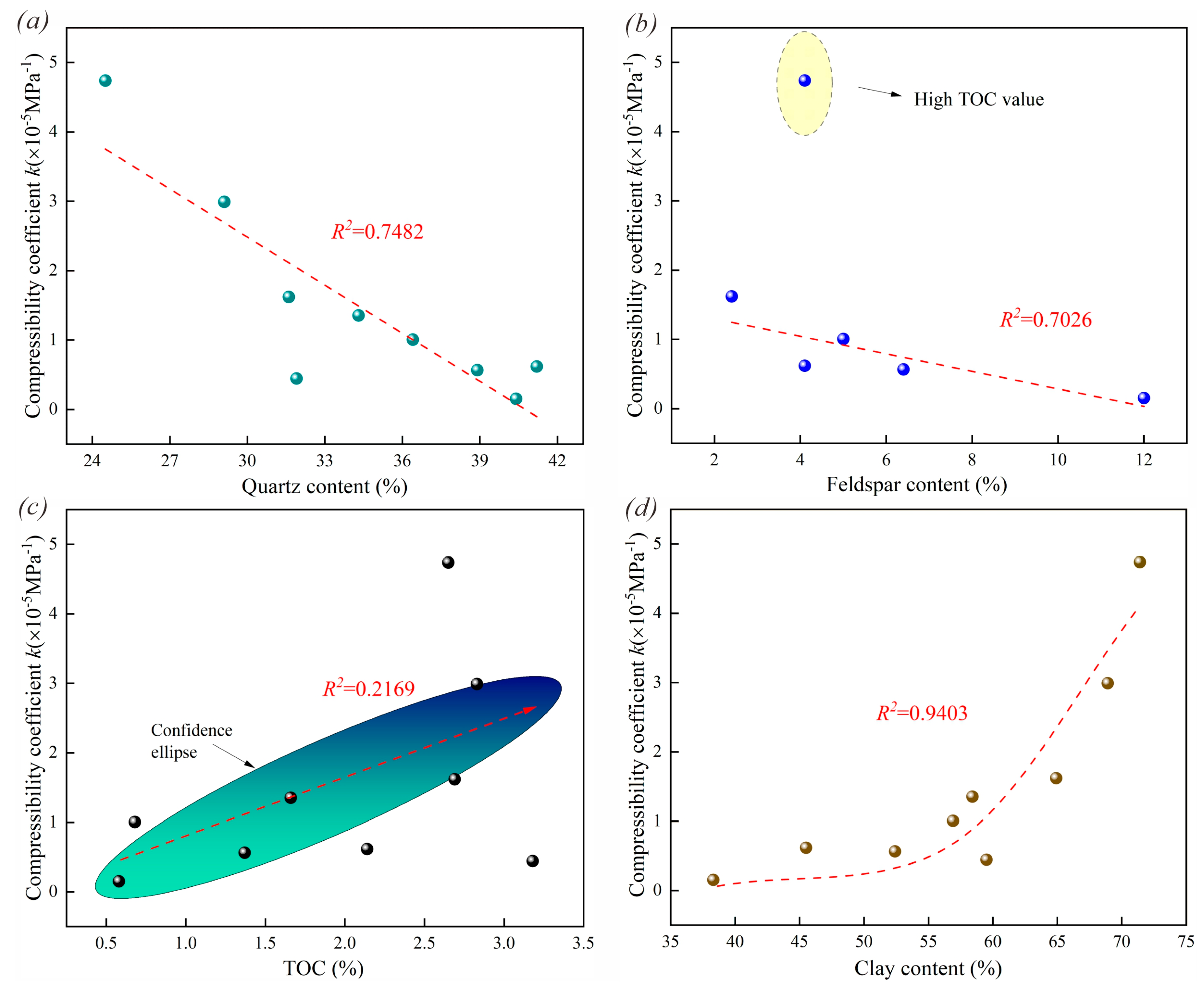
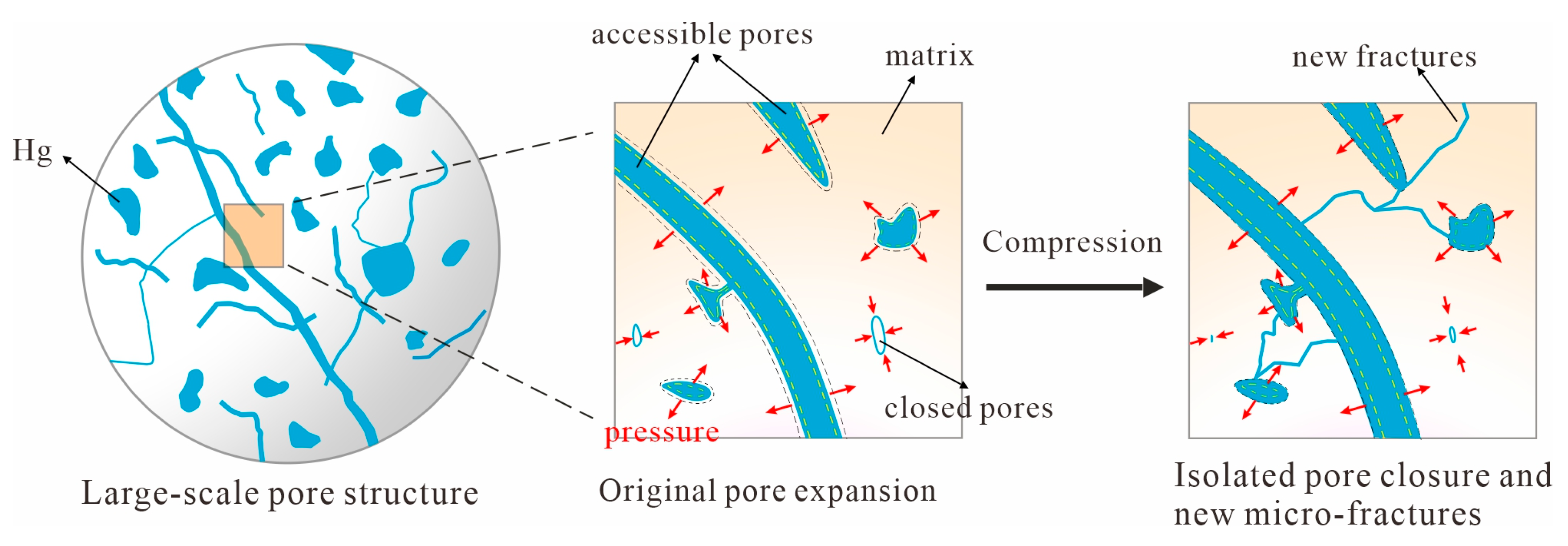
4.1. Influencing Factors of Matrix Compression
4.2. Effect of Matrix Compressibility on Multifractal Characterization
4.3. Heterogeneity Analysis by Multifractal Singular Spectrum
4.4. Heterogeneity Analysis by Multifractal Dimension Spectrum
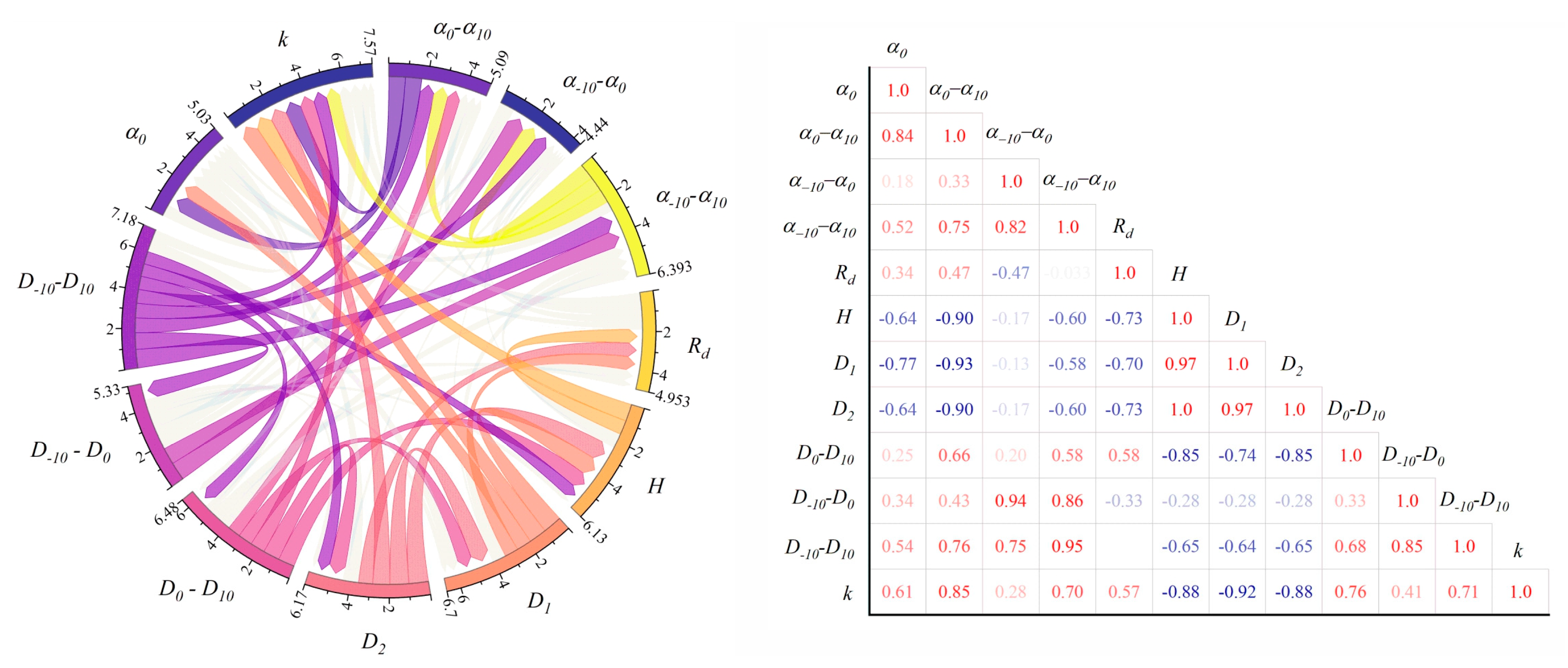
4.5. Influencing Factors of Pore Heterogeneity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Hammes, U. Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. AAPG Bull. 2012, 96, 1071–1098. [Google Scholar] [CrossRef]
- Pan, Y.; Hui, D.; Luo, P.; Zhang, Y.; Sun, L.; Wang, K. Experimental investigation of the geochemical interactions between supercritical CO2 and shale: Implications for CO2 storage in gas-bearing shale formations. Energy Fuels 2018, 32, 1963–1978. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, Z.; Liu, Q.; Jiang, S.; Liu, K.; Tan, J.; Gao, F. Mechanism of shale gas occurrence: Insights from comparative study on pore structures of marine and lacustrine shales. Mar. Pet. Geol. 2019, 104, 200–216. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Zheng, S.; Luo, Z.; Sheng, Y.; Wang, X. Full-scale pore structure and its controlling factors of the Wufeng–Longmaxi shale, southern Sichuan Basin, China: Implications for pore evolution of highly overmature marine shale. J. Nat. Gas Sci. Eng. 2019, 67, 134–146. [Google Scholar] [CrossRef]
- Feng, G.; Zhu, Y.; Chen, S.; Wang, Y.; Ju, W.; Hu, Y.; You, Z.; Wang, G. Supercritical methane adsorption on shale over wide pressure and temperature ranges: Implications for Gas-in-Place estimation. Energy Fuels 2020, 34, 3121–3134. [Google Scholar] [CrossRef]
- Liu, D.; Tian, T.; Liang, R.; Yang, F.; Ye, F. Characterization of shale pore structure by multitechnique combination and multifractal analysis and its significance. Geofluids 2020, 2020, 8896940. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Cheng, H. Gas adsorption characterization of pore structure of organic-rich shale: Insights into contribution of organic matter to shale pore network. Nat. Resour. Res. 2021, 30, 2377–2395. [Google Scholar] [CrossRef]
- Inan, S.; Al Badairy, H.; Inan, T.; Al Zahrani, A. Formation and occurrence of organic matter-hosted porosity in shales. Int. J. Coal Geol. 2018, 199, 39–51. [Google Scholar] [CrossRef]
- Huang, H.; Li, R.; Jiang, Z.; Li, J.; Chen, L. Investigation of variation in shale gas adsorption capacity with burial depth: Insights from the adsorption potential theory. J. Nat. Gas Sci. Eng. 2020, 73, 103043. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, L.; Hu, Q.; Pan, Z.; Yu, B.; Sun, L.; Bai, L.; Fu, H.; Zhang, Y.; Zhang, C. Multiscale connectivity characterization of marine shales in southern China by fluid intrusion, small-angle neutron scattering (SANS), and FIB-SEM. Mar. Pet. Geol. 2020, 112, 104101. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, J.; Xu, Z.; Wang, Z.; Hu, T.; Chen, D.; Li, Q.; Li, Y. Organic matter pore characterization in lacustrine shales with variable maturity using nanometer-scale resolution X-ray computed tomography. Energy Fuels 2017, 31, 2669–2680. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Zhou, J.; Gentzis, T.; Rezaee, R. Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 2017, 209, 567–578. [Google Scholar] [CrossRef]
- Gou, Q.; Xu, S.; Hao, F.; Yang, F.; Zhang, B.; Shu, Z.; Zhang, A.; Wang, Y.; Lu, Y.; Cheng, X. Full-scale pores and micro-fractures characterization using FE-SEM, gas adsorption, nano-CT and micro-CT: A case study of the Silurian Longmaxi Formation shale in the Fuling area, Sichuan Basin, China. Fuel 2019, 253, 167–179. [Google Scholar] [CrossRef]
- Sun, M.; Yu, B.; Hu, Q.; Zhang, Y.; Li, B.; Yang, R.; Melnichenko, Y.B.; Cheng, G. Pore characteristics of Longmaxi shale gas reservoir in the Northwest of Guizhou, China: Investigations using small-angle neutron scattering (SANS), helium pycnometry, and gas sorption isotherm. Int. J. Coal Geol. 2017, 171, 61–68. [Google Scholar] [CrossRef]
- Chen, L.; Zuo, L.; Jiang, Z.; Jiang, S.; Liu, K.; Tan, J.; Zhang, L. Mechanisms of shale gas adsorption: Evidence from thermodynamics and kinetics study of methane adsorption on shale. Chem. Eng. J. 2019, 361, 559–570. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Sun, L.; Zou, J.; Yuan, Y.; Gentzis, T.; Zhang, Y.; Carvajal-Ortiz, H.; Rezaee, R. A comprehensive pore structure study of the Bakken Shale with SANS, N2 adsorption and mercury intrusion. Fuel 2019, 245, 274–285. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Cheng, H. Pore structure of Triassic Yanchang mudstone, Ordos Basin: Insights into the impact of solvent extraction on porosity in lacustrine mudstone within the oil window. J. Pet. Sci. Eng. 2020, 195, 107944. [Google Scholar] [CrossRef]
- Feng, C.; Li, X.; Xu, E.; Sui, H.; Xue, F.; Xie, H. Microstructure characteristics of tectonic coal and primary coal: A case study of Guizhou, China. Nat. Resour. Res. 2023, 32, 2901–2926. [Google Scholar] [CrossRef]
- Ritter, H.L. Pore-size distribution in porous materials. Pressure porosimeter and determination of complete macropore size distributions. Ind. Eng. Chem. Anal. Ed. 1945, 17, 782–786. [Google Scholar] [CrossRef]
- Friesen, W.; Mikula, R. Mercury porosimetry of coals: Pore volume distribution and compressibility. Fuel 1988, 67, 1516–1520. [Google Scholar] [CrossRef]
- Cai, Y.; Li, Q.; Liu, D.; Zhou, Y.; Lv, D. Insights into matrix compressibility of coals by mercury intrusion porosimetry and N2 adsorption. Int. J. Coal Geol. 2018, 200, 199–212. [Google Scholar] [CrossRef]
- Zhang, M.; Fu, X.; Duan, C.; Li, Y. Influencing factor analysis of the coal matrix compressibility of middle-high rank coals. J. Nat. Gas Sci. Eng. 2020, 81, 103462. [Google Scholar]
- Feng, G.; Li, W.; Zhu, Y.; Wang, X.; Wang, Y.; Song, Y.; Zheng, S.; Shang, F. Matrix Compressibility and Multifractal Nature of Nanoporous Shale. Energy Fuels 2024, 38, 4057–4075. [Google Scholar] [CrossRef]
- Zhang, X.; Han, H.; Peng, J.; Gou, Y. Multifractal Analysis of Pore Structure and Evaluation of Deep-Buried Cambrian Dolomite Reservoir with Image Processing: A Case from Tarim Basin, NW China. Geofluids 2020, 2020, 7131573. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hu, Y. Comparative evaluation of pore structure heterogeneity in low-permeability tight sandstones using different fractal models based on NMR technology: A case study of Benxi Formation in the Central Ordos Basin. Energy Fuels 2020, 34, 13924–13942. [Google Scholar] [CrossRef]
- Hazra, B.; Wood, D.A.; Vishal, V.; Varma, A.K.; Sakha, D.; Singh, A.K. Porosity controls and fractal disposition of organic-rich Permian shales using low-pressure adsorption techniques. Fuel 2018, 220, 837–848. [Google Scholar] [CrossRef]
- Song, W.; Wang, D.; Yao, J.; Li, Y.; Sun, H.; Yang, Y.; Zhang, L. Multiscale image-based fractal characteristic of shale pore structure with implication to accurate prediction of gas permeability. Fuel 2019, 241, 522–532. [Google Scholar] [CrossRef]
- Han, W.; Zhou, G.; Zhang, Q.; Pan, H.; Liu, D. Experimental study on modification of physicochemical characteristics of acidified coal by surfactants and ionic liquids. Fuel 2020, 266, 116966. [Google Scholar] [CrossRef]
- Han, W.; Zhou, G.; Gao, D.; Zhang, Z.; Wei, Z.; Wang, H.; Yang, H. Experimental analysis of the pore structure and fractal characteristics of different metamorphic coal based on mercury intrusion-nitrogen adsorption porosimetry. Powder Technol. 2020, 362, 386–398. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W. Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals. Int. J. Coal Geol. 2008, 73, 27–42. [Google Scholar] [CrossRef]
- Yang, F.; Ning, Z.; Liu, H. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China. Fuel 2014, 115, 378–384. [Google Scholar] [CrossRef]
- Li, A.; Ding, W.; He, J.; Dai, P.; Yin, S.; Xie, F. Investigation of pore structure and fractal characteristics of organic-rich shale reservoirs: A case study of Lower Cambrian Qiongzhusi formation in Malong block of eastern Yunnan Province, South China. Mar. Pet. Geol. 2016, 70, 46–57. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Wang, Y.; Chen, S. Fractal Characteristics of Nanoscale Pores in Shale and its Implications on Methane Adsorption Capacity. Fractals 2019, 27, 1940014. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Pan, Z.; Niu, X.; Yu, Y.; Meng, S. Pore structure and its fractal dimensions of transitional shale: A cross-section from east margin of the Ordos Basin, China. Fuel 2019, 241, 417–431. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Song, X. Multifractal analysis of Hg pore size distributions of tectonically deformed coals. Int. J. Coal Geol. 2015, 144, 138–152. [Google Scholar] [CrossRef]
- Muller, J.; Mccauley, J.L. Implication of fractal geometry for fluid flow properties of sedimentary rocks. Transp. Porous Media 1992, 8, 133–147. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Boast, C.W.; Bulock, D.G. Multifractal analyses of soil properties. Agron. J. 1999, 91, 1033–1041. [Google Scholar] [CrossRef]
- Posadas, A.N.; Giménez, D.; Quiroz, R.; Protz, R. Multifractal characterization of soil pore systems. Soil Sci. Soc. Am. J. 2003, 67, 1361–1369. [Google Scholar] [CrossRef]
- Montero, E.; Martín, M.Á. Hölder spectrum of dry grain volume-size distributions in soil. Geoderma 2003, 112, 197–204. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R.; Rother, G.; Allard, L.F.; Jackson, A.J.; Littrell, K.C. Diagenetic changes in macro-to nano-scale porosity in the St. Peter Sandstone: An (ultra) small angle neutron scattering and backscattered electron imaging analysis. Geochim. Cosmochim. Acta 2013, 102, 280–305. [Google Scholar] [CrossRef]
- Liang, Z.; Jiang, Z.; Li, Z.; Song, Y.; Gao, F.; Liu, X.; Xiang, S. Nanopores Structure and Multifractal Characterization of Bulk Shale and Isolated Kerogen—An Application in Songliao Basin, China. Energy Fuels 2021, 35, 5818–5842. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, Z.; Han, Y.; Wang, H.; Hou, M.; Yan, G.; Feng, G.; Zhang, X.; Yin, T.; Zhang, H. Pore-Fracture Distribution Heterogeneity of Shale Reservoirs Determined by using HPMI and LPN2 GA Tests. Acta Geo. Sin-Engl. 2022, 96, 1659–1672. [Google Scholar] [CrossRef]
- Li, F.; Jiang, B.; Cheng, G.; Song, Y.; Tang, Z. Structural and evolutionary characteristics of pores-microfractures and their influence on coalbed methane exploitation in high-rank brittle tectonically deformed coals of the Yangquan mining area, northeastern Qinshui basin, China. J. Petrol. Sci. Eng. 2019, 174, 1290–1302. [Google Scholar]
- Chong, H.; Liu, X.; Xi, D.; Zhang, J.; Vandeginste, V.; Wang, D.; Yao, P. Quantitative Description of Pore and Fracture Distribution Heterogeneity Using Mercury Removal Curve and Applicability of Fractal Models. Processes 2024, 12, 917. [Google Scholar] [CrossRef]
- GB/T 19145-2022; Determination for Total Organic Carbon in Sedimentary Rock. Standards Press of China: Beijing, China, 2022.
- GB/T 35210.1-2023; Determination of Isothermal Adsorption/Desorption of Methane in Shale—Part 1: Static Volumetric Method. Standards Press of China: Beijing, China, 2023.
- Song, Y.; Jiang, B.; Li, M.; Liu, J.; Cheng, G.; Tang, Z. Nano-porous structural evolution and tectonic control of low-medium metamorphic tectonically deformed coals—Taking Suxian mine field as an example. J. Nanosci. Nanotechnol. 2017, 17, 6083–6095. [Google Scholar] [CrossRef]
- Song, Y.; Jiang, B.; Shao, P.; Wu, J. Matrix compression and multifractal characterization for tectonically deformed coals by Hg porosimetry. Fuel 2018, 211, 661–675. [Google Scholar]
- Li, Y.H.; Lu, G.Q.; Rudolph, V. Compressibility and fractal dimension of fine coal particles in relation to pore structure characterisation using mercury porosimetry. Part. Part. Syst. Charact. 1999, 16, 25–31. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Nucl. Phys. B 1987, 2, 501–511. [Google Scholar] [CrossRef]
- Ferreiro, J.P.; Vázquez, E.V. Multifractal analysis of Hg pore size distributions in soils with contrasting structural stability. Geoderma 2010, 160, 64–73. [Google Scholar] [CrossRef]
- Zhang, M.; Duan, C.; Li, G.; Fu, X.; Zhong, Q.; Liu, H.; Dong, Z. Determinations of the multifractal characteristics of the pore structures of low-, middle-, and high-rank coal using high-pressure mercury injection. J. Petrol. Sci. Eng. 2021, 203, 108656. [Google Scholar] [CrossRef]
- Chhabra, A.B.; Meneveau, C.; Jensen, R.V.; Sreenivasan, K.R. Direct determination of the f (α) singularity spectrum and its application to fully developed turbulence. Phys. Rev. A 1989, 40, 5284. [Google Scholar] [CrossRef]
- Ning, S.; Xia, P.; Hao, F.; Tian, J.; Fu, Y.; Wang, K. Pore Fractal Characteristics between Marine and Marine–Continental Transitional Black Shales: A Case Study of Niutitang Formation and Longtan Formation. Fractal. Fract. 2024, 8, 288. [Google Scholar] [CrossRef]
- Chen, S.; Gong, Z.; Li, X.; Wang, H.; Wang, Y.; Zhang, Y. Pore structure and heterogeneity of shale gas reservoirs and its effect on gas storage capacity in the Qiongzhusi Formation. Geosci. Front. 2021, 12, 101244. [Google Scholar] [CrossRef]
- Xu, Z.; Shi, W.; Zhai, G.; Peng, N.; Zhang, C. Study on the characterization of pore structure and main controlling factors of pore development in gas shale. J. Nat. Gas Geosci. 2020, 5, 255–271. [Google Scholar] [CrossRef]
- Muller, J. Characterization of pore space in chalk by multifractal analysis. J. Hydrol. 1996, 187, 215–222. [Google Scholar] [CrossRef]
- Peng, J.; Han, H.; Xia, Q.; Li, B. Evaluation of the pore structure of tight sandstone reservoirs based on multifractal analysis: A case study from the Kepingtage Formation in the Shuntuoguole uplift, Tarim Basin, NW China. J. Geophys. 2018, 15, 1122–1136. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Zou, J.; Gentzis, T.; Rezaee, R.; Bubach, B.; Carvajal-Ortiz, H. Multifractal analysis of gas adsorption isotherms for pore structure characterization of the Bakken Shale. Fuel 2018, 219, 296–311. [Google Scholar] [CrossRef]
- Guan, M.; Liu, X.; Jin, Z.; Lai, J. The heterogeneity of pore structure in lacustrine shales: Insights from multifractal analysis using N2 adsorption and mercury intrusion. Mar. Pet. Geol. 2020, 114, 104150. [Google Scholar] [CrossRef]
- Caniego, F.J.; Martí, M.A.; San José, F. Rényi dimensions of soil pore size distribution. Geoderma 2003, 112, 205–216. [Google Scholar] [CrossRef]
- Feng, G.; Li, W.; Zhu, Y.; Wang, Y.; Song, Y.; Zheng, S.; Shang, F. Scale-Dependent Fractal Properties and Geological Factors for the Pore Structure in Shale: Insights from Field Emission Scanning Electron Microscopy and Fluid Intrusion. Energy Fuels 2023, 37, 16519–16535. [Google Scholar] [CrossRef]



| Sample ID | TOC(%) | Whole-Rock Minerals(%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Total Clays | Quartz | Feldspar | Calcite | Dolomite | Siderite | Pyrite | ||
| QS-1 | 2.69 | 64.9 | 31.6 | 2.4 | 1.1 | 0 | 0 | 0 |
| QS-2 | 0.58 | 38.3 | 40.4 | 12 | 0 | 6.6 | 2.7 | 0 |
| QS-3 | 1.37 | 52.4 | 38.9 | 6.4 | 0 | 0 | 2.3 | 0 |
| QS-4 | 2.14 | 45.5 | 41.2 | 4.1 | 0 | 0 | 9.2 | 0 |
| QS-5 | 2.65 | 71.4 | 24.5 | 4.1 | 0 | 0 | 0 | 0 |
| QS-6 | 2.83 | 68.9 | 29.1 | 0 | 0 | 0 | 2 | 0 |
| QS-7 | 0.68 | 56.9 | 36.4 | 5 | 0 | 0 | 1.7 | 0 |
| QS-8 | 1.66 | 58.4 | 34.3 | 0 | 0 | 3.9 | 0 | 3.4 |
| QS-9 | 3.18 | 59.5 | 31.9 | 0 | 0 | 0 | 2.4 | 6.2 |
| Sample ID | VS, Matrix Volume (cm3/g) | (10−5 MPa−1) | (cm3/g) | (cm3/g) | Compression Ratio (%) | |
|---|---|---|---|---|---|---|
| QS-1 | 0.4465 | 0.7239 | 1.6210 | 0.0061 | 0.0047 | 31.08 |
| QS-2 | 0.4327 | 0.0665 | 0.1540 | 0.0101 | 0.0100 | 1.21 |
| QS-3 | 0.4438 | 0.2512 | 0.5660 | 0.0055 | 0.0050 | 9.93 |
| QS-4 | 0.4451 | 0.2757 | 0.6190 | 0.0072 | 0.0067 | 7.49 |
| QS-5 | 0.4433 | 2.0884 | 4.7110 | 0.0115 | 0.0073 | 57.74 |
| QS-6 | 0.4337 | 1.2975 | 2.9920 | 0.0076 | 0.0050 | 52.46 |
| QS-7 | 0.4321 | 0.4350 | 1.0070 | 0.0060 | 0.0051 | 17.28 |
| QS-8 | 0.4370 | 0.5916 | 1.3540 | 0.0047 | 0.0036 | 30.32 |
| QS-9 | 0.4381 | 0.1955 | 0.4460 | 0.0048 | 0.0044 | 8.64 |
| Sample ID | α0 | α0 − α10 | α−10 − α0 | α−10 − α10 | Rd | H | D0 | D1 | D2 | D0 − D10 | D−10 − D0 | D−10 − D10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QS-1 | 1.071 | 0.696 | 0.488 | 1.183 | 0.208 | 0.815 | 0.944 | 0.790 | 0.631 | 0.519 | 0.478 | 0.998 |
| QS-2 | 1.051 | 0.416 | 0.336 | 0.752 | 0.080 | 0.889 | 0.944 | 0.845 | 0.777 | 0.278 | 0.353 | 0.631 |
| QS-3 | 1.079 | 0.559 | 0.477 | 1.036 | 0.082 | 0.856 | 0.944 | 0.812 | 0.712 | 0.387 | 0.472 | 0.859 |
| QS-4 | 1.079 | 0.646 | 0.315 | 0.961 | 0.331 | 0.832 | 0.944 | 0.794 | 0.663 | 0.469 | 0.351 | 0.820 |
| QS-5 | 1.147 | 0.777 | 0.383 | 1.160 | 0.395 | 0.791 | 0.944 | 0.732 | 0.583 | 0.481 | 0.424 | 0.904 |
| QS-6 | 1.132 | 0.704 | 0.328 | 1.032 | 0.375 | 0.809 | 0.944 | 0.750 | 0.618 | 0.481 | 0.424 | 0.904 |
| QS-7 | 1.128 | 0.734 | 0.392 | 1.126 | 0.342 | 0.808 | 0.944 | 0.754 | 0.616 | 0.510 | 0.455 | 0.965 |
| QS-8 | 1.174 | 0.741 | 0.768 | 1.510 | -0.027 | 0.830 | 0.944 | 0.760 | 0.660 | 0.465 | 0.828 | 1.293 |
| QS-9 | 1.083 | 0.580 | 0.325 | 0.905 | 0.256 | 0.848 | 0.944 | 0.803 | 0.697 | 0.402 | 0.372 | 0.774 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, B.; Zhu, Y.; Feng, G.; Xiang, J.; Wang, Y. Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis. Fractal Fract. 2024, 8, 580. https://doi.org/10.3390/fractalfract8100580
Zhong B, Zhu Y, Feng G, Xiang J, Wang Y. Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis. Fractal and Fractional. 2024; 8(10):580. https://doi.org/10.3390/fractalfract8100580
Chicago/Turabian StyleZhong, Baoyuan, Yanming Zhu, Guangjun Feng, Jie Xiang, and Yang Wang. 2024. "Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis" Fractal and Fractional 8, no. 10: 580. https://doi.org/10.3390/fractalfract8100580
APA StyleZhong, B., Zhu, Y., Feng, G., Xiang, J., & Wang, Y. (2024). Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis. Fractal and Fractional, 8(10), 580. https://doi.org/10.3390/fractalfract8100580








