Analytic Approach Solution to Time-Fractional Phi-4 Equation with Two-Parameter Fractional Derivative
Abstract
1. Introduction
2. Some Definitions and Theorems of Fractional Calculus
3. Analytic Approach
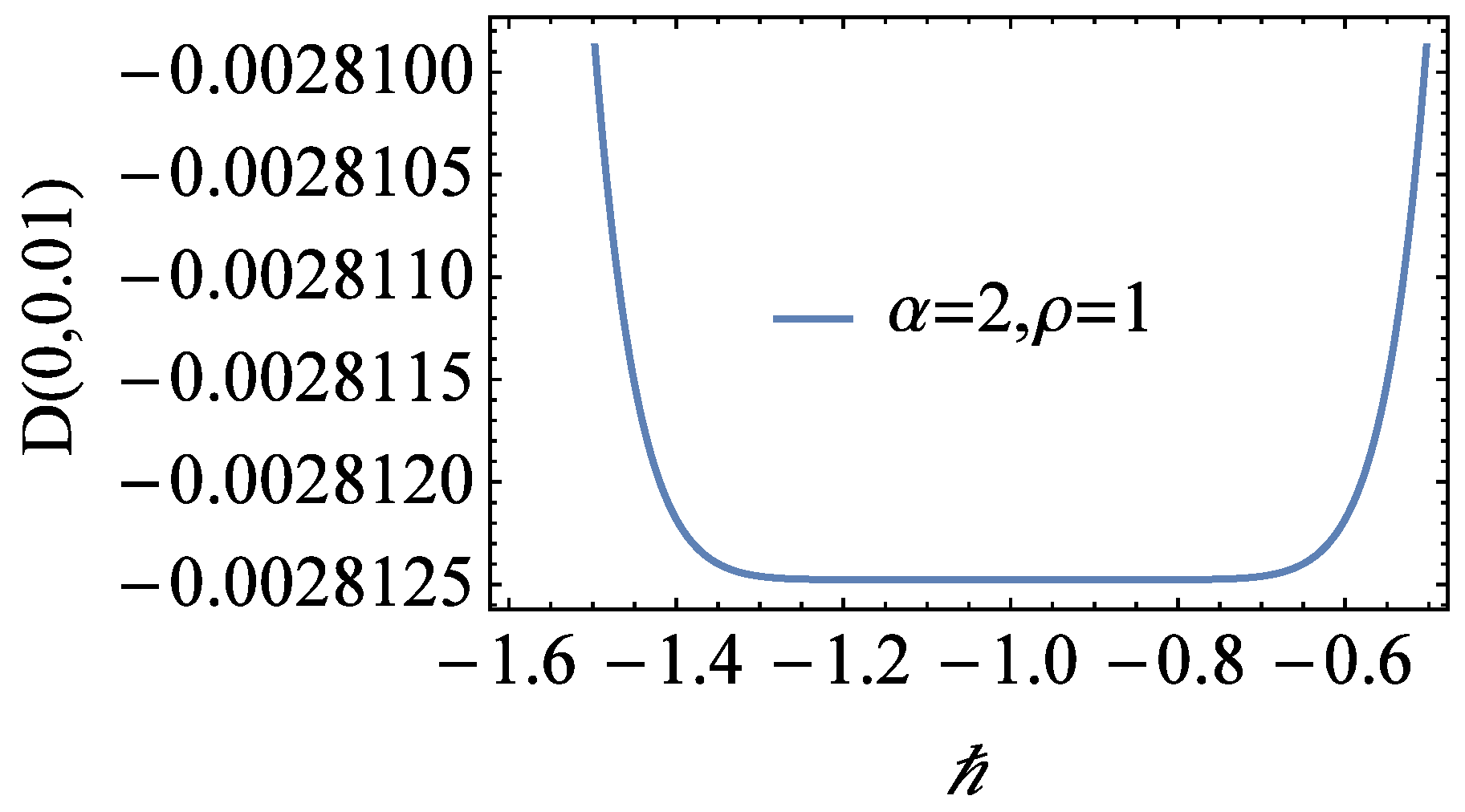
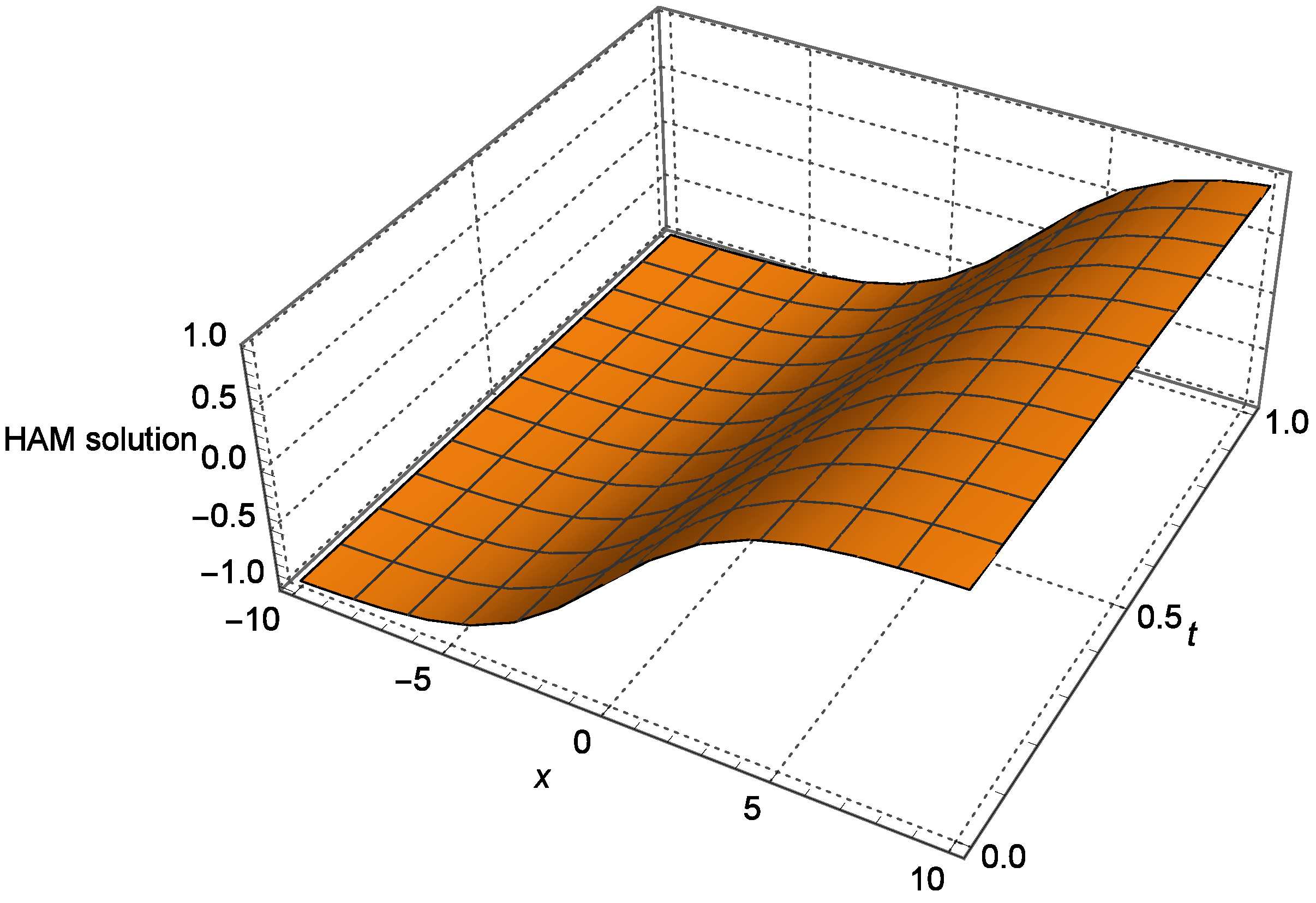
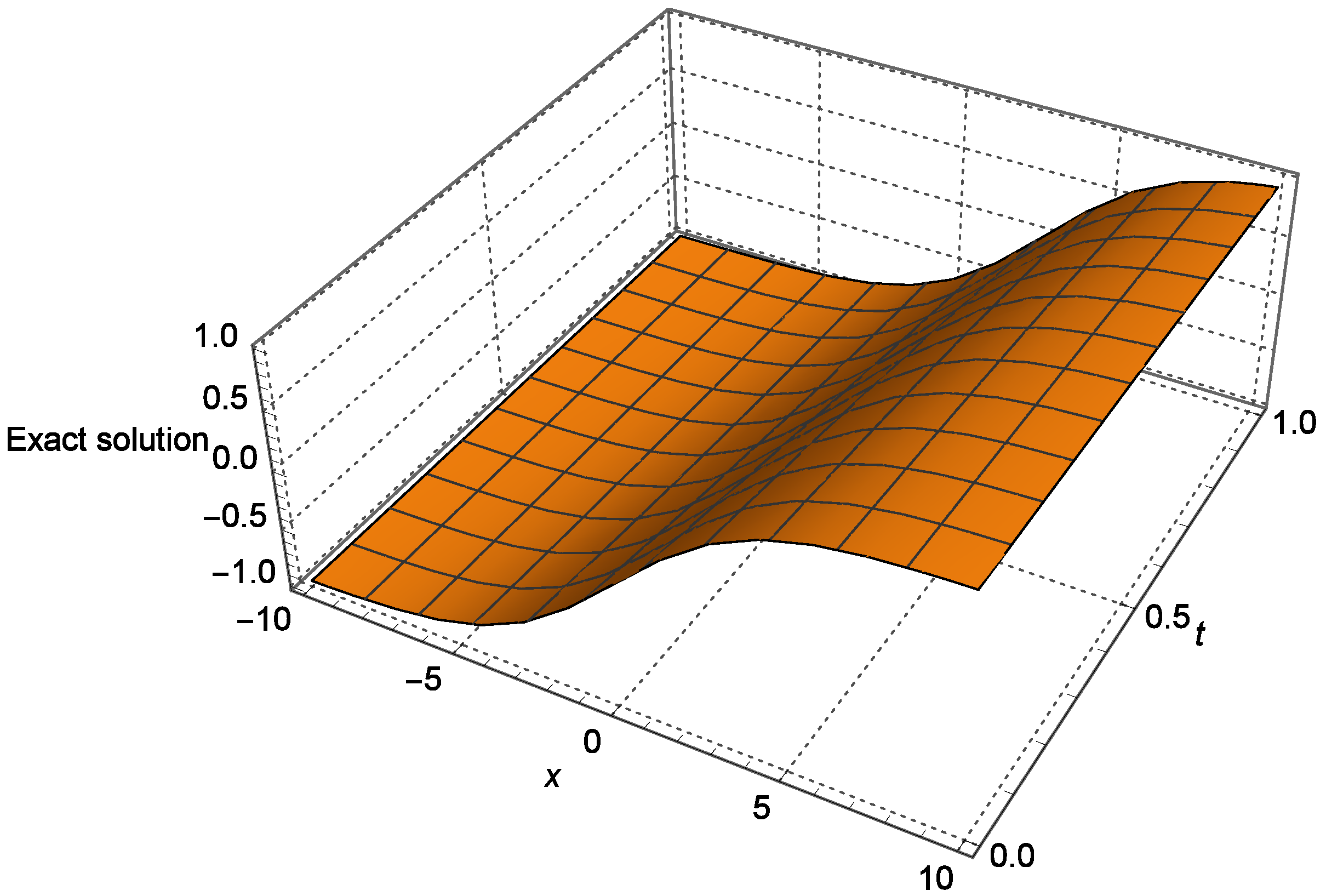
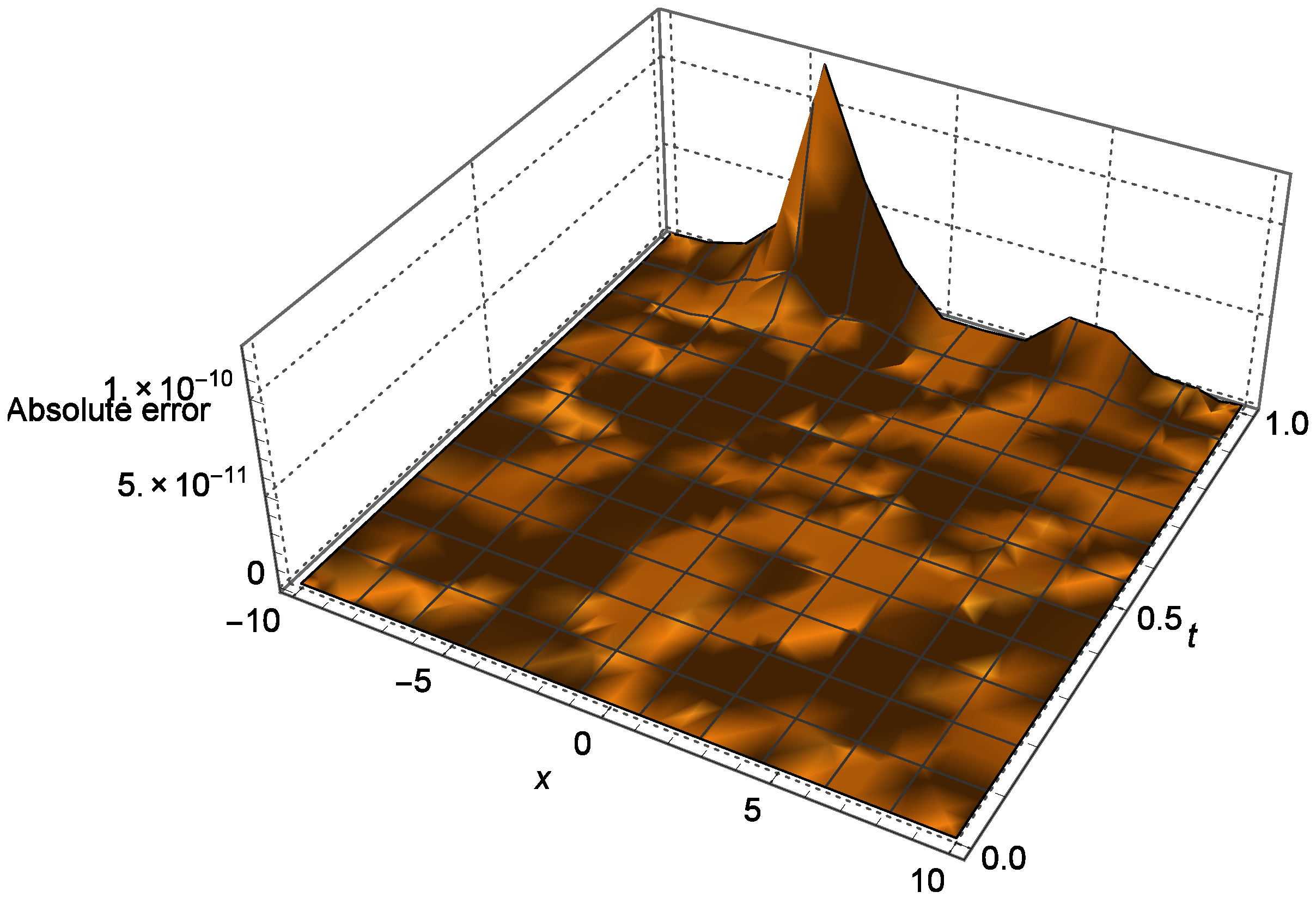
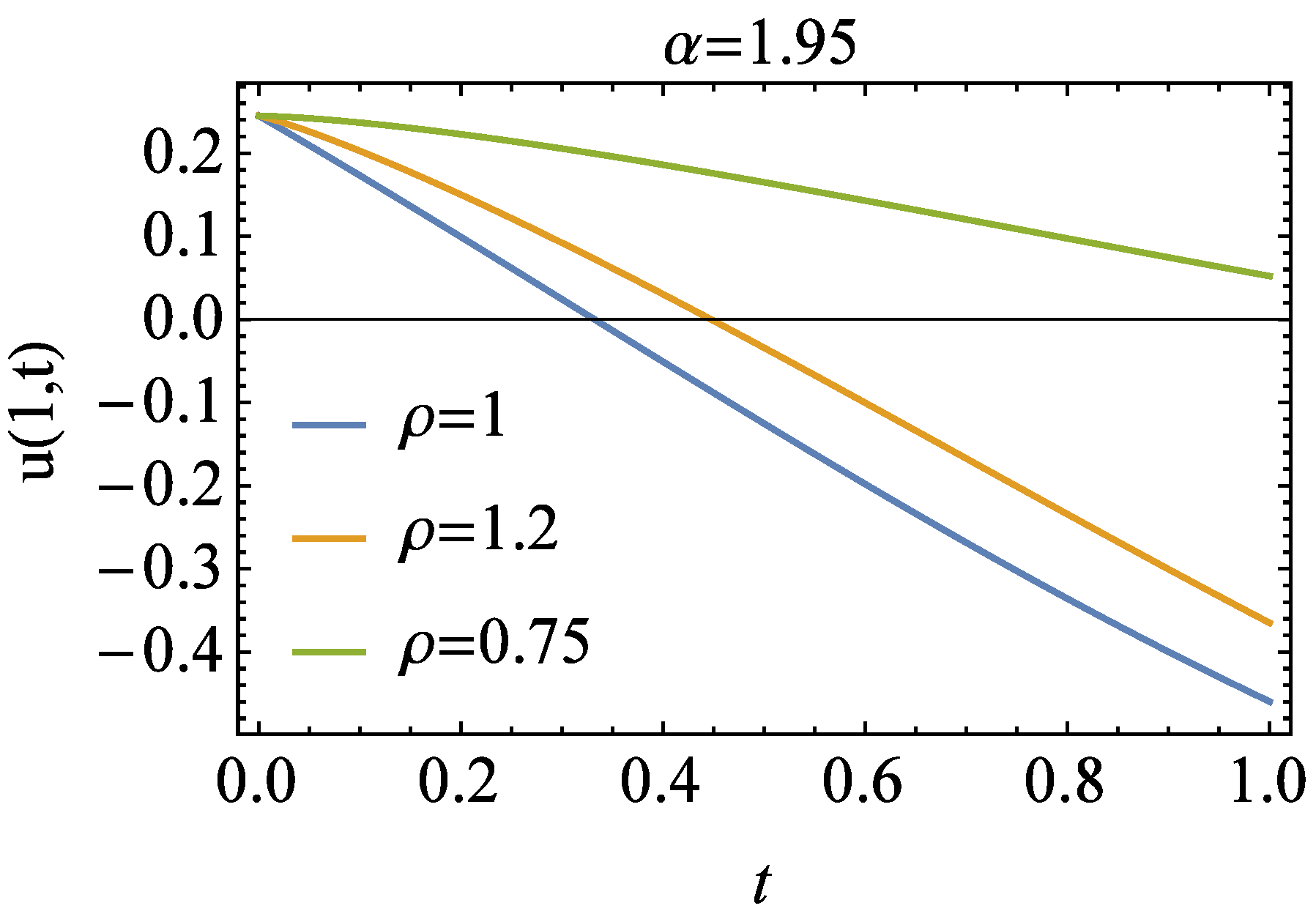
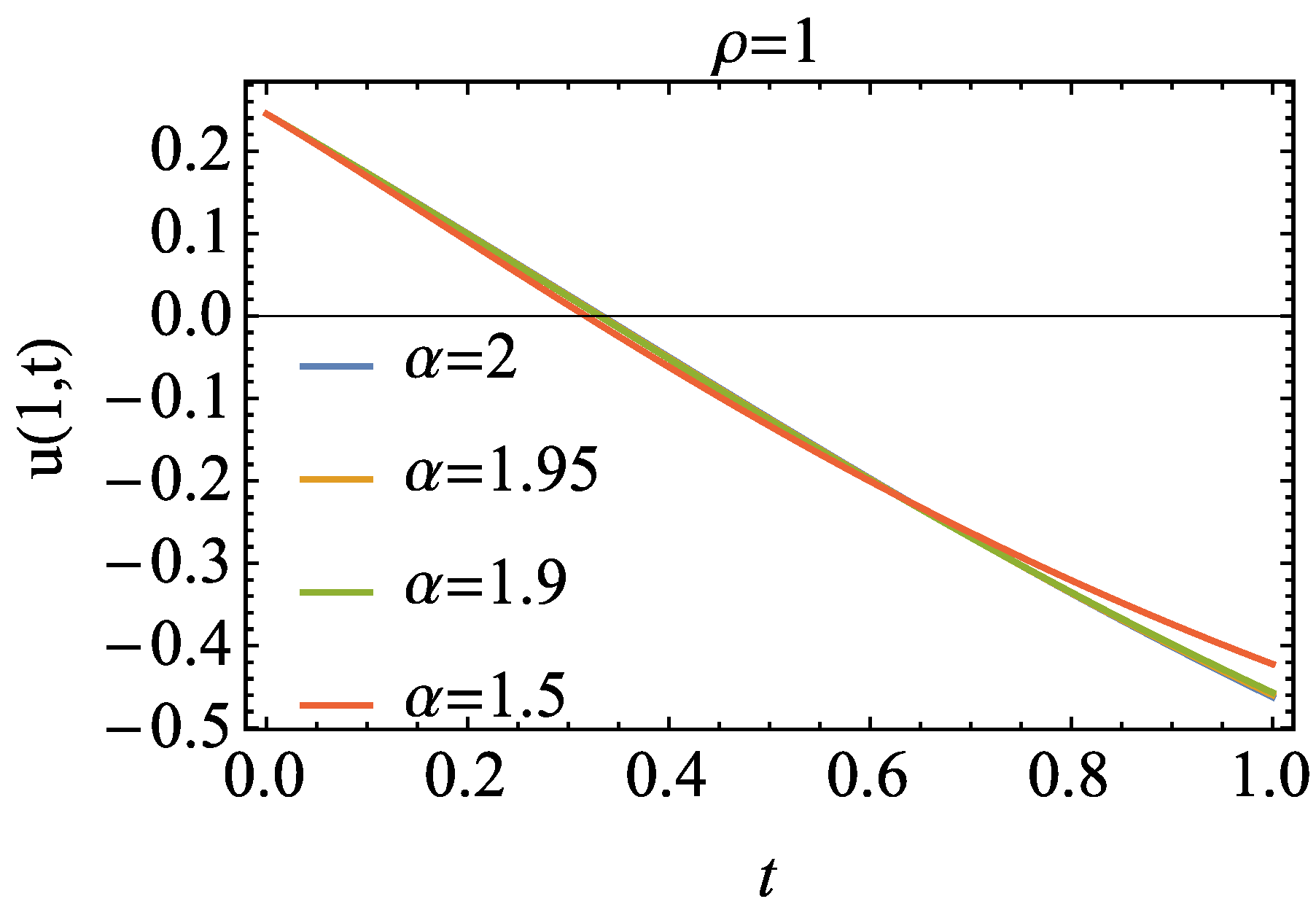
4. Numerical Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gómez-Aguilar, J.F.; Razo-Hernández, R.; Granados-Lieberman, D. A physical interpretation of fractional calculus in observables terms: Analysis of the fractional time constant and the transitory response. Rev. Mex. Física 2014, 60, 32–38. [Google Scholar]
- Agarwal, R.; Hristova, S.; O’Regan, D. Applications of Lyapunov functions to Caputo fractional differential equations. Mathematics 2018, 6, 229. [Google Scholar] [CrossRef]
- Alomari, A.K.; Drabseh, G.A.; Al-Jamal, M.F.; AlBadarneh, R.B. Numerical simulation for fractional phi-4 equation using homotopy Sumudu approach. Int. J. Simul. Process. Model. 2021, 16, 26–33. [Google Scholar] [CrossRef]
- Albuohimad, B.; Adibi, H.; Kazem, S. A numerical solution of time-fractional coupled Korteweg-de Vries equation by using spectral collection method. Ain Shams Eng. J. 2018, 9, 1897–1905. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M.; Baleanu, D. Natural transform decomposition method for solving fractional-order partial differential equations with proportional delay. Mathematics 2019, 7, 532. [Google Scholar] [CrossRef]
- Alquran, M.; Jarrah, A.; Krishnan, E.V. Solitary Wave Solutions of the Phi-Four Equation and the Breaking Soliton System by Means of Jacobi Elliptic Sine-Cosine Expansion Method. Nonlinear Dyn. Syst. Theory 2018, 18, 233–240. [Google Scholar]
- Zahra, W.K. Trigonometric B-Spline Collocation Method for Solving PHI-Four and Allen-Cahn Equations. Mediterr. J. Math. 2017, 14, 122. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Assas, L.M.; Alghamdi, M.A. An efficient spectral collocation algorithm for nonlinear Phi-four equations. Bound. Value Probl. 2013, 2013, 87. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, H.M.; Syam, M.I. Analytical solution of the time-fractional phi-4 equation by using modified residual power series method. Nonlinear Dyn. 2017, 90, 2525–2529. [Google Scholar] [CrossRef]
- Ehsani, F.; Ehsani, F.; Hadi, A.; Hadi, N. Analytical solution of Phi-Four equation. Tech. J. Eng. Appl. Sci. 2013, 14, 1378–1388. [Google Scholar]
- Tariq, H.; Akram, G. New approach for exact solutions of time-fractional Cahn-Allen equation and time fractional Phi-4 equation. Phys. A 2017, 473, 352–362. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New numerical results for the time-fractional Phi-four equation using a novel analytical approach. Symmetry 2020, 12, 478. [Google Scholar] [CrossRef]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Numerical Investigation of Time-Fractional Phi-Four Equation via Novel Transform. Symmetry 2023, 15, 687. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S. Notes on the homotopy analysis method: Some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 983–997. [Google Scholar] [CrossRef]
- Liao, S. Homotopy Analysis Method in Non Linear Differential Equations; Springer: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2012. [Google Scholar]
- Saad, K.M.; L-Shareef, E.H.F.A.; Alomari, A.K.; Baleanud, D.; Gómez-Aguilar, J.F. On exact solutions for time-fractional Korteweg-de Vries and Korteweg-de Vries-Burger’s equations using homotopy analysis transform method. Chin. J. Phys. 2020, 63, 149–162. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional Differential Equations With Dependence on the Caputo-Katugampola Derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional operators with generalized Mittag-Leffler kernels and their iterated differintegrals. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023102. [Google Scholar] [CrossRef]
- Alomari, A.K.; Abdeljawad, T.; Baleanu, D.; Saad, K.; Al-Mdallal, Q. Numerical solutions of fractional parabolic equations with generalized Mittag-Leffler kernels. Numer. Methods Partial. Differ. Equ. 2024, 40, e22699. [Google Scholar] [CrossRef]
- Alomari, A.K.; Alshbeel, A.; Azmi, A. Caputo-type of two parameters for fuzzy fractional differential equations using OHAM technique. Results Nonlinear Anal. 2023, 6, 157–176. [Google Scholar]
- Oliveira, D.S.; Oliveira, E. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2019, 10, 81–91. [Google Scholar] [CrossRef]
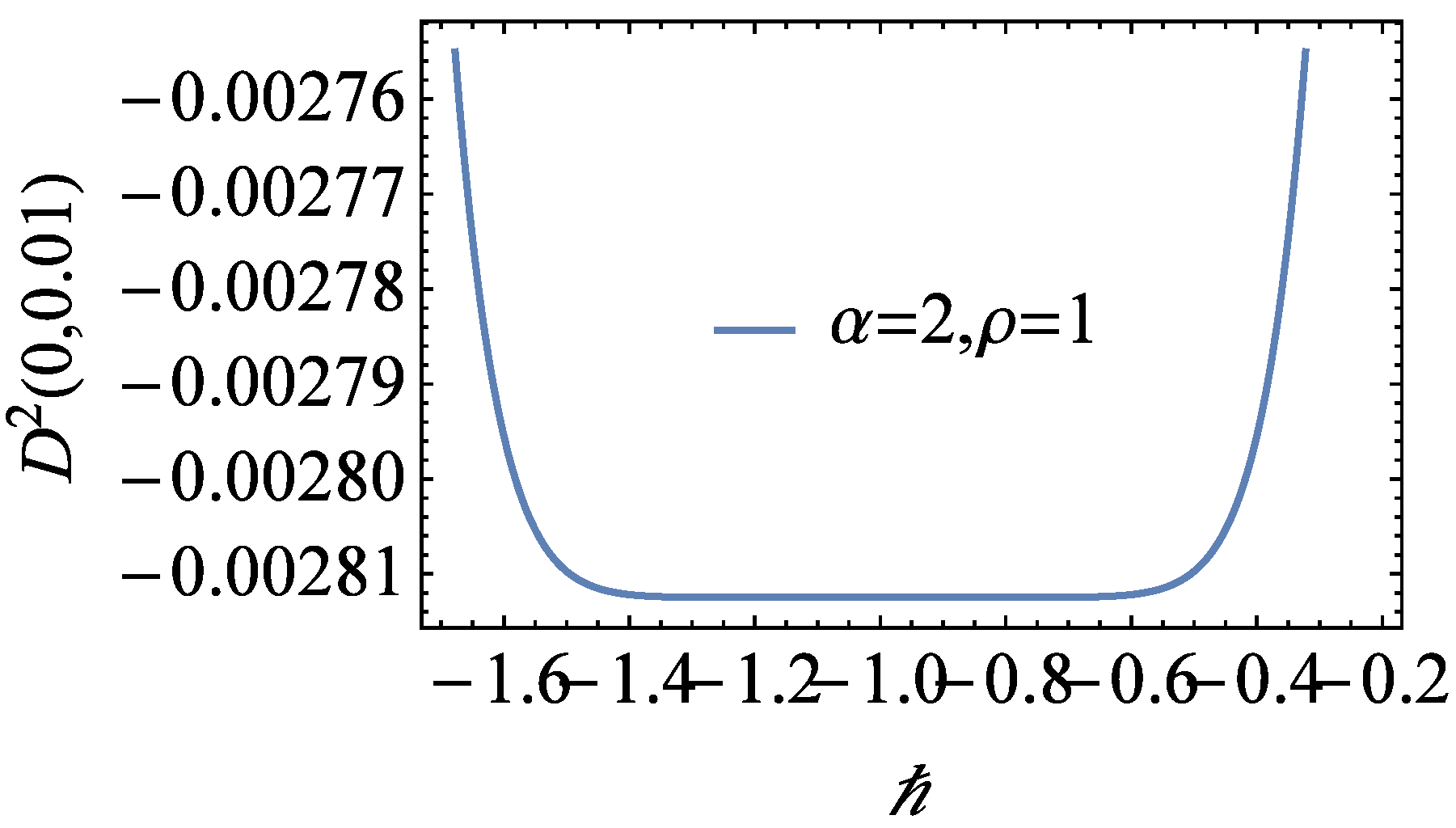

| x | |||
|---|---|---|---|
| −5 | |||
| −3 | |||
| −1 | |||
| 1 | |||
| 3 | |||
| 5 |
| x | t | Exact | |||||
|---|---|---|---|---|---|---|---|
| Solution | |||||||
| 0.5 | |||||||
| 1 | |||||||
| 1.5 | |||||||
| 2 | |||||||
| 2.5 | |||||||
| HAM Error | q-HATM Error | YTDM Error | HAM Error | q-HATM Error | YTDM Error | |
|---|---|---|---|---|---|---|
| x|t | 0.01 | 0.01 | 0.01 | 0.05 | 0.05 | 0.05 |
| −5 | ||||||
| −3 | ||||||
| −1 | ||||||
| 1 | ||||||
| 3 | ||||||
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massoun, Y.; Alomari, A.-K.; Cesarano, C. Analytic Approach Solution to Time-Fractional Phi-4 Equation with Two-Parameter Fractional Derivative. Fractal Fract. 2024, 8, 576. https://doi.org/10.3390/fractalfract8100576
Massoun Y, Alomari A-K, Cesarano C. Analytic Approach Solution to Time-Fractional Phi-4 Equation with Two-Parameter Fractional Derivative. Fractal and Fractional. 2024; 8(10):576. https://doi.org/10.3390/fractalfract8100576
Chicago/Turabian StyleMassoun, Youssouf, Abedel-Karrem Alomari, and Clemente Cesarano. 2024. "Analytic Approach Solution to Time-Fractional Phi-4 Equation with Two-Parameter Fractional Derivative" Fractal and Fractional 8, no. 10: 576. https://doi.org/10.3390/fractalfract8100576
APA StyleMassoun, Y., Alomari, A.-K., & Cesarano, C. (2024). Analytic Approach Solution to Time-Fractional Phi-4 Equation with Two-Parameter Fractional Derivative. Fractal and Fractional, 8(10), 576. https://doi.org/10.3390/fractalfract8100576








