Fractal Analysis of Doped Strontium Titanate Photocatalyst
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Doping of SrTiO3
2.3. Characterization of Samples
3. Results and Discussion
3.1. FTIR Analysis of Particles
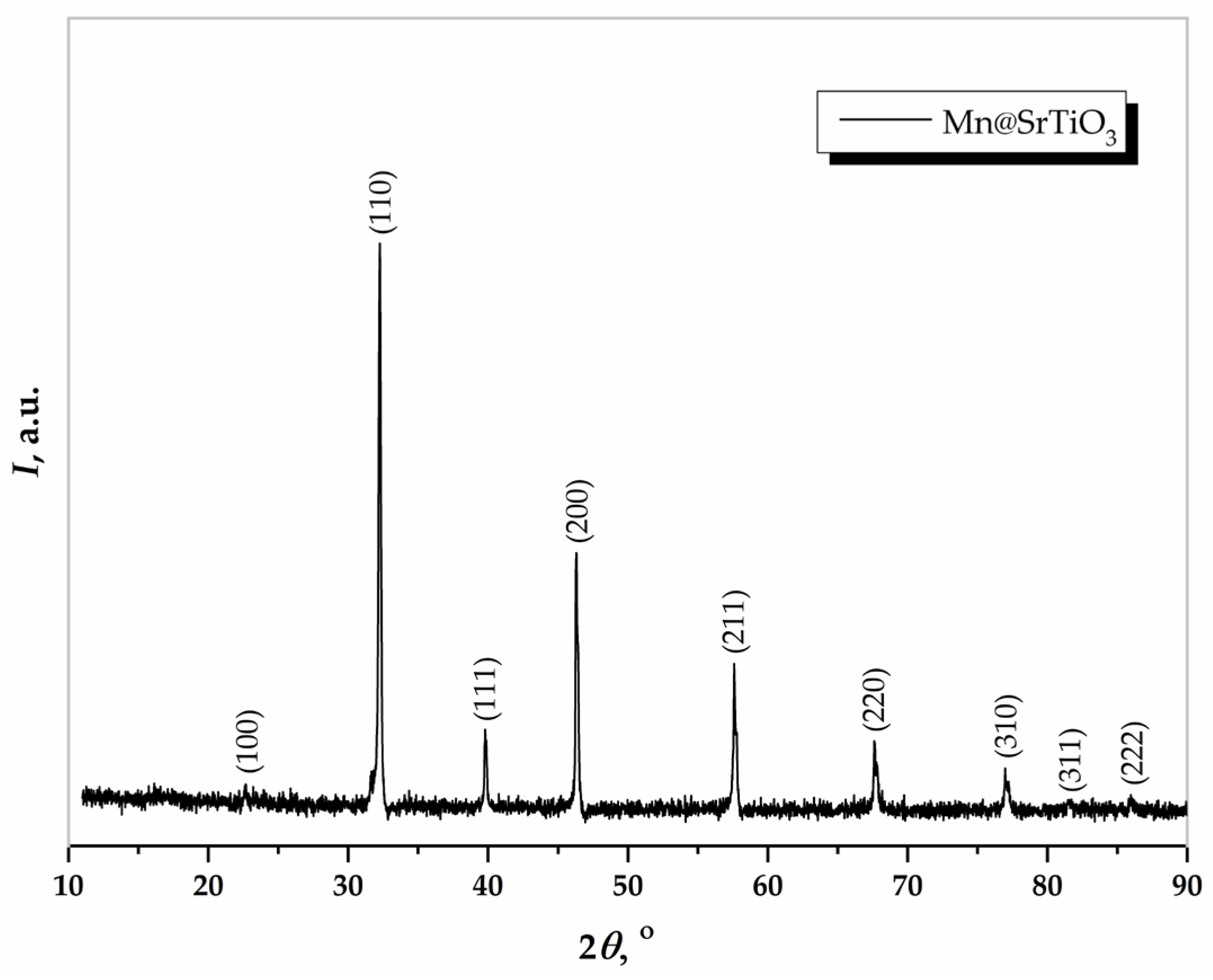
3.2. XRD Analysis of Mn@SrTiO3
3.3. FESEM Analysis of Grains
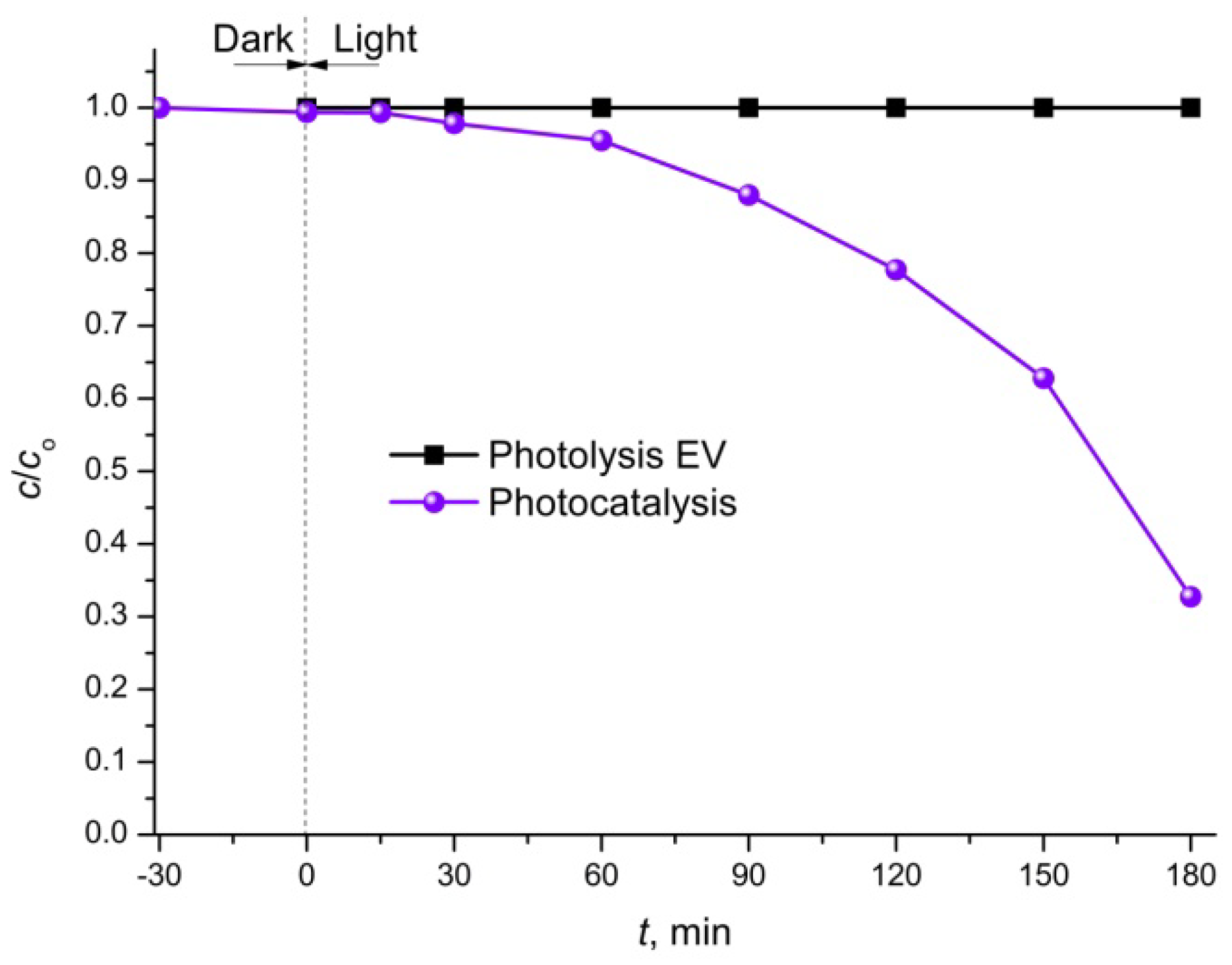
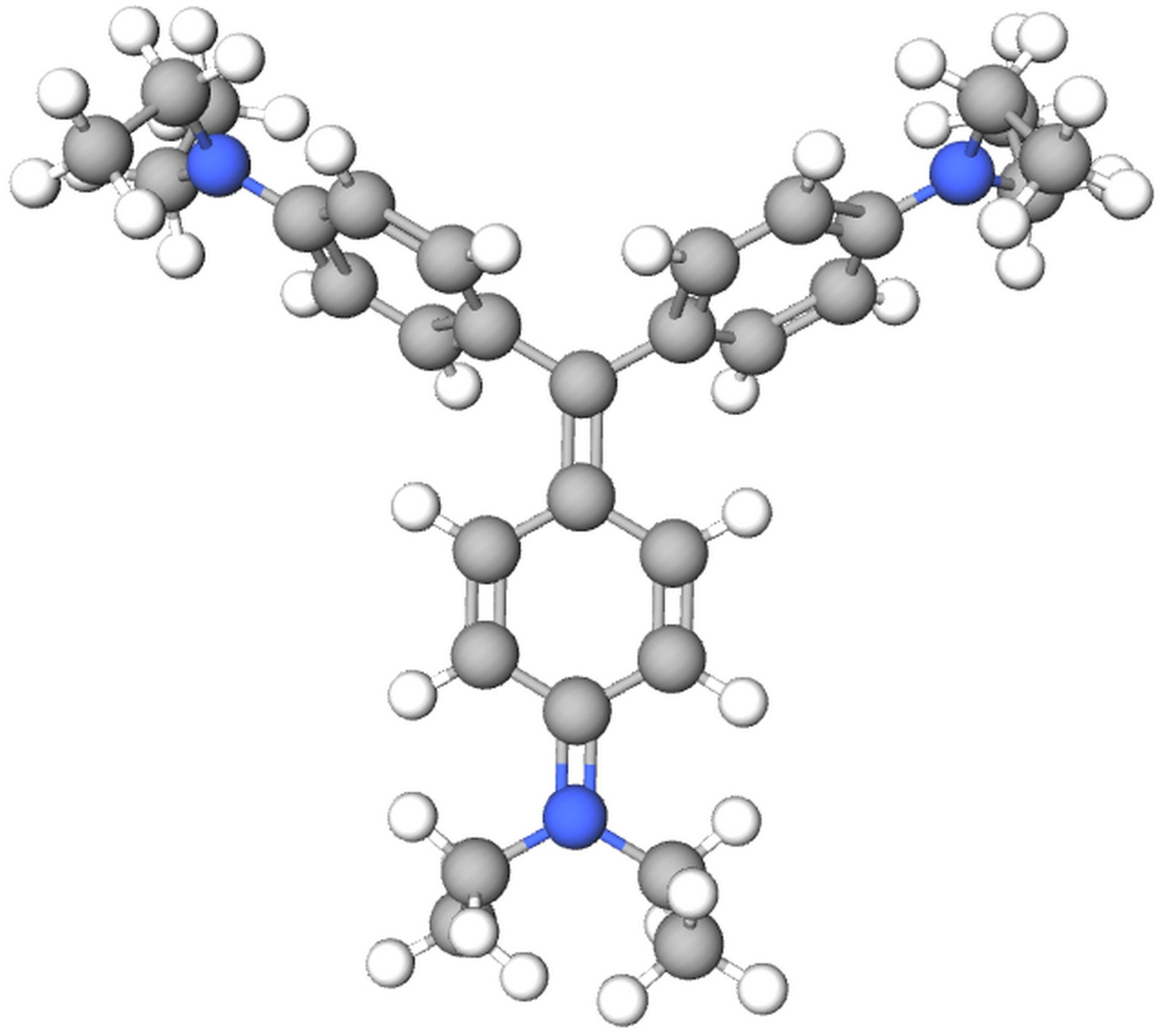
3.4. Photocatalytic Activity of Mn@SrTiO3
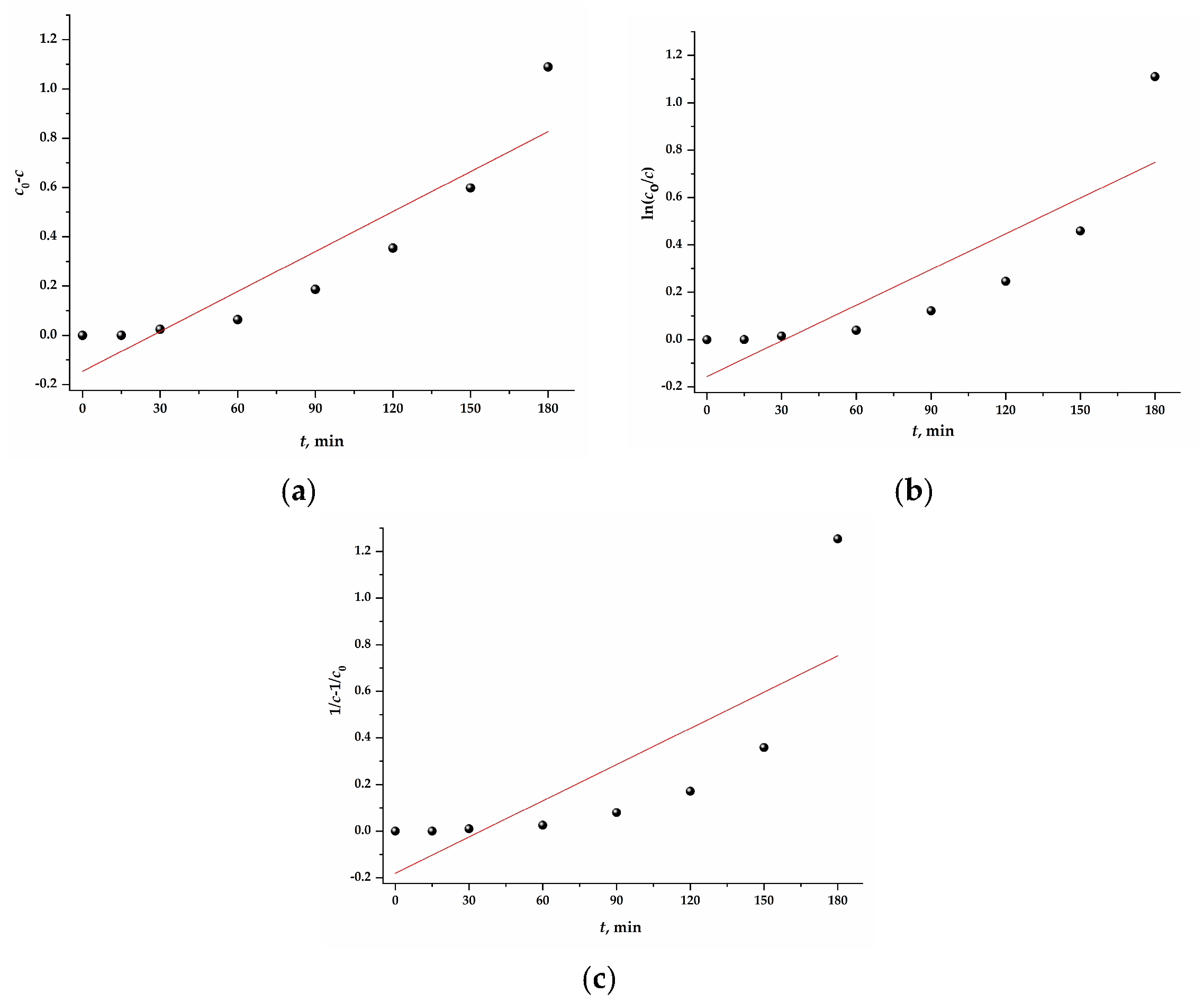
3.5. Kinetics Modeling of the Photocatalytic Degradation of EV Dye
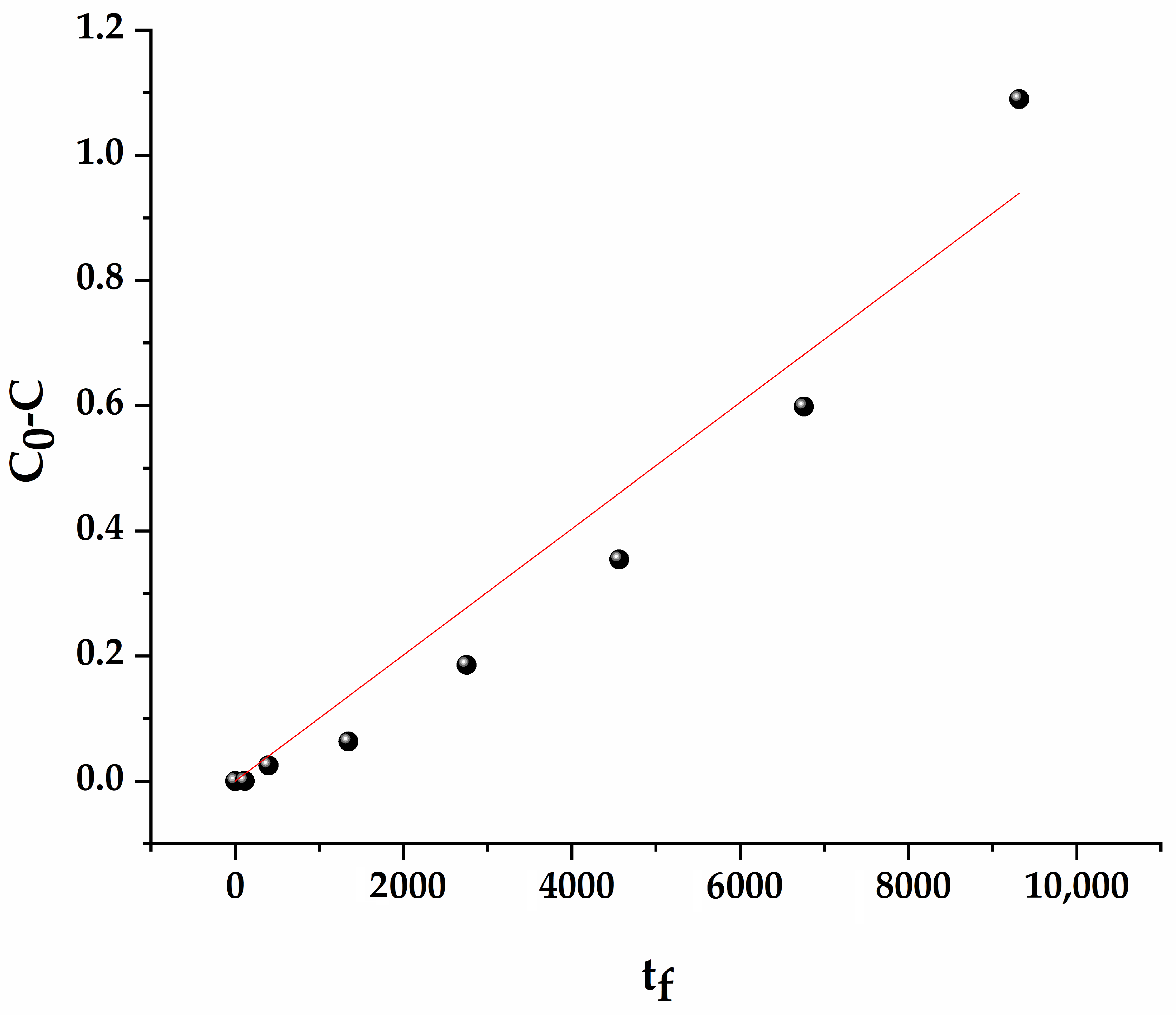
3.6. Fractal Analysis of Mn@SrTiO3
3.7. Fractal-like Photodegradation Reaction Kinetics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Tang, S. Investigation and Application of Fractals in Civil Engineering Materials. Fractal Fract. 2023, 7, 369. [Google Scholar] [CrossRef]
- Boeing, G. Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Qiang, C.; Deng, Y.; Cheong, K.H. Information Fractal Dimension of Mass Function. Fractals 2022, 30, 2250110. [Google Scholar] [CrossRef]
- Duan, Q.; An, J.; Mao, H.; Liang, D.; Li, H.; Wang, S.; Huang, C. Review about the Application of Fractal Theory in the Research of Packaging Materials. Materials 2021, 14, 860. [Google Scholar] [CrossRef] [PubMed]
- Gordillo-Cruz, E.; Alvarez-Ramirez, J.; González, F.; De Los Reyes, J.A. Fractal Analysis of X-ray Diffraction Patterns of Zirconia–Alumina Mixed Oxides. Phys. A Stat. Mech. Its Appl. 2018, 512, 635–643. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, Y.; Zhao, H.; Li, Z.; Feng, P.; Feng, F. Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal Fract. 2022, 6, 135. [Google Scholar] [CrossRef]
- Paun, M.-A.; Nichita, M.-V.; Paun, V.-A.; Paun, V.-P. Fractal Analysis of Four Xerogels Based on TEGylated Phenothiazine and Chitosan. Gels 2023, 9, 435. [Google Scholar] [CrossRef]
- Stajcic, I.; Stajcic, A.; Serpa, C.; Vasiljevic-Radovic, D.; Randjelovic, B.; Radojevic, V.; Fecht, H. Microstructure of Epoxy-Based Composites: Fractal Nature Analysis. Fractal Fract. 2022, 6, 741. [Google Scholar] [CrossRef]
- Peng, D.; Li, X. Fractal Contact Analysis for Transversely Isotropic Piezoelectric Materials: Theoretical and Numerical Predictions. Tribol. Int. 2023, 181, 108323. [Google Scholar] [CrossRef]
- Wei, H.; Lv, X.; Zhao, Y.; Li, C.; Yan, H.; Sun, R.; Kang, M. Quantitative Description of Filler Dispersion in Composite Materials by Fractal Analysis and Fluorescent labeling-LSCM Visualization Technology. Polym. Compos. 2022, 43, 3598–3608. [Google Scholar] [CrossRef]
- Li, C.; Xu, Y.; Jiang, Z.; Yu, B.; Xu, P. Fractal Analysis on the Mapping Relationship of Conductivity Properties in Porous Material. Fractal Fract. 2022, 6, 527. [Google Scholar] [CrossRef]
- Khamoushi, K.; Serpa, C. Fractal Analysis and Microwave Properties of La (Mg ½ Ti ½) O3. Mater. Today Commun. 2024, 38, 107995. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Mahmoud, S.A.; Mohamed, A.A. Unveiling the Photocatalytic Potential of Graphitic Carbon Nitride (g-C3N4): A State-of-the-Art Review. RSC Adv. 2024, 14, 25629–25662. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Noor, T.; Iqbal, N.; Yaqoob, L. Photocatalytic Dye Degradation from Textile Wastewater: A Review. ACS Omega 2024, 9, 21751–21767. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Ponce, N.T.; Banerjee, A.; Bandopadhyay, R.; Rajendran, S.; Lichtfouse, E. Green Polymeric Nanomaterials for the Photocatalytic Degradation of Dyes: A Review. Environ. Chem. Lett. 2020, 18, 1569–1580. [Google Scholar] [CrossRef]
- Sarkodie, B.; Amesimeku, J.; Frimpong, C.; Howard, E.K.; Feng, Q.; Xu, Z. Photocatalytic Degradation of Dyes by Novel Electrospun Nanofibers: A Review. Chemosphere 2023, 313, 137654. [Google Scholar] [CrossRef]
- Shabil Sha, M.; Anwar, H.; Musthafa, F.N.; Al-Lohedan, H.; Alfarwati, S.; Rajabathar, J.R.; Khalid Alahmad, J.; Cabibihan, J.-J.; Karnan, M.; Kumar Sadasivuni, K. Photocatalytic Degradation of Organic Dyes Using Reduced Graphene Oxide (rGO). Sci. Rep. 2024, 14, 3608. [Google Scholar] [CrossRef]
- Deepracha, S.; Ayral, A.; Ogawa, M. Acceleration of the Photocatalytic Degradation of Organics by In-Situ Removal of the Products of Degradation. Appl. Catal. B Environ. 2021, 284, 119705. [Google Scholar] [CrossRef]
- Günnemann, C.; Curti, M.; Sieland, F.; Bahnemann, D.W. Charge Carriers in Commercial Photocatalysts: Fractal Kinetics and Effect of “Inert” Additives. Top. Catal. 2021, 64, 737–747. [Google Scholar] [CrossRef]
- Wang, C.L. Fractional Kinetics of Photocatalytic Degradation. J. Adv. Dielect. 2018, 8, 1850034. [Google Scholar] [CrossRef]
- Sieland, F.; Schneider, J.; Bahnemann, D.W. Fractal Charge Carrier Kinetics in TiO2. J. Phys. Chem. C 2017, 121, 24282–24291. [Google Scholar] [CrossRef]
- Dobrescu, G.; Papa, F.; State, R.; Raciulete, M.; Berger, D.; Balint, I.; Ionescu, N.I. Modified Catalysts and Their Fractal Properties. Catalysts 2021, 11, 1518. [Google Scholar] [CrossRef]
- Hou, D.; Hu, X.; Ho, W.; Hu, P.; Huang, Y. Facile Fabrication of Porous Cr-Doped SrTiO3 Nanotubes by Electrospinning and Their Enhanced Visible-Light-Driven Photocatalytic Properties. J. Mater. Chem. A 2015, 3, 3935–3943. [Google Scholar] [CrossRef]
- Siqueira, F.B.L.B.; Campos, D.C. Application of Impedance Spectroscopy to Analyze the Electrical Properties of Cobalt Doped SrTiO3. Solid State Ion. 2023, 391, 116140. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Zhai, X.; Xue, Y.; Hao, L.; Zhu, H.; Liu, C.; Cheng, H.; Ouyang, J. Energy Storage Properties of Sol–Gel-Processed SrTiO3 Films. Materials 2022, 16, 31. [Google Scholar] [CrossRef]
- Xie, T.; Wang, Y.; Liu, C.; Xu, L. New Insights into Sensitization Mechanism of the Doped Ce (IV) into Strontium Titanate. Materials 2018, 11, 646. [Google Scholar] [CrossRef]
- Sharma, N.; Hernadi, K. The Emerging Career of Strontium Titanates in Photocatalytic Applications: A Review. Catalysts 2022, 12, 1619. [Google Scholar] [CrossRef]
- Fadlallah, M.M.; Gogova, D. Theoretical Study on Electronic, Optical, Magnetic and Photocatalytic Properties of Codoped SrTiO3 for Green Energy Application. Micro Nanostruct. 2022, 168, 207302. [Google Scholar] [CrossRef]
- Rocha-Rangel, E.; Pech-Rodríguez, W.J.; López-Hernández, J.; Calles-Arriaga, C.A.; Armendáriz-Mireles, E.N.; Castillo-Robles, J.A.; Rodríguez-García, J.A. Synthesis of SrTiO3 by the Calcination of SrCO3 and TiO2 Mixtures Intensively Ground by Means of High Energy Milling. Arch. Metall. Mater. 2020, 65, 621–626. [Google Scholar] [CrossRef]
- Yuan, Z.; Guo, M.; Shi, Q.; Liang, S.; Chen, Z.; Wang, S.; Chen, D.; Jiang, X.; Wei, F.; Liang, Z. Preparation and Piezoelectric Assisted Photocatalytic Degradation of BaTiO3/SrTiO3 Nanocomposites. Ceram. Int. 2024, 50, S0272884224027123. [Google Scholar] [CrossRef]
- Xin, X.; Zou, H.; Du, S.; Bao, Y.; Zhang, F. Visible-Light Harvesting SrTiO3 Solid Solutions for Photocatalytic Hydrogen Evolution from Water. ChemSusChem 2024, e202400533. [Google Scholar] [CrossRef] [PubMed]
- Basumatary, P.; Saha, S.; Ramchiary, A.; Konwar, D. Development of Bifunctional SrTiO3/SrMoO4 Heterojunction Catalyst for Efficient Adsorption and Photocatalytic Performance Evaluation. J. Phys. Chem. Solids 2024, 188, 111939. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, X.; Wang, Z.-H.; Peng, Y.; Liu, Y.; Yang, S.; Sun, C.; Xu, X.; Zhang, X.; Kang, J.; et al. Crystal Facet Engineering on SrTiO3 Enhances Photocatalytic Overall Water Splitting. J. Am. Chem. Soc. 2024, 146, 6618–6627. [Google Scholar] [CrossRef] [PubMed]
- Kala, K.; Jeyalakshmi, M.S.; Mohandoss, S.; Chandrasekaran, R. Evolution of Anticancer, Antioxidant and Photocatalytic Activities of Biosynthesized MnO2 Nanoparticles Using Aqueous Extract of Sida Acuta. Surf. Interfaces 2023, 40, 103136. [Google Scholar] [CrossRef]
- Malhotra, M.; Poonia, K.; Singh, P.; Khan, A.A.P.; Thakur, P.; Van Le, Q.; Helmy, E.T.; Ahamad, T.; Nguyen, V.-H.; Thakur, S.; et al. An Overview of Improving Photocatalytic Activity of MnO2 via the Z-Scheme Approach for Environmental and Energy Applications. J. Taiwan Inst. Chem. Eng. 2024, 158, 104945. [Google Scholar] [CrossRef]
- Arunpandian, M.; Oh, T.H.; Sriram, G. Breakthrough in High-Efficiency Photocatalytic Degradation of Acebutolol by Advanced Binary CeO2–MnO2 Oxide System. Molecules 2024, 29, 2854. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, K.; Prasad, T.; Rai, S.; Chaudhary, A.; Tungala, K.; Das, A. Fabrication of Cationic Microgels Doped MnO2/Fe3O4 Nanocomposites, and Study of Their Photocatalytic Performance and Reusability in Organic Transformations. Polym. Adv. Technol. 2024, 35, e6295. [Google Scholar] [CrossRef]
- Elhmali, H.T.; Stajcic, I.; Stajcic, A.; Pesic, I.; Jovanovic, M.; Petrovic, M.; Radojevic, V. Influence of Novel SrTiO3/MnO2 Hybrid Nanoparticles on Poly (Methyl Methacrylate) Thermal and Mechanical Behavior. Polymers 2024, 16, 278. [Google Scholar] [CrossRef]
- Meneses-Franco, A.; Campos-Vallette, M.; Vásquez, S.O.; Soto-Bustamante, E.A. Er-Doped Nanostructured BaTiO3 for NIR to Visible Upconversion. Materials 2018, 11, 1950. [Google Scholar] [CrossRef]
- Charan Prasanth, S.; Jose, R.; Vijay, A.; Vineetha, P.; Venkata Saravanan, K. An Investigation of Thermoelectric Power Factor of Mn and Nb Doped SrTiO3 Ceramics. Mater. Today Proc. 2022, 51, 1751–1753. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Mote, V.; Purushotham, Y.; Dole, B. Williamson-Hall Analysis in Estimation of Lattice Strain in Nanometer-Sized ZnO Particles. J. Theor. Appl. Phys. 2012, 6, 6. [Google Scholar] [CrossRef]
- Hassanzadeh-Tabrizi, S.A. Precise Calculation of Crystallite Size of Nanomaterials: A Review. J. Alloys Compd. 2023, 968, 171914. [Google Scholar] [CrossRef]
- Fiat Varol, S.; Babür, G.; Çankaya, G.; Kölemen, U. Synthesis of Sol–Gel Derived Nano-Crystalline ZnO Thin Films as TCO Window Layer: Effect of Sol Aging and Boron. RSC Adv. 2014, 4, 56645–56653. [Google Scholar] [CrossRef]
- Kelly, M.N.; Rheinheimer, W.; Hoffmann, M.J.; Rohrer, G.S. Anti-Thermal Grain Growth in SrTiO3: Coupled Reduction of the Grain Boundary Energy and Grain Growth Rate Constant. Acta Mater. 2018, 149, 11–18. [Google Scholar] [CrossRef]
- Chen, C.-C.; Lu, C.-S.; Chung, Y.-C. Photocatalytic Degradation of Ethyl Violet in Aqueous Solution Mediated by TiO2 Suspensions. J. Photochem. Photobiol. A Chem. 2006, 181, 120–125. [Google Scholar] [CrossRef]
- Lam, S.-M.; Sin, J.-C.; Abdullah, A.Z.; Mohamed, A.R. Degradation of Wastewaters Containing Organic Dyes Photocatalysed by Zinc Oxide: A Review. Desalin. Water Treat. 2012, 41, 131–169. [Google Scholar] [CrossRef]
- Konstantinou, I.K.; Albanis, T.A. TiO2-Assisted Photocatalytic Degradation of Azo Dyes in Aqueous Solution: Kinetic and Mechanistic Investigations. Appl. Catal. B Environ. 2004, 49, 1–14. [Google Scholar] [CrossRef]
- Brites, F.F.; Santana, V.S.; Fernandes-Machado, N.R.C. Effect of Support on the Photocatalytic Degradation of Textile Effluents Using Nb2O5 and ZnO: Photocatalytic Degradation of Textile Dye. Top Catal. 2011, 54, 264–269. [Google Scholar] [CrossRef]
- Ran, X.; Wang, L.; Xiao, B.; Lei, L.; Zhu, J.; Liu, Z.; Xi, X.; Feng, G.; Li, R.; Feng, J. Effective Removal of Methylene Blue on EuVO4/g-C3N4 Mesoporous Nanosheets via Coupling Adsorption and Photocatalysis. Int. J. Mol. Sci. 2022, 23, 10003. [Google Scholar] [CrossRef]
- Li, X.; Anwer, S.; Guan, Q.; Li, B.; Chan, V.; Palmisano, G.; Zheng, L. Surface Diffusion Induced Degradation Enhancement and Zero-Order Kinetics in Edge-Connected MoS2/Au/TiO2 Z-Scheme Photocatalytic System. Chem. Eng. Sci. 2024, 284, 119501. [Google Scholar] [CrossRef]
- Buescu, J.; Serpa, C. Fractal and Hausdorff Dimensions for Systems of Iterative Functional Equations. J. Math. Anal. Appl. 2019, 480, 123429. [Google Scholar] [CrossRef]
- Kopelman, R. Fractal Reaction Kinetics. Science 1988, 241, 1620–1626. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.Y.; Zhong, B.; Peng, S.Y. Kinetics of the First-Order Reaction on Fractals and Monte Carlo Simulations. Chem. Phys. Lett. 1995, 242, 228–231. [Google Scholar] [CrossRef]

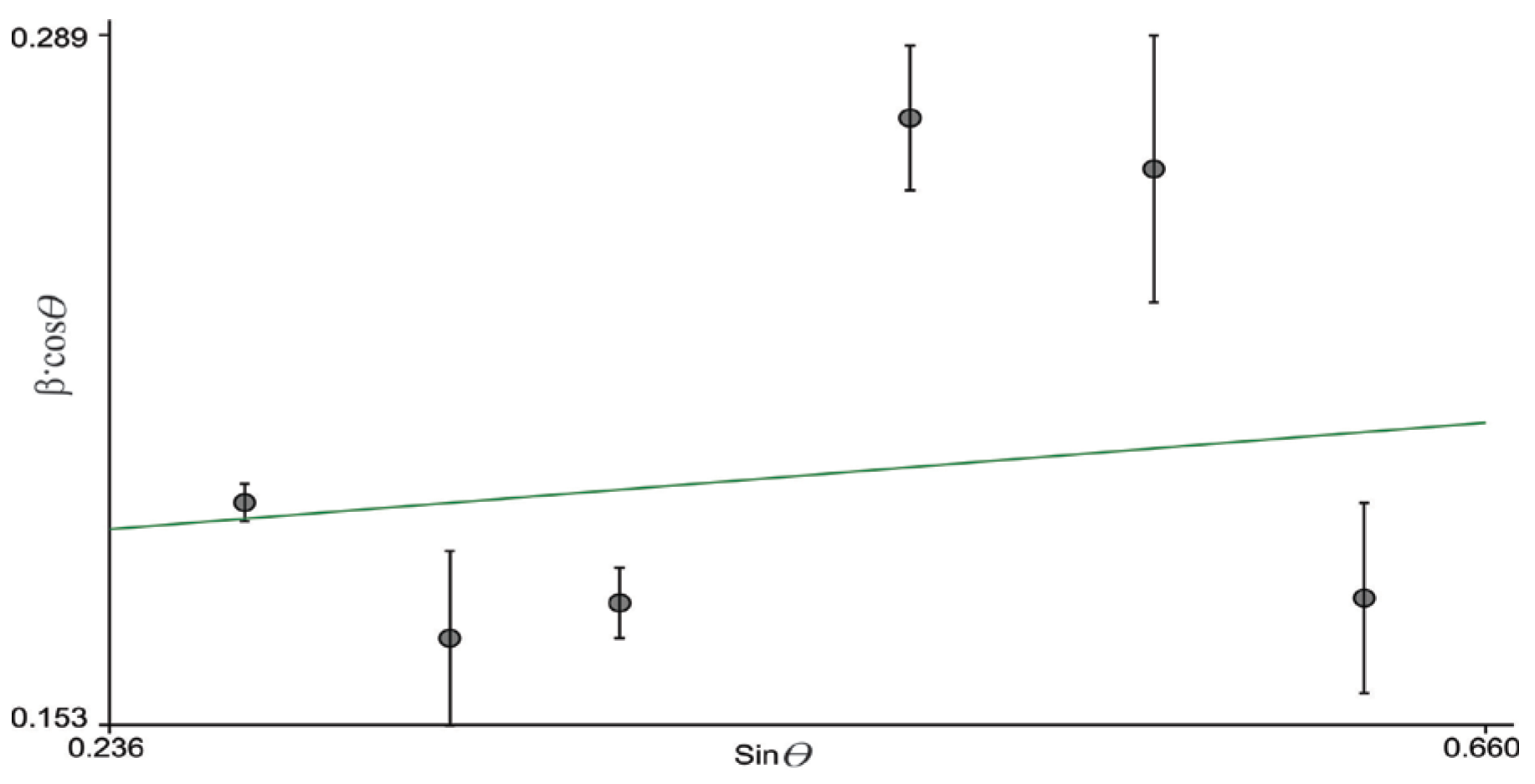



| Sample | Unit Cell Parameter (Å) and Volume (Å3) | Scherrer Method | W–H Method | ||
|---|---|---|---|---|---|
| D (nm) | D (nm) | ε (%) | δ (nm–2) | ||
| Mn@SrTiO3 | a = 3.903(5) V = 59.46(5) | 41(1) | 44(3) | 0.02(2) | 5.2 × 10–4 |
| Sample | Pseudo-Zero Order c0 – c = k0t | Pseudo-First Order ln(c0/c) = k1t | Pseudo-Second Order 1/c – 1/c0 = k2t | |||
|---|---|---|---|---|---|---|
| k0 (min−1) | R2 | k1 (min–1) | R2 | k2 (min−1) | R2 | |
| Mn@SrTiO3 | 0.0054(9) | 0.822 | 0.005(1) | 0.700 | 0.005(2) | 0.566 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −0.061 | −0.023 | 0.304 | 0.026 | −0.001 | −0.045 | 0.186 | −0.08 | 0.031 | 0.038 | −0.051 | 0.035 | |
| −0.577 | 0.448 | 0.247 | −0.22 | 0.052 | −0.131 | −0.461 | 0.013 | 0.346 | 0.194 | −0.564 | 0.311 | |
| 3.256 | 2.559 | 2.502 | 3.426 | 3.298 | 3.431 | 2.903 | 2.991 | 2.837 | 3.002 | 3.569 | 2.771 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stajcic, I.; Serpa, C.; Simovic, B.; Jankovic Castvan, I.; Dodevski, V.; Radojevic, V.; Stajcic, A. Fractal Analysis of Doped Strontium Titanate Photocatalyst. Fractal Fract. 2024, 8, 560. https://doi.org/10.3390/fractalfract8100560
Stajcic I, Serpa C, Simovic B, Jankovic Castvan I, Dodevski V, Radojevic V, Stajcic A. Fractal Analysis of Doped Strontium Titanate Photocatalyst. Fractal and Fractional. 2024; 8(10):560. https://doi.org/10.3390/fractalfract8100560
Chicago/Turabian StyleStajcic, Ivana, Cristina Serpa, Bojana Simovic, Ivona Jankovic Castvan, Vladimir Dodevski, Vesna Radojevic, and Aleksandar Stajcic. 2024. "Fractal Analysis of Doped Strontium Titanate Photocatalyst" Fractal and Fractional 8, no. 10: 560. https://doi.org/10.3390/fractalfract8100560
APA StyleStajcic, I., Serpa, C., Simovic, B., Jankovic Castvan, I., Dodevski, V., Radojevic, V., & Stajcic, A. (2024). Fractal Analysis of Doped Strontium Titanate Photocatalyst. Fractal and Fractional, 8(10), 560. https://doi.org/10.3390/fractalfract8100560







