Analysis of Caputo-Type Non-Linear Fractional Differential Equations and Their Ulam–Hyers Stability

Abstract

This study presents two novel frameworks, termed a quasi-modular b-metric space and a non-Archimedean quasi-modular b-metric space, and various topological properties are provided. Using comparison and simulation functions, this paper rigorously proves several fixed point theorems in the non-Archimedean quasi-modular b-metric space. As a useful application, it also establishes Ulam–Hyers stability for the fixed point problem. Finally, this study concludes with a unique solution to a non-linear fractional differential equation, making a substantial contribution to the discipline.

1. Introduction and Preliminaries

From this point forward, the symbols $\mathbb{R}$, ${\mathbb{R}}^{+}$, and $\mathbb{N}$ will be exclusively employed to denote the set of all real numbers, the set of all non-negative real numbers, and the set of all positive integer numbers, respectively. This notation will be consistently utilized throughout this document to maintain clarity and precision in mathematical discourse.

Fixed point theory remains a dynamically evolving and vibrant area within the mathematical sciences. Its foundational principles and methodological approaches offer broad applications across diverse disciplines, positioning them as indispensable tools for problem-solving within various mathematical contexts. The ensuing references are aimed at shedding light on specific recent advancements within the realm of fixed point theory [1].

One significant advancement within the realm of metric fixed point theory is the generalization of the metric space structure. This expansion broadens the conceptual framework of metric spaces and marks one of the most vibrant and fruitful areas of contemporary research. The adaptation and enhancement of the metric function have facilitated the introduction of numerous novel topological constructs within scholarly discourse. These modifications, whether through the alteration of the distance function or the incorporation of novel attributes, have paved the way for the emergence of innovative structures. This evolution is particularly pertinent across various specialized fields, including summability theory, sequence spaces, fuzzy theory, and the geometry of Banach spaces, among others, where these newly developed metric functions are extensively utilized.

The renowned question concerning the stability of functional equations, initially formulated by Ulam [2], presented an intriguing challenge in the field:

Let us consider two distinct structures, where $D_1$ represents a group and $D_2$ denotes a metric group endowed with a metric denoted by d. Given a positive real number $\epsilon$, the inquiry centers on whether it is possible to ascertain the existence of a positive real number $\delta$, such that if a function $\beth :D_1\to D_2$ satisfies the inequality

$$d\left(\beth \left(\sout{\lambda }\hslash \right),\beth \left(\sout{\lambda }\right)\beth \left(\hslash \right)\right)<\delta$$

for all elements $\sout{\lambda },\hslash \in D_1,$ it can then be established that a homomorphism $P:D_1\to D_2$ exists fulfilling the condition

$$d\left(\beth \left(z\right),P\left(z\right)\right)<\epsilon$$

for every element $z\in D_1.$

The discourse on Ulam stability, initially put forth by Ulam [2], has burgeoned into a significant domain of inquiry within the mathematical research field capturing the scholarly interest of numerous researchers. For those endeavoring to attain an enhanced comprehension of this subject, it is highly advisable to delve into the foundational works by D.H. Hyers et al. in [3] and M.T. Rassias in [4].

The research area of “Fractional Differential Equations” (FDEs) has experienced a notable surge in interest over recent years, attributed to its broad applicability across various real-world scenarios within the realms of science, thermodynamics, economics, and modeling, among potentially other fields [5,6]. This burgeoning attention stems from the recognition that, while traditional calculus serves as a foundational tool for explaining and simulating the complex behaviour inherent in numerous disciplines, fractional differential equations offer a more nuanced and precise framework for evaluating the intricate dynamics of complex natural systems. Examples of such applications include but are not limited to the mathematical modeling of infectious diseases, diffusion processes for image reconstruction, and the intricate interactions between cancer cells and the immune system. The conventional methodologies fall short of capturing the true essence of these complex dynamics, thereby rendering fractional differential equations a more suitable alternative to ordinary differential equations for such purposes [7]. In light of this, there has been a significant thrust toward the development of novel scientific methodologies and findings specifically tailored to fractional differential equations. This has led to a concentrated effort among researchers to delve into initial and boundary value problems that incorporate various types of derivatives, including but not limited to Atangana–Baleanu, Caputo–Fabrizio, and Caputo derivatives. The recent period has witnessed a remarkable expansion in the volume of research dedicated to this topic, yielding a plethora of both intriguing and practically relevant outcomes, as evidenced by the literature [8,9,10,11,12].

A notable example of such advancements is the introduction of the b-metric function, distinguished by the inclusion of a coefficient within the triangle inequality. This function, pioneered by Czerwik [13,14], represents the most significant extension of the metric function concept over the past four decades. Specifically, a function $d:\Xi \times \Xi \to {\mathbb{R}}^{+}$ is identified as a b-metric function on a non-empty set $\Xi$ provided it adheres to the revised axiom:

$$d\left(\sout{\lambda },z\right)\le \mathfrak{s}\left[d\left(\sout{\lambda },\hslash \right)+d\left(\hslash ,z\right)\right],$$

where $\mathfrak{s}$ is a constant greater than 1, thereby introducing a scalable factor to the traditional metric space definition, facilitating a broader spectrum of analytical and geometrical applications.

The concept of a quasi-metric was initially elucidated in 1931, delineating a foundational aspect within the domain of mathematical analysis. The definition provided is as follows:

Definition 1 

([15,16,17]). Consider a non-empty set Ξ, on which we define a function $q:\Xi \times \Xi \to {\mathbb{R}}^{+}$ that maps pairs of elements from Ξ to positive real numbers. For all $x,y,z\in \Xi$, q is designated as a quasi-pseudo-metric on Ξ if it fulfills the ensuing terms:

$\left(q_1\right)$

$q\left(\sout{\lambda },\sout{\lambda }\right)=0$;

$\left(q_2\right)$

$q\left(\sout{\lambda },z\right)\le q\left(\sout{\lambda },\hslash \right)+q\left(\hslash ,z\right).$

Moreover, a quasi-pseudo-metric q ascends to the status of a quasi-metric, provided it adheres to an additional stipulation:

$\left(q_3\right)$

$q(\sout{\lambda },\hslash )=q(\hslash ,\sout{\lambda })=0\Rightarrow \sout{\lambda }=\hslash$, which introduces a symmetric condition leading to the identification of distinct elements.

Expanding upon this framework, a quasi-metric q is recognized as a $T_1$-quasi-metric on Ξ if it encounters a further criterion:

$\left(q_4\right)$

$q\left(\sout{\lambda },\hslash \right)=0\Rightarrow \sout{\lambda }=\hslash$.

This exposition into the realm of quasi-metrics not only underscores their theoretical significance but also amplifies their applicability across diverse mathematical landscapes.

In the seminal work of Nakano [18], the concept of a modular space was introduced, marking a pivotal moment in the field. Following this foundational development, Chistyakov [19,20] significantly advanced the discourse on modular spaces by proposing the notion of a modular metric space. This concept has garnered considerable attention and achieved remarkable success, particularly over the past decade, largely due to its compelling physical interpretation, enhancing its appeal within the realm of metric functions.

Definition 2 

([19,20]). Let $\Xi \ne \varnothing$. A function ${\mu }_{\eta }:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$, defined by $\mu \left(\eta ,\sout{\lambda },\hslash \right)={\mu }_{\eta }\left(\sout{\lambda },\hslash \right)$, is called a modular metric on Ξ if it satisfies the subsequent axioms for all $\sout{\lambda },\hslash ,z\in \Xi$:

$\left({\mu }_1\right)$ 

${\mu }_{\eta }\left(\sout{\lambda },\hslash \right)=0$ for all $\eta >0$⇔$\sout{\lambda }=\hslash$;

$\left({\mu }_2\right)$ 

${\mu }_{\eta }\left(\sout{\lambda },\hslash \right)={\mu }_{\eta }\left(\hslash ,\sout{\lambda }\right)$ for all $\eta >0$;

$\left({\mu }_3\right)$ 

${\mu }_{\eta +\ell }\left(\sout{\lambda },\hslash \right)\le {\mu }_{\eta }\left(\sout{\lambda },z\right)+{\mu }_{\ell }\left(z,\hslash \right)$ for all $\eta ,\ell >0.$

In the event that the axiom $\left({\mu }_{1^{\prime }}\right)$, delineated below, is furnished in place of $\left({\mu }_1\right)$, ${\mu }_{\eta }$ is designated as a pseudo-modular metric on the set $\Xi$. This can be articulated as follows:

$\left({\mu }_{1^{\prime }}\right)$ 

For every $\eta >0$, it holds that ${\mu }_{\eta }(\sout{\lambda },\sout{\lambda })=0$.

This formulation is essential for extending the traditional scope of modular metrics, facilitating a broader spectrum of mathematical analysis and topology applications.

The introduction of the concept of modular b-metric spaces was initially put forth by Ege and Alaca [21] in 2018, marking a pivotal moment in the domain of metric space analysis. This foundational work proposed a nuanced alteration to the requirement $\left({\mu }_3\right)$ within the established Definition 2, thereby extending the theoretical framework and potential applicability of modular metric spaces. This novel adjustment has subsequently facilitated the opening of new pathways for investigation and exploration within the discipline, underscoring the perpetual evolution and profundity of mathematical inquiry:

$\left({\mu }_{3^{\prime }}\right)$ 

an element $\mathfrak{s}\ge 1$ exists such that, for all $\sout{\lambda },\hslash ,z\in \Xi$ and for all $\eta ,\ell >0$,

$${\mu }_{\eta +\ell }\left(\sout{\lambda },\hslash \right)\le \mathfrak{s}\left[{\mu }_{\eta }\left(\sout{\lambda },z\right)+{\mu }_{\ell }\left(z,\hslash \right)\right].$$

It is established that a modular metric space can be derived from a modular b-metric space under the condition that $\mathfrak{s}=1$. Also, the set

$${\Xi }_{{\mu }_{\eta }}^{*}\left({\sout{\lambda }}_0\right)=\left\{\sout{\lambda }\in \Xi :\exists \eta >0\mathrm{such}\mathrm{that}{\mu }_{\eta }\left(\sout{\lambda },{\sout{\lambda }}_0\right)<\infty \right\}$$

is known as a modular b-metric space (around ${\lambda }_0$). Further, refer to [22,23,24,25,26,27] to learn more.

In 2019, Girgin and Öztürk [28] innovatively merged existing principles to develop what is known as a quasi-modular metric space, presenting a novel generalized metric space framework. Further, they elucidated specific topological characteristics inherent to this space, marking a significant contribution to the field. Beyond these foundational developments, the duo proposed various fixed point theorems, opening avenues for practical applications through the establishment of a non-Archimedean quasi-modular metric space. Notably, when the emphasized space was integrated with a directed graph, the application of a simulation function facilitated the derivation of fixed point results, underscoring the practical implications and versatility of their work [29].

Definition 3. 

Let $q^{\mu }:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$ be a function on a non-void set Ξ. If the statements

$\left({q^{\mu }}_1\right)$

$\sout{\lambda }=\hslash \iff {q^{\mu }}_{\eta }\left(\sout{\lambda },\hslash \right)=0$ for all $\eta >0$ and

$\left({q^{\mu }}_2\right)$

${q^{\mu }}_{\eta +\ell }\left(\sout{\lambda },\hslash \right)\le {q^{\mu }}_{\eta }\left(\sout{\lambda },z\right)+{q^{\mu }}_{\ell }\left(z,\hslash \right)$ for all $\eta ,\ell >0$ and $\sout{\lambda },\hslash ,z\in \Xi$

are provided, then $q^{\mu }$ is termed a quasi-modular metric on Ξ, and ${\Xi }_{q^{\mu }}$ is a quasi-modular metric space, which is abbreviated by $\mathcal{Q}\mathcal{M}\mathcal{M}\mathcal{S}$.

Moreover, if we consider the below condition instead of $\left({q^{\mu }}_2\right)$, then we gain the features of non-Archimedean space; that is, ${\Xi }_{q^{\mu }}$ is a non-Archimedean quasi-modular metric space (briefly $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}\mathcal{M}\mathcal{M}\mathcal{S}$).

$\left({q^{\tilde{\mu }}}_{2^{\prime }}\right)$

${q^{\mu }}_{max\left\{\eta ,\ell \right\}}\left(\sout{\lambda },\hslash \right)\le {q^{\mu }}_{\eta }\left(\sout{\lambda },z\right)+{q^{\mu }}_{\ell }\left(z,\hslash \right).$

In the pursuit of enhancing productivity within the realm of fixed point theory, numerous scholars have embarked on an endeavor to augment the Banach contraction principle through the incorporation of auxiliary functions across various abstract spaces. This area of research is currently in a state of active exploration. A noteworthy advancement in this field is the identification of a novel class known as simulation functions, a contribution made by Khojasteh et al. (2015) [30], delineating a considerable milestone in the evolving landscape of fixed point theory.

Definition 4 

([30]). A function $\xi :\left[0,\infty \right)\times \left[0,\infty \right)\to \mathbb{R}$ is a simulation function if the following statements are ensured:

$\left({\xi }_1\right)$

$\xi \left(0,0\right)=0$;

$\left({\xi }_2\right)$

$\xi \left(\widehat{f},\widehat{q}\right)<\widehat{q}-\widehat{f}$ for all $\widehat{f},\widehat{q}>0$;

$\left({\xi }_3\right)$

If $\left\{{\widehat{f}}_{\mathfrak{y}}\right\}$, $\left\{{\widehat{q}}_{\mathfrak{y}}\right\}$ are sequences in $\left(0,\infty \right)$ such that $\underset{n\to \infty }{lim}{\widehat{f}}_{\mathfrak{y}}=\underset{n\to \infty }{lim}{\widehat{q}}_{\mathfrak{y}}>0$, then

$$\underset{n\to \infty }{limsup}\xi \left({\widehat{f}}_{\mathfrak{y}},{\widehat{q}}_{\mathfrak{y}}\right)<0.$$

In addition, from $\left({\xi }_2\right)$, it consequently ensues that $\xi \left(\widehat{f},\widehat{q}\right)<0$ for all $\widehat{f}\ge \widehat{q}>0$.

It is hereby acknowledged that the notation $\mathcal{Z}$ accurately denotes the comprehensive set of all simulation functions.

Definition 5 

([30]). A mapping $\beth :\Xi \to \Xi$ on a metric space $\left(\Xi ,d\right)$ is entitled as a $\mathcal{Z}$ contraction with respect to $\xi \in \mathcal{Z}$ if the inequality

$$\xi \left(d\left(\beth \sout{\lambda },\beth \hslash \right),d\left(\sout{\lambda },\hslash \right)\right)\ge 0$$

is fulfilled for all $\sout{\lambda },\hslash \in \mathcal{U}.$

In exploring the realm of Banach contraction mappings, one can elucidate their nature through the employment of simulation functions, denoted as $\xi \in \mathcal{Z}$. These functions are characterized by the relationship $\xi \left(\widehat{f},\widehat{q}\right)=\gamma \widehat{q}-\widehat{f}$, which is applicable for every $\widehat{f},\widehat{q}\in \left[0,\infty \right)$, where $\gamma$ is constrained within the interval $\left[0,1\right)$. This relationship underscores the foundational principle of contraction mappings within the context of mathematical analysis, offering a nuanced perspective on the dynamics between functions within specified domains.

Building upon the foundational work in the field, Samet et al. [31] introduced the notion of $\alpha$-admissible mappings, significantly contributing to the domain’s understanding. Following this pioneering effort, Karapınar et al. [32] expanded upon the initial concept, offering a broader generalization that has been widely noted and appreciated in subsequent academic discussions and analyses.

Definition 6 

([31]). Let $\beth :\Xi \to \Xi$ and $\alpha :\Xi \times \Xi \to \left[0,\infty \right)$ be two mappings. Then, ℶ is named α-admissible if the statement

$$\alpha \left(\sout{\lambda },\hslash \right)\ge 1\Rightarrow \alpha \left(\beth \sout{\lambda },\beth \hslash \right)\ge 1$$

is fulfilled for all $\sout{\lambda },\hslash \in \Xi .$

Definition 7 

([32]). Let $\beth :\Xi \to \Xi$ and $\alpha :\Xi \times \Xi \to \left[0,\infty \right)$ be two mappings. The mapping ℶ is called triangular α-admissible if the axioms

$\left(i\right)$

$\alpha \left(\sout{\lambda },\hslash \right)\ge 1\Rightarrow \alpha \left(\beth \sout{\lambda },\beth \hslash \right)\ge 1$ and

$\left(ii\right)$

$\alpha \left(\sout{\lambda },z\right)\ge 1$ and $\alpha \left(z,\hslash \right)\ge 1$, then $\alpha \left(\sout{\lambda },\hslash \right)\ge 1$

are provided for all $\sout{\lambda },\hslash ,z\in \Xi .$

On the other hand, let $\varpi :\left[0,\infty \right)\to \left[0,\infty \right)$ be a function providing the subsequent statements:

$\left({\varpi }_1\right)$

$\varpi$ is nondecreasing;

$\left({\varpi }_2\right)$

${\displaystyle \sum _{n=1}^{\infty }}{\varpi }^n\left(\rho \right)<\infty$, where ${\varpi }^n$ represents the $n-$times composition of $\varpi$.

Thereupon, $\varpi$ is referred to as $\mathfrak{c}-$comparison functions, and note that $\varpi \left(\rho \right)<\rho$ for any $\rho >0$. Also, let $\mathcal{L}$ symbolize the family of all such functions.

In 1996, Berinde [33] enhanced the idea of a $\mathfrak{c}-$comparison function to broaden the applicability of fixed point theorems to the category of b-metric spaces.

Definition 8 

([33]). Let $\psi :\left[0,\infty \right)\to \left[0,\infty \right)$ be a function and $\mathfrak{s}\in \mathbb{R}$ with $\mathfrak{s}\ge 1$. If the following circumstances are met, then the mapping ψ is termed a $\mathfrak{b}-$comparison function:

$\left({\psi }_1\right)$

ψ is nondecreasing;

$\left({\psi }_2\right)$

There exist ${\vartheta }_0\in \mathbb{N}$, $\gamma \in \left(0,1\right)$ and a convergent series of non-negative terms ${\displaystyle \sum _{\vartheta =1}^{\infty }}{v}_{\vartheta }$ such that

$${\mathfrak{s}}^{\vartheta +1}{\psi }^{\vartheta +1}\left(\rho \right)\le \gamma {\mathfrak{s}}^{\vartheta }{\psi }^{\vartheta }\left(\rho \right)+v_{\vartheta },$$

for $\vartheta \ge {\vartheta }_0$ and any $\rho \in \left[0,\infty \right)$.

Moreover, the family ${\mathcal{L}}_{♭}$ is denoted to symbolize all such functions.

Besides that, a $\mathfrak{b}-$comparison function and a $\mathfrak{c}-$comparison function coincide in the case of $\mathfrak{s}=1$.

The lemma is essential at the stage of proving our main results.

Lemma 1. 

Let $\psi :\left[0,\infty \right)\to \left[0,\infty \right)$ be a $\mathfrak{b}-$comparison function. Thus, the ensuing circumstances exist:

$\left({\psi }_3\right)$

The series ${\displaystyle \sum _{\vartheta =0}^{\infty }}{\mathfrak{s}}^{\vartheta }{\psi }^{\vartheta }\left(\rho \right)$ converges for any $\rho >0$;

$\left({\psi }_4\right)$

The function $p_{\mathfrak{s}}:\left[0,\infty \right)\to \left[0,\infty \right)$ defined by $p_{\mathfrak{s}}\left(\rho \right)={\displaystyle \sum _{\vartheta =0}^{\infty }}{\mathfrak{s}}^{\vartheta }{\psi }^{\vartheta }\left(\rho \right),$$\rho \in \left[0,\infty \right)$ is increasing and continuous at the point $0.$

In work presented by Samet et al., a novel notation is introduced, which is meticulously developed with consideration toward admissible mappings. This conceptual framework is outlined in their study, referenced [31].

Definition 9. 

Let $\beth :\Xi \to \Xi$ be a given mapping on a complete metric space $\left(\Xi ,d\right)$. If there exist $\alpha :\Xi \times \Xi \to \left[0,\infty \right)$ and $\varpi \in \mathcal{L}$ satisfying the inequality

$$\alpha \left(\sout{\lambda },\hslash \right)d\left(\beth \sout{\lambda },\beth \hslash \right)\le \varpi \left(d\left(\sout{\lambda },\hslash \right)\right)$$

for all $\sout{\lambda },\hslash \in \Xi$, then the mapping ℶ is entitled $\alpha -\varpi -$contractive.

Building upon the foundational concepts introduced earlier, this study aims to delineate and explore the nuances of quasi-modular b-metric spaces alongside their non-Archimedean counterparts. Furthermore, this discourse delineates specific topological characteristics inherent within these spaces. Subsequently, the investigation unveils novel findings related to fixed points by proposing a framework for generalized simulative ${\mathcal{Z}}_{\psi }-$contraction within the realm of non-Archimedean quasi-modular b-metric spaces.

2. Some Topological Features in the Setting of a Quasi-Modular $\mathit{b}-$Metric Space

The current section extends the idea of $QMMS$ through a b-metric function, which is referred to as a quasi-modular b-metric space, as mentioned below:

Definition 10. 

Let Ξ be a non-void set. A function $q^{\tilde{\mu }}:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$ is entitled a quasi-modular b-metric (briefly $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$) with $\mathfrak{s}\ge 1$ on Ξ if the statements

$\left({q^{\tilde{\mu }}}_1\right)$

$\sout{\lambda }=\hslash \iff {q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)=0$ for all $\eta >0$,

$\left({q^{\tilde{\mu }}}_2\right)$

${q^{\tilde{\mu }}}_{\eta +\ell }\left(\sout{\lambda },\hslash \right)\le s\left[{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },z\right)+{q^{\tilde{\mu }}}_{\ell }\left(z,\hslash \right)\right]$ for all $\eta ,\ell >0$ and $\sout{\lambda },\hslash ,z\in \Xi$

are met, and thence, ${\Xi }_{q^{\tilde{\mu }}}$ is a quasi-modular b-metric space denoted by $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$.

Moreover, we replace the condition of $\left({q^{\tilde{\mu }}}_1\right)$ with the following one; then, $q^{\tilde{\mu }}$ is entitled as a quasi-pseudo-modular b metric on $\Xi$:

$\left({q^{\tilde{\mu }}}_{1^{\prime }}\right)$

${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\sout{\lambda }\right)=0$ for all $\eta >0$ and $\sout{\lambda }\in \Xi .$

Also, a $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$$q^{\tilde{\mu }}$ on $\Xi$ is termed as regular if the below weaker criteria hold instead of $\left({q^{\tilde{\mu }}}_1\right)$:

$\left({q^{\tilde{\mu }}}_3\right)$

$\sout{\lambda }=\hslash$ if and only if ${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)=0$ for some $\eta >0.$

Additionally, $q^{\tilde{\mu }}$ is termed convex if for $\eta ,\ell >0$ and $\lambda ,\hslash ,z\in \Xi$ the inequality provides:

$\left({q^{\tilde{\mu }}}_4\right)$

${q^{\tilde{\mu }}}_{\eta +\ell }\left(\sout{\lambda },\hslash \right)\le {\displaystyle \frac{\eta }{\eta +\ell }}{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },z\right)+{\displaystyle \frac{\ell }{\eta +\ell }}{q^{\tilde{\mu }}}_{\ell }\left(z,\hslash \right).$

Definition 11. 

In the definition of $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$, if we replace $\left({q^{\tilde{\mu }}}_2\right)$ with

$\left({q^{\tilde{\mu }}}_5\right)$

${q^{\tilde{\mu }}}_{max\left\{\eta ,\ell \right\}}\left(\sout{\lambda },\hslash \right)\le \mathfrak{s}\left[{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },z\right)+{q^{\tilde{\mu }}}_{\ell }\left(z,\hslash \right)\right]$

for all $\eta ,\ell >0$ and $\sout{\lambda },\hslash ,z\in \Xi$, then ${\Xi }_{q^{\tilde{\mu }}}$ is named non-Archimedean quasi-modular b-metric space, which is specified by $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$.

Since the axiom $\left({q^{\tilde{\mu }}}_5\right)$ implies $\left({q^{\tilde{\mu }}}_2\right)$, every $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ is a $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$.

Remark 1. 

Taking the aforementioned information into account, we yield that

$\left(i\right)$

For a $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$$q^{\tilde{\mu }}$ on Ξ, the conjugate $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$${q^{\tilde{\mu }}}^{-1}$ on Ξ of $q^{\tilde{\mu }}$ is defined by ${q^{\tilde{\mu }}}_{\eta }^{-1}\left(\sout{\lambda },\hslash \right)={q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\sout{\lambda }\right)$;

$\left(ii\right)$

If $q^{\tilde{\mu }}$ is a $T_0$-quasi-pseudo-modular b metric on Ξ, then ${q^{\tilde{\mu }}}^E$ is represented by ${q^{\tilde{\mu }}}^E={q^{\tilde{\mu }}}^{-1}\vee q^{\tilde{\mu }}$, that is,

$${q^{\tilde{\mu }}}_{\eta }^E\left(\sout{\lambda },\hslash \right)=max\left\{{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\sout{\lambda }\right)\right\},$$

defines modular b-metric spaces.

Each $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$$q^{\tilde{\mu }}$ on $\Xi$ induces $T_0$ topology ${\tau }_{q^{\tilde{\mu }}}$ on $\Xi$, which owns, as a base, the family of open $q^{\tilde{\mu }}-$balls

$$\left\{{\mathrm{B}}_{\eta }\left(\sout{\lambda },r\right):\sout{\lambda }\in \Xi ,r>0,\mathrm{and}\eta >0\right\},$$

where

$${\mathrm{B}}_{\eta }\left(\sout{\lambda },\epsilon \right)=\left\{\hslash \in \Xi :{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)<\epsilon \right\}$$

for all $\lambda \in \Xi$, $r>0$ and $\eta >0$. If ${\tau }_{q^{\tilde{\mu }}}$ is a $T_1$ topology on $\Xi$, then $q^{\tilde{\mu }}$ is a $T_1-$$\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$ on $\Xi$.

Definition 12. 

Let ${\left\{{\sout{\lambda }}_p\right\}}_{p\in \mathbb{N}}$ be a sequence in a $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ ${\Xi }_{q^{\tilde{\mu }}}$ provided that ${\sout{\lambda }}_p\to \sout{\lambda }$. Then, the sequence ${\left\{{\sout{\lambda }}_p\right\}}_{p\in \mathbb{N}}$ is termed

$\left(1\right)$

$q^{\tilde{\mu }}-$convergent or left convergent if ${\sout{\lambda }}_p\to \sout{\lambda }\iff {q^{\tilde{\mu }}}_m\left(\sout{\lambda },{\sout{\lambda }}_p\right)\to 0.$

$\left(2\right)$

${q^{\tilde{\mu }}}^{-1}-$convergent or right convergent if ${\sout{\lambda }}_p\to \sout{\lambda }\iff {q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_p,\sout{\lambda }\right)\to 0.$

$\left(3\right)$

${q^{\tilde{\mu }}}^E-$convergent if ${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },{\sout{\lambda }}_p\right)\to 0$ and ${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_p,\sout{\lambda }\right)\to 0.$

$\left(4\right)$

Left (right) $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy if for every $\epsilon >0$, $p_{\epsilon }\in \mathbb{N}$ exists such that ${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_k,{\sout{\lambda }}_p\right)<\epsilon$ for all $p,k\in \mathbb{N}$ with $p_{\epsilon }\le k\le p\left(p_{\epsilon }\le p\le k\right)$ and for all $\eta >0$.

$\left(5\right)$

${q^{\tilde{\mu }}}^E-$Cauchy if, for every $\epsilon >0$, there exists $p_{\epsilon }\in \mathbb{N}$ such that ${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_p,{\sout{\lambda }}_k\right)<\epsilon$ for all $p,k\in \mathbb{N}$ with $p,k\ge n_{\epsilon }$.

Definition 13. 

Those below can be expressed through the above definition:

$\left(i\right)$

A sequence is left $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy with regard to $q^{\tilde{\mu }}$⇔ it is right-$q^{\tilde{\mu }}-\mathcal{K}-$Cauchy with regard to ${q^{\tilde{\mu }}}^{-1}$;

$\left(ii\right)$

A sequence is ${q^{\tilde{\mu }}}^E-$Cauchy ⇔ it is left and right $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy.

Definition 14. 

A $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ ${\Xi }_{q^{\tilde{\mu }}}$ is called:

$\left(i\right)$

Left $q^{\tilde{\mu }}-\mathcal{K}-$complete if every left $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy is $q^{\tilde{\mu }}-$convergent.

$\left(ii\right)$

$q^{\tilde{\mu }}-$Smyth-complete if every left $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy sequence is ${q^{\tilde{\mu }}}^E-$convergent.

$\left(iii\right)$

$q^{\tilde{\mu }}-$bicomplete if ${\Xi }_{{q^{\tilde{\mu }}}^E}$ is a complete general modular b-metric space.

Every $q^{\tilde{\mu }}-$Smyth-complete $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ is left as a $q^{\tilde{\mu }}-\mathcal{K}-$complete space. The contrary is not accurate in general.

Example 1. 

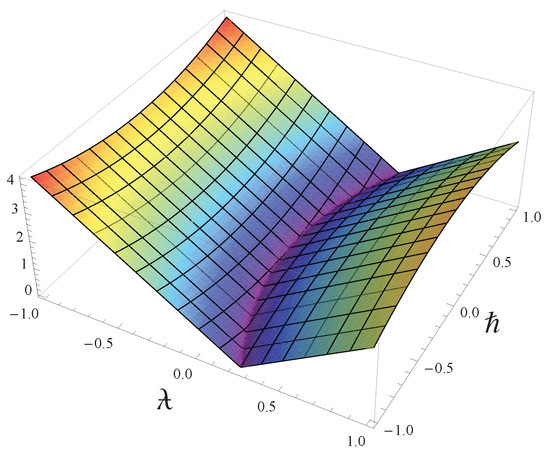
Let $\Xi =\left[-1,1\right]$, and consider the quasi-modular b metric $q^{\tilde{\mu }}:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$ by

$${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)=\left\{\begin{array}{c}0,\mathrm{iff}\sout{\lambda }=\hslash \hfill \\ {\displaystyle \frac{{\left|\sout{\lambda }-\frac{\hslash }{2}\right|}^2}{\eta }},\mathrm{otherwise}\hfill \end{array}\right..$$

(1)

In Figure 1, we present an illustration of Equation (1), specifically when $\varrho =1$ and within the interval $\left[-1,1\right]$:

Figure 1. A 3D representation of Equation (1).

Indeed, note that ${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\ge 0$ for all $\sout{\lambda },\hslash \in \Xi$ and ${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)=0\iff \sout{\lambda }=\hslash$ for all $\eta >0$. Moreover, $q^{\tilde{\mu }}$ is not symmetric provided that ${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)={q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\sout{\lambda }\right)\iff \sout{\lambda }=\hslash$ for all $\eta >0$. Assuming $\sout{\lambda }=1$, $\hslash =0$, and $z=-1$, we may deduce that the inequality

$$\begin{array}{cc}\hfill {q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },z\right)={q^{\tilde{\mu }}}_{\eta }\left(1,-1\right)={\displaystyle \frac{9}{4\eta }}& \le s\left[{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)+{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,z\right)\right]\hfill \\ & =\mathfrak{s}\left[{q^{\tilde{\mu }}}_{\eta }\left(1,0\right)+{q^{\tilde{\mu }}}_{\eta }\left(0,-1\right)\right]=\mathfrak{s}{\displaystyle \frac{5}{4\eta }}\hfill \end{array}$$

is not satisfied in the case of $\mathfrak{s}=1$, i.e., $q^{\tilde{\mu }}$ is not a non-Archimedian quasi-modular metric function. However, by taking $\mathfrak{s}\ge 2$, we yield that $q^{\tilde{\mu }}$ is a non-Archimedian quasi-modular b metric, and consequently, ${\Xi }_{q^{\tilde{\mu }}}$ is a $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$.

3. Fixed Point Results

In the analysis that follows, we make use of the following property:

$\left(\Omega \right)$

ℶ is a triangular $\alpha$-admissible mapping, and an element ${\sout{\lambda }}_0\in {\Xi }_{q^{\tilde{\mu }}}$ exists such that $\alpha \left({\sout{\lambda }}_0,\beth {\sout{\lambda }}_0\right)\ge 1$.

Definition 15. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ and $\beth :{\Xi }_{q^{\tilde{\mu }}}\to {\Xi }_{q^{\tilde{\mu }}}$ be a given mapping. Then, the mapping ℶ is entitled a generalized simulative ${\mathcal{Z}}_{\psi }$ contraction if there exist $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$, $\psi \in {\mathcal{L}}_{♭}$, and $\xi \in \mathcal{Z}$ such that

$$\xi \left(\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right),\psi \left(\mathcal{M}\left(\sout{\lambda },\hslash \right)\right)\right)\ge 0,$$

(2)

where

$$\mathcal{M}\left(\sout{\lambda },\hslash \right)=max\left\{{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\beth \sout{\lambda }\right),{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\beth \hslash \right)\right\}$$

(3)

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}}.$

Theorem 1. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1.$ Presume that ℶ is a generalized simulative ${\mathcal{Z}}_{\psi }$ contraction and provides the subsequent statements:

$\left(i\right)$

The condition $\left(\Omega \right)$ is met;

$\left(ii\right)$

The mapping ℶ is continuous.

Then, ℶ admits a fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

Proof. 

Assume that ${\sout{\lambda }}_0\in {\Xi }_{q^{\tilde{\mu }}}$ exists such that $\alpha \left({\sout{\lambda }}_0,\beth {\sout{\lambda }}_0\right)\ge 1$. Form the sequence ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ in ${\Xi }_{q^{\tilde{\mu }}}$ by ${\sout{\lambda }}_{\mathfrak{y}+1}=\beth {\sout{\lambda }}_{\mathfrak{y}},$ for all $\mathfrak{y}\in \mathbb{N}.$ If ${\sout{\lambda }}_{\mathfrak{y}+1}={\sout{\lambda }}_{\mathfrak{y}}$ for some $\mathfrak{y}\in \mathbb{N},$ then ${\sout{\lambda }}^{*}={\sout{\lambda }}_{\mathfrak{y}}$ is a fixed point for ℶ and the proof has been concluded. As a result, we conclude that ${\sout{\lambda }}_{\mathfrak{y}+1}\ne {\sout{\lambda }}_{\mathfrak{y}}$ for all $\mathfrak{y}\in \mathbb{N}.$ Because ℶ is triangular $\alpha$-admissible, we have $\alpha \left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)=\alpha \left({\sout{\lambda }}_0,\beth {\sout{\lambda }}_0\right)\ge 1$⇒$\alpha \left(\beth {\sout{\lambda }}_0,\beth {\sout{\lambda }}_1\right)=\alpha \left({\sout{\lambda }}_1,\beth {\sout{\lambda }}_2\right)\ge 1.$ By induction, we obtain

$$\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\ge 1,$$

(4)

for all $\mathfrak{y}\in \mathbb{N}.$ Regarding (2), we attain

$$\begin{array}{c}0\le \xi \left(\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}_{\mathfrak{y}-1}\right),\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right)\right)\right)\hfill \\ \\ <\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right)\right)-\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}_{\mathfrak{y}-1}\right).\hfill \end{array}$$

(5)

Then, from (5), we have

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\le \alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}_{\mathfrak{y}-1}\right)<\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}-1}\right)\right)$$

(6)

where

$$\begin{array}{c}\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right)=max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},\beth {\sout{\lambda }}_{\mathfrak{y}-1}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}_{\mathfrak{y}}\right)\right\}\hfill \\ \\ =max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\right\}\hfill \\ \\ =max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\right\}.\hfill \end{array}$$

If $\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right)={q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right),$ then, from (6), we gain

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\right)<{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right),$$

which is a contradiction. Thence, $\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right)={q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right),$ and we obtain

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}-1},{\sout{\lambda }}_{\mathfrak{y}}\right)\right).$$

By induction, we obtain

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\le {\psi }^n\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right),$$

(7)

for all $\mathfrak{y}\in \mathbb{N}.$ From (7) and by using $\left({q^{\tilde{\mu }}}_2\right)$ and the non-Archimedean property of our space, for all $z\ge 1,$ we have

$$\begin{array}{c}{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{n+z}\right)\le \mathfrak{s}{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)+{\mathfrak{s}}^2{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}+1},{\sout{\lambda }}_{n+2}\right)+\dots \hfill \\ +{\mathfrak{s}}^{z-1}{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{n+z-2},{\sout{\lambda }}_{n+z-1}\right)+{\mathfrak{s}}^z{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{n+z-1},{\sout{\lambda }}_{n+z}\right)\hfill \\ \\ \le \mathfrak{s}{\psi }^n\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)+{\mathfrak{s}}^2{\psi }^{n+1}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)+\dots \hfill \\ +{\mathfrak{s}}^{z-1}{\psi }^{n+z-2}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)+{\mathfrak{s}}^z{\psi }^{n+z-1}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)\hfill \\ \\ ={\displaystyle \frac{1}{{\mathfrak{s}}^{n-1}}}\left[{\mathfrak{s}}^n{\psi }^n\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)\right.+{\mathfrak{s}}^{n+1}{\psi }^{n+1}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)+\dots \hfill \\ +{\mathfrak{s}}^{n+z-2}{\psi }^{n+z-2}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)+\left.{\mathfrak{s}}^{n+z-1}{\psi }^{n+z-1}\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)\right].\hfill \end{array}$$

By denoting $Z_{\mathfrak{y}}={\displaystyle \sum _{k=0}^n}{\mathfrak{s}}^k{\psi }^k\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right),\mathfrak{y}\ge 1$, we attain

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{n+z}\right)\le {\displaystyle \frac{1}{{\mathfrak{s}}^{\mathfrak{y}-1}}}\left[Z_{\mathfrak{y}+z-1}-Z_{\mathfrak{y}-1}\right],z\ge 1.$$

(8)

Thereupon, from Lemma 1, we learn that the series ${\displaystyle \sum _{k=0}^{\mathfrak{y}}}{\mathfrak{s}}^k{\psi }^k\left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_0,{\sout{\lambda }}_1\right)\right)$ is convergent. Hence, there exists $Z=\underset{\mathfrak{y}\to \infty }{lim}{Z}_{\mathfrak{y}}\in \left[0,\infty \right).$ Considering $\mathfrak{s}\ge 1$ and inequality (8), we obtain that ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ is a left $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy sequence. Since ${\Xi }_{q^{\tilde{\mu }}}$ is a $q^{\tilde{\mu }}-$Symth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$, there exists ${\sout{\lambda }}^{*}\in {\Xi }_{q^{\tilde{\mu }}}$ such that ${\sout{\lambda }}_{\mathfrak{y}}\to {\sout{\lambda }}^{*}$ as $\mathfrak{y}\to \infty .$ The continuity of ℶ provides that ${\sout{\lambda }}_{\mathfrak{y}+1}=\beth {\sout{\lambda }}_{\mathfrak{y}}\to \beth {\sout{\lambda }}^{*}$ as $\mathfrak{y}\to \infty .$ By the uniqueness of the limit, we achieve ${\sout{\lambda }}^{*}=\beth {\sout{\lambda }}^{*},$ which means that ${\sout{\lambda }}^{*}$ is a fixed point of $\beth .$ □

Next, we present a new result by disregarding the continuity of ℶ.

Theorem 2. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1.$ Assume that ℶ is a generalized simulative ${\mathcal{Z}}_{\psi }$ contraction provided that the below statements hold:

$\left(i\right)$

The condition $\left(\Omega \right)$ holds;

$\left(ii\right)$

If ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ is a sequence in ${\Xi }_{q^{\tilde{\mu }}}$ such that $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\ge 1$ for all $\mathfrak{y}\in \mathbb{N}$, and ${\sout{\lambda }}_{\mathfrak{y}}\to \sout{\lambda }\in {\Xi }_{q^{\tilde{\mu }}}$ as $\mathfrak{y}\to \infty ,$ then $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},\sout{\lambda }\right)\ge 1$ for all $\mathfrak{y}\in \mathbb{N}.$

Then, ℶ admits a fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

Proof. 

By continuing as in the proof of Theorem 1, we procure that ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ is a left $q^{\tilde{\mu }}-\mathcal{K}-$Cauchy sequence in the $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ ${\Xi }_{q^{\tilde{\mu }}}$. So, there exists ${\sout{\lambda }}^{*}\in {\Xi }_{q^{\tilde{\mu }}}$ such that ${\sout{\lambda }}_{\mathfrak{y}}\to {\sout{\lambda }}^{*}$ as $\mathfrak{y}\to \infty .$ Also, from (4) and Hypothesis $\left(ii\right)$, we achieve

$$\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)\ge 1,$$

(9)

for all $\mathfrak{y}\in \mathbb{N}$. Here, we presume that ${\sout{\lambda }}^{*}\ne \beth {\sout{\lambda }}^{*}$ and using the triangular inequality and the expressions (2) and (9), we derive

$$\begin{array}{c}0\le \xi \left(\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}^{*}\right),\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)\right)\right)\hfill \\ \\ =\xi \left(\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right){q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}+1},\beth {\sout{\lambda }}^{*}\right),\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)\right)\right)\hfill \\ \\ <\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)\right)-\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right){q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}+1},\beth {\sout{\lambda }}^{*}\right),\hfill \end{array}$$

(10)

which is equivalent to

$$\begin{array}{cc}\hfill {q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}+1},\beth {\sout{\lambda }}^{*}\right)={q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}^{*}\right)& \le \alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}^{*}\right)\hfill \\ & <\psi \left(\mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)\right),\hfill \end{array}$$

(11)

where

$$\begin{array}{cc}\hfill \mathcal{M}\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right)& =max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},\beth {\sout{\lambda }}_{\mathfrak{y}}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},\beth {\sout{\lambda }}^{*}\right)\right\}\hfill \\ & =max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}^{*}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},\beth {\sout{\lambda }}^{*}\right)\right\}.\hfill \end{array}$$

(12)

Here, by letting $\mathfrak{y}\to \infty$ in (10)–(12), from the property of $\psi$, we conclude that

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},\beth {\sout{\lambda }}^{*}\right)=0,$$

which is a contradiction, that is, ${\sout{\lambda }}^{*}=\beth {\sout{\lambda }}^{*}.$ □

The following hypothesis is sufficient to obtain the uniqueness of the fixed point of ℶ.

$\left(\mathcal{U}\right)$

For all $\sout{\lambda },\hslash \in Fix\left\{\beth \right\},$ where $Fix\left\{\beth \right\}$ is the set of all fixed points of ℶ, we obtain $\alpha \left(\sout{\lambda },\hslash \right)\ge 1.$

Theorem 3. 

Besides the conditions of Theorem 1 (resp. Theorem 2), if we attach $\left(\mathcal{U}\right)$, then we yield the uniqueness of the fixed point of ℶ in ${\Xi }_{q^{\tilde{\mu }}}$.

Proof. 

We presume that ${\hslash }^{*}$ is an another fixed point of ℶ, which means that ${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\ne 0.$ From the hypotheses $\left(\mathcal{U}\right)$, we obtain $\alpha \left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\ge 1.$ Since ℶ is a generalized simulative ${\mathcal{Z}}_{\psi }$ contraction, we have

$$\begin{array}{c}0\le \xi \left(\alpha \left({\sout{\lambda }}^{*},{\hslash }^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right),\psi \left(\mathcal{M}\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right)\right)\hfill \\ \\ <\psi \left(\mathcal{M}\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right)-\alpha \left({\sout{\lambda }}^{*},{\hslash }^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right),\hfill \end{array}$$

which is equivalent to

$$\begin{array}{cc}\hfill {q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)={q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right)& \le \alpha \left({\sout{\lambda }}^{*},{\hslash }^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right)\hfill \\ & <\psi \left(\mathcal{M}\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right),\hfill \end{array}$$

where

$$\mathcal{M}\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)=max\left\{{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right),{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},\beth {\sout{\lambda }}^{*}\right),{q^{\tilde{\mu }}}_{\eta }\left({\hslash }^{*},\beth {\hslash }^{*}\right)\right\}={q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right).$$

Thus, we obtain

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right)<{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right),$$

which is a contradiction. Hence, ℶ has a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$. □

Considering the inherent characteristics of simulation functions, deducing the subsequent outcome directly from these properties is possible.

Corollary 1. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1.$ Presume that ℶ is a self mapping on ${\Xi }_{q^{\tilde{\mu }}}$ such that the following statements are fulfilled:

$\left(i\right)$

Two functions $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and $\psi \in {\mathcal{L}}_{♭}$ exist such that

$$\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \psi \left(\mathcal{M}\left(\sout{\lambda },\hslash \right)\right);$$

(13)

where $\mathcal{M}\left(\sout{\lambda },\hslash \right)$ as defined in (3), for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}},$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is satisfied;

$\left(iii\right)$

ℶ is continuous;

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is provided.

Thereby, ℶ admits a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

Example 2. 

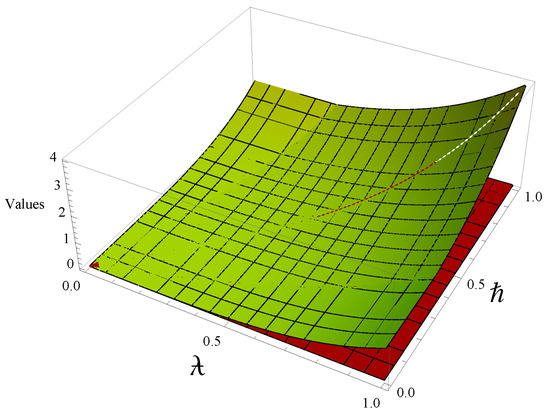
Let $\Xi =\left[0,\infty \right)$. Regarding the quasi-modular b metric $q^{\tilde{\mu }}:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$ and the function $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ by

$${q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)=\left\{\begin{array}{c}0,\sout{\lambda }=\hslash \\ {\displaystyle \frac{{\left({\sout{\lambda }}^2+{\hslash }^2\right)}^2}{\eta }},\sout{\lambda }\ne \hslash \hfill \end{array}\right.$$

and

$$\alpha \left(\sout{\lambda },\hslash \right)=\left\{\begin{array}{c}1,\sout{\lambda }\in \left[0,1\right]\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.,$$

respectively. In light of the preceding discourse, it is imperative to assert that ${\Xi }_{q^{\tilde{\mu }}}$ epitomizes a $q^{\tilde{\mu }}-$Smyth-complete entity within the framework of $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$, wherein $\mathfrak{s}$ is posited to equal 2. Concurrently, it is essential to delineate the functions of the mapping ℶ alongside ψ, which is a member of ${\mathcal{L}}_{♭}$. The function ℶ is hereby defined as $\beth \sout{\lambda }={\displaystyle \frac{\sout{\lambda }}{3}}$, and ψ is articulated through the relationship $\psi \left(t\right)={\displaystyle \frac{t}{2}}$, presenting a foundational underpinning for further academic inquiry within this domain. We aim to prove that the inequality (13) holds, that is,

$$\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \psi \left(max\left\{{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\beth \sout{\lambda }\right),{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\beth \hslash \right)\right\}\right).$$

The subsequent figure illustrates the contractive condition applicable for all elements $\sout{\lambda },\hslash$ within the closed interval $\left[0,1\right]$.

Moreover, in the case of $\sout{\lambda },\hslash \in \Xi -\left[0,1\right]$, it is clear that the results are satisfied. Therefore, for all $\sout{\lambda },\hslash \in \Xi$ with $\sout{\lambda }\ne \hslash$ and $\sout{\lambda },\hslash \in \left[0,1\right]$, we have

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)={q^{\tilde{\mu }}}_{\eta }\left({\displaystyle \frac{\sout{\lambda }}{3}},{\displaystyle \frac{\hslash }{3}}\right)={\displaystyle \frac{{\left({\sout{\lambda }}^2+{\hslash }^2\right)}^2}{81\eta }}\hfill \\ \\ \le {\displaystyle \frac{1}{2}}max\left\{{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\beth \sout{\lambda }\right),{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\beth \hslash \right)\right\}\hfill \\ \\ ={\displaystyle \frac{1}{2}}max\left\{{\displaystyle \frac{{\left({\sout{\lambda }}^2+{\hslash }^2\right)}^2}{\eta }},{\displaystyle \frac{{\left(10{\sout{\lambda }}^2\right)}^2}{81\eta }},{\displaystyle \frac{{\left(10{\hslash }^2\right)}^2}{81\eta }}\right\}.\hfill \end{array}$$

Using simple calculations, we yield that

$$max\left\{{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),{q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\beth \sout{\lambda }\right),{q^{\tilde{\mu }}}_{\eta }\left(\hslash ,\beth \hslash \right)\right\}={q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right),$$

for all $\sout{\lambda },\hslash \in \Xi$ and $\eta >0$. So, we achieve that the inequality

$${\displaystyle \frac{{\left({\sout{\lambda }}^2+{\hslash }^2\right)}^2}{81\eta }}\le {\displaystyle \frac{{\left({\sout{\lambda }}^2+{\hslash }^2\right)}^2}{2\eta }}$$

is satisfied, so inequality (13) is met which is represented as in Figure 2. As a result, the hypotheses of Corollary 1 are contended, and the point $\sout{\lambda }=0$ is the fixed point of the mapping ℶ.

Figure 2. A 3D representation of inequality (13).

Corollary 2. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1.$ Presume that ℶ is a self mapping on ${\Xi }_{q^{\tilde{\mu }}}$ such that the following statements are fulfilled:

$\left(i\right)$

Two functions $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and $\psi \in {\mathcal{L}}_{♭}$ exist such that

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\right)\hfill \end{array}$$

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}};$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is satisfied;

$\left(iii\right)$

ℶ is continuous;

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is provided.

Thereby, ℶ admits a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

Corollary 3. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1$, and $\beth :$ be a self mapping on ${\Xi }_{q^{\tilde{\mu }}}$. If the following circumstances are provided, then ℶ owns a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$:

$\left(i\right)$

A function $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and an element $\lambda \in \left(0,1\right)$ exist such that

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \lambda {q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\hfill \end{array}$$

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}};$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is met;

$\left(iii\right)$

ℶ is continuous;

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is satisfied.

Corollary 4. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1$ and ℶ be a self mapping on ${\Xi }_{q^{\tilde{\mu }}}$. Assume that the follow circumstances are met:

$\left(i\right)$

There exist two functions $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and $\psi \in {\mathcal{L}}_{♭}$ such that

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\right)\hfill \end{array}$$

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}};$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is provided;

$\left(iii\right)$

If ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ is a sequence in ${\Xi }_{q^{\tilde{\mu }}}$ such that $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\ge 1$ for all n and ${\sout{\lambda }}_{\mathfrak{y}}\to \sout{\lambda }\in {\Xi }_{q^{\tilde{\mu }}}$ as $\mathfrak{y}\to \infty ,$ then $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},\sout{\lambda }\right)\ge 1$ for all $n;$

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is fulfilled.

Thus, ℶ owns a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

Corollary 5. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1.$ Assume that ℶ is a self mapping on ${\Xi }_{q^{\tilde{\mu }}}$, satisfying the below axioms:

$\left(i\right)$

There exist functions $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and $\lambda \in \left(0,1\right)$ such that

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \lambda {q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\hfill \end{array}$$

(14)

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}};$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is met;

$\left(iii\right)$

If ${\left\{{\sout{\lambda }}_{\mathfrak{y}}\right\}}_{\mathfrak{y}\in \mathbb{N}}$ is a sequence in ${\Xi }_{q^{\tilde{\mu }}}$ such that $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},{\sout{\lambda }}_{\mathfrak{y}+1}\right)\ge 1$ for all n and ${\sout{\lambda }}_{\mathfrak{y}}\to \sout{\lambda }\in {\Xi }_{q^{\tilde{\mu }}}$ as $\mathfrak{y}\to \infty ,$ then $\alpha \left({\sout{\lambda }}_{\mathfrak{y}},\sout{\lambda }\right)\ge 1$ for all n.

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is provided.

Thereupon, ℶ owns a unique fixed point in ${\Xi }_{q^{\tilde{\mu }}}$.

4. An Application to Ulam–Hyers Stability

This section endeavors to contextualize the principal outcomes of the study within the framework of the Ulam–Hyers stability conundrum. Notably, many scholarly contributions exist addressing the results of Ulam–Hyers stability in the realm of fixed point theorems, as evidenced by the literature [34,35,36,37].

Definition 16. 

Let $\beth :\Xi \to \Xi$ be an operator on $(\Xi ,d)$, where $(\Xi ,d)$ is a metric space. The below fixed point equation

$$\sout{\lambda }=\beth \left(\sout{\lambda }\right)$$

(15)

is termed Ulam–Hyers stable of general type if the function $\psi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, which is increasing, is continuous at 0 and $\psi \left(0\right)=0$ such that, for every $ϵ>0$ and for each ${\hslash }^{*}\in \Xi$, there is an ϵ solution to (15), which means that ${\hslash }^{*}$ provides the inequality

$$d\left({\hslash }^{*},\beth {\hslash }^{*}\right)\le \epsilon .$$

(16)

A solution ${\sout{\lambda }}^{*}\in \Xi$ to Equation (15) exists such that

$$d\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\le \psi \left(\epsilon \right).$$

If an element $\iota >0$ exists such that $\psi \left(\rho \right)=\iota \rho$, for each $\rho \in {\mathbb{R}}^{+}$, the fixed point Equation (15) is considered Ulam–Hyers stable.

Theorem 4. 

Let ${\Xi }_{q^{\tilde{\mu }}}$ be a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with $\mathfrak{s}>1$. Presume that the below statements are met:

$\left(i\right)$

There exist two functions $\alpha :{\Xi }_{q^{\tilde{\mu }}}\times {\Xi }_{q^{\tilde{\mu }}}\to \left[0,\infty \right)$ and $\psi \in {\mathcal{L}}_{♭}$ such that

$$\begin{array}{c}\alpha \left(\sout{\lambda },\hslash \right){q^{\tilde{\mu }}}_{\eta }\left(\beth \sout{\lambda },\beth \hslash \right)\le \psi \left({q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\right)\hfill \end{array}$$

for all $\sout{\lambda },\hslash \in {\Xi }_{q^{\tilde{\mu }}};$

$\left(ii\right)$

The condition $\left(\Omega \right)$ is met;

$\left(iii\right)$

ℶ is continuous;

$\left(iv\right)$

The axiom $\left(\mathcal{U}\right)$ is satisfied;

$\left(v\right)$

The function $\sigma :\left[0,\infty \right)\to \left[0,\infty \right),$$\sigma \left(r\right)=r-\mathfrak{s}\psi \left(r\right)$ is strictly increasing.

Thereupon, (15), the fixed point equation is Ulam–Hyers stable of a general type.

Proof. 

Owing to the fact that ℶ is a Picard operator, $fix\left(\beth \right)=\left\{{\sout{\lambda }}^{*}\right\}.$ Let $\epsilon >0$ and ${\hslash }^{*}$ be solutions to (16), i.e.,

$${q^{\tilde{\mu }}}_{\eta }\left({\hslash }^{*},\beth {\hslash }^{*}\right)\le \epsilon .$$

Also, by using the conditions $\left(ii\right)$ and $\left(iv\right)$, we obtain

$$\begin{array}{c}{q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)={q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},{\hslash }^{*}\right)={q^{\tilde{\mu }}}_{max\left\{\eta ,\eta \right\}}\left(\beth {\sout{\lambda }}^{*},{\hslash }^{*}\right)\hfill \\ \\ \le \mathfrak{s}\left[{q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right)+{q^{\tilde{\mu }}}_{\eta }\left(\beth {\hslash }^{*},{\hslash }^{*}\right)\right]\hfill \\ \\ \le \mathfrak{s}\left[\alpha \left({\sout{\lambda }}^{*},{\hslash }^{*}\right){q^{\tilde{\mu }}}_{\eta }\left(\beth {\sout{\lambda }}^{*},\beth {\hslash }^{*}\right)+\epsilon \right]\hfill \\ \\ \le \mathfrak{s}\left[\psi \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right)+\epsilon \right].\hfill \end{array}$$

Therefore,

$$\sigma \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right):={q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)-s\psi \left({q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\right)\le \mathfrak{s}\epsilon ,$$

that is,

$${q^{\tilde{\mu }}}_{\eta }\left({\sout{\lambda }}^{*},{\hslash }^{*}\right)\le {\sigma }^{-1}\left(\mathfrak{s}\epsilon \right).$$

Consequently, (15) is Ulam–Hyers stable of a general type. □

5. An Application to a Non-Linear Fractional Differential Equation

This section focuses on investigating Caputo-type non-linear fractional differential equations in the setting of a $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$:

$$\begin{array}{c}{D}^{\delta }\omega \left(\varrho \right)+G\left(\varrho ,\omega \left(\varrho \right)\right)=0,\varrho \in I=\left[0,1\right],1<\delta <2\hfill \\ \\ \omega \left(0\right)=0,\omega \left(1\right)=0,\hfill \end{array}$$

(17)

where $D^{\delta }$ denotes the Caputo fractional derivative of order $\delta ,$$\varrho \in \left(C\left[0,1\right],\mathbb{R}\right)$, and $G:I\times \mathbb{R}\to \mathbb{R}$ is a continuous function (for further information, see [38,39,40]). We keep in mind that $\Xi =\left\{\omega :\omega \in \left(C\left[0,1\right],\mathbb{R}\right)\right\}$, with the supremum norm

$$∥\omega ∥={\displaystyle \frac{1}{\eta }}\underset{\varrho \in \left[0,1\right]}{sup}\left|\omega \left(\varrho \right)\right|,\eta >0$$

being a Banach space. Also, $\Xi :=C\left(\left[0,1\right],\mathbb{R}\right)$ is a $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ with the function

$$\begin{array}{c}{q^{\tilde{\mu }}}_{\eta }:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]\hfill \\ \\ \left(\omega ,v\right)\to {q^{\tilde{\mu }}}_{\eta }\left(\omega ,v\right)={\displaystyle \frac{1}{\eta }}∥\omega -v∥\hfill \\ \\ ={\displaystyle \frac{1}{\eta }}\underset{\varrho \in \left[0,1\right]}{sup}\left|\omega \left(\varrho \right)-v\left(\varrho \right)\right|,\hfill \end{array}$$

(18)

for all $\eta >0$. Then, ${\Xi }_{q^{\tilde{\mu }}}$ is a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$. A solution to (17) is a fixed point of the integral equation

$$\begin{array}{c}\beth \omega \left(\varrho \right)={\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)G\left(\varsigma ,\omega \left(\varsigma \right)\right)d\varsigma \hfill \\ \\ +{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}G\left(\varsigma ,\omega \left(\varsigma \right)\right)d\varsigma .\hfill \end{array}$$

(19)

Theorem 5. 

Assume $G:I\times \mathbb{R}\to \mathbb{R}$ is a continuous function fulfilling

$$\left|G\left(\varsigma ,\omega \left(\varsigma \right)\right)-G\left(\varsigma ,v\left(\varsigma \right)\right)\right|\le {\displaystyle \frac{\Gamma \left(\delta +1\right)}{5}}\lambda \left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|,$$

(20)

for each $\varsigma \in [0,1],$ for some $\lambda \in [0,1]$, and all $\omega ,v\in {\Xi }_{q^{\tilde{\mu }}}.$ The stated boundary conditions result in a unique solution to the fractional differential Equation (17).

Proof. 

$\Xi :=C\left(\left[0,1\right],\mathbb{R}\right)$ is endowed with $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}$$q^{\tilde{\mu }}:\left(0,\infty \right)\times \Xi \times \Xi \to \left[0,\infty \right]$ stated as

$$E_{\eta }\left(\omega ,v\right)={\displaystyle \frac{1}{\eta }}∥\omega -v∥={\displaystyle \frac{1}{\eta }}\underset{\varrho \in \left[0,1\right]}{sup}\left|\omega \left(\varrho \right)-v\left(\varrho \right)\right|,\eta >0.$$

Then, ${\Xi }_{q^{\tilde{\mu }}}$ is a $q^{\tilde{\mu }}-$Smyth-complete $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$. We define $\beth :{\Xi }_{q^{\tilde{\mu }}}\to {\Xi }_{q^{\tilde{\mu }}}$ as in (19); so, ℶ is continuous. Here, for all $\varrho \in [0,1]$, we obtain

$$\begin{array}{c}\left|\beth \omega \left(\varrho \right)-\beth v\left(\varrho \right)\right|=\left|{\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)G\left(\varsigma ,\omega \left(\varsigma \right)\right)d\varsigma \right.\hfill \\ +{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}G\left(\varsigma ,\omega \left(\varsigma \right)\right)d\varsigma \hfill \\ -{\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)G\left(\varsigma ,v\left(\varsigma \right)\right)d\varsigma \hfill \\ \left.-{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}G\left(\varsigma ,v\left(\varsigma \right)\right)d\varsigma \right|\hfill \\ \\ \le {\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)\left|G\left(\varsigma ,\omega \left(\varsigma \right)\right)-G\left(\varsigma ,v\left(\varsigma \right)\right)\right|d\varsigma \hfill \\ +{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}\left|G\left(\varsigma ,\omega \left(\varsigma \right)\right)-G\left(\varsigma ,v\left(\varsigma \right)\right)\right|d\varsigma \hfill \\ \\ \le {\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)\left[{\displaystyle \frac{\Gamma \left(\delta +1\right)}{5}}\lambda \underset{\varsigma \in \left[0,1\right]}{sup}\left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|\right]d\varsigma \hfill \\ +{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}\left[{\displaystyle \frac{\Gamma \left(\delta +1\right)}{5}}\lambda \underset{\varsigma \in \left[0,1\right]}{sup}\left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|\right]d\varsigma \hfill \\ \\ \le \left[{\displaystyle \frac{\Gamma \left(\delta +1\right)}{5}}\lambda \underset{\varsigma \in \left[0,1\right]}{sup}\left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|\right]\hfill \\ \times \underset{\varrho \in \left[0,1\right]}{sup}\left({\displaystyle \frac{1}{\Gamma \left(\delta \right)}}\underset{0}{\overset{\varrho }{\int }}\left(\varrho {\left(1-\varsigma \right)}^{\delta -1}-{\left(\varrho -\varsigma \right)}^{\delta -1}\right)d\varsigma +{\displaystyle \frac{t}{\Gamma \left(\delta \right)}}\underset{\varrho }{\overset{1}{\int }}{\left(1-\varsigma \right)}^{\delta -1}d\varsigma \right)\hfill \\ \\ \le \lambda \underset{a\in \left[0,1\right]}{sup}\left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|\hfill \end{array}$$

for all $\omega ,v\in {\Xi }_{q^{\tilde{\mu }}}.$ Thus, for all $\eta >0,$ we achieve

$$\begin{array}{c}{q^{\tilde{\mu }}}_{\eta }\left(\beth \omega ,\beth v\right)={\displaystyle \frac{1}{\eta }}\underset{\varrho \in \left[0,1\right]}{sup}\left|\beth \omega \left(\varrho \right)-\beth v\left(\varrho \right)\right|\hfill \\ \\ \le {\displaystyle \frac{1}{\eta }}\lambda \underset{\varsigma \in \left[0,1\right]}{sup}\left|\omega \left(\varsigma \right)-v\left(\varsigma \right)\right|\le \lambda {q^{\tilde{\mu }}}_{\eta }\left(\omega ,v\right).\hfill \end{array}$$

By choosing

$$\psi \left(\iota \right)=\lambda \iota ,\mathcal{M}\left(\sout{\lambda },\hslash \right)={q^{\tilde{\mu }}}_{\eta }\left(\sout{\lambda },\hslash \right)\mathrm{and}\alpha \left(\sout{\lambda },\hslash \right)=1$$

in Corollary 1, all requirements for Corollary 1 are met. This implies that ℶ possesses a unique fixed point, and (17) has a unique solution. □

6. Conclusions and Future Directions

In this investigation, we began by delineating the constructs $\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ and $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$, followed by an exposition of their topological characteristics. We proceeded to establish a series of fixed point theorems for generalized $\alpha -{\psi }_b-$contractive mappings within the context of $\mathfrak{non}\mathbb{A}\mathfrak{rc}-\mathcal{Q}{\mathcal{M}}_{♭}\mathcal{M}\mathcal{S}$ spaces.

As a practical application of our theoretical findings, we derived Ulam–Hyers stability results pertinent to fixed point problems. Additionally, the framework of fixed point theory was utilized to address and resolve a distinctive Caputo-type non-linear fractional differential equation, showcasing the versatility and applicability of our results.

Looking forward, the exploration of contractive conditions, including but not limited to F contraction, $\theta$ contraction, and interpolative contraction, within quasi-modular b-metric spaces, presents an intriguing avenue for further research. Moreover, pursuing optimal proximity results and examining multivalued contractions within these spaces hold considerable promise. A particularly compelling direction for future inquiry would involve the formulation and analysis of a common fixed point theorem that extends the existing body of knowledge in the realm of quasi-modular b-metric spaces.

For future work, the work conducted in this article can be extended to multivalued mappings and graphical structures in control system optimization, and it will be interesting to find the proximal point results for the contractions utilized in this work.