Abstract
The computation of the sign function of a matrix plays a crucial role in various mathematical applications. It provides a matrix-valued mapping that determines the sign of each eigenvalue of a nonsingular matrix. In this article, we present a novel iterative algorithm designed to efficiently calculate the sign of an invertible matrix, emphasizing the enlargement of attraction basins. The proposed solver exhibits convergence of order four, making it highly efficient for a wide range of matrices. Furthermore, the method demonstrates global convergence properties. We validate the theoretical outcomes through numerical experiments, which confirm the effectiveness and efficiency of our proposed algorithm.
MSC:
65F60; 41A25
1. Introductory Notes
The matrix sign function, also known as the matrix signum function or simply matrix sign, is a mathematical function that operates on matrices, returning a matrix of the same size with elements representing the signs of the corresponding elements in the input matrix. The concept of the sign function can be traced back to the scalar sign function, which operates on individual real numbers ([1], Chapter 11). The scalar sign function offers +1 for positive numbers, for negative numbers, and 0 for zero.
The extension of the sign function to matrices emerged as a natural generalization. This function was introduced to facilitate the study of matrix theory and to develop new algorithms for solving matrix equations and systems. This function provides valuable information about the structure and properties of matrices. The earliest references to the matrix sign could be found in the mathematical literature in the late 1960s and early 1970s [2]. This function for a square nonsingular matrix , i.e.,
can be expressed as follows [3] (p. 107):
where I is is the unit matrix.
Several authors who contributed to the development and study of the matrix sign function include Nicholas J. Higham, Charles F. Van Loan, and Gene H. Golub; see the textbook [3]. Since its introduction, it has found applications in various areas of mathematics and scientific computing. It has been utilized in numerical analysis, linear algebra algorithms, control theory, graph theory, and stochastic differential equations; see, e.g., [4]. In recent years, research has focused on refining algorithms for efficiently computing the matrix sign function, higher-order iterative methods, and exploring its connections to other matrix functions and properties. This function has proven to be a fruitful tool for characterizing and manipulating matrices in a wide range of disciplines. Expanding the discussion, the work by Al-Mohy and Higham [5], while primarily centered on the matrix exponential, introduced a highly influential algorithm that serves as a fundamental basis for computing various other matrix functions, including (1).
Here are some areas where this function finds utility. 1. Stability analysis: In control theory and dynamical systems, the matrix sign function is employed to analyze the stability of linear time-invariant systems. By examining the signs of the eigenvalues of a system’s matrix representation, the matrix sign function helps determine stability properties, such as asymptotic stability or instability [6]. 2. Matrix fraction descriptions: This function plays a key appearance in representing matrix fraction descriptions of linear time-invariant sets. Matrix fractions are used in system theory to describe transfer functions, impedance matrices, and other related quantities. Then, (1) is employed in the realization theory of these matrix fractions [7]. 3. Robust control: Robust control techniques aim to design control systems that can handle uncertainties and disturbances. This function is utilized in robust control algorithms to assess the stability and performance of uncertain systems. It helps analyze the worst-case behavior of the system under varying uncertain conditions [2]. 4. Discrete-time systems: In the analysis and design of discrete-time systems, the matrix sign function aids in studying the stability and convergence properties of difference equations. It allows one the examination of the spectral radius of a matrix and determination of the long-term behavior of discrete-time systems [3]. 5. Matrix equations: This function is employed in solving matrix equations. For example, it can be employed in the calculation of the matrix square root or the matrix logarithm, which have applications in numerical methods, optimization, and signal processing [8].
It is an interesting choice to compute (1) by numerical iterative methods which are mainly constructed by resolving the following nonlinear matrix equations:
The matrix from (1) is the solution of (3) since it satisfies the definition of . In this work, we focus on proposing a new solver for (3) in the scalar format and then extending for the matrix environment in order to be computationally economic when compared to the famous iteration solvers of the same type to find (1) of a nonsingular matrix.
The remainder of this work is arranged as follows. In Section 2, we look at some important methods for figuring out the sign of a matrix. Then, in Section 3, we explain why higher-order methods are useful and introduce a solver for solving nonlinear scalar equations. We extend this solver to work with matrices and prove its effectiveness through detailed analysis, showing that it has a convergence order of four. We also examine the attraction basins to ensure the solver works globally and covers a wider range compared to similar methods. We discuss its stability as well. In Section 4, we present the results of our numerical study to validate our theoretical findings, demonstrating the usefulness of our method. Finally, in Section 5, we provide our conclusions.
2. Iteration Methods
Kenney and Laub in [9] presented a general and important family of iterations for finding (1) via the application of the Padé approximations: We assume now that the -Padé fraction approximate to is given as where Q, P are polynomials of suitable degrees in the Padé approximation and . Then, [9] discussed that the iteration method below,
converges with convergence speed to . Thus, the second-order Newton’s method (NIM) can be constructed as follows:
where
is the starting matrix and M represents the input matrix as given in (1). We note that the reciprocal Padé-approximations can be defined based on reciprocals of (4). Newton’s method provides an iterative approach to approximating (1). It starts with an initial matrix and then improves the approximation in each iteration until convergence is achieved. This iterative nature makes it useful when dealing with complex matrices or large matrices where direct methods may be computationally expensive.
Newton’s iterative scheme plays an important role in finding (1) due to its effectiveness in approximating the solution iteratively. Some reasons highlighting the importance of Newton’s iteration for computing (1) lie in the advantages of iterative approximation (see [10]). It has quadratic convergence properties, especially when the initial matrix is close to the desired solution. Also, it needs the calculation of the derivative of the function being approximated. In the case of finding (1), this involves the derivative of the sign function, which can be derived analytically. Utilizing the derivative information can help guide the iterative process towards the solution.
Employing (4), the subsequent renowned techniques, namely the locally convergent inversion-free Newton–Schulz solver,
and Halley’s solver,
can be extracted, as in [11]. A quartically convergent solver is proposed in [12] as follows:
Parameter is an independent real constant. Additionally, two alternative quartically convergent methods are derived from (4) with global convergence, which can be expressed as follows:
3. A New Numerical Method
Higher-order iteration solvers to compute (1) offer several advantages compared to lower-order methods [13,14]. To discuss further, higher-order iterative methods typically converge faster than lower-order methods. By incorporating more information from the matrix and its derivatives, these methods can achieve faster convergence rates, leading to fewer iterations required to reach a desired level of accuracy. This can improve the computational efficiency of the matrix sign function computation.
Higher-order iterative methods may provide higher accuracy in approximating the matrix sign function. This is particularly beneficial when dealing with matrices that have small eigenvalues or require high precision computations. Such methods often exhibit improved robustness compared to lower-order methods. They are typically more stable and less sensitive to variations in the input matrix. This robustness is particularly advantageous in situations where the matrix may have a non-trivial eigenvalue distribution or when dealing with ill-conditioned matrices. Higher-order methods can provide more reliable and accurate results in such cases. In addition, such iterations are applicable to a wide range of matrix sizes and types. They can handle both small and large matrices efficiently. Moreover, these methods can be adapted to handle specific matrix structures or properties, such as symmetric or sparse matrices, allowing for versatile applications across different domains.
It is significant to note that the choice of the appropriate iterative method relies on various factors, including the characteristics of the matrix, computational resources, desired accuracy, and specific application requirements. While higher-order iterative methods offer advantages, they may also come with increased memory requirements if not treated well. Thus, a careful consideration of these trade-offs is necessary and an efficient method must be constructed. To propose an efficient one, we proceed as follows.
We now examine the scalar form of Equation (3), that is to say, . Here, is the scalar version of the nonlinear matrix Equation (3), which means that . In this paper, we employ uppercase letter “H” when addressing matrices, while utilizing lowercase letter “h” to denote scalar inputs. We propose a refined adaptation of the Newton’s scheme, comprising three sequential steps as outlined below:
where is a divided difference operator. For further insights into solving nonlinear scalar equations using high-order iterative methods, refer to works [15,16,17]. Additionally, valuable information can be found in modern textbooks such as [18,19] or classical textbooks like [20]. The second substep in (12) represents a significant improvement over the approach presented in [21]. The coefficients involved in this substep are computed through a method of unknown coefficients, which involves rigorous computations. Initially, these coefficients are considered unknown, and then they are carefully determined to achieve a fourth order of convergence. Furthermore, this process is designed to expand the basins of attraction, providing an advantage over other solvers with similar characteristics.
Theorem 1.
Assume as a simple root of , which is an enough smooth function. By considering an enough close guess the method (12) converges to ρ and the rate of convergence is four.
Proof.
The proof entails a meticulous derivation of Taylor’s expansion for each sub-step of the iterative process around the simple root . Nonetheless, it is observed that (12) satisfies the subsequent error equation,
where and . Considering that the method (12) belongs to the category of fixed-point type methods, similar to Newton’s method, its convergence is local. This implies that the initial guess should be sufficiently close to the root to guarantee convergence. The proof finishes now. □
To illustrate more on the mathematical derivation of the second substep (12), in fact, first, we consider (12) as follows:
which offers the following error equation:
The relationship (16) results in selecting , consequently transforming the error equation into
Therefore, we need to determine the remaining unspecified coefficients in a way that ensures , reducing the term in (16). Moreover, their selection should aim to minimize the subsequent error equation, namely . This leads us to a choice of , and .
Now, we can solve (3) by the iterative method (12). Pursuing this yields
with the initial value (6). To clarify the derivation in detail, we provide a simple yet efficient Mathematica code for this purpose as follows:
ClearAll[‘‘Global‘*’’] f[x_] := x^2 - 1 fh = f[h]; fh1 = f’[h]; y = h - fh/fh1; fy = f[y]; x = h - ((21 fh - 22 fy)/(21 fh - 43 fy)) fh/fh1 // FullSimplify; ddo1 = (x - h)^-1 (f[x] - f[h]); h1 = x - f[x]/ddo1 // FullSimplifyLikewise, we acquire the reciprocal expression of (17) through the following procedure:
Theorem 2.
Proof.
We consider B to be a non-singular, non-unique transformation matrix, and represent the Jordan canonical form in the following form:
where the eigenvalues of M are distinct and . For function f which possesses degrees of differentiability at for , [22] and is given on the spectrum of M, the matrix function can be expressed by
wherein
with
Considering as the jth Jordan block size associated to , we have
To continue, we employ the Jordan block matrix J and decompose M by utilizing a nonsingular matrix B of identical dimensions, leading to the following decomposition:
Through the utilization of this decomposition and an analysis of the solver’s structure, we derive an iterative sequence for the eigenvalues from iterate l to iterate in the following manner:
where
In a broad sense and upon performing certain matrix simplifications, the iterative process (25) reveals that the eigenvalues converge to , viz.,
Equation (27) indicates the convergence of the eigenvalues toward . With each iteration, the eigenvalues tend to cluster closer to . Having analyzed the theoretical convergence of the method, we now focus on examining the rate of convergence. For this purpose, we consider
Utilizing (28) and recognizing that represents rational functions of M while also demonstrating commutativity with N within a similar manner as M, we can express
Using (29) and a 2-norm, it is possible to obtain
This shows the convergence rate of order four under a suitable selection of the initial matrix, such as (6). □
We note that the proofs of the theorems in this section are new and were obtained for our proposed method.
Attraction basins are useful in understanding the global convergence behavior of iteration schemes to calculate (1). In the context of iterative methods, the basins of attraction refer to regions in the input space where the iterative process converges to a specific solution or behavior. When designing a solver for computing (1), it is crucial to ensure that the method tends to the desired solution regardless of the initial guess. The basins of attraction provide insights into the convergence behavior by identifying the regions of the input space that lead to convergence and those that lead to divergence or convergence to different solutions.
By studying the basins of attraction, one can analyze the stability and robustness of an iterative method for computing (1). In general, here is how basins of attraction help in understanding global convergence [23]:
- Convergence Analysis: Basins of attraction provide information about the convergence properties of the iterative sequence. The regions in the input space that belong to the basin of attraction of a particular solution indicate where the method converges to that solution. By analyzing the size, shape, and location of these basins, one can gain insights into the convergence behavior and determine the conditions under which convergence is guaranteed.
- Stability Assessment: Basins of attraction reveal the stability of the iterative method. If the basins of attraction are well-behaved and do not exhibit fractal or intricate structures, it indicates that the method is stable and robust. On the other hand, if the basins are complex and exhibit fractal patterns, it suggests that the method may be sensitive to initial conditions and can easily diverge or converge to different solutions.
- Optimization and Method Refinement: Analyzing the basins of attraction can guide the optimization and refinement of the iterative method. By identifying regions of poor convergence or instability, adjustments can be made to the algorithm to improve its performance. This may involve modifying the iteration scheme, incorporating adaptive techniques, or refining the convergence criteria.
- Algorithm Comparison: Basins of attraction can be used to compare various iteration methods for finding (1). By studying the basins associated with different methods, one can assess their convergence behavior, stability, and efficiency. This information can aid in selecting the most suitable method for a particular problem or in developing new algorithms that overcome the limitations of existing approaches.
We introduced techniques (17) and (18) with the aim of expanding the attraction regions pertaining to these methods in the solution of . To provide greater clarity, we proceed to explore how the proposed methods exhibit global convergence and enhanced convergence radii by visually representing their respective attraction regions in the complex domain,
when solving . In pursuit of this objective, we partition the complex plane into numerous points using a mesh, and subsequently assess the behavior of each point as an initial value to ascertain whether it converges or diverges. Upon convergence, the point is shaded in accordance with the number of iterations, leading to the following termination criterion: Figure 1, Figure 2 and Figure 3 include the basins of attractions for different methods. We recal that the fractal behavior of iterative methods in a complex plane determine their local or global convergence under certain conditions. They reveal that for (17) and (18), they own larger radii of convergence in comparison to their same-order competitors from (4). The presence of a lighter area indicates the expansion of the convergence radii as they extend to encompass (1).
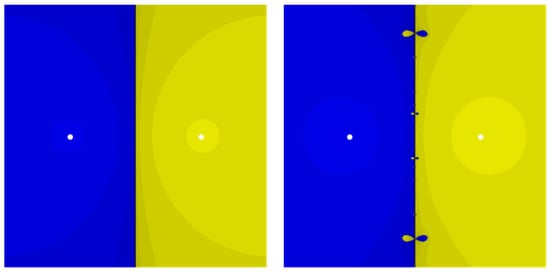
Figure 2.
Attraction basins of (10) on the left, and locally convergent Padé [1,3] on the right.
Theorem 3.
According to Equation (18) and assuming an invertible matrix M, the sequence with is asymptotically stable.
Proof.
We consider a perturbed calculation of in the iterate of performing the numerical solver,; for more, see [24]. And we define the following relation per cycle:
Throughout the remainder of the proof, we assume the validity of relation for , which holds true under the condition of performing a first-order error analysis, considering the smallness of . We obtain
In the phase of convergence, it is considered that
utilizing the following established facts (pertaining to the invertible matrix H and an arbitrary matrix E) as referenced in [25] (p. 188),
We also utilize and (which are special cases of ) and , ) to obtain
By further simplifications and using , we can find
This leads to the conclusion that (18) at the iterate is bounded, thus offering us
Therefore, the sequence produced via (17) is stable. □
We end this section by noting that our proposed method comes with error estimation techniques that enable the estimation of the approximation error during the computation. This provides valuable information about the quality of the calculated resolution. Additionally, its higher-order nature allows for better control over the accuracy of the approximation by adjusting the order of the method or specifying convergence tolerances. Additionally, our method can take advantage of parallel computing architectures to accelerate the computation process. It can be parallelized to distribute the computational workload across multiple processing units, enabling faster computations for large matrices or in high-performance computing environments.
4. Computational Study
Here, we evaluate the performance of the proposed solvers for various types of problems. The whole implementations are run by Mathematica (see [26]). Computational issues such as convergence detection are considered. We divide the tests into two parts, tests of theoretical values and tests of practical values. The following methods are compared: (5) denoted by NIM, (8), denoted by HM, (11), shown by Padé, (17) shown by P1, (18) shown by P2. We also compare the results with the Zaka Ullah et al. method (ZM) [21] as follows:
For all the compared iterative methods, we employ the initial matrix by (6). The calculation of the absolute error is performed as follows:
Here, represents the stopping value. Observing that the reported times are based on a single execution of the entire program, it is important to note that these reported times encompass all calculations, including the computation of norm residuals and other relevant operations.
Example 1.
Ten real random matrices are generated using a random seed and their matrix sign functions are computed and compared. We produce ten random matrices in the interval of the sizes till under .
Numerical comparisons for Example 1 are presented in Table 1 and Table 2, substantiating the effectiveness of the methods proposed in this paper. Notably, both P1 and P2 contribute to a decrease in the required number of iterations for determining the matrix sign, resulting in a noticeable reduction in elapsed CPU time (measured in seconds). This reduction is evident in the average CPU times across ten randomly generated matrices of varying dimensions.

Table 1.
Computational comparisons based on the number of iterates in Example 1.

Table 2.
Computational comparisons based on the CPU times (in seconds) for Example 1.
Example 2.
In this test, the matrix sign function is computed for ten complex random matrices with the same seed as in Example 1 under by the piece of Mathematica code below:
number = 10;
Table[M[n] = RandomComplex[{-20 - 20 I,
20 + 20 I}, {100 n, 100 n}];, {n, number}];
Table 3 and Table 4 provide numerical comparisons for Example 2, further reaffirming the efficiency of the proposed method in determining the sign of ten randomly generated complex matrices. Comparable computational experiments conducted for various analogous problems consistently corroborate the aforementioned findings, with P1 emerging as the superior solver.

Table 3.
Computational comparisons based on the number of iterates in Example 2.

Table 4.
Computational comparisons based on CPU times (in seconds) for Example 2.
Stabilized Solution of a Riccati Equation
We take into account the ARE, also known as the algebraic Riccati equation, arising in optimal control problems in continuous/discrete time as follows [27]:
where is positive definite, is positive semi-definite, , , and are the unknown matrix. Typically, we seek a solution that stabilizes the system, meaning the eigenvalues of have negative real parts. It is important to notice that if the pair is stabilizable, and is detectable, then there exists a stabilizing unique resolution Y for Equation (40) in . Furthermore, this solution Y is both symmetric and positive semi-definite. Assuming Y is the stabilizing resolution for the ARE in Equation (40), all eigenvalues of have negative real parts, which can be seen from the following equation:
We obtain
for a suitable matrix K, wherein
Now, we find Y as follows:
and thus
which implies
After determining the sign of H, solving the required solution becomes feasible by addressing the overdetermined system (46). This can be achieved through standard algorithms designed for solving such systems. In our test scenario, we utilize P1 with the termination condition (39) in the infinity norm, along with a tolerance of to compute the sign of H during the solution of the ARE (40). As a practical instance, this procedure involves the following input matrices:
The resulting matrix, which serves as the solution to (40), is
To verify the accuracy of matrix Y, we calculate the residual norm of (40) in using (51), resulting in . This value affirms the precision of the approximation we attained for (40) through the matrix sign function and P1 approach.
5. Conclusions
In this paper, we provided details on why higher-order methods are necessary for finding the sign of invertible matrices. Then, it was discussed by basins of attractions that the proposed method to compute (1) has global convergence, and its convergence radii were wider than those of its competitors. The stability of the method was discussed in detail, and computational results supported the theoretical outcomes. Several other tests were conducted by the authors and upheld the efficiency of the presented iterative scheme in computing the matrix sign. Future works can be pursued on extension of the presented solver to find the matrix sector function. In fact, this function is a generalization of the sign function, and it is necessary to compute such a matrix function by high-order iterative methods. On the other hand, it would be interesting and of practical use to propose more efficient variants of (17) to have larger basins of attractions but with the same number of matrix multiplications. These could be our future research directions.
Author Contributions
Conceptualization, L.S., M.Z.U. and H.K.N.; formal analysis, L.S., M.Z.U., M.A. and S.S.; funding acquisition, S.S.; investigation, L.S., M.Z.U. and M.A.; methodology, H.K.N., M.A. and S.S.; supervision, L.S., M.Z.U. and H.K.N.; validation, M.Z.U., M.A. and S.S.; writing—original draft, L.S. and M.Z.U.; writing—review and editing, L.S. and M.Z.U. All authors have read and agreed to the published version of the manuscript.
Funding
Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, Saudi Arabia, under grant no. (IFPIP: 383-247-1443).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Regarding the data availability statement, it is confirmed that data sharing does not apply to this article, as no new data were generated during the course of this paper.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 383-247-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia. The authors express their gratitude to referees for providing valuable feedback, comments, and corrections on an earlier version of this submission. Their help have significantly improved the readability and reliability of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hogben, L. Handbook of Linear Algebra; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Roberts, J.D. Linear model reduction and solution of the algebraic Riccati equation by use of the sign function. Int. J. Cont. 1980, 32, 677–687. [Google Scholar] [CrossRef]
- Higham, N.J. Functions of Matrices: Theory and Computation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Soheili, A.R.; Amini, M.; Soleymani, F. A family of Chaplygin–type solvers for Itô stochastic differential equations. Appl. Math. Comput. 2019, 340, 296–304. [Google Scholar] [CrossRef]
- Al-Mohy, A.; Higham, N. A scaling and squaring algorithm for the matrix exponential. SIAM J. Matrix Anal. Appl. 2009, 31, 970–989. [Google Scholar] [CrossRef]
- Denman, E.D.; Beavers, A.N. The matrix sign function and computations in systems. Appl. Math. Comput. 1976, 2, 63–94. [Google Scholar] [CrossRef]
- Tsai, J.S.H.; Chen, C.M. A computer-aided method for solvents and spectral factors of matrix polynomials. Appl. Math. Comput. 1992, 47, 211–235. [Google Scholar] [CrossRef]
- Ringh, E. Numerical Methods for Sylvester-Type Matrix Equations and Nonlinear Eigenvalue Problems. Doctoral Thesis, Applied and Computational Mathematics, KTH Royal Institute of Technology, Stockholm, Sweden, 2021. [Google Scholar]
- Kenney, C.S.; Laub, A.J. Rational iterative methods for the matrix sign function. SIAM J. Matrix Anal. Appl. 1991, 12, 273–291. [Google Scholar] [CrossRef]
- Soleymani, F.; Stanimirović, P.S.; Shateyi, S.; Haghani, F.K. Approximating the matrix sign function using a novel iterative method. Abstr. Appl. Anal. 2014, 2014, 105301. [Google Scholar] [CrossRef]
- Gomilko, O.; Greco, F.; Ziȩtak, K. A Padé family of iterations for the matrix sign function and related problems. Numer. Lin. Alg. Appl. 2012, 19, 585–605. [Google Scholar] [CrossRef]
- Cordero, A.; Soleymani, F.; Torregrosa, J.R.; Zaka Ullah, M. Numerically stable improved Chebyshev–Halley type schemes for matrix sign function. J. Comput. Appl. Math. 2017, 318, 189–198. [Google Scholar] [CrossRef]
- Rani, L.; Soleymani, F.; Kansal, M.; Kumar Nashine, H. An optimized Chebyshev-Halley type family of multiple solvers: Extensive analysis and applications. Math. Meth. Appl. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Liu, T.; Zaka Ullah, M.; Alshahrani, K.M.A.; Shateyi, S. From fractal behavior of iteration methods to an efficient solver for the sign of a matrix. Fractal Fract. 2023, 7, 32. [Google Scholar] [CrossRef]
- Khdhr, F.W.; Soleymani, F.; Saeed, R.K.; Akgül, A. An optimized Steffensen-type iterative method with memory associated with annuity calculation. Eur. Phy. J. Plus 2019, 134, 146. [Google Scholar] [CrossRef]
- Dehghani-Madiseh, M. A family of eight-order interval methods for computing rigorous bounds to the solution to nonlinear equations. Iran. J. Numer. Anal. Optim. 2023, 13, 102–120. [Google Scholar]
- Ogbereyivwe, O.; Izevbizua, O. A three-free-parameter class of power series based iterative method for approximation of nonlinear equations solution. Iran. J. Numer. Anal. Optim. 2023, 13, 157–169. [Google Scholar]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials—Part I; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials—Part II; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: New York, NY, USA, 1964. [Google Scholar]
- Zaka Ullah, M.; Muaysh Alaslani, S.; Othman Mallawi, F.; Ahmad, F.; Shateyi, S.; Asma, M. A fast and efficient Newton-type iterative scheme to find the sign of a matrix. AIMS Math. 2023, 8, 19264–19274. [Google Scholar] [CrossRef]
- Bhatia, R. Matrix Analysis; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1997; Volume 169. [Google Scholar]
- Soleymani, F.; Kumar, A. A fourth-order method for computing the sign function of a matrix with application in the Yang–Baxter-like matrix equation. Comput. Appl. Math. 2019, 38, 64. [Google Scholar] [CrossRef]
- Iannazzo, B. Numerical Solution of Certain Nonlinear Matrix Equations. Ph.D. Thesis, Universita Degli Studi di Pisa, Pisa, Italy, 2007. [Google Scholar]
- Stewart, G.W. Introduction to Matrix Computations; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Styś, K.; Styś, T. Lecture Notes in Numerical Analysis with Mathematica; Bentham eBooks: Sharjah, United Arab Emirates, 2014. [Google Scholar]
- Soheili, A.R.; Toutounian, F.; Soleymani, F. A fast convergent numerical method for matrix sign function with application in SDEs. J. Comput. Appl. Math. 2015, 282, 167–178. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

