A Mechanical Picture of Fractal Darcy’s Law

Abstract

The main goal of this manuscript is to generalize Darcy’s law from conventional calculus to fractal calculus in order to quantify the fluid flow in subterranean heterogeneous reservoirs. For this purpose, the inherent features of fractal sets are scrutinized. A set of fractal dimensions is incorporated to describe the geometry, morphology, and fractal topology of the domain under study. These characteristics are known through their Hausdorff, chemical, shortest path, and elastic backbone dimensions. Afterward, fractal continuum Darcy’s law is suggested based on the mapping of the fractal reservoir domain given in Cartesian coordinates $x_i$ into the corresponding fractal continuum domain expressed in fractal coordinates ${\xi }_i$ by applying the relationship ${\xi }_i={ϵ}_0{(x_i/{ϵ}_0)}^{{\alpha }_i-1}$, which possesses local fractional differential operators used in the fractal continuum calculus framework. This generalized version of Darcy’s law describes the relationship between the hydraulic gradient and flow velocity in fractal porous media at any scale including their geometry and fractal topology using the ${\alpha }_i$-parameter as the Hausdorff dimension in the fractal directions ${\xi }_i$, so the model captures the fractal heterogeneity and anisotropy. The equation can easily collapse to the classical Darcy’s law once we select the value of 1 for the alpha parameter. Several flow velocities are plotted to show the nonlinearity of the flow when the generalized Darcy’s law is used. These results are compared with the experimental data documented in the literature that show a good agreement in both high-velocity and low-velocity fractal Darcian flow with values of alpha equal to $0<{\alpha }_1<1$ and $1<{\alpha }_1<2$, respectively, whereas ${\alpha }_1=1$ represents the standard Darcy’s law. In that way, the alpha parameter describes the expected flow behavior which depends on two fractal dimensions: the Hausdorff dimension of a porous matrix and the fractal dimension of a cross-section area given by the intersection between the fractal matrix and a two-dimensional Cartesian plane. Also, some physical implications are discussed.

1. Introduction

Fractals are useful for modeling physical and applied sciences phenomena which are scale-invariant and exhibit dimensions that transcend integer values as well as self-similarity [1,2]. A fractal object is defined as an irregular geometrical shape such that its Hausdorff dimension, $d_{\mathcal{H}}$, is larger than its topological dimension, $d_t$ (see [3,4] and references therein).

Many natural structures have irregular geometries exhibiting statistical scale invariance over a great range of length scales L [5]. Specifically, it has been proved that naturally fractured reservoirs possess pore and fracture networks whose heterogeneity is almost always fractal [6]. So, there is a complex fluid flow path that cannot be described by traditional geometry [7,8].

Multiphase flows in porous materials is one of most important issues of hydrological and petroleum engineering. Likewise, Darcy’s law is a popular model which describes the characteristics of fluid movement through a porous medium. The standard Darcy’s equation takes the form [9]

$$\begin{array}{c}\hfill q=-\frac{k}{\mu }\frac{dp}{d{x}_1},\end{array}$$

(1)

where q is the the flux, k represents the absolute permeability of the porous domain, $\mu$ is the dynamic viscosity of the liquid, and $dp/d{x}_1$ denotes the pressure gradient. The above equation describes a linear relationship between the velocity field and the pressure gradient [10,11] and it is only valid for very low velocities or at low Reynolds numbers $Re<10$. Nevertheless, in the case of relatively fast flow ($Re>10$) or relatively high Knudsen numbers ($Kn>0.1$) [12,13], Darcy’s linear relation between the velocity and pressure drop is no longer valid; therefore, Equation (1) is not enough to describe this flow behavior, which is called non-Darcian flow, specifically in fractal objects, which present a nonlinear relationship between the flow velocity and hydraulic gradient (for a short review, see [14]).

Accordingly, several empirical formulas using ordinary calculus have been proposed to model flows that are different to the Darcian regime in fractured reservoirs. An increase in the flow rate captured by nonlinear equations was observed, such as the power function [15,16], exponential function [17], and Gamma function [18].

Fractional calculus is another efficient tool to obtain a better description of the flux and of the hydraulic gradient through generalized Darcy’s equations [14].

Although fractional calculus has been used from L’Opital and Leibniz (1965) [19,20], specifically the concept of fractional hydrology was put forward around 1990 [21] and has remained popular even nowadays. Consequently, a huge number of different models of Darcy’s law with fractional geometry were developed [22,23,24,25,26].

In this regard, a novel description on spatial fractional Darcy’s law controlled by Riemann–Liouville operators was introduced by [27] as

$$\begin{array}{c}\hfill q=-\frac{k_{\alpha }}{\mu }\frac{d^{\alpha }p}{d{x}_1^{\alpha }},\end{array}$$

(2)

where $k_{\alpha }$ is the fractional permeability and $0<\alpha \le 1$. If $\alpha =1$ in Equation (2), then Equation (1) is obtained. Another formulation relating the flux to the pressure gradient on the sample of length $x_1$ in the flow direction using fractional calculus was suggested by [28], which has dimensionless variables,

$$\begin{array}{c}\hfill q_{\beta ,D}=-{\delta }_{\beta ,D}\frac{{\partial }^{\beta }}{\partial r_D^{\beta }}{p}_D\end{array}$$

(3)

using Weyl’s fractional differential operator of order $\beta ={\Re }^{+}$. When $\beta =1$, the fraction mechanic in Equation (3) reduces to a classical mechanic description given by Equation (1).

All fractional Darcy’s equations have shown to be better models than the standard Darcy’s equation to describe nonlinearity between the fluid flux and hydraulic gradient. However, validation of non-Darcian models seems to be an endless challenge because alternative models lead to very different solutions of the same problems for fractal porous media. That is why the generalizations from conventional to fractional calculus use standard measures [21] such as length which is not a suitable measure for fractal sets [29]. A more complete model of physical phenomena must include scaling laws and fractality in fractional mechanics [30,31].

In this context, a solution of physical problems on fractal sets was formulated by some researchers using non-standard measures like the Hausdorff measure in different frameworks, for example, fractal geometry [32,33,34] and the fractal continuum [35,36,37]. These include both non-integer dimensions and self-similar properties in order to characterize the geometry and fractal topology of the fractal object under study.

Fractal continuum calculus (${\mathcal{F}}^{\alpha }$-CC) is a vector local differential calculus developed by Balankin and Elizarraraz [37,38] to provide a generalization of ordinary calculus to include fractal sets ${\mathcal{F}}^n$. ${\mathcal{F}}^{\alpha }$-CC consists of mapping mechanical problems for fractal media embedded in the Euclidean space $x_i\in E^n$ into the corresponding problems for the fractal continuum with spatial coordinates ${\xi }_i\in {\mathcal{F}}^{\alpha }$ [39]. The formulation employs local fractional differential operators [38]. This calculus makes possible an approximation of the non-differentiable functions defined on fractals by differentiable analytic envelopes [39].

Fractal continuum calculus has been applied to solve several mechanical problems on fractals mapped onto boundary value problems in a fractal continuum, such as hydrodynamics and the Newtonian fractal fluid equations [37,38]; Maxwell and diffusion equations [40,41]; and the Euler–Bernoulli bending beam [42,43].

The goal of this work is to generalize Darcy’s law, relating the flux to the pressure drop across a sample length of a porous media and similar phenomena. The mathematical tools of non-integer-dimensions calculus and fractal geometry and topology, along with the self-similar properties of naturally fractured reservoirs, allow for a more complete depiction of transport phenomena away from the traditional Darcy’s law, which is impossible to describe by conventional calculus, because non-conventional reservoirs have discontinuous points and non-differentiable continuous functions. By contrast, ordinary calculus deals with smooth and continuous functions on Euclidean spaces, where concepts such as limits, derivatives, and continuity are well-defined.

The manuscript’s structure is outlined as follows: In Section 2, we provide an overview of fractal continuum calculus, and Section 3 introduces the fractal Darcy’s law in the fractal continuum calculus sense. Section 4 presents an analysis and discussion of the mechanical implications and Section 5 finishes the article with conclusions.

2. Mathematical Background

In this section, we review and define the mathematical tools needed for the forthcoming analysis.

2.1. Spatial Coordinates Embedded in Euclidean Space $x_i\in E^3$ of a Fractal ${\mathcal{F}}^3$

The property of a fractal domain is that it does not depend on the unit of measurement and it is ruled by the scaling law [1] $N\sim {\left(L/ϵ\right)}^{d_{\mathcal{H}}}$, where the value of $d_{\mathcal{H}}$ remains constant within a bounded range of length scales ${ϵ}_0\le ϵ\le L<{ϵ}_C$, with ${ϵ}_0$ and ${ϵ}_C$ being the lower and upper cutoffs. Its Hausdorff dimension exceeds its topological dimension and at the same time cannot continuously fill the Euclidean space $E^d$ where it resides [44], such that $d_t<d_{\mathcal{H}}<d$. Therefore, the functions on the fractal space are non-differentiable and discontinuous [42].

In addition, the Hausdorff dimension is associated with the Euclidean metric ($ϵ$) defined in $E^3$. Nonetheless, the fractal domain can be characterized by another metric without reference to the embedding into the Euclidean space [44], called the geodesic metric (${ϵ}_{\ell }$). Hence, the fractal topology is characterized by the chemical dimension $d_{\ell }$ [41] as $N\sim {\left(L/{ϵ}_{\ell }\right)}^{d_{\ell }}$, where the value of $d_{\ell }$ keeps constant within a bounded range of the length scales $d_t\le {ϵ}_{\ell }\le L\le n$, with $d_t$ and $n=3$ being the lower and upper cutoffs, respectively. In addition, the integer part of the chemical dimension $\lfloor d_{\ell }\rfloor$ determines the number of orthogonal fractional coordinates on the fractal domain under study [39]: (${\xi }_i$ and $A_{{\mathcal{F}}_i}$).

On the other hand, we recall the following fractal parameters:

i

The fractal distance $x_{\mathcal{F}}$ is defined by $x_{\mathcal{F}}={ϵ}_0{\left(L/{ϵ}_0\right)}^{{\alpha }_i}$, where $\alpha$ is the fractal dimension of the fractal coordinates ${\xi }_i$.

 ii

The fractal area of the cross section $A_{\mathcal{F}}$ of the fractal domain (see Figure 1) with respect to its linear size L is given by $A_{\mathcal{F}}={ϵ}_0^2{\left(L/{ϵ}_0\right)}^{d_{{\mathcal{A}}_i}}$, with $d_{{\mathcal{A}}_i}$ being the fractal dimension of the cross-sectional area given by the intersection between the fractal and a two-dimensional Cartesian plane in $E^3$.

 iii

The fractal mass $M_{\mathcal{F}}$, which scales with the region size L as [35] $M_{\mathcal{F}}={\rho }_0{x}_{\mathcal{F}}{A}_{\mathcal{F}}={\rho }_0{ϵ}_0^3{\left(L/{ϵ}_0\right)}^{d_{\mathcal{H}}}$, where

$${\alpha }_i=d_{\mathcal{H}}-d_{{\mathcal{A}}_i},$$

(4)

and ${\rho }_0$ is the mass density.

Taking into account these concepts, we used the fractal parameters of the Menger sponge path-connected fractal. It is known that the Menger sponge can be constructed from a middle-$\gamma$ Cantor set for $0<\gamma <1$, which is defined as ${\mathcal{C}}^{\gamma }={\cap }_{n=1}^{\infty }{\mathcal{C}}_n^{\gamma }$ [45], where n denotes the iteration number. Accordingly, the Sierpinski carpet and Menger sponge are the two- and three-dimensional versions of the middle-$\gamma$ Cantor set [46] as is sketched in Figure 1. The Hausdorff dimension of these fractals is given by

$$\begin{array}{c}\hfill d_{\mathcal{H}}=d·\frac{log\left(L/{ϵ}_0-\beta \right)}{log(L/{ϵ}_0)}\end{array}$$

(5)

where d is the dimension of the embedding Euclidean space, $L/{ϵ}_0$ is the size of the boxes covering the fractal mass, and $\beta$ denotes the deleted boxes of the fractal mass. The fractal mass can be the length of a line or the area of a surface or the volume of an object. So, in Equation (5), $d=1,2,3$ represent the Haudorff dimension of the Cantor set, Sierpinski carpet, and Menger sponge, respectively [47].

2.2. Spatial Coordinates in the Fractal Continuum ${\xi }_i\in F^{\alpha }$

The fractal continuum is a three-dimensional domain ${\mathcal{F}}^3\subset E^3$ filled with continuous matter [39]. It is equipped with rules pertaining to integro-differential calculus, such that its properties are continuous and differentiable functions (see [39]). Then, the topological dimension is given by $d_t=3>d_{\mathcal{H}}$. A path-connected fractal where $\lfloor d_{\ell }\rfloor <3$ as the Menger sponge having $d_{\ell }=d_{\mathcal{H}}\approx 2.72$ and $\lfloor d_{\ell }\rfloor =2$ possesses a pair of mutually orthogonal fractal coordinates (${\xi }_i,A_{{\mathcal{F}}_i}$) associated with the decomposition of the infinitesimal volume element ${\mathcal{F}}_{2.72}^3$ [39]:

$$\begin{array}{ccc}\hfill d{V}_{2.72}& =& d{\xi }_i\left(x_i\right)d{A}_{{\mathcal{F}}_i}\hfill \\ & =& c_1^{\left(i\right)}\left(x_i\right)c_2^{\left(i\right)}d{x}_{i}d{A}_i\hfill \\ & =& c_3\left(x_k\right)dV\hfill \\ & =& c_{3}d{x}_{1}d{x}_{2}d{x}_3,\hfill \end{array}$$

(6)

where $d{A}_i=d{x}_j·d{x}_k$ and $d{A}_{{\mathcal{F}}_i}$ are the infinitesimal area elements on the intersection between ${\mathcal{F}}^3$ and the two-dimensional plane perpendicular to the i-axis in $E^3$ and in ${\mathcal{F}}^3\subset E^3$, respectively, while $c_2^{\left(i\right)}\left(x_{j\ne i}\right)$ is the density of the admissible states in the plane of this intersection. From Equation (6) and the fractal mass $M_{\mathcal{F}}={\rho }_0{ϵ}_0^3{\left(L/{ϵ}_0\right)}^{d_{\mathcal{H}}}$, the transformation functions in ${\mathcal{F}}^3\subset E^3$ obey the following relationship [38]

$$\begin{array}{c}\hfill c_3\left(x_i\right)=c_1^{\left(k\right)}\left(x_k\right)c_2^{\left(k\right)},\end{array}$$

(7)

where

$$\begin{array}{c}\hfill c_2^{\left(k\right)}(x_i,x_j)\ne c_1^{\left(i\right)}\left(x_i\right)c_1^{\left(j\right)}\left(x_j\right),\end{array}$$

(8)

because a choice of the coordinate pair (${\xi }_i,A_{{\mathcal{F}}_i}$) is not unique. Accordingly, to fulfill the constitutive requirement (4), the densities of admissible states ${\mathcal{F}}^3\subset {\Re }^3$ should obey the following scaling relations

$$\begin{array}{c}\hfill \begin{array}{c}\int dV{c}_3\sim {ϵ}_0^{3-d_{\mathcal{H}}}{L}^{d_{\mathcal{H}}},\hfill \\ \int d{A}_i{c}_2^{\left(i\right)}\sim {ϵ}_0^{2-d_{\mathcal{A}}}{L}^{d_{\mathcal{A}}},\hfill \\ \int d{\xi }_i\sim {ϵ}_0^{1-{\alpha }_i}{L}^{{\alpha }_i},\hfill \end{array}\end{array}$$

(9)

where $\int d{\xi }_i=\int d{x}_i{c}_1^{\left(i\right)}$, the index i denotes a Cartesian direction and the scaling exponent ${\alpha }_i=d_{\mathcal{H}}-d_{\mathcal{A}}$. From Equation (7), it is deduced that ${\xi }_i={ϵ}_0^{1-{\alpha }_i}{x}_i^{{\alpha }_i}$, and so it holds that

$$\begin{array}{c}\hfill x_i\mapsto {\xi }_i={ϵ}_0{\left(\frac{x_i}{{ϵ}_0}\right)}^{{\alpha }_i},\end{array}$$

(10)

whose geometrical interpretation is detailed in Figure 2, where the mapping ${\mathcal{F}}_3^{d_{\mathcal{H}}}\mapsto {\mathcal{F}}_{d_{\mathcal{H}}}^3$ is sketched. From the above equations, it is deduced that

$$\begin{array}{c}\hfill c_1^{\left(i\right)}={\alpha }_i{ϵ}_0^{1-{\alpha }_i}{x}_i^{{\alpha }_i-1}\end{array}$$

(11)

where ${\alpha }_i$ is the Hausdorff dimension of coordinates ${\chi }_i$, such that ${\alpha }_i=d_{\mathcal{H}}-d_{{\mathcal{A}}_i}$.

2.3. Conservation Laws for Fractal Continuum Flow

Within the fractal continuum approach, the conservation equations used for the model flow of Newtonian or non-Newtonian fluids are as follows [38]: for the continuity equation,

$$\begin{array}{c}\hfill \frac{\partial {\rho }_c}{\partial t}=-di{v}_{\mathcal{H}}\left({\rho }_c\overrightarrow{u}\right)\end{array}$$

(12)

where the Hausdorff divergence is defined by

$$\begin{array}{c}\hfill di{v}_{\mathcal{H}}f={\xi }_1\frac{\partial f_1}{\partial x_1}+{\xi }_2\frac{\partial f_2}{\partial x_2}+{\xi }_3\frac{\partial f_3}{\partial x_3}.\end{array}$$

(13)

The equation of the balance of the energy density $e(x_i,t)$ in the fractal continuum flow is given as

$$\begin{array}{c}\hfill {\rho }_c\left(\frac{d}{dt}\right)e={\sigma }_{ij}{\nabla }_j^H{u}_i+{\rho }_c{\nabla }_i^H\overrightarrow{q},\end{array}$$

(14)

where ${\sigma }_{ij}$ is the stress tensor, $\overrightarrow{q}=q_{i}n$ is the density of the heat flux, and the term ${\nabla }_i^{\mathcal{H}}$ denotes the Hausdorff derivative (see [37,48]):

$$\begin{array}{c}\hfill {\nabla }_i^{\mathcal{H}}f=\underset{x_i\to x_i^{\prime }}{lim}\frac{f\left(x_i^{\prime }\right)-f\left(x_i\right)}{\Delta \left(x_i^{\prime },x_i\right)}=\frac{1}{{\alpha }_i}{\left(\frac{x_i}{{ϵ}_0}\right)}^{1-{\alpha }_i}\frac{\partial }{\partial x_i}f\end{array}$$

(15)

where $\partial /\partial x_i$ means the conventional partial derivative. Meanwhile, the balance of the density of the momentum is governed by

$$\begin{array}{c}\hfill \left(\frac{d}{dt}\right){\upsilon }_k=f_k+{\rho }_c^{-1}{\nabla }_i^H{\sigma }_{ki},\end{array}$$

(16)

where $f_k$ is the density of the volume forces and

$$\begin{array}{c}\hfill {\upsilon }_i={\alpha }_i{\left(\frac{x_i}{{ϵ}_0}\right)}^{{\alpha }_i-1}{u}_i.\end{array}$$

(17)

3. Differential Equations of Darcy’s Law for Fractal Continuum

This section is devoted to deducing the fractal Darcy’s law by applying the ideas reviewed in the previous part.

Darcy’s law in the fractal continuum space is given in fractal coordinates ${\xi }_i\in {\mathcal{F}}^{\alpha }$ and is analogous to the ordinary Darcy’s law given in Cartesian coordinates. Then, the following expression is obtained:

$$\begin{array}{c}\hfill q_{\alpha }=-\frac{k_{{\alpha }_1}}{\mu }\frac{dp}{d{\xi }_1},\end{array}$$

(18)

where p represents pressure, ${\xi }_1$ denotes the fractal length of the sample, and $k_{{\alpha }_1}$ represents the fractal permeability, which can be obtained using Equations (36) or (6) of Refs. [49,50], respectively. When the porous matrix is of the classical Menger sponge type (where $d_{\mathcal{H}}=log20/log3$), the fractal permeability of porous media can be computed as $k_{{\alpha }_1}({\varphi }_{{\xi }_1}=0.3)=k_{{\xi }_1}{\lambda }^{-0.12}$, with ${\varphi }_{{\xi }_1}={(20/27)}^n=3^{-(3-d_{\mathcal{H}})n}$ being the global porosity and $n=1,2,3,\dots ,\infty$ is the iteration number of the Menger sponge [51]. In the case of a core sample, the overall porosity is obtained with a criterion based on the fractal statistical properties of porous media (see [52] and references therein).

The mapping of Equation (18) using fractal continuum calculus (${\mathcal{F}}^{\alpha }$-CC) from fractal coordinates to Cartesian coordinates is carried out using Equations (10) and (17) in order to generalize Darcy’s law as follows (see Figure 3):

$$\begin{array}{c}\hfill q_{{\alpha }_1}=-\frac{k_{{\alpha }_1}}{\mu }{ϵ}_0^{{\alpha }_1-1}\frac{dp}{d{x}_1^{{\alpha }_1}}.\end{array}$$

(19)

It is worth noting that for the Hausdorff dimension ${\alpha }_1=d_{\mathcal{H}}-d_A=1$ (in both coordinates Cartesian and fractals, $x_1$ and ${\xi }_1$, respectively), Equation (19) takes the form of the standard Darcy’s law given in Equation (1). Here, the cross-sectional area is in the Cartesian $x_2{x}_3$-plane and fractal ${\xi }_2{\xi }_3$-plane.

The mechanical picture shown in Figure 3 exhibits the link between the pressure gradient and velocity by the fractal Darcy’s law model (19) in a porous media with heterogeneous mechanical features, which correspond to values $0<{\alpha }_1\le 2$.

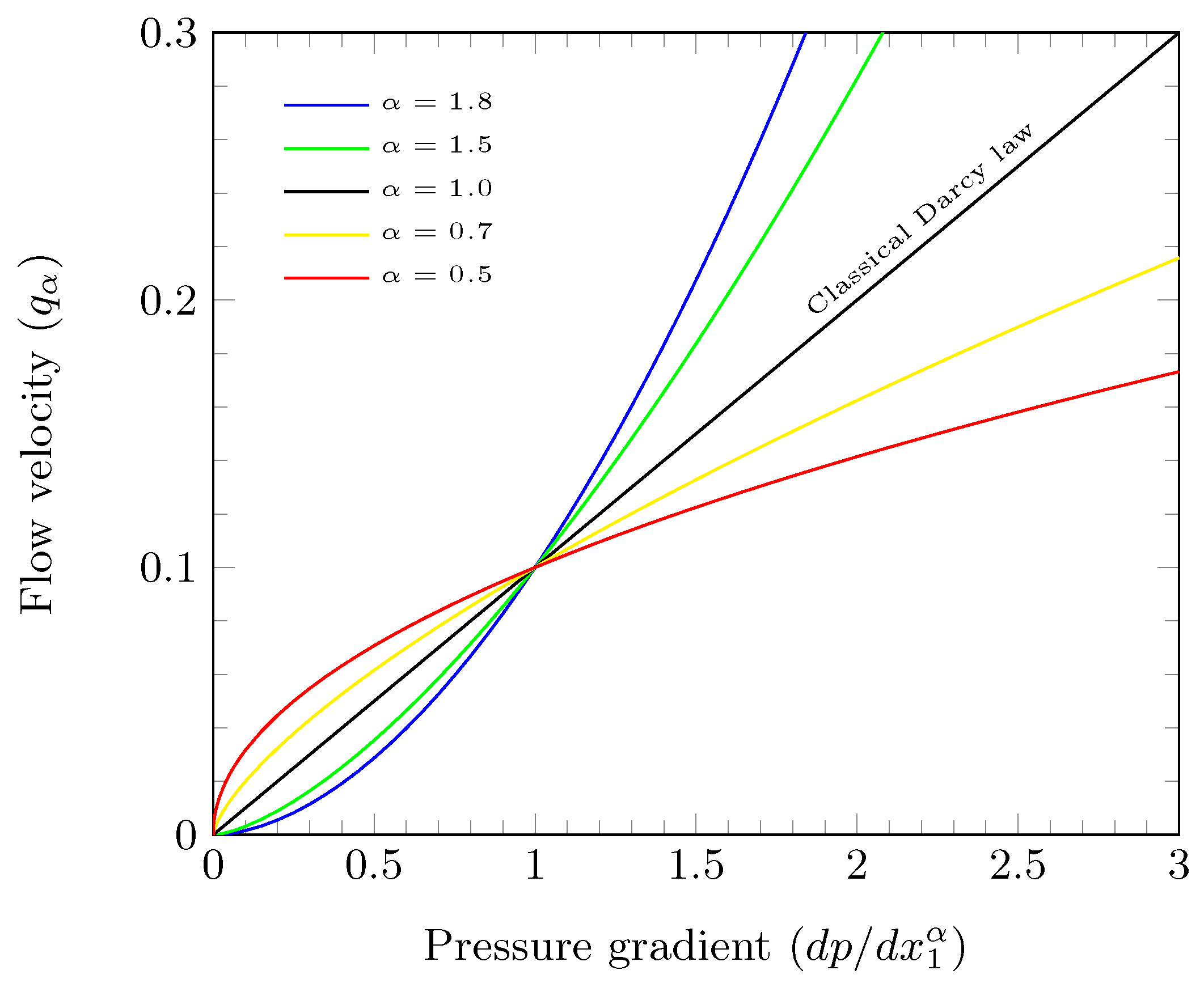
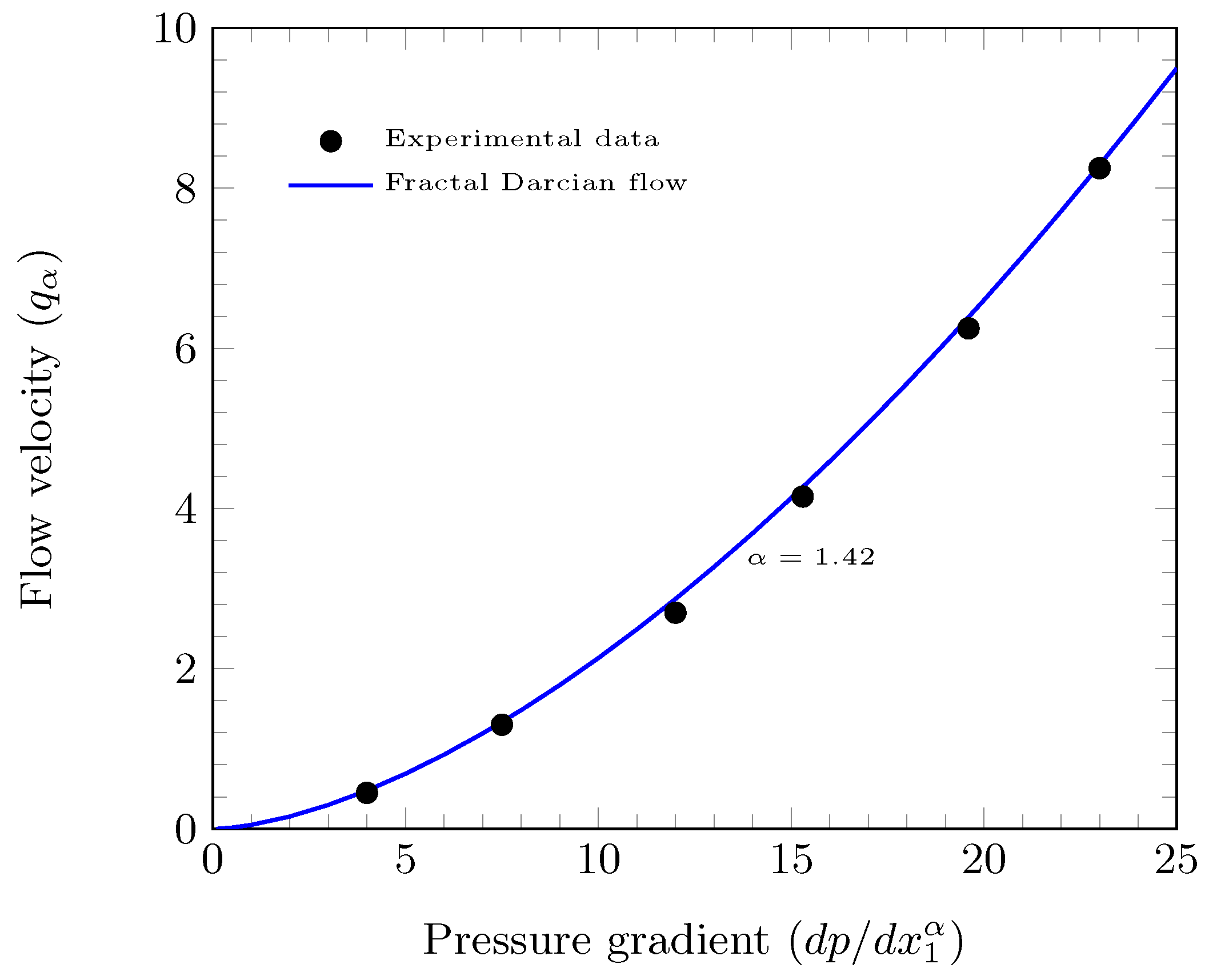
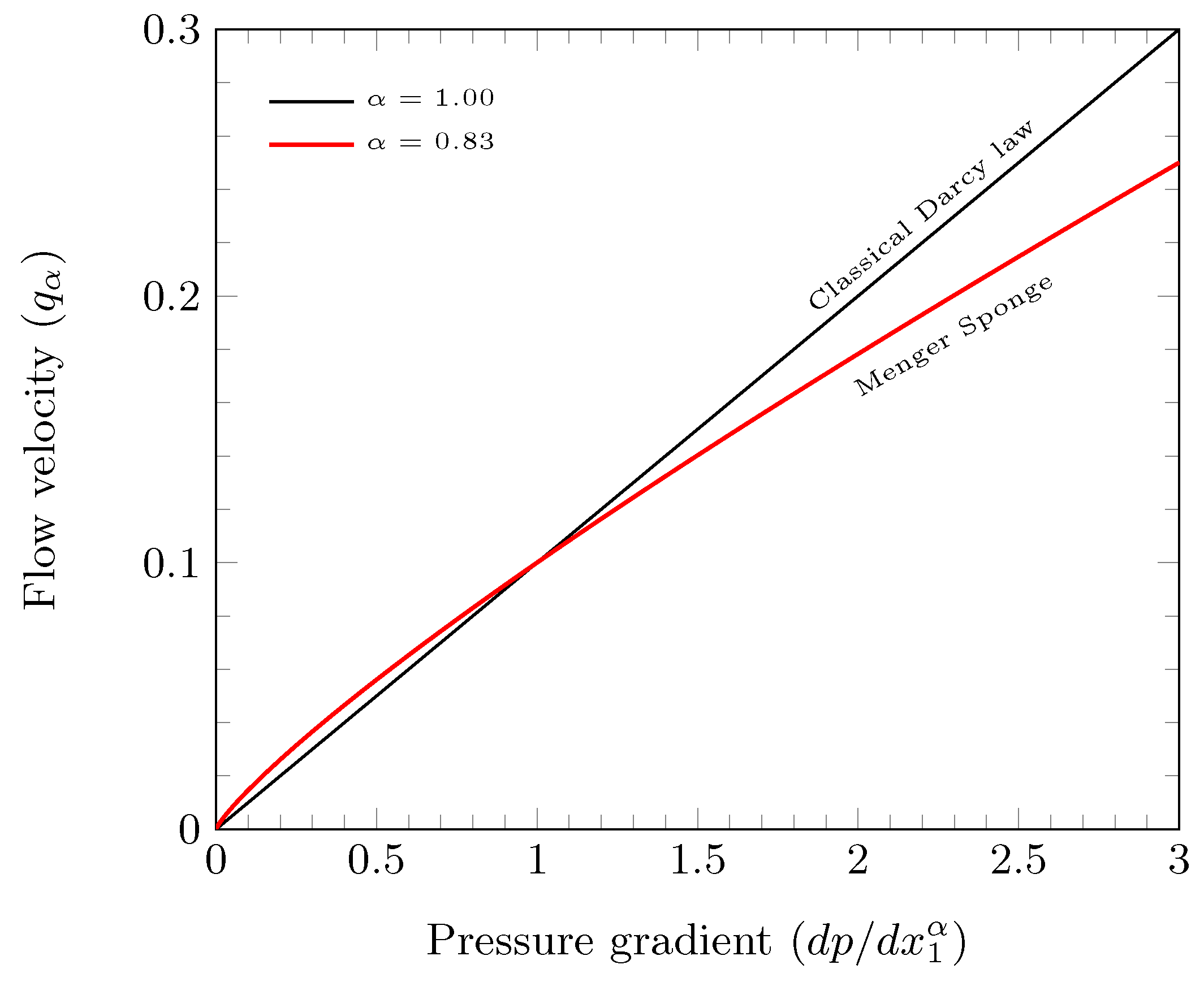
4. Theoretical Implementations and Discussions of Suggested Formulation

In this section, we show the validity of the developed model and the discussion of the effectiveness of fractal continuum calculus on non-Darcian flow.

For the purpose of the model’s dependability evaluation (which was suggested in Equation (19)), it is compared with both the experimental test carried out by [53] and the fractional Darcy law introduced in [14]. The experimental results of the non-Darcian flow of high velocity match the result of the fractal Darcy equation when ${\alpha }_1=0.68$, and it is consistent with the numerical result of the Zhou–Yang fractional model as can be observed in Figure 4, where the straight line represents the standard Darcian flow and the curved lines are non-Darcian flow cases. At first glance, it can be seen in Figure 4 that the blue line perfectly fits the behavior described by the experimental data (solid circle in black color). On the other hand, in this particular case, our formulation is consistent with the Zhou fractional model.

Moreover, another application of the fractal Darcy’s equation is shown in Figure 5; it is a non-Darcian flow of low velocity. Again, the flow behavior displayed by Equation (19), in blue, is a good description of the experimental data (reported in Ref. [14]), which matches with other non-Darcian models. For example, in this particular case, the blue curve is the same as the one obtained using a fractional Darcy equation suggested by Chang–Sun (for details, see Equation (2.9) in [54] and figures therein). However, it is easy to see that there is a discrepancy between the experimental data and the results produced by the Chang–Sun model and ours. Unfortunately, the mathematical models do not exactly describe the experimental behavior; however, they do give a close description of the actual behavior of the flow.

In addition, a numerical analysis on the inverse of the Menger sponge was carried out in order to describe the fluid flow through fractal porosity using the well-known fractal parameters of the classical Menger sponge, and then the formulation suggested in this work was applied. Figure 6 shows a non-Darcian flow of high velocity with ${\alpha }_1=0.83$.

In this manuscript, it is argued that in addition to the fractal geometry of the porous medium, its fractal topology must be considered, as a way of having a more complete description of the heterogeneity of the medium. It is well-known that the Hausdorff dimension tells us nothing about the fractal topology and it can be treated as the degree to which a set “fills” the Euclidean space in which it is embedded. There are mathematical and physical fractals with the same Hausdorff dimension and with different chemical, spectral, or lacunarity dimensions, for example, the classical Weierstrass fractal, three-dimensional Cantor dust, and Sierpinski carpet have $d_{\mathcal{H}}=log8/log3$, whilst the von Koch curve and two-dimensional Cantor dust have the same Hausdorff dimension $d_{\mathcal{H}}=log4/log3$.

However, to our best knowledge, the non-homogeneous media can be quantifiably set apart by this group of dimension numbers in order to further characterize a fractal set under study. It is a straightforward matter to see that Equation (19) holds these aspects through the Hausdorff and chemical dimensions, which are involved in the alpha parameters as defined in Equation (4). We emphasize that the fractal permeability was out of the scope of this work, because there are studies that delve into that topic, for example, Refs. [49,55,56].

In this regard, the physical significance of the fractal Darcy’s law refers to a theoretical framework or mathematical relationship that generalizes Darcy’s law in order to describe fluid flow through porous media that exhibit non-conventional characteristics. This could potentially involve considering the complex and irregular nature of porous materials on different scales and how it influences fluid flow behavior. One can more easily picture the importance of a fractal description in terms of the relationship between fluid flow and friction in two dimensions: a flow over a smooth horizontal surface (line) with a no-slip boundary condition behaves very differently than a rough line (one can think of a sawtooth or wavy line with zero mean as the simplest cases). The fractal dimensions give a mathematical idea of the complexity of that boundary/line/case, even if on average (or viewed from the distance) it is a straight line. One can extrapolate the concept to three (or more) fractal dimensions and infer that their characteristics have a rich mathematical behavior, from which the traditional Darcian flow is a particular case.

Another benefit of the continuous fractal approach used in this work is the value that ${\alpha }_1$ in Equation (19) can be $0<{\alpha }_1<2$. Therefore, the Darcy fractal model can be applied for high-velocity non-Darcian flow for $0<{\alpha }_1<1$ and for low-velocity non-Darcian flow for $1<{\alpha }_1<2$.

5. Conclusions

The objective of the present work is to give a description of the non-Darcian flow behavior by applying fractal continuum calculus. A fractal Darcy’s equation is suggested, which is applicable for both high-velocity non-Darcian flow as sketched in Figure 4 and low-velocity non-Darcian flow as is plotted in Figure 5.

When compared to experimental data, the information obtained from different models as well as the one proposed here indicates that the flow models with local fractional differential operators mentioned in this work are able to provide a better description of the characteristics of the non-Darcian flow with higher precision and pliability.

The present model not only has a resemblance to the results acquired in models that incorporate fractional geometry but also includes fractal geometry through the different Hausdorff dimensions of the porous medium and fractal topology using its (connectivity) chemical dimension, and consequently, it permits capturing the heterogeneity (with the alpha parameter) of the porous medium in a single expression, which is called the fractal Darcy’s law.

In addition, the discussion about the effectiveness of fractal continuum calculus shows that fractal continuum models can be used to describe the non-Darcian flow in porous media. It is noted that when the Hausdorff dimension ${\alpha }_i$ of Cartesian coordinates $x_i\in E^3$ is the integer order (${\alpha }_i=1$), the conventional Darcy’s equation is obtained as a particular case of the fractal Darcian model.

On the other hand, the fractal continuum calculus framework can be used to model complex problems in other areas of physics, for example, wave propagation in fractal media, mechanical vibrations, and fracture mechanics, among others.