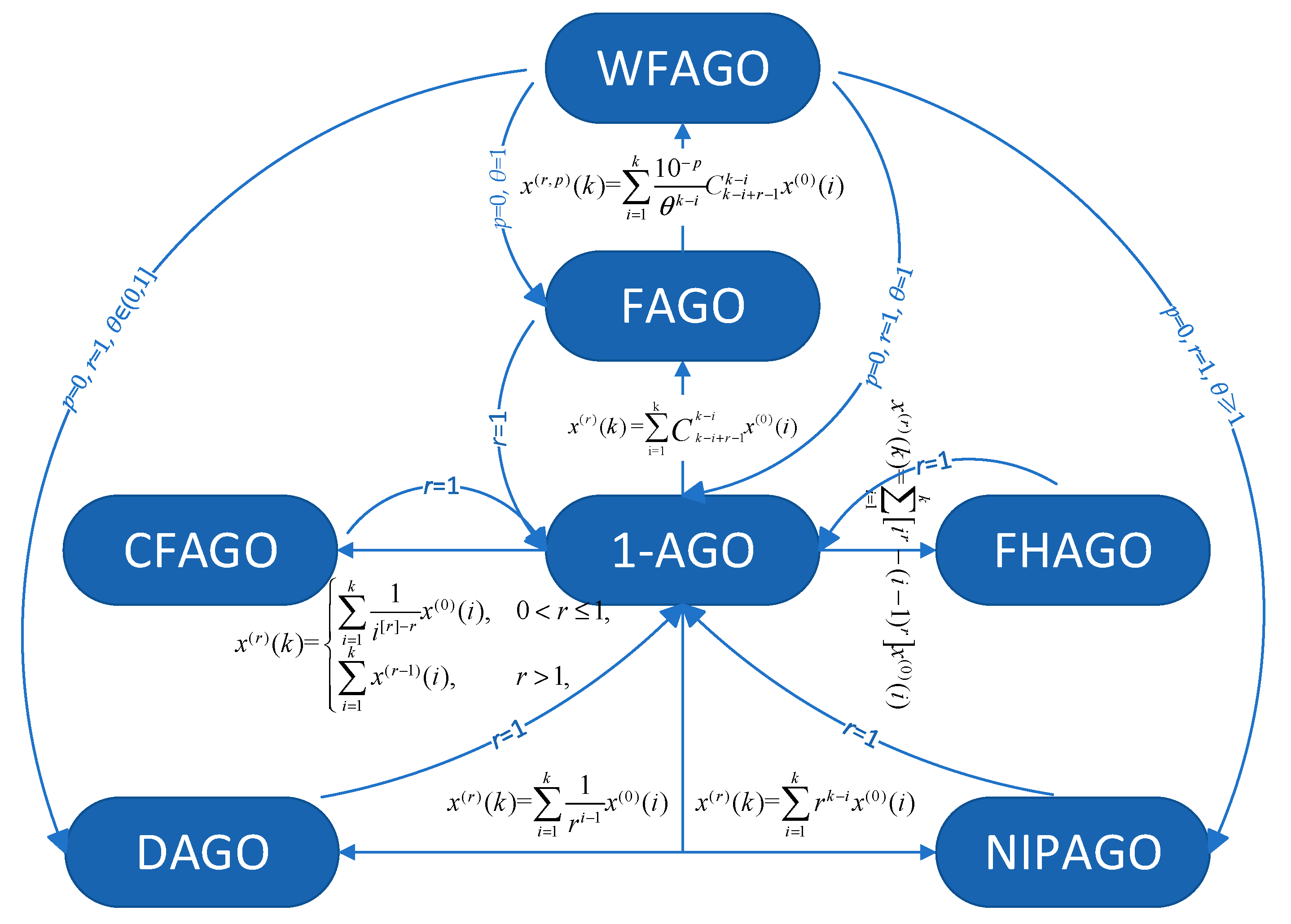
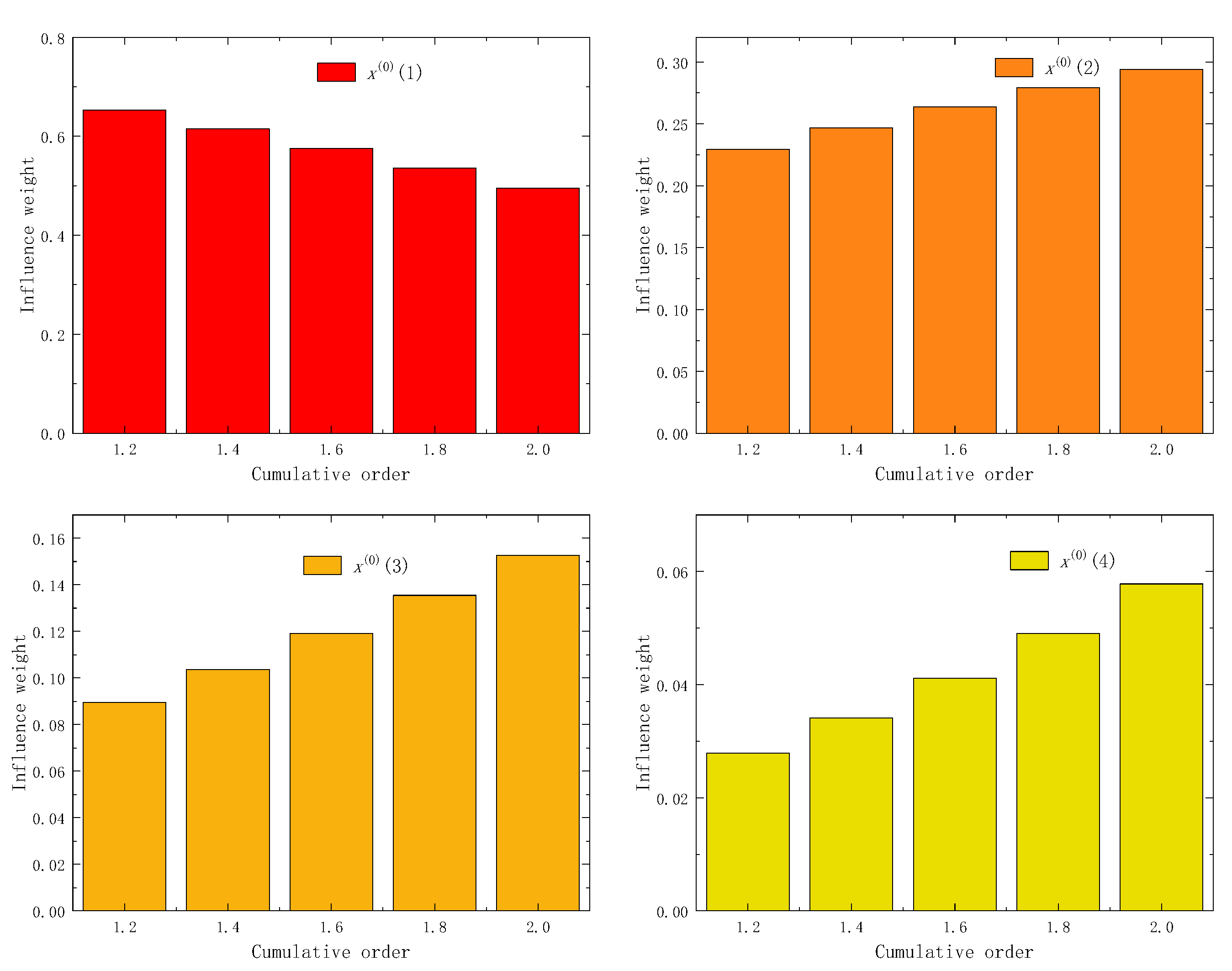
Figure 1.
The relation between the 1-AGO and other AGOs.
Figure 1.
The relation between the 1-AGO and other AGOs.
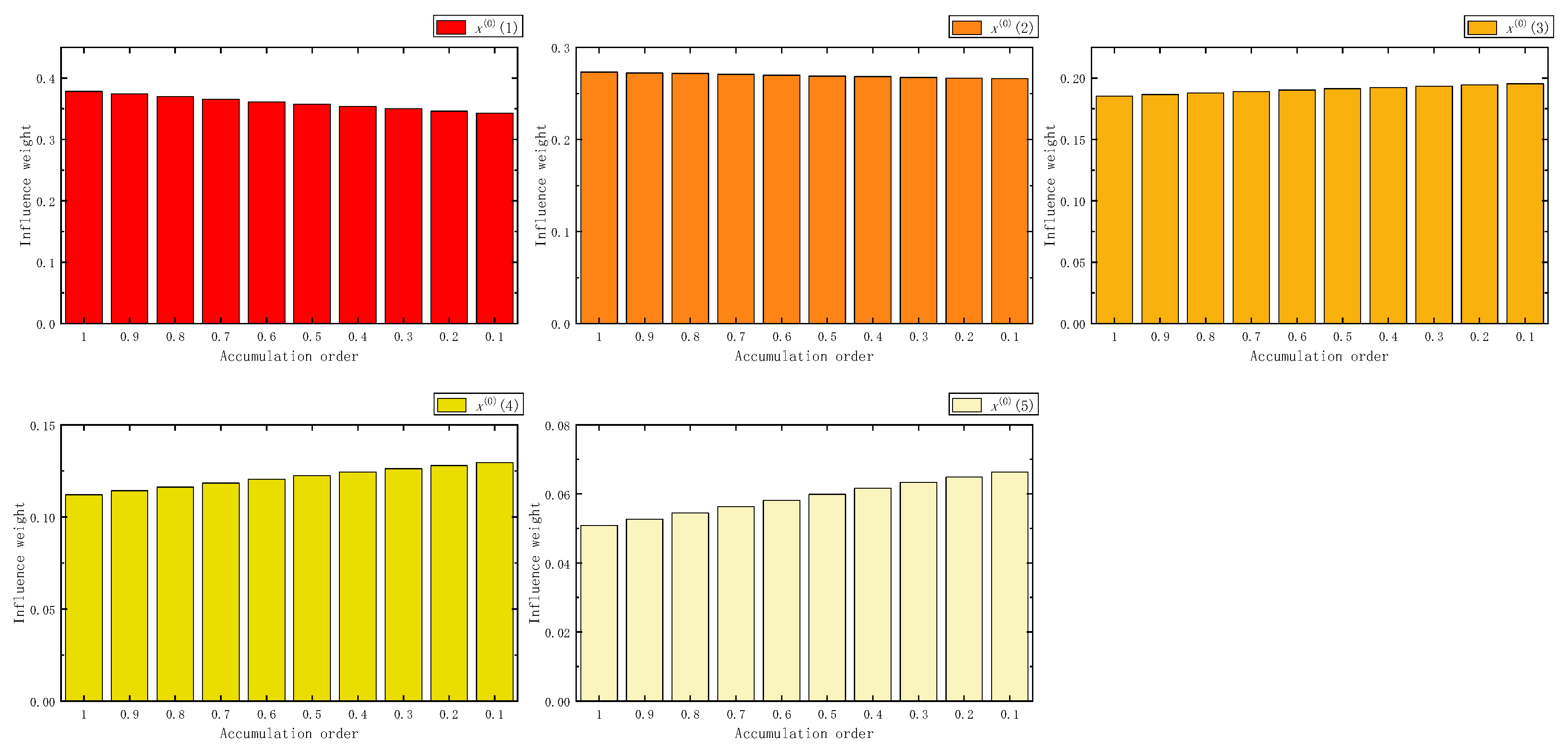
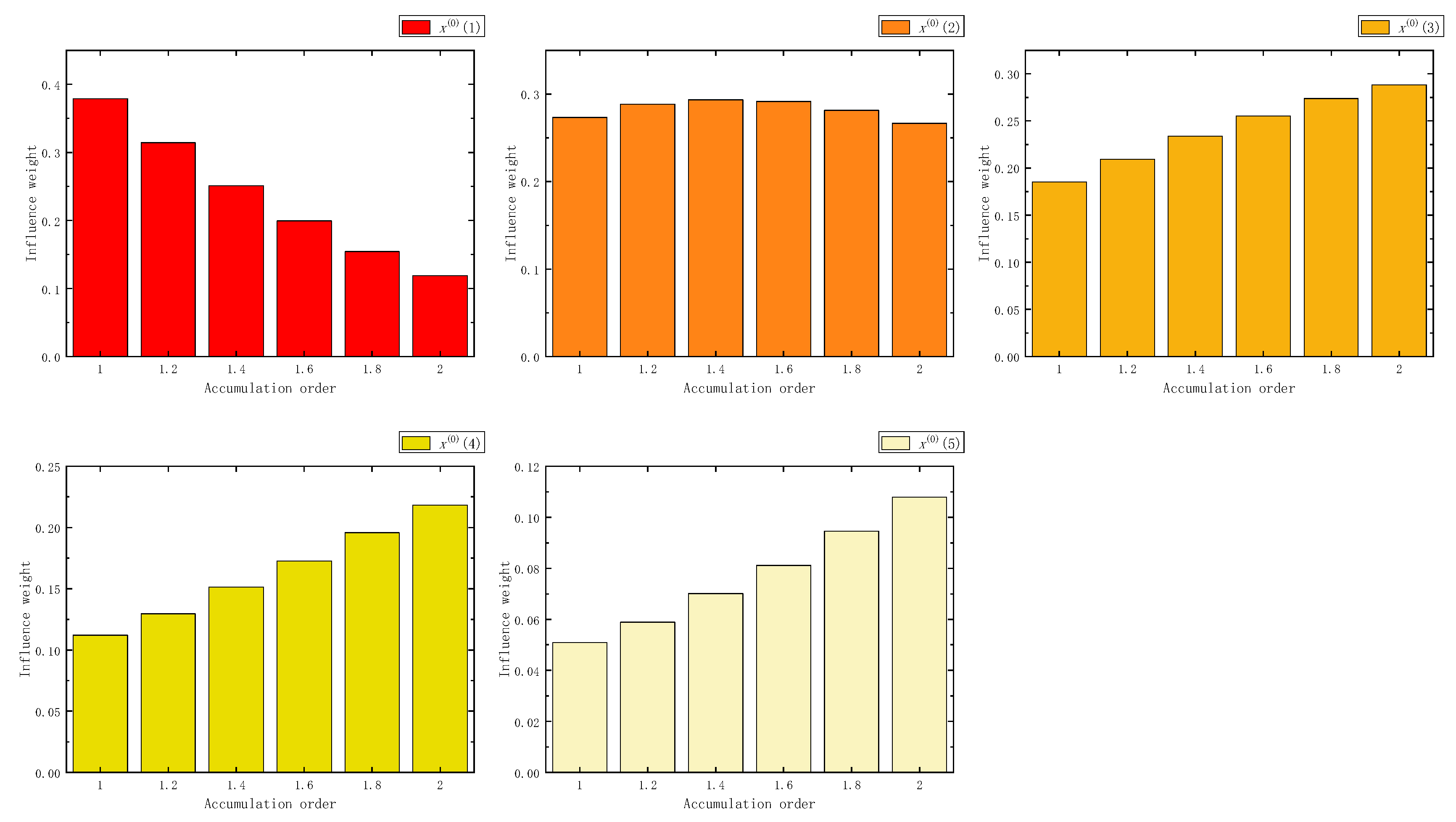
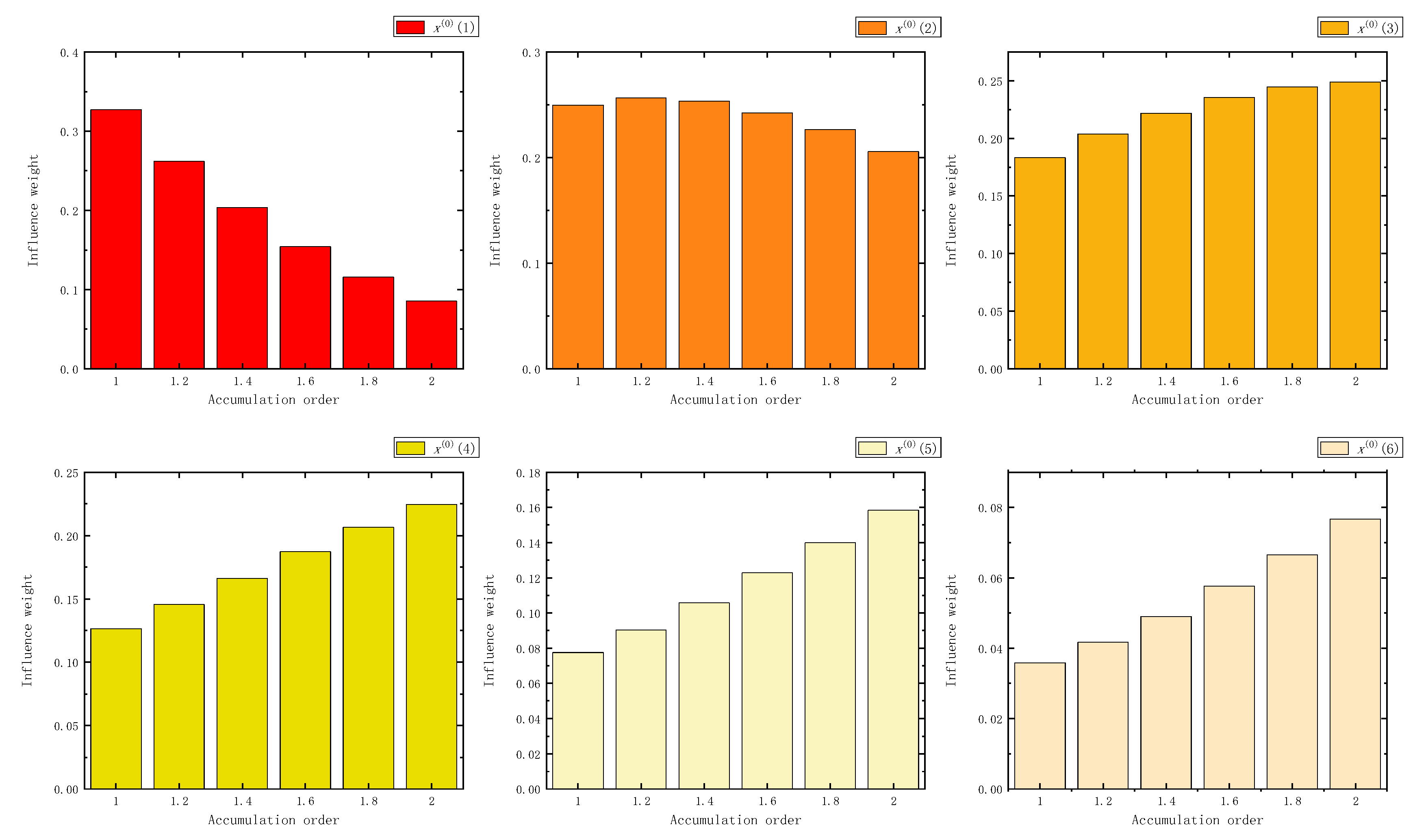
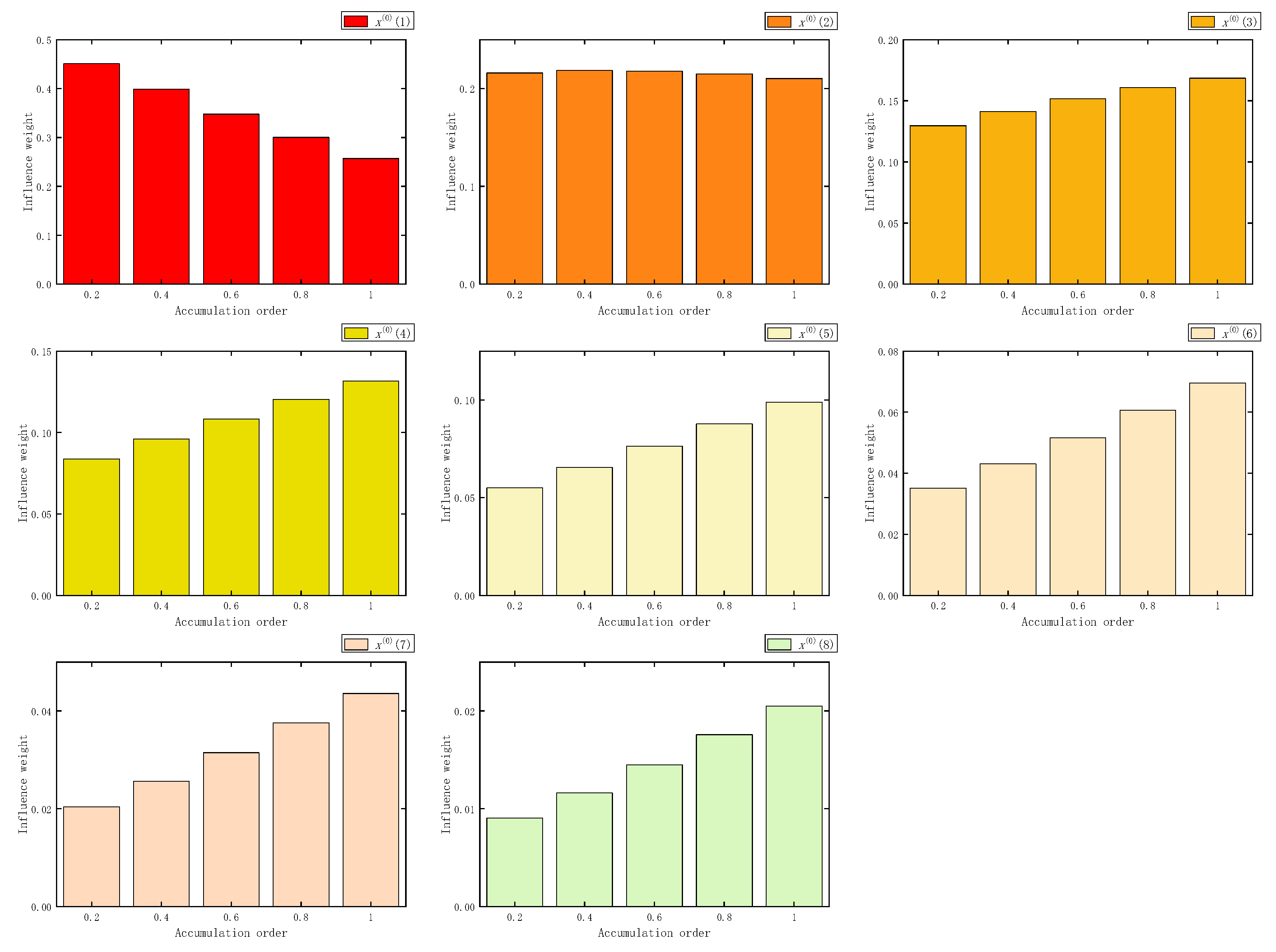
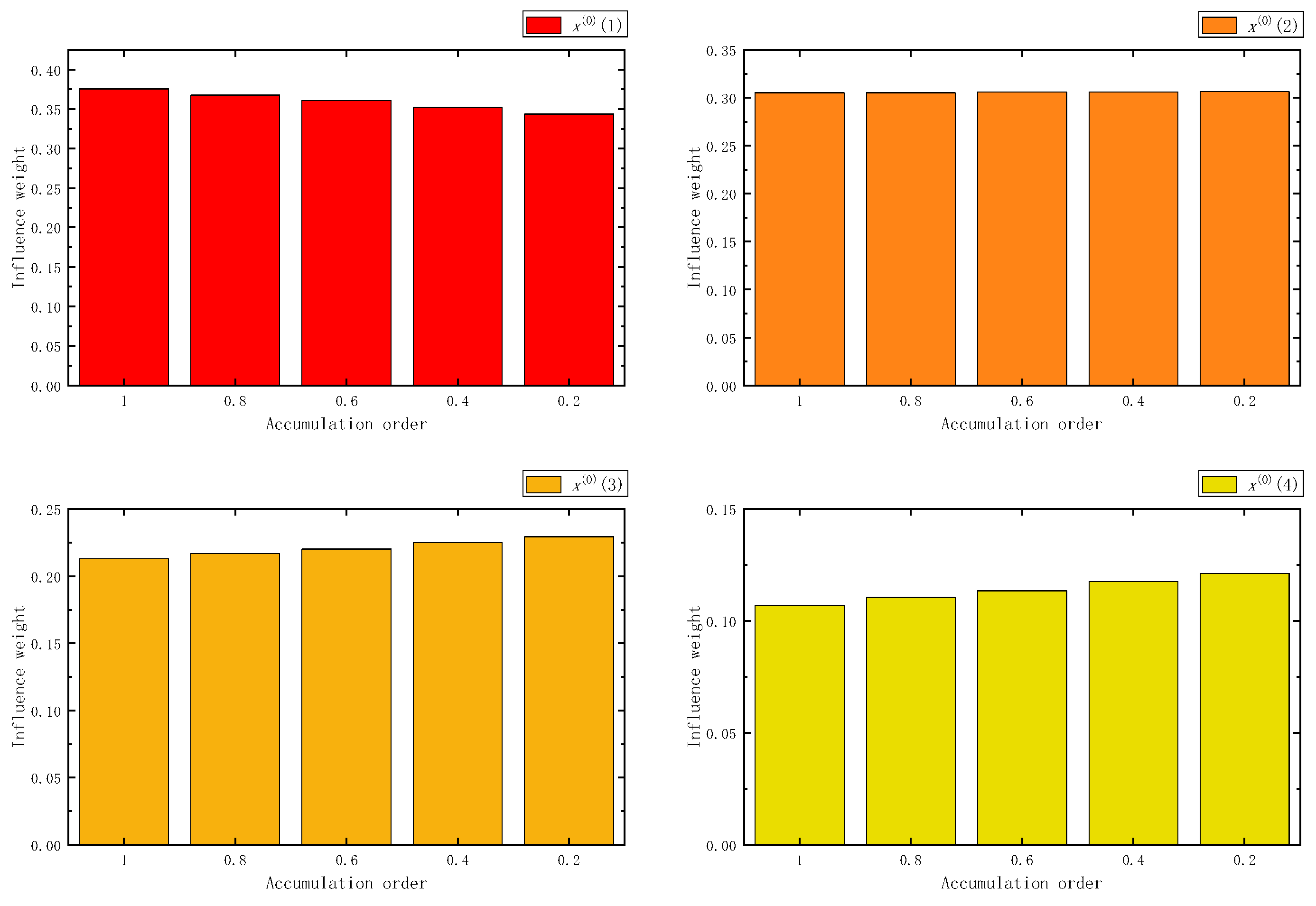
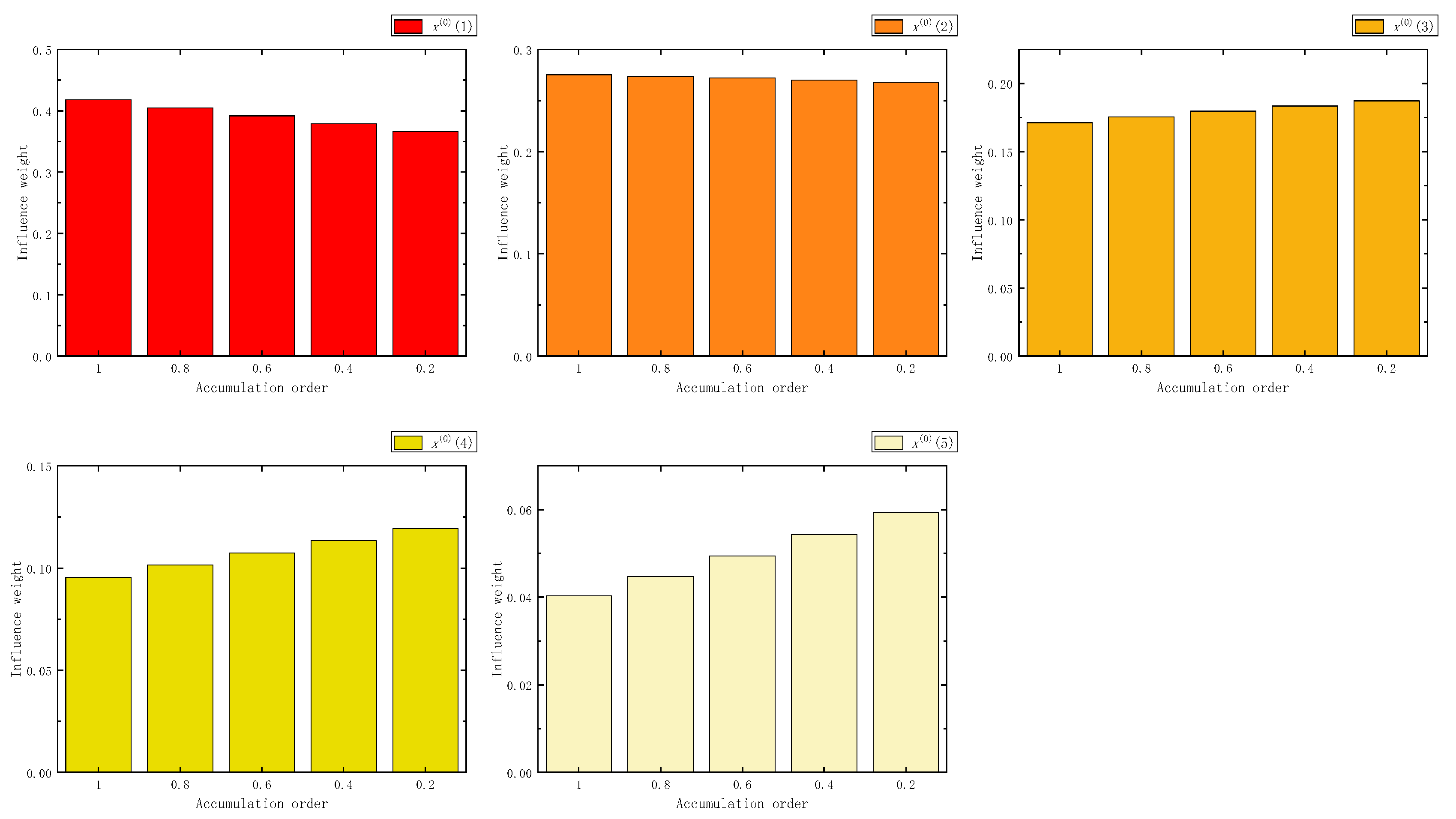
Figure 2.
The influence weight of five samples in FAGO.
Figure 2.
The influence weight of five samples in FAGO.
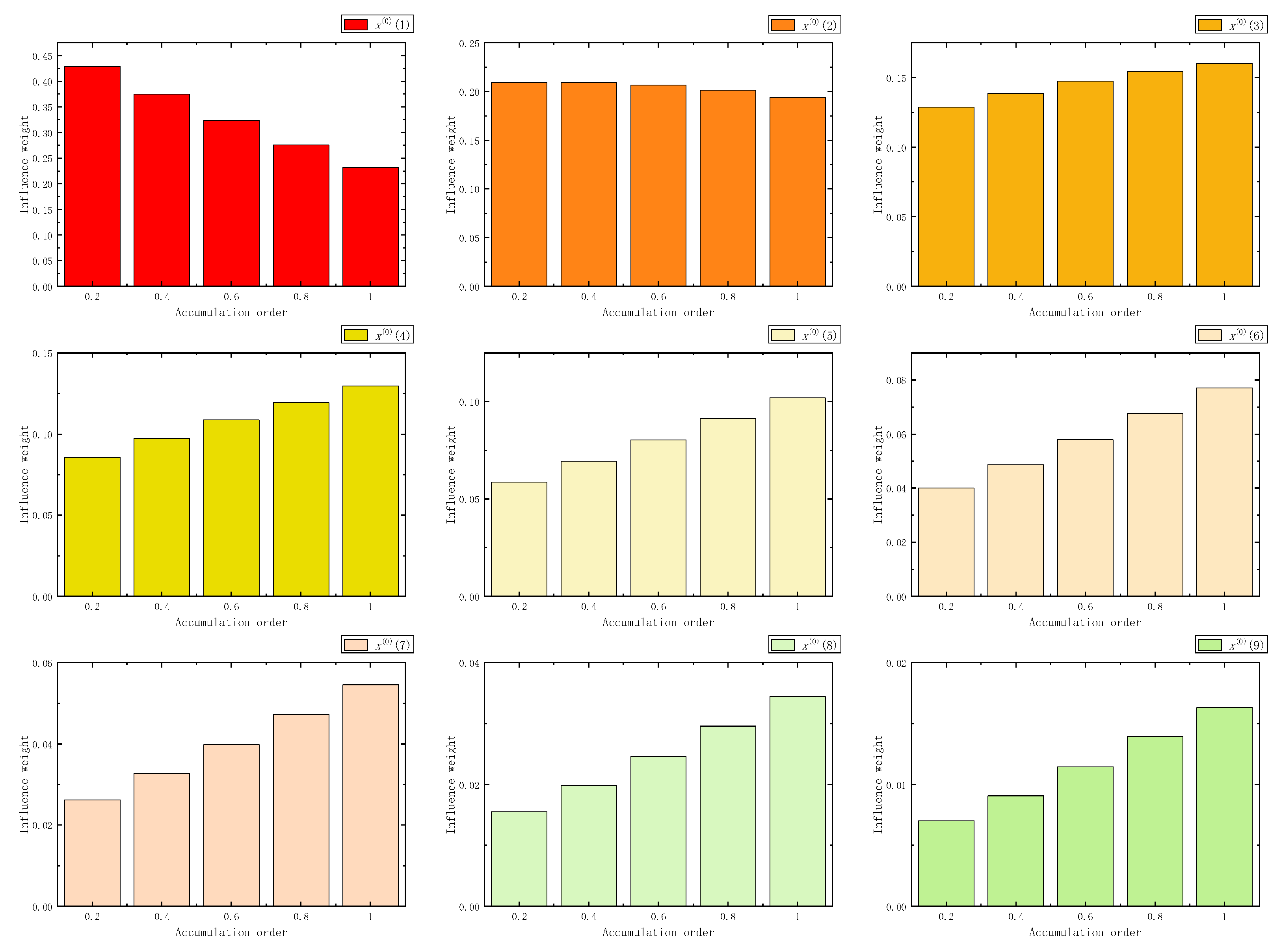
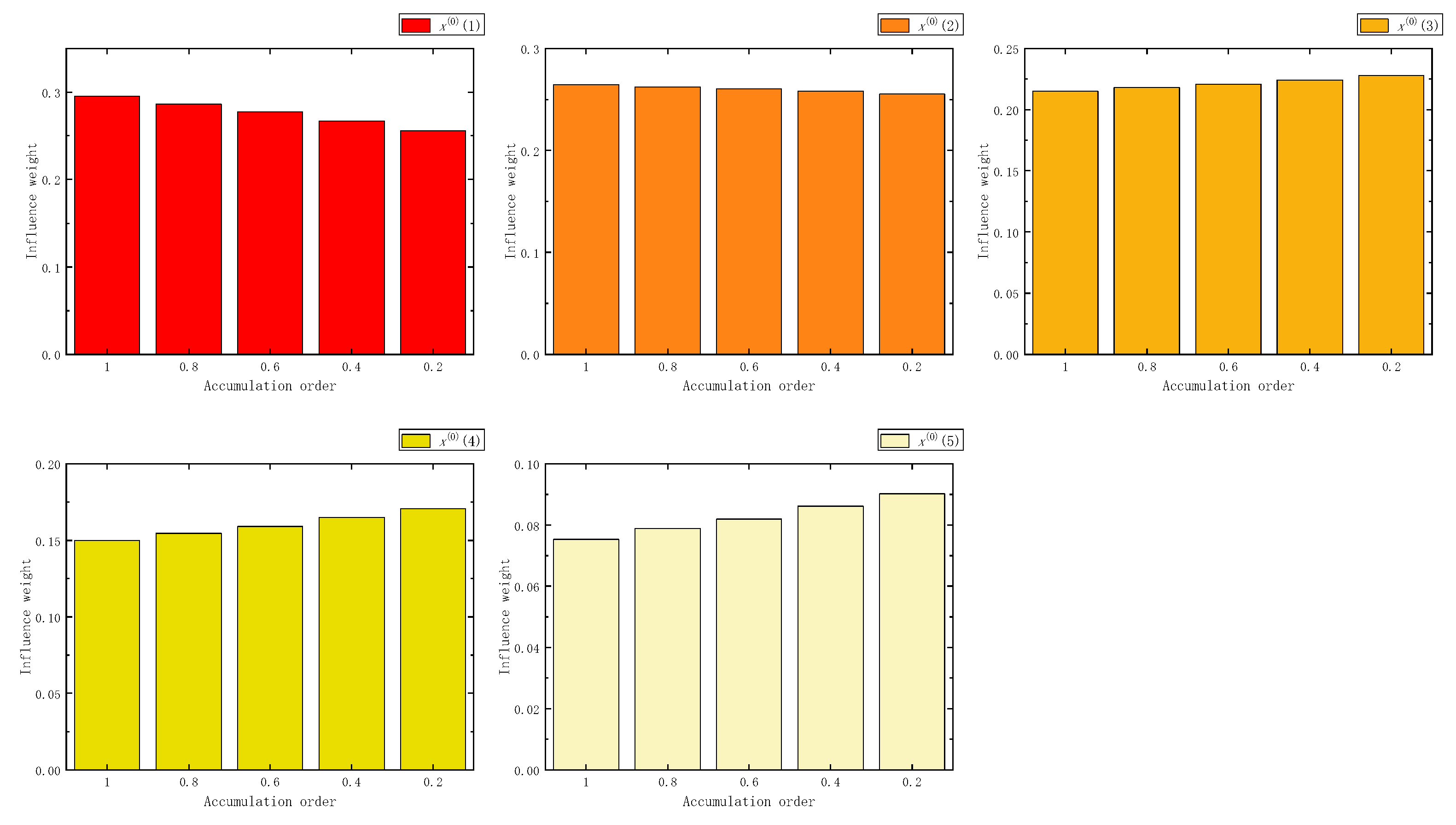
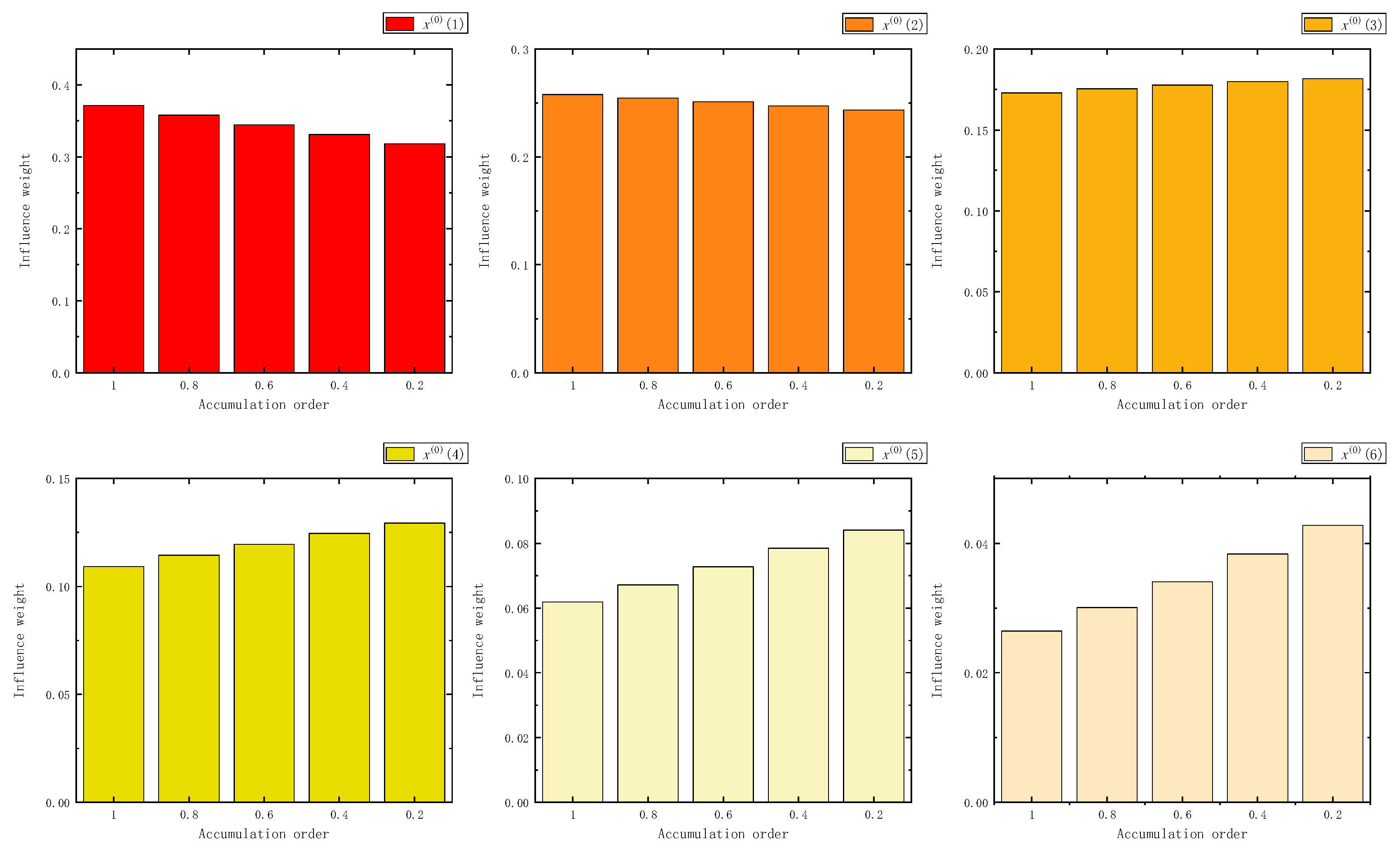
Figure 3.
The influence weight of six samples in FAGO.
Figure 3.
The influence weight of six samples in FAGO.
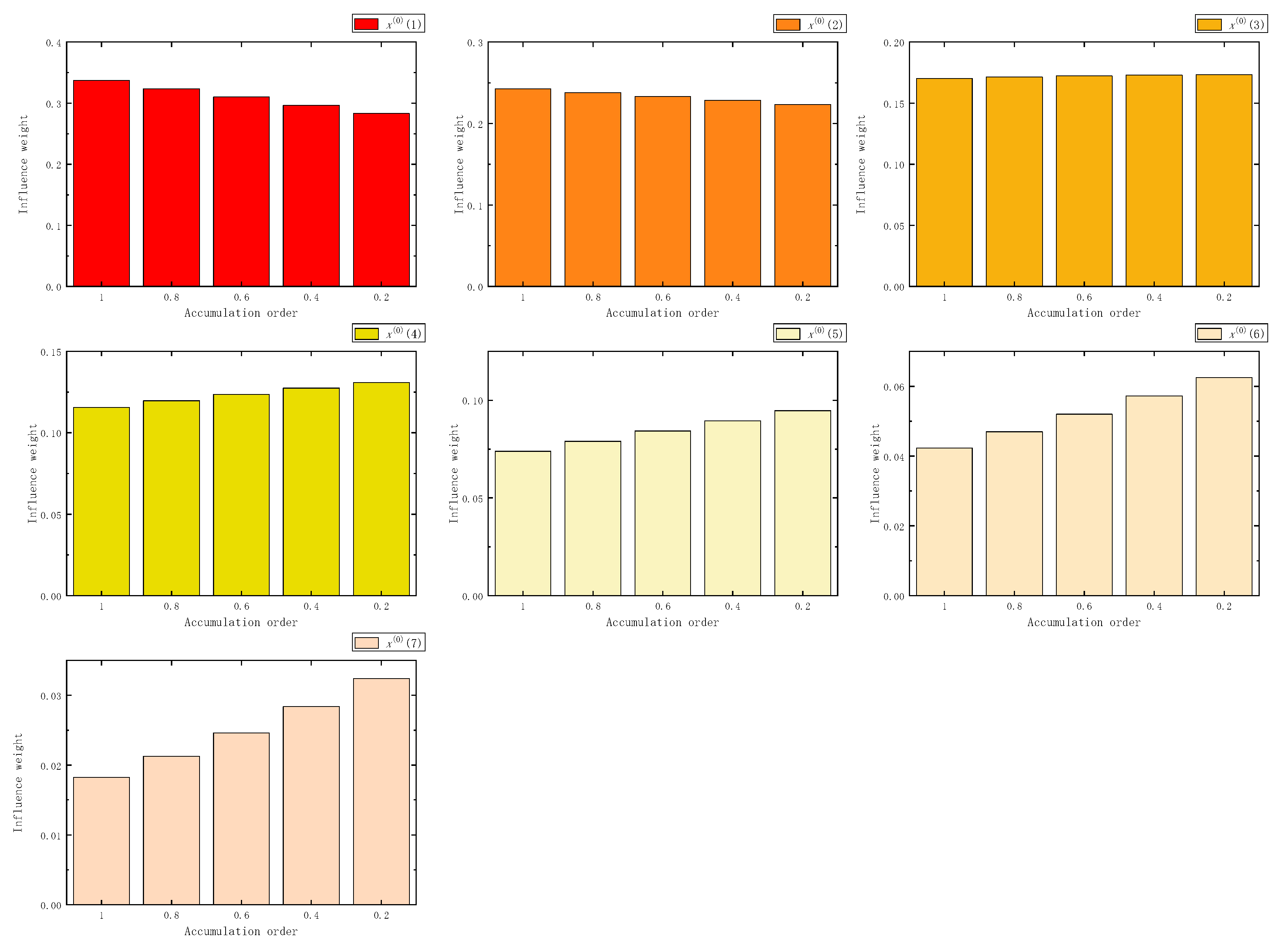
Figure 4.
The influence weight of seven samples in FAGO.
Figure 4.
The influence weight of seven samples in FAGO.
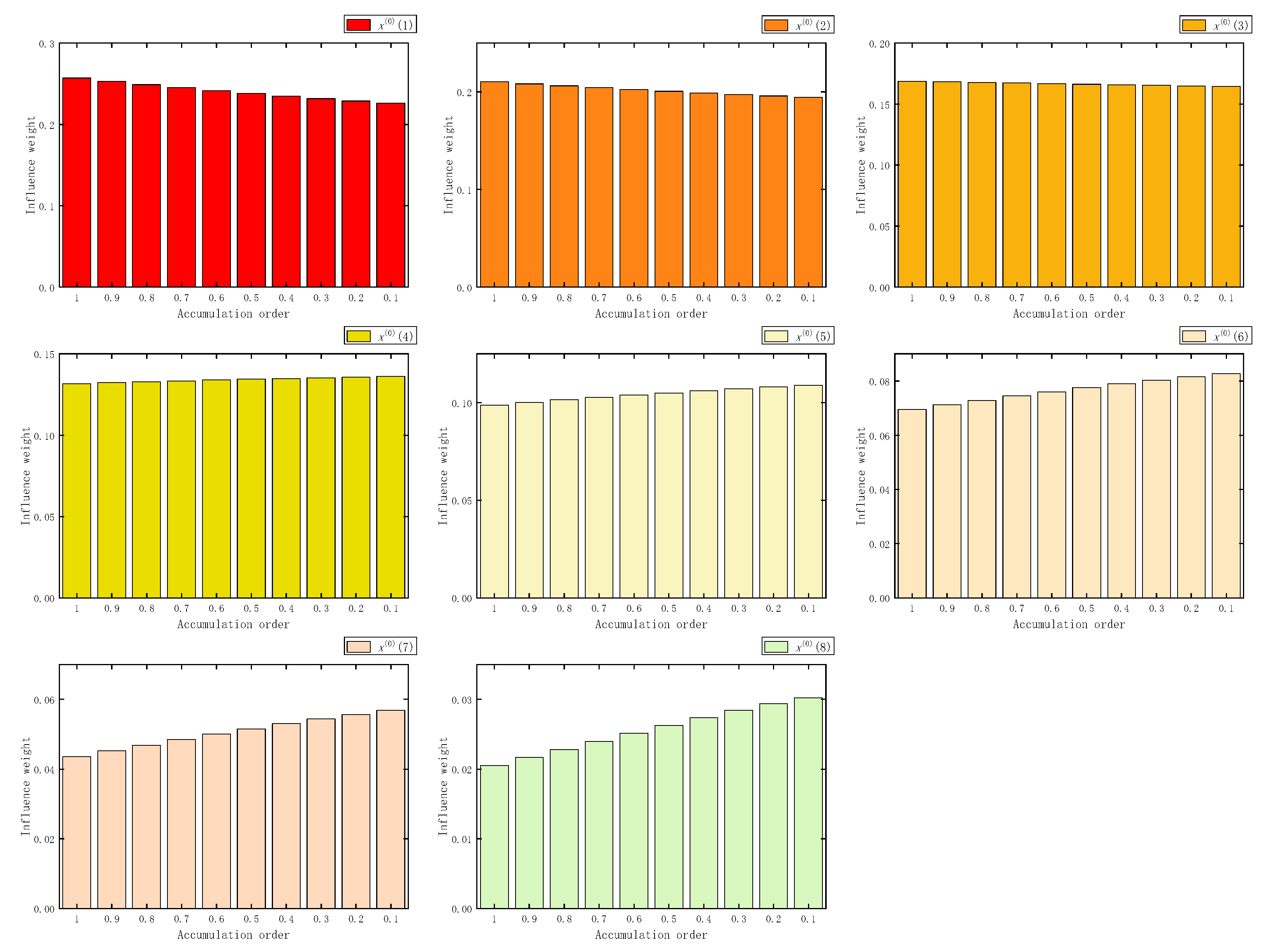
Figure 5.
The influence weight of eight samples in FAGO.
Figure 5.
The influence weight of eight samples in FAGO.
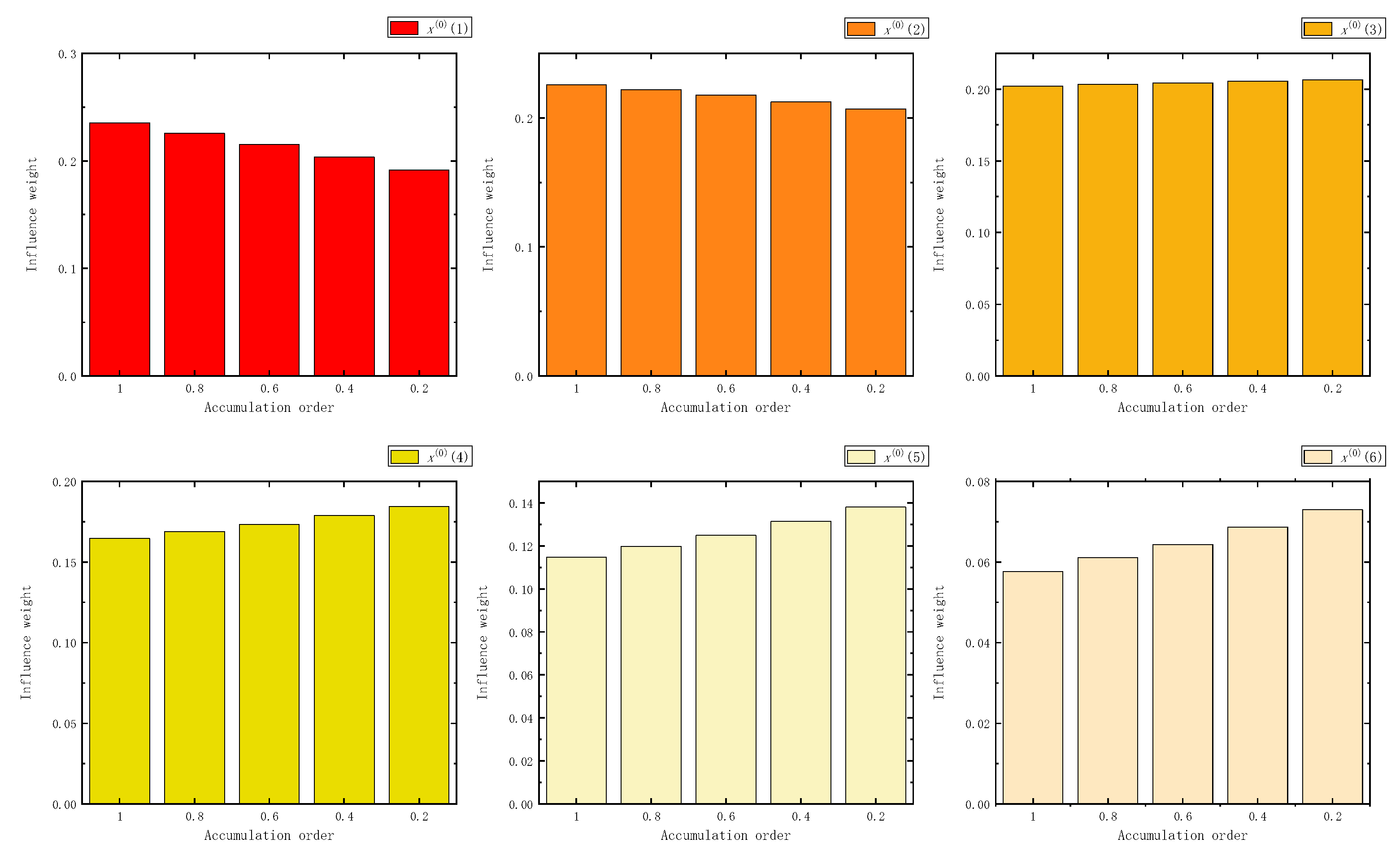
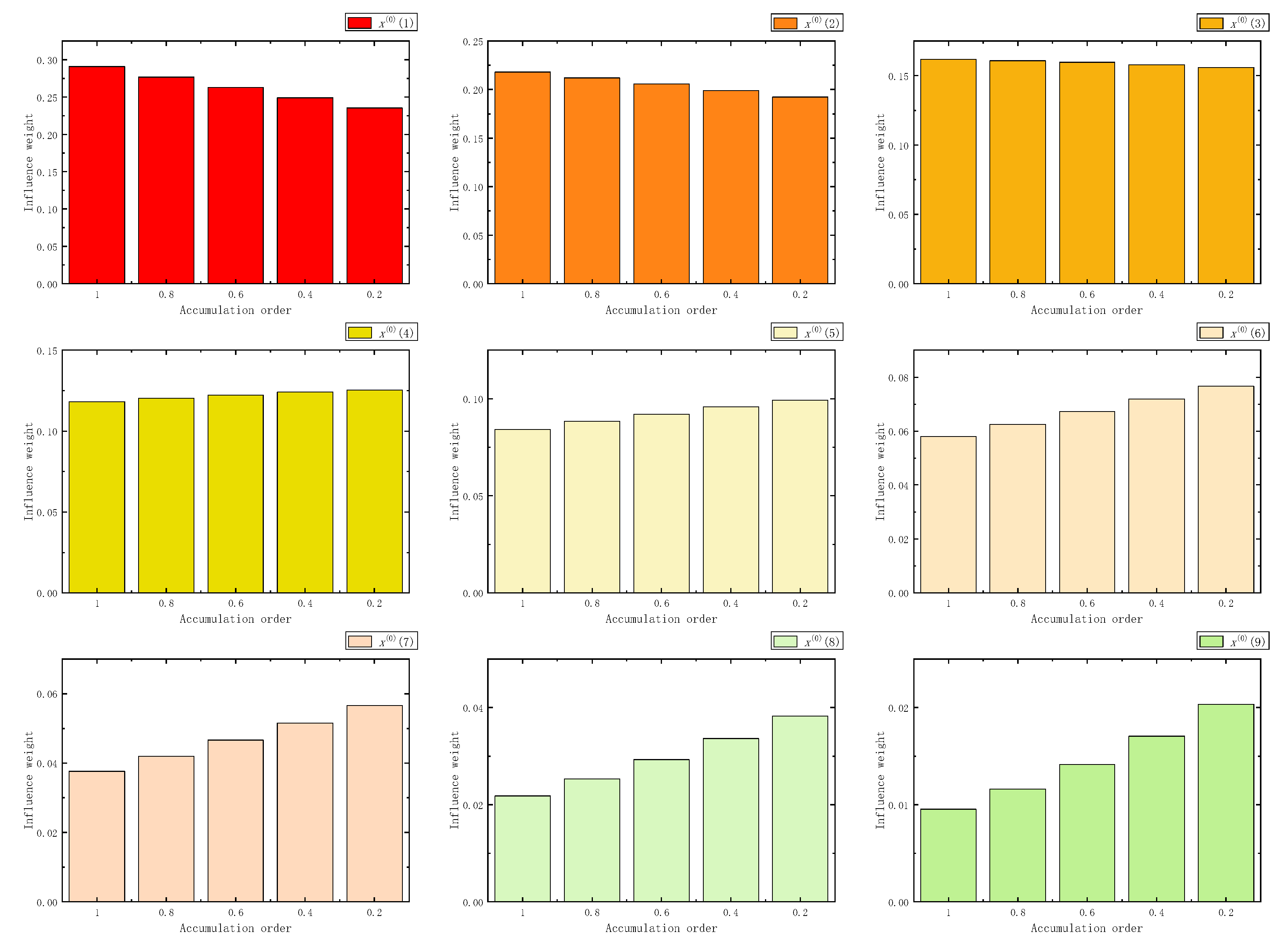
Figure 6.
The influence weight of nine samples in FAGO.
Figure 6.
The influence weight of nine samples in FAGO.
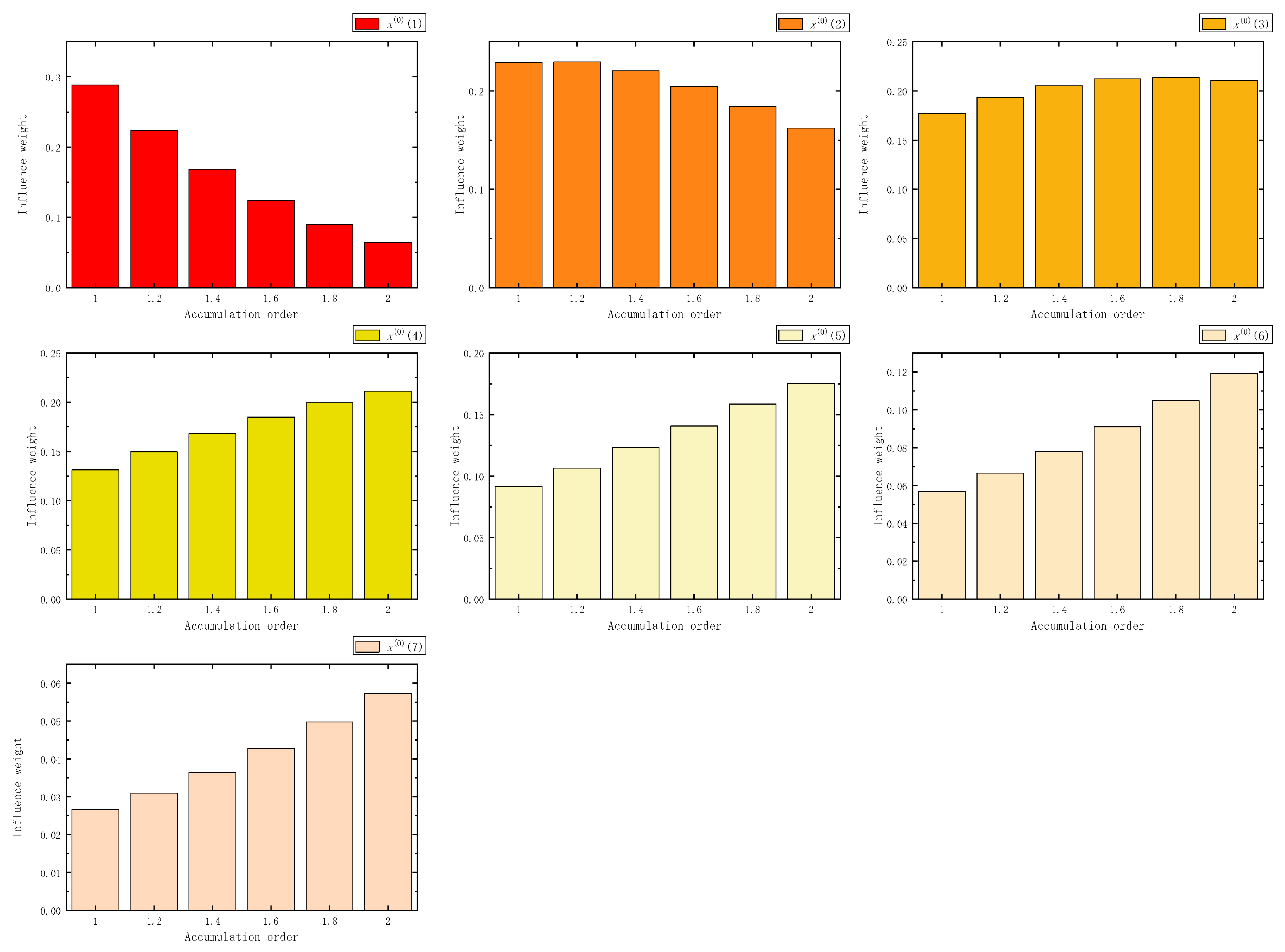
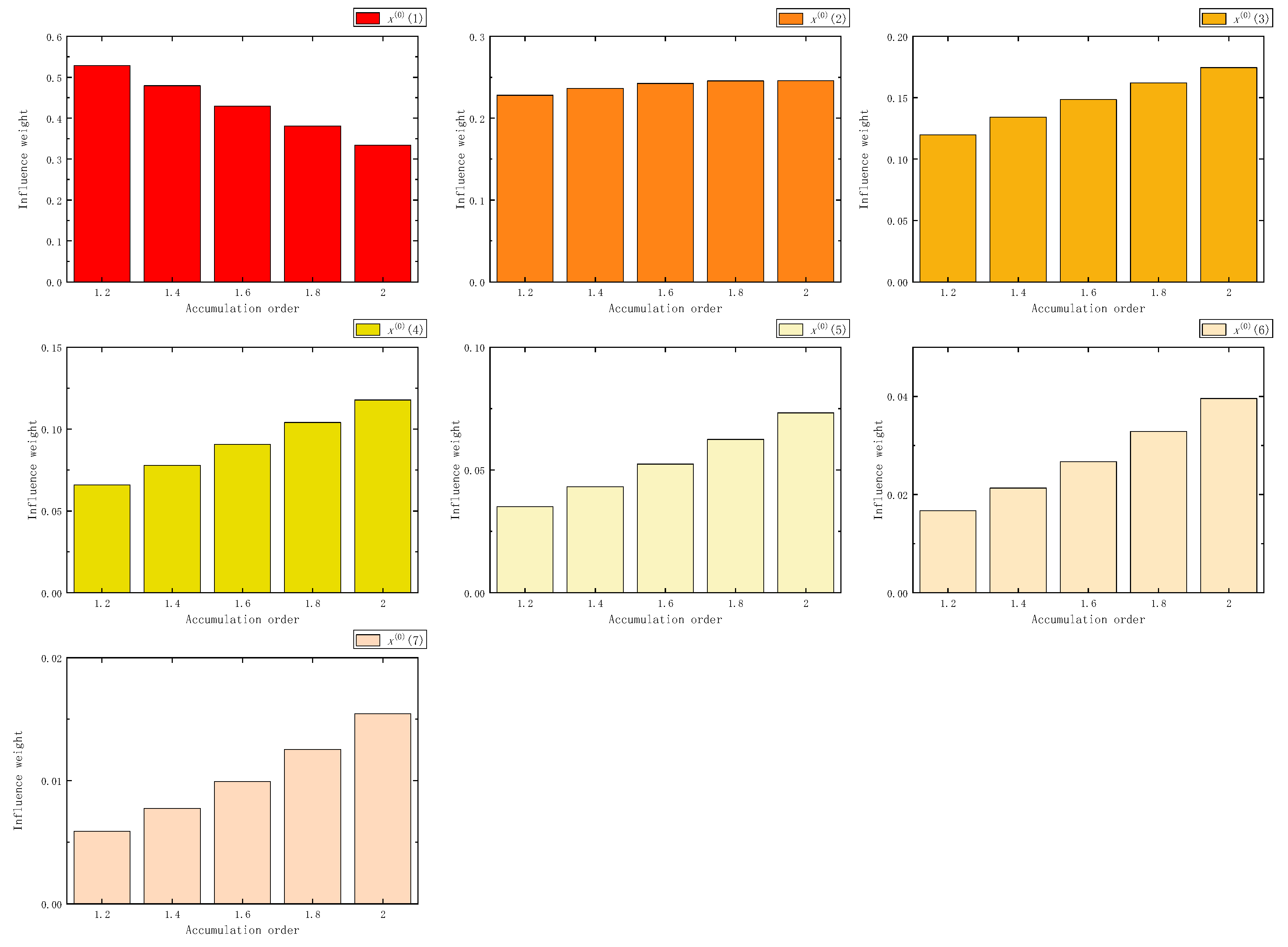
Figure 7.
The influence weight of 10 samples in FAGO.
Figure 7.
The influence weight of 10 samples in FAGO.
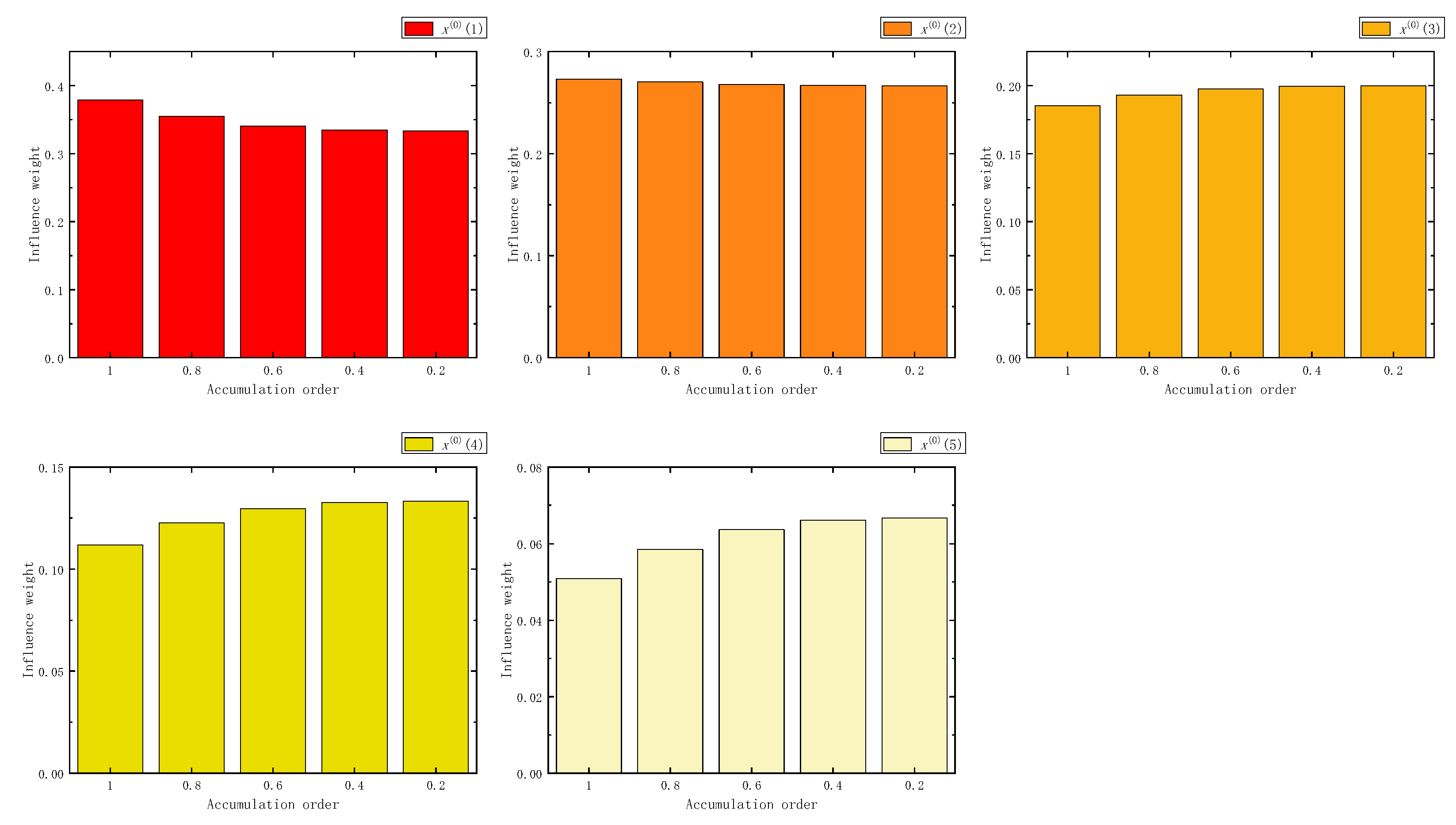
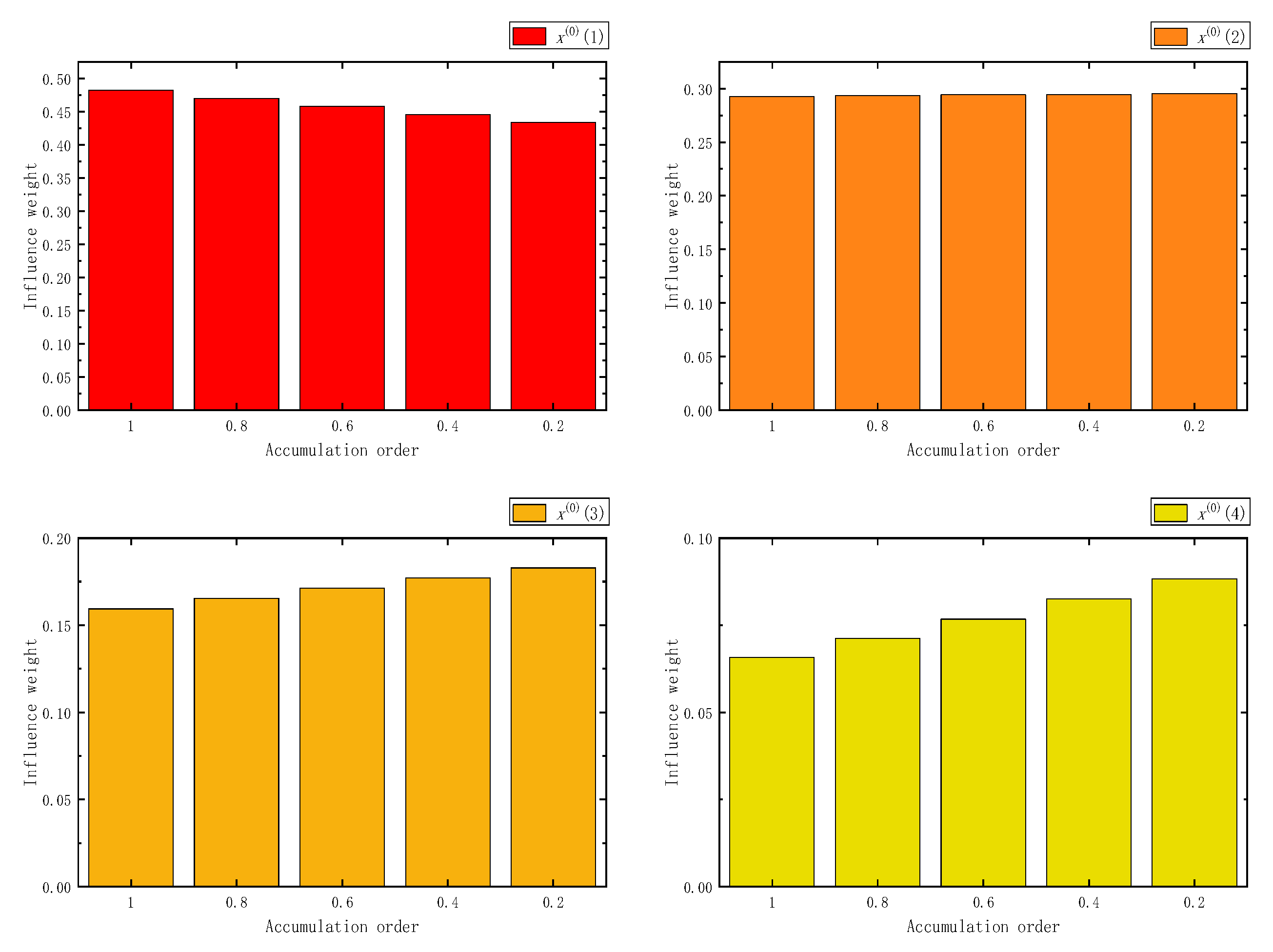
Figure 8.
The influence weight of five samples in FHAGO.
Figure 8.
The influence weight of five samples in FHAGO.
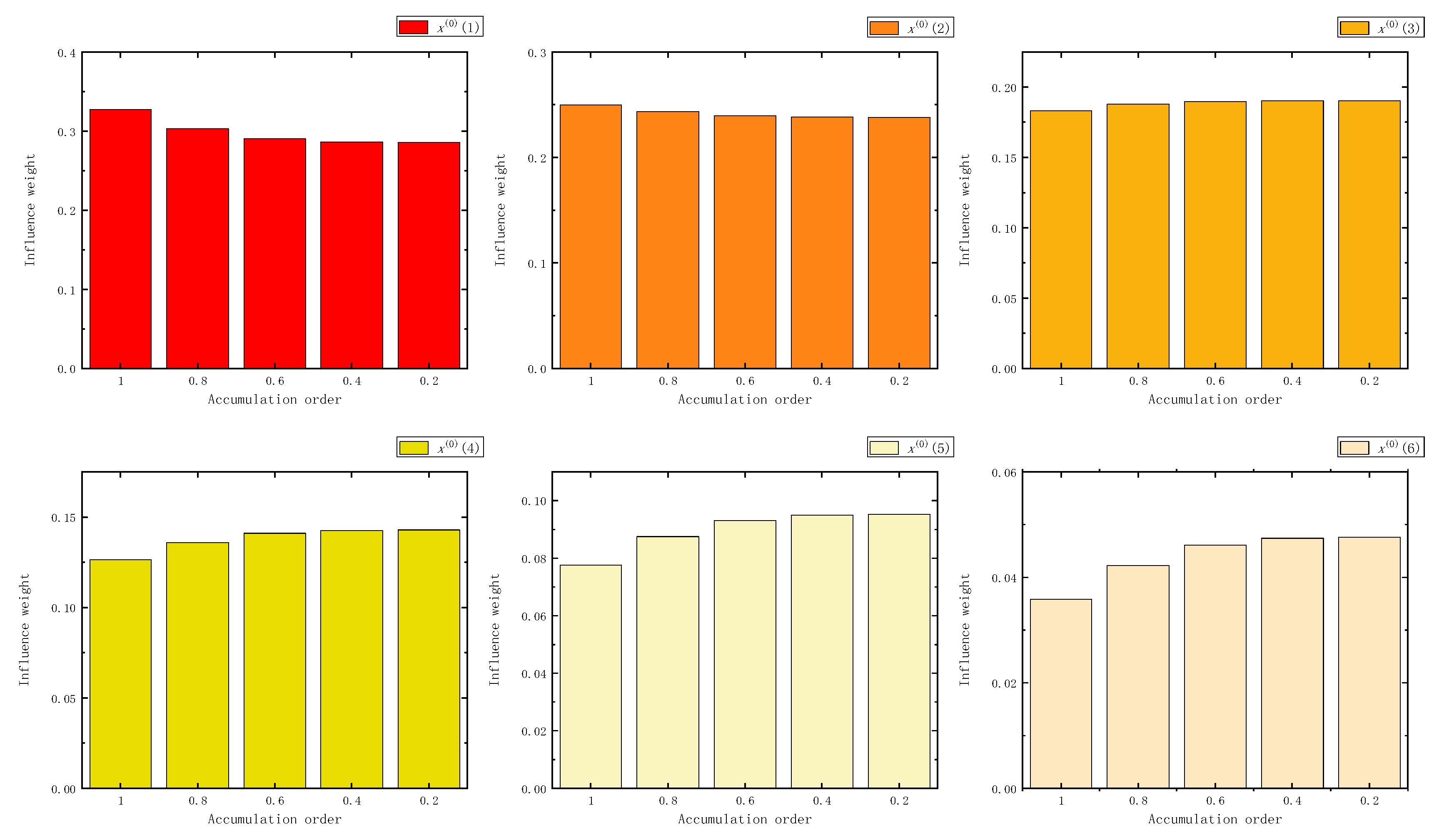
Figure 9.
The influence weight of six samples in FHAGO.
Figure 9.
The influence weight of six samples in FHAGO.
Figure 10.
The influence weight of seven samples in FHAGO.
Figure 10.
The influence weight of seven samples in FHAGO.
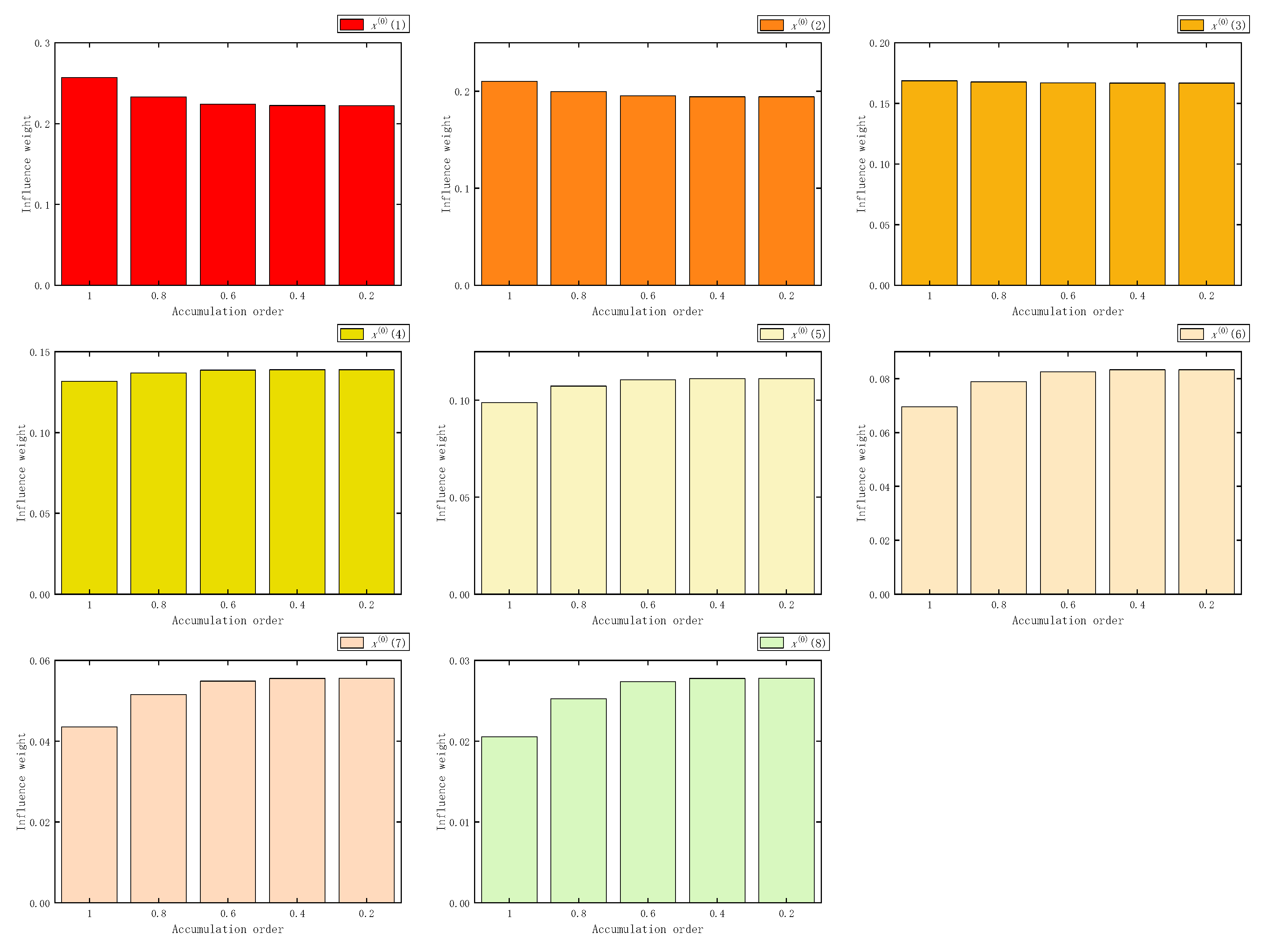
Figure 11.
The influence weight of eight samples in FHAGO.
Figure 11.
The influence weight of eight samples in FHAGO.
Figure 12.
The influence weight of nine samples in FHAGO.
Figure 12.
The influence weight of nine samples in FHAGO.
Figure 13.
The influence weight of 10 samples in FHAGO.
Figure 13.
The influence weight of 10 samples in FHAGO.
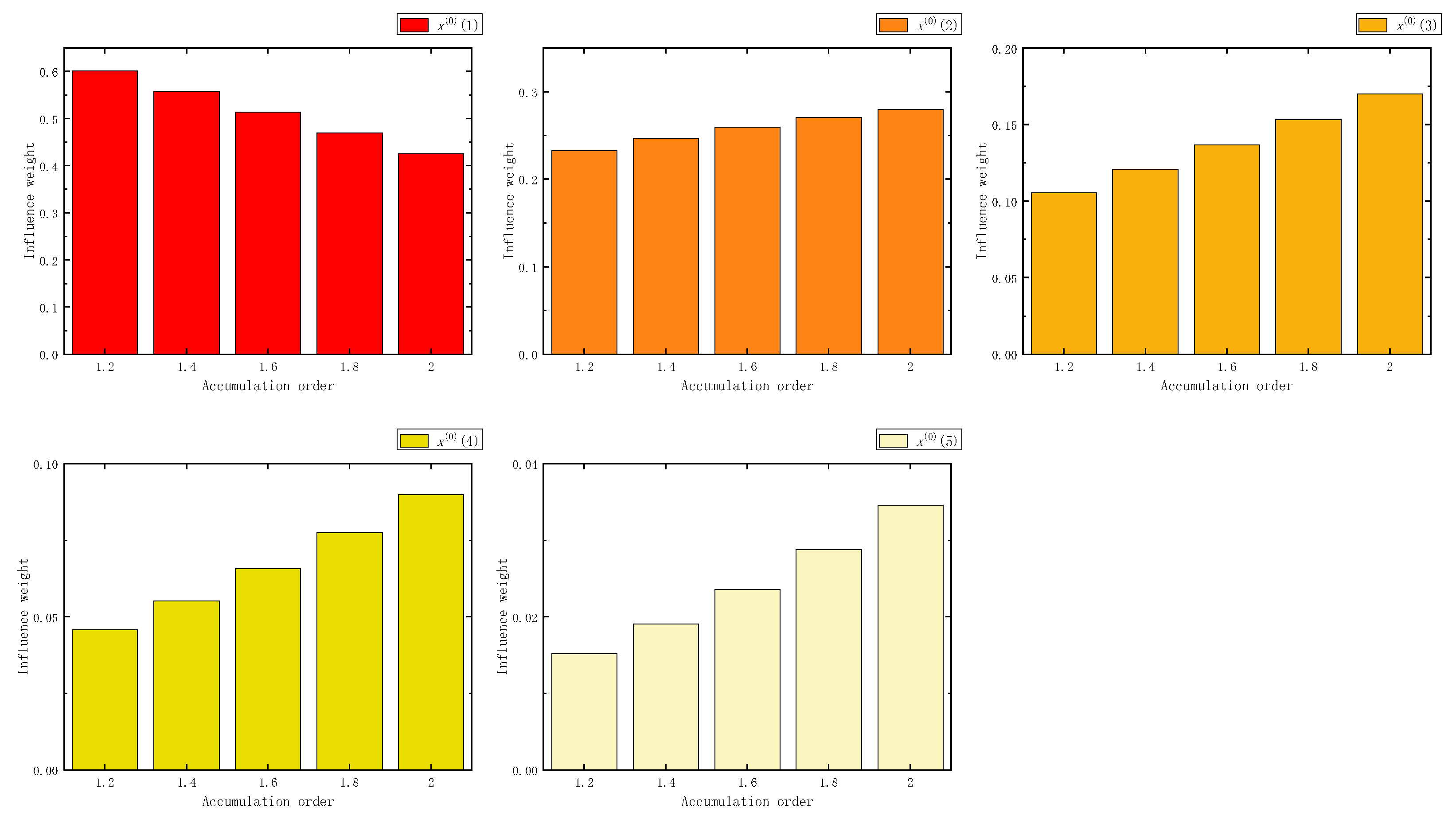
Figure 14.
The influence weight of five samples in CFAGO when .
Figure 14.
The influence weight of five samples in CFAGO when .
Figure 15.
The influence weight of six samples in CFAGO when .
Figure 15.
The influence weight of six samples in CFAGO when .
Figure 16.
The influence weight of seven samples in CFAGO when .
Figure 16.
The influence weight of seven samples in CFAGO when .
Figure 17.
The influence weight of eight samples in CFAGO when .
Figure 17.
The influence weight of eight samples in CFAGO when .
Figure 18.
The influence weight of nine samples in CFAGO when .
Figure 18.
The influence weight of nine samples in CFAGO when .
Figure 19.
The influence weight of 10 samples in CFAGO when .
Figure 19.
The influence weight of 10 samples in CFAGO when .
Figure 20.
The influence weight of five samples in CFAGO when .
Figure 20.
The influence weight of five samples in CFAGO when .
Figure 21.
The influence weight of six samples in CFAGO when .
Figure 21.
The influence weight of six samples in CFAGO when .
Figure 22.
The influence weight of seven samples in CFAGO when .
Figure 22.
The influence weight of seven samples in CFAGO when .
Figure 23.
The influence weight of eight samples in CFAGO when .
Figure 23.
The influence weight of eight samples in CFAGO when .
Figure 24.
The influence weight of nine samples in CFAGO when .
Figure 24.
The influence weight of nine samples in CFAGO when .
Figure 25.
The influence weight of 10 samples in CFAGO when .
Figure 25.
The influence weight of 10 samples in CFAGO when .
Figure 26.
The influence weight of five samples in NIPAGO.
Figure 26.
The influence weight of five samples in NIPAGO.
Figure 27.
The influence weight of six samples in NIPAGO.
Figure 27.
The influence weight of six samples in NIPAGO.
Figure 28.
The influence weight of seven samples in NIPAGO.
Figure 28.
The influence weight of seven samples in NIPAGO.
Figure 29.
The influence weight of eight samples in NIPAGO.
Figure 29.
The influence weight of eight samples in NIPAGO.
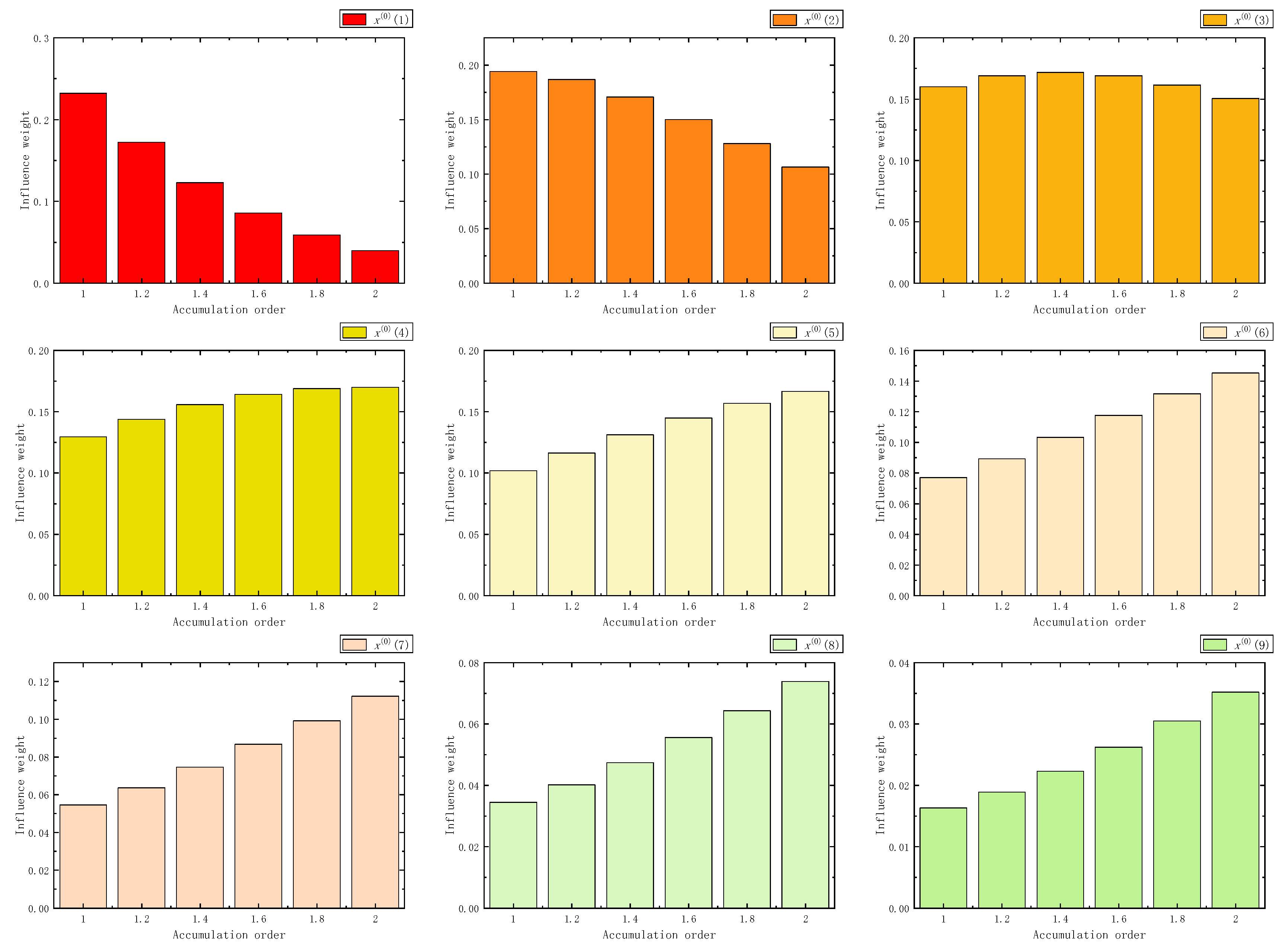
Figure 30.
The influence weight of nine samples in NIPAGO.
Figure 30.
The influence weight of nine samples in NIPAGO.
Figure 31.
The influence weight of 10 samples in NIPAGO.
Figure 31.
The influence weight of 10 samples in NIPAGO.
Figure 32.
The influence weight of five samples in DAGO.
Figure 32.
The influence weight of five samples in DAGO.
Figure 33.
The influence weight of six samples in DAGO.
Figure 33.
The influence weight of six samples in DAGO.
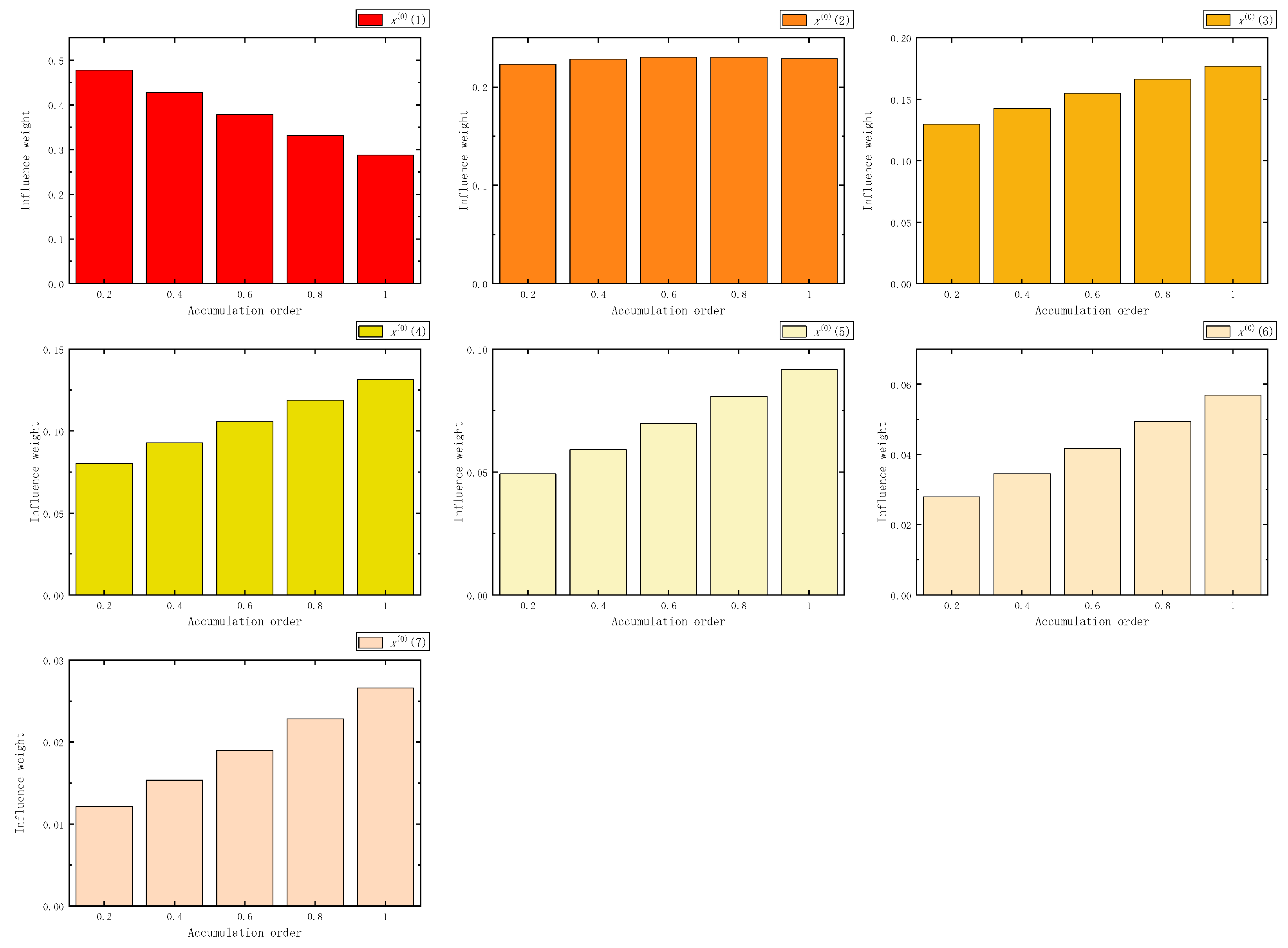
Figure 34.
The influence weight of seven samples in DAGO.
Figure 34.
The influence weight of seven samples in DAGO.
Figure 35.
The influence weight of eight samples in DAGO.
Figure 35.
The influence weight of eight samples in DAGO.
Figure 36.
The influence weight of nine samples in DAGO.
Figure 36.
The influence weight of nine samples in DAGO.
Figure 37.
The influence weight of 10 samples in DAGO.
Figure 37.
The influence weight of 10 samples in DAGO.
Figure 38.
The influence weight of five samples in WFAGO.
Figure 38.
The influence weight of five samples in WFAGO.
Figure 39.
The influence weight of six samples in WFAGO.
Figure 39.
The influence weight of six samples in WFAGO.
Figure 40.
The influence weight of seven samples in WFAGO.
Figure 40.
The influence weight of seven samples in WFAGO.
Figure 41.
The influence weight of eight samples in WFAGO.
Figure 41.
The influence weight of eight samples in WFAGO.
Figure 42.
The influence weight of nine samples in WFAGO.
Figure 42.
The influence weight of nine samples in WFAGO.
Figure 43.
The influence weight of 10 samples in WFAGO.
Figure 43.
The influence weight of 10 samples in WFAGO.
Table 1.
Research process regarding grey AGOs.
Table 1.
Research process regarding grey AGOs.
Author’s
Information | AGOs | Contribution |
|---|
| Wu (2013) [17] | Fractional accumulated generating operator (FAGO) | Reducing inherent randomness in data and enhancing the performance of the model for nonlinear forecasting problems. |
| Chen (2020) [22] | Fractional Hausdorff accumulated generating operator (FHAGO) | Improving the predictive accuracy of traditional grey model and validating its applicability through three cases. |
| Ma (2020) [23] | Conformable fractional accumulated generating operator (CFAGO) | Predicting natural gas consumption in 11 countries to demonstrate its higher efficiency in long-term and non-stationary time series prediction. |
| Zhou (2017) [24] | New information priority accumulated generating operator (NIPAGO) | Further reflecting the information priority and validating the effectiveness of the model. |
| Liu (2021) [25] | Damping accumulated generating operator (DAGO) | Flexibly adjusting the trend component and correcting the results and validating the applicability through four cases. |
| Zhu (2022) [26] | Weakened fractional order accumulated generating operator (WFAGO) | Reducing the ill-condition of the discrete grey system and improving its performance and verifying the feasibility by predicting electricity consumption in Zhejiang and Heilongjiang. |
| Zhao (2020) [19] | Adjacent accumulated generating operator (AAGO) | Demonstrating its stability and high predictive accuracy, predicting the renewable energy consumption in the Asia–Pacific Economic Cooperation region. |
| Xiao (2017) [27] | Cycle truncation accumulated generating operator (CAGO) | Converting the traffic flow sequence of seasonal fluctuation into a flat sequence and verifying performance through predicting the traffic flow in China and Canada. |
| Li (2022) [28] | Generalized accumulated generating operator (GAGO) | Introducing a new information priority generalized accumulative grey model and forecasting greenhouse gas emissions in Shanghai Cooperation Organization member states. |
| Guo (2021) [29] | Quarterly compound accumulated generating operator (QAGO) | Introducing two seasonal parameters into the model and forecasting air quality in 22 cities. |
| Che (2013) [30] | Opposite-direction accumulated generating operator (OAGO) | Making full use of the new information and validating its applicability by predicting fatigue experimental data of Ti alloy. |
Table 2.
The comparison of different AGOs.
Table 2.
The comparison of different AGOs.
| AGOs | Advantages | Disadvantages |
|---|
| FAGO | It can handle nonlinear data and reveal trends in complex or irregular data. | High computational requirements. |
| FHAGO | It can satisfy the high stability of the model solution and simplify the integration operation process. | Unable to utilize initial value |
| CFAGO | It can maintain data consistency and stability, possess linear characteristics, and have relatively simple calculations. | Significant errors may occur when dealing with non-linear data. |
| NIPAGO | It assigns increasing weights to historical data through series operations to ensure that new data has greater importance than old data. | The contribution of older data may be excessively disregarded. |
| DAGO | During the accumulation process, each data point is given the same weight, so that the accumulation sequence still has monotonicity. | There may be significant errors for non-linear data. |
| WFAGO | It can alleviate the pathological state of the system by reducing the differences between system elements. | High computational requirements. |
Table 3.
The direct relation matrix A.
Table 3.
The direct relation matrix A.
| | x(0) (1) | x(0) (2) | x(0) (3) | x(0) (4) | x(0) (5) |
|---|
| x(0) (1) | 0 | 1 | 1 | 1 | 1 |
| x(0) (2) | 0 | 0 | 1 | 1 | 1 |
| x(0) (3) | 0 | 0 | 0 | 1 | 1 |
| x(0) (4) | 0 | 0 | 0 | 0 | 1 |
| x(0) (5) | 0 | 0 | 0 | 0 | 0 |
Table 4.
The normalized relation matrix Z.
Table 4.
The normalized relation matrix Z.
| | x(0) (1) | x(0) (2) | x(0) (3) | x(0) (4) | x(0) (5) |
|---|
| x(0) (1) | 0 | 0.25 | 0.25 | 0.25 | 0.25 |
| x(0) (2) | 0 | 0 | 0.25 | 0.25 | 0.25 |
| x(0) (3) | 0 | 0 | 0 | 0.25 | 0.25 |
| x(0) (4) | 0 | 0 | 0 | 0 | 0.25 |
| x(0) (5) | 0 | 0 | 0 | 0 | 0 |
Table 5.
The total relation matrix C.
Table 5.
The total relation matrix C.
| | x(0) (1) | x(0) (2) | x(0) (3) | x(0) (4) | x(0) (5) |
|---|
| x(0) (1) | 0 | 0.25 | 0.31 | 0.39 | 0.49 |
| x(0) (2) | 0 | 0 | 0.25 | 0.31 | 0.39 |
| x(0) (3) | 0 | 0 | 0 | 0.25 | 0.31 |
| x(0) (4) | 0 | 0 | 0 | 0 | 0.25 |
| x(0) (5) | 0 | 0 | 0 | 0 | 0 |
Table 6.
The influence degree of each sample.
Table 6.
The influence degree of each sample.
| | x(0) (1) | x(0) (2) | x(0) (3) | x(0) (4) | x(0) (5) |
|---|
| Influence degree | 1.44 | 0.95 | 0.56 | 0.25 | 0 |
Table 7.
The influence degree of each sample under different accumulation orders.
Table 7.
The influence degree of each sample under different accumulation orders.
| Influence Degree | Accumulation Orders |
|---|
| 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
|---|
| x(0) (1) | 1.44 | 1.48 | 1.51 | 1.55 | 1.60 | 1.65 | 1.70 | 1.77 | 1.84 | 1.91 |
| x(0) (2) | 0.95 | 0.99 | 1.02 | 1.06 | 1.10 | 1.15 | 1.20 | 1.25 | 1.31 | 1.38 |
| x(0) (3) | 0.56 | 0.59 | 0.62 | 0.65 | 0.68 | 0.72 | 0.75 | 0.80 | 0.84 | 0.89 |
| x(0) (4) | 0.25 | 0.27 | 0.28 | 0.30 | 0.32 | 0.34 | 0.37 | 0.39 | 0.42 | 0.45 |
| x(0) (5) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 8.
The influence weight of each sample under different accumulation orders after processing.
Table 8.
The influence weight of each sample under different accumulation orders after processing.
| Influence Weight | Accumulation Orders |
|---|
| 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
|---|
| x(0) (1) | 0.45 | 0.44 | 0.44 | 0.44 | 0.43 | 0.43 | 0.42 | 0.42 | 0.42 | 0.41 |
| x(0) (2) | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 |
| x(0) (3) | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 |
| x(0) (4) | 0.08 | 0.08 | 0.08 | 0.08 | 0.09 | 0.09 | 0.09 | 0.09 | 0.10 | 0.10 |
| x(0) (5) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 9.
Influence degree regularity under different AGOs.
Table 9.
Influence degree regularity under different AGOs.
| AGOs | Accumulation Order | Influence Degree |
|---|
| | | New Information | Old Information |
|---|
| 1-AGO | Fixed | Fixed | Fixed |
| FAGO | Decreasing | Increasing | Decreasing |
| FHAGO | Increasing | Significantly increasing | Significantly decreasing |
| CFAGO | Increasing | Significantly increasing | Significantly decreasing |
| NIPAGO | Decreasing | Increasing | Decreasing |
| DAGO | Decreasing | Significantly increasing | Significantly decreasing |
| WFAGO | Decreasing | Increasing | Decreasing |