Two-Dimensional Fractional Order Iterative Learning Control for Repetitive Processes
Abstract
:1. Introduction
2. Preliminaries
3. Robust FOILC Design
3.1. System Description
3.2. Control Law Design
4. Parameters Tuning
4.1. Fractional Order Parameters Tuning
- I.
- Phase margin specification
- II.
- Gain crossover frequency specification
4.2. Learning Gain Synthesis Conditions
5. Control Performance Analysis
5.1. Convergence Analysis
5.2. Robustness Analysis
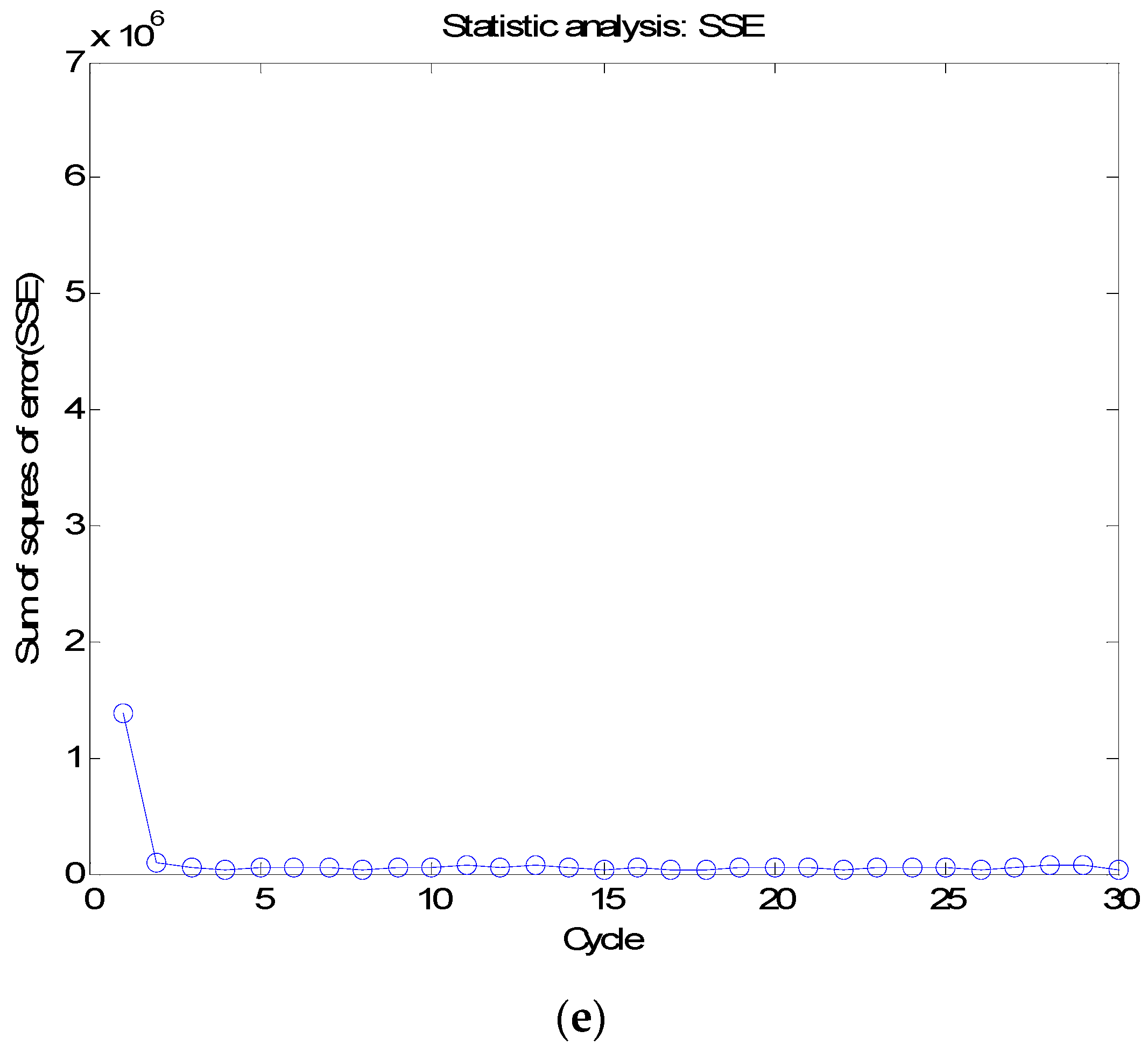
6. Simulation Results
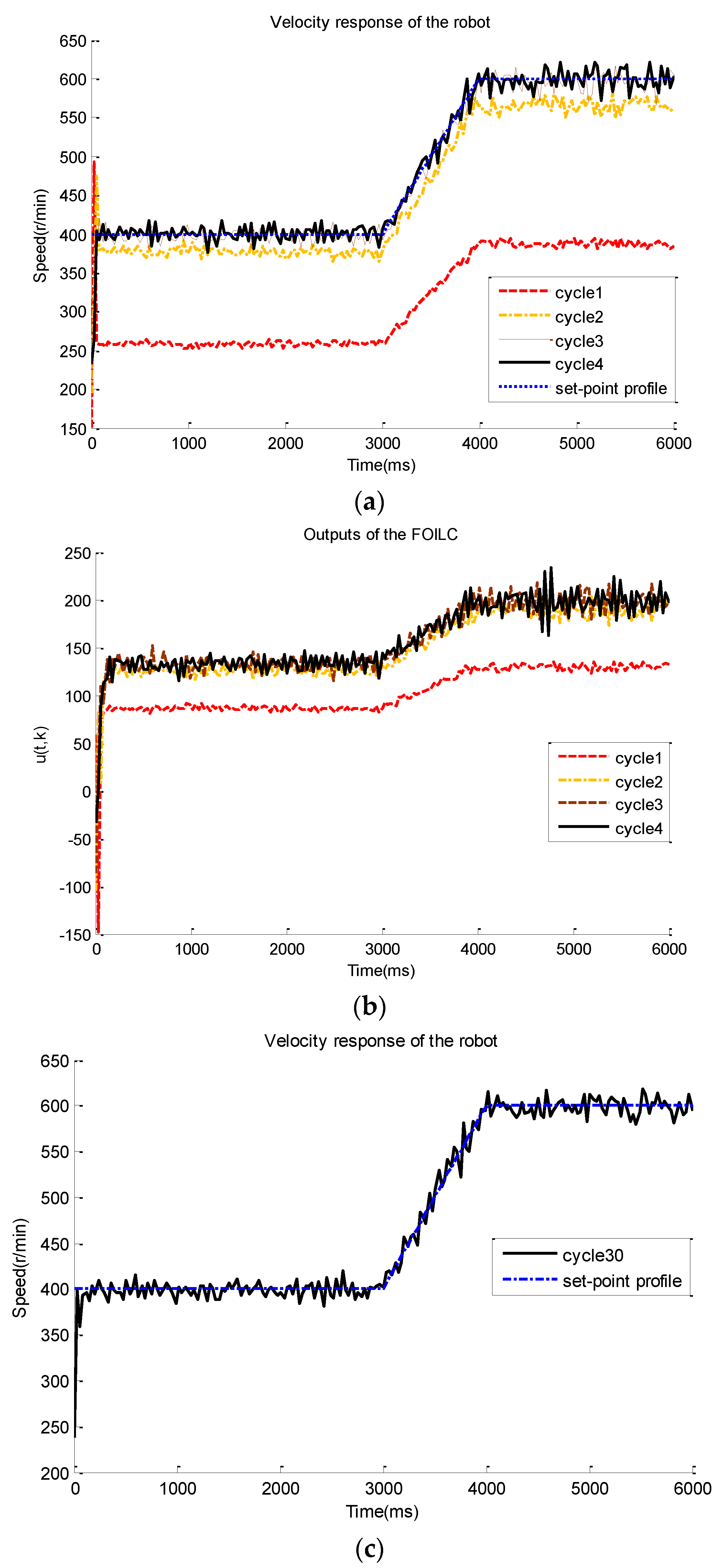
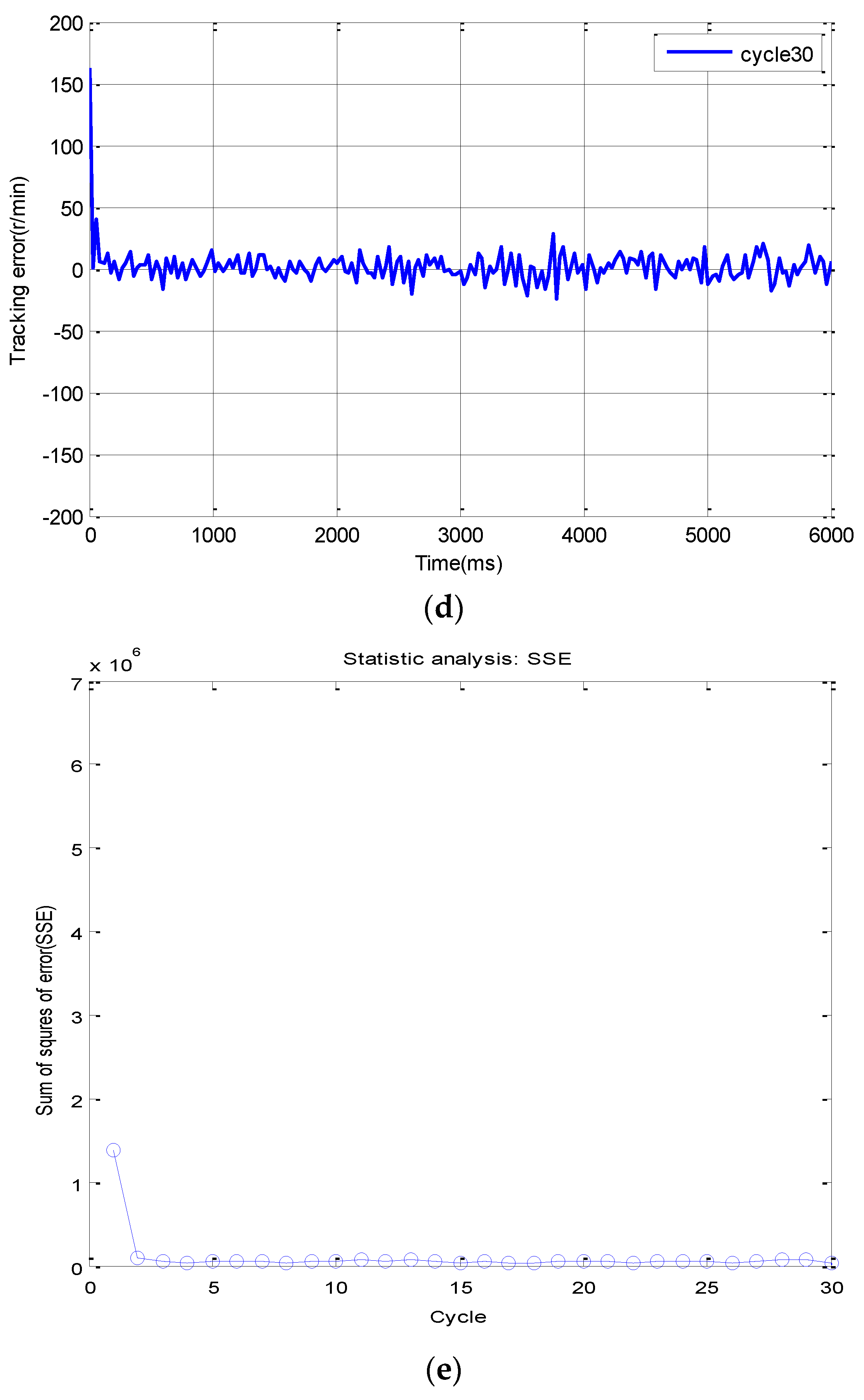
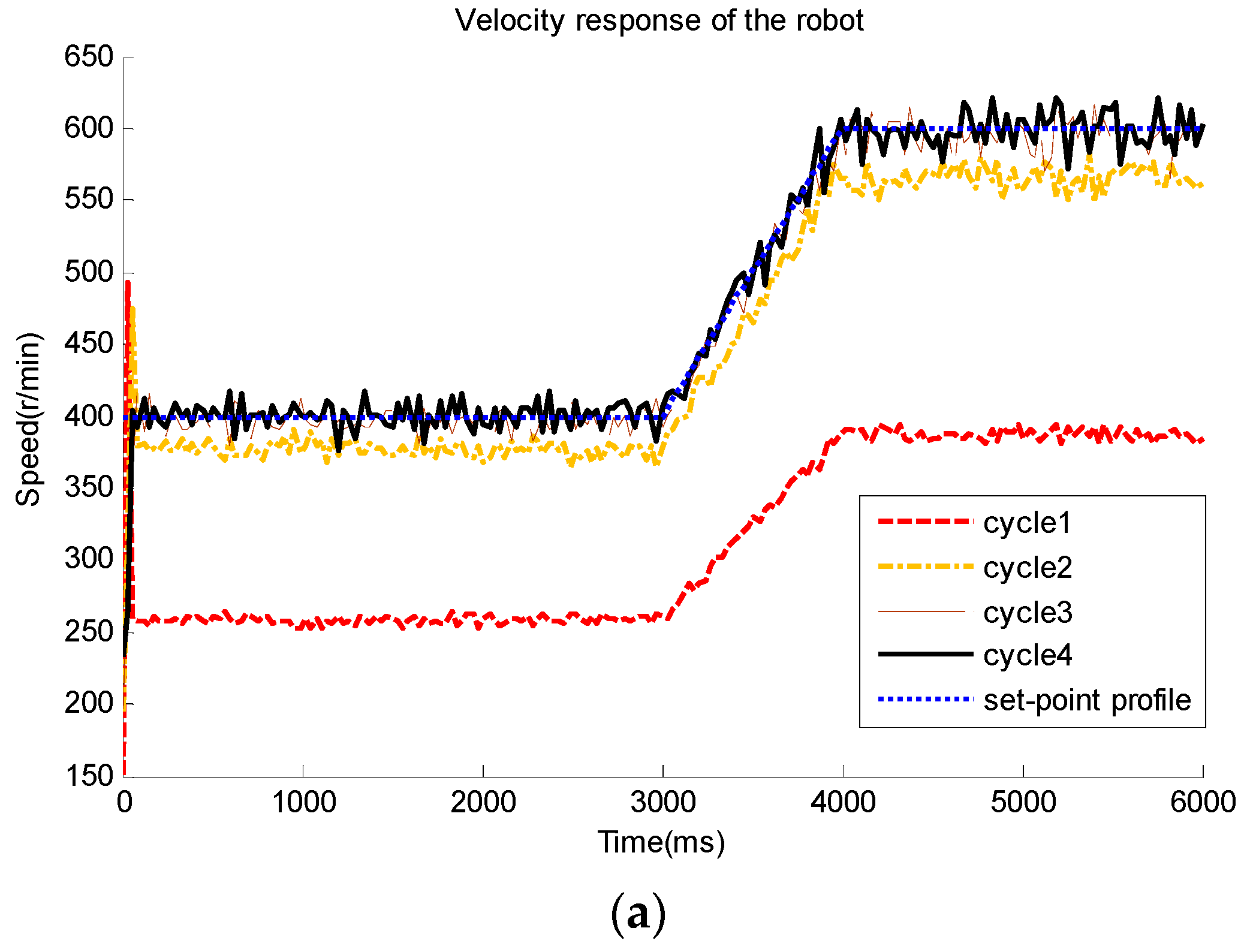
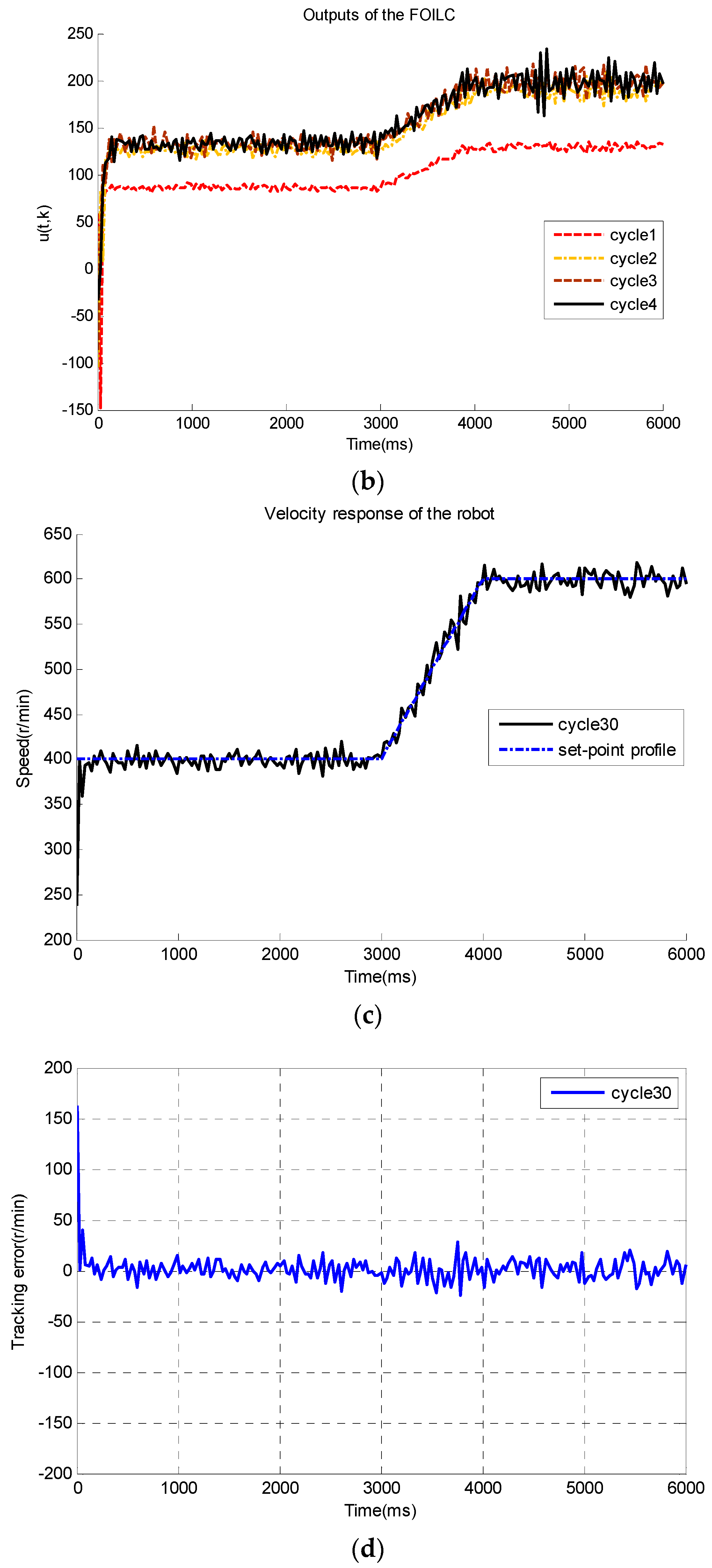
7. Experimental Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sammons, P.M.; Gegel, M.L.; Bristow, D.A.; Landers, R.G. Repetitive Process Control of Additive Manufacturing with Application to Laser Metal Deposition. IEEE Trans. Control Syst. Technol. 2019, 27, 566–575. [Google Scholar] [CrossRef]
- Mooren, N.; Witvoet, G.; Oomen, T. Gaussian process repetitive control: Beyond periodic internal models through kernels. Automatica 2022, 140, 1–13. [Google Scholar] [CrossRef]
- Steinbuch, M. Repetitive control for systems with uncertain period-time. Automatica 2002, 38, 2103–2109. [Google Scholar] [CrossRef]
- Moore, K.L.; Dahleh, M.; Bhattacharyya, S.P. Iterative learning control: A survey and new results. J. Robot. Syst. 1992, 9, 563–594. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. A Practical Nonlinear Adaptive Control of Hydraulic Servomechanisms with Periodic-Like Disturbances. IEEE/ASME Trans. Mechatron. 2015, 20, 2752–2760. [Google Scholar] [CrossRef]
- Arimoto, S.; Kawamura, S.; Miyazaki, F. Bettering operation of robots by learning. J. Robot. Syst. 1984, 1, 123–140. [Google Scholar] [CrossRef]
- Xu, J.-X.; Bien, Z.Z. The frontiers of iterative learning control. In Iterative Learning Control: Analysis, Design, Integration and Application; Kluwer Academic Publishers: Boston, MA, USA; Dordrecht, The Netherlands; London, UK, 1998; pp. 9–35. [Google Scholar]
- Amann, N.; Owens, D.H.; Rogers, E. Iterative learning control using optimal feedback and feedforward actions. Int. J. Control 1996, 65, 277–293. [Google Scholar] [CrossRef]
- Amann, N.; Owens, D.H.; Rogers, E. Predictive optimal iterative learning control. Int. J. Control 1998, 69, 203–226. [Google Scholar] [CrossRef]
- Moon, J.-H.; Doh, T.-Y.; Chung, M.J. A robust approach to iterative learning control design for uncertain systems. Automatica 1998, 34, 1001–1004. [Google Scholar] [CrossRef]
- Tayebi, A.; Zaremba, M.B. Robust iterative learning control design is straightforward for uncertain LTI systems satisfying the robust performance condition. IEEE Trans. Autom. Control 2003, 48, 101–106. [Google Scholar] [CrossRef]
- Shi, J.; Gao, F.; Wu, T.-J. Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system. J. Process Control 2005, 15, 907–924. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, H.; Cao, Z.; Jiang, Q. A design method for indirect iterative learning control based on two-dimensional generalized predictive control algorithm. J. Process Control 2014, 24, 1527–1537. [Google Scholar] [CrossRef]
- Li, D.W.; Xi, Y.G.; Lu, J.Y.; Gao, F.R. Synthesis of real-time feedback-based 2Diterative learning control model predictive control for constrained batch processes with unknown input nonlinearity. Ind. Eng. Chem. Res. 2016, 55, 13074–13084. [Google Scholar] [CrossRef]
- Han, C.; Jia, L.; Peng, D.G. Model predictive control of batch processes based on two-dimensional integration frame. Nonlinear Anal. Hybrid Syst. 2018, 28, 75–86. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, S.; Tao, J. A new design of predictive functional control strategy for batch processes in the two-dimensional framework. IEEE Trans. Ind. Inform. 2019, 15, 2905–2914. [Google Scholar] [CrossRef]
- Hao, S.; Liua, T.; Gao, F. PI based indirect-type iterative learning control for batch processes with time-varying uncertainties: A 2D FM model based approach. J. Process Control 2019, 78, 57–67. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Wei, S.; Zhou, D.; Huang, B. Control performance assessment for ILC-controlled batch processes in a 2-D system framework. IEEE Trans. Syst. Man Cybern. 2018, 48, 1493–1504. [Google Scholar] [CrossRef]
- Zhou, L.; Jia, L.; Wang, Y.-L. An integrated robust iterative learning control strategy for batch processes based on 2D system. J. Process Control 2020, 85, 136–148. [Google Scholar] [CrossRef]
- Hao, S. Two-dimensional delay compensation based iterative learning control scheme for batch processes with both input and state delays. J. Frankl. Inst. 2019, 356, 8118–8137. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, L.; Yu, J.; Zhang, R.; Gao, F. A hybrid 2D fault-tolerant controller design for multi-phase batch processes with time delay. J. Process Control. 2018, 69, 138–157. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, R. A two-dimensional design of model predictive control for batch processes with two-dimensional (2D) dynamics using extended non-minimal state space structure. J. Process Control 2019, 81, 172–189. [Google Scholar] [CrossRef]
- Mandra, S.; Galkowski, K.; Rogers, E.; Rauh, A.; Aschemann, H. Performance-Enhanced Robust Iterative Learning Control with Experimental Application to PMSM Position Tracking. IEEE Trans. Control Syst. Technol. 2019, 27, 1813–1819. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Ahn, H.-S. Fractional-order iterative learning control for fractional-order linear systems. Asian J. Control 2011, 13, 1–10. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Tenreiro Machado, J.A. (Eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Li, Y.; Chen, Y.; Ahn, H.-S. A Survey on Fractional-Order Iterative Learning Control. J. Optim. Theory Appl. 2013, 156, 127–140. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Moore, K.L. On Dα-type iterative learning control. Proc. IEEE Conf. Decis. Control. 2001, 5, 4451–4456. [Google Scholar]
- Ye, Y.; Tayebi, A.; Liu, X. All-pass filtering in iterative learning control. Automatica 2009, 45, 257–264. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. Equilibrium points, stability and numerical solutions of fractional-order predator prey and rabies models. J. Math. Anal. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Lan, Y.-H. Iterative learning control with initial state learning for fractional order nonlinear systems. Comput. Math. Appl. 2012, 64, 3210–3216. [Google Scholar] [CrossRef]
- Yan, L.; Wei, J. Fractional order nonlinear systems with delay in iterative learning control. Appl. Math. Comput. 2015, 257, 546–552. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.R. Fractional order iterative learning control with randomly varying trial lengths. J. Frankl. Inst. 2017, 354, 967–992. [Google Scholar] [CrossRef]
- Luo, D.; Wang, J.; Shen, D. Iterative learning control for fractional-order multi-agent systems. J. Frankl. Inst. 2019, 356, 6328–6351. [Google Scholar] [CrossRef]
- Luo, D.; Wang, J.; Shen, D. Iterative Learning Control for Locally Lipschitz Nonlinear Fractional-order Multi-agent Systems. J. Frankl. Inst. 2020, 357, 6671–6693. [Google Scholar] [CrossRef]
- Mandra, S.; Galkowski, K.; Aschemann, H. Robust guaranteed cost ILC with dynamic feedforward and disturbance compensation for accurate PMSM position control. Control Eng. Pract. 2017, 65, 36–47. [Google Scholar] [CrossRef]
- Du, C.; Xie, L.; Zhang, C. H∞ control and robust stabilization of two-dimensional systems in Roesser models. Automatica 2001, 37, 205–211. [Google Scholar] [CrossRef]
- Cao, Y.Y.; Sun, Y.X.; Lam, J. Delay dependent robust H∞ for uncertain systems with time-varying delays. IEEE Proc. Control Theory Appl. 1998, 143, 338–344. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Luo, H. Two-Dimensional Fractional Order Iterative Learning Control for Repetitive Processes. Fractal Fract. 2023, 7, 624. https://doi.org/10.3390/fractalfract7080624
Zhang B, Luo H. Two-Dimensional Fractional Order Iterative Learning Control for Repetitive Processes. Fractal and Fractional. 2023; 7(8):624. https://doi.org/10.3390/fractalfract7080624
Chicago/Turabian StyleZhang, Bitao, and Haobo Luo. 2023. "Two-Dimensional Fractional Order Iterative Learning Control for Repetitive Processes" Fractal and Fractional 7, no. 8: 624. https://doi.org/10.3390/fractalfract7080624
APA StyleZhang, B., & Luo, H. (2023). Two-Dimensional Fractional Order Iterative Learning Control for Repetitive Processes. Fractal and Fractional, 7(8), 624. https://doi.org/10.3390/fractalfract7080624





