Solvability of a ϱ-Hilfer Fractional Snap Dynamic System on Unbounded Domains
Abstract
1. Introduction
2. Preliminaries
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (i)
- The sequence converges to a fixed point ;
- (ii)
- is the unique fixed point of Λ in ;
- (iii)
- If , then .
3. The Existence and Uniqueness Results
4. The Stability
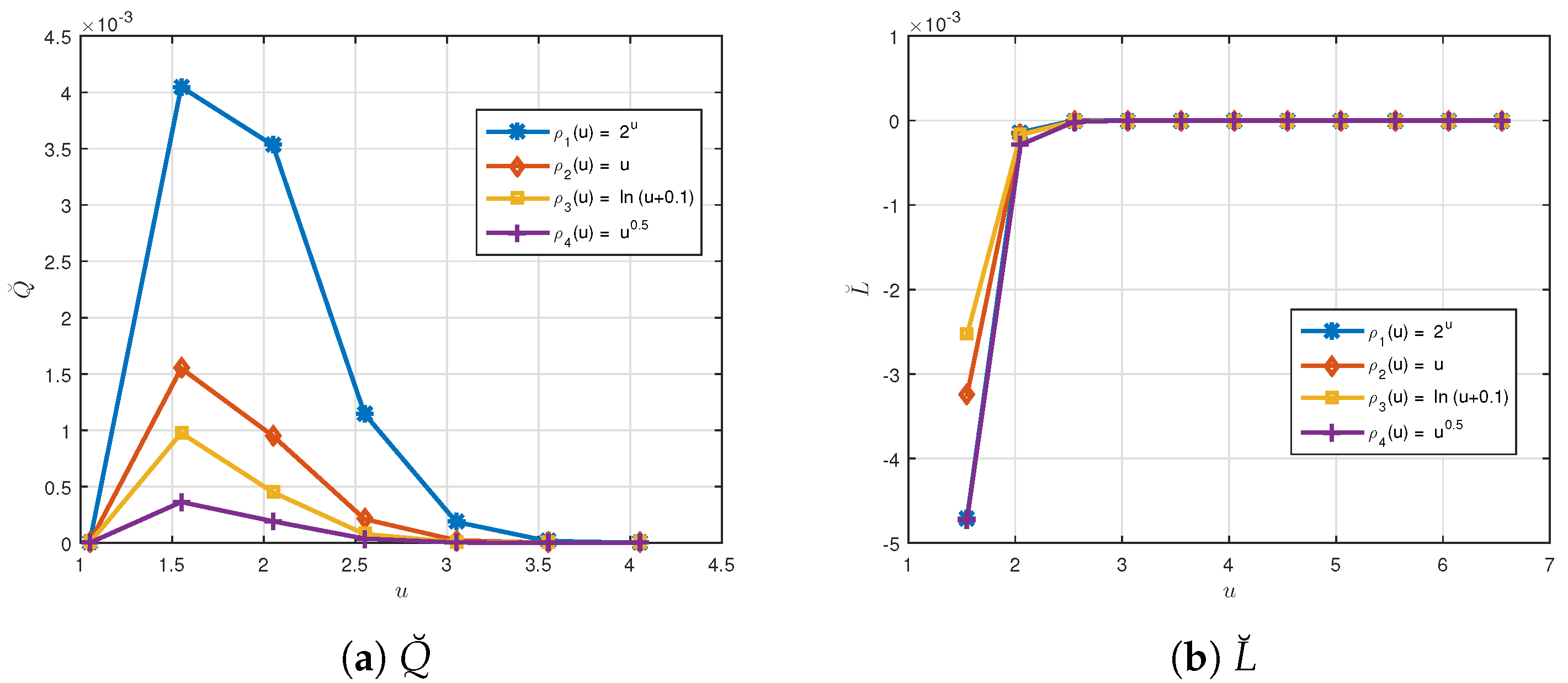
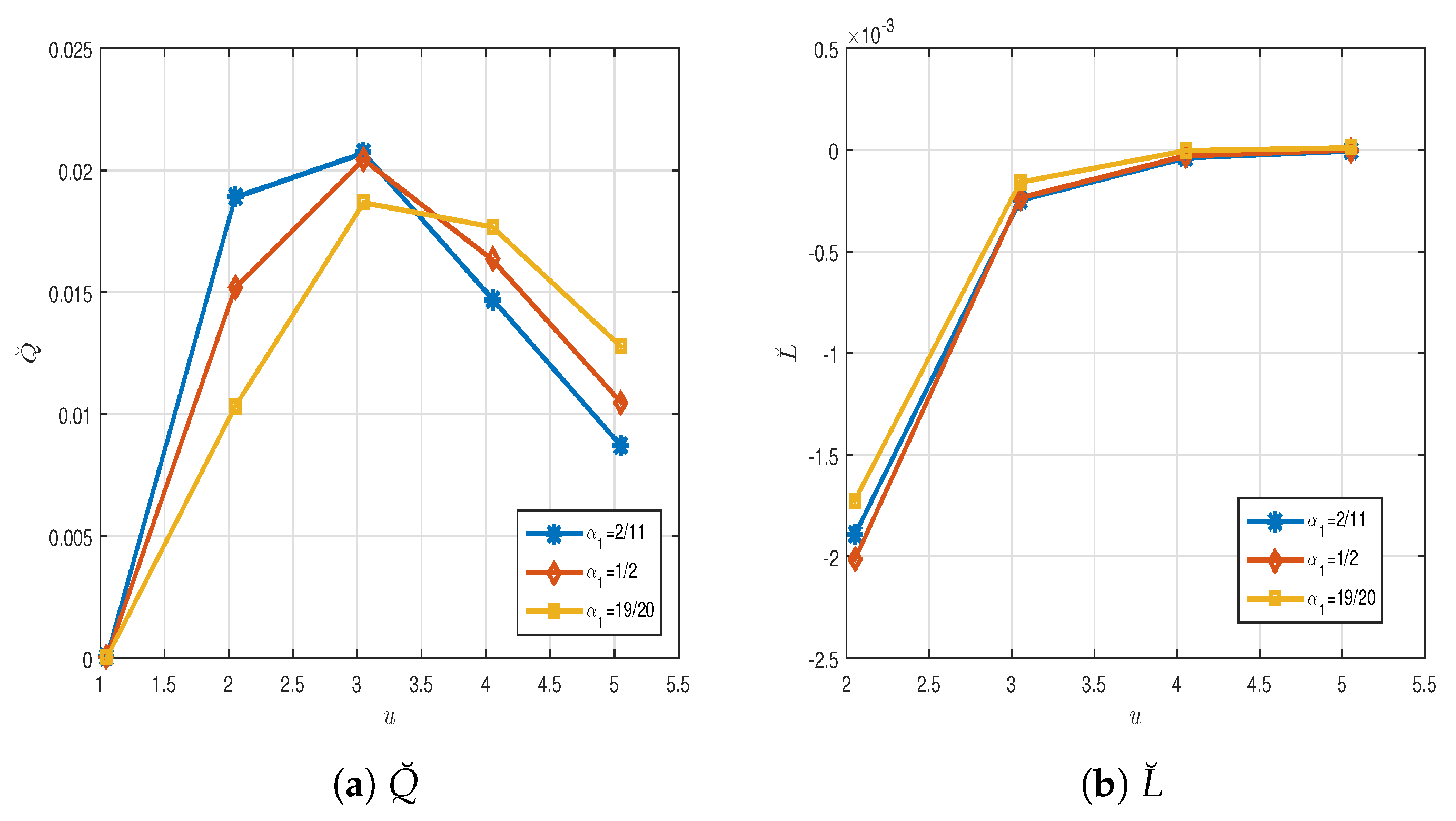
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdo, M.S. Boundary value problem for fractional neutral differential equations with infinite delay. Abhath J. Basic Appl. Sci. 2022, 1, 1–18. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Thabet, S.T.M.; Dhakne, M.B.; Salman, M.A.; Gubran, R. Generalized fractional Sturm-Liouville and Langevin equations involving Caputo derivative with nonlocal conditions. Prog. Fract. Differ. Appl. 2020, 6, 225–237. [Google Scholar] [CrossRef]
- Amiri, P.; Samei, M.E. Existence of Urysohn and Atangana-Baleanu fractional integral inclusion systems solutions via common fixed point of multi-valued operators. Chaos Solitons Fractals 2022, 165, 112822. [Google Scholar] [CrossRef]
- Abbas, M.I.; Ghaderi, M.; Rezapour, S.; Thabet, S.T.M. On a coupled system of fractional differential equations via the generalized proportional fractional derivatives. J. Funct. Spaces 2022, 2022, 4779213. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Lakshmikantham, V. Theory of fractional functional differential equations. Nonlinear Anal. 2008, 69, 3337–3343. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Elsonbaty, A.R.; El-Sayed, A.M.A. Further nonlinear dynamical analysis of simple jerk system with multiple attractors. Nonlinear Dyn. 2017, 87, 1169–1186. [Google Scholar] [CrossRef]
- Sousa, J.V.C.; Oliveira, E.C. On the ψ-Hilfer fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Abdo, M.; Panchal, S. Fractional integro-differential equations involving ψ-Hilfer fractional derivative. Adv. Appl. Math. Mech. 2019, 11, 338–359. [Google Scholar]
- Abdo, M.S.; Saeed, A.M.; Panchal, S.K. Fractional boundary value problem with ψ-Caputo fractional derivative. Proc. Indian Acad. Sci. Math. Sci. 2019, 129, 65. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Abdo, M.S.; Panchal, S.K. Existence and Ulam–Hyers–Mittag–Leffler stability results of ψ-Hilfer nonlocal Cauchy problem. Rend. Circ. Mat. Palermo Ser. 2 2020, 11, 57–77. [Google Scholar] [CrossRef]
- Almeidal, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Elsayed, E.; Kanagarajan, K. Existence and uniqueness results for fractional pantograph equations involving ψ-Hilfer fractional derivative. Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal. 2018, 25, 319–328. [Google Scholar]
- Vanterler, D.C.; Sousa, J.; Capelas, D.O.E. On the Ulam-Hyers-Rassias stability for nonlinear fractional differential equations using the ψ-Hilfer operator. J. Fixed Point Theory Appl. 2018, 20, 96. [Google Scholar] [CrossRef]
- Baitiche, Z.; Derbazi, C.; Benchohra, M. ψ-Caputo fractional differential equations with multi-point boundary conditions by topological degree theory. Results Nonlinear Anal. 2020, 3, 167–178. [Google Scholar]
- Bachir, F.S.; Abbas, S.; Benbachir, M.; Benchohra, M. Hilfer-Hadamard fractional differential equations; Existence and attractivity. Adv. Theory Nonlinear Anal. Its Appl. 2021, 5, 49–57. [Google Scholar]
- Thabet, S.T.M.; Dhakne, M.B. On positive solutions of higher order nonlinear fractional integro-differential equations with boundary conditions. Malaya J. Mat. 2019, 7, 20–26. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Dhakne, M.B. On boundary value problems of higher order abstract fractional integro-differential equations. Int. J. Nonlinear Anal. Appl. 2016, 7, 165–184. [Google Scholar]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. Caputo-type modification of the Hadamard fractional derivatives. Adv. Differ. Equ. 2012, 2012, 142. [Google Scholar] [CrossRef]
- Adjabi, Y.; Jarad, F.; Baleanu, D.; Abdeljawad, T. On Cauchy problems with Caputo-Hadamard fractional derivatives. J. Comput. Anal. Appl. 2016, 21, 661–681. [Google Scholar]
- Palve, L.A.; Abdo, M.S.; Panchal, S.K. Fractional functional differential equations with delay involving Hilfer-Hadamard type. Palest. J. Math. 2022, 11, 614–625. [Google Scholar]
- Ali, A.; Mahariq, I.; Shah, K.; Abdeljawad, T.; Al-Sheikh, B. Stability analysis of initial value problem of pantograph-type implicit fractional differential equations with impulsive conditions. Adv. Differ. Equ. 2021, 2021, 55. [Google Scholar] [CrossRef]
- Ali, A.; Shah, K.; Abdeljawad, T. Study of implicit delay fractional differential equations under anti-periodic boundary conditions. Adv. Differ. Equ. 2020, 2020, 139. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Dhakne, M.B. On nonlinear fractional integro-differential equations with two boundary conditions. Adv. Stud. Contemp. Math. 2016, 26, 513–526. [Google Scholar]
- Mahmudov, N.; Matar, M.M. Existence of mild solution for hybrid differential equations with arbitrary fractional order. TWMS J. Pure Appl. Math. 2017, 8, 160–169. [Google Scholar]
- Boutiara, A.; Guerbati, K.; Benbachir, M. Caputo-Hadamard fractional differential equation with three-point boundary conditions in Banach spaces. Aims Math. 2020, 5, 259–272. [Google Scholar] [CrossRef]
- Matar, M.M.; Ahmad, M.; Zada, A.; Etemad, S.; Rezapour, S. On the existence and stability of two positive solutions of a hybrid differential system of arbitrary fractional order via Avery–Anderson–Henderson criterion on cones. Adv. Differ. Equ. 2021, 2021, 423. [Google Scholar] [CrossRef]
- Abo Amra, I.E.; Matar, M.M. Coupled system of fractional differential equations with impulsive and nonlocal coupled boundary conditions. Bol. Soc. Mat. Mex. 2020, 26, 477–497. [Google Scholar] [CrossRef]
- Alqahtani, B.; Aydi, H.; Karapinar, E.; Rakocevic, V. A solution for Volterra fractional integral equations by hybrid contractions. Mathematics 2019, 7, 694. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Alzabut, J. On Riemann-Liouville fractional q–difference equations and their application to retarded logistic type model. Math. Methods Appl. Sci. 2018, 41, 8953–8962. [Google Scholar] [CrossRef]
- Baghani, H.; Alzabut, J.; Nieto, J. A coupled system of Langevin differential equations of fractional order and associated to anti-periodic boundary conditions. Math. Meth. Appl. Sci. 2020, 2020, 1–11. [Google Scholar]
- Rezapour, S.; Thabet, S.T.M.; Matar, M.M.; Alzabut, J.; Etemad, S. Some existence and stability criteria to a generalized FBVP having fractional composite p-Laplacian operator. J. Funct. Spaces 2021, 2021, 9554076. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.; Jafari, S.; Alsaadi, F.E. Chaos in a simple snap system with only one nonlinearity, its adaptive control and real circuit design. Arch. Control Sci. 2019, 29, 73–96. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Higazy, M.; Alkinani, M.H. Application of triple compound combination anti-synchronization among parallel fractional snap systems and electronic circuit implementation. Adv. Differ. Equ. 2021, 2021, 211. [Google Scholar] [CrossRef]
- Samei, M.E.; Matar, M.M.; Etemad, S.; Rezapour, S. On the generalized fractional snap boundary problems via G-Caputo operators: Existence and stability analysis. Adv. Differ. Equ. 2021, 2021, 498. [Google Scholar] [CrossRef]
- Wang, X.; Berhail, A.; Tabouche, N.; Matar, M.M.; Samei, M.E.; Kaabar, M.K.A.; Yue, X.G. A Novel Investigation of Non-Periodic snap BVP in the G-Caputo Sense. Axioms 2022, 11, 390. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Matar, M.M.; Salman, M.A.; Samei, M.E.; Vivas-Cortez, M. On coupled snap system with integral boundary conditions in the G-Caputo sense. Aims Math. 2023, 8, 12576–12605. [Google Scholar] [CrossRef]
- Adjabi, Y.; Samei, M.E.; Matar, M.M.; Alzabut, J. Langevin differential equation in frame of ordinary and Hadamard fractional derivatives under three point boundary conditions. Aims Math. 2021, 6, 2796–2843. [Google Scholar] [CrossRef]
- Diaz, J.; Margolis, B. A fixed point theorem of the alternative for contractions on a generalized complete metric space. Bull. Am. Math. Soc. 1968, 74, 305–309. [Google Scholar] [CrossRef]
- Su, X.; Zhang, S. Unbounded solutions to a boundary value problem of fractional order on the halfline. Comput. Math. Appl. 2011, 61, 1079–1087. [Google Scholar] [CrossRef]
- Su, X. Solutions to boundary value problem of fractional order on unbounded domains in a Banach space. Nonlinear Anal. Theory Methods Appl. 2011, 74, 2844–2852. [Google Scholar] [CrossRef]
- Kou, C.; Zhou, H.; Yan, Y. Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis. Nonlinear Anal. Theory Methods Appl. 2011, 74, 5975–5986. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Kedim, I. Study of nonlocal multiorder implicit differential equation involving Hilfer fractional derivative on unbounded domains. J. Math. 2023, 2023, 8668325. [Google Scholar] [CrossRef]
- Oliveira, E.C.; Sousa, J.V.C. Ulam-Hyers-Rassias stability for a class of fractional integro-differential equations. Results Math. 2018, 73, 111. [Google Scholar] [CrossRef]
- Cădariu, L.; Găvruţa, L.; Găvruţa, P. Weighted space method for the stability of some nonlinear equations. Appl. Anal. Discret. Math. 2012, 6, 126–139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thabet, S.T.M.; Vivas-Cortez, M.; Kedim, I.; Samei, M.E.; Ayari, M.I. Solvability of a ϱ-Hilfer Fractional Snap Dynamic System on Unbounded Domains. Fractal Fract. 2023, 7, 607. https://doi.org/10.3390/fractalfract7080607
Thabet STM, Vivas-Cortez M, Kedim I, Samei ME, Ayari MI. Solvability of a ϱ-Hilfer Fractional Snap Dynamic System on Unbounded Domains. Fractal and Fractional. 2023; 7(8):607. https://doi.org/10.3390/fractalfract7080607
Chicago/Turabian StyleThabet, Sabri T. M., Miguel Vivas-Cortez, Imed Kedim, Mohammad Esmael Samei, and M. Iadh Ayari. 2023. "Solvability of a ϱ-Hilfer Fractional Snap Dynamic System on Unbounded Domains" Fractal and Fractional 7, no. 8: 607. https://doi.org/10.3390/fractalfract7080607
APA StyleThabet, S. T. M., Vivas-Cortez, M., Kedim, I., Samei, M. E., & Ayari, M. I. (2023). Solvability of a ϱ-Hilfer Fractional Snap Dynamic System on Unbounded Domains. Fractal and Fractional, 7(8), 607. https://doi.org/10.3390/fractalfract7080607









