An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool
Abstract
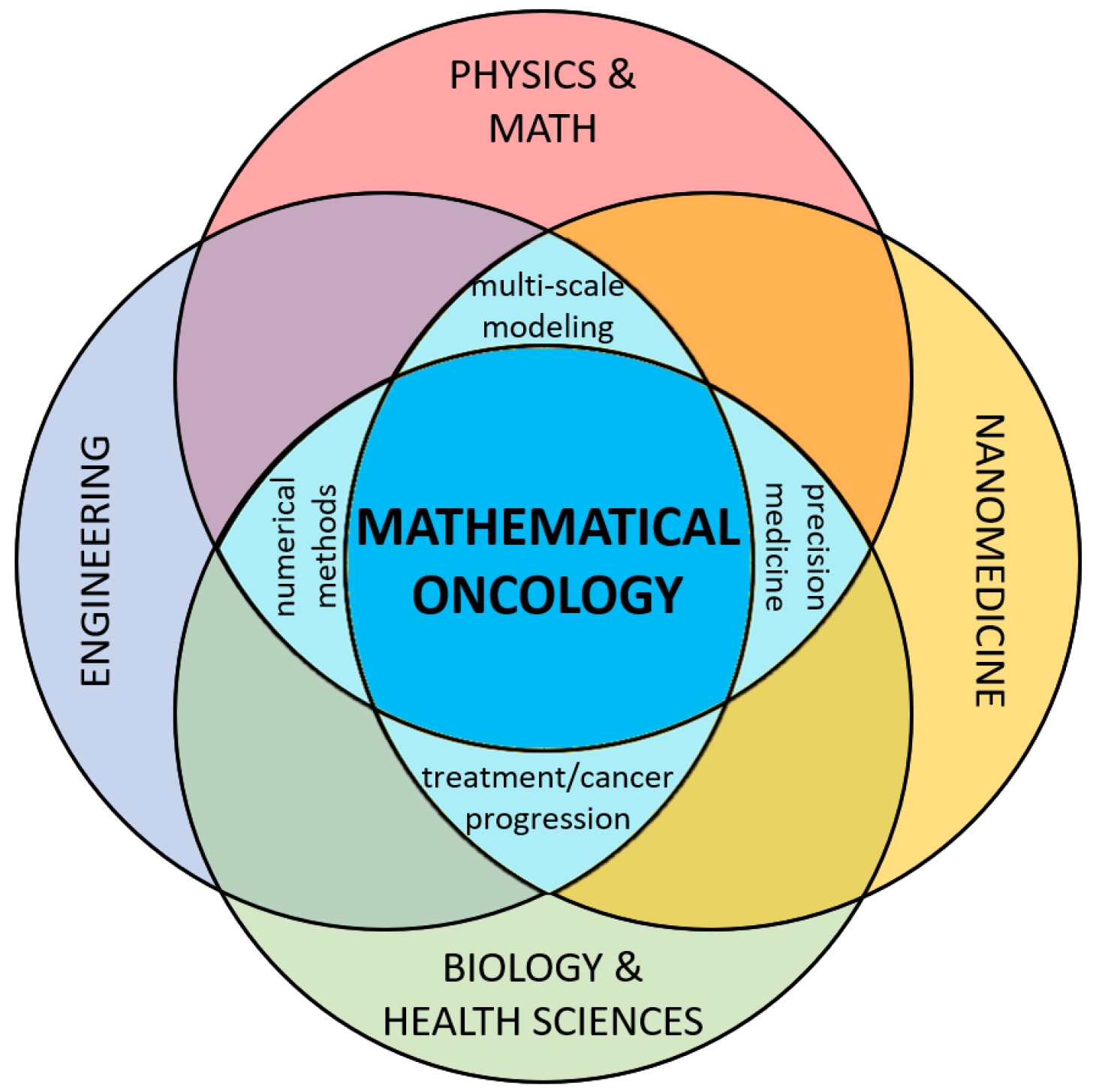
1. Introduction
2. Mathematical Modelling in Oncology
2.1. White-, Grey- and Black-Box Modelling
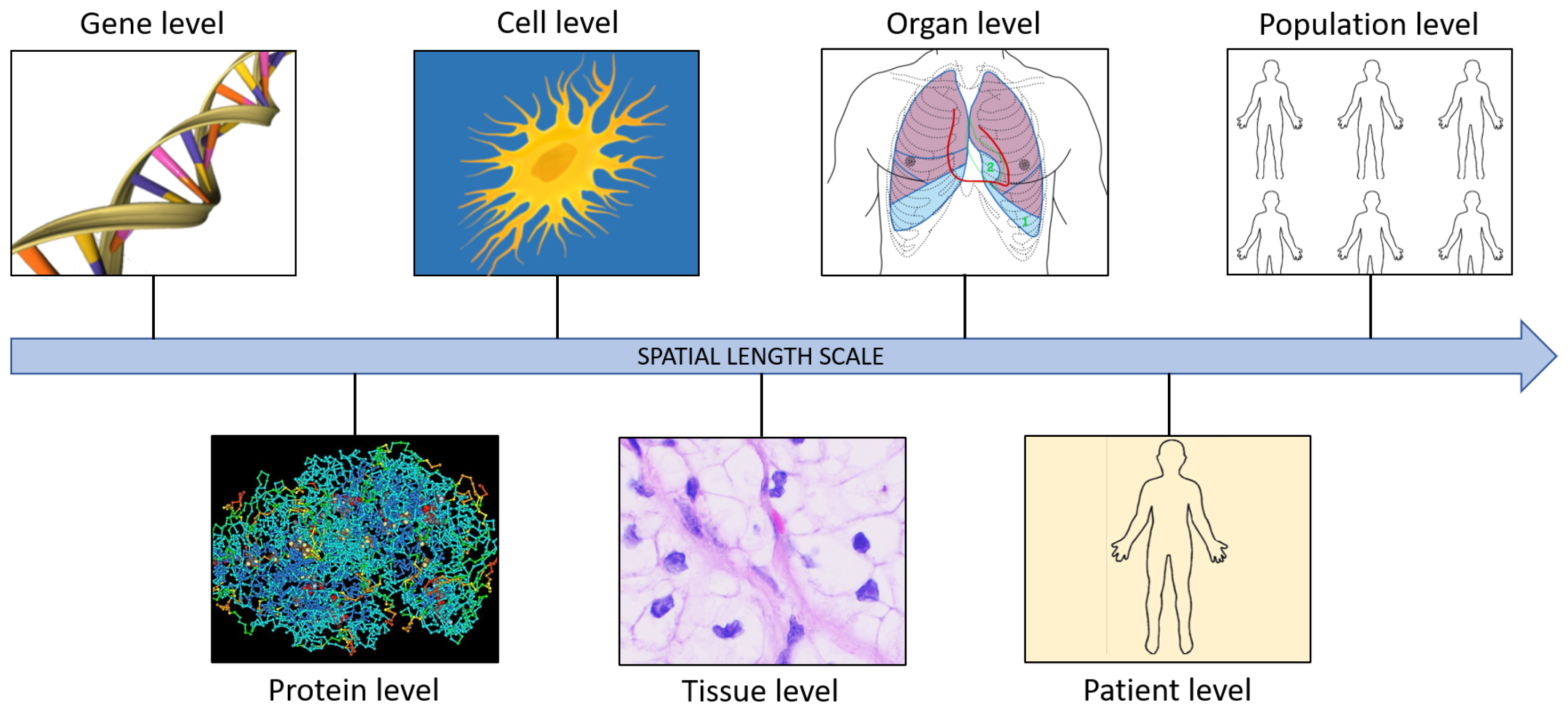
2.2. The Spatial Scale
2.3. Models of Ordinary and Partial Differential Equations
2.4. Other Modelling Techniques
2.5. General Modelling Assumptions
2.6. Modelling Treatment Intervention
2.7. General Modelling Limitations
2.8. Mathematical Oncology or Oncological Mathematics?
3. Fractional Calculus in Mathematical Modelling
3.1. Early Development
3.2. The Memory Effect
3.3. General Applications
3.4. Modelling Biological Phenomena
3.5. Toward a Fractional Mathematical Oncology
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tabassum, S.; Rosli, N.; Mazalan, M. Mathematical Modelling of Cancer Growth Process: A Review. J. Phys. Conf. Ser. 2019, 1366, 012018. [Google Scholar] [CrossRef]
- Cancer Treatment Centers of America. What Is Cancer, Is It Common & How Do You Get It. 2022. Available online: https://www.cancercenter.com/what-is-cancer (accessed on 11 August 2022).
- National Cancer Institute (NCI). What Is Cancer? 2021. Available online: https://www.cancer.gov/about-cancer/understanding/what-is-cancer (accessed on 13 August 2022).
- Stanford Health Care (SHC). Cancer. Available online: https://stanfordhealthcare.org/medical-conditions/cancer/cancer.html (accessed on 23 August 2022).
- Cancer Treatment Centers of America. What’s the Difference? Benign and Malignant Tumours. 2017. Available online: https://www.cancercenter.com/community/blog/2017/12/whats-the-difference-benign-and-malignant-tumours (accessed on 26 August 2022).
- Basanta, D.; Anderson, A.R. Homeostasis Back and Forth: An Ecoevolutionary Perspective of Cancer. Cold Spring Harb. Perspect. Med. 2017, 7, a028332. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.; Maini, P.K. Mathematical oncology. Bull. Math. Biol. 2018, 80, 945–953. [Google Scholar] [CrossRef] [PubMed]
- National Cancer Institute (NCI). Types of Cancer Treatment. Available online: https://www.cancer.gov/about-cancer/treatment/types (accessed on 11 August 2022).
- World Health Organization. Cancer. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 15 August 2022).
- American Cancer Society. Cancer Facts & Figures 2021. Available online: https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/cancer-facts-figures-2021.html (accessed on 20 August 2022).
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer statistics, 2022. CA Cancer J. Clin. 2022, 72, 7–33. [Google Scholar] [CrossRef]
- Dogra, P.; Butner, J.; Chuang, Y.; Caserta, S.; Goel, S.; Brinker, C.; Cristini, V.; Wang, Z. Mathematical modelling in cancer nanomedicine: A review. Biomed. Microdevices 2019, 21, 40. [Google Scholar] [CrossRef] [PubMed]
- Rockne, R.C.; Hawkins-Daarud, A.; Swanson, K.R.; Sluka, J.P.; Glazier, J.A.; Macklin, P.; Hormuth, D.A. The 2019 mathematical oncology roadmap. Phys. Biol. 2019, 16, 041005. [Google Scholar] [CrossRef]
- Brady, R.; Enderling, H. Mathematical Models of Cancer: When to Predict Novel Therapies, and When Not to. Bull. Math. Biol. 2019, 81, 3722–3731. [Google Scholar] [CrossRef]
- Malinzi, J.; Basita, K.B.; Padidar, S.; Adeola, H.A. Prospect for application of mathematical models in combination cancer treatments. Inform. Med. Unlocked 2021, 23, 100534. [Google Scholar] [CrossRef]
- dePillis, L.G.; Eladdadi, A.; Radunskaya, A.E. Modelling cancer-immune responses to therapy. J. Pharmacokinet. Pharmacodyn. 2014, 41, 461–478. [Google Scholar] [CrossRef]
- Agarwal, R.; Kritika; Purohit, S.D. Chapter 5: Fractional order mathematical model for the cell cycle of a tumour cell. In Fractional Calculus in Medical and Health Science; Kumar, D., Singh, J., Eds.; CRC Press: Boca Raton, FL, USA, 2020; pp. 129–147. [Google Scholar] [CrossRef]
- Valentim, C.A.; Rabi, J.A.; David, S.A. Fractional Mathematical Oncology: On the potential of non-integer order calculus applied to interdisciplinary models. Biosystems 2021, 204, 104377. [Google Scholar] [CrossRef]
- Altrock, P.M.; Liu, L.L.; Michor, F. The mathematics of cancer: Integrating quantitative models. Nat. Rev. Cancer 2015, 15, 730–745. [Google Scholar] [CrossRef] [PubMed]
- Bekisz, S.; Geris, L. Cancer modelling: From mechanistic to data-driven approaches, and from fundamental insights to clinical applications. J. Comput. Sci. 2020, 46, 101198. [Google Scholar] [CrossRef]
- Chauviere, A.H.; Hatzikirou, H.; Lowengrub, J.S.; Frieboes, H.B.; Thompson, A.M.; Cristini, V. Mathematical oncology: How Are the Mathematical and Physical Sciences Contributing to the War on Breast Cancer? Curr. Breast Cancer Rep. 2010, 2, 121–129. [Google Scholar] [CrossRef][Green Version]
- Anderson, A.R.; Quaranta, V. Integrative mathematical oncology. Nat. Rev. Cancer 2008, 8, 227–234. [Google Scholar] [CrossRef]
- Araujo, R.P.; McElwain, D.L.S. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef] [PubMed]
- Jean-Quartier, C.; Jeanquartier, F.; Jurisica, I.; Holzinger, A. In silico cancer research towards 3R. BMC Cancer 2018, 18, 408. [Google Scholar] [CrossRef] [PubMed]
- Sneddon, L.U.; Halsey, L.G.; Bury, N.R. Considering aspects of the 3Rs principles within experimental animal biology. J. Exp. Biol. 2017, 220, 3007–3016. [Google Scholar] [CrossRef] [PubMed]
- DiMasi, J.A.; Hansen, R.W.; Grabowski, H.G. The price of innovation: New estimates of drug development costs. J. Health Econ. 2003, 22, 151–185. [Google Scholar] [CrossRef]
- Rozova, V.; Alexander, B. Therapy strategy in tumour cells and immune system interaction mathematical model. Appl. Anal. 2016, 95, 1548–1559. [Google Scholar] [CrossRef]
- Mahlbacher, G.; Reihmer, K.; Frieboes, H. Mathematical modelling of tumour-immune cell interactions. J. Theor. Biol. 2019, 469, 47–60. [Google Scholar] [CrossRef]
- Song, W.; Lin, X.; Liao, X.; Hu, D.; Lin, J.; Sarpel, U.; Ye, Y.; Feferman, Y.; Labow, D.M.; Walsh, M.J. Multiscale network analysis reveals molecular mechanisms and key regulators of the tumour microenvironment in gastric cancer. Int. J. Cancer 2020, 146, 1268–1280. [Google Scholar] [CrossRef] [PubMed]
- Sancho-Araiz, A.; Mangas-Sanjuan, V.; Trocóniz, I. The Role of Mathematical Models in Immuno-Oncology: Challenges and Future Perspectives. Pharmaceutics 2021, 13, 1016. [Google Scholar] [CrossRef]
- Byrne, H.M. Dissecting cancer through mathematics: From the cell to the animal model. Nat. Rev. Cancer 2010, 10, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Bull, J.A.; Byrne, H.M. The Hallmarks of Mathematical Oncology. Proc. IEEE 2022, 110, 523–540. [Google Scholar] [CrossRef]
- Yin, A.; Moes, D.J.; Hasselt, J.G.; Swen, J.J.; Guchelaar, H. A review of mathematical models for tumour dynamics and treatment resistance evolution of solid tumours. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 720–737. [Google Scholar] [CrossRef]
- Winther, R.G. Mathematical Modelling in Biology: Philosophy and Pragmatics. Front. Plant Sci. 2012, 3, 102. [Google Scholar] [CrossRef]
- Kalmykov, L.; Kalmykov, V. Mechanistic mechanisms of competition and biodiversity. Nat. Preced. 2012. [Google Scholar] [CrossRef]
- de Pillis, L.; Fister, K.R.; Gu, W.; Collins, C.; Daub, M.; Gross, D.; Moore, J.; Preskill, B. Mathematical model creation for cancer chemo-immunotherapy. Comput. Math. Methods Med. 2009, 10, 165–184. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Hanczar, B.; Zehraoui, F.; Issa, T.; Arles, M. Biological interpretation of deep neural network for phenotype prediction based on Gene expression. BMC Bioinform. 2020, 21, 501. [Google Scholar] [CrossRef]
- Deisboeck, T.S.; Wang, Z.; Macklin, P.; Cristini, V. Multiscale cancer modelling. Annu. Rev. Biomed. Eng. 2011, 13, 127–155. [Google Scholar] [CrossRef]
- Wikimedia Commons. Available online: https://commons.wikimedia.org/wiki/File:DNA_Double_Helix.png (accessed on 27 June 2023).
- Wikimedia Commons. Available online: https://upload.wikimedia.org/wikipedia/commons/thumb/3/31/ProteinStructure.jpg/640px-ProteinStructure.jpg (accessed on 27 June 2023).
- Wikimedia Commons. Available online: https://commons.wikimedia.org/wiki/File:Cells_001.png (accessed on 27 June 2023).
- Wikimedia Commons. Available online: https://upload.wikimedia.org/wikipedia/commons/thumb/9/92/Grade_2_clear_cell_renal_cell_carcinoma.jpg/640px-Grade_2_clear_cell_renal_cell_carcinoma.jpg (accessed on 27 June 2023).
- Wikimedia Commons. Available online: https://upload.wikimedia.org/wikipedia/commons/thumb/4/47/Birikaren_zokoguneak_1.png/640px-Birikaren_zokoguneak_1.png (accessed on 27 June 2023).
- Wikimedia Commons. Available online: https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/Human_body_outline.png/640px-Human_body_outline.png (accessed on 27 June 2023).
- Tracqui, P. Biophysical models of tumour growth. Rep. Prog. Phys. 2009, 72, 056701. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Sagotsky, J.A.; Deisboeck, T.S. Multiscale agent-based cancer modelling. J. Math. Biol. 2008, 58, 545–559. [Google Scholar] [CrossRef]
- Tzamali, E.; Tzedakis, G.; Sakkalis, V. Modelling how heterogeneity in cell cycle length affects cancer cell growth dynamics in response to treatment. Front. Oncol. 2020, 10, 1552. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Phillips, C.M.; Wu, C.; Lima, E.A.B.F.; Lorenzo, G.; Jha, P.K.; Jarrett, A.M.; Oden, J.T.; Yankeelov, T.E. Biologically-Based Mathematical Modelling of Tumour Vasculature and Angiogenesis via Time-Resolved Imaging Data. Cancers 2021, 13, 3008. [Google Scholar] [CrossRef]
- Sarapata, E.; de Pillis, L. A comparison and catalog of intrinsic tumour growth models. Bull. Math. Biol. 2014, 76, 2010–2024. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumour Growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef]
- Eftimie, R.; Bramson, J.; Earn, D. Interactions Between the Immune System and Cancer: A Brief Review of Non-spatial Mathematical Models. Bull. Math. Biol. 2010, 73, 2–32. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Radunskaya, A. A mathematical tumour model with immune resistance and drug therapy: An optimal control approach. J. Theor. Med. 2001, 3, 79–100. [Google Scholar] [CrossRef]
- Darandis, N.; Nazari, M. A mathematical model for chemo-immunotherapy of cancer considering macrophages polarization and cytokine dynamics. Authorea 2020. [Google Scholar] [CrossRef]
- Pillis, L.G.; Radunskaya, A.E. Best practices in mathematical modelling. In Computational Toxicology; Methods in Molecular Biology; Humana: Totowa, NJ, USA, 2013; pp. 51–74. [Google Scholar] [CrossRef]
- Valentim, C.A.; Oliveira, N.A.; Rabi, J.A.; David, S.A. Can fractional calculus help improve tumour growth models? J. Comput. Appl. Math. 2020, 379, 112964. [Google Scholar] [CrossRef]
- Murphy, H.; Jaafari, H.; Dobrovolny, H. Differences in predictions of ODE models of tumour growth: A cautionary example. BMC Cancer 2016, 16, 163. [Google Scholar] [CrossRef] [PubMed]
- Fahimi, M.; Nouri, K.; Torkzadeh, L. Chaos in a stochastic cancer model. Phys. A Stat. Mech. Appl. 2020, 545, 123810. [Google Scholar] [CrossRef]
- Xu, J.; Vilanova, G.; Gomez, H. A mathematical model coupling tumour growth and angiogenesis. PLoS ONE 2016, 11, e0149422. [Google Scholar] [CrossRef]
- Lefebvre, G.; Cornelis, F.; Cumsille, P.; Colin, T.; Poignard, C.; Saut, O. Spatial modelling of tumour drug resistance: The case of GIST liver metastases. Math. Med. Biol. 2016, 34, 151–176. [Google Scholar] [CrossRef]
- Polovinkina, M.V.; Debbouche, A.; Polovinkin, I.P.; David, S.A. Stability of stationary solutions for the glioma growth equations with radial or axial symmetries. Math. Methods Appl. Sci. 2021, 44, 12021–12034. [Google Scholar] [CrossRef]
- Mohammadi, V.; Dehghan, M.; De Marchi, S. Numerical simulation of a prostate tumour growth model by the RBF-FD scheme and a semi-implicit time discretization. J. Comput. Appl. Math. 2021, 388, 113314. [Google Scholar] [CrossRef]
- Osborne, J.M.; Fletcher, A.G.; Pitt-Francis, J.M.; Maini, P.K.; Gavaghan, D.J. Comparing individual-based approaches to modelling the self-organization of multicellular tissues. PLoS Comput. Biol. 2017, 13, e1005387. [Google Scholar] [CrossRef]
- Benecchi, L. Neuro-fuzzy system for prostate cancer diagnosis. Urology 2006, 68, 357–361. [Google Scholar] [CrossRef]
- Behinaein, B.; Rudie, K.; Sangrar, W. Petri Net Siphon Analysis and Graph Theoretic Measures for Identifying Combination Therapies in Cancer. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 231–243. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef]
- Ghadiri, M.; Heidari, M.; Marashi, S.A.; Mousavi, S.H. A multiscale agent-based framework integrated with a constraint-based metabolic network model of cancer for simulating avascular tumour growth. Mol. BioSyst. 2017, 13, 1888–1897. [Google Scholar] [CrossRef] [PubMed]
- Tsai, F.C.; Wang, M.C.; Lo, J.F.; Chou, C.M.; Lin, Y.L. Spatiotemporal dynamics of the biological interface between cancer and the microenvironment: A fractal anomalous diffusion model with microenvironment plasticity. Theor. Biol. Med. Model. 2012, 9, 36. [Google Scholar] [CrossRef]
- Kim, E.; Brown, J.S.; Eroglu, Z.; Anderson, A.R. Adaptive Therapy for Metastatic Melanoma: Predictions from Patient Calibrated Mathematical Models. Cancers 2021, 13, 823. [Google Scholar] [CrossRef]
- de Pillis, L.G.; Gu, W.; Radunskaya, A. Mixed immunotherapy and chemotherapy of tumours: Modelling, applications and biological interpretations. J. Theor. Biol. 2006, 238, 841–862. [Google Scholar] [CrossRef]
- Akman Yıldız, T.; Arshad, S.; Baleanu, D. New observations on optimal cancer treatments for a fractional tumour growth model with and without singular kernel. Chaos Solitons Fractals 2018, 117, 226–239. [Google Scholar] [CrossRef]
- Engelhart, M.; Lebiedz, D.; Sager, S. Optimal control for selected cancer chemotherapy ODE models: A view on the potential of optimal schedules and choice of objective function. Math. Biosci. 2011, 229, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Coelho, R.; Neto, J.; Valério, D.; Vinga, S. Chapter 4: Dynamic Biochemical and Cellular Models of Bone Physiology: Integrating Remodelling Processes, Tumour Growth, and Therapy. In The Computational Mechanics of Bone Tissue; Belinha, J., Manzanares-Céspedes, M.C., Completo, A.M.G., Eds.; Lecture Notes in Computational Vision and Biomechanics Series; Springer: Cham, Switzerland, 2020; Volume 35, pp. 95–128. [Google Scholar] [CrossRef]
- Farayola, M.F.; Shafie, S.; Mohd Siam, F.; Mahmud, R.; Ajadi, S.O. Mathematical modelling of cancer treatments with fractional derivatives: An overview. Malays. J. Fundam. Appl. Sci. 2021, 17, 389–401. [Google Scholar] [CrossRef]
- Divoli, A.; Mendonça, E.; Evans, J.; Rzhetsky, A. Conflicting biomedical assumptions for mathematical modelling: The case of cancer metastasis. PLoS Comput. Biol. 2011, 7, e1002132. [Google Scholar] [CrossRef]
- Karolak, A.; Markov, D.; McCawley, L.; Rejniak, K. Towards personalized computational oncology: From spatial models of tumour spheroids, to organoids, to tissues. J. R. Soc. Interface 2018, 15, 20170703. [Google Scholar] [CrossRef]
- Komarova, N.; Wodarz, D. Drug resistance in cancer: Principles of emergence and prevention. Proc. Natl. Acad. Sci. USA 2005, 102, 9714–9719. [Google Scholar] [CrossRef] [PubMed]
- Tongen, A.L.; Adam, M.B. Ethics Involved in Simulation-Based Medical Planning. Ethics Med. 2006, 22, 23–29. [Google Scholar]
- Gatenby, R.A.; Maini, P.K. Mathematical oncology: Cancer summed up. Nature 2003, 421, 321. [Google Scholar] [CrossRef] [PubMed]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Ross, B. The development of fractional calculus 1695–1900. Hist. Math. 1977, 4, 75–89. [Google Scholar] [CrossRef]
- Valério, D.; Sá da Costa, J. An Introduction to Fractional Control; IET Control Engineering Series; The Institution of Engineering and Technology: London, UK, 2013; Volume 91. [Google Scholar] [CrossRef]
- Ortigueira, M.D. An introduction to the fractional continuous-time linear systems: The 21st century systems. IEEE Circuits Syst. Mag. 2008, 8, 19–26. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D. Fractional Signals and Systems; Fractional Calculus in Applied Sciences and Engineering Series; De Gruyter: Berlin, Germany, 2020; Volume 7. [Google Scholar] [CrossRef]
- Baleanu, D.; Agarwal, R.P. Fractional calculus in the sky. Adv. Differ. Equ. 2021, 2021, 117. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers, 1st ed.; Lecture Notes in Electrical Engineering Series; Springer: Dordecht, The Netherlands, 2011; Volume 84. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.D.; Lopes, A.M. How many fractional derivatives are there? Mathematics 2022, 10, 737. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D.; Machado, J.T. Variable Order Fractional Systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 231–243. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V. The chronicles of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 307–336. [Google Scholar] [CrossRef]
- Rahimy, M. Applications of Fractional Differential Equations. Appl. Math. Sci. 2010, 4, 2453–2461. [Google Scholar]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar] [CrossRef]
- Velasco, M.P.; Usero, D.; Jiménez, S.; Vázquez, L.; Vázquez-Poletti, J.L.; Mortazavi, M. About some possible implementations of the fractional calculus. Mathematics 2020, 8, 893. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Westerlund, S. Dead matter has memory! Phys. Scr. 1991, 43, 174–179. [Google Scholar] [CrossRef]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.T.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems of Fractional Systems Theory, 1st ed.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- West, B.J. Nature’s Patterns and the Fractional Calculus; Fractional Calculus in Applied Sciences and Engineering; De Gruyter: Berlin, Germany, 2017; Volume 2. [Google Scholar] [CrossRef]
- Mitkowski, W.; Kacprzyk, J.; Baranowski, J. (Eds.) Advances in the Theory and Applications of Non-Integer Order Systems, Proceedings of the 5th Conference on Non-Integer Order Calculus and Its Applications, Cracow, Poland, 4–5 July 2013, 1st ed.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2013; Volume 257. [Google Scholar] [CrossRef]
- Babiarz, A.; Czornik, A.; Klamka, J.; Niezabitowski, M. (Eds.) Theory and Applications of Non-Integer Order Systems, Proceedings of the 8th Conference on Non-Integer Order Calculus and Its Applications, Zakopane, Poland, 20–21 September 2016, 1st ed.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2016; Volume 407. [Google Scholar] [CrossRef]
- Malinowska, A.B.; Mozyrska, D.; Sajewski, Ł. (Eds.) Advances in Non-Integer Order Calculus and Its Applications, Proceedings of the 10th International Conference on Non-Integer Order Calculus and Its Applications, Białystok, Poland, 20–21 September 2018, 1st ed.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2019; Volume 559. [Google Scholar] [CrossRef]
- Mathieu, B.; Melchior, P.; Oustaloup, A.; Ceyral, C. Fractional differentiation for edge detection. Signal Process. 2003, 83, 2421–2432. [Google Scholar] [CrossRef]
- David, S.; Inacio, C., Jr.; Nunes, R.; Machado, J.T. Fractional and fractal processes applied to cryptocurrencies price series. J. Adv. Res. 2021, 32, 85–98. [Google Scholar] [CrossRef]
- Farman, M.; Aslam, M.; Akgül, A.; Ahmad, A. Modelling of fractional-order COVID-19 epidemic model with quarantine and social distancing. Math. Methods Appl. Sci. 2021, 44, 9334–9350. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Tchier, F.; Singh, J.; Baleanu, D. An efficient computational technique for fractal vehicular traffic flow. Entropy 2018, 20, 259. [Google Scholar] [CrossRef] [PubMed]
- Valentim, C.A., Jr.; Bannwart, F.; David, S.A. Fractional calculus applied to linear thermoacoustics: A generalization of Rott’s model. In Proceedings of the 17th Brazilian Congress of Thermal Sciences and Engineering, São Carlos, Brazil, 25–28 November 2018. [Google Scholar] [CrossRef]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20200050. [Google Scholar] [CrossRef] [PubMed]
- Petráš, I.; Terpák, J. Fractional calculus as a simple tool for modelling and analysis of long memory process in industry. Mathematics 2019, 7, 511. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional-calculus-based electromagnetic tool to study pulse propagation in arbitrary dispersive dielectrics. Phys. Status Solidi (a) 2018, 216, 1800557. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st ed.; Mathematics in Science and Engineering Series; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A Review. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J. The role of fractional calculus in Modelling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Chen, Y. Variable-order fractional differential operators in Anomalous Diffusion Modelling. Phys. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Oliveira, F.A.; Ferreira, R.M.; Lapas, L.C.; Vainstein, M.H. Anomalous Diffusion: A Basic Mechanism for the Evolution of Inhomogeneous Systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous diffusion modelling by fractal and fractional derivatives. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Manimaran, J.; Shangerganesh, L.; Debbouche, A.; Antonov, V. Numerical Solutions for time-fractional cancer invasion system with nonlocal diffusion. Front. Phys. 2019, 7, 93. [Google Scholar] [CrossRef]
- Valentim, C.A.; Rabi, J.A.; David, S.A.; Machado, J.T. On multistep tumour growth models of fractional variable-order. Biosystems 2021, 199, 104294. [Google Scholar] [CrossRef] [PubMed]
- Neto, J. Dynamic Modelling of Bone Remodelling, Tumour Growth and Therapy: Simplifying and Diffusing with Variable Order Derivatives. Master’s Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2017. [Google Scholar]
- Abaid Ur Rehman, M.; Ahmad, J.; Hassan, A.; Awrejcewicz, J.; Pawlowski, W.; Karamti, H.; Alharbi, F.M. The dynamics of a fractional-order mathematical model of cancer tumour disease. Symmetry 2022, 14, 1694. [Google Scholar] [CrossRef]
- Tang, T.Q.; Shah, Z.; Bonyah, E.; Rashid, J.; Shutaywi, M.; Alreshidi, N. Modelling and Analysis of Breast Cancer with Adverse Reactions of Chemotherapy Treatment through Fractional Derivative. Comput. Math. Methods Med. 2022, 2022, 5636844. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumour. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Damor, R.; Shukla, A. Numerical simulation of fractional Bioheat equation in hyperthermia treatment. J. Mech. Med. Biol. 2014, 14, 1450018. [Google Scholar] [CrossRef]
- Rihan, F.; Hashish, A.; Al-Maskari, F.; Sheek-Hussein, M.; Ahmed, E.; Riaz, M.; Radouane, Y. Dynamics of Tumour-Immune System with Fractional-Order. J. Tumour Res. 2016, 2, 109. [Google Scholar] [CrossRef]
- Ionescu, C.; Copot, D.; De Keyser, R. Modelling Doxorubicin effect in various cancer therapies by means of fractional calculus. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1283–1288. [Google Scholar] [CrossRef]
- Kumar, D.; Rai, K. Numerical simulation of time fractional dual-phase-lag model of heat transfer within skin tissue during thermal therapy. J. Therm. Biol. 2017, 67, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Neto, J.P.; Valério, D.; Vinga, S. Chapter 1—Variable Order Fractional Derivatives and Bone Remodelling in the Presence of Metastases. In Mathematical Techniques of Fractional Order Systems; Azar, A.T., Radwan, A.G., Vaidyanathan, S., Eds.; Advances in Nonlinear Dynamics and Chaos (ANDC); Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–36. [Google Scholar] [CrossRef]
- Awadalla, M.; Yameni Noupoue, Y.Y.; Abuasbeh, K. A new Fractional Model for the Cancer Treatment by Radiotherapy Using Hadamard Fractional Derivative. Online Math. J. 2019, 1, 1–12. Available online: https://www.researchgate.net/publication/332130754 (accessed on 27 June 2023).
- Silva, J.G.; Ribeiro, A.C.; Camargo, R.F.; Mancera, P.F.; Santos, F.L. Stability analysis and numerical simulations via fractional calculus for tumour dormancy models. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 528–543. [Google Scholar] [CrossRef]
- Atıcı, F.M.; Atıcı, M.; Nguyen, N.; Zhoroev, T.; Koch, G. A study on discrete and discrete fractional pharmacokinetics-pharmacodynamics models for tumour growth and anti-cancer effects. Comput. Math. Biophys. 2019, 7, 10–24. [Google Scholar] [CrossRef]
- Bonyah, E.; Zarin, R.; Fatmawati, F. Mathematical modelling of cancer and hepatitis co-dynamics with non-local and non-singular kernel. Commun. Math. Biol. Neurosci. 2020, 2020, 91. [Google Scholar] [CrossRef]
- Farayola, M.F.; Shafie, S.; Siam, F.M.; Khan, I. Mathematical modelling of radiotherapy cancer treatment using Caputo fractional derivative. Comput. Methods Programs Biomed. 2020, 188, 105306. [Google Scholar] [CrossRef]
- Ahmed, N.; Vieru, D.; Zaman, F. Memory effects on the proliferative function in the cycle-specific of chemotherapy. Math. Model. Nat. Phenom. 2021, 16, 14. [Google Scholar] [CrossRef]
- Ganji, R.; Jafari, H.; Moshokoa, S.; Nkomo, N. A mathematical model and numerical solution for brain tumour derived using fractional operator. Results Phys. 2021, 28, 104671. [Google Scholar] [CrossRef]
- Özköse, F.; Yilmaz, S.; Yavuz, M.; Öztürk, I.; Tamerşenel, M.; Bağcı, B.c.; Dogan, M.; Önal, O. A Fractional Modelling of Tumour-Immune System Interaction Related to Lung Cancer with Real Data. Eur. Phys. J. Plus 2021, 137, 40. [Google Scholar] [CrossRef]
- Lawson, J.; Levere, K.M. Comparison of Fractional-Order and Integer-Order Cancer Tumour Growth Models: An Inverse Approach. In Recent Developments in Mathematical, Statistical and Computational Sciences, Proceedings of the V AMMCS International Conference, Waterloo, ON, Canada, 18–23 August 2019; Kilgour, D.M., Kunze, H., Makarov, R., Melnik, R., Wang, X., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 555–564. [Google Scholar]
- Tang, T.Q.; Shah, Z.; Rashid, J.; Alzahrani, E. Modelling the dynamics of tumour–immune cells interactions via fractional calculus. Eur. Phys. J. Plus 2022, 137, 367. [Google Scholar] [CrossRef]
| Estimated New Cases | |||||
| Males | Females | ||||
| Prostate | 268,490 | 27% | Breast | 287,850 | 31% |
| Lung and bronchus | 117,910 | 12% | Lung and bronchus | 118,830 | 13% |
| Colon and rectum | 80,690 | 8% | Colon and rectum | 70,340 | 8% |
| Urinary bladder | 61,700 | 6% | Uterine corpus | 65,950 | 7% |
| Melanoma of the skin | 57,180 | 6% | Melanoma of the skin | 42,600 | 5% |
| Kidney and renal pelvis | 50,290 | 5% | Non-Hodgkin lymphoma | 36,350 | 4% |
| Non-Hodgkin lymphoma | 44,120 | 4% | Thyroid | 31,940 | 3% |
| Oral cavity and pharynx | 38,700 | 4% | Pancreas | 29,240 | 3% |
| Leukaemia | 35,810 | 4% | Kidney and renal pelvis | 28,710 | 3% |
| Pancreas | 32,970 | 3% | Leukaemia | 24,840 | 3% |
| All Sites | 983,160 | 100% | All Sites | 934,870 | 100% |
| Estimated Deaths | |||||
| Males | Females | ||||
| Lung and bronchus | 68,820 | 21% | Lung and bronchus | 61,360 | 21% |
| Prostate | 34,500 | 11% | Breast | 43,250 | 15% |
| Colon and rectum | 28,400 | 9% | Colon and rectum | 24,180 | 8% |
| Pancreas | 25,970 | 8% | Pancreas | 23,860 | 8% |
| Liver and intrahepatic bile duct | 20,420 | 6% | Ovary | 12,810 | 4% |
| Leukaemia | 14,020 | 4% | Uterine corpus | 12,550 | 4% |
| Esophagus | 13,250 | 4% | Liver and intrahepatic bile duct | 10,100 | 4% |
| Urinary bladder | 12,120 | 4% | Leukaemia | 9980 | 3% |
| Non-Hodgkin lymphoma | 11,700 | 4% | Non-Hodgkin lymphoma | 8550 | 3% |
| Brain and other nervous system | 10,710 | 3% | Brain and other nervous system | 7570 | 3% |
| All Sites | 322,090 | 100% | All Sites | 287,270 | 100% |
| Year | Title | Type of Cancer | Treatment | Fractional Operator | Ref. |
|---|---|---|---|---|---|
| 2014 | A fractional diffusion equation model for cancer tumour | Not specified | Not specified | Caputo | [125] |
| 2014 | Numerical simulation of fractional bioheat equation in hyperthermia treatment | Not specified | Hyperthermia | Caputo | [126] |
| 2016 | Dynamics of tumour-immune system with fractional-order | Not specified | Immunotherapy | Caputo | [127] |
| 2016 | Modelling doxorubicin effect in various cancer therapies by means of fractional calculus | Not specified | Chemotherapy | Grünwald–Letnikov | [128] |
| 2017 | Numerical simulation of time fractional dual-phase-lag model of heat transfer within skin tissue during thermal therapy | Not specified | Hyperthermia | Caputo | [129] |
| 2018 | New observations on optimal cancer treatments for a fractional tumour growth model with and without singular kernel | Obesity-associated cancer | Chemotherapy, Immunotherapy and Combined | Caputo and Caputo–Fabrizio | [71] |
| 2018 | Variable order fractional derivatives and bone remodelling in the presence of metastases | Not specified | Chemotherapy | Grünwald–Letnikov | [130] |
| 2019 | A new fractional model for the cancer treatment by radiotherapy using the Hadamard fractional derivative | Not specified | Radiotherapy | Hadamard | [131] |
| 2019 | Numerical solutions for time-fractional cancer invasion system with nonlocal diffusion | Not specified | — | Caputo | [120] |
| 2019 | Stability analysis and numerical simulations via fractional calculus for tumour dormancy models | Not specified | — | Caputo | [132] |
| 2019 | A study on discrete and discrete fractional pharmacokinetics pharmacodynamics models of tumour growth and anti-cancer effects | Colon carcinoma | Not specified | Rieman–Liouville | [133] |
| 2020 | On multistep tumour growth models of fractional variable-order | Breast cancer | — | Caputo | [121] |
| 2020 | Can fractional calculus help improve tumour growth models? | Breast cancer | — | Caputo | [56] |
| 2020 | Mathematical modelling of cancer and hepatitis co-dynamics with non-local and non-singular kernel | Co-infection of cancer & hepatitis | — | ABC | [134] |
| 2020 | Mathematical modelling of radiotherapy cancer treatment using Caputo fractional derivative | Uterine cervical cancer | Radiotherapy | Caputo | [135] |
| 2021 | Memory effects on the proliferative function in the cycle-specific of chemotherapy | Breast & ovarian cancer | Chemotherapy | Caputo | [136] |
| 2021 | A mathematical model and numerical solution for brain tumour derived using fractional operator | Glioblastoma | Chemotherapy and Surgery | Caputo | [137] |
| 2021 | A fractional modelling of tumour-immune system interaction related to lung cancer with real data | Lung cancer | — | Caputo | [138] |
| 2021 | Comparison of fractional-order and integer-order cancer tumour growth models: an inverse approach | Prostate cancer | Chemotherapy | Caputo | [139] |
| 2022 | Modelling and analysis of breast cancer with adverse reactions of chemotherapy treatment through fractional derivative | Breast cancer | Chemotherapy | Caputo–Fabrizio | [124] |
| 2022 | The dynamics of a fractional-order mathematical model of cancer tumour disease | Not specified | Chemotherapy | Caputo | [123] |
| 2022 | Modelling the dynamics of tumour-immune cells interactions via fractional calculus | Not specified | Immunotherapy | Caputo | [140] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, L.C.; Costa, R.S.; Valério, D. An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool. Fractal Fract. 2023, 7, 595. https://doi.org/10.3390/fractalfract7080595
Vieira LC, Costa RS, Valério D. An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool. Fractal and Fractional. 2023; 7(8):595. https://doi.org/10.3390/fractalfract7080595
Chicago/Turabian StyleVieira, Lourenço Côrte, Rafael S. Costa, and Duarte Valério. 2023. "An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool" Fractal and Fractional 7, no. 8: 595. https://doi.org/10.3390/fractalfract7080595
APA StyleVieira, L. C., Costa, R. S., & Valério, D. (2023). An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool. Fractal and Fractional, 7(8), 595. https://doi.org/10.3390/fractalfract7080595







