Dynamic of Some Relapse in a Giving Up Smoking Model Described by Fractional Derivative
Abstract
1. Introduction
2. Preliminary
- -
- The Riemann–Liouville fractional integral of order is defined bywhere is the order of integration, and is the gamma function.
- -
- The Caputo fractional derivatives of order are defined aswhere , with being the integer part of .
- -
- The Caputo derivative and the Riemann–Liouville integral satisfy the following properties:
- (a)
- .
- (b)
- , where .
- (c)
- .
- (d)
- If is such that , then .
3. Mathematical Modeling of a Giving Up Smoking Model
4. Mathematical Analysis
4.1. Existence and Uniqueness
4.2. Non-Negative Solutions
- If , then the function f is nondecreasing for all .
- If , then the function f is nonincreasing for all .
4.3. Equilibrium and Smokers Generation Number
- If , then , which gives and ; then there is no positive solution.
- If , then . Consequently, , so we obtain one positive solution
- If , then ; if, in addition, , then there is no positive solution. However, we can write A asThen, to ensure that A remains positive, we take ; that is, .
4.4. Local Stability for the Free Smoker Equilibrium Point
4.5. Local Stability for the Present Equilibrium Point
4.6. Global Stability
5. Numerical Simulations and Discussions
Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. WHO Report on the Global Tobacco Epidemic, 2008: The MPOWER Package; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Anjam, Y.N.; Shafqat, R.; Sarris, I.E.; Rahman, M.U.; Touseef, S.; Arshad, M. A fractional order investigation of smoking model using caputo-fabrizio differential operator. Fractal Fract. 2022, 6, 623. [Google Scholar] [CrossRef]
- Rezapour, S.; Etemad, S.; Sinan, M.; Alzabut, J.; Vinodkumar, A. A mathematical analysis on the new fractal-fractional model of second-hand smokers via the power law type kernel: Numerical solutions, equilibrium points, and sensitivity analysis. J. Funct. Spaces 2022, 2022, 3553021. [Google Scholar] [CrossRef]
- Hecht, S.S. Cigarette smoking: Cancer risks, carcinogens, and mechanisms. Langenbeck’s Arch. Surg. 2006, 391, 603–613. [Google Scholar] [CrossRef]
- Castillo-Garsow, C.; Jordan-Salivia, G.; Rodriguez-Herrera, A. Mathematical Models for the Dynamics of Tobacco Use, Recovery and Relapse. 1997. Available online: https://www.semanticscholar.org/paper/Mathematical-Models-for-the-Dynamics-of-Tobacco-and-Castillo-Garsow-Jordan-Salivia/d29de75a1ea86e9b7649e65070431c4dd78a96c0 (accessed on 11 June 2023).
- Zaman, G. Optimal campaign in the smoking dynamics. Comput. Math. Methods Med. 2011, 2011, 163834. [Google Scholar] [CrossRef]
- Rahman, G.u.; Agarwal, R.P.; Din, Q. Mathematical analysis of giving up smoking model via harmonic mean type incidence rate. Appl. Math. Comput. 2019, 354, 128–148. [Google Scholar] [CrossRef]
- Huo, H.; Zhu, C. Influence of relapse in a giving up smoking model. Abstr. Appl. Anal. 2013, 2013, 525461. [Google Scholar] [CrossRef]
- de Barros, L.C.; Lopes, M.M.; Pedro, F.S.; Esmi, E.a.; Santos, J.P.C.d.; Sánchez, D.E. The memory effect on fractional calculus: An application in the spread of COVID-19. Comput. Appl. Math. 2021, 40, 72. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Zaman, G.; Momani, S. A numeric–analytic method for approximating a giving up smoking model containing fractional derivatives. Comput. Math. Appl. 2012, 64, 3065–3074. [Google Scholar] [CrossRef]
- Lubin, J.H.; Caporaso, N.E. Cigarette smoking and lung cancer: Modeling total exposure and intensity. Cancer Epidemiol. Biomarkers Prev. 2006, 15, 517–523. [Google Scholar] [CrossRef] [PubMed]
- Alkhudhari, Z.; Al-Sheikh, S.; Al-Tuwairqi, S. Global dynamics of a mathematical model on smoking. Int. Sch. Res. Not. 2014, 2014, 847075. [Google Scholar] [CrossRef]
- Khalid, M.; Khan, F.S.; Iqbal, A. Perturbation-iteration algorithm to solve fractional giving up smoking mathematical model. Int. J. Comput. Appl. 2016, 142, 975–8887. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Qurashi, M.A.; Baleanu, D. A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, 2017, 88. [Google Scholar] [CrossRef]
- Ahmad, A.; Farman, M.; Ghafar, A.; Inc, M.; Ahmad, M.O.; Sene, N. Analysis and simulation of fractional order smoking epidemic model. Comput. Math. Methods Med. 2022, 2022, 9683187. [Google Scholar] [CrossRef] [PubMed]
- Addai, E.; Zhang, L.; Asamoah, J.K.K.; Essel, J.F. A fractional order age-specific smoke epidemic model. Appl. Math. Model. 2023, 119, 99–118. [Google Scholar] [CrossRef]
- Addai, E.; Adeniji, A.; Peter, O.J.; Agbaje, J.O.; Oshinubi, K. Dynamics of age-structure smoking models with government intervention coverage under fractal-fractional order derivatives. Fractal Fract. 2023, 7, 370. [Google Scholar] [CrossRef]
- Zeb, A.; Kumar, S.; Saeed, T. A robust computational dynamics of fractional-order smoking model with relapse habit. Fractals 2022, 30, 2240034. [Google Scholar] [CrossRef]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 1999, 198, 340. [Google Scholar]
- Sumeyr, U.; Esmehan, U.; Necati, O.; Zakia, H. Mathematical analysis and numerical simulation for smoking model with atangana-baleanu derivative. Chaos Solitons Fractals 2019, 118, 300–306. [Google Scholar]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Almeida, R.; Artur, M.C.; Natalia, M.; Teresa, M. An epidemiological mseir model desribed by the caputo fractional derivative. Int. J. Dyn. Control. 2019, 7, 776–784. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosiences 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963. [Google Scholar]
- Li, H.; Muhammadhaji, A.; Zhang1, L.; Teng1, Z. Stability analysis of a fractional-order predator–prey model incorporating a constant prey refuge and feedback control. Adv. Differ. Equ. 2018, 2018, 325. [Google Scholar] [CrossRef]
- David, R.M. Introduction to the Theory of Stability; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Vargas de León, C. Volterra-type lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duate-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
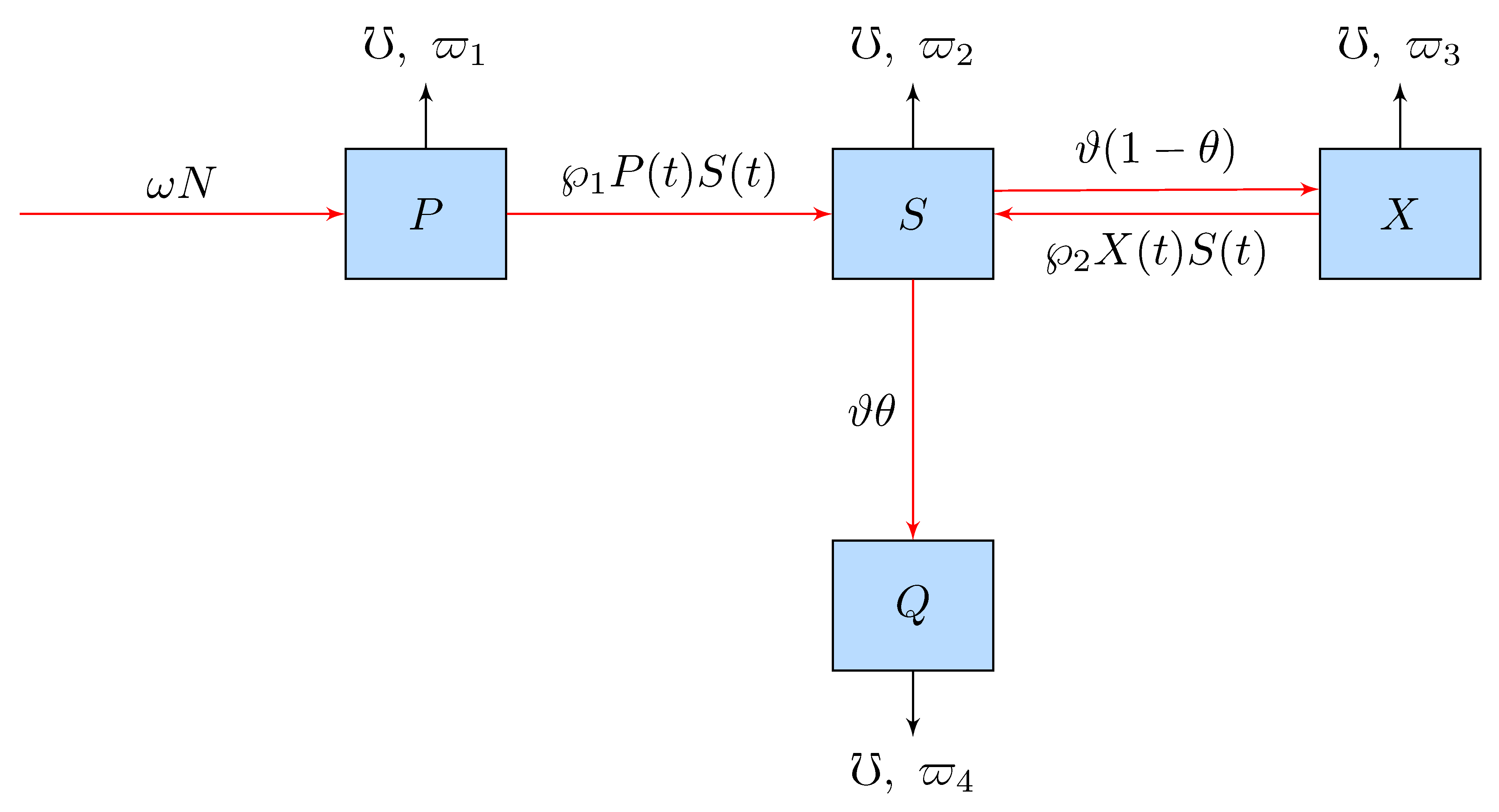


| Parameter | Description |
|---|---|
| The overall recruits number into the considered homogeneously mixed population. | |
| The rate of spread from potential to persistent smokers. | |
| The relapse rate of temporally recovered smokers who contact persistent smokers. | |
| The rate of smokers who temporarily stop. | |
| The rate of people who have successfully stopped smoking. | |
| ℧ | The natural rate of mortality. |
| The mortality rate from smoking. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alalhareth, F.K.; Boudaoui, A.; El hadj Moussa, Y.; Laksaci, N.; Alharbi, M.H. Dynamic of Some Relapse in a Giving Up Smoking Model Described by Fractional Derivative. Fractal Fract. 2023, 7, 543. https://doi.org/10.3390/fractalfract7070543
Alalhareth FK, Boudaoui A, El hadj Moussa Y, Laksaci N, Alharbi MH. Dynamic of Some Relapse in a Giving Up Smoking Model Described by Fractional Derivative. Fractal and Fractional. 2023; 7(7):543. https://doi.org/10.3390/fractalfract7070543
Chicago/Turabian StyleAlalhareth, Fawaz K., Ahmed Boudaoui, Yacine El hadj Moussa, Noura Laksaci, and Mohammed H. Alharbi. 2023. "Dynamic of Some Relapse in a Giving Up Smoking Model Described by Fractional Derivative" Fractal and Fractional 7, no. 7: 543. https://doi.org/10.3390/fractalfract7070543
APA StyleAlalhareth, F. K., Boudaoui, A., El hadj Moussa, Y., Laksaci, N., & Alharbi, M. H. (2023). Dynamic of Some Relapse in a Giving Up Smoking Model Described by Fractional Derivative. Fractal and Fractional, 7(7), 543. https://doi.org/10.3390/fractalfract7070543









