Co-Dynamics of COVID-19 and Viral Hepatitis B Using a Mathematical Model of Non-Integer Order: Impact of Vaccination
Abstract
1. Introduction
Preliminaries
2. Model Formulation
2.1. Basic Reproduction Number
2.2. Local Asymptotic Stability of System (1)
3. Existence and Uniqueness of the Fractional Model’s Solution
4. Ulam–Hyers (UH) Stability
- i.
- .
- ii.
- ,.
5. Numerical Schemes and Simulations
5.1. Numerical Simulations
6. Conclusions
- (i.)
- The basic analysis/properties of the fractional-order system (1) are investigated.
- (ii.)
- The derivation of appropriate conditions for the existence of a unique solution of the formulated fractional-order system is carried out in Section 3, with the help of Theorem 2.
- (iii.)
- Stability analyses of the formulated model in the framework of Ulam–Hyers are discussed in Section 4, with the help of Theorem 3.
- (iv.)
- (i.)
- (ii.)
- The 3D plots of the COVID-19-associated reproduction number as a function of the transmission rate and vaccination parameters are presented in Figure 2a,b, respectively. It was observed from both figures that an increase in the transmission rate results in a subsequent rise in the value of the reproduction number, as expected. However, from Figure 2a, it is noticed that increasing the COVID-19 vaccination rate causes a decrease in the reproduction number, and also in the disease burden within the population. However, increasing the vaccine inefficacy causes an increase in the reproduction number, as observed in Figure 2b.
- (iii.)
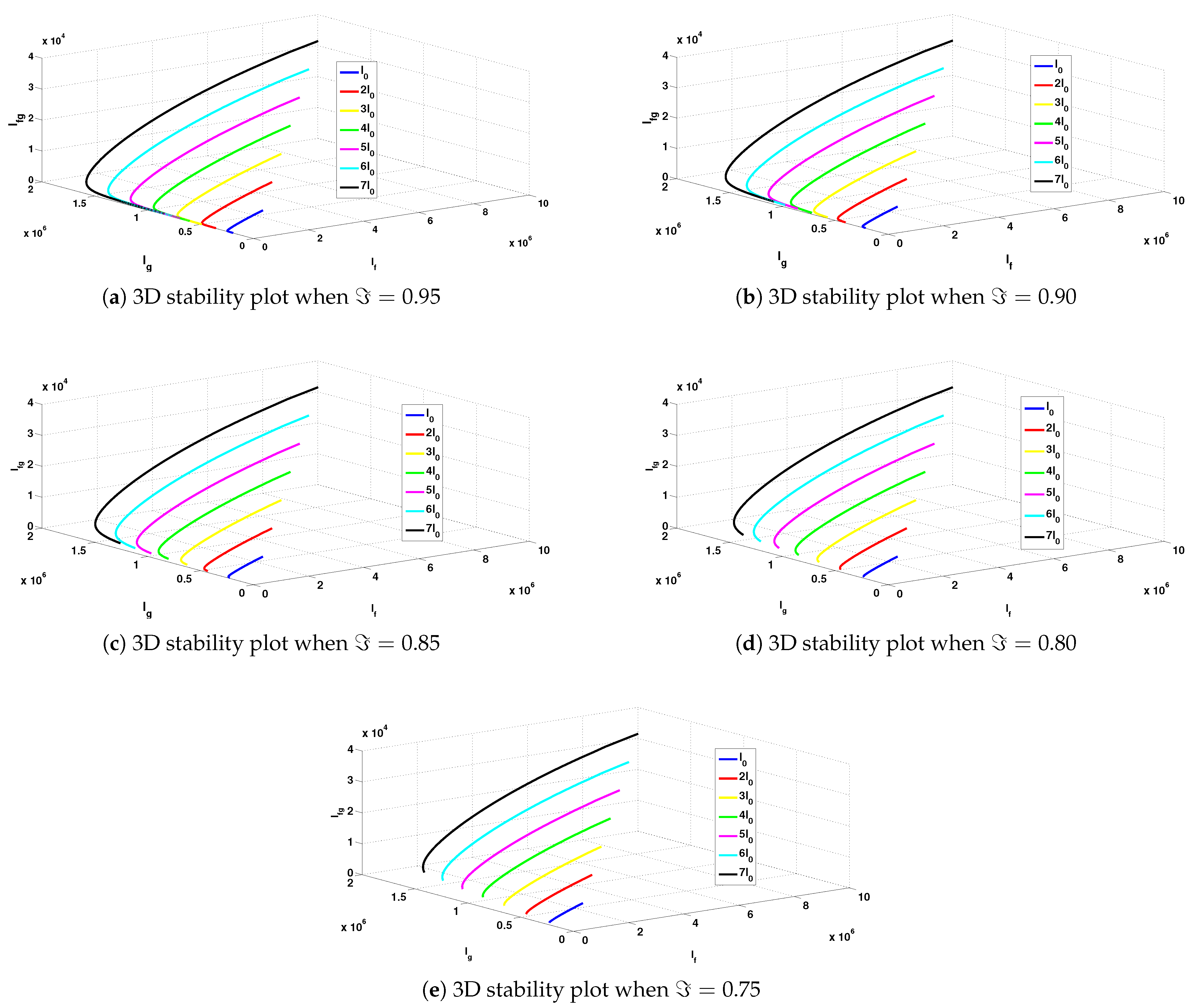
- The different trajectories for the epidemiological states at various orders of the derivative, when the reproduction number , are presented in Figure 3a–i. It was observed that the trajectory diagrams tend towards the infection-free steady state. Phase portraits confirming the behavior of the infected components of the model are also depicted in Figure 4a–e. One important observation from these figures is that for different initial conditions assumed for the disease classes, their trajectories still point towards the infection-free steady states over the passage of time, regardless of the order of the fractional derivative. These results also confirm the local asymptotic stability and the Ulam–Hyers stability results established in Section 2.2 and Section 4, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Theorem 3
References
- Johns Hopkins Coronavirus Resource Center [Internet]. Available online: https://coronavirus.jhu.edu/map.html (accessed on 19 February 2023).
- Tao, Y.; Jiang, J.; Yan, L.; Wang, C.; Ding, Y.; Yu, J.; Zhao, D.; Chi, X.; Wang, X.; Wu, R.; et al. Epidemiological study of hepatitis B and hepatitis C infections in Northeastern China and the beneficial effect of the vaccination strategy for hepatitis B: A cross-sectional study. BMC Public Health 2018, 18, 1088. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. About Global Hepatitis B [Internet]. Available online: https://www.cdc.gov/globalhealth/immunization/diseases/hepatitis-b/about/index.html (accessed on 19 February 2023).
- Vos, T.; Flaxman, A.D.; Naghavi, M.; Lozano, R.; Michaud, C.; Ezzati, M.; Shibuya, K.; Salomon, J.A.; Abdalla, S.; Aboyans, V.; et al. Years lived with disability (YLDs) for 1160 sequelae of 289 diseases and injuries 1990–2010: A systematic analysis for the global burden of disease study 2010. Lancet 2012, 380, 2163–2196. [Google Scholar] [CrossRef] [PubMed]
- Lozano, R.; Naghavi, M.; Foreman, K.; Lim, S.; Shibuya, K.; Aboyans, V.; Abraham, J.; Adair, T.; Aggarwal, R.; Ahn, S.Y.; et al. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: A systematic analysis for the global burden of disease study 2010. Lancet 2012, 380, 2095–2128. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Bi, S.; Yang, W.; Wang, L.; Cui, G.; Cui, F.; Zhang, Y.; Liu, J.; Gong, X.; Chen, Y.; et al. Epidemiological serosurvey of hepatitis B in China–declining HBV prevalence due to hepatitis B vaccination. Vaccine 2009, 27, 6550–6557. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, A.M.; Moghadami, M.; Seif, M.; Mirahmadizadeh, A. Association of Routine Hepatitis B Vaccination and Other Effective Factors with Hepatitis B Virus Infection: 25 Years Since the Introduction of National Hepatitis B Vaccination in Iran. Iran. J. Med. Sci. 2021, 46, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Yousafzai, M.T.; Qasim, R.; Khalil, R.; Kakakhel, M.F.; Rehman, S.U. Hepatitis B vaccination among primary health care workers in Northwest Pakistan. Int. J. Health Sci. 2014, 8, 67–76. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, L.; Wang, F.S. Liver injury in COVID-19: Management and challenges. Lancet Gastroenterol. Hepatol. 2020, 5, 428–430. [Google Scholar] [CrossRef]
- McGill COVID-19 Vaccine Tracker [Internet]. Available online: https://covid19.trackvaccines.org/ (accessed on 19 February 2023).
- Mohammed, I.; Nauman, A.; Paul, P.; Ganesan, S.; Chen, K.H.; Jalil, S.M.S.; Jaouni, S.H.; Kawas, H.; Khan, W.A.; Vattoth, A.L.; et al. The efficacy and effectiveness of the COVID-19 vaccines in reducing infection, severity, hospitalization, and mortality: A systematic review. Hum. Vaccin Immunother. 2022, 18, 2027160. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, X.; Zhou, Y.H. Hepatitis B vaccine development and implementation. Hum. Vaccin Immunother. 2020, 16, 1533–1544. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, F.Z.; Zhang, G.M.; Cui, F.Q.; Wu, Z.H.; Miao, N.; Sun, X.J.; Liang, X.F.; Li, L. An economic analysis of adult hepatitis B vaccination in China. Vaccine 2015, 33, 6831–6839. [Google Scholar] [CrossRef]
- Rihan, F.A.; Baleanu, D.; Lakshmanan, S.; Rakkiyappan, R. On Fractional SIRC Model with Salmonella Bacterial Infection. Abstr. Appl. Anal. 2014, 2014, 136263. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical Modeling of Fractional-Order Biological Systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef]
- Asamoah, J.K.K. Fractal-fractional model and numerical scheme based on Newton polynomial for Q fever disease under Atangana-Baleanu derivative. Results Phys. 2022, 34, 105189. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–3. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and applications to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Baleanu, D.; Abadi, M.H.; Jajarmi, A.; Vahid, K.Z.; Nieto, J.J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Vahid, K.Z.; Mobayen, S. A general fractional formulation and tracking control for immunogenic tumor dynamics. Math. Methods Appl. Sci. 2022, 45, 667–680. [Google Scholar]
- Chu, Y.-M.; Zarin, R.; Khan, A.; Murtaza, S. A vigorous study of fractional order mathematical model for SARS-CoV-2 epidemic with Mittag-Leffler kernel. Alex. Eng. J. 2023, 71, 565–579. [Google Scholar] [CrossRef]
- Gul, N.; Bilal, R.; Algehyne, E.A.; Alshehri, M.G.; Khan, M.A.; Chu, Y.-M.; Islam, S. The dynamics of fractional order Hepatitis B virus model with asymptomatic carriers. Alex. Eng. J. 2021, 60, 3945–3955. [Google Scholar] [CrossRef]
- Shen, W.-Y.; Chu, Y.-M.; ur Rahman, M.; Mahariq, I.; Zeb, A. Mathematical analysis of HBV and HCV co-infection model under nonsingular fractional order derivative. Results Phys. 2021, 28, 104582. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Onyenegecha, C.P. A fractional order model for the co-interaction of COVID-19 and Hepatitis B virus. Results Phys. 2022, 37, 105498. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M. Modeling SARS-CoV-2 and HBV co-dynamics with optimal control. Phys. A 2023, 615, 128607. [Google Scholar] [CrossRef] [PubMed]
- Din, A.; Li, Y.; Omame, A. A stochastic stability analysis of a HBV-COVID-19 co-infection model in resource limitation settings. Waves Random Complex Media 2022, 1–33. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- [Internet]. Available online: https://www.indexmundi.com/pakistan/demographics_profile.html (accessed on 19 February 2023).
- Din, A.; Li, Y.; Yusuf, A. Delayed hepatitis B epidemic model with stochastic analysis. Chaos Solitons Fractals 2021, 146, 110839. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Din, A. Global asymptotic stability, extinction and ergodic stationary distribution in a stochastic model for dual variants of SARS-CoV-2. Math. Comput. Simul. 2023, 204, 302–336. [Google Scholar] [CrossRef]
- Nanduri, S.; Pilishvili, T.; Derado, G.; Soe, M.M.; Dollard, P.; Wu, H.; Li, Q.; Bagchi, S.; Dubendris, H.; Link-Gelles, R.; et al. Effectiveness of Pfizer-BioNTech and Moderna Vaccines in Preventing SARS-CoV-2 Infection among Nursing Home Residents before and during Widespread Circulation of the SARS-CoV-2 B.1.617.2 (Delta) Variant—National Healthcare Safety Network, March 1–August 1, 2021. Morb. Mortal. Wkly Rep. 2021, 70, 1163–1166. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishers: New York, NY, USA, 1960. [Google Scholar]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Pakistan: Coronavirus Pandemic Country Profile. [Internet]. [cited 2023 February 19]. Available online: https://ourworldindata.org/coronavirus/country/pakistan (accessed on 11 January 2023).
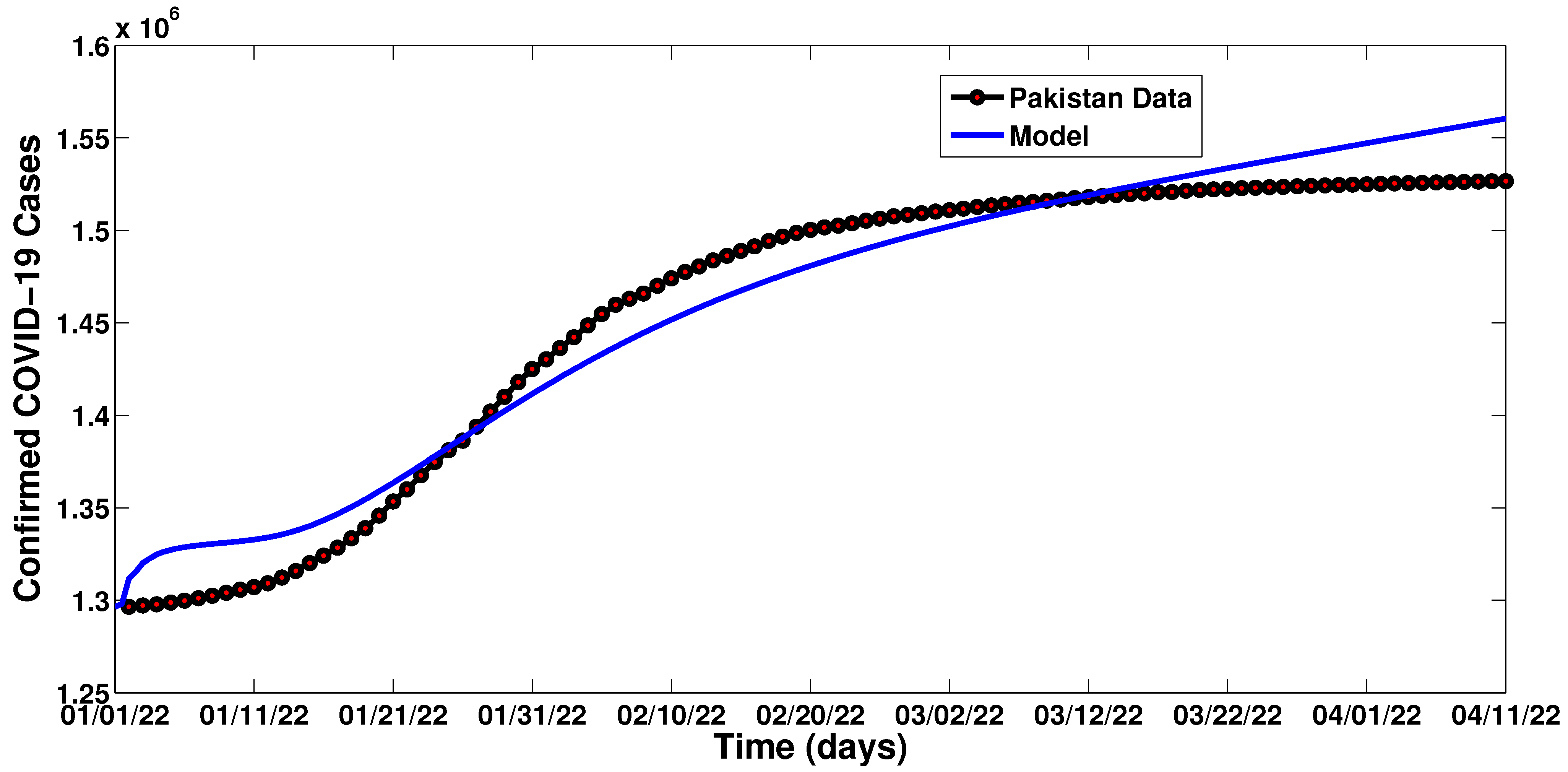





| Parameter | Description | Value | Reference |
|---|---|---|---|
| COVID-19 transmission rate | 0.0237 | Fitted | |
| Viral hepatitis B transmission rate | 0.7571 | Fitted | |
| Recruitment rate into the population | day | [30] | |
| Natural death rate | day | [30] | |
| COVID-19 recovery rate | day | [26] | |
| Viral hepatitis B recovery rate | day | [31] | |
| Recovery rate for co-infected persons | [26] | ||
| COVID-19-induced death rate | 0.0020 | Fitted | |
| Viral hepatitis B induced death rate | 0.05 | [31] | |
| Co-infection death rate | 0.05 | [26] | |
| COVID-19 primary vaccination rate | 0.0015 | Assumed | |
| Viral hepatitis B primary vaccination rate | 0.0100 | Assumed | |
| COVID-19 booster vaccination rate | 0.9998 | Assumed | |
| Viral hepatitis B booster vaccination rate | 0.0010 | Assumed | |
| Waning immunity due to COVID-19 vaccination | 0.010–0.015 | [32] | |
| Waning immunity due to viral hepatitis B vaccination | 0.010–0.015 | Assumed | |
| COVID-19 vaccine inefficacy rate | (1–0.85) | [33] | |
| Viral hepatitis B vaccine inefficacy rate | (1–0.85) | [31] | |
| Modification parameter for vulnerability to a second infection | 0.15 | Assumed |
| Date (January) | Cases | Date (February) | Cases | Date (March) | Cases | Date (April) | Cases |
|---|---|---|---|---|---|---|---|
| 01/01/2022 | 1,296,527 | 01/02/2022 | 1,436,413 | 01/03/2022 | 1,510,986 | 01/04/2022 | 1,525,181 |
| 02/01/2022 | 1,297,235 | 01/02/2022 | 1,442,263 | 02/03/2022 | 1,511,754 | 02/04/2022 | 1,525,466 |
| 03/01/2022 | 1,297,865 | 03/02/2022 | 1,448,663 | 03/03/2022 | 1,512,707 | 03/04/2022 | 1,525,620 |
| 04/01/2022 | 1,298,763 | 04/02/2022 | 1,454,800 | 04/03/2022 | 1,513,503 | 04/04/2022 | 1,525,775 |
| 05/01/2025 | 1,299,848 | 05/02/2022 | 1,459,773 | 05/03/2022 | 1,514,258 | 05/04/2022 | 1,525,923 |
| 06/01/2022 | 1,301,141 | 06/02/2022 | 1,463,111 | 06/03/2022 | 1,515,014 | 06/04/2022 | 1,526,093 |
| 07/01/2022 | 1,302,486 | 07/02/2022 | 1,465,910 | 07/03/2022 | 1,515,392 | 07/04/2022 | 1,526,234 |
| 08/01/2022 | 1,304,058 | 08/02/2022 | 1,470,161 | 08/03/2022 | 1,516,150 | 08/04/2022 | 1,526,472 |
| 09/01/2022 | 1,305,707 | 09/02/2022 | 1,474,075 | 09/03/2022 | 1,516,789 | 09/04/2022 | 1,526,568 |
| 10/01/2022 | 1,307,174 | 10/02/2022 | 1,477,573 | 10/03/2022 | 1,517,512 | 10/04/2022 | 1,526,666 |
| 11/01/2022 | 1,309,248 | 11/02/2022 | 1,480,592 | 11/03/2022 | 1,518,083 | ||
| 12/01/2022 | 1,312,267 | 12/02/2022 | 1,483,798 | 12/03/2022 | 1,518,692 | ||
| 13/01/2022 | 1,315,834 | 13/02/2022 | 1,486,361 | 13/03/2022 | 1,519,154 | ||
| 14/01/2022 | 1,320,120 | 14/02/2022 | 1,488,958 | 14/03/2022 | 1,519,627 | ||
| 15/01/2022 | 1,324,147 | 15/02/2022 | 1,491,423 | 15/03/2022 | 1,520,120 | ||
| 16/01/2022 | 1,328,487 | 16/02/2022 | 1,494,293 | 16/03/2022 | 1,520,634 | ||
| 17/01/2022 | 1,333,521 | 17/02/2022 | 1,496,693 | 17/03/2022 | 1,520,817 | ||
| 18/01/2022 | 1,338,993 | 18/02/2022 | 1,498,676 | 18/03/2022 | 1,521,513 | ||
| 19/01/2022 | 1,345,801 | 19/02/2022 | 1,500,320 | 19/03/2022 | 1,521,888 | ||
| 20/01/2025 | 1,353,479 | 20/02/2022 | 1,501,680 | 20/03/2022 | 1,522,191 | ||
| 21/01/2022 | 1,360,019 | 21/02/2022 | 1,502,641 | 21/03/2022 | 1,522,419 | ||
| 22/01/2022 | 1,367,605 | 22/02/2022 | 1,503,873 | 22/03/2022 | 1,522,862 | ||
| 23/01/2022 | 1,374,800 | 23/02/2022 | 1,505,328 | 23/03/2022 | 1,523,072 | ||
| 24/01/2022 | 1,381,152 | 24/02/2022 | 1,506,450 | 24/03/2022 | 1,523,401 | ||
| 25/01/2022 | 1,386,348 | 25/02/2022 | 1,507,657 | 25/03/2022 | 1,523,590 | ||
| 26/01/2022 | 1,393,887 | 26/02/2022 | 1,508,504 | 26/03/2022 | 1,523,900 | ||
| 27/01/2022 | 1,402,070 | 27/02/2022 | 1,509,360 | 27/03/2022 | 1,524,086 | ||
| 28/01/2022 | 1,410,033 | 28/02/2022 | 1,510,221 | 28/03/2022 | 1,524,355 | ||
| 29/01/2022 | 1,417,991 | 29/03/2022 | 1,524,549 | ||||
| 30/01/2022 | 1,425,039 | 30/03/2022 | 1,524,793 | ||||
| 31/01/2022 | 1,430,366 | 31/03/2022 | 1,524,973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omame, A.; Onyenegecha, I.P.; Raezah, A.A.; Rihan, F.A. Co-Dynamics of COVID-19 and Viral Hepatitis B Using a Mathematical Model of Non-Integer Order: Impact of Vaccination. Fractal Fract. 2023, 7, 544. https://doi.org/10.3390/fractalfract7070544
Omame A, Onyenegecha IP, Raezah AA, Rihan FA. Co-Dynamics of COVID-19 and Viral Hepatitis B Using a Mathematical Model of Non-Integer Order: Impact of Vaccination. Fractal and Fractional. 2023; 7(7):544. https://doi.org/10.3390/fractalfract7070544
Chicago/Turabian StyleOmame, Andrew, Ifeoma P. Onyenegecha, Aeshah A. Raezah, and Fathalla A. Rihan. 2023. "Co-Dynamics of COVID-19 and Viral Hepatitis B Using a Mathematical Model of Non-Integer Order: Impact of Vaccination" Fractal and Fractional 7, no. 7: 544. https://doi.org/10.3390/fractalfract7070544
APA StyleOmame, A., Onyenegecha, I. P., Raezah, A. A., & Rihan, F. A. (2023). Co-Dynamics of COVID-19 and Viral Hepatitis B Using a Mathematical Model of Non-Integer Order: Impact of Vaccination. Fractal and Fractional, 7(7), 544. https://doi.org/10.3390/fractalfract7070544









