Approximation of Aperiodic Signals Using Non-Integer Harmonic Series: The Generalized NAFASS Approach
Abstract
:1. Introduction
2. The Description of the Algorithm and Possible Generalizations
3. Results and Verification on Real Data
3.1. The Treatment of Economic Data
- S1. Calculation of the inoculating/seed frequencies forming the corresponding branches that are calculated with respect to iteration Formula (A5) (see Mathematical Appendix A) and have initially d = 1, 2 and 3 inoculating/seed frequencies. We also chose a reasonable value for the limiting frequency ΩK=50 that was sufficient for providing a fit with the calculated value of the relative error from expression (5), not exceeding 6.5%. These frequencies are shown in Figure 2.
- S2. The next step is the selection of the optimal frequency branch based on expression (5). The results of this procedure are illustrated by Figure 3 and Figure 4. As follows from Figure 4, the averaged frequency branch <Ωk> and the optimal frequency branch Ωk (obtained from criterion (5) and illustrated in Figure 3) cannot coincide with each other. Substitution of the optimal frequency branch Ωk allows the fitting of the initial random function for Al prices. It is obvious that the desired amplitudes from (1) are evaluated by the linear least square method (LLSM). The fit for this Al price distribution, realized in the frame of the hypothesis (1), is presented in Figure 5. Actually, these two steps solve the first problem mentioned above. Together with this fit, we also show the AFR in Figure 6. We should stress, here, that this AFR has different behavior and does not progress to the monotone decreasing of the amplitudes that is expected in the F-transformation and to providing the convergence of the corresponding Fourier series. This becomes sensitive to some parts of the trend that is observed for the initial Al prices analyzed and needs the specific analysis of an experienced expert who works professionally with economic data.
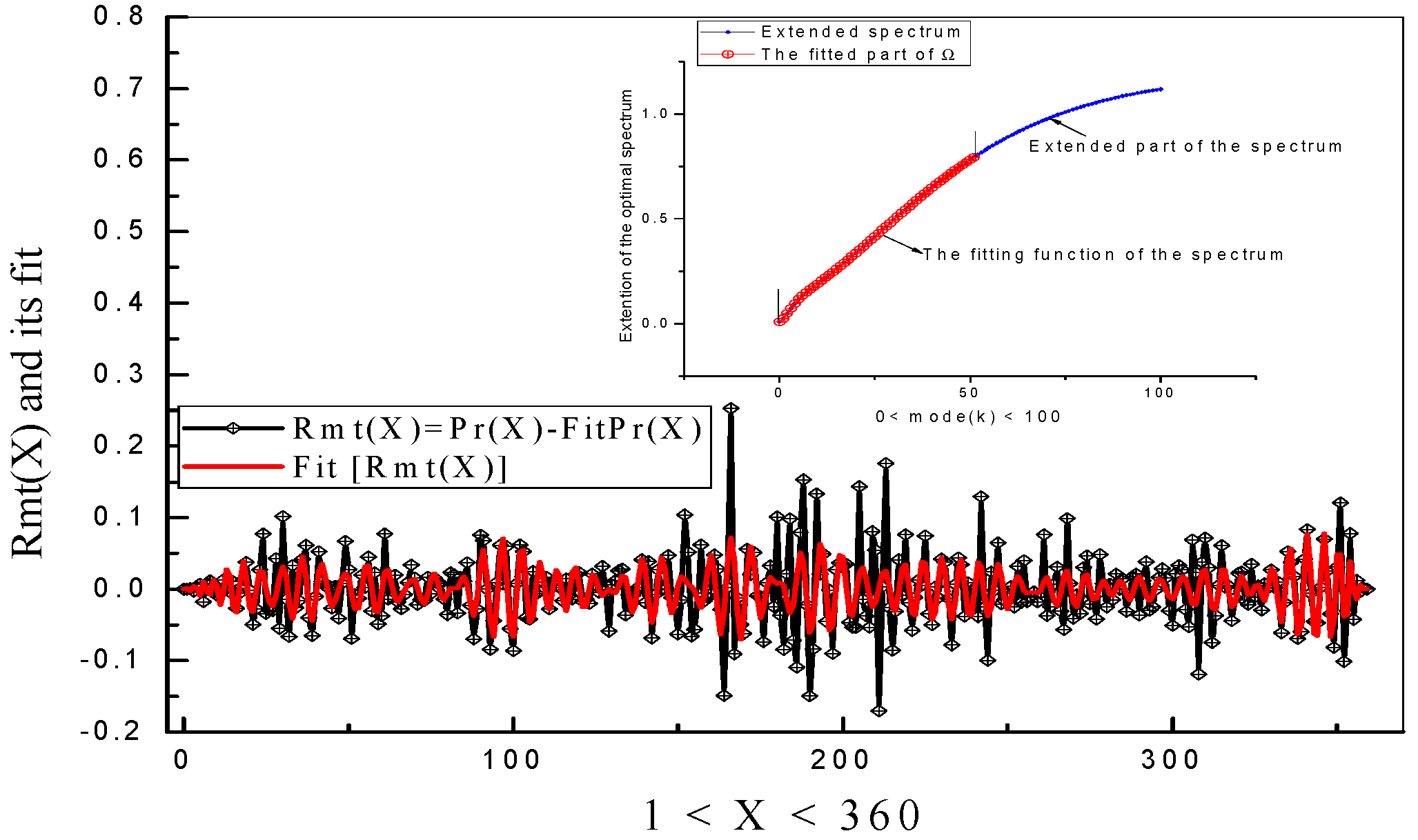
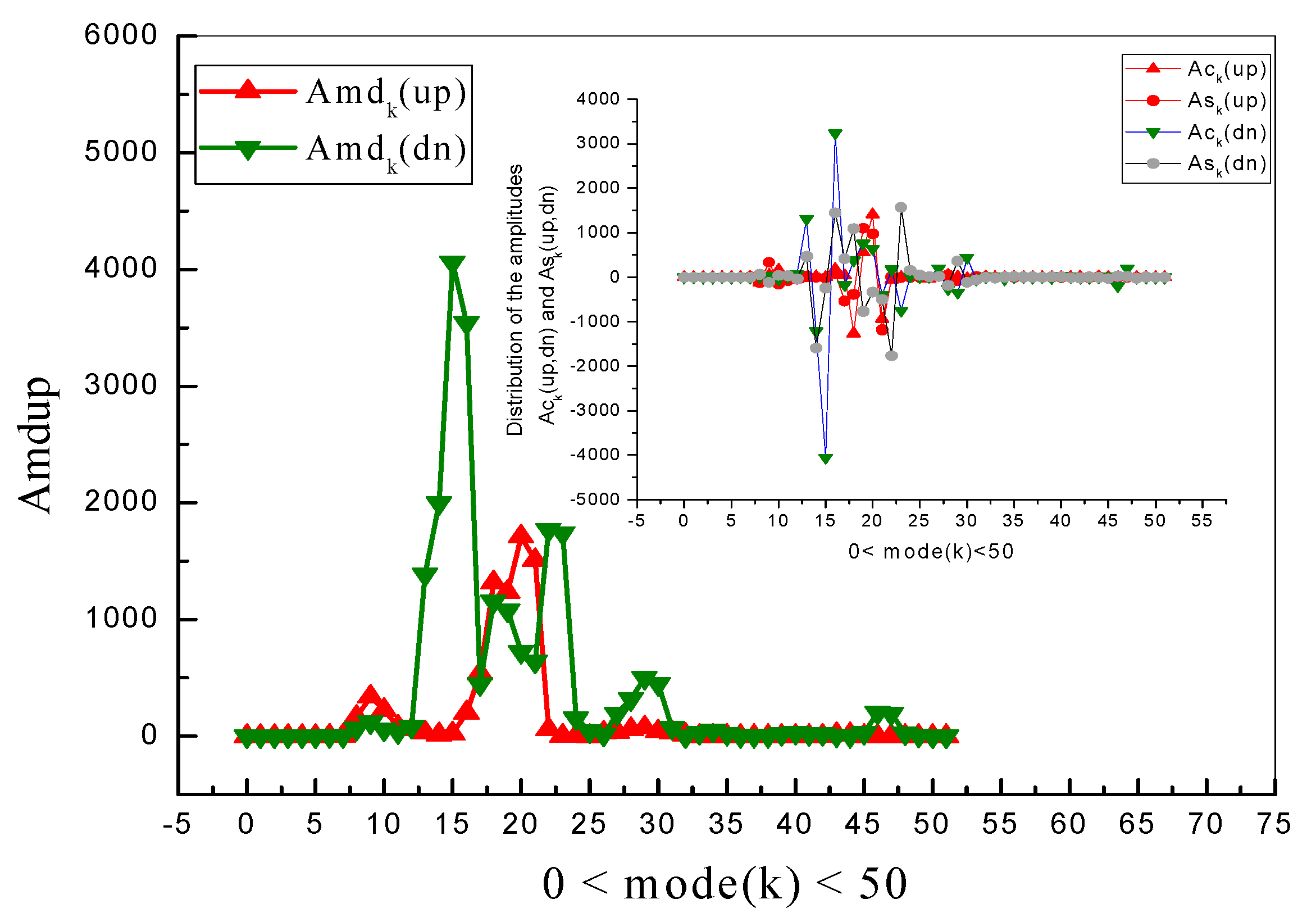
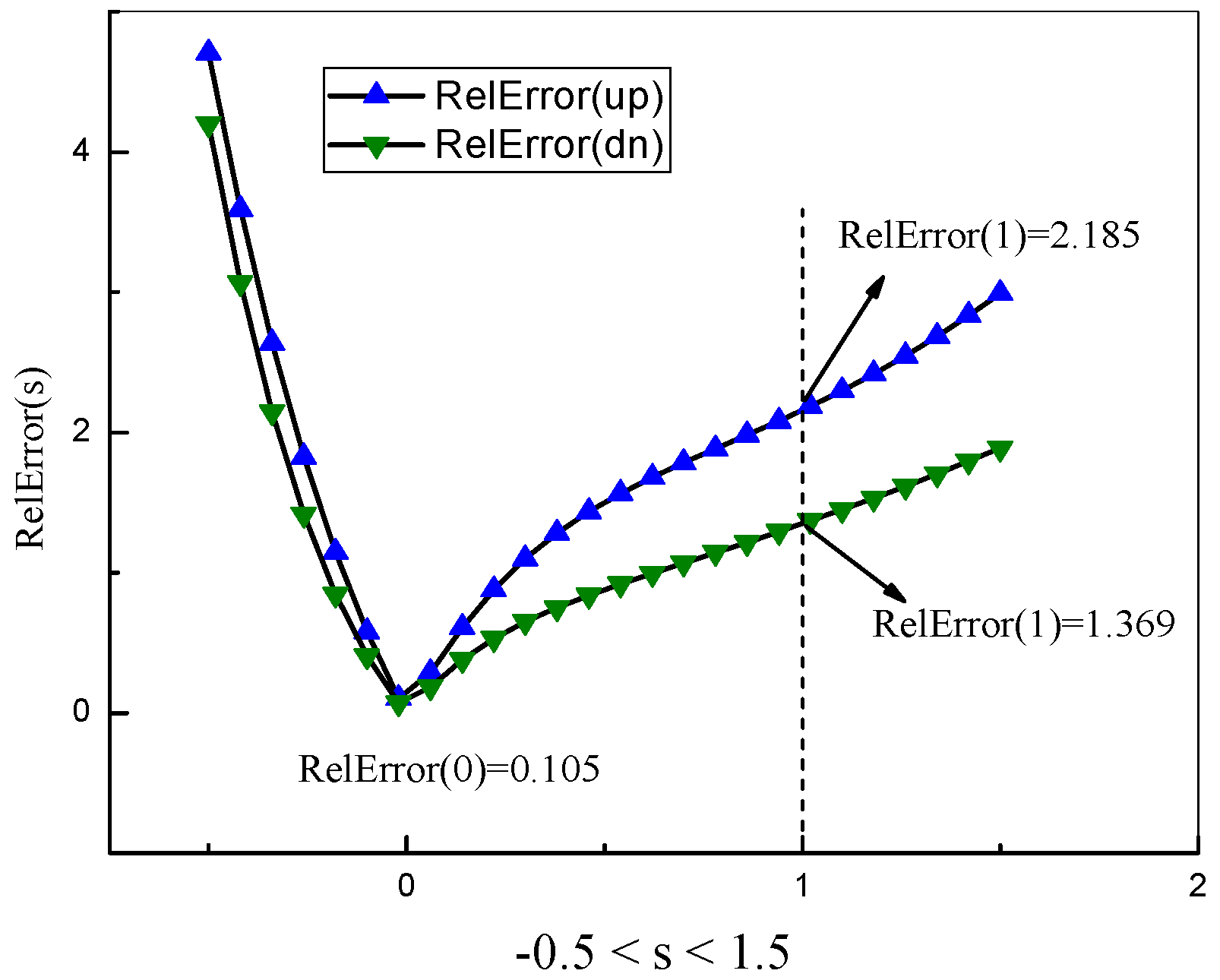
- S3. To solve the second problem, we formed the function (6) and calculated its relative error for a minimal value of p = 3. We also considered the case p = 2; however, for the same conditions, this case had a large value of the fitting error exceeding 7% and, therefore, we were forced to consider the case p = 3 as the most probable. In the behavior of the relative error, we expected that the case s = 1 would be optimal. This expectation was confirmed by our previous calculations, realized in [30]. However, to our deep amazement, this assumption was not confirmed for all four metals that were subjected to this analysis. The behavior of this function has the clearly expressed minimal value at s = 0, not s = 1! Earlier, for the results presented in paper [30], we did not have this criterion and we analyzed available data in the frame of an approximation corresponding to the linear hypothesis (2) with s = 1. Therefore, this key plot shown in Figure 7 confirms that for the available data analyzed, the hypothesis with s = 0 (expression (3)) that describes the fit of the optimal frequencies is the most real. Figure 7 demonstrates this behavior in detail for the optimal branch of frequencies corresponding to the prices for Al. For the other three metals, a similar behavior for the fitting error related to the function Φk = ln(Ωk) is conserved. The corresponding values of error (0) for all four metals are provided in Table 1. The fit of the optimal frequency with two equivalent functions expressed by relationships (3) and (11) are shown in Figure 8. How do we confirm, in addition, the selection of the chosen hypothesis (3)? The fitting function (11) allows us to increase the frequency range if we extend the initial interval for mode(k) [0, 50] up to the interval [0, 100] and consider the fit of the remnant function that is obtained as the difference between the initial price distribution and its fitting function, provided by expression (1). Additional frequencies help to realize this fit approximately, as shown in Figure 9, with the value of the relative error close to 6%. The AFR for this remnant function confirms, in general, this behavior. With an increasing number of the higher frequencies (q > 50), the behavior of the amplitudes Acq and Asq becomes chaotic. These functions, including their module entering to the AFR, are shown in Figure 10. For the other three metals (Cu, Ni, and Pb), the treatment procedure explained above, in the form of steps S1–S3, is conserved and, therefore, for them we show only the desired fit that is presented in Figure 11. The necessary numeric parameters are also listed in Table 1, Table 2 and Table 3.
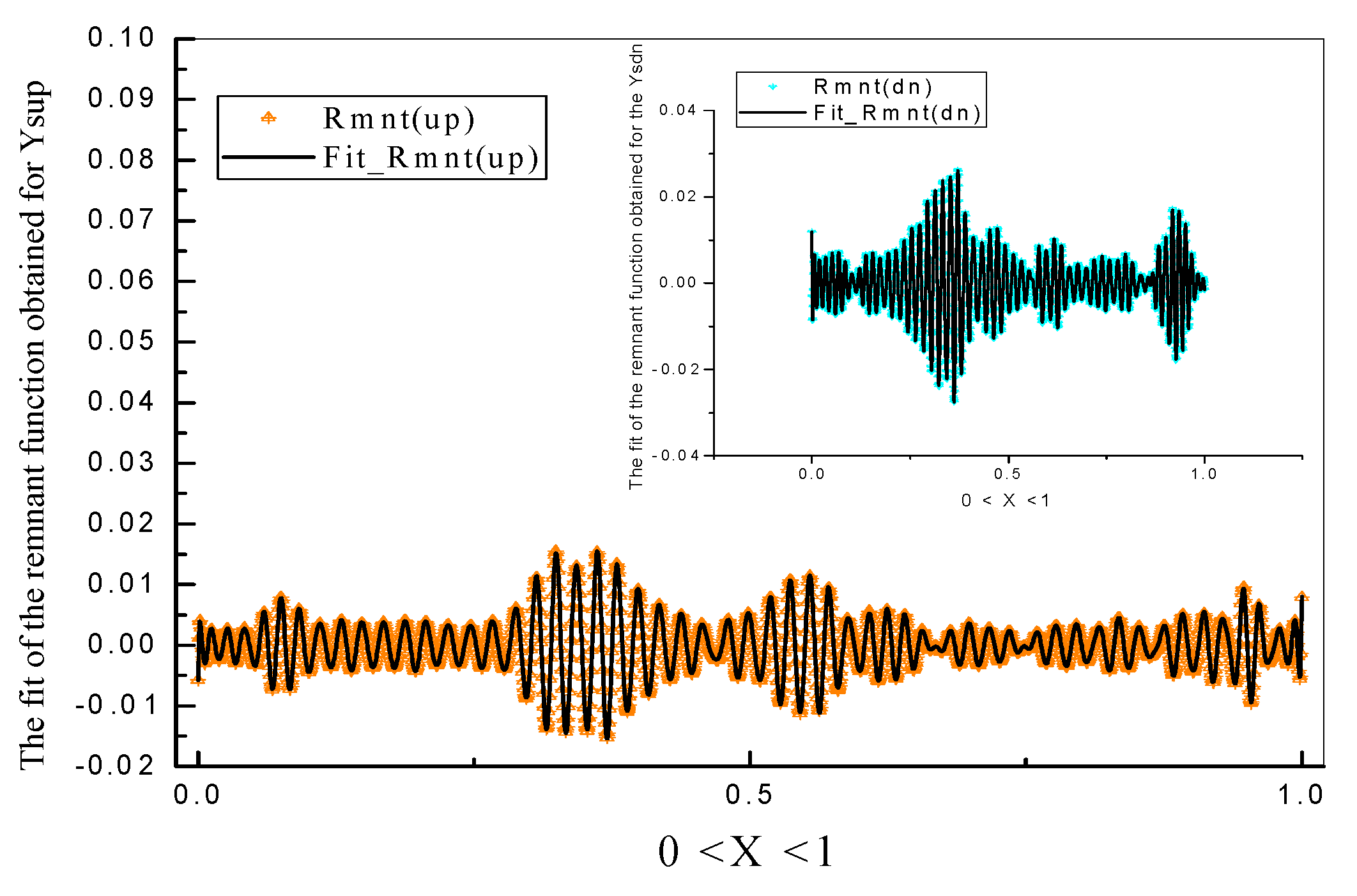
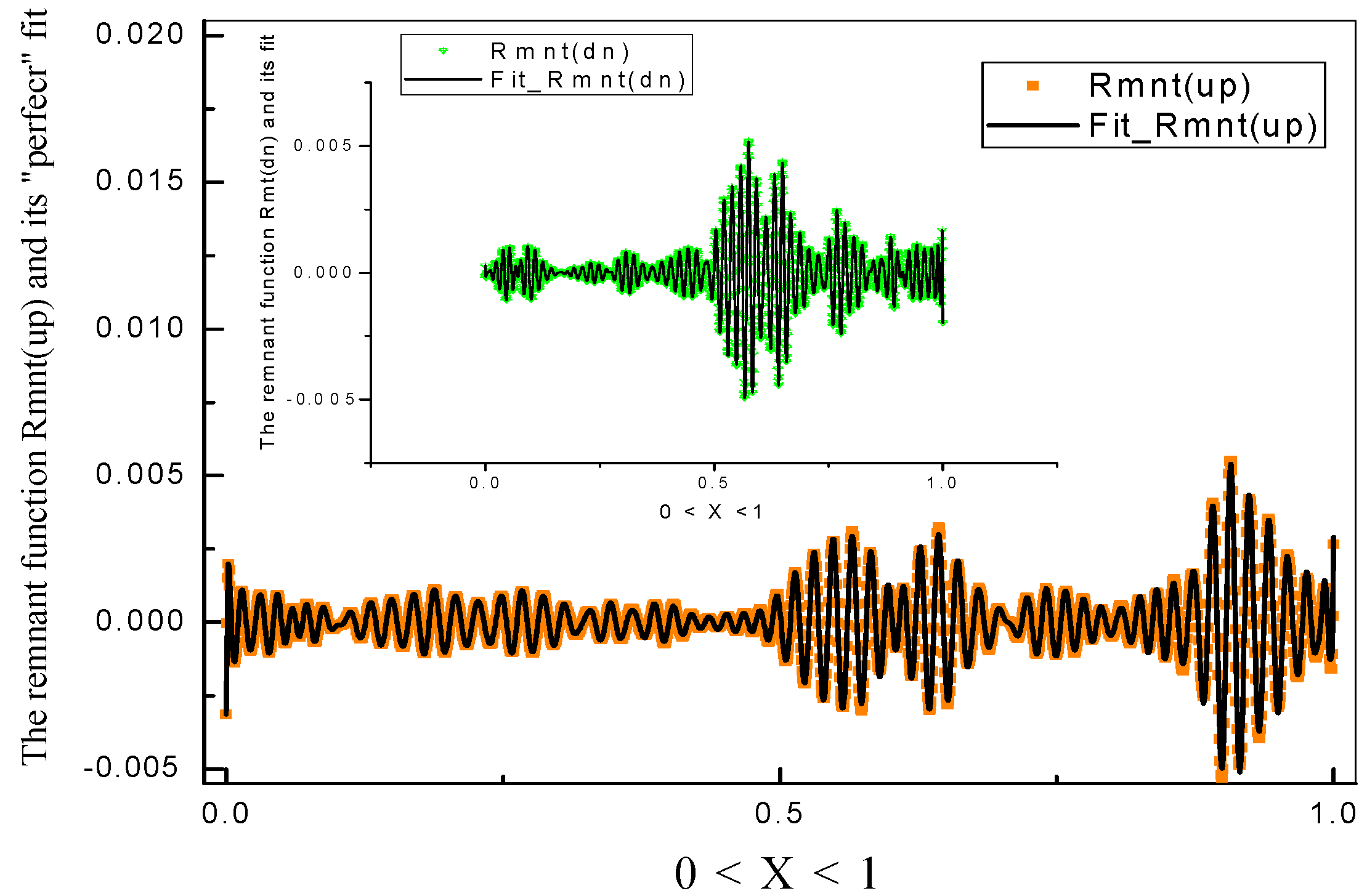
3.2. The Treatment of Acoustic Data
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Isermann, R.; Münchhof, M. Identification of Dynamic Systems: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 85. [Google Scholar]
- Mertins, A. Signal Analysis: Wavelets, Filter Banks, Time-Frequency Transforms and Applications; Wiley: Chichester, UK, 1999. [Google Scholar]
- Arecchi, F.; Meucci, R.; Puccioni, G.; Tredicce, J. Experimental evidence of subharmonic bifurcations, multistability, and turbulence in a Q-switched gas laser. Phys. Rev. Lett. 1982, 49, 1217–1220. [Google Scholar] [CrossRef]
- Chen, J.; Chau, K.; Chan, C.; Jiang, Q. Subharmonics and chaos in switched reluctance motor drives. IEEE Trans. Energy Convers. 2002, 17, 73–78. [Google Scholar] [CrossRef]
- Lauterborn, W.; Cramer, E. Subharmonic route to chaos observed in acoustics. Phys. Rev. Lett. 1981, 47, 1445. [Google Scholar] [CrossRef]
- Wilden, I.; Herzel, H.; Peters, G.; Tembrock, G. Subharmonics, biphonation, and deterministic chaos in mammal vocalization. Bioacoustics 1998, 9, 171–196. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice Hall Press: Upple Sadle River, NJ, USA, 1995; Volume 778. [Google Scholar]
- Almeida, L.B. The fractional Fourier transform and time-frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Stanković, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Tao, R.; Kang, X. Analysis and comparison of discrete fractional Fourier transforms. Signal Process. 2019, 160, 284–298. [Google Scholar] [CrossRef]
- Portnoff, M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Qian, S.; Chen, D. Joint time-frequency analysis. IEEE Signal Process. Mag. 1999, 16, 52–67. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Zhi, S.; Wang, T.; Chu, F. Short-time Fourier transform using odd symmetric window function. J. Dyn. Monit. Diagn. 2022, 1, 37–45. [Google Scholar] [CrossRef]
- Hlubina, P.; Luňáček, J.; Ciprian, D.; Chlebus, R. Windowed Fourier transform applied in the wavelength domain to process the spectral interference signals. Opt. Commun. 2008, 281, 2349–2354. [Google Scholar] [CrossRef] [Green Version]
- Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef] [PubMed]
- Qian, S.; Chen, D. Discrete Gabor transform. IEEE Trans. Signal Process. 1993, 41, 2429–2438. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Krolak, P.; Steele, C. The generalized Gabor transform. IEEE Trans. Image Process. 1995, 4, 978–988. [Google Scholar] [PubMed]
- Zhao, Z.; Tao, R.; Li, G.; Wang, Y. Clustered fractional Gabor transform. Signal Process. 2020, 166, 107240. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Burlington, MA, USA, 1999. [Google Scholar]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Kumar, A. Wavelet signal processing: A review for recent applications. Int. J. Eng. Tech. 2020, 6, 12. [Google Scholar] [CrossRef]
- Peng, Z.K.; Peter, W.T.; Chu, F.L. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Zayed, A.I. Hilbert transform associated with the fractional Fourier transform. IEEE Signal Process. Lett. 1998, 5, 206–208. [Google Scholar] [CrossRef]
- de Souza, U.B.; Escola, J.P.L.; da Cunha Brito, L. A survey on Hilbert-Huang transform: Evolution, challenges and solutions. Digit. Signal Process. 2022, 120, 103292. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Singh, L.; Pachori, R.B. Fourier–Bessel series expansion based empirical wavelet transform for analysis of non-stationary signals. Digit. Signal Process. 2018, 78, 185–196. [Google Scholar] [CrossRef]
- Chaudhary, P.K.; Gupta, V.; Pachori, R.B. Fourier-Bessel representation for signal processing: A review. Digit. Signal Process. 2023, 135, 103938. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Khamzin, A.A.; Machado, J.T. Detection of quasi-periodic processes in complex systems: How do we quantitatively describe their properties? Phys. Scr. 2013, 89, 015201. [Google Scholar] [CrossRef] [Green Version]
- Nigmatullin, R.; Rakhmatullin, R. Detection of quasi-periodic processes in repeated measurements: New approach for the fitting and clusterization of different data. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4080–4093. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. Detection of Quasi-Periodic Processes in Experimental Measurements: Reduction to an “Ideal Experiment”. In Complex Motions and Chaos in Nonlinear Systems, Nonlinear Systems and Complexity; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–37. [Google Scholar]
- Nigmatullin, R.R.; Maione, G.; Lino, P.; Saponaro, F.; Zhang, W. The general theory of the quasi-reproducible experiments: How to describe the measured data of complex systems? Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 324–341. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Lopes, A.M. Approximation of data using non-integer harmonics series. Nonlinear Dyn. 2017, 89, 2845–2854. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Alexandrov, V.S.; Agarwal, P.; Jain, S.; Ozdemir, N. Description of multi-periodic signals generated by complex systems: NOCFASS-New possibilities of the Fourier analysis. Numer. Algebra Control. Optim. 2022, 1–19. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Gubaidullin, I.A. NAFASS: Fluctuation spectroscopy and the Prony spectrum for description of multi-frequency signals in complex systems. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 252–269. [Google Scholar] [CrossRef]
- Baleanu, M.C.; Nigmatullin, R.R.; Okur, S.; Osakoglu, K. New Approach for Consideration of Adsorption/Desorption Data. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4649–4656. [Google Scholar] [CrossRef] [Green Version]
- Ciurea, M.L.; Lazanu, S.; Stavarache, I.; Lepadatu, A.M.; Iancu, V.; Mitroi, M.R.; Baleanu, C.M. Stress-induced traps in multilayered structures. J. Appl. Phys. 2011, 109, 013717. [Google Scholar] [CrossRef] [Green Version]
- Beckenbach, E.F.; Bellman, R. Inequalities; Springer Science & Business Media: New York, NY, USA, 2012; Volume 30. [Google Scholar]

















| Metal | w2 | w1 | w0 | Error(Ωopt, Ωk(fit)) (%) | RelError(0) (%) |
|---|---|---|---|---|---|
| Al | 2.53693 | −2.08913 | 0.5522 | 2.07977 | 0.0171 |
| Cu | 2.57315 | −2.15859 | 0.58544 | 2.50774 | 0.00605 |
| Ni | 2.58633 | −2.18624 | 0.59991 | 3.07769 | 0.00801 |
| Pb | 2.52498 | −2.07013 | 0.54515 | 4.0708 | 3.3452 × 10−5 |
| Metal | C0 | C1 | C2 | λ1 | λ2 |
|---|---|---|---|---|---|
| Al | 0.18097 | −2.39532 | −2.6291 | 0.57265 | 0.96428 |
| Cu | 0.35232 | −2.47294 | −2.61073 | 0.6042 | 0.96896 |
| Ni | 0.21646 | −2.24152 | −2.5588 | 0.6223 | 0.96403 |
| Pb | −0.03681 | −1.79219 | −2.6155 | 0.57214 | 0.95284 |
| Metal | Ω0 (opt) | ΩK (opt) (K = 50) | A0 | MinErr (%) | Max (Amd) |
|---|---|---|---|---|---|
| Al | 0.00884 | 0.79845 | −613.59 | 2.60589 | 28023.2 |
| Cu | 0.00998 | 0.83988 | 14.5714 | 3.76527 | 4163.16 |
| Ni | 0.01117 | 0.87714 | 61.2108 | 6.34594 | 759.972 |
| Pb | 0.01321 | 0.82796 | 14.1491 | 5.14134 | 81097.5 |
| Envelopes of Insects | w2 | w1 | w0 | Error(Ωopt,Ωk(fit)) (%) | RelError(0) (%) |
|---|---|---|---|---|---|
| Ysup(1) | 2.62716 | −2.26616 | 0.63901 | 4.27366 | 0.02533 |
| Ysdn(1) | 2.65023 | −2.30832 | 0.6581 | 4.86923 | 0.01613 |
| Ysup(2) | 2.6001 | −2.2124 | 0.6123 | 3.44258 | 0.1051 |
| Ysdn(2) | 2.67842 | −2.36338 | 0.68496 | 2.46499 | 0.1047 |
| Envelopes of Insects | C0 | C1 | C2 | λ1 | λ2 |
|---|---|---|---|---|---|
| Ysup(1) | 6.04624 | −1.87786 | −2.39444 | 0.66225 | 0.96491 |
| Ysdn(1) | 6.48627 | −2.17 | −2.67748 | 0.6744 | 0.97583 |
| Ysup(2) | 6.18376 | −1.99235 | −2.64792 | 0.63339 | 0.96671 |
| Ysdn(2) | 6.52706 | −2.35381 | −2.58688 | 0.70024 | 0.97818 |
| Envelopes of Insects | Ω0 (opt) | ΩK (opt) (K = 50) | A0 | MinErr (%) | Max (Amd) |
|---|---|---|---|---|---|
| Ysup(1) | 6.07508 | 306.747 | 0.24827 | 1.39285 | 38,985.8 |
| Ysdn(1) | 5.92548 | 348.423 | −0.58799 | 1.99317 | 4063.01 |
| Ysup(2) | 5.30349 | 326.084 | 0.23301 | 0.86607 | 89.2284 |
| Ysdn(2) | 5.28291 | 300.306 | −0.16851 | 0.88903 | 14,036.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigmatullin, R.R.; Khamzin, A.A.; Chen, Y. Approximation of Aperiodic Signals Using Non-Integer Harmonic Series: The Generalized NAFASS Approach. Fractal Fract. 2023, 7, 498. https://doi.org/10.3390/fractalfract7070498
Nigmatullin RR, Khamzin AA, Chen Y. Approximation of Aperiodic Signals Using Non-Integer Harmonic Series: The Generalized NAFASS Approach. Fractal and Fractional. 2023; 7(7):498. https://doi.org/10.3390/fractalfract7070498
Chicago/Turabian StyleNigmatullin, Raoul R., Airat A. Khamzin, and Yangquan Chen. 2023. "Approximation of Aperiodic Signals Using Non-Integer Harmonic Series: The Generalized NAFASS Approach" Fractal and Fractional 7, no. 7: 498. https://doi.org/10.3390/fractalfract7070498
APA StyleNigmatullin, R. R., Khamzin, A. A., & Chen, Y. (2023). Approximation of Aperiodic Signals Using Non-Integer Harmonic Series: The Generalized NAFASS Approach. Fractal and Fractional, 7(7), 498. https://doi.org/10.3390/fractalfract7070498








