Analysis of a High-Accuracy Numerical Method for Time-Fractional Integro-Differential Equations

Abstract

A high-order finite difference numerical scheme based on the compact difference operator is proposed in this paper for time-fractional partial integro-differential equations with a weakly singular kernel, where the time-fractional derivative term is defined in the Riemann-Liouville sense. Here, the stability and convergence of the constructed compact finite difference scheme are proved in $L^{\infty }$ norm, with the accuracy order $O({\tau }^2+h^4)$, where $\tau$ and h are temporal and spatial step sizes, respectively. The advantage of this numerical scheme is that arbitrary parameters can be applied to achieve the desired accuracy. Some numerical examples are presented to support the theoretical analysis.

1. Introduction

In this paper, we will consider the following Riemann-Liouville time-fractional partial integro-differential equation with a weakly singular kernel:

$$\left\{\begin{array}{cc}{}_0\mathcal{D}_t^{\alpha }u(x,t)={\mathcal{I}}^{\beta }\Delta u(x,t)+f(x,t),\hfill & (x,t)\in \mathsf{\Omega },\\ u(0,t)=g_1\left(t\right),u(L,t)=g_2\left(t\right),\hfill & t\in (0,T),\\ u(x,0)=\phi \left(x\right),\hfill & x\in (0,L),\end{array}\right.$$

(1)

where $\mathsf{\Omega }=[0,L]\times [0,T]$, $\alpha ,\beta \in (0,1)$ and $\Delta u(x,t)=u_{xx}(x,t)$. $g_1\left(t\right),g_2\left(t\right),\phi \left(x\right)$ and $f(x,t)$ are given smooth functions. ${}_0\mathcal{D}_t^{\alpha }$ and ${\mathcal{I}}^{\beta }$ are defined in Definition 1. The existence and uniqueness of the solution for Equation (1) have been considered in [1].

Definition 1

([2,3,4]). (1) The α-order fractional Riemann-Liouville derivatives of the function $u(x,t)$ is defined as

$${}_0\mathcal{D}_t^{\alpha }u(x,t)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}\frac{d}{dt}{\int }_0^t{(t-s)}^{-\alpha }u(x,s)ds.$$

(2) The β-order fractional Riemann-Liouville integral of the function $u(x,t)$ is defined as

$${\mathcal{I}}^{\beta }u(x,t)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}u(x,s)ds,$$

where $\mathsf{\Gamma }(·)$ is the Euler’s gamma function.

At present, Riemann-Liouville and Caputo derivatives are commonly used in engineering and the sciences. The properties of the Riemann-Liouville derivative are different from those of the Caputo derivative. Furthermore, the Riemann-Liouville derivative is singular at zero, and its mathematical analysis is more sophisticated [5]. The Riemann-Liouville derivative naturally arises in real-world phenomena in several diverse disciplines, such as viscoelastic materials [6,7], mathematical biology [8] and electrochemistry [9]. More application details can refer to [10]. Indeed, the exact solutions of many fractional integral or differential equations cannot be found, so it is therefore necessity to find the numerical solutions. Due to this circumstance, we need to apply the appropriate methods to find numerical solutions of the fractional equations, for instance, finite difference methods [11], finite element methods [12], integral transform methods [13] and radial basis function methods [14,15].

Up to now, the fractional integral or differential equations have abundant research results. For example, Fakhar-Izadi [16] considered the spectral Galerkin method in time and space for solving 1D and 2D fourth-order time-fractional partial integro-differential equations. Wang and Zhu [17] achieved the fractional integro-differential equations transformed into a system of algebraic equations using an operational matrix. Ghanbari and Kumar [18] studied a fractional predator-prey pathogen model, and the stability and convergence results wer obtained. Zhang and Li [19] proposed a numerical algorithm to solve a second-order-delay integro-differential equations based on the generalized Störmer-Cowell methods and compound quadrature rules.

In recent years, an increasing number of researchers have chosen to study high-order and highly dimensional numerical discrete schemes. It is well-known that the compact finite difference method is useful for constructing high-accuracy numerical schemes. The following articles contain the results of compact difference methods. In [20], a generalized framework for deriving the approximation of an arbitrary-order derivative was proposed by Caban and Tyliszczak based on the compact difference method. Ding and Li [21] constructed a novel high-order numerical algorithm by using the tempered Grünwald difference operator and fourth-order compact numerical differential formulas to solve 2D partial differential equation with the Riesz derivative. In [22], Vong and Wang constructed a high-accuracy numerical algorithm for the time-fractional Fokker-Planck equations with variable convection. In [23], Ding solved the 2D diffusion-wave equations, and the following convergence order was achieved: $O({\tau }^2+h_1^2+h_2^2)$. Zhai et al. [24] solved a 3D time-fractional convection-diffusion equation using the ADI compact difference method and proved the higher-order algorithm is unconditionally stable. Xu et al. [25] developed a higher-order finite difference method for the fourth-order time-fractional integro-differential equation with a Caputo derivative.

Concerning integro-difference equations with Riemann-Liouville derivatives, some results can be found as follows. Dehghan and Abbaszadeh [26,27] studied a numerical algorithm for fractional integro-differential equations with Riemann-Liouville and Riesz derivatives. In [28], Diethelm et al. proposed a second-order method to approximate the integral term. Chen et al. [29] studied the fractional evolution equation with a Riemann-Liouville integral term and obtained the convergence order $O\left({\tau }^{1+\alpha }\right)$. Guo and Xu [30] found that the Caputo derivative numerical scheme has the convergence order $O\left({\tau }^{2-\alpha }\right)$. Up to now, there are the most results for integro-difference equations with Caputo derivatives and few results for Equation (1). Inspired by the results of [28,29], we want to construct a fully discrete high-order difference scheme for Equation (1). By using the second-order shifted and weighted Grünwald difference operator and fourth-order compact difference method, we construct a high order difference scheme for Equation (1). Compared with the result in [29], it can be found that the convergence order in the temporal direction can reach the second order, which is better than the result in [29].

The structure of this article is as follows. In the next section, necessary notations are listed, and a numerical scheme based on a compact difference operator for Equation (1) is studied. In Section 3, the stability analysis and convergence of the established numerical scheme are carried out. In Section 4, several experimental results are stated to support the efficiency of the established discrete scheme.

2. Numerical Scheme

Let M and N be two positive integers, and let $h=L/M$ and $\tau =T/N$ be the spatial step size and time step size, respectively. C is a constant, which may be different in different locations.

For $j=0,1,\dots ,M$ and $n=0,1,\dots ,N$, the mesh point $(x_j,t_n)$ is defined as $x_j=jh$ and $t_n=n\tau$. Let $u_j^n$ be the exact solution and $U_j^n$ be the approximate solution at each mesh point $(x_j,t_n)$ of Equation (1). The following notations and lemmas will be used throughout this paper:

$${\delta }_x^2{U}_j=\frac{U_{j-1}-2U_j+U_{j+1}}{h^2},\hspace{1em}{\delta }_x{U}_j=\frac{U_j-U_{j-1}}{h},$$

(2)

$$\mathcal{H}{U}_j=\left\{\begin{array}{cc}\frac{1}{12}(U_{j-1}+10U_j+U_{j+1})=(1+\frac{h^2}{12}{\delta }_x^2)U_j,\hfill & \hfill j=1,2,\dots ,M-1,\hfill \\ U_j,\hfill & \hfill j=0,M.\hfill \end{array}\right.$$

(3)

Using the shifted and weighted Grünwald difference method to approximation derivatives, we can obtain a discrete scheme with a second-order convergence rate in the temporal direction.

Lemma 1

([31]). Suppose that $u\in L^{1+\alpha }\left(R\right)$, and let

$${}_{-\infty }\mathcal{D}_t^{\alpha }u\left(t\right)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}\frac{d}{dt}{\int }_{-\infty }^t{(t-s)}^{-\alpha }u\left(s\right)ds.$$

The shifted and weighted Grünwald difference operator is defined as follows:

$$A_{\tau ,p}^{\left(\alpha \right)}u\left(t\right)=\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^{\infty }{g}_i^{\left(\alpha \right)}u(t-(i-p)\tau ),$$

(4)

where p is an integer according to Equation (4). Then, we obtain that

$$A_{\tau ,p}^{\left(\alpha \right)}u\left(t\right)={}_{-\infty }\mathcal{D}_t^{\alpha }u\left(t\right)+O\left(\tau \right),$$

uniformly for $t\in$ R as $\tau \to 0$. The coefficients $g_i^{\left(\alpha \right)}(0<\alpha \le 1)$ are defined as follows:

$$g_0^{\left(\alpha \right)}=1,\hspace{1em}{g}_i^{\left(\alpha \right)}=(1-\frac{\alpha +1}{i})g_{i-1}^{\alpha },i=1,2,\cdots .$$

In addition, if $\alpha =0$, we stipulate $g_0^{\left(\alpha \right)}=1$ and $g_i^{\left(\alpha \right)}$ when $i\ge 1$.

Lemma 2

([32]). Let $u\in L^{2+\alpha }\left(R\right)$, ${}_{-\infty }\mathcal{D}_t^{\alpha +2}u$ and its Fourier transform belong to $L^{2+\alpha }\left(R\right)$, and define the shifted and weighted Grünwald difference operator as follows:

$${}_L\mathcal{D}_{\tau ,p,q}^{\alpha }u\left(t\right)=\frac{\alpha -2q}{2(p-q)}{A}_{\tau ,p}^{\left(\alpha \right)}u\left(t\right)+\frac{2p-\alpha }{2(p-q)}{A}_{\tau ,q}^{\left(\alpha \right)}u\left(t\right).$$

(5)

Then, uniformly for $t\in R$ as $\tau \to 0$, we obtain

$${}_L\mathcal{D}_{\tau ,p,q}^{\alpha }u\left(t\right)={}_{-\infty }\mathcal{D}_t^{\alpha }u\left(t\right)+O({\tau }^2),\hspace{1em}p\ne q,$$

where p and q are integers.

Furthermore, we define ${}_L\mathcal{D}_{\tau ,p,q}^{\alpha }={}_L\mathcal{D}_{\tau ,q,p}^{\alpha }$. A finite difference approximations to discrete derivative in time is as follows (see [31]):

$$\left((1+\frac{\alpha }{2})A_{\tau ,0}^{\left(\alpha \right)}-\frac{\alpha }{2}{A}_{\tau ,-1}^{\left(\alpha \right)}\right)u\left(t\right)={\tau }^{-\alpha }\sum _{i=0}^{\infty }{w}_i^{\left(\alpha \right)}u(t-i\tau )={}_{-\infty }\mathcal{D}_t^{\alpha }u\left(t\right)+O\left({\tau }^2\right),0<\alpha <1,$$

where

$$\begin{array}{cc}{w}_0^{\left(\alpha \right)}=(1+\frac{\alpha }{2})g_0^{\left(\alpha \right)}=1+\frac{\alpha }{2},\hfill & \\ w_i^{\left(\alpha \right)}=(1+\frac{\alpha }{2})g_i^{\left(\alpha \right)}-\frac{\alpha }{2}{g}_{i-1}^{\left(\alpha \right)},\hfill & i\ge 1.\hfill \end{array}$$

(6)

Combining the above equality, we obtain

$${}_0\mathcal{D}_t^{\alpha }u(x_j,t_n)=\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}u(x_j,t_{n-i})+O\left({\tau }^2\right).$$

Lemma 3

([31,33,34,35]). Let function $u\in C^6[x_{j-1},x_{j+1}]$ and $\xi (s)={(1-s)}^3[5-3{(1-s)}^2]$; then, we get

$$\begin{array}{c}\frac{u″(x_{j+1})+10u″(x_j)+u″(x_{j-1})}{12}\hfill \\ =\frac{1}{h^2}(u(x_{j+1})-2u(x_j)+u(x_{j-1}))+\frac{h^4}{360}{\int }_0^1(u^{\left(6\right)}(x_j-sh)+u^{\left(6\right)}(x_j+sh))\xi (s)ds.\hfill \end{array}$$

Lemma 4

([28,36]). Suppose that $\mathcal{L}\left(t\right)\in C^2[0,T]$; then, there exists a positive constant C which depends only on β$(0<\beta <1)$ such that

$$|{\int }_0^{t_n}{(t_n-s)}^{\beta -1}\mathcal{L}\left(s\right)ds-\sum _{i=0}^n{\kappa }_{n-i,n}^n\mathcal{L}\left(t_{n-i}\right)|\le C\underset{0\le t\le T}{\max }|\mathcal{L}″\left(t\right)|t_n^{\beta }{\tau }^2,\hspace{1em}1\le n\le N,$$

where

$${\kappa }_{n-i,n}^n=\frac{{\tau }^{\beta }}{\beta (\beta +1)}\times \left\{\begin{array}{cc}{(n-1)}^{\beta +1}-(n-1-\beta )n^{\beta },\hfill & i=n,\hfill \\ {(i+1)}^{\beta +1}-2{\left(i\right)}^{\beta +1}+{(i-1)}^{\beta +1},\hfill & 1\le i\le n-1,\hfill \\ 1,\hfill & i=0.\hfill \end{array}\right.$$

(7)

Lemma 5.

For any ${\kappa }_{n-i,n}^n(1\le i\le n-1,2\le n\le N)$satisfying the definition of Equation (7), the sequence $\{{\kappa }_{n-i,n}^n\}$ decreases monotonically depending on k.

Proof. 

By Equation (7), we have

$${\kappa }_{n-i,n}^n=\frac{{\tau }^{\beta }}{\beta (\beta +1)}\times ({(i+1)}^{\beta +1}-2i^{\beta +1}+{(i-1)}^{\beta +1}).$$

Let $g(\lambda )=\frac{{\tau }^{\beta }}{\beta (\beta +1)}\times ({(\lambda +1)}^{\beta +1}-2{\lambda }^{\beta +1}+{(\lambda -1)}^{\beta +1})$, then

$$g\prime (\lambda )=\frac{{\tau }^{\beta }}{\beta }\times ({(\lambda +1)}^{\beta }-2{\lambda }^{\beta }+{(\lambda -1)}^{\beta }).$$

By the mean value theorem, we get

$$g\prime (\lambda )={\tau }^{\beta }({\xi }_1^{\beta -1}-{\xi }_2^{\beta -1}),$$

where ${\xi }_1\in (\lambda ,\lambda +1)$, ${\xi }_2\in (\lambda -1,\lambda )$, therefore $g\prime \left(\lambda \right)\le 0$. Then, the sequence $\{{\kappa }_{n-i,n}^n\}$ decreases monotonically in $[1,\infty )$. □

Lemma 6

([36]). Let ${\kappa }_{i,n}^n(1\le n\le N)$ be defined as Equation (7), and for all β $(0<\beta <1)$, we obtain

 (i)$\begin{array}{c}0<{\kappa }_{0,n}^n<\frac{{\tau }^{\beta }}{\beta +1},\hfill \end{array}$

 (ii)$\begin{array}{c}\sum _{i=1}^{n-1}|{\kappa }_{i,n}^n|\le \frac{T^{\beta }}{\beta }.\hfill \end{array}$

Assume that $u(x,t)\in C_{x,t}^{6,2}([0,L]\times [0,T])$ and consider Equation (1) on grid point $(x_j,t_n)$ and apply compact difference operator $\mathcal{H}$ to both sides. We thus have

$${}_0\mathcal{D}_t^{\alpha }u(x_j,t_n)={\mathcal{I}}^{\beta }\mathcal{H}{u}_{xx}(x_j,t_n)+\mathcal{H}f(x_j,t_n).$$

(8)

For the left term of Equation (8), by Lemma 2, we get

$${}_0\mathcal{D}_t^{\alpha }\mathcal{H}u(x_j,t_n)=\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}\mathcal{H}u(x_j,t_{n-i})+O({\tau }^2).$$

(9)

For the first term on the right of Equation (8), Lemma 3 and Lemma 4 imply that

$${\mathcal{I}}^{\beta }\mathcal{H}{u}_{xx}(x_j,t_n)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n{\delta }_x^{2}u(x_j,t_{n-i})+O({\tau }^2+h^4).$$

(10)

Substituting Equation (9) and Equation (10) into Equation (1), it follows that

$$\begin{array}{c}\hfill \frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}\mathcal{H}{u}_j^{n-i}=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n{\delta }_x^2{u}_j^{n-i}+\mathcal{H}{f}_j^n+R_j^n,\end{array}$$

(11)

where $f_j^n=f(x_j,t_n),|R_j^n|\le C({\tau }^2+h^4).$

Neglecting the small term $R_j^n$ in Equation (11), when $1\le j\le M-1, 1\le n\le N$, the compact finite difference scheme for Equation (1) is given as follows:

$$\left\{\begin{array}{c}\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}\mathcal{H}{U}_j^{n-i}=\frac{1}{\mathsf{\Gamma }(\beta )}\sum _{i=0}^n{\kappa }_{n-i,n}^n{\delta }_x^2{U}_j^{n-i}+\mathcal{H}{f}_j^n,\hfill \\ U_0^n=g_1(t_n),U_M^n=g_2(t_n),\hfill \\ U_j^0={[\phi \left(x_1\right),\phi \left(x_2\right),\cdots ,\phi \left(x_{M-1}\right)]}^T.\hfill \end{array}\right.$$

(12)

At each time level, the compact difference scheme Equation (12) is a system of linear algebraic equations with a strictly diagonally dominant matrix as its coefficient matrix. We can obtain the following theorem.

Theorem 1

([30]). The compact difference scheme Equation (12) permits a unique solution.

3. Stability and Convergence

In this section, we first give some notations and lemmas which will be used in the subsequent discussions. Then, the stability analysis and error estimates of the compact finite difference scheme for Equation (12) are obtained.

Denote ${\mathfrak{V}}_h=\left\{v\right|v=(v_0,v_1\dots ,v_M)$ as the space of grid functions, and $v_0=v_M=0$. For each $u,v\in {\mathfrak{V}}_h$, the inner product and norm are denoted as follows:

$$\begin{array}{cc}(u,v)=h\sum _{j=1}^{M-1}{u}_j{v}_j{, \Vert u\Vert }^2=(u,u),\hfill & {\Vert u\Vert }_{\infty }=\underset{0\le j\le M}{\max }\left|u_j\right|,\hfill \\ {(u,v)}_{\mathcal{A}}=(u,v)-\frac{h^2}{12}({\delta }_{x}u,{\delta }_{x}v),\hfill & {\Vert u\Vert }_{\mathcal{A}}^2={(u,u)}_{\mathcal{A}}.\hfill \end{array}$$

Lemma 7

([31,37]). Let ${\{w_i^{\left(\alpha \right)}\}}_{n=0}^{\infty }$ be defined as Equation (6); then, for each positive integer m and for any ${(p^0,p^1,\cdots ,p^m)}^T\in {\mathbb{R}}^{m+1}$, we have

$$\sum _{n=0}^m(\sum _{i=0}^n{w}_i^{\left(\alpha \right)}{p}^{n-i})p^n\ge 0.$$

Lemma 8

([36]). Assume that $u,v\in {\mathfrak{V}}_h$; then, $({\delta }_x^{2}u,v)=-({\delta }_{x}u,{\delta }_{x}v).$

Lemma 9

([38]). If $u\in {\mathfrak{V}}_h$, then $\frac{2}{3}{\Vert {\delta }_x{u}^n\Vert }^2\le -({\delta }_x^2{U}^n,\mathcal{H}{u}^n).$

Lemma 10

([39]). For all grid function $u\in {\mathfrak{V}}_h$, then

$$\begin{array}{cc}{\Vert u\Vert }_{\infty }\le \frac{\sqrt{L}}{2}\Vert {\delta }_{x}u\Vert ,\hfill & \Vert u\Vert \le \frac{L}{\sqrt{6}}\Vert {\delta }_{x}u\Vert ,\hfill \\ \frac{\sqrt{6}}{3}\Vert u\Vert \le {\Vert u\Vert }_{\mathcal{A}}\le \Vert u\Vert ,\hfill & \Vert \mathcal{H}u\Vert \le \Vert u\Vert .\hfill \end{array}$$

Lemma 11

([36,40]). Define $\{{\zeta }_n\}$ as a sequence of non-negative real numbers if it satisfies the following inequality

$${\zeta }_n\le \sum _{k=0}^{n-1}{\varrho }_k{\zeta }_k+b_n,n\ge 0,$$

where $b_n$ is a nondecreasing sequence of non-negative numbers, and ${\varrho }_k\ge 0$. It thus holds that

$${\zeta }_n\le b_{n}exp\left(\sum _{k=0}^{n-1}{\varrho }_k\right),n\ge 0.$$

Lemma 12

([41]). $\left(\check{C}eby\check{s}evinequality\right)$ If $\eta =({\eta }_1,{\eta }_2,\dots ,{\eta }_n)$ is a nonincreasing sequence and $\mu =({\mu }_1,{\mu }_2,\dots ,{\mu }_n)$ is a nondecreasing sequence, then we obtain

$$\sum _{i=1}^n{\eta }_i{\mu }_i\le \frac{1}{n}\sum _{i=1}^n{\eta }_i\sum _{i=1}^n{\mu }_i.$$

Lemma 13.

If $v\in {\mathfrak{V}}_h$, then $({\delta }_x^2{v}^{n-i},\mathcal{H}{v}^n)\le \Vert {\delta }_x{v}^{n-i}{\Vert }_{\mathcal{A}}{\Vert {\delta }_x{v}^n\Vert }_{\mathcal{A}}.$

Proof. 

By definition of ${(u,v)}_{\mathcal{A}}$, Equation (3) and Lemma 8, we have

$$\begin{array}{cc}\hfill ({\delta }_x^2{v}^{n-i},\mathcal{H}{v}^n)& =\left({\delta }_x^2{v}^{n-i},(1+\frac{h^2}{12}{\delta }_x^2)v^n\right)\hfill \\ & =({\delta }_x^2{v}^{n-i},v^n)+\frac{h^2}{12}({\delta }_x^2{v}^{n-i},{\delta }_x^2{v}^n)\hfill \\ & =-({\delta }_x{v}^{n-i},{\delta }_x{U}^n)+\frac{h^2}{12}({\delta }_x^2{v}^{n-i},{\delta }_x^2{v}^n)\hfill \\ & =-{({\delta }_x{v}^{n-i},{\delta }_x{v}^n)}_{\mathcal{A}}\hfill \\ & \le \Vert {\delta }_x{v}^{n-i}{\Vert }_{\mathcal{A}}{\Vert {\delta }_x{v}^n\Vert }_{\mathcal{A}},\hfill \end{array}$$

from which the desired result is obtained. □

Lemma 14.

Let ${\kappa }_{n-i,n}^n$ and ${\delta }_x{U}^{n-i}$ be defined in Equation (7) and Equation (2), respectively; then,

$$\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert \le \frac{M^{\ast }{T}^{\beta }}{(n-1)\beta }\sum _{i=1}^{n-1}\frac{\Vert {\delta }_x{U}^i\Vert }{M_i},\hspace{1em}2\le n\le N,$$

where $M^{\ast }$=$\underset{1\le i\le n-1}{\max }\Vert {\delta }_x{U}^{n-i}\Vert$ and $M_i=\Vert {\delta }_x{U}^i\Vert$.

Proof. 

Let $M^{\ast }=\underset{1\le i\le n-1}{\max }\Vert {\delta }_x{U}^{n-i}\Vert$ and $M_i=\Vert {\delta }_x{U}^i\Vert$. By Lemma 5 and Lemma 12, we get

$$\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert \le \sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|M^{\ast }\le \frac{1}{n-1}\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\sum _{i=1}^{n-1}{M}^{\ast }.$$

(13)

For the left term of Equation (13), by Lemma 6, we have

$$\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert \le \frac{1}{(n-1)}\sum _{i=1}^{n-1}\frac{T^{\beta }{M}^{\ast }}{\beta }.$$

Since function $u(x,t)$ is continuous on Ω, it is bounded. Let $M=\underset{1\le i\le n-1}{\max }{M}^{\ast }/M_i$. We thus have

$$\begin{array}{c}\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert \hfill \\ \le \frac{T^{\beta }{M}^{\ast }}{(n-1)\beta }\left(\frac{\Vert {\delta }_x{U}^1\Vert }{M_1}+\dots +\frac{\Vert {\delta }_x{U}^{n-1}\Vert }{M_{n-1}}\right)\hfill \\ =\frac{T^{\beta }}{(n-1)\beta }\sum _{i=1}^{n-1}\frac{M^{\ast }\Vert {\delta }_x{U}^i\Vert }{M_i}\hfill \\ \le \frac{M{T}^{\beta }}{(n-1)\beta }\sum _{i=1}^{n-1}\Vert {\delta }_x{U}^{n-i}\Vert .\hfill \end{array}$$

The proof is completed. □

Theorem 2.

If $U^n$ is the approximation solution of Equation (12) with the given initial and boundary conditions in the sense that for all $\tau >0$; if ${\tau }^{1-\beta }N\le C_1$ and $T\ge 1$, then

$$\tau \sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \le C\left(\Vert {\delta }_x{U}^0\Vert +\underset{0\le n\le m}{\max }\Vert f^n\Vert \right),\hspace{1em}1\le m\le N,$$

where C and $C_1$ are positive constants, and they depend on T.

Proof. 

By Equation (12), we obtain

$$\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}\mathcal{H}{U}^{n-i}=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n{\delta }_x^2{U}^{n-i}+\mathcal{H}{f}^n.$$

(14)

Taking the inner product of Equation (14) with $\tau \mathcal{H}{U}^n$, then

$$\begin{array}{cc}\hfill & {\tau }^{1-\alpha }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{U}^{n-i},\mathcal{H}{U}^n)\hfill \\ \hfill & =\frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n({\delta }_x^2{U}^{n-i},\mathcal{H}{U}^n)+\tau (\mathcal{H}{f}^n,\mathcal{H}{U}^n).\hfill \end{array}$$

(15)

By Equation (7), Equation (15) and Lemma 9, we have

$$\begin{array}{cc}\hfill & {\tau }^{1-\alpha }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{U}^{n-i},\mathcal{H}{U}^n)\hfill \\ \hfill & =\frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=1}^n{\kappa }_{n-i,n}^n({\delta }_x^2{U}^{n-i},\mathcal{H}{U}^n)+\frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}{\kappa }_{n,n}^n({\delta }_x^2{U}^n,\mathcal{H}{U}^n)+\tau (\mathcal{H}{f}^n,\mathcal{H}{U}^n)\hfill \\ \hfill & \le \frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=1}^n{\kappa }_{n-i,n}^n({\delta }_x^2{U}^{n-i},\mathcal{H}{U}^n)-\frac{2{\tau }^{\beta +1}}{3\mathsf{\Gamma }(\beta +2)}{\Vert {\delta }_x{U}^n\Vert }^2+\tau (\mathcal{H}{f}^n,\mathcal{H}{U}^n).\hfill \end{array}$$

(16)

By inequality (16) and Lemma 13, we get that

$$\begin{array}{c}{\tau }^{1-\alpha }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{U}^{n-i},\mathcal{H}{U}^n)+\frac{2{\tau }^{\beta +1}}{3\mathsf{\Gamma }(\beta +2)}{\Vert {\delta }_x{U}^n\Vert }^2\hfill \\ \le \frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=1}^n|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}{\Vert }_{\mathcal{A}}\Vert {\delta }_x{U}^n{\Vert }_{\mathcal{A}}+\tau \Vert \mathcal{H}{f}^n\Vert \Vert \mathcal{H}{U}^n\Vert \hfill \\ \le \frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=1}^n|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert \Vert {\delta }_x{U}^n\Vert +\frac{\tau L}{\sqrt{6}}\Vert f^n\Vert \Vert {\delta }_x{U}^n\Vert .\hfill \end{array}$$

(17)

By inequality (17), we obtain

$$\begin{array}{cc}\hfill & \frac{{\tau }^{1-\alpha -\beta }}{\Vert {\delta }_x{U}^n\Vert }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{U}^{n-i},\mathcal{H}{U}^n)+\frac{2\tau }{3\mathsf{\Gamma }(\beta +2)}\Vert {\delta }_x{U}^n\Vert \hfill \\ \hfill & \le \frac{{\tau }^{1-\beta }}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=1}^n|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert +\frac{{\tau }^{1-\beta }L}{\sqrt{6}}\Vert f^n\Vert .\hfill \end{array}$$

(18)

By inequality (18) and summing the above expression from n = 1 to m and $1\le m\le N$, we get

$$\begin{array}{cc}\hfill & {\tau }^{1-\alpha -\beta }\sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{U}^{n-i},\mathcal{H}{U}^n)+\frac{2\tau }{3\mathsf{\Gamma }(\beta +2)}\sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \hfill \\ \hfill & \le \frac{{\tau }^{1-\beta }}{\mathsf{\Gamma }\left(\beta \right)}\sum _{n=0}^m\sum _{i=1}^n|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert +\frac{{\tau }^{1-\beta }L}{\sqrt{6}}\sum _{n=0}^m\Vert f^n\Vert .\hfill \end{array}$$

(19)

By Lemma 6, Lemma 7, Lemma 14 and inequality (19), we obtain

$$\begin{array}{cc}\hfill & \tau \sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \hfill \\ \hfill & \le \frac{3{\tau }^{1-\beta }}{2{({\beta }^2+\beta )}^{-1}}\sum _{n=0}^m\sum _{i=1}^n|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert +\frac{3{\tau }^{1-\beta }\mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}}\sum _{n=0}^m\Vert f^n\Vert \hfill \\ \hfill & \le \frac{3{\tau }^{1-\beta }}{2{({\beta }^2+\beta )}^{-1}}\sum _{n=0}^m\left(\sum _{i=1}^{n-1}|{\kappa }_{n-i,n}^n|\Vert {\delta }_x{U}^{n-i}\Vert +|{\kappa }_{0,n}^n|\Vert {\delta }_x{U}^0\Vert \right)+\frac{3\tau \mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}{\tau }^{\beta }}\sum _{n=0}^m\Vert f^n\Vert \hfill \\ \hfill & \le \frac{3{\tau }^{1-\beta }}{2{({\beta }^2+\beta )}^{-1}}\sum _{n=0}^m\left(\frac{M{T}^{\beta }}{(n-1)\beta }\sum _{i=1}^{n-1}\Vert {\delta }_x{U}^{n-i}\Vert +\frac{{\tau }^{\beta }\Vert {\delta }_x{U}^0\Vert }{\beta +1}\right)+\frac{3\tau \mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}{\tau }^{\beta }}\sum _{n=0}^m\Vert f^n\Vert .\hfill \end{array}$$

(20)

By inequality (20) and $T\ge 1$, we get

$$\begin{array}{cc}\hfill & \tau \sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \hfill \\ \hfill & \le \sum _{i=1}^{n-1}\frac{3M{T}^{\beta }(\beta +1)}{2(n-1){\tau }^{\beta }}\tau \sum _{n=0}^m\Vert {\delta }_x{U}^{n-i}\Vert +\sum _{n=0}^m\left(\frac{3\tau \beta }{2}\Vert {\delta }_x{U}^0\Vert +\frac{3\tau \mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}{\tau }^{\beta }}\underset{0\le n\le m}{\max }\Vert f^n\Vert \right)\hfill \\ \hfill & \le \sum _{i=1}^{n-1}\frac{3MT(\beta +1)}{2(n-1){\tau }^{\beta }}\tau \sum _{n=0}^m\Vert {\delta }_x{U}^{n-i}\Vert +\sum _{n=0}^m\left(\frac{3\tau \beta }{2}\Vert {\delta }_x{U}^0\Vert +\frac{3\tau \mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}{\tau }^{\beta }}\underset{0\le n\le m}{\max }\Vert f^n\Vert \right)\hfill \\ \hfill & \le \sum _{i=1}^{n-1}\frac{3M{C}_1(\beta +1)}{2(n-1)}\tau \sum _{n=0}^m\Vert {\delta }_x{U}^{n-i}\Vert +\sum _{n=0}^m\left(\frac{3\tau \beta }{2}\Vert {\delta }_x{U}^0\Vert +\frac{3\tau \mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}{\tau }^{\beta }}\underset{0\le n\le m}{\max }\Vert f^n\Vert \right).\hfill \end{array}$$

Let $b_n=\frac{3\tau \beta }{2}{\sum }_{n=0}^m\Vert {\delta }_x{U}^0\Vert +\frac{3{\tau }^{1-\beta }\mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}}{\sum }_{n=0}^m\underset{0\le n\le m}{\max }\Vert f^n\Vert$. We can thus obtain that $b_n$ is a positive nondecreasing sequence with respect to n. Hence, by the above inequalities and Lemma 11, we have

$$\begin{array}{cc}\hfill & \tau \sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \hfill \\ \hfill & \le \left(\frac{3\tau \beta }{2}\sum _{n=0}^m\Vert {\delta }_x{U}^0\Vert +\frac{3{\tau }^{1-\beta }\mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}}\sum _{n=0}^m\underset{0\le n\le m}{\max }\Vert f^n\Vert \right)exp\left(\sum _{i=1}^{n-1}\frac{3M{C}_1(\beta +1)}{2(n-1)}\right)\hfill \\ \hfill & \le \left(\frac{3\tau \beta }{2}\sum _{n=0}^m\Vert {\delta }_x{U}^0\Vert +\frac{3C_1\mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}}\underset{0\le n\le m}{\max }\Vert f^n\Vert \right)exp\left(\frac{3M{C}_1(\beta +1)}{2}\right).\hfill \end{array}$$

Let $C=max\{\frac{3T\beta }{2},\frac{3C_1\mathsf{\Gamma }(\beta +2)}{2\sqrt{6}{L}^{-1}}\}\exp (\frac{3M{C}_1(\beta +1)}{2})$, the following inequality holds

$$\begin{array}{c}\hfill \tau \sum _{n=0}^m\Vert {\delta }_x{U}^n\Vert \le C\left(\Vert {\delta }_x{U}^0\Vert +\underset{0\le n\le m}{\max }\Vert f^n\Vert \right),\end{array}$$

which is the desired result. □

Define $e_j^n=u_j^n-U_j^n$ ($0\le j\le M,0\le n\le N$) as errors at each mesh point $(x_j,t_n)$; then, the error bound of our numerical scheme will be considered as follows. (To make the following expression succinct, the subscript j will be neglected.)

Theorem 3.

Let $u^n\in C_{x,t}^{6,2}([0,L]\times [0,T])$ be the exact solution of Equation (1) and $U^n$ be the numerical solution of Equation (12), if ${\tau }^{1-\beta }N\le C_1$ and $T\ge 1$; then, the error bound is as follows:

$$\tau \sum _{n=0}^m{\Vert e^n\Vert }_{\infty }\le C({\tau }^2+h^4),$$

where C is a positive constant, and it depends on T.

Proof. 

By definition of $e^n$, then the error equation is as follows

$$\frac{1}{{\tau }^{\alpha }}\sum _{i=0}^n{w}_i^{\left(\alpha \right)}\mathcal{H}{e}^{n-i}=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n{\delta }_x^2{e}^{n-i}+R^n.$$

(21)

Taking the inner product of inequality (21) with $\tau \mathcal{H}{e}^n$, we obtain

$$\begin{array}{c}\hfill {\tau }^{1-\alpha }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{e}^{n-i},\mathcal{H}{e}^n)=\frac{\tau }{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n({\delta }_x^2{e}^{n-i},\mathcal{H}{e}^n)+\tau (R^n,\mathcal{H}{e}^n).\end{array}$$

(22)

By Equation (7), Lemma 9 and inequality (22), we have

$$\begin{array}{cc}\hfill & {\tau }^{1-\alpha -\beta }\sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{e}^{n-i},\mathcal{H}{e}^n)+\frac{2\tau }{3\mathsf{\Gamma }(\beta +2)}{\Vert {\delta }_x{e}^n\Vert }^2\hfill \\ \hfill & \le \frac{{\tau }^{1-\beta }}{\mathsf{\Gamma }\left(\beta \right)}\sum _{i=0}^n{\kappa }_{n-i,n}^n({\delta }_x^2{e}^{n-i},\mathcal{H}{e}^n)+{\tau }^{1-\beta }(R^n,\mathcal{H}{e}^n).\hfill \end{array}$$

(23)

By inequality (18), inequality (23) and summing the above expression from n = 1 to m and $1\le m\le N$, we obtain

$$\begin{array}{cc}\hfill & {\tau }^{1-\alpha -\beta }\sum _{n=0}^m\Vert {\delta }_x{e}^n\Vert \sum _{i=0}^n{w}_i^{\left(\alpha \right)}(\mathcal{H}{e}^{n-i},\mathcal{H}{e}^n)+\frac{2\tau }{3\mathsf{\Gamma }(\beta +2)}\sum _{n=0}^m\Vert {\delta }_x{e}^n\Vert \hfill \\ \hfill & \le \frac{{\tau }^{1-\beta }}{\mathsf{\Gamma }\left(\beta \right)}\sum _{n=0}^m\sum _{i=0}^n{\kappa }_{n-i,n}^n\Vert {\delta }_x{e}^{n-i}\Vert +\frac{{\tau }^{1-\beta }L}{\sqrt{6}}\sum _{n=0}^m\Vert R^n\Vert .\hfill \end{array}$$

(24)

From Theorem 2, we get

$$\begin{array}{c}\hfill \tau \sum _{n=0}^m\Vert {\delta }_x{e}^n\Vert \le C_1\left(\Vert {\delta }_x{e}^0\Vert +\tau \sum _{n=0}^m\Vert R^n\Vert \right).\end{array}$$

(25)

By inequality (25) and Lemma 10, then

$$\begin{array}{cc}\hfill \tau \sum _{n=0}^m{\Vert e^n\Vert }_{\infty }& \le \frac{C_1{C}_2\sqrt{L}}{2}\left(\tau \sum _{n=0}^m{\Vert R^n\Vert }_{\infty }\right)\hfill \\ \hfill & \le C({\tau }^2+h^4),\hfill \end{array}$$

where C, $C_1$ and $C_2$ are the constants, and the desired result is obtained. □

4. Numerical Experiments

We will present several experiments which support the theoretical analysis in Section 3. All numerical tests were performed on an AMD Ryzen 7 4700U with Radeon Graphics (2.00 GHz) and 16 Gb of RAM, using MATLAB (R2020b).

Let N and M be two constants, and define $\tau =T/N$ and $h=L/M$ to be temporal step size and spatial step size, respectively. Let $u(x_j,t_n)$ be the exact solution of Equation (1) and $U_j^n$ be numerical solution of Equation (12). As in [14,25], we consider the $L^{\infty }$-norm errors and corresponding convergence rates in the following:

$$E_{\infty }(\tau ,h)=\underset{1\le j\le M,1\le n\le N}{\max }|u(x_j,t_n)-U_j^n|,Rat{e}^x=log(E_1/E_2)/log(h_1/h_2),$$

where $E_1$ and $E_2$ are errors correspond to grids with mesh sizes $h_1$ and $h_2$, respectively. In addition, we have

$$Rat{e}^t=log(E_1/E_2)/log({\tau }_1/{\tau }_2),$$

where $E_1$ and $E_2$ are errors correspond to grids with mesh sizes ${\tau }_1$ and ${\tau }_2$, respectively.

If we perform an $\alpha$-order Riemann-Liouville fractional integral on both sides of Equation (1), we can obtain new ($\alpha +\beta$)-order partial integro-differential equations. In [29], for $h_1=h_2=h$, the scheme is convergent with the order $O({\tau }^{1+\alpha }+h^2)$ when $u_{tt}(x,t)$ is singular at $t=0$ and $O({\tau }^2+h^2)$ when $u_{tt}(x,t)$ is smooth at $t=0$. According to the results of the following three examples, we find that our scheme is convergent with the order $O({\tau }^2+h^4)$.

Example 1.

In the first example, we choose $L=2$, $T=4$ and the force term as follows:

$$\begin{array}{c}\hfill f(x,t)=\left(\frac{t^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}+\frac{t^{\beta }{\pi }^2}{\mathsf{\Gamma }(\beta +1)}\right)sin\left(\pi x\right)-\left(\frac{96t^{4-\alpha }}{\mathsf{\Gamma }(5-\alpha )}+\frac{384{\pi }^2{t}^{\beta +4}}{\mathsf{\Gamma }(\beta +5)}\right)sin\left(2\pi x\right),\end{array}$$

where the corresponding initial term is $\phi \left(x\right)=sin\left(\pi x\right)$ and the exact solution is $u(x,t)=-4t^{4}sin\left(2\pi x\right)+sin\left(\pi x\right)$.

Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the numerical results of Example 1. Table 1, Table 2 and Table 3 give the time convergence rates and the corresponding errors for a given $M=100$ and different values of N. For different $\beta$ values, the experiment presents the error in the case of $\alpha =0.15$, 0.5 and 0.75. This experiment shows that convergence order in the temporal direction can achieve the global second order. Table 4, Table 5 and Table 6 show the convergence rates in space and the corresponding $L^{\infty }$ norm errors for $N=1000$ and different values of M. For different $\beta$ values, this experiment shows the errors in the case of $\alpha =0.15$, 0.5 and 0.75. The experiment demonstrates that convergence order in the spatial direction can be of the fourth order. One can see that they are in good agreement with the theoretical results.

Table 1. $L^{\infty }$ norm errors, convergence orders in temporal direction with $\alpha =0.15$ ($M=100$).

N	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet
20	1.0757 $\times {10}^{-1}$	–	1.4878 $\times {10}^{-1}$	–	1.5525 $\times {10}^{-1}$	–
30	4.8826 $\times {10}^{-2}$	1.95	6.6068 $\times {10}^{-2}$	2.00	6.8492 $\times {10}^{-2}$	2.02
40	2.7637 $\times {10}^{-2}$	2.00	3.6888 $\times {10}^{-2}$	2.03	3.8097 $\times {10}^{-2}$	2.04
50	1.7601 $\times {10}^{-2}$	2.02	2.3315 $\times {10}^{-2}$	2.06	2.4020 $\times {10}^{-2}$	2.07
60	1.2063 $\times {10}^{-2}$	2.07	1.5917 $\times {10}^{-2}$	2.09	1.6370 $\times {10}^{-2}$	2.10

Table 2. $L^{\infty }$ norm errors, convergence orders in temporal direction with $\alpha =0.5$ ($M=100$).

N	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet
20	1.0536 $\times {10}^{-1}$	–	1.4749 $\times {10}^{-1}$	–	1.5446 $\times {10}^{-1}$	–
30	4.7949 $\times {10}^{-2}$	1.94	6.5576 $\times {10}^{-2}$	2.00	6.8171 $\times {10}^{-2}$	2.02
40	2.7171 $\times {10}^{-2}$	2.00	3.6666 $\times {10}^{-2}$	2.02	3.7937 $\times {10}^{-2}$	2.04
50	1.7338 $\times {10}^{-2}$	2.01	2.3213 $\times {10}^{-2}$	2.05	2.3933 $\times {10}^{-2}$	2.06
60	1.1907 $\times {10}^{-2}$	2.06	1.5877 $\times {10}^{-2}$	2.08	1.6321 $\times {10}^{-2}$	2.10

Table 3. $L^{\infty }$ norm errors, convergence orders in temporal direction with $\alpha =0.75$ ($M=100$).

N	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet
20	1.0451 $\times {10}^{-1}$	–	1.4728 $\times {10}^{-1}$	–	1.5458 $\times {10}^{-1}$	–
30	4.7727 $\times {10}^{-2}$	1.93	6.5637 $\times {10}^{-2}$	2.00	6.8332 $\times {10}^{-2}$	2.01
40	2.7162 $\times {10}^{-2}$	2.00	3.6817 $\times {10}^{-2}$	2.01	3.8107 $\times {10}^{-2}$	2.03
50	1.7423 $\times {10}^{-2}$	2.00	2.3402 $\times {10}^{-2}$	2.03	2.4103 $\times {10}^{-2}$	2.05
60	1.2040 $\times {10}^{-2}$	2.03	1.6085 $\times {10}^{-2}$	2.06	1.6490 $\times {10}^{-2}$	2.08

Table 4. $L^{\infty }$ norm errors, convergence orders in spatial direction with $\alpha =0.15$ ($N=1000$).

M	$\mathit{\beta }$ = 0.1		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.9
	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex
20	6.2623 $\times {10}^{-1}$	–	6.2607 $\times {10}^{-1}$	–	6.2657 $\times {10}^{-1}$	–
25	2.6760 $\times {10}^{-1}$	3.81	2.6752 $\times {10}^{-1}$	3.81	2.6773 $\times {10}^{-1}$	3.81
30	1.2819 $\times {10}^{-1}$	4.04	1.2814 $\times {10}^{-1}$	4.04	1.2824 $\times {10}^{-1}$	4.04
35	6.9359 $\times {10}^{-2}$	4.00	6.9319 $\times {10}^{-2}$	4.00	6.9375 $\times {10}^{-2}$	4.00
40	4.0633 $\times {10}^{-2}$	4.00	4.0600 $\times {10}^{-2}$	4.00	4.0632 $\times {10}^{-2}$	4.01

Table 5. $L^{\infty }$ norm errors, convergence orders in spatial direction with $\alpha =0.5$ ($N=1000$).

M	$\mathit{\beta }$ = 0.1		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.9
	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex
20	6.2606 $\times {10}^{-1}$	–	6.2645 $\times {10}^{-1}$	–	6.2753 $\times {10}^{-1}$	–
25	2.6755 $\times {10}^{-1}$	3.81	2.6772 $\times {10}^{-1}$	3.81	2.6815 $\times {10}^{-1}$	3.81
30	1.2817 $\times {10}^{-1}$	4.04	1.2825 $\times {10}^{-1}$	4.04	1.2844 $\times {10}^{-1}$	4.04
35	6.9328 $\times {10}^{-2}$	4.00	6.9330 $\times {10}^{-2}$	4.00	6.9477 $\times {10}^{-2}$	4.00
40	4.0638 $\times {10}^{-2}$	4.00	4.0660 $\times {10}^{-2}$	4.00	4.0699 $\times {10}^{-2}$	4.01

Table 6. $L^{\infty }$ norm errors, convergence orders in spatial direction with $\alpha =0.75$ ($N=1000$).

M	$\mathit{\beta }$ = 0.1		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.9
	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex
20	6.2632 $\times {10}^{-1}$	–	6.2722 $\times {10}^{-1}$	–	6.2905 $\times {10}^{-1}$	–
25	2.6772 $\times {10}^{-1}$	3.81	2.6813 $\times {10}^{-1}$	3.81	2.6906 $\times {10}^{-1}$	3.81
30	1.2830 $\times {10}^{-1}$	4.03	1.2854 $\times {10}^{-1}$	4.03	1.2917 $\times {10}^{-1}$	4.02
35	6.9255 $\times {10}^{-2}$	4.00	6.9231 $\times {10}^{-2}$	4.01	6.9506 $\times {10}^{-2}$	4.02
40	4.0741 $\times {10}^{-2}$	4.00	4.0859 $\times {10}^{-2}$	4.00	4.1272 $\times {10}^{-2}$	4.00

Example 2.

In this example, we choose $L=T=1$ and the force term as follows:

$$\begin{array}{cc}\hfill f(x,t)=& \frac{24t^{4-\alpha }}{\mathsf{\Gamma }(5-\alpha )}{x}^4{(1-x)}^4\hfill \\ \hfill & -\frac{24t^{\beta +4}}{\mathsf{\Gamma }(5+\beta )}\left(12x^2{(1-x)}^4-32x^3{(1-x)}^3+12x^4{(1-x)}^2\right)\hfill \end{array}$$

For this test, the reference solution is under a very fine mesh ($N=M=2000$).

Table 7, Table 8, Table 9 and Table 10 show the numerical results of Example 2. Table 7 and Table 8 show the time convergence rates and corresponding numerical errors for $M=100$ and different values of N. Table 7 shows the results of $\alpha$ = 0.2 at $\beta$ = 0.2, 0.5 and 0.8. Table 8 shows the results of $\alpha$ = 0.5 at $\beta$ = 0.2, 0.5 and 0.8. Table 9 shows the space convergence rates and corresponding numerical errors for N = 1000 and different values of M, where $\alpha$ = 0.5 and $\beta$ = 0.2, 0.5 and 0.8. Table 10 shows the space convergence rates and corresponding numerical errors for $N=1000$ and different values of M, where $\alpha$ = 0.8 and $\beta$ = 0.2, 0.5 and 0.8.

Table 7. $L^{\infty }$ norm errors, convergence orders in temporal direction with $\alpha =0.2$ ($M=100$).

N	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet
80	3.5587 $\times {10}^{-7}$	–	4.7904 $\times {10}^{-7}$	–	4.7745 $\times {10}^{-7}$	–
120	1.6399 $\times {10}^{-7}$	$1.91$	2.1471 $\times {10}^{-7}$	$1.98$	2.1239 $\times {10}^{-7}$	$2.00$
160	9.4460 $\times {10}^{-8}$	$1.92$	1.2141 $\times {10}^{-7}$	$1.98$	1.1955 $\times {10}^{-7}$	$2.00$
200	6.1535 $\times {10}^{-8}$	$1.92$	7.8011 $\times {10}^{-8}$	$1.98$	7.6549 $\times {10}^{-8}$	$2.00$
240	4.3346 $\times {10}^{-8}$	$1.92$	5.4349 $\times {10}^{-8}$	$1.98$	5.3185 $\times {10}^{-8}$	$2.00$

Table 8. $L^{\infty }$ norm errors, convergence orders in temporal direction with $\alpha =0.5$ ($M=100$).

N	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet	E∞(τ,h)	Ratet
80	2.6455 $\times {10}^{-7}$	–	3.6887 $\times {10}^{-7}$	–	3.4948 $\times {10}^{-7}$	–
120	1.2312 $\times {10}^{-7}$	$1.89$	1.6556 $\times {10}^{-7}$	$1.98$	1.5537 $\times {10}^{-7}$	$2.00$
160	7.1366 $\times {10}^{-8}$	$1.90$	9.3688 $\times {10}^{-8}$	$1.98$	8.7392 $\times {10}^{-8}$	$2.00$
200	4.6695 $\times {10}^{-8}$	$1.90$	6.0216 $\times {10}^{-8}$	$1.98$	5.5918 $\times {10}^{-8}$	$2.00$
240	3.3001 $\times {10}^{-8}$	$1.91$	4.1955 $\times {10}^{-8}$	$1.98$	3.8817 $\times {10}^{-8}$	$2.00$

Table 9. $L^{\infty }$ norm errors, convergence orders in spatial direction with $\alpha =0.5$ ($N=1000$).

M	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex
5	1.9612 $\times {10}^{-4}$	–	1.6038 $\times {10}^{-4}$	–	1.4915 $\times {10}^{-4}$	–
10	1.1815 $\times {10}^{-5}$	$3.84$	1.1132 $\times {10}^{-5}$	$3.85$	1.0256 $\times {10}^{-5}$	$3.86$
20	7.8367 $\times {10}^{-7}$	$3.91$	7.4692 $\times {10}^{-7}$	$4.00$	6.9964 $\times {10}^{-7}$	$3.90$
40	4.9249 $\times {10}^{-8}$	$4.00$	4.6857 $\times {10}^{-8}$	$4.00$	4.3776 $\times {10}^{-8}$	$4.00$
80	3.1877 $\times {10}^{-9}$	$4.00$	2.9625 $\times {10}^{-9}$	$4.00$	2.6208 $\times {10}^{-9}$	$4.06$

Table 10. $L^{\infty }$ norm errors, convergence orders in spatial direction with $\alpha =0.8$ ($N=1000$).

M	$\mathit{\beta }$ = 0.2		$\mathit{\beta }$ = 0.5		$\mathit{\beta }$ = 0.8
	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex	E∞(τ,h)	Ratex
5	1.6038 $\times {10}^{-4}$	–	1.4915 $\times {10}^{-4}$	–	1.3523 $\times {10}^{-4}$	–
10	1.1132 $\times {10}^{-5}$	$3.85$	1.0256 $\times {10}^{-5}$	$3.86$	9.4517 $\times {10}^{-6}$	$3.84$
20	7.4663 $\times {10}^{-7}$	$3.90$	6.9930 $\times {10}^{-7}$	$3.90$	6.4053 $\times {10}^{-7}$	$3.90$
40	4.6564 $\times {10}^{-8}$	$4.00$	4.3441 $\times {10}^{-8}$	$4.00$	3.9510 $\times {10}^{-8}$	$4.02$
80	2.5944 $\times {10}^{-9}$	$4.17$	2.2607 $\times {10}^{-9}$	$4.26$	1.8297 $\times {10}^{-9}$	$4.43$

The numerical results of this example show that the convergence order in the temporal and spatial directions can reach the second and fourth orders, respectively. The results of Example 2 show that the convergence orders match the theoretical ones.

Example 3.

For the last test, we choose $L=T=1$. The force term is the following:

$$\begin{array}{cc}\hfill & f(x,t)=\left(\frac{t^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}-\frac{24t^{4-\alpha }}{\mathsf{\Gamma }(5-\alpha )}+\frac{25{\pi }^2{t}^{\beta +1}}{\mathsf{\Gamma }(\beta +2)}-\frac{600{\pi }^2{t}^{\beta +4}}{\mathsf{\Gamma }(\beta +5)}\right)sin\left(5\pi x\right),\hfill \end{array}$$

where the corresponding initial term is $\phi \left(x\right)=0$ and the exact solution is $u(x,t)=(t-t^4)sin(5\pi x)$.

Let $M=100$ and $N=2000$. In Figure 1, we display the exact solution and numerical solution and the corresponding absolute error and contour plot absolute error with $\alpha =0.1$ and $\beta =0.1$. Similarly, the exact solution, numerical solution and corresponding error are presented in Figure 2 with $\alpha =0.9$ and $\beta =0.9$. One can obviously see that our method can achieve the desired accuracy.

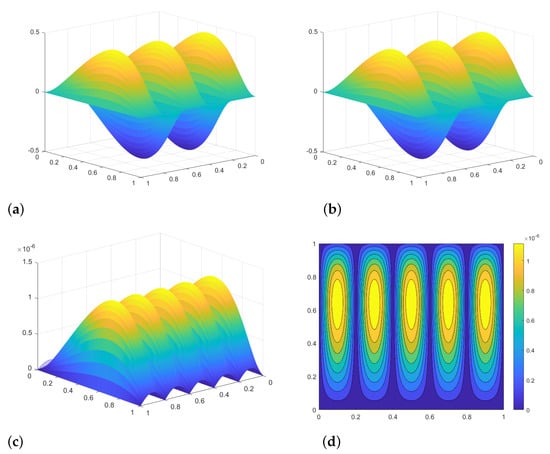
Figure 1. Exact solution, numerical solution, absolute error and contour plot of absolute error for Example 3 with $\alpha =\beta =0.1$, $M=100$ and $N=2000$: (a) Exact solution; (b) Numerical solution; (c) Absolute Error; (d) Contour plot absolute error.

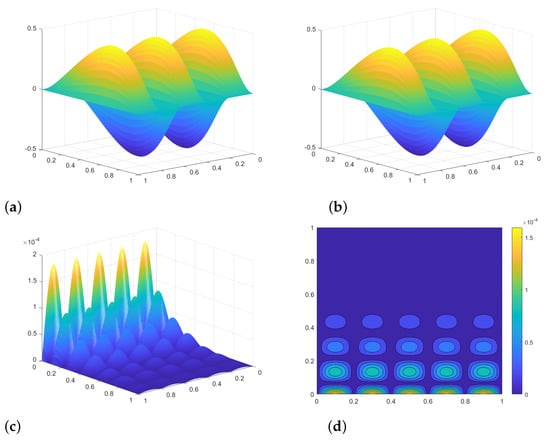
Figure 2. Exact solution, numerical solution, absolute error and contour plot of absolute error for Example 3 with $\alpha =\beta =0.9$, $M=100$ and $N=2000$: (a) Exact solution; (b) Numerical solution; (c) Absolute Error; (d) Contour plot absolute error.

5. Conclusions

The main result of this work is that an efficient finite difference numerical scheme is proposed and analyzed for time-fractional integro-differential equations, in which the derivative is defined as a Riemann-Liouville derivative. The stability analysis and error bound of the presented numerical method are carried out, and the convergence order is $O({\tau }^2+h^4)$. Several numerical experiments are given to support the theoretical analysis. Furthermore, the accuracy of the discrete scheme constructed in this paper is not affected by the parameters $\alpha$ and $\beta$. Development of fast and parallel-in-time methods [42,43] for accelerating the numerical schemes of time-fractional PDEs can be carried out in our future work. At the same time, we will try to study the high-order numerical schemes of fractional integro-difference equations to solve nonlinear and high-dimensional problems.