Abstract
In real-life control problems, such as power systems, there are large-scale high-ranked discrete-time algebraic Riccati equations (DAREs) from fractional systems that require stabilizing solutions. However, these solutions are no longer numerically low-rank, which creates difficulties in computation and storage. Fortunately, the potential structures of the state matrix in these systems (e.g., being banded-plus-low-rank) could be beneficial for large-scale computation. In this paper, a factorized structure-preserving doubling algorithm (FSDA) is developed under the assumptions that the non-linear and constant terms are positive semidefinite and banded-plus-low-rank. The detailed iteration scheme and a deflation process for FSDA are analyzed. Additionally, a technique of partial truncation and compression is introduced to reduce the dimensions of the low-rank factors. The computation of residual and the termination condition of the structured version are also redesigned. Illustrative numerical examples show that the proposed FSDA outperforms SDA with hierarchical matrices toolbox (SDA_HODLR) on CPU time for large-scale problems.
1. Introduction
Consider the fractional system [1,2]
where and () represents the order of the fractional derivative, , and with . If is approximated by the Grünwald–Letnikov rule [3] at , the system (1) is equivalent to the discrete-time linear system
where and . The corresponding optimal control and the feedback gain can be expressed in terms of the unique positive semidefinite stabilizing solution of the discrete-time algebraic Riccati Equation (DARE)
There have been numerous methods, including classical and state-of-the-art techniques, developed over the past few decades to solve this equation in a numerically stable manner. See [4,5,6,7,8,9,10,11,12,13,14,15] and the references therein for more details.
In many large-scale control problems, the matrix in the non-linear term and in the constant term are of low-rank with , , , , and . Then the unique positive definite stabilizing solution in the DARE (3) or its dual equation can be approximated numerically by a low-rank matrix [16,17]. However, when the constant term H in the DARE equation has a high-rank structure, the stabilizing solution is no longer numerically low-ranked, making its storage and outputting difficult. To solve this issue, an adapted version of the doubling algorithm, named SDA_h, was proposed in [18]. The main idea behind SDA_h is to take advantage of the numerical low-rank of the stabilizing solution in the dual equation to estimate the residual of the original DARE. In this way, SDA_h can efficiently evaluate the residual and output the feedback gain. An interesting question up to now is:
- Can SDA solve the large-scale DAREs efficiently when both G and H are of high-rank?
The main difficulty, in this case, lies in that the stabilizing solutions both in DARE (3) and its dual equation are not of low-rank, making the direct application of SDA difficult for large-scale problems, especially the estimation of residuals and the realization of algorithmic termination. This paper attempts to overcome this obstacle. Rather than answering the above question completely, DARE (3) with the banded-plus-low-rank structure
is considered, where is a banded matrix, , are low-rank matrices and is the kernel matrix with . The assumption of (4) is not necessary when G and H are of low rank, i.e., in that case A is allowed to be any (sparse) matrix. We also assume that the high-rank non-linear item and the constant item are of the form
where , are positive semidefinite banded matrices, , , and are symmetric and (here and might be zero). In addition, we assume that , , and are all banded matrices with banded inverse (BMBI), which has some applications in the power system [19,20,21]. See also [22,23,24,25,26,27,28,29], as well as their references for other applications.
The main contributions in this paper are:
- Although the hierarchical (e.g., HODLR) structure [30,31] can be employed to run the SDA to cope with large-scale DAREs with both high-rank H and G, it is the first to develop SDA to the factorized form—FSDA—to deal with such DAREs.
- The structure of the FSDA iterative sequence is explicitly revealed to consist of two parts—the banded part and the low-rank part. The banded part can iterate independently while the low-rank part relies heavily on the product of the banded part and the low-rank part.
- A deflation process of the low-rank factors is proposed to reduce the column number of the low-rank part. The conventional truncation and compression in [17,18] for the whole low-rank factor does not to work as it destroys the implicit structure and makes the subsequent deflation infeasible. Instead, a partial truncation and compression (PTC) technique is then devised to impose merely on the exponentially increasing part (after deflation), effectively slimming the dimensions of the low-rank factors.
- The termination criterion of FSDA consists of two parts. The residual of the banded part is considered in the pre-termination, and only if it is small enough, the actual termination criterion involving the low-rank factors is computed. This way, the time-consuming detection of the terminating condition is reduced in complexity.
The research in this field is also motivated by other applications, such as the finite element methods (FEM). In FEM, the matrices resulting from discretizing the matrix equations exhibit a sparse and structured pattern [32,33]. By capitalizing on these advantages, iterative methods designed for such matrices can significantly enhance computational efficiency, minimize memory usage, and lead to quicker solutions for large-scale problems.
The whole paper is organized as follows. Section 2 describes the FSDA for DAREs (3) with high-rank non-linear and constant terms. The deflation process for the low-rank factors and kernels is given in Section 3. Section 4 dwells on the technique of PTC to slim the dimensions of low-rank factors and kernels. The way to compute the residual, as well as the concrete implementation of the FSDA, is described in Section 5. Numerical experiments are listed in Section 6 to show the effectiveness of the FSDA.
Notation 1.
(or simply I) is the identity matrix. For a matrix , denotes the spectral radius of A. For symmetric matrices A and , we say () if is a positive definite (semi-definite) matrix. Unless stated otherwise, the norm is the F-norm of a matrix. For a sequence of matrices , . For a banded matrix B, represents the bandwidth. Additionally, the Sherman–Morrison–Woodbury (SMW) formula (see [34] for example), is required in the analysis of iterative scheme.
2. SDA and the Structured Iteration for DARE
For DARE
and its dual equation
SDA [7] generates a sequence of matrices, for
with , , . Under some conditions (see also Theorem 1), converges to the zero matrix and and converge to the stabilizing solutions of and , respectively.
2.1. FSDA for High-Rank Terms
Given banded matrices , and , low-rank matrices , , , and , and kernels , , and in the structured initial matrices (4) and (5), the FSDA is described inductively as follows, where
with sparse banded matrices , low-rank factors , , , , kernel matrices , , and . Without loss of generality, we assume that and . Otherwise, and fulfill the assumption.
We first elaborate the concrete format of banded parts and low-rank factors for and . Note that banded parts are capable of iterating independently, regardless of the low-rank parts and kernels.
Case for .
In the first step, we will assume that and , i.e., these matrices have no low-rank part. Note that this is only performed in order to simplify exposition. The fully general case with non-trivial low-rank parts will be shown in the case .
Insert the initial matrices , , and and low-rank matrices and into SDA (7). It follows from the SMW formula that
with
It follows from [35] (Lem 4.5) that the iteration (9) is well defined if and are both positive semidefinite.
Case for general .
By inserting the banded matrices , and and the low-rank factors , , , and and the kernels , and into SDA (7), banded matrices at the k-th iteration are
with
The corresponding low-rank factors are
To express the kernels explicitly, let
and
with
Define the kernel components
and
Then the kernel matrices corresponding to , , and () at the k-th step are
and
Remark 1.
1. The banded parts in (13) in the FSDA can iterate independently of the low-rank parts, motivating to the pre-termination criterion in Section 5.
2. Low-rank factors in (14)–(17) are seen growing in dimension on a scale of , obviously intolerable for large-scale problems. So a deflation process and a truncation and compression technique are required to reduce the dimensions of the low-rank factors.
3. In real implementations, low-rank factors and kernels for are actually deflated, truncated, and compressed, as described in the next two sections, where a superscript “” is added to the upper right corner of each low-rank factor. Correspondingly, column numbers , , , and are the ones after deflation, truncation, and compression. Here, we temporarily omit this superscript “” just for the convenience when describing the successive iteration process.
2.2. Convergence and the Evolution of the Bandwidth
To obtain the convergence, we further assume that
and
The following theorem concludes the convergence of SDA (7), see [35] (Thm 4.3, Thm 4.6) or [36] (Thm 3.1).
Theorem 1.
Corollary 1.
Proof.
Corollary 2.
Under the conditions of Theorem 1 and Corollary 1, the symmetric positive semidefinite solutions and to DARE (3) and its dual equation have the decompositions
Moreover, for the sequences generated by FSDA, and converge to zero, and converge to and and, and converge to and , respectively, all quadratically.
Proof.
It follows from (26) that converges to zero. Then the decomposition in (8) together with imply that the sequence will converge to zero quadratically.
Additionally, as the sequences and converge quadratically, by (26), to the unique solutions and , respectively, and
in (8). So, given the initial banded matrices and , the iterations and in (9) and (13) are independent of the low-ranked part and have the unique limits and , respectively. Consequently, the sequences and converge quadratically to the matrices and , respectively. □
Remark 2.
1. Although the product converges to zero, it follows from (15), (17) and (23) that the kernel and low-rank factors and might still not converge to zero, respectively.
2. If the convergence of SDA (or the corresponding FSDA) is quadratic, the number of the iterations k is not big when termination occurs, then the matrices and are generally of numerical low-rank.
To show the evolution of the bandwidth of , and , we first require the following result [37].
Theorem 2.
Let be an matrix. Assume that there is a number m such that if and that and for some and . Then for , there are numbers and depending only on , and m, such that
We now consider the evolution of the bandwidth for the banded parts.
Theorem 3.
Proof.
It follows from [35] (Thm 4.6) that and are non-singular for all k. This together with (29) indicate that there is an integer such that and the increment of and in (13) satisfies
where is the given the truncation tolerance. On the other hand for , it follows from Theorem 2 that there are and independent of k, such that
Then one has
for . Now recalling the iteration (9), the bandwidths of the first iteration admit the bounds
3. Deflation of Low-Rank Factors and Kernels
It has been shown that there is an exponential increase in the dimension of low-rank factors and kernels. Nevertheless, it is clear that the first three items in and (see (15) and (17)) are same as the second to the fourth item in and (see (14) and (16)), respectively. Then the deflation of low-rank factors and kernels is needed to keep these matrices low-ranked. To see this process clearly, we start with the case .
Case for .
Consider the deflation of the low-rank factors firstly. It follows from (14)–(17) that
with
Expanding the above low-rank factors with the initial and , one can see from Appendix A that and (or and ) occur twice in (or ). To reduce the dimension of , we remove the duplicated in (or in ) and retain the one in (or ). Furthermore, we remove in (or in ) and keep the one in (or ). Then the original (or ) is deflated to (or ) of a smaller dimension, where the superscript “d ” indicates the matrix after deflation. Analogously, as and appear twice in and , we apply the same deflation process to and , respectively, obtaining and in Appendix A, where the left blank in each factor corresponds to the deleted matrix and the black bold matrices inherit from the undeflated ones. Note that the deflated matrices , , and are still denoted by , , and , respectively, in next iteration to simplify notations.
For the kernels at , one has
and
with non-zero components defined in (18)–(20). Here, details of the deflation of are explained explicitly and that for is similar. In fact, there are 10 block rows and block columns with each of initial size in . Due to the deflation of the L-factors described above, we add the first and the ninth row to the third and the seventh row and then remove the first and the ninth row, respectively. We also add the the first and the ninth column to the third and the seventh column and then remove the first and the ninth column, respectively, completing the deflation of .
Analogously, there are eight block rows and block columns, each of the initial size in . The deflation process simultaneously adds the seventh column and row subblocks to the third column and row subblocks, respectively. Then the first column sub-block of the upper right and the first row sub-block of the lower-left overlap with the first column sub-block of and the first row sub-block of , respectively, completing the deflation of .
The whole process is described in Figure 1 and Figure 2 where each small square is of size and each block with gray background represents the non-zero component in and . The little white squares in and inherit from the originally undeflated submatrices and the little black squares in and represent the submatrices after summation.
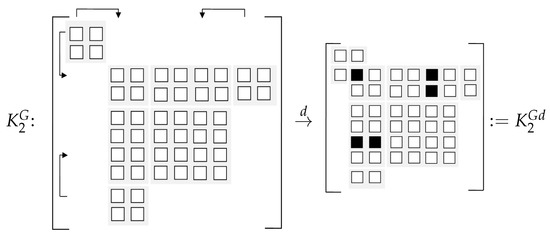
Figure 1.
The deflation process of (or ).
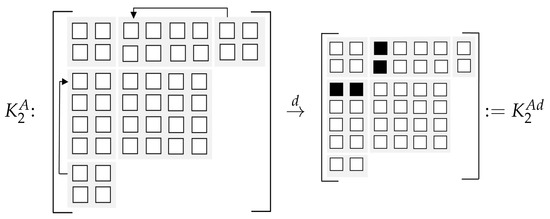
Figure 2.
The deflation process of .
Case for .
After the -th deflation, the deflated matrices , , and are denoted by , , and for simplicity. Now there are (or ) columns in and (or and ) and (or ) columns in and (or and ) that are identical. Then, one can remove columns of
and
and keep the columns of
and
in (A1) (or (A3)), respectively. So there are matrices, each of order , that are left in (or ), i.e., in (A1) (or in (A3)) in Appendix B. Meanwhile, only one matrix of order is left in , (or ), i.e., the last item in (A1) (or in (A3)) of Appendix B. We also take as an example to describe the above deflation more clearly in Appendix C.
To deflate (), columns of
are removed but the columns of
are retained in (or ). So only one matrix of order is left in (or ), i.e., the last item in (A2) (or in (A4)) of Appendix B. Note that the low-rank factors in the -th iteration are the ones after deflation, truncation and compression, deleting the superscript “d” for the simplicity. We take as an example to describe the above deflation more clearly in Appendix D.
Correspondingly, the kernel matrices , , and are deflated according to their low-rank factors. Here, we describe the deflation of and that of is essentially the same. By recalling the place of non-zero sub-matrices (the block with gray background in Figure 3) of in (21), the deflation process essentially adds to , columns to and rows to , respectively. See Figure 3 for illustration.
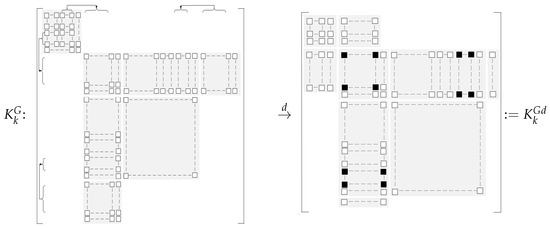
Figure 3.
The deflation process of (or ).
Similarly, by recalling the positions of non-zero matrices (the block with gray background in Figure 4) of in (23), the deflation process will add columns to columns and rows to rows . See Figure 4 for illustration.
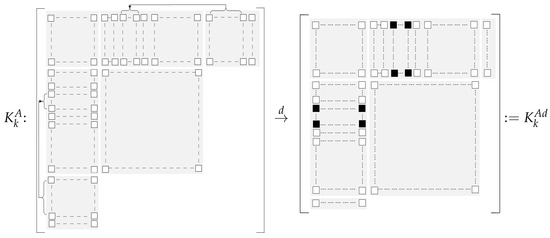
Figure 4.
The deflation process of .
4. Partial Truncation and Compression
Although the deflation of the low-rank factors and kernels in the last section can reduce dimensional growth, the exponential increment of the undeflated part is still rapid, making large-scale computation and storage infeasible. Conventionally, one efficient way to shrink the column number of low-rank factors is by truncation and compression (TC) [17,18], which, unfortunately, is hard to be applied to our case due to the following two main obstacles.
- Direct application of TC to , , , , and their corresponding kernels , and at the k-th step will require four QR decompositions, resulting in a relatively high computational complexity and CPU consumption.
- The TC process applied to the whole low-rank factors at current step breaks up the implicit structure, causing the deflation to be unrealized in the next iteration.
In this section, we will instead present a technique of partial truncation and compression (PTC) to overcome the above difficulties. Our PTC only requires two QR decompositions of the exponentially increasing (not the entire) parts of low-rank factors, keeping the successive deflation for subsequent iterations.
PTC for low-rank factors. Recall the deflated forms (A1) and (A3) in Appendix B. and can be divided to three parts
The number of columns in
and
increases only linearly with k, and the last parts
and
are always of size . So we only truncate and compress the dominantly growing parts
and
by orthogonalization. Consider the QR decompositions with column pivoting of
where and are permutation matrices such that the diagonal elements of ( or H) are decreasing in absolute value, , and and are some small tolerances controlling PTC of and , respectively, and are the respective column numbers of and bounded above by some given . Then their ranks satisfy
with . Furthermore, and are orthonormal and and are full-rank with . Then and can be truncated and reorganized as
with and .
Similarly, recalling the deflated forms in (A2) and (A4) in Appendix B, and are also divided into two parts,
with
Since and have been compressed to and , respectively, one has the truncated and compressed factors
with and , finishing the PTC process for the low-rank factors in the k-th iteration.
It is worth noting that the above PTC process can proceed to the next iteration. In fact, one has
after the k-th PTC. As is equal to and is equal to , one can deflate and to
with
Applying PTC to and , respectively, again, one has
where and are unitary matrices from QR decomposition and the PTC in the -th iteration is completed.
To eliminate items less than and in the low-rank factors and kernels, an additional monitoring step is imposed after the PTC process. Specifically, the last item in (or in ) will be discarded if its norm is less than (or ). Similarly, in (or in ) will be abandoned if its norm is less than (or ). In this way, the growth of column dimension in the low-rank factors , , and , as well as the kernels , , , will be controlled efficiently while sacrificing a hopefully negligible bit of accuracy. Additionally, their sizes after PTC will be further restricted by setting a reasonable upper bound .
5. Algorithm and Implementation
5.1. Computation of Residuals
The computation of relative residuals, such as , is commonly used in the context of solving the DARE using SDA, as mentioned in [4]. Typically, the FSDA algorithm is designed to stop when the relative residual is sufficiently small, which guarantees that the approximated solution is close to the exact solution of the DARE [35]. However, computing directly can be computationally expensive due to the high rank of and . To overcome this difficulty, the residual is divided into two parts, the banded part and the low-ranked part, under the assumptions of Equations (4) and (5). The residual for the banded part can be computed relatively easily and serves as a pre-termination condition, followed by the termination of the entire FSDA algorithm based on the residual for the low-ranked part.
5.1.1. Residual for the Banded Part
Define
and
With the current approximated solution , the residual for DARE (3) is
where the banded part, the low-rank part and the kernel are
respectively, and
It is not difficult to see that the main flop counts in the kernel lie in forming matrices
To avoid calculating them in each iteration, we first verify if
with and being the band tolerance. Here, the norm is the matrix spectral norm, which is not easy to compute and is replaced by -matrix norm in practice. This is feasible as the residual of comes from two relatively independent parts, i.e., the banded part and the low-rank part.
5.1.2. Residual for the Low-Rank Part
When the pre-termination (39) is satisfied, matrices in (38) are then constructed, followed by the deflation, truncation, and compression of the low-rank factor . Specifically, the columns are removed and columns of are kept such that is deflated to , i.e.,
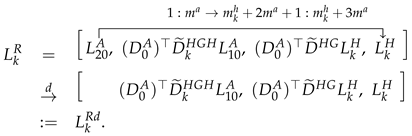
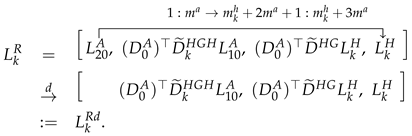
Let , . The kernel in (37) is correspondingly deflated as
where all elements in are same to those in except .
After deflation, the truncation and compression are applied to with QR decomposition
where is the permutation matrix such that the diagonal elements of are decreasing in absolute value, and is the given tolerance, is orthonormal and is full-ranked. Since , the terminating condition of the whole algorithm is chosen to be
with being the low-rank tolerance.
5.2. Algorithm and Operation Counts
The process of deflation and PTC together with the computation of residuals (39) and (40) are summarized in the FSDA Algorithm 1.
| Algorithm 1 FSDA. Solve DAREs with high-ranked G and H |
|
Remark 3.
1. At each iteration, elements in the banded matrices , , and with an absolute value less than are eliminated.
2. The deflation process involves merging selected rows and columns in the kernels , , and based on overlapping columns in the low-rank factors , , , and . This requires adding some columns and rows.
3. The PTC is applied to and . The column numbers of and increase linearly with respect to while those of and remain unchanged. Elements in , , , and with an absolute value less than are removed to minimize the column size of the low-rank factors.
To further analyze the complexity and the memory requirement of the FSDA, the bandwidth of , , and at each iteration are assumed to be , and (), respectively. We also set , , , and for the convenience of counting flops. The table in Appendix E lists the time and memory requirement for different components in the k-th iteration of the FSDA, where the estimations are upper bounds due to the truncation errors , and .
6. Numerical Examples
In this section, we will demonstrate the effectiveness of the FSDA algorithm in computing the approximate solution of the DARE (3). The FSDA algorithm was implemented using MATLAB 2014a [38] on a 64-bit PC running Windows 10. The PC had a 3.0 GHz Intel Core i5 processor with 6 cores and 6 threads, 32GB RAM, and a machine unit round-off value of eps = . The residual for the DARE was estimated using the upper bound formula
where B_RRes in (39) and LR_RRes in (40) are the relative residuals for the banded part and the low-rank part, respectively. The tolerance values for truncation and compression were set to , and the termination tolerance values were set to . We also tried eps as the tolerance value for , and in our experiments, but found that it had no impact on the residual accuracy. The maximum permitted column number in the low-rank factors was set to . As a comparison, we also ran the ordinary SDA algorithm with hierarchical structure (i.e., HODLR) using the hm-toolbox (http://github.com/numpi/hm-toolbox, accessed on 1 June 2023) [39,40]. The SDA algorithm with hierarchical structure is referred to as SDA_HODLR in this paper. The derived relative residual for SDA_HODLR is denoted by . In our numerical experiments, the initial bandwidths of all banded matrices in Examples 1 and 3 were relatively small, while those in Example 2 were non-trivial.
Example 1.
The first example is of the medium scale, measuring the error between the true solution and the computed one. Given the constant, where ζ and η are positive numbers such that θ is real. Let with e the random vector satisfying , , , then . Set , . The solution of the DARE is of the form with and .
It is not difficult to see that the solution is stabilizing since the spectral radius of is less than unity when .
We first took and to calculate B_RRes, followed by LR_RRes as well as the upper bound of residual of DARE . In our implementations, the relative error between the approximated solution (denoted by when terminated at the j-th iteration) and the true stabilizing solution was evaluated, and the numerical results are presented in Table 1. It is seen that for different scales () FSDA was able to attain the prescribed banded accuracy in five iterations. Residuals LR_Res and were then evaluated, attaining the order . The relative error with the computational time being not included in the CPU time, also reflects that approximates the true solution very well. On the other hand, SDA_HODLR also attains the prescribed residual accuracy in five iterations, but cost more CPU time (in seconds).

Table 1.
Residual and actual errors in Example 1.
We then took to make the spectral radius of close to 1 and recorded the numerical performance of the FSDA with . It is seen from Table 1 that the FSDA costs seven iterations before termination, obtaining almost the same banded residual histories (B_RRes) for different N. As before, LR_RRes and were of and , respectively, showing that is a good approximation to the true solution to DARE (3). The last relative error also validates this fact. Analogously, SDA_HODLR requires seven iterations to arrive at the residual level . It is also seen that the FSDA costs less CPU time than SDA_HODLR for all N.
Example 2.
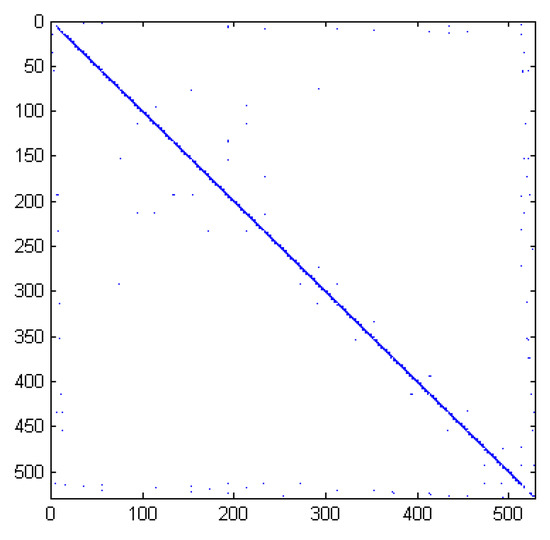
Consider a generalized model of power system labelled by PI Sections 20–80 (https://sites.google.com/site/rommes/software, “S10PI_n1.mat” accessed on 1 June 2023). All transmission lines in the network are modelled by RLC ladder networks, of cascaded RLC PI-circuits [41]. The original band-plus-low-rank matrix A has a small scale of 528 (Figure 5) and is then extended to larger ones. Specifically, we extract the banded part of the bandwidth 217 from the original matrix and tile it along the diagonal direction for 20 times to obtain . We then implement an SVD of the matrix to produce the singular value matrix and the unitary matrices and . The low-ranked parts and are then constructed by tiling and 20 times and multiplying from the right, respectively, where is the number of singular values in less than . Let and be block diagonal matrices with each diagonal block the random matrix (generated by‘rand(3)’). Let and be also diagonal block matrices with the top left element a random number, the last diagonal block random matrix and others random matrices. Define matrices G and H as
with , .

Figure 5.
Structured matrix of size in Example 2.
We ran the FSDA with three different , each conducting five random experiments. In all experiments, B_RRes and LR_RRes (in ) were observed attaining the pre-terminating condition (39) and the terminating condition (40), respectively.
Figure 6 plots the obtained numerical results for five experiments, where Rk is the upper bound of the residual of the DARE, BRes and LRes are the absolute residuals of the banded part and the low-rank part (i.e., the numerators in B_RRes and LR_RRes), respectively. It is seen that the relative residual levels of LR_RRes and B_RRes (between and ) are lower than those of LRes and BRes (between and ) in all experiments. Particularly, the gap between them increases as becomes larger. On the other hand, the residual line of Rk is above the residual lines of B_RRes or LR_RRes, attaining the level between and . This demonstrates that the FSDA can obtain a relatively high residual accuracy.
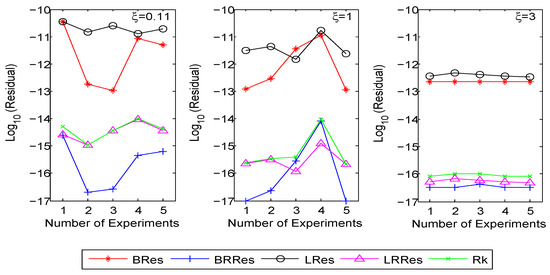
Figure 6.
Residual of the banded part and the low-rank part for different .
To clearly see the evolution of the bandwidth of the banded matrices and the dimensional increase in the low-rank factors for five iterations, we listed the history of bandwidths of , , and (denoted by , , and , respectively) and the column numbers of and (denoted by and , respectively) in Table 2, where the CPU row recorded the consumed CPU time in seconds. It is obviously seen that, for , and 3, the FSDA requires 5, 4, and 3 iterations to reach the prescribed accuracy, respectively. Further experiments show that the required number of iterations, when terminated, will decrease as goes larger. Additionally, we see that bandwidths and rise much in the second iteration but keep almost unchanged for the remaining iterations. Nevertheless, decreases gradually after reaching the maximal value in the second iteration, which is consistent with the convergence of in Corollary 1. On the other hand, we see from and that the column numbers in the second iteration are about fourfold of those in the first iteration since the FSDA does not deflate the low-rank factors at the first iteration. However, the column numbers in the fifth iteration (if it exists) are less than twofold of those in the fourth iteration. This reflects that deflation and PTC are efficient in reducing the dimensions of low-rank factors. In our experiments, we also found that nearly half of the CPU time in the FSDA was consumed in forming in the pre-termination. However, such a time expense might decrease if the initial bandwidths , , and are narrow.

Table 2.
CPU times and history of bandwidth of banded matrices and column numbers of low-rank factors in Example 2.
To further compare numerical performances between the FSDA and SDA_HODLR for larger problems, we extended the original scale to N = 15,840, 21,120, 26,400 and 31,680 at and ran both algorithms until convergence. The results are listed in Table 3, where one can see that both the FSDA and SDA_HODLR (i.e., SDA_HD in the table) attain the prescribed residual accuracy within three iterations, and SDA_HODLR requires less CPU time than FSDA does. However, there seems a strong tendency that the FSDA will outperform the SDA_HODLR on CPU time for larger problems, as the CPU time of the SDA_HODLR appears to surge at N = 26,400 and SDA_HODLR used up memory at N = 31,680 without producing any numerical results (denoted by “—”). The symbols “*” in the SDA_HODLR column represent no related records for bandwidth and column number of the low-rank factors.

Table 3.
Numerical results for FSDA and SDA_HODLR in Example 2 at . The symbol * stands for no related records.
We further modified this example to have a simpler banded part to test both algorithms. Specifically, the relatively data-concentrated banded part of bandwidth 3 is extracted and tiled along the diagonal direction for 20 times to form . As before, an SVD is imposed on the rest matrix to construct the low-ranked parts and after tiling the derived unitary matrices 20 times and multiplying from the right. We still selected and ran both the FSDA and SDA_HODLR at scales N = 15,840, 21,120, 26,400 and 31,680 again. The obtained results are recorded in Table 4, where it is readily seen that the FSDA outperforms the SDA_HODLR on CPU time. Once again, the SDA_HODLR ran out of memory for the case N = 31,680.

Table 4.
Numerical results for FSDA and SDA_HODLR in relatively simpler banded part of Example 2 at . The symbol * stands for no related records.
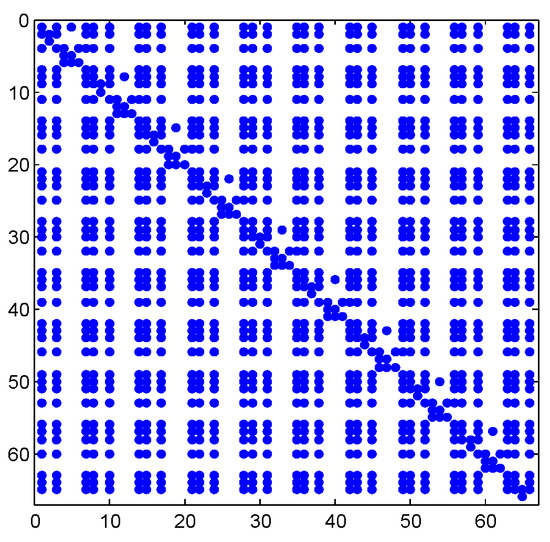
Example 3.
This example is an extension of small-scale electric power systems networks to a large-scale one which is used for signal stability analysis [19,20,21]. The corresponding matrix is from the power system of New England (https://sites.google.com/site/rommes/software, “ww_36_pemc_36.mat”, accessed on 1 June 2023). Figure 7 presents the original structure of the matrix A of order 66. We properly modified elements , , ; , , , . Then the banded part is extracted from blocks (1:6, 1:6), (7:13, 7:13), (14:20, 14:20), (21:27, 21:27), (28:34, 28:34), (35:41, 35:41), (42:48, 42:48), (49:55, 49:55), (56:62, 56:62), and (63:66, 63:66), admitting the bandwidth of 4. After tiling 200, 400, and 600 times along the diagonal direction, we obtain banded matrix of scales N = 13,200, 26,400 and 39,600. For the low-rank factors, an SVD of the matrix is firstly implemented to produce the diagonal singular value matrix and the unitary matrices and . The low-ranked parts and are then constructed by tiling and 200, 400, and 600 times and dividing their F-norms, respectively, where is the number of singular values in less than . The matrices G and H are
with .

Figure 7.
Structured matrix A of order (1194 non-zeros) in Example 3.
We took different and ran the FSDA to compute the stabilizing solution for different dimensions N = 13,200, 26,400, and 39,600. In our experiments, the FSDA always satisfied the pre-terminating condition (39) first and then terminated at LR_RRes . We picked and listed derived results in Table 5, where BRes (or LRes) and B_RRes (or LR_RRes) record the absolute and the relative residual for the banded part (or the low-rank part), respectively, and , record histories of the upper bound of the residual of DARE, the bandwidths of , and and the column numbers of the low-rank factors and , respectively. Particularly, the column describes the accumulated time to compute residuals (excluding the data marked with “*”).

Table 5.
Residuals, column numbers of low-rank factors, and CPU times at in Example 3.
Obviously, for different N, the FSDA is capable of achieving the prescribed accuracy after five iterations. The residuals BRes, B_RRes, LRes, and LR_RRes indicate that the FSDA tended to converge quadratically. Especially, BRes (or B_RRes) at different N are of nearly same order and terminate at (or ). Similarly, LRes (or LR_RRes) at different N attain the order (or ). More iterations seemed useless in improving the accuracy of LRes and LR_RRes. Note that data labelled with the superscript “*” in columns LRes, LR_RRes and come from the re-running of the FSDA to complement the residual in each iteration, and their corresponding CPU time is not included in the column . Lastly, indicate that the bandwidths of , , and are invariant and the column numbers of the low-rank factors grow less than twice in each iteration, demonstrating the effectiveness of the deflation and PTC.
We also ran the FSDA to compute the solution of the DARE of and the results were recorded in Table 6. In this case, the FSDA requires seven iterations to reach the prescribed accuracy. As before, the last few residuals in the column BRes (or B_RRes) at different N are almost the same of (or ). The residuals LRes (or LR_RRes) at different N terminate at (or ). In particular, BRes and B_RRes showed that the FSDA attained the prescribed accuracy at the 5th iteration, but the corresponding residual of the low-rank part was still between and . So two additional iterations were required to meet the termination condition (40), even if the residual level in B_RRes kept stagnant in the last three iterations. From a structured point of view, it seems that the low-rank part is approaching the critical case while the banded part still lies in the non-critical case. Similarly, [] indicate that , , and are all block diagonal with block sizes and the deflation and PTC for the low-rank factors are effective. Moreover, shows that the CPU times at the current iteration were less than twice that of the previous iteration when .

Table 6.
Residuals, spans of columns, and CPU times at in Example 3.
We further compare numerical performances between the FSDA and SDA_HODLR for large-scale problems. Different values of have been tried and the compared numerical behaviors of both algorithms are analogous. We list the results of and in Table 7, where one can see that the FSDA requires less iterations and CPU time to satisfy the stop criterion than the SDA_HODLR. Particularly, the SDA_HODLR depleted all memory at N = 39,600 and did not yield any numerical results (denoted by “—”). The symbols “*” in the SDA_HODLR column represent no related records for bandwidths and column numbers of the low-rank factors.

Table 7.
Numerical results between FSDA and SDA_HODLR of Example 3. The symbol * stands for no related records.
7. Conclusions
The stabilizing solution of the discrete-time algebraic Riccati Equation (DARE) from the fractional system, with high-rank non-linear term G and constant term H, is not of numerical low-rank. The structure-preserving doubling algorithm (SDA_h) proposed in [18] is no longer applicable for large scale problems. In some applications, such as in power systems, the state matrix A is of banded-plus-low-rank, and in those cases SDA can be further developed to the factorized structure-preserving doubling algorithm (FSDA) to solve large scale DAREs with high-rank non-linear and constant terms. Under the assumption that G and H are positive semidefinite and and are banded matrices with banded inverse (BMBI), we presented the iterative scheme of FSDA, as well as the convergence of the banded and the low-ranked parts. A deflation process and the technique of PCT are subsequently proposed to efficiently control the growth of the number of columns of low-rank factors. Numerical experiments have demonstrated that the FSDA always reaches the economical pre-terminating condition associated with the banded part before the real terminating condition related to the low-rank part, yielding good approximated solutions and to the DARE and its dual, respectively. Moreover, our FSDA is superior to the existing SDA_HODLR on the CPU time for large-scale DAREs. For future work, the computation of the stabilizing solution for CAREs might be further investigated. This will be more complicated as the Cayley transformation is incorporated and the selection of the corresponding parameter does not seem easy. In addition, other sparse structures of A and high-rank H and G might be investigated.
Author Contributions
Conceptualization, B.Y.; methodology, B.Y.; software, N.D.; validation, N.D.; and formal analysis, B.Y. All authors have read and agreed to the final version of this manuscript.
Funding
This work was supported in part by the NSF of China (11801163), the NSF of Hunan Province (2021JJ50032, 2023JJ50165), the foundation of Education Department of Hunan Province (HNJG-2021-0129) and Degree & Postgraduate Education Reform Project of Hunan University of Technology and Hunan Province (JG2315, 2023JGYB210).
Acknowledgments
Part of the work occurred when the first author visited Monash University. The authors also thank the editor and three anonymous referees for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Matrices , , and are actually the deflated, truncated and compressed low-rank factors , , and , respectively. We omit the superscript “dt” for the simpler notation.
Appendix B

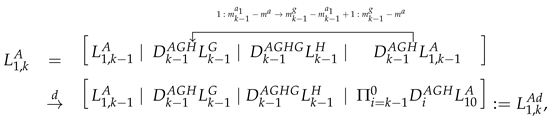
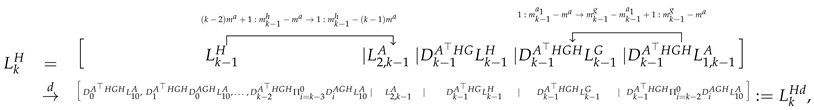
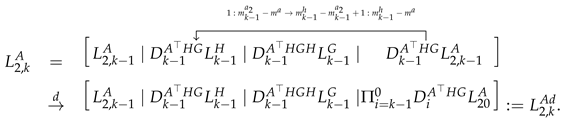
Matrices , , and are actually the deflated, truncated and compressed low-rank factors , , and , respectively. We omit the superscript “dt” for convenience.
Appendix C. Description for the Deflation of
After the previous deflation, there are columns in and (items marked with bold type in (A2) and (A3)) and columns (items marked with bold type in (A4) and (A5)) in and are identical. Then, one can remove columns of in (A2) and in (A5) (i.e., items with bold type in (A2) and (A5)), keep columns of in (A3) and in (A4) (i.e., items with bold type in (A3) and (A4)), respectively. Then there are two matrices with each of order are left in and only one matrix of order left in .
Note that matrices , , and are actually the deflated, truncated and compressed low-rank factors , , and , respectively.
Appendix D. Description for the Deflation of
To deflate , columns of are removed (i.e., items marked with bold type in (A7)) but columns of (i.e., items marked with bold type in (A6)) are retained in . So only one matrix of order is left in , i.e., the last item in (A8).
Note that matrices , and are actually the deflated, truncated, and compressed low-rank factors , , and , respectively.
Appendix E

Table A1.
Complexity and memory requirement at k-th iteration in the FSDA.
Table A1.
Complexity and memory requirement at k-th iteration in the FSDA.
| Items | Flops | Memory |
|---|---|---|
| Banded part | ||
| , * | ||
| , , | ||
| Low-rank part and kernels | ||
| , , | ||
| , , | ||
| , , | ||
| , , | ||
| , | ||
| , | ||
| , , | ||
| , | ||
| *, , | ||
| , ** | ||
| , , | ||
| , | ||
| Residual part | ||
| , | ||
| * | ||
| ** | ||
* LU factorization and Gaussian elimination is used [42]. ** Householder QR decomposition is used [12].
References
- Nosrati, K.; Shafiee, M. On the convergence and stability of fractional singular Kalman filter and Riccati equation. J. Frankl. Inst. 2020, 357, 7188–7210. [Google Scholar]
- Trujillo, J.J.; Ungureanu, V.M. Optimal control of discrete-time linear fractional-order systems with multiplicative noise. Int. J. Control 2018, 91, 57–69. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Benner, P.; Fassbender, H. The symplectic eigenvalue problem, the butterfly form, the SR algorithm, and the Lanczos method. Linear Algebra Appl. 1998, 275–276, 19–47. [Google Scholar]
- Chen, C.-R. A structure-preserving doubling algorithm for solving a class of quadratic matrix equation with M-matrix. Electron. Res. Arch. 2022, 30, 574–581. [Google Scholar]
- Chu, E.K.-W.; Fan, H.-Y.; Lin, W.-W. A structure-preserving doubling algorithm for continuous-time algebraic Riccati equations. Linear Algebra Appl. 2005, 396, 55–80. [Google Scholar]
- Chu, E.K.-W.; Fan, H.-Y.; Lin, W.-W.; Wang, C.-S. A structure-preserving doubling algorithm for periodic discrete-time algebraic Riccati equations. Int. J. Control 2004, 77, 767–788. [Google Scholar]
- Kleinman, D. On an iterative technique for Riccati equation computations. IEEE Trans. Autom. Control 1968, 13, 114–115. [Google Scholar] [CrossRef]
- Lancaster, P.; Rodman, L. Algebraic Riccati Equations; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Laub, A.J. A Schur method for solving algebraic Riccati equation. IEEE Trans. Autom. Control 1979, AC-24, 913–921. [Google Scholar]
- Li, T.-X.; Chu, D.-L. A structure-preserving algorithm for semi-stabilizing solutions of generalized algebraic Riccati equations. Electron. Trans. Numer. Anal. 2014, 41, 396–419. [Google Scholar]
- Mehrmann, V.L. The Autonomous Linear Quadratic Control Problem; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 1991; Volume 163. [Google Scholar]
- Mohammad, I. Fractional polynomial approximations to the solution of fractional Riccati equation. Punjab Univ. J. Math. 2019, 51, 123–141. [Google Scholar]
- Tvyordyj, D.A. Hereditary Riccati equation with fractional derivative of variable order. J. Math. Sci. 2021, 253, 564–572. [Google Scholar] [CrossRef]
- Yu, B.; Li, D.-H.; Dong, N. Low memory and low complexity iterative schemes for a nonsymmetric algebraic Riccati equation arising from transport theory. J. Comput. Appl. Math. 2013, 250, 175–189. [Google Scholar] [CrossRef]
- Benner, P.; Saak, J.A. Galerkin-Newton-ADI method for solving large-scale algebraic Riccati equations. In DFG Priority Programme 1253 “Optimization with Partial Differential Equations”; Preprint SPP1253-090; DFG: Bonn, Germany, 2010. [Google Scholar]
- Chu, E.K.-W.; Weng, P.C.-Y. Large-scale discrete-time algebraic Riccati equations—Doubling algorithm and error analysis. J. Comput. Appl. Math. 2015, 277, 115–126. [Google Scholar] [CrossRef]
- Yu, B.; Fan, H.-Y.; Chu, E.K.-W. Large-scale algebraic Riccati equations with high-rank constant terms. J. Comput. Appl. Math. 2019, 361, 130–143. [Google Scholar] [CrossRef]
- Martins, N.; Lima, L.; Pinto, H. Computing dominant poles of power system transfer functions. IEEE Trans. Power Syst. 1996, 11, 162–170. [Google Scholar] [CrossRef]
- Freitas, F.D.; Martins, N.; Varricchio, S.L.; Rommes, J.; Veliz, F.C. Reduced-Order Transfer Matrices from RLC Network Descriptor Models of Electric Power Grids. IEEE Trans. Power Syst. 2011, 26, 1905–1916. [Google Scholar] [CrossRef]
- Rommes, J.; Martins, N. Efficient computation of multivariable transfer function dominant poles using subspace acceleration. IEEE Trans. Power Syst. 2006, 21, 1471–1483. [Google Scholar] [CrossRef]
- Dahmen, W.; Micchelli, C.C. Banded matrices with banded inverses, II: Locally finite decomposition of spline spaces. Constr. Approx. 1993, 9, 263–281. [Google Scholar] [CrossRef]
- Cantero, M.J.; Moral, L.; Velázquez, L. Five-diagonal matrices and zeros of orthogonal polynomials on the unit circle. Linear Algebra Appl. 2003, 362, 29–56. [Google Scholar] [CrossRef]
- Kimura, H. Generalized Schwarz form and lattice-ladder realizations of digital filters. IEEE Trans. Circuits Syst. 1985, 32, 1130–1139. [Google Scholar] [CrossRef]
- Kavcic, A.; Moura, J. Matrices with banded inverses: Inversion algorithms and factorization of Gauss–Markov processes. IEEE Trans. Inf. Theory 2000, 46, 1495–1509. [Google Scholar] [CrossRef]
- Strang, G. Fast transforms: Banded matrices with banded inverses. Proc. Natl. Acad. Sci. USA 2010, 107, 12413–12416. [Google Scholar] [CrossRef] [PubMed]
- Strang, G. Groups of banded matrices with banded inverses. Proc. Am. Math. Soc. 2011, 139, 4255–4264. [Google Scholar] [CrossRef]
- Strang, G.; Nguyen, T. Wavelets and Filter Banks; Wellesley-Cambridge Press: Cambridge, UK, 1996. [Google Scholar]
- Olshevsky, V.; Zhlobich, P.; Strang, G. Green’s matrices. Linear Algebra Appl. 2010, 432, 218–241. [Google Scholar] [CrossRef]
- Grasedyck, L.; Hackbusch, W.; Khoromskij, B.N. Solution of large scale algebraic matrix Riccati equations by use of hierarchical matrices. Computing 2003, 70, 121–165. [Google Scholar] [CrossRef]
- Kressner, D.; Krschner, P.; Massei, S. Low-rank updates and divide-and-conquer methods for quadratic matrix equations. Numer. Algorithms 2020, 84, 717–741. [Google Scholar] [CrossRef]
- Benner, P.; Saak, J. A Semi-Discretized Heat Transfer Model for Optimal Cooling of Steel Profiles. In Dimension Reduction of Large-Scale Systems; Benner, P., Sorensen, D.C., Mehrmann, V., Eds.; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2005; Volume 45. [Google Scholar]
- Korvink, G.; Rudnyi, B. Oberwolfach Benchmark Collection. In Dimension Reduction of Large-Scale Systems; Benner, P., Sorensen, D.C., Mehrmann, V., Eds.; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2005; Volume 45. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Huang, C.-M.; Li, R.-C.; Lin, W.-W. Structure-Preserving Doubling Algorithms for Nonlinear Matrix Equations; SIAM: Washington, DC, USA, 2018. [Google Scholar]
- Lin, W.-W.; Xu, S.-F. Convergence analysis of structure-preserving doubling algorithms for Riccati-type matrix equations. SIAM J. Matrix Anal. Appl. 2006, 28, 26–39. [Google Scholar] [CrossRef]
- Demko, S. Inverses of band matrices and local convergence of spline projections. SIAM J. Numer. Anal. 1977, 14, 616–619. [Google Scholar] [CrossRef]
- Mathworks. MATLAB User’s Guide; Mathworks: Natick, MA, USA, 2010. [Google Scholar]
- Massei, S.; Palitta, D.; Robol, L. Solving rank structured Sylvester and Lyapunov equations. SIAM J. Matrix Anal. Appl. 2018, 39, 1564–1590. [Google Scholar] [CrossRef]
- Massei, S.; Robol, L.; Kressner, D. hm-toolbox: Matlab software for HODLR and HSS matrices. SIAM J. Sci. Comput. 2020, 42, C43–C68. [Google Scholar] [CrossRef]
- Watson, N.; Arrillaga, J. Power Systems Electromagnetic Transients Simulation; IET, Digital Libray: London, UK, 2003. [Google Scholar]
- Arbenz, P.; Gander, W. A Survey of Direct Parallel Algorithms for Banded Linear Systems; Tech. Report 221; Departement Informatik, Institut für Wissenschaftliches Rechnen, ETH Zürich: Zurich, Switzerland, 1994. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).