Investigation of Fractal Characteristics of Karman Vortex for NACA0009 Hydrofoil
Abstract
1. Introduction
2. Research Objective
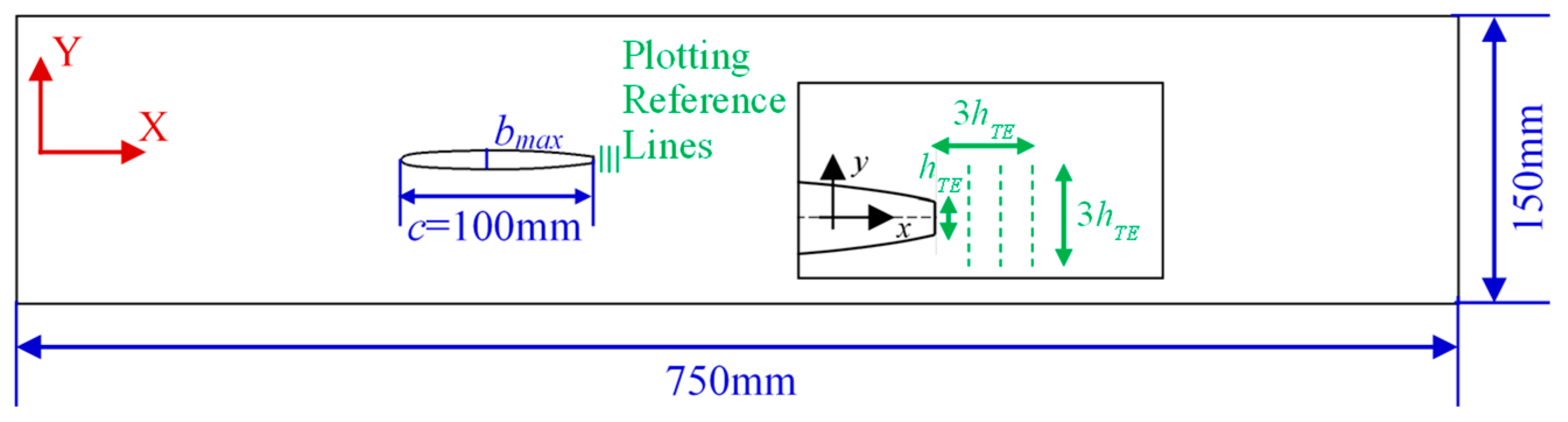
3. Numerical Simulation and Experiment
3.1. Turbulence Model
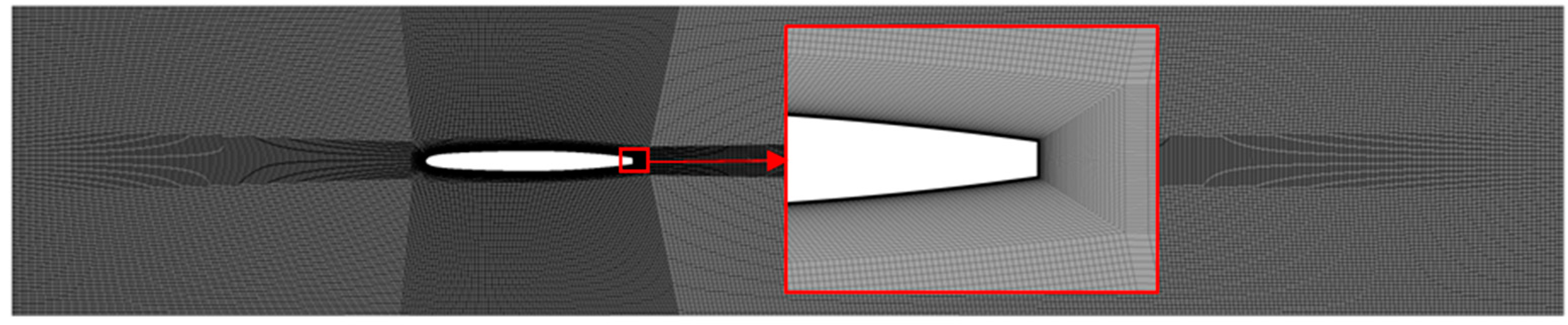
3.2. CFD Setup
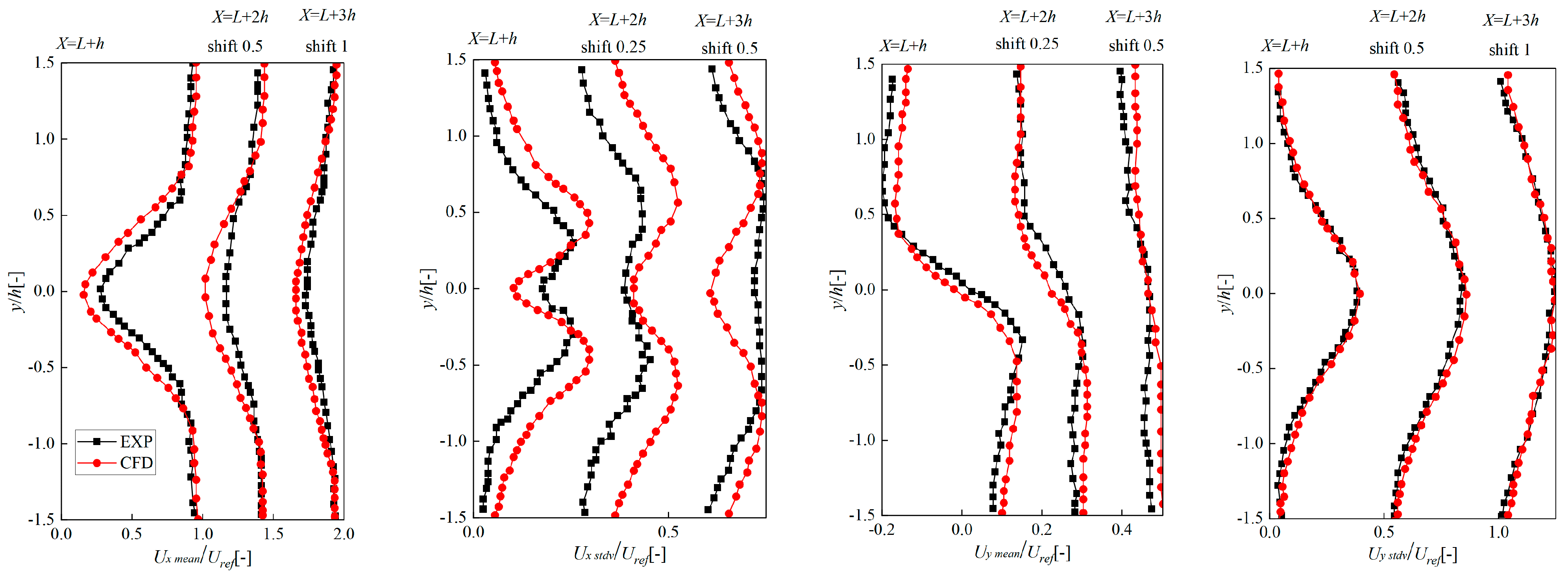
3.3. Experimental Validation
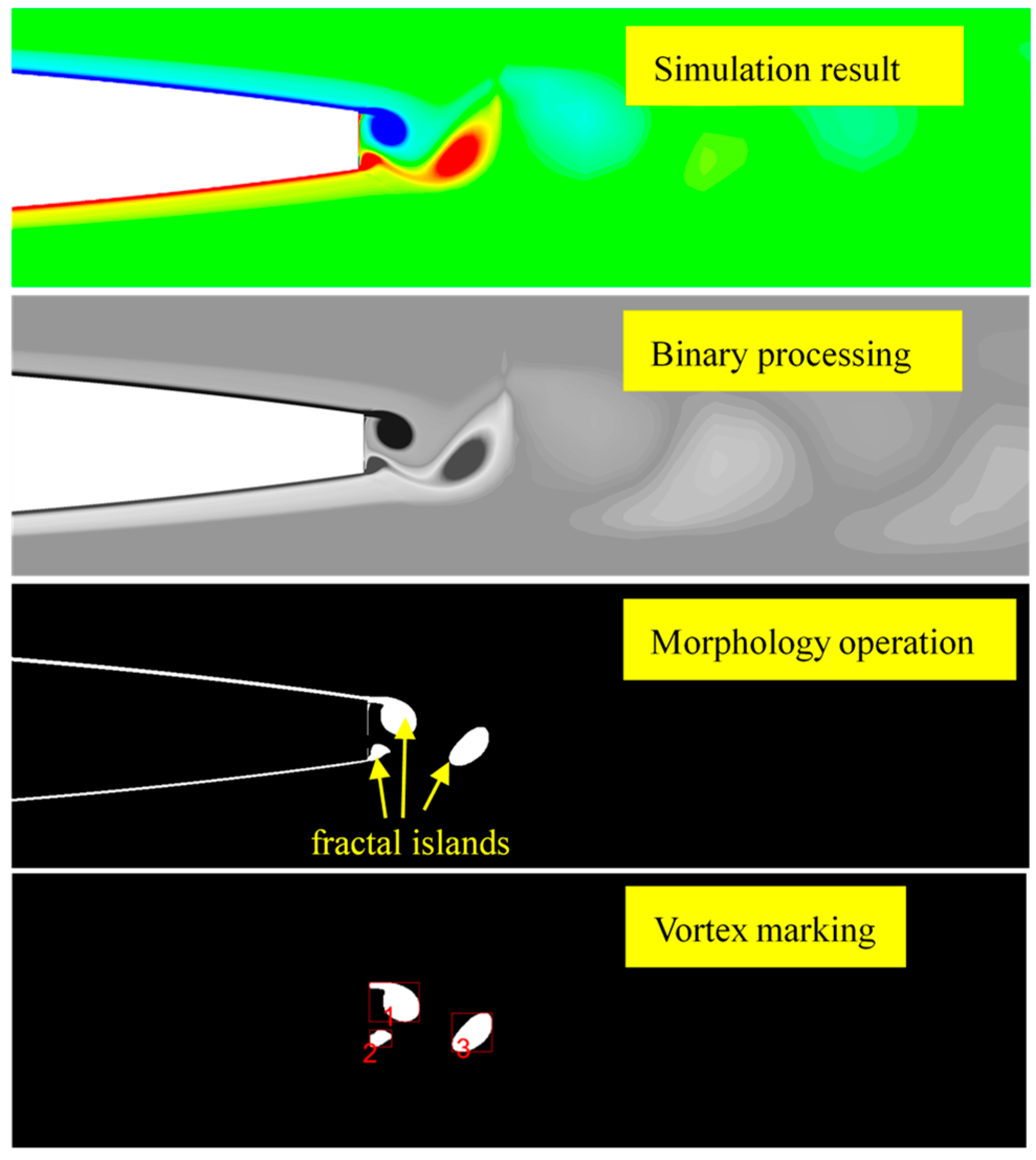
4. Fractal Dimension
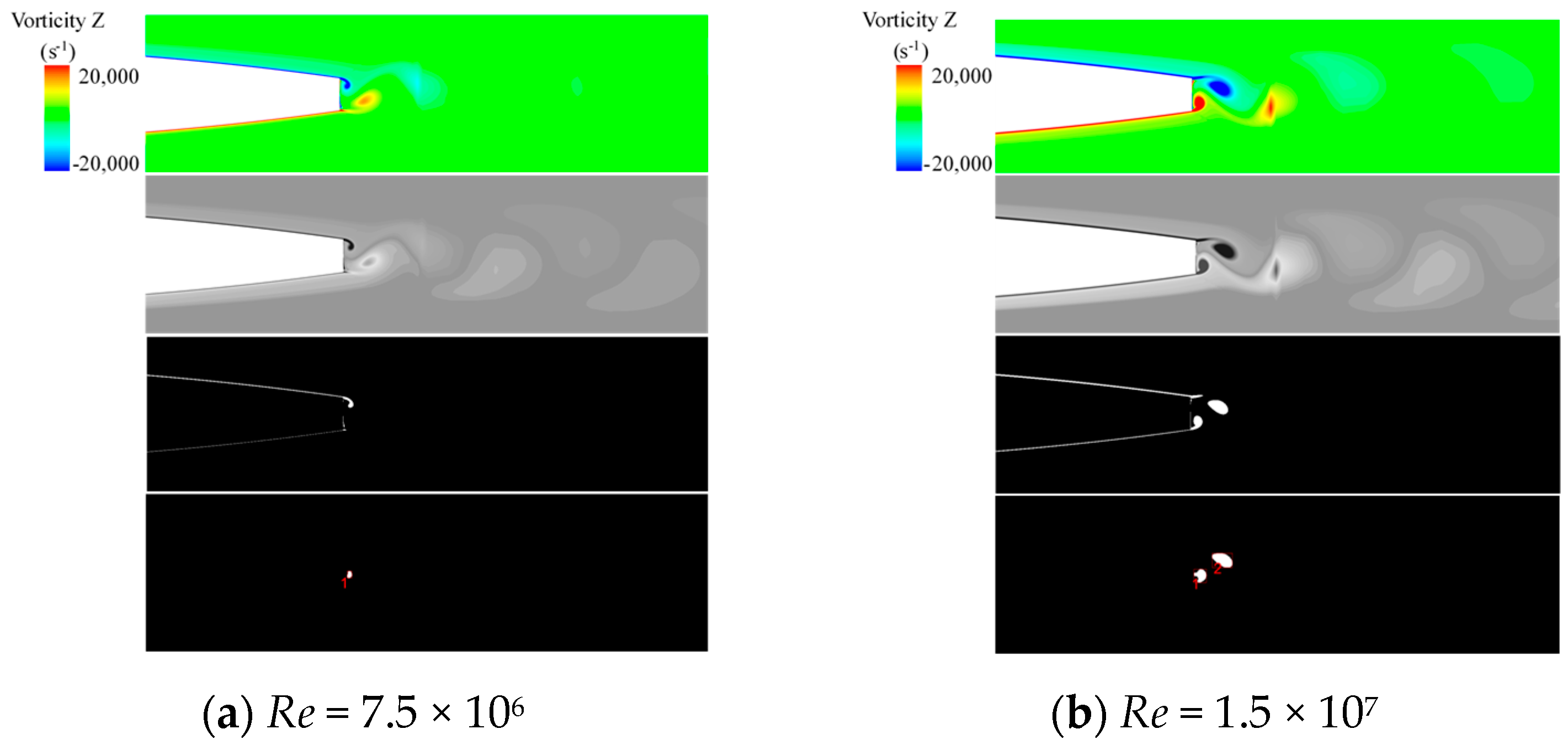
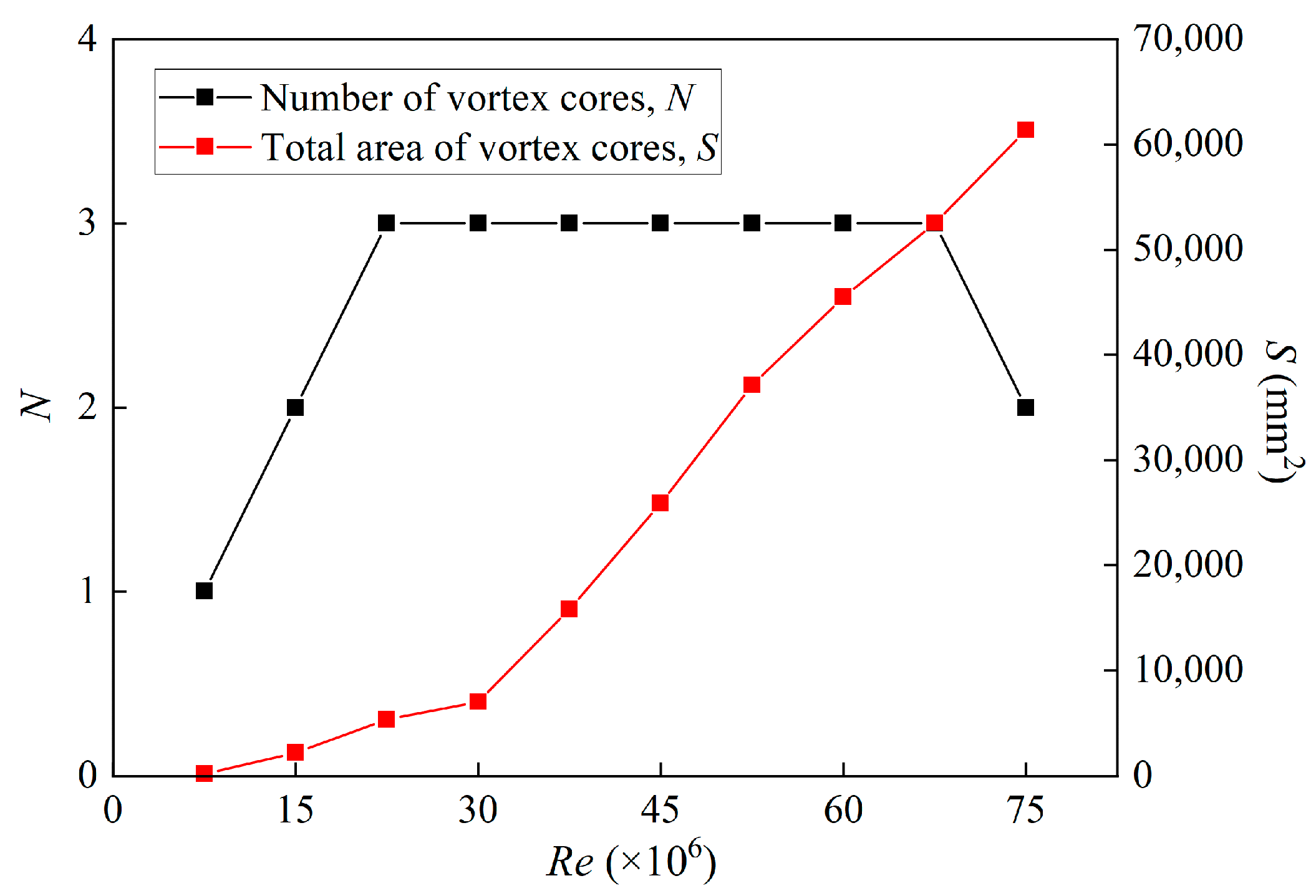
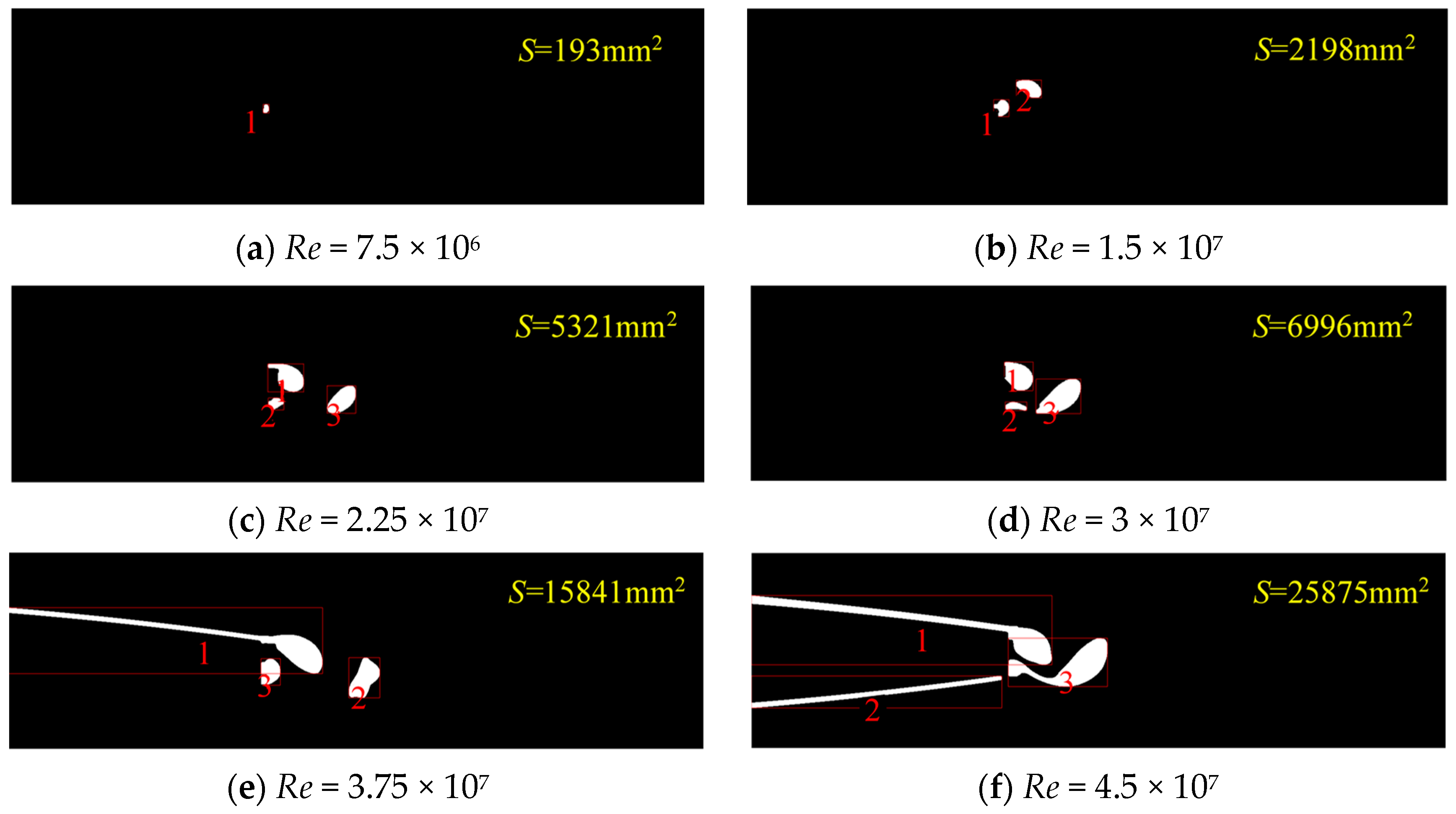
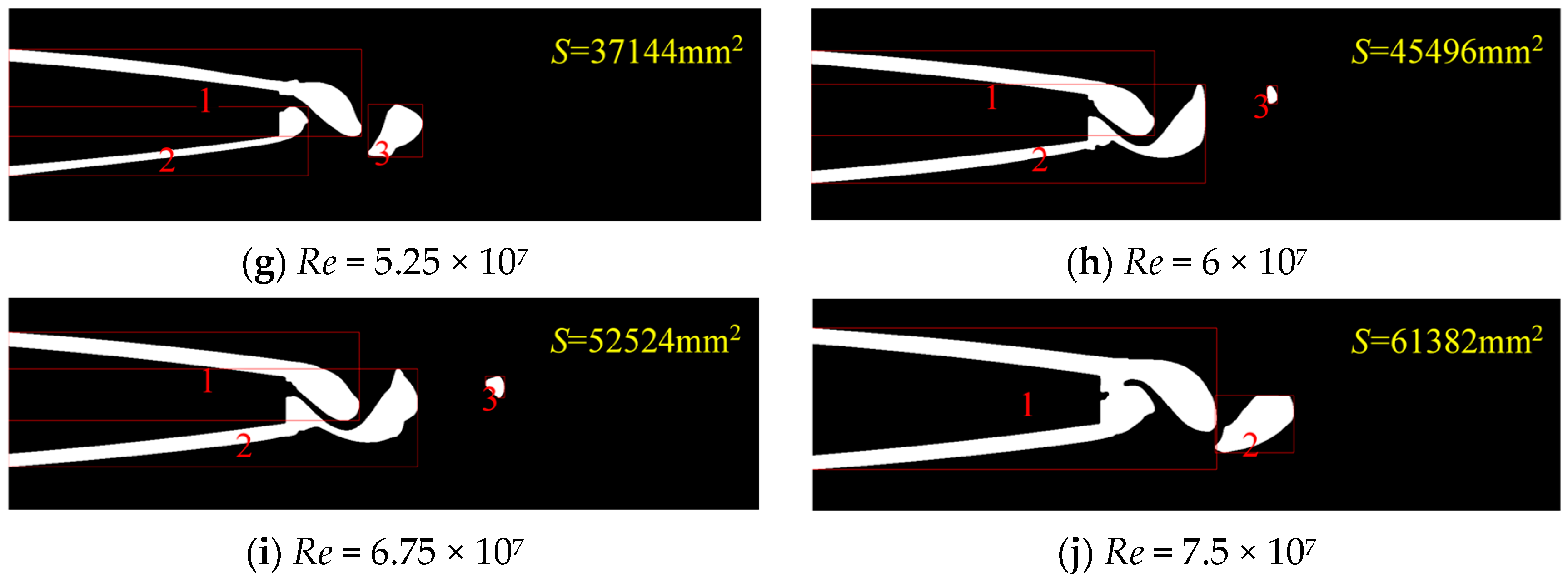
5. Research Results and Analysis
6. Conclusions
- (1)
- By combining binary and morphological operations and CFD numerical simulation, image segmentation methods were applied to recognize the shape of the Karman vortex. The results show that this method can efficiently and intuitively obtain the shedding intensity and shape of the vortex. This method can also be extended to related research on the characteristics and evolution of the vortex flow in hydraulic machinery.
- (2)
- Based on the fractal dimension method of the area and perimeter, the number of vortex cores and the total area of the Karman vortex at trailing edge of hydrofoil were analyzed at different Reynolds numbers. The results show that with the increase in the Reynolds number, the number of vortex cores first increases from 1 to 3 and then decreases to 2, while the total area of the vortex cores keeps increasing.
- (3)
- Conclusion (2) was obtained by combining the results of the numerical simulation of the vorticity contours. As the Reynolds number increases, the turbulence level increases, leading to the appearance of vortex clusters at the trailing edge of the hydrofoil. The total area of the vortex clusters increases, especially when Re > 3 × 107, and the growth rate of the vortex core area also increases due to the increase in turbulence.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ai, C.; Zhang, L.; Gao, W.; Yang, G.; Wu, D.; Chen, L.; Chen, W.; Plummer, A. A review of energy storage technologies in hydraulic wind turbines. Energy Convers. Manag. 2022, 264, 115584. [Google Scholar] [CrossRef]
- Qin, Y.; Li, D.; Wang, H.; Liu, Z.; Wei, X.; Wang, X. Investigation on hydraulic loss component and distribution in hydraulic machinery: A case study of pump-turbine in pump mode. J. Energy Storage 2022, 52, 104932. [Google Scholar] [CrossRef]
- Zhang, F.; Fang, M.; Pan, J.; Tao, R.; Zhu, D.; Liu, W.; Xiao, R. Guide vane profile optimization of pump-turbine for grid connection performance improvement. Energy 2023, 274, 127369. [Google Scholar] [CrossRef]
- Wang, D.; Chiu, C.; Pham, H. Electromagnetic energy harvesting from vibrations induced by Kármán vortex street. Mechatronics 2012, 22, 746–756. [Google Scholar] [CrossRef]
- Luna-Ramírez, A.; Campos-Amezcua, A.; Dorantes-Gómez, O.; Mazur-Czerwiec, Z.; Muñoz-Quezada, R. Failure analysis of runner blades in a Francis hydraulic turbine—Case study. Eng. Fail. Anal. 2016, 59, 314–325. [Google Scholar] [CrossRef]
- Roig, R.; Chen, J.; de la Torre, O.; Escaler, X. Understanding the Influence of Wake Cavitation on the Dynamic Response of Hydraulic Profiles under Lock-In Conditions. Energies 2021, 14, 6033. [Google Scholar] [CrossRef]
- Demori, M.; Ferrari, M.; Bonzanini, A.; Poesio, P.; Ferrari, V. Autonomous Sensors Powered by Energy Harvesting from von Karman Vortices in Airflow. Sensors 2017, 17, 2100. [Google Scholar] [CrossRef]
- Chamoun, G.; Kanso, E.; Newton, P.K. Von Karman vortex streets on the sphere. Phys. Fluids 2009, 21, 116603. [Google Scholar] [CrossRef]
- Kreuzahler, S.; Schulz, D.; Homann, H.; Ponty, Y.; Grauer, R. Numerical study of impeller-driven von Kármán flows via a volume penalization method. New J. Phys. 2014, 16, 103001. [Google Scholar] [CrossRef]
- Xing, T. Direct numerical simulation of Open Von Kármán Swirling Flow. J. Hydrodyn. 2014, 26, 165–177. [Google Scholar] [CrossRef]
- Hernández, E.S.; Llewellyn Smith, S.G.; Cros, A. Resonance of a flexible plate immersed in a von Kármán vortex street. J. Mech. Sci. Technol. 2020, 34, 1459–1465. [Google Scholar] [CrossRef]
- Ausoni, P.; Farhat, M.; Escaler, X.; Egusquiza, E.; Avellan, F. Cavitation Influence on von Kármán Vortex Shedding and Induced Hydrofoil Vibrations. J. Fluids Eng.-Trans. ASME 2007, 129, 966–973. [Google Scholar] [CrossRef]
- Leung, R.C.K.; So, R.M.C. Noise Generation of Blade–Vortex Resonance. J. Sound Vib. 2001, 245, 217–237. [Google Scholar] [CrossRef]
- Su, W.; Li, S.; Zhang, Q.; Li, J.; Ye, Q.; Wang, N. Influence of thermal inhibitor position and temperature on vortex-shedding-driven pressure oscillations. Chin. J. Aeronaut. 2013, 26, 544–553. [Google Scholar] [CrossRef]
- Kumar, B.; Mittal, S. On the origin of the secondary vortex street. J. Fluid Mech. 2012, 711, 641–666. [Google Scholar] [CrossRef]
- Atrah, A.; Ab-Rahman, M.; Salleh, H.; Nuawi, M.; Mohd Nor, M.; Jamaludin, N. Karman Vortex Creation Using Cylinder for Flutter Energy Harvester Device. Micromachines 2017, 8, 227. [Google Scholar] [CrossRef]
- Yao, G.; Wang, H.; Yang, C.; Wen, L. Research and design of underwater flow-induced vibration energy harvester based on Karman vortex street. Mod. Phys. Lett. B 2017, 31, 1750076. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Yang, Y.; Duan, Z. New omega vortex identification method, Science China Physics. Mech. Astron. 2016, 59, 684711. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Wang, Y.; Liu, C. Objective Omega vortex identification method. J. Hydrodyn. 2019, 31, 455–463. [Google Scholar] [CrossRef]
- Xu, H.; Cai, X.; Liu, C. Liutex (vortex) core definition and automatic identification for turbulence vortex structures. J. Hydrodyn. 2019, 31, 857–863. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.; Liu, Y.; Wang, F.; Li, S.; Liu, J. A CNN-based vortex identification method. J. Vis. 2019, 22, 65–78. [Google Scholar] [CrossRef]
- Li, P.; Tao, R.; Yang, S.; Zhu, D.; Xiao, R. Temporal and Spatial Analysis on the Fractal Characteristics of the Helical Vortex Rope. Fractal Fract. 2022, 6, 477. [Google Scholar] [CrossRef]
- Hu, Z.; Zhu, D.; Xiao, R.; Tao, R. Comparative Evaluation of the Immersed-Solid Method for Simulating the Flow Field around Hydrofoil. Sustainability 2023, 15, 3493. [Google Scholar] [CrossRef]
- Del-Pozo-Velázquez, J.; Chamorro-Posada, P.; Aguiar-Pérez, J.M.; Pérez-Juárez, M.Á.; Casaseca-De-La-Higuera, P. Water Detection in Satellite Images Based on Fractal Dimension. Fractal Fract. 2022, 6, 657. [Google Scholar] [CrossRef]
- Ma, C.; Shen, L.; Deng, H.; Li, J. Synaptic clef segmentation method based on fractal dimension for ATUM-SEM image of mouse cortex. Int. J. Wavelets Multiresolution Inf. Process. 2022, 20, 2150038. [Google Scholar] [CrossRef]
- Zhuang, Z.; Lei, N.; Joseph Raj, A.N.; Qiu, S. Application of fractal theory and fuzzy enhancement in ultrasound image segmentation. Med. Biol. Eng. Comput. 2019, 57, 623–632. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Chen, J.; Zhou, Y.; Antonia, R.A.; Zhou, T.M. The turbulent Kármán vortex. J. Fluid Mech. 2019, 871, 92–112. [Google Scholar] [CrossRef]
- Ausoni, P. Turbulent Vortex Shedding from a Blunt Trailing Edge Hydrofoil. Ph.D. Thesis, Swiss Federal Institute of Technology Lausanne, Lausanne, Switzerland, 2009. [Google Scholar]
- Prażmowska, M.; Prażmowski, K.; Żynel, M. Euclidean geometry of orthogonality of subspaces. Aequ. Math. 2008, 76, 151–167. [Google Scholar] [CrossRef]
- Izard, V.; Pica, P.; Spelke, E.S. Visual foundations of Euclidean geometry. Cogn. Psychol. 2022, 136, 101494. [Google Scholar] [CrossRef]
- Balogh, Z.M.; Tyson, J.T.; Warhurst, B. Sub-Riemannian vs. Euclidean dimension comparison and fractal geometry on Carnot groups. Adv. Math. 2009, 220, 560–619. [Google Scholar] [CrossRef]

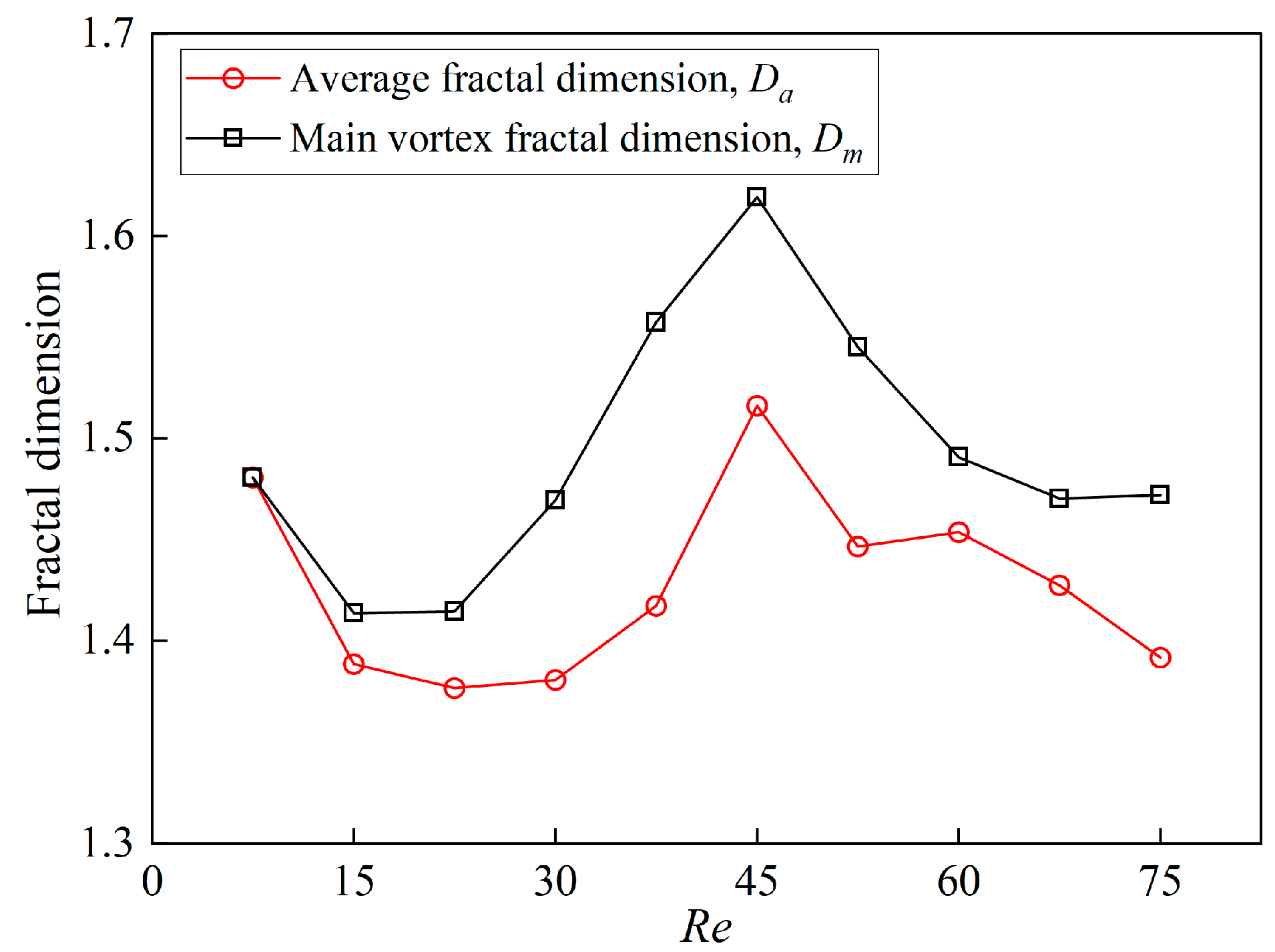
| Re (×106) | 7.5 | 15 | 22.5 | 30 | 37.5 | 45 | 52.5 | 60 | 67.5 | 75 |
|---|---|---|---|---|---|---|---|---|---|---|
| Da | 1.48 | 1.39 | 1.38 | 1.38 | 1.42 | 1.52 | 1.45 | 1.45 | 1.43 | 1.39 |
| Dm | 1.48 | 1.41 | 1.41 | 1.47 | 1.56 | 1.62 | 1.55 | 1.49 | 1.47 | 1.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zuo, Y.; Zhu, D.; Tao, R.; Xiao, R. Investigation of Fractal Characteristics of Karman Vortex for NACA0009 Hydrofoil. Fractal Fract. 2023, 7, 467. https://doi.org/10.3390/fractalfract7060467
Zhang F, Zuo Y, Zhu D, Tao R, Xiao R. Investigation of Fractal Characteristics of Karman Vortex for NACA0009 Hydrofoil. Fractal and Fractional. 2023; 7(6):467. https://doi.org/10.3390/fractalfract7060467
Chicago/Turabian StyleZhang, Fangfang, Yaju Zuo, Di Zhu, Ran Tao, and Ruofu Xiao. 2023. "Investigation of Fractal Characteristics of Karman Vortex for NACA0009 Hydrofoil" Fractal and Fractional 7, no. 6: 467. https://doi.org/10.3390/fractalfract7060467
APA StyleZhang, F., Zuo, Y., Zhu, D., Tao, R., & Xiao, R. (2023). Investigation of Fractal Characteristics of Karman Vortex for NACA0009 Hydrofoil. Fractal and Fractional, 7(6), 467. https://doi.org/10.3390/fractalfract7060467








