On Entropy of Some Fractal Structures

Abstract

Shannon entropy, also known as information entropy or entropy, measures the uncertainty or randomness of probability distribution. Entropy is measured in bits, quantifying the average amount of information required to identify an event from the distribution. Shannon’s entropy theory initiates graph entropies and develops information-theoretic magnitudes for structural computational evidence of organic graphs and complex networks. Graph entropy measurements are valuable in several scientific fields, such as computing, chemistry, biology, and discrete mathematics. In this study, we investigate the entropy of fractal-type networks by considering cycle, complete, and star networks as base graphs using degree-based topological indices.

1. Introduction

In information theory, entropy measures the amount of uncertainty or randomness in a dataset. It is often used to quantify the amount of information in a message or signal. The entropy of a probability distribution is defined as the negative sum of the probabilities of each event multiplied by the logarithm of the probabilities. A high entropy indicates that the data are highly uncertain or random. In contrast, a low entropy suggests that the data are more predictable or certain.

Graph entropy is a measure used to quantify the randomness or disorder of a graph. It is based on the concept of entropy from information theory. It is used to analyze the structure of complex networks. The entropy of a graph measures the number of ways that the edges of the graph can be rearranged while preserving the number of vertices and edges. Modern information theory was started by Shannon’s seminal work [1] in the late nineteen-forties and developed the information-theoretic magnitudes for computation skeleton evidence of organic and multifaceted graphs [2,3]. Shannon’s entropy formulas were applied to explore a structure’s structural information content. The participation of Rashevsky and Trucco [4,5] is closely associated with investigating the living body, e.g., chemical and biological systems, using networks.

Furthermore, entropy measures have been broadly valuable for computer science, biology, and structural chemistry. Widely speaking, to investigate the biological or chemical characteristics of molecular structures, entropic measures are applied. Tan and Wu [6] introduced the entropy measures, which depend on vertex degree to reveal network heterogeneity. It is used in various fields such as network science, complex systems, computer science, social science, and physics to study the complexity and randomness of the network, classify the network, compare the network with other networks, and identify the most random parts of the network [7,8,9,10,11,12,13].

There are presently two ways to employ information entropy in chemistry. It is a structural descriptor for determining how complex chemical compounds are, according to information [14]. Entropy is helpful in this context for categorizing natural products and synthetic compounds [15,16], numerically identifying organic molecule isomers [17], and correlating structural and physicochemical properties. A different application of information entropy is in physicochemical processes. Kobozev proved its usefulness in analyzing physicochemical processes that simulate information transmission as a result. Entropy values were employed to research the chemical processes of molecular compounds by Manzoor et al. [18]. Abraham et al. obtained the entropy measures by computing systematic expressions of the self-powered degree-based topological indices for three reticular metal–organic frameworks with a zinc-based central unit and stringed binding linkers with varying benzene molecule counts [19]. Shabbir and Nadeem gave a comprehensive computational analysis of entropies based on degree-based topological indices and carbon nanotube Y-junctions [20]. Shanmukha et al. investigated the graph entropies of porous graphene using topological indices [21].

Fractal geometry is a fascinating field that explores self-similar shapes and patterns that can be observed ubiquitously in nature, including trees, rivers, coastlines, mountains, shells, and hurricanes. The study of fractals contributes to our understanding of the inherent beauty and complexity of the natural world but also has far-reaching applications in various scientific disciplines, such as biology, computer networks, physical sciences, and chemical graph theory. Sierpiński-type structures, in particular, have been extensively examined in both fractal theory and practice, with a wealth of research demonstrating their relevance and usefulness across diverse fields [22,23,24].

One significant aspect of fractal structures that warrants further investigation is their entropy, which measures the degree of disorder or randomness within a system. The entropy of fractals has important implications for understanding the thermodynamics, information content, and stability of these complex systems, which can, in turn, impact a wide range of practical applications, such as the design of more efficient data storage and compression techniques, the modeling of complex biological processes, and the optimization of computer networks. Given the ubiquity and significance of fractal structures in nature and their various applications across various scientific fields, a comprehensive study of their entropy is timely and essential. Thus, a thorough exploration of the entropy of fractal structures not only addresses a critical gap in the current literature but also holds the potential to uncover novel insights and advance our understanding of these intricate systems. We hope this paper will serve as a valuable contribution to the ongoing discourse on fractals and their entropy, providing readers with a compelling reason to delve deeper into this intriguing and impactful topic.

Let $\mathcal{G}(V,E)$ be a graph of order $p,$ and t a positive integer. We denote by $V^t$ the set of words of length t on alphabet $V.$ The letters of a word u of length t are denoted by $u_1,u_2,\cdots u_t.$ The chain of two words u and w is denoted by $uw$. Klavžar and Milutinović defined the graph $S(K_n,t),$ with vertex set $V^t$, where $\{u,w\}$ is an edge if and only if there exists $i\in \{1,2,\cdots ,t\}$ such that [25].

• $u_j=w_j$ if $j<i$
• $u_i\ne w_i$ and $u_i,w_i\in E\left(\mathcal{G}\right)$
• $u_j=w_i$ and $u_i=w_j$ if $j>i.$

Subsequently, the term Sierpiński graphs was named in [26], and since then, they have been investigated from various perspectives. For example, Imran et al. investigated the topological properties of Sierpiński graphs [27]. Gravier et al. investigated identifying codes, locating-dominating codes, and total-dominating codes in Sierpiński graphs [28]. Hinz and Heide defined an algorithm that uses three automata and the fact that there are at most two internally vertex disjoint shortest paths between any two vertices to determine all shortest paths in Sierpiński graphs [29]. Kalvzar et al. proved that for any $n\ge 1$ and $t\ge 1,$ the Sierpiński graph $S(K_n,t)$ has a unique 1-perfect code if t is even, and $S(K_n,t)$ has precisely n 1-perfect codes if t is odd. The concept of almost-extreme vertex of $S(K_n,t)$ was introduced by Klavzar and Zemljic in [30] as a vertex that is either adjacent to an extreme vertex of $S(K_n,t)$ or is incident to an edge between two subgraphs of $S(K_n,t)$ isomorphic to $S(K_n,t-1).$ They also deduced explicit formulas for the distance in $S(K_n,t)$ between an arbitrary vertex and an almost-extreme vertex. Hinz and Parisse studied the eccentricity of an arbitrary vertex of Sierpiński graphs in [31] where the main result gave an expression for the average eccentricity of $S(K_n,t).$ Rodríguez-Velázquez et al. obtained closed formulae for several parameters of generalized Sierpiński graphs $S(\mathcal{G},t)$ in terms of parameters of the base graph $\mathcal{G};$ especially, they studied the chromatic, vertex cover, clique, and domination numbers [32]. Ishfaq et al. computed the Zagreb and forgotten invariants for extended Sierpiński graphs. They also obtained sharp bounds by applying different parameters [33]. For more details and general background on Sierpiński graphs, refer to the comprehensive survey [34].

This construction of Sierpiński graphs was generalized by Gravier et al. [35] for any graph $\mathcal{G}=(V,E),$ by defining the $t-$th generalized Sierpiński graph of $\mathcal{G},$ denoted by $S(\mathcal{G},t),$ as the graph with vertex set $V^t$ and edge set defined as follows: $u,w$ is an edge if and only if there exists $i\in \{1,\cdots ,t\}$ such that

• $u_j=w_j$ if $j<i$
• $u_i\ne w_i$ and $u_i,w_i\in E\left(\mathcal{G}\right)$
• $u_j=w_i$ and $u_i=w_j$ if $j>i.$

Notice that if $\{u,v\}$ is an edge of $S(G,t),$ there is an edge $\{x,y\}$ of G and a word w such that $u=wxyy\dots y$ and $v=wyxx\dots x.$ In general, $S(G,t)$ can be constructed recursively from G with the following process: $S(\mathcal{G},1)=\mathcal{G}$ and, for $t\ge 2,$ we copy n times $S(\mathcal{G},t-1)$ and add the letter x at the beginning of each label of the vertices belonging to the copy of $S(\mathcal{G},t-1)$ corresponding to $x.$ Then, for every edge $\{x,y\}$ of $\mathcal{G},$ add an edge between vertex $xyy\dots y$ and vertex $yxx\dots x.$ Vertices of the form $xx\dots x$ are called extreme vertices. For any graph G of order n and any integer $t\ge 2,$$S(G,t)$ has n extreme vertices and, if x has degree $d_{\mathcal{G}}\left(x\right)$ in $G,$ then the extreme vertex $xx\dots x$ of $S(\mathcal{G},t)$ also has degree $d_{\mathcal{G}}\left(x\right).$ Moreover, the degrees of two vertices $yxx\dots x$ and $xyy\dots y,$ which connect two copies of $S(\mathcal{G},t-1),$ are equal to $d_{\mathcal{G}}\left(x\right)+1$ and $d_{\mathcal{G}}\left(y\right)+1,$ respectively. Moreover, an extended Sierpiński graph $ES\left(\mathcal{G},t\right)$ is attained by introducing a vertex x in generalized Sierpiński graph and connecting with extreme vertices.

Topological descriptors are widely used in the field of chemical graph theory [36,37]. These descriptors can help estimate the physical and chemical properties of chemical networks. Over the past several decades, numerous topological invariants have been established and studied in chemical literature [38,39], and have been applied to understand various effects of organic materials that depend on their molecular shape. The first topological descriptor was introduced by the chemist Wiener in 1947 to determine the boiling points of paraffin [40].

Gutman et al. in [41,42] defined the Zagreb indices:

$$M_1\left(\mathcal{G}\right)=\sum _{x\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}{\left(x\right)}^2=\sum _{xy\in E\left(\mathcal{G}\right)}\left(d_{\mathcal{G}}\left(x\right)+d_{\mathcal{G}}\left(y\right)\right)$$

(1)

$$M_2\left(\mathcal{G}\right)=\sum _{xy\in E\left(\mathcal{G}\right)}\left(d_{\mathcal{G}}\left(x\right)d_{\mathcal{G}}\left(y\right)\right)$$

(2)

Furtuala et al. [43] proposed the forgotten topological index, defined as

$$F\left(\mathcal{G}\right)=\sum _{x\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}{\left(x\right)}^3=\sum _{xy\in E\left(\mathcal{G}\right)}\left(d_{\mathcal{G}}{\left(x\right)}^2+d_{\mathcal{G}}{\left(y\right)}^2\right)$$

(3)

In this paper, we consider simple and finite graphs. A graph $\mathcal{G}=\left(V,E\right)$ consists of a set of nodes and the connections between them, called edges. The order and size of a graph $\mathcal{G}$ are represented by the number of nodes and edges, respectively, and are usually denoted as p and q. The degree of a vertex v, denoted by $d_v$, is the number of edges adjacent to the vertex. A graph $\mathcal{G}$ is considered complete if a unique edge connects every pair of distinct vertices. We use $S_p$, $C_p$, and $K_p$ to represent star, cycle, and complete graphs of order p, respectively. In this paper, we will employ the notations $d_{\mathcal{G}}\left(x\right)=\zeta \left(x\right)$ and $d_{\mathcal{G}}\left(y\right)=\zeta \left(y\right)$ for the degrees of vertices x and y.

1.1. General Entropy of Graphs

Chen et al. [44] introduced the concept of edge partition graph entropy in 2014. The edge partition graph entropy is measured in Equation (4):

$$EN{T}_{\chi }\left(\mathcal{G}\right)=-\sum _{x^{\prime }{y}^{\prime }\in E\left(\mathcal{G}\right)}\frac{\chi \left(x^{\prime }{y}^{\prime }\right)}{{\sum }_{xy\in E\left(\mathcal{G}\right)}\chi \left(xy\right)}ln\left[\frac{\chi \left(x^{\prime }{y}^{\prime }\right)}{{\sum }_{xy\in E\left(\mathcal{G}\right)}\chi \left(xy\right)}\right]$$

(4)

1.1.1. The First Zagreb Entropy

If $\chi \left(xy\right)=\zeta \left(x\right)+\zeta \left(y\right)$, then

$$\sum _{xy\in E\left(\mathcal{G}\right)}\chi \left(xy\right)=\sum _{xy\in E\left(\mathcal{G}\right)}\left(\zeta \left(x\right)+\zeta \left(y\right)\right)=M_1\left(\mathcal{G}\right)$$

The first Zagreb entropy is obtained by simplifying Equation (4) as follows:

$$EN{T}_{M_1\left(\mathcal{G}\right)}=ln\left(M_1\left(\mathcal{G}\right)\right)-\frac{1}{\left(M_1\left(\mathcal{G}\right)\right)}ln\left[\prod _{xy\in E\left(\mathcal{G}\right)}{\left[\zeta \left(x\right)+\zeta \left(y\right)\right]}^{\left[\zeta \left(x\right)+\zeta \left(y\right)\right]}\right]$$

(5)

1.1.2. The Second Zagreb Entropy

If $\chi \left(xy\right)=\zeta \left(x\right)\times \zeta \left(y\right)$, then

$$\sum _{xy\in E\left(\mathcal{G}\right)}\chi \left(xy\right)=\sum _{xy\in E\left(\mathcal{G}\right)}\left(\zeta \left(x\right)\times \zeta \left(y\right)\right)=M_2\left(\mathcal{G}\right)$$

The second Zagreb entropy is obtained by simplifying Equation (4) as follows:

$$EN{T}_{M_2\left(\mathcal{G}\right)}=ln\left(M_2\left(\mathcal{G}\right)\right)-\frac{1}{\left(M_2\left(\mathcal{G}\right)\right)}ln\left[\prod _{xy\in E\left(\mathcal{G}\right)}{\left[\zeta \left(x\right)\times \zeta \left(y\right)\right]}^{\left[\zeta \left(x\right)\times \zeta \left(y\right)\right]}\right]$$

(6)

1.1.3. The Forgotten Entropy

If $\chi \left(xy\right)=\left[{\left(\zeta \left(x\right)\right)}^2+{\left(\zeta \left(y\right)\right)}^2\right]$, then

$$\sum _{xy\in E\left(\mathcal{G}\right)}\chi \left(xy\right)=\sum _{xy\in E\left(\mathcal{G}\right)}{\left(\zeta \left(x\right)\right)}^2+{\left(\zeta \left(y\right)\right)}^2=F\left(\mathcal{G}\right)$$

The forgotten entropy is obtained by simplifying Equation (4) as follows:

$$EN{T}_{F\left(\mathcal{G}\right)}=ln\left(F\left(\mathcal{G}\right)\right)-\frac{1}{\left(F\left(\mathcal{G}\right)\right)}ln\left[\prod _{xy\in E\left(\mathcal{G}\right)}{\left[{\left(\zeta \left(x\right)\right)}^2+{\left(\zeta \left(y\right)\right)}^2\right]}^{\left[{\left(\zeta \left(x\right)\right)}^2+{\left(\zeta \left(y\right)\right)}^2\right]}\right]$$

(7)

We apply the edge partition method to Sierpiński graphs, which has not been previously performed. We analyze the entropy of these fractal-type networks using first and second Zagreb and forgotten topological indices. We provide a comparative analysis of entropies calculated using Zagreb and forgotten indices by considering different base graphs (cycle, star, and complete graph) for the Sierpiński network. This comparison enables researchers to evaluate the performance of these indices in terms of their ability to capture the complexity and randomness of Sierpiński networks.

2. Results and Discussion

In this part of the paper, we obtained the entropy of Sierpiński graphs by using first and second Zagreb, and forgotten topological indices by considering cycle graph as a base graph $\mathcal{G}$. Furthermore, we compare entropies for the Sierpiński graph by using Zagreb and forgotten indices.

2.1. Results for Sierpiński Graph When Cycle Is a Base Graph

Figure 1 shows the generalized Sierpiński graphs $S(1,C_4)$ and $S(2,C_4)$. The data in Table 1 are obtained by partitioning the graph’s edges $S(C_p,t)$ according to the degrees of their end vertices. The first column shows that three are different types of edges, while the second column presents the frequency of each edge type. From Figure 1, it can be seen that the extended Sierpiński graph $S(1,C_4)$ has only one type of edge partition. This specific partition consists of edges that connect end vertices, each having a degree of 2, while the extended Sierpiński graph $S(2,C_4)$ has all three types of edges.

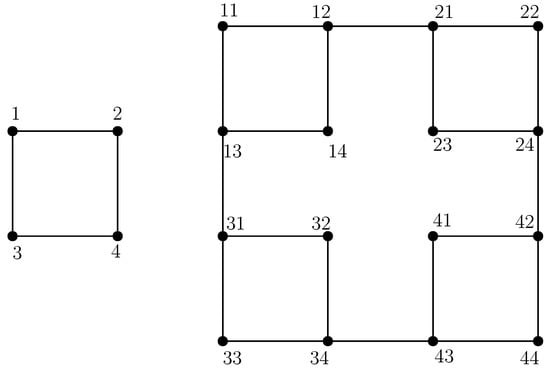
Figure 1. Sierpiński graphs $S(C_4,1)$ and $S(C_4,2)$.

Table 1. Degree-based edge partition of $S(C_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(2,2)$	$p^{t-1}(p-4)$	$E_1$
$(2,3)$	$4p{(p-1)}^{t-2}$	$E_2$
$(3,3)$	$\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}$	$E_3$

2.1.1. First Zagreb Entropy

To compute the first Zagreb index-entropy of $S(C_p,t)$, we first calculate the value of the first Zagreb index of $S(C_p,t)$ by using the edge partition given in Table 1 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(S(C_p,t)\right)& =\frac{4p^{t+1}+10p^t-8p^{t-1}-4p{(p-1)}^{t-1}-6p}{p-1}\hfill \end{array}\end{array}$$

Now, by using this computed value of first Zagreb index and values given in Table 1, we obtain the first Zagreb entropy:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln[p^{t-1}(p-4){\left(4\right)}^4\times 4p{(p-1)}^{t-2}{\left(5\right)}^5\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right){\left(6\right)}^6]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(\frac{4p^{t+1}+10p^t-8p^{t-1}-4p{(p-1)}^{t-1}-6p}{p-1}\right)\hfill \\ & -\frac{ln\left[p^{t-1}(p-4)\times {\left(4\right)}^4\right]}{\left(\frac{4p^{t+1}+10p^t-8p^{t-1}-4p{(p-1)}^{t-1}-6p}{p-1}\right)}\hfill \\ & -\frac{ln\left[4p{(p-1)}^{t-2}\times {\left(5\right)}^5\right]}{\left(\frac{4p^{t+1}+10p^t-8p^{t-1}-4p{(p-1)}^{t-1}-6p}{p-1}\right)}\hfill \\ & -\frac{ln\left[\left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right)\times {\left(6\right)}^6\right]}{\left(\frac{4p^{t+1}+10p^t-8p^{t-1}-4p{(p-1)}^{t-1}-6p}{p-1}\right)}\hfill \end{array}\end{array}$$

2.1.2. Second Zagreb Entropy

To compute the second Zagreb index-entropy of $S(C_p,t)$, we first calculate the value of the second Zagreb index of $S(C_p,t)$ by using the edge partition given in Table 1 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(S(C_p,t)\right)& =\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}-9p}{p-1}\hfill \end{array}\end{array}$$

Now, by using this computed value of second Zagreb index and values given in Table 1, we obtain the second Zagreb entropy:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln[p^{t-1}(p-4){\left(4\right)}^4\times 4p{(p-1)}^{t-2}{\left(6\right)}^6\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right){\left(9\right)}^9]\hfill \end{array}\end{array}$$

$$EN{T}_{M_2}=ln\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}-9p}{p-1}\right)$$

$$-\frac{ln\left[p^{t-1}(p-4)\times {\left(4\right)}^4\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}-9p}{p-1}\right)}$$

$$-\frac{ln\left[4p{(p-1)}^{t-2}\times {\left(6\right)}^6\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}-9p}{p-1}\right)}$$

$$-\frac{ln\left[\left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right)\times {\left(9\right)}^9\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}-9p}{p-1}\right)}$$

2.1.3. Forgotten Entropy

To compute forgotten index-entropy of $S(C_p,t)$, we first calculate the value of the forgotten index of $S(C_p,t)$ by using the edge partition given in Table 1 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(S(C_p,t)\right)& =\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}-18p}{p-1}\hfill \end{array}\end{array}$$

By incorporating the computed value of the forgotten index and the values found in Table 1, we can obtain the forgotten entropy.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln[p^{t-1}(p-4){\left(8\right)}^8\times 4p{(p-1)}^{t-2}{\left(13\right)}^{13}\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right){\left(18\right)}^{18}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}-18p)}{p-1}\right)\hfill \\ & -\frac{ln\left[p^{t-1}(p-4)\times {\left(8\right)}^8\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}-18p}{p-1}\right)}\hfill \\ & -\frac{ln\left[4p{(p-1)}^{t-2}\times {\left(13\right)}^{13}\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}-18p}{p-1}\right)}\hfill \\ & -\frac{ln\left[\left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right)\times {\left(18\right)}^{18}\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}-18p}{p-1}\right)}\hfill \end{array}\end{array}$$

2.2. Results for the Sierpiński Graph When Star Is a Base Graph

The Sierpiński graph $S(S_p,t)$ is shown in Figure 2. The edge partition based on the degree of the end vertices of each edge is shown in Table 2.

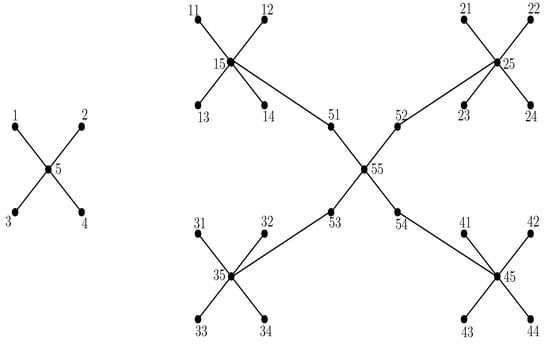
Figure 2. Sierpiński graph $S(S_5,1$) and $S(S_5,2$).

Table 2. Degree-based edge partition of $S(S_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(1,p)$	$p^{t-1}(p-2)+1$	$E_1$
$(2,p)$	$2p^{t-1}-p-1$	$E_2$
$(2,p-1)$	$p-1$	$E_3$

2.2.1. First Zagreb Entropy

By using the values of edge partitions given in Table 2, we obtained the first Zagreb index of $\left(S(S_p,t)\right)$ as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(S(S_p,t)\right)& =p^{t+1}+(p+2)p^{t-1}-2(p+1)\hfill \end{array}\end{array}$$

Now, Equation (5) by using Table 2 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln[((p-2)p^{t-1}+1){(1+p)}^{1+p}\times (2p^{t-1}-p-1){(2+p)}^{2+p}\hfill \\ & \times (p-1){(1+p)}^{1+p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(p^{t+1}+(p+2)p^{t-1}-2(p+1)\right)\hfill \\ & -\frac{ln\left[((p-2)p^{t-1}+1)\times {(1+p)}^{1+p}\right]}{p^{t+1}+(p+2)p^{t-1}-2(p+1)}\hfill \\ & -\frac{ln\left[(2p^{t-1}-p-1)\times {(2+p)}^{2+p}\right]}{p^{t+1}+(p+2)p^{t-1}-2(p+1)}\hfill \\ & -\frac{ln\left[(p-1)\times {(1+p)}^{1+p}\right]}{p^{t+1}+(p+2)p^{t-1}-2(p+1)}\hfill \end{array}\end{array}$$

2.2.2. Second Zagreb Entropy

To compute the second Zagreb index-entropy of $S(S_p,t)$ we first calculate the value of the second Zagreb index of $S(S_p,t)$ by using the edge partition given in Table 2 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(S(S_p,t)\right)& =(p+2)p^t-5p+2\hfill \end{array}\end{array}$$

Now, by using this computed value of the second Zagreb index and values given in Table 2, we obtain the second Zagreb entropy:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln[((p-2)p^{t-1}+1){\left(p\right)}^p\times (2p^{t-1}-p-1){\left(2p\right)}^{2p}\hfill \\ & \times (p-1){(2p-2)}^{2p-2}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left((p+2)p^t-5p+2\right)\hfill \\ & -\frac{ln\left[\left((p-2)p^{t-1}+1\right)\times {\left(p\right)}^p\right]}{(p+2)p^t-5p+2}\hfill \\ & -\frac{ln\left[\left(2p^{t-1}-p-1\right)\times {\left(2p\right)}^{2p}\right]}{(p+2)p^t-5p+2}\hfill \\ & -\frac{ln\left[(p-1)\times {(2p-2)}^{2p-2}\right]}{(p+2)p^t-5p+2}\hfill \end{array}\end{array}$$

2.2.3. Forgotten Entropy

The forgotten index of the star-based Sierpiński graph, calculated using Table 2, is given as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(S(S_p,t)\right)& =(p+6)p^{t-1}+p^{t+2}-3p^2+3p-4\hfill \end{array}\end{array}$$

Now, Equation (7) by using Table 2 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln[\left((p-2)p^{t-1}+1\right){(1+p^2)}^{1+p^2}\times \left(2p^{t-1}-p-1\right){(4+p^2)}^{4+p^2}\hfill \\ & \times (p-1){(p^2-2p+5)}^{(p^2-2p+5)}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left((p+6)p^{t-1}+p^{t+2}-3p^2+3p-4\right)\hfill \\ & -\frac{ln\left[\left((p-2)p^{t-1}+1\right)\times {(1+p^2)}^{1+p^2}\right]}{(p+6)p^{t-1}+p^{t+2}-3p^2+3p-4}\hfill \\ & -\frac{ln\left[\left(2p^{t-1}-p-1\right)\times {(4+p^2)}^{4+p^2}\right]}{(p+6)p^{t-1}+p^{t+2}-3p^2+3p-4}\hfill \\ & -\frac{ln\left[(p-1)\times {(p^2-2p+5)}^{(p^2-2p+5)}\right]}{(p+6)p^{t-1}+p^{t+2}-3p^2+3p-4}\hfill \end{array}\end{array}$$

2.3. Results for the Sierpiński Graph When Complete Graph Is a Base Graph

Figure 3 displays the generalized Sierpiński graphs $S(K_4,1)$ and $S(K_4,2)$. The values in Table 1 were derived by categorizing the edges of the graph $S(K_p,t)$ based on the degrees of their end vertices. The first column reveals two distinct types of edges, while the second column indicates the frequency of each edge type. Observing Figure 3, we can see that the extended Sierpiński graph $S(K_4,1)$ has only one type of edge partition. This particular partition is composed of edges connecting end vertices, each with a degree of 3. In contrast, the extended Sierpiński graph $S(K_p,t)$ features all types of edges.

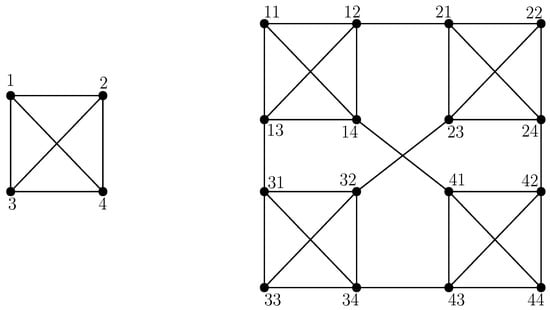
Figure 3. Sierpiński graph S($K_4$, 1) and S($K_4$, 2).

2.3.1. First Zagreb Entropy

First, we calculate the value of the first Zagreb index of $S(K_p,t)$ by using the edge partition given in Table 3 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(S(K_p,t)\right)& =p^{t+2}-2p^2+p\hfill \end{array}\end{array}$$

Table 3. Degree-based edge partition of $S(K_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(p,p-1)$	$p(p-1)$	$E_1$
$(p,p)$	$\frac{p^{t+1}-2p^2+p}{2}$	$E_2$

Now, by using this computed value and values given in Table 3 we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln[p(p-1){(2p-1)}^{2p-1}\hfill \\ & \times \left(\frac{p^{t+1}-2p^2+p}{2}\right){\left(2p\right)}^{2p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(p^{t+2}-2p^2+p\right)\hfill \\ & -\frac{ln\left[p(p-1)\times {(2p-1)}^{2p-1}\right]}{p^{t+2}-2p^2+p}\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}-2p^2+p}{2}\right)\times {\left(2p\right)}^{2p}\right]}{p^{t+2}-2p^2+p}\hfill \end{array}\end{array}$$

2.3.2. Second Zagreb Entropy

The second Zagreb index of complete Sierpiński graph is obtained by using Table 3 as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(S(K_p,t)\right)& =\frac{p^{t+3}-3p^3+2p^2}{2}\hfill \end{array}\end{array}$$

Now, Equation (6) by using Table 3 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln\left[p(p-1){(p^2-p)}^{p^2-p}\times \left(\frac{p^{t+1}-2p^2+p}{2}\right){\left(p^2\right)}^{p^2}\right]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(\frac{p^{t+3}-3p^3+2p^2}{2}\right)\hfill \\ & -\frac{ln\left[p(p-1)\times {(p^2-p)}^{p^2-p}\right]}{\frac{p^{t+3}-3p^3+2p^2}{2}}\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}-2p^2+p}{2}\right)\times {\left(p^2\right)}^{p^2}\right]}{\frac{p^{t+3}-3p^3+2p^2}{2}}\hfill \end{array}\end{array}$$

2.3.3. Forgotten Entropy

The values of forgotten index and forgotten index index-entropy of $S(K_p,t)$ obtained by using Table 3 are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(S(K_p,t)\right)& =p^{t+3}-3p^3+3p^2-p\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln[p(p-1){(1+2p^2-2p)}^{1+2p^2-2p}\hfill \\ & \times \left(\frac{p^{t+1}-2p^2+p}{2}\right){\left(2p^2\right)}^{2p^2}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left(p^{t+3}-3p^3+3p^2-p\right)\hfill \\ & -\frac{ln\left[p(p-1)\times {(1+2p^2-2p)}^{1+2p^2-2p}\right]}{p^{t+3}-3p^3+3p^2-p}\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}-2p^2+p}{2}\right)\times {\left(2p^2\right)}^{2p^2}\right]}{p^{t+3}-3p^3+3p^2-p}\hfill \end{array}\end{array}$$

2.4. Results for Extended Sierpiński Graphs

In this section, we obtain the entropy of extended Sierpiński graphs using Zagreb and forgotten topological indices by considering cycle, star, and complete graph as a base graph.

2.4.1. Results for the Extended Sierpiński Graph When Cycle Is a Base Graph

Figure 4 presents the extended Sierpiński graph $ES(C_4,2)$. This graph is created by adding a new vertex to the generalized Sierpiński graph $ES(C_4,2)$ and connecting it to the extreme vertices.

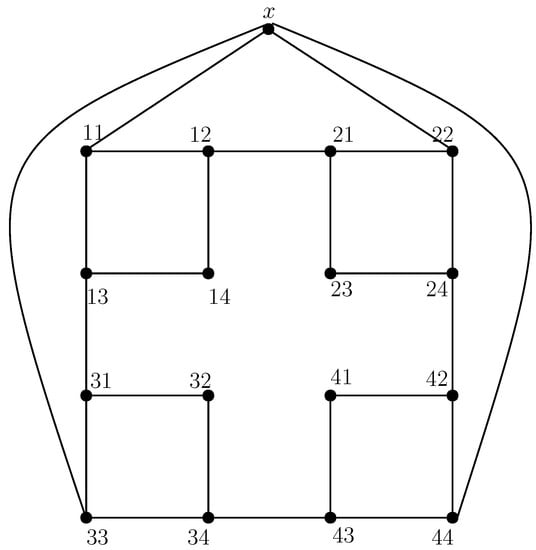
Figure 4. Extended Sierpiński graph $ES$($C_4$, 2).

The values in Table 4 are obtained by computing the number of edges of the graph $ES(C_p,t)$ based on the degrees of their end vertices. The first column reveals that there are four distinct types of edges, while the second column indicates the frequency of each edge type.

Table 4. Degree-based edge partition of $ES(C_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(2,2)$	$p^{t-1}(p-4)$	$E_1$
$(2,3)$	$4p{(p-1)}^{t-2}-2p$	$E_2$
$(3,3)$	${\displaystyle \frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-3p+2p^2}{p-1}}$	$E_3$
$(3,p)$	p	$E_4$

2.4.2. First Zagreb Entropy

The first Zagreb index of the cycle-based extended Sierpiński graph is computed by using Table 4 and is given as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(ES(C_p,t)\right)& =\frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}\hfill \end{array}\end{array}$$

The value of the first Zagreb index entropy is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln[\left(p^{t-1}(p-4)\right){\left(4\right)}^4\times \left(4p{(p-1)}^{t-2}-2p\right){\left(5\right)}^5\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-3p+2p^2}{p-1}\right){\left(6\right)}^6\times p{(3+p)}^{3+p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left({\displaystyle \frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}}\right)\hfill \\ & -{\displaystyle \frac{ln\left[p^{t-1}(p-4)\times {\left(4\right)}^4\right]}{\left({\displaystyle \frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}}\right)}}\hfill \\ & -{\displaystyle \frac{ln\left[(4p{(p-1)}^{t-2}-2p)\times {\left(5\right)}^5\right]}{\left({\displaystyle \frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}}\right)}}\hfill \\ & -{\displaystyle \frac{ln\left[\left({\displaystyle \frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-3p+2p^2}{p-1}}\right)\times {\left(6\right)}^6\right]}{\left({\displaystyle \frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}}\right)}}\hfill \\ & -{\displaystyle \frac{ln\left[p\times {(3+p)}^{3+p}\right]}{\left({\displaystyle \frac{4p^{t+1}+10p^t-12p^{t-1}-4p{(p-1)}^{t-1}+p^3+4p^2-11p}{p-1}}\right)}}\hfill \end{array}\end{array}$$

2.4.3. Second Zagreb Entropy

By using the values of edge partitions given in Table 4, we obtained the second Zagreb index of $\left(ES(C_p,t)\right)$ as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(ES(C_p,t)\right)& =\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\hfill \end{array}\end{array}$$

The second Zagreb index entropy of $\left(ES(C_p,t)\right)$ is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln[\left(p^{t-1}(p-4)\right){\left(4\right)}^4\times \left(4p{(p-1)}^{t-2}\right){\left(6\right)}^6\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\right){\left(9\right)}^9\times p{\left(3p\right)}^{3p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\right)\hfill \\ & -\frac{ln\left[p^{t-1}(p-4)\times {\left(4\right)}^4\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\right)}\hfill \\ & -\frac{ln\left[4p{(p-1)}^{t-2}\times {\left(6\right)}^6\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\right)}\hfill \\ & -\frac{ln\left[\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\times {\left(9\right)}^9\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\right)}\hfill \\ & -\frac{ln\left[p\times {\left(3p\right)}^{3p}\right]}{\left(\frac{4p^{t+1}+25p^t-20p^{t-1}-12p{(p-1)}^{t-1}+3p^3+3p^2-15p}{p-1}\right)}\hfill \end{array}\end{array}$$

2.4.4. Forgotten Entropy

The forgotten index of the cycle-based extended Sierpiński graph is computed by using Table 4 and is given as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(ES(C_p,t)\right)& =\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\hfill \end{array}\end{array}$$

The value of forgotten entropy of $ES(C_p,t)$ is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln[\left(p^{t-1}(p-4)\right){\left(8\right)}^8\times (4p{(p-1)}^{t-2}-2p){\left(13\right)}^{13}\hfill \\ & \times \left(\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-3p+2p^2}{p-1}\right){\left(18\right)}^{18}\times p{(9+p^2)}^{9+p^2}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\right)\hfill \\ & -\frac{ln\left[p^{t-1}(p-4)\times {\left(8\right)}^8\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\right)}\hfill \\ & -\frac{ln\left[4p{(p-1)}^{t-2}\times {\left(13\right)}^{13}\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\right)}\hfill \\ & -\frac{ln\left[\frac{5p^t-4p{(p-1)}^{t-1}-4p^{t-1}-p}{p-1}\times {\left(18\right)}^{18}\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\right)}\hfill \\ & -\frac{ln\left[p\times {(9+p^2)}^{9+p^2}\right]}{\left(\frac{8p^{t+1}+50p^t-40p^{t-1}-20p{(p-1)}^{t-1}+p^4-p^3+19p^2-37p}{p-1}\right)}\hfill \end{array}\end{array}$$

2.5. Results for the Extended Sierpiński Graph When Star Is a Base Graph

In this section, we compute the results for the extended Sierpiński graph $ES(S_5,2),$ shown in Figure 5 by using the partition of edges given in Table 5.

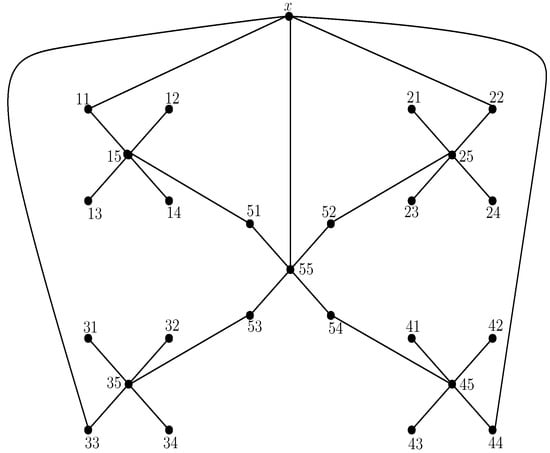
Figure 5. Extended Sierpiński graph $ES(S_5,2)$.

Table 5. Degree-based edge partition of $ES(S_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(1,p)$	$(p-2)p^{t-1}-p+2$	$E_1$
$(p,p)$	1	$E_2$
$(2,p)$	$2p^{t-1}+2p-4$	$E_3$

2.5.1. First Zagreb Entropy

First, we compute the first Zagreb index by using Table 5 as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(ES(S_p,t)\right)& =p^{t+1}+p^t+2p^{t-1}+p^2+3p-6\hfill \end{array}\end{array}$$

Now, by using the above computed first Zagreb index, we obtain the first Zagreb entropy:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln[\left((p-2)p^{t-1}-p+2\right){(1+p)}^{1+p}\times {\left(2p\right)}^{2p}\hfill \\ & \times (2p^{t-1}+2p-4){(2+p)}^{2+p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(p^{t+1}+p^t+2p^{t-1}+p^2+3p-6\right)\hfill \\ & -\frac{ln\left[((p-2)p^{t-1}-p+2)\times {(1+p)}^{1+p}\right]}{p^{t+1}+p^t+2p^{t-1}+p^2+3p-6}\hfill \\ & -\frac{ln\left[1\times {\left(2p\right)}^{2p}\right]}{p^{t+1}+p^t+2p^{t-1}+p^2+3p-6}\hfill \\ & -\frac{ln\left[(2p^{t-1}+2p-4)\times {(2+p)}^{2+p}\right]}{p^{t+1}+p^t+2p^{t-1}+p^2+3p-6}\hfill \end{array}\end{array}$$

2.5.2. Second Zagreb Entropy

Similarly, the second Zagreb index is calculated by using Table 5.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(ES(S_p,t)\right)& =p^{t+1}+2p^t+4p^2-6p\hfill \end{array}\end{array}$$

Now, Equation (6) by using Table 5 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln[((p-2)p^{t-1}-p+2){\left(p\right)}^p\times {\left(p^2\right)}^{p^2}\hfill \\ & \times (2p^{t-1}+2p-4){\left(2p\right)}^{2p}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(p^{t+1}+2p^t+4p^2-6p\right)\hfill \\ & -\frac{ln\left[((p-2)p^{t-1}-p+2)\times {\left(p\right)}^p\right]}{p^{t+1}+2p^t+4p^2-6p}\hfill \\ & -\frac{ln\left[1\times {\left(2p\right)}^{2p}\right]}{p^{t+1}+2p^t+4p^2-6p}\hfill \\ & -\frac{ln\left[(2p^{t-1}+2p-4)\times {\left(2p\right)}^{2p}\right]}{p^{t+1}+2p^t+4p^2-6p}\hfill \end{array}\end{array}$$

2.5.3. Forgotten Entropy

The forgotten index of the star-based extended Sierpiński graph by using Table 5 is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(ES(S_p,t)\right)& =p^{t+2}+p^t+6p^{t-1}+p^3+7p-14\hfill \end{array}\end{array}$$

Now, the forgotten entropy is computed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln[((p-2)p^{t-1}-p+2){(1+p^2)}^{1+p^2}\times {\left(2p^2\right)}^{2p^2}\hfill \\ & \times (2p^{t-1}+2p-4){(4+p^2)}^{(4+p^2)}]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left(p^{t+2}+p^t+6p^{t-1}+p^3+7p-14\right)\hfill \\ & -\frac{ln\left[((p-2)p^{t-1}-p+2)\times {(1+p^2)}^{1+p^2}\right]}{p^{t+2}+p^t+6p^{t-1}+p^3+7p-14}\hfill \\ & -\frac{ln\left[1\times {\left(2p^2\right)}^{2p^2}\right]}{p^{t+2}+p^t+6p^{t-1}+p^3+7p-14}\hfill \\ & -\frac{ln\left[(2p^{t-1}+2p-4)\times {(4+p^2)}^{4+p^2}\right]}{p^{t+2}+p^t+6p^{t-1}+p^3+7p-14}\hfill \end{array}\end{array}$$

2.6. Results for the Extended Sierpiński Graph When Complete Graph Is a Base Graph

Figure 6 displays the extended Sierpiński graphs $S(K_4,2).$ The values in Table 6 are derived by categorizing the edges of the graph $S(K_p,t)$ based on the degrees of their end vertices. The first column reveals that there is only type of edges, while the second column indicates the frequency of this edge type.

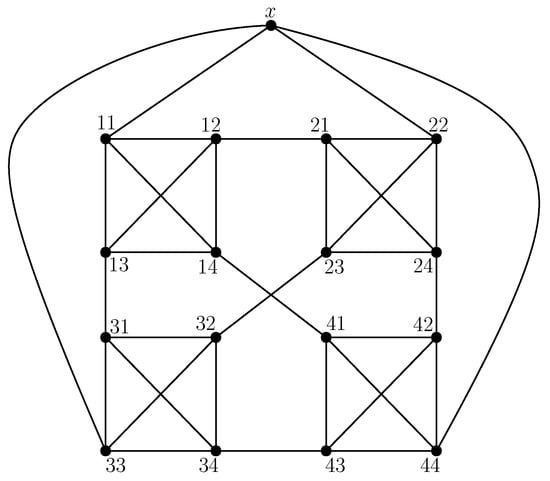
Figure 6. Extended Sierpiński graph $ES$($K_4$ 2).

Table 6. Degree-based edge partition of $ES(K_p,t)$ with respect to end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{x}),\mathit{\zeta }(\mathit{y}\left)\right)$	Frequency	Set of Edges
$(p,p)$	$\frac{p^{t+1}+p}{2}$	$E_1$

2.6.1. First Zagreb Entropy

The first Zagreb index of the extended Sierpiński graph $ES(K_p,t)$ computed by using the Table 6 is given as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_1\left(ES(K_p,t)\right)& =p^{t+2}+p^2\hfill \end{array}\end{array}$$

Now, Equation (5) by using Table 6 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(M_1\right)-\frac{1}{M_1}ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(2p\right)}^{2p}\right]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_1}& =ln\left(p^{t+2}+p^2\right)\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(2p\right)}^{2p}\right]}{p^{t+2}+p^2}\hfill \end{array}\end{array}$$

2.6.2. Second Zagreb Entropy

The second Zagreb index of the complete-based extended Sierpiński graph by using Table 6 is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_2\left(ES(K_p,t)\right)& =\frac{p^{t+3}+p^3}{2}\hfill \end{array}\end{array}$$

Now, Equation (6) by using Table 6 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(M_2\right)-\frac{1}{M_2}ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(p^2\right)}^{p^2}\right]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_{M_2}& =ln\left(\frac{p^{t+3}+p^3}{2}\right)\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(p^2\right)}^{p^2}\right]}{\frac{p^{t+3}+p^3}{2}}\hfill \end{array}\end{array}$$

2.6.3. Forgotten Entropy

The forgotten index of the complete-based extended Sierpiński graph computed by using Table 6 is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F\left(ES(K_p,t)\right)& =p^{t+3}+p^3\hfill \end{array}\end{array}$$

Now, Equation (7) by using Table 6 can be written as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F& =ln\left(F\right)-\frac{1}{F}ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(2p^2\right)}^{2p^2}\right]\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill EN{T}_F=& ln\left(p^{t+3}+p^3\right)\hfill \\ & -\frac{ln\left[\left(\frac{p^{t+1}+p}{2}\right)\times {\left(2p^2\right)}^{2p^2}\right]}{p^{t+3}+p^3}\hfill \end{array}\end{array}$$

3. Comparison of Entropies for Sierpiński and Extended Sierpiński Graphs

Table 7 shows that first and second Zagreb entropy of the cycle-based Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 7.

Table 7. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $S(C_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$4.357112342$	$4.664564435$	$5.567854535$
$[5,3]$	$6.639791916$	$6.891116333$	$7.615514617$
$[6,4]$	$8.964062757$	$9.207471830$	$9.929721543$
$[7,5]$	$11.48388097$	$11.71375468$	$12.43132469$
$[8,6]$	$14.19293087$	$14.40905918$	$15.12320522$
$[9,7]$	$17.06553261$	$17.26874688$	$17.98038607$

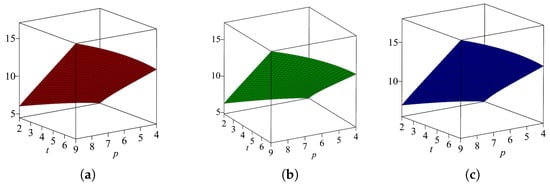
Figure 7. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $S(C_p,t)$.

Table 8 shows that first and second Zagreb entropy of the star-based Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 8.

Table 8. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $S(S_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$3.956203890$	$3.878174010$	$4.775322330$
$[5,3]$	$6.612869027$	$6.680438886$	$7.986139517$
$[6,4]$	$9.151850317$	$9.236229738$	$10.77683658$
$[7,5]$	$11.84344655$	$11.92589558$	$13.65463845$
$[8,6]$	$14.70122917$	$14.77917286$	$16.66703026$
$[9,7]$	$17.70513351$	$17.77846370$	$19.80399526$

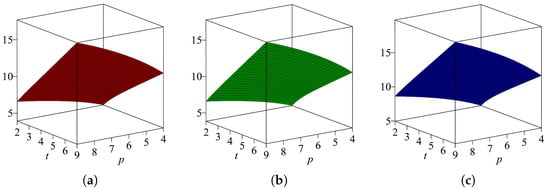
Figure 8. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $S(S_p,t)$.

Table 9 shows that first and second Zagreb entropy of the complete-based Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 9.

Table 9. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $S(K_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$5.269786874$	$5.882539495$	$6.549911825$
$[5,3]$	$8.015882977$	$8.922939944$	$9.613624196$
$[6,4]$	$10.74768073$	$11.84537046$	$12.53832187$
$[7,5]$	$13.62115712$	$14.87384670$	$15.56698092$
$[8,6]$	$16.63551904$	$18.02180861$	$18.71495506$
$[9,7]$	$19.77502049$	$21.27909762$	$21.97224476$

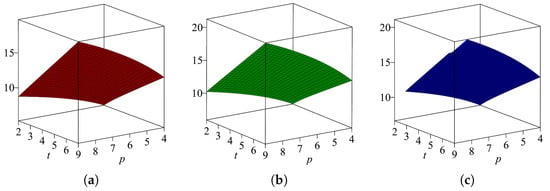
Figure 9. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $S(K_p,t)$.

Table 10 shows that first and second Zagreb entropy of the cycle-based extended Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 10.

Table 10. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $ES(C_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$6.744250951$	$7.122475043$	$7.835251712$
$[5,3]$	$6.744250951$	$7.122475043$	$7.835251712$
$[6,4]$	$9.004999353$	$9.340076797$	$10.04341609$
$[7,5]$	$11.51369249$	$11.81866854$	$12.51813906$
$[8,6]$	$14.21965179$	$14.50110779$	$15.19901406$
$[9,7]$	$17.09036043$	$17.35195472$	$18.04896784$

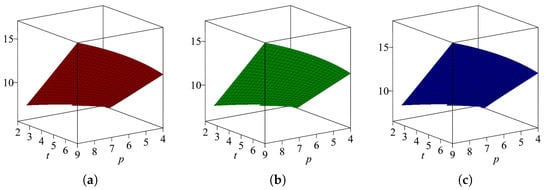
Figure 10. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $ES(C_p,t)$.

Table 11 shows that first and second Zagreb entropy of the star-based extended Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 11.

Table 11. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $ES(S_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$4.349468252$	$4.400006480$	$5.330242762$
$[5,3]$	$6.663257691$	$6.727725774$	$8.065541871$
$[6,4]$	$9.151850317$	$9.239941749$	$10.79751281$
$[7,5]$	$11.84344655$	$11.92613288$	$13.65800141$
$[8,6]$	$14.70122917$	$14.77918398$	$16.66247189$
$[9,7]$	$17.70513351$	$17.77846402$	$19.79538648$

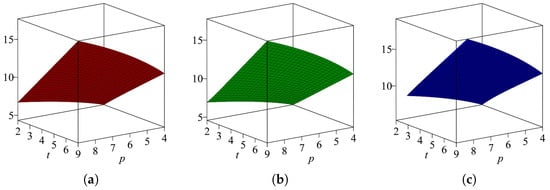
Figure 11. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $ES(S_p,t)$.

Table 12 shows that first and second Zagreb entropy of the complete-based extended Sierpiński graph is almost the same, while forgotten entropy is greater than first and second Zagreb entropy, and their graphical comparison is shown in Figure 12.

Table 12. Comparison of $EN{T}_{M_1}$, $EN{T}_{M_2}$, and $EN{T}_F$ entropies for $ES(K_p,t)$.

$[\mathit{p},\mathit{t}]$	${\mathit{ENT}}_{{\mathit{M}}_1}$	${\mathit{ENT}}_{{\mathit{M}}_2}$	${\mathit{ENT}}_{\mathit{F}}$
$[4,2]$	$5.502085580$	$5.737909410$	$6.888379941$
$[5,3]$	$8.036895597$	$8.538590153$	$9.646333509$
$[6,4]$	$10.74920362$	$11.44128855$	$12.54096309$
$[7,5]$	$13.62124385$	$14.46844837$	$15.56715400$
$[8,6]$	$16.63552293$	$17.61634557$	$18.71496447$
$[9,7]$	$19.77502063$	$20.87363251$	$21.97224520$

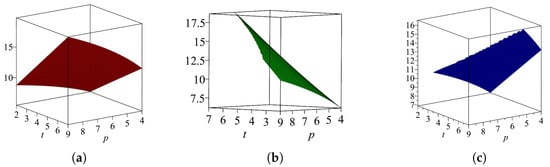
Figure 12. (a) $EN{T}_{M_1}$, (b) $EN{T}_{M_2}$, and (c) $EN{T}_F$ for $ES(K_p,t)$.

4. Conclusions

In this paper, we computed the entropy of fractal-type graphs, namely, Sierpiński and extended Sierpiński graphs, using cycle, star, and complete graph as a base graph. Topological indices used in this article were first Zagreb index, second Zagreb index, and forgotten index. Moreover, we compared the entropies relevant to the above used topological indices, which shows that the entropy of cycle-based fractals is more significant, while the entropy of star-based fractals is smaller and the entropy of complete-based fractals is in between cycle- and star-based fractals.