Mathematical Analysis of Fractal-Fractional Mathematical Model of COVID-19
Abstract
1. Introduction
2. Preliminaries
Formulation of the Proposed Model of COVID-19
3. Equilibrium Points and Stability
3.1. Equilibrium Points
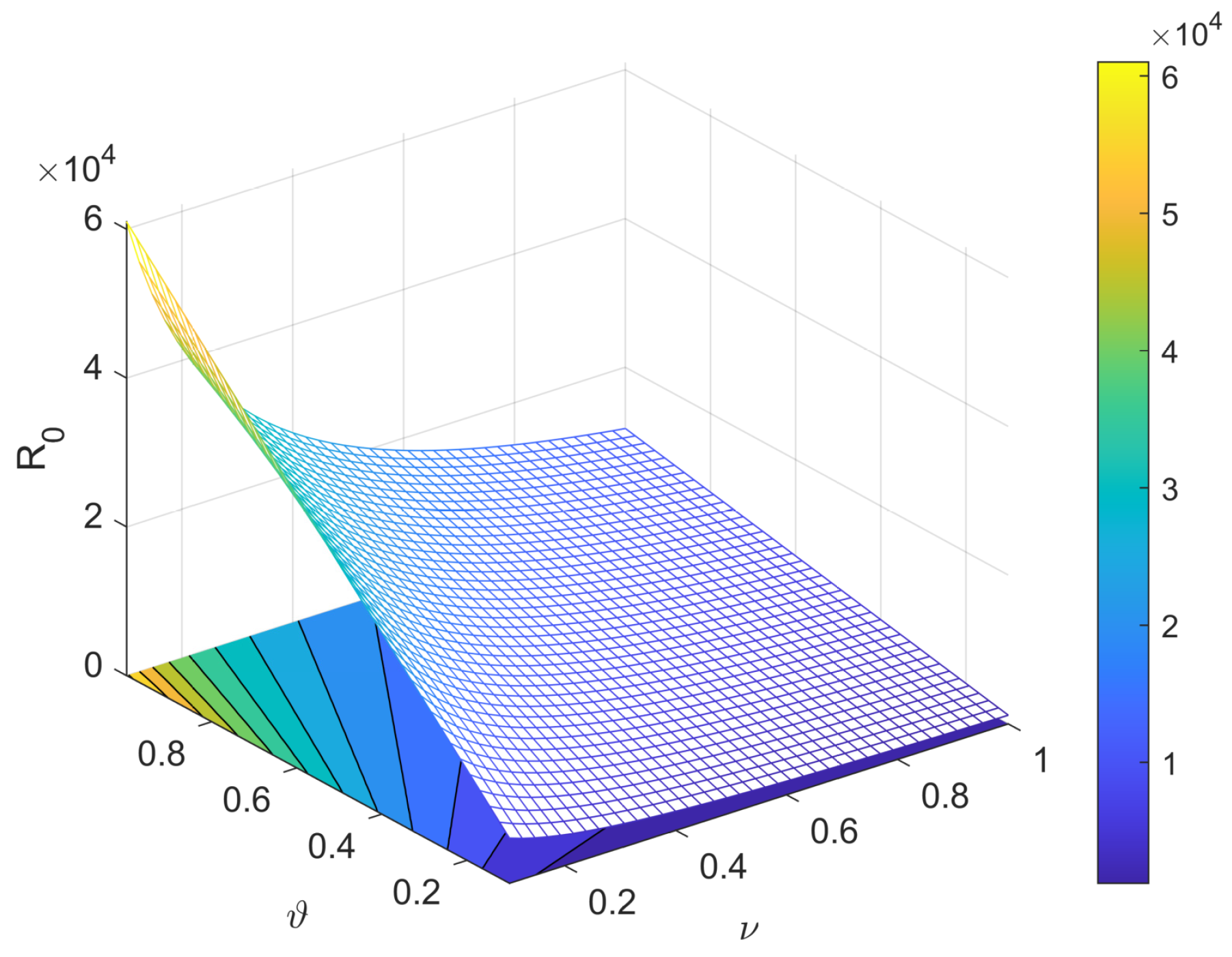
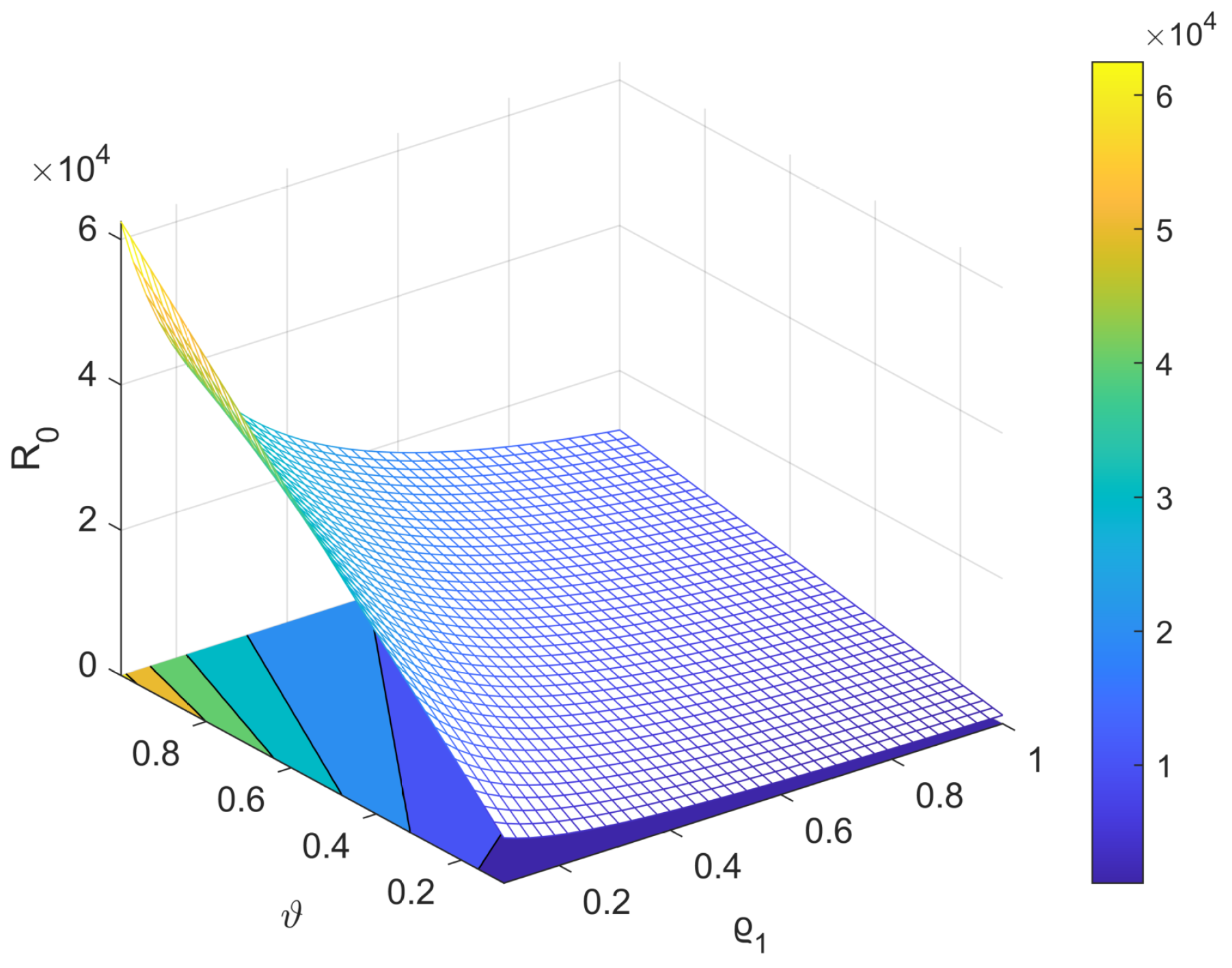
3.2. Basic Reproduction Number
3.3. Stability Analysis
4. Bifurcation Analysis
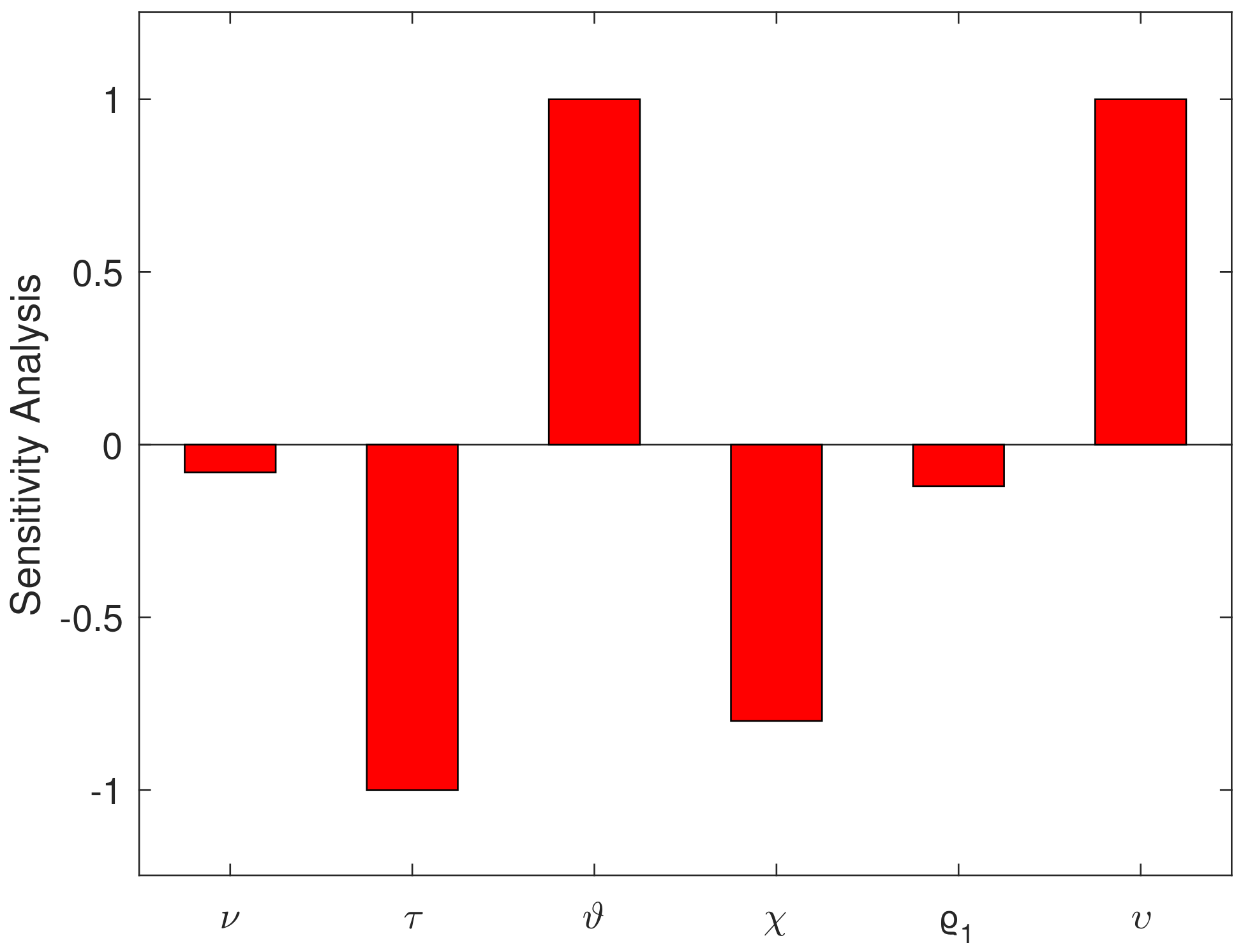
5. Sensitivity Analysis
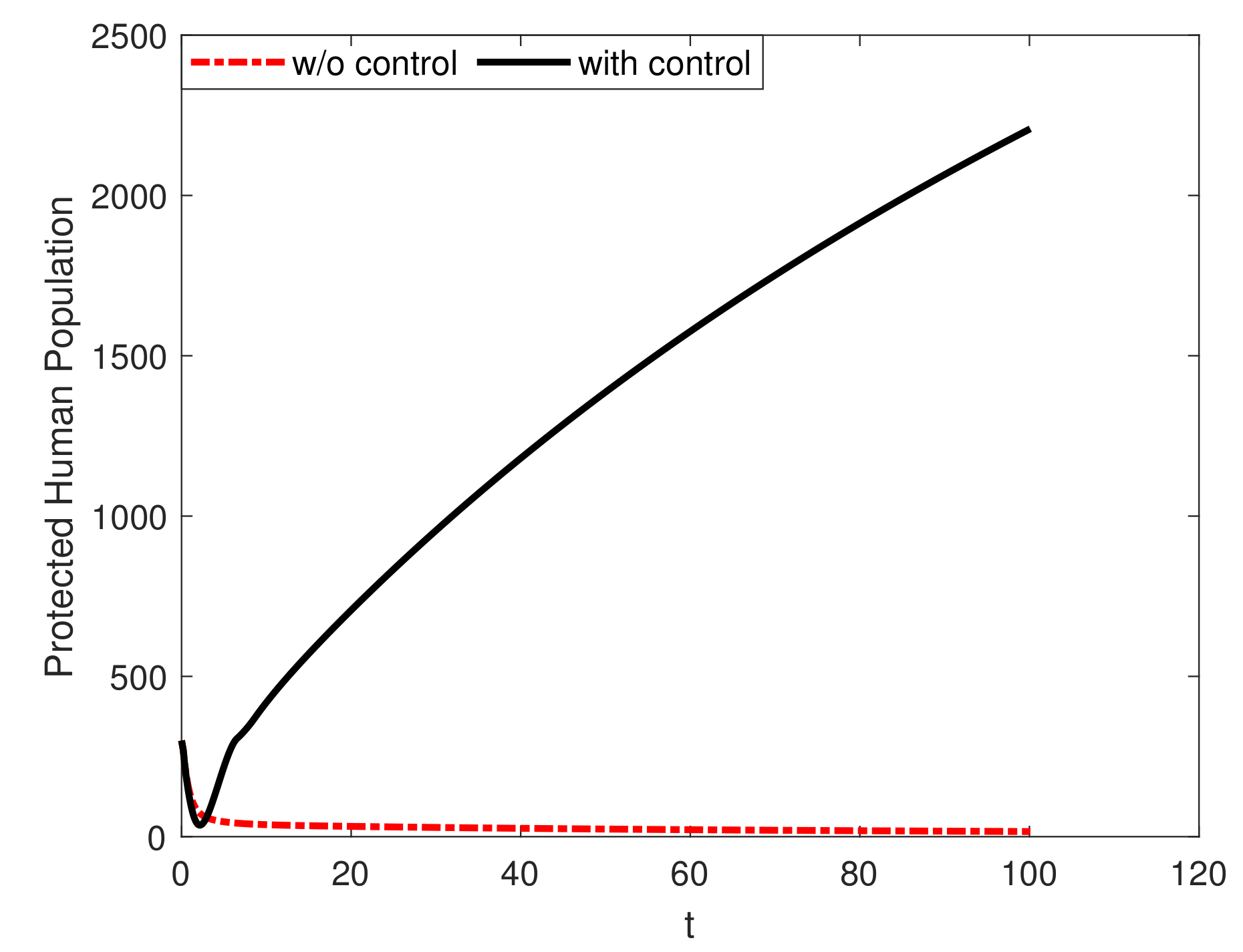
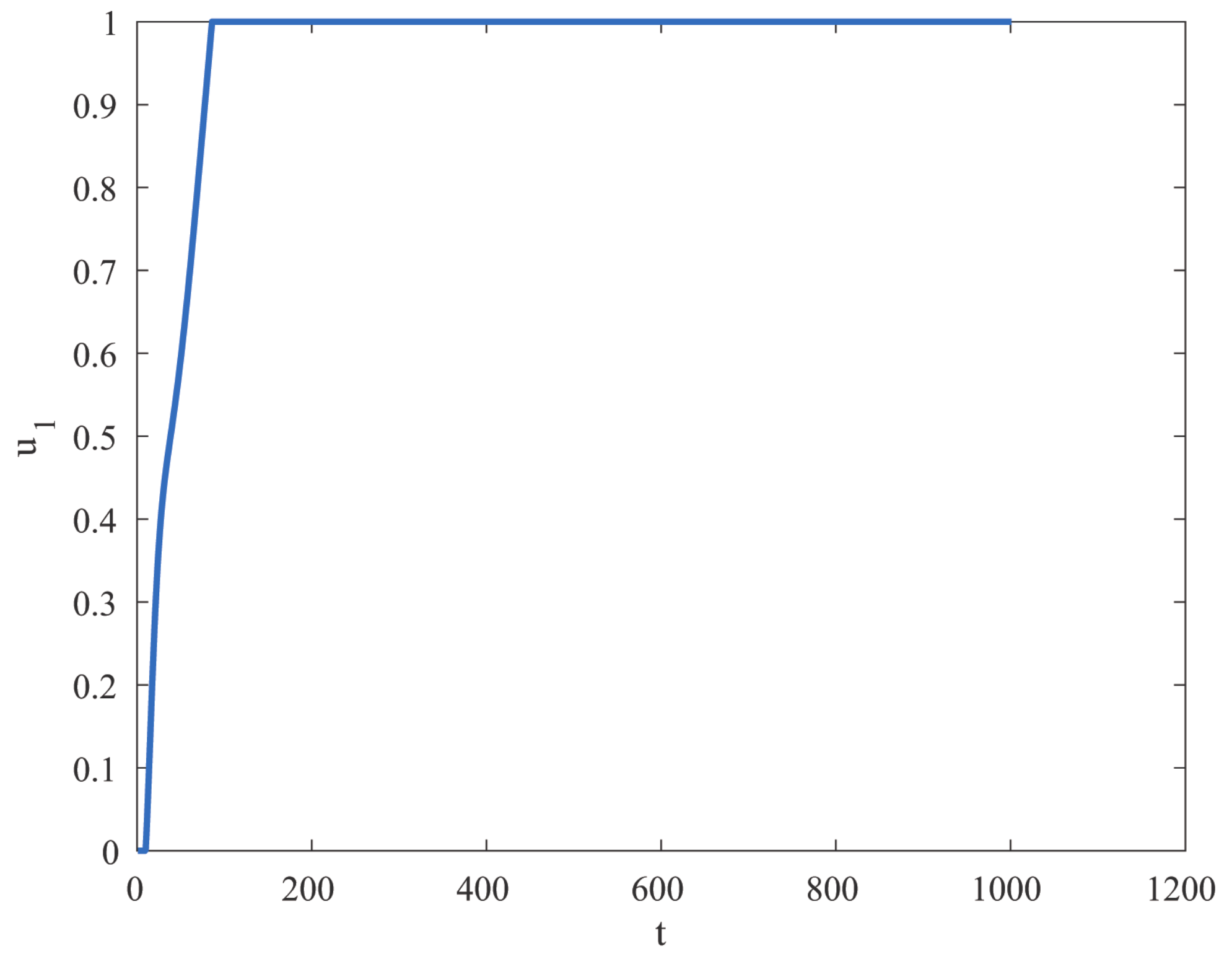
6. Optimal Control Strategies
Characterization of an Optimal Control
7. Numerical Scheme for the Fractal-Fractional Model
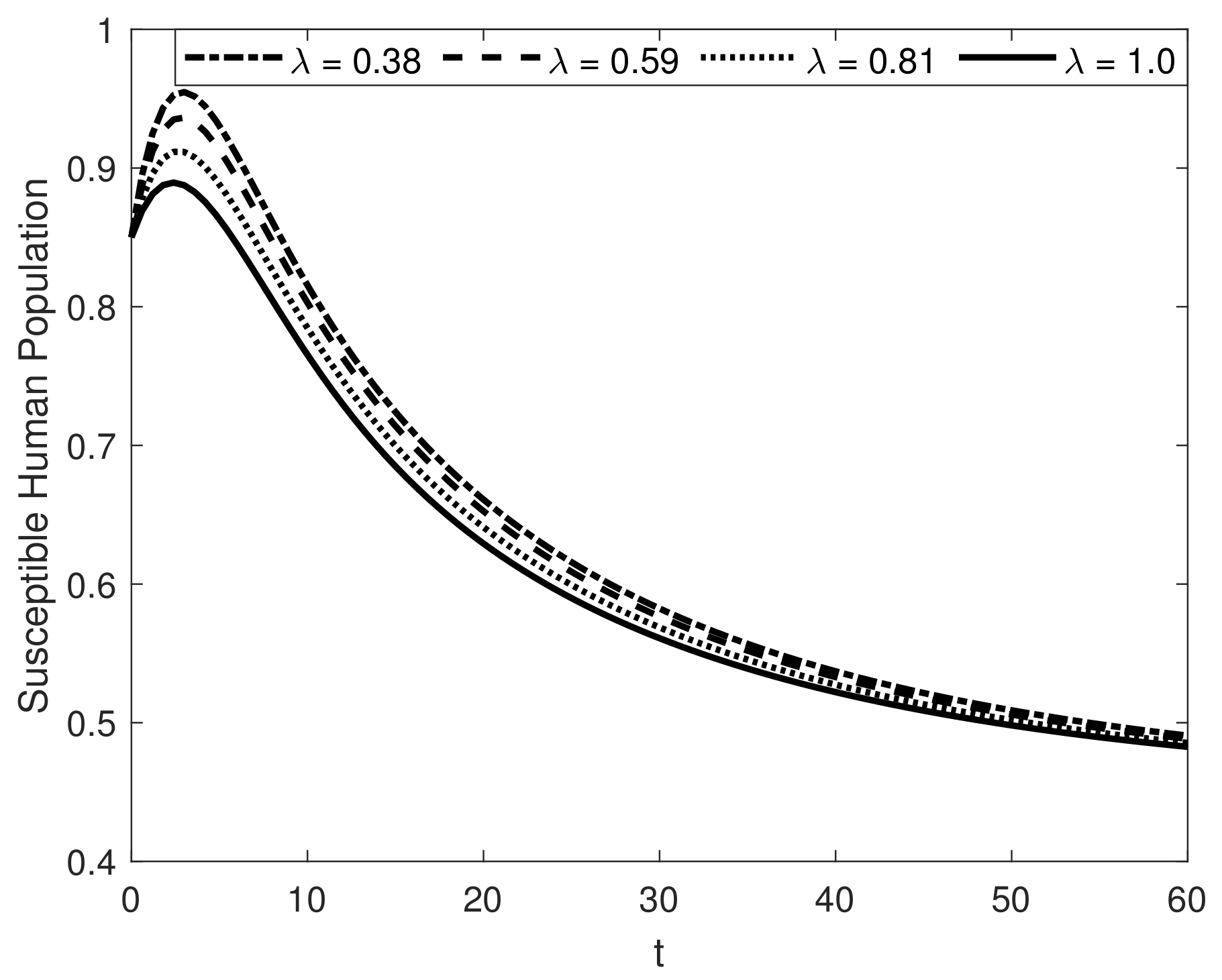
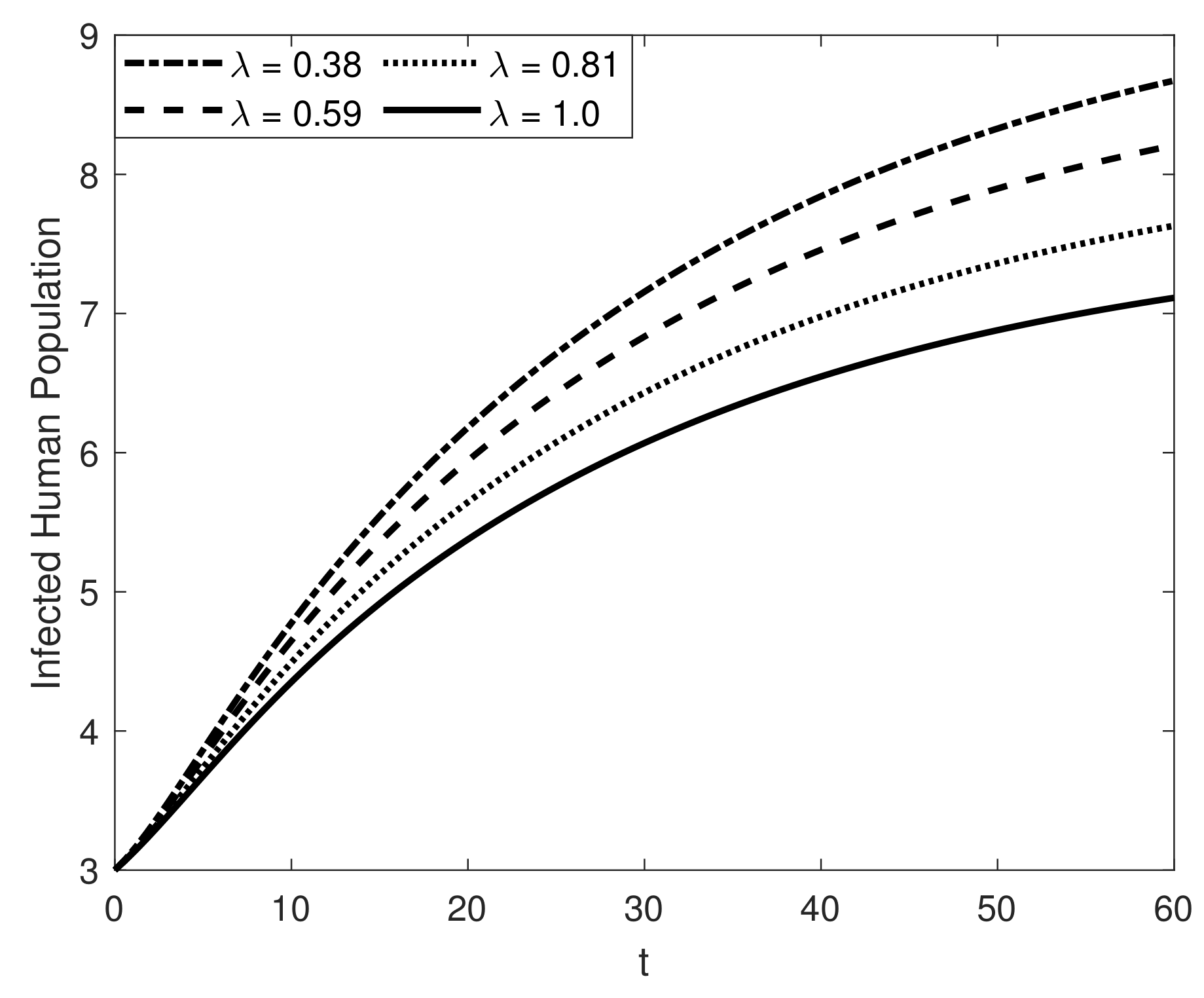
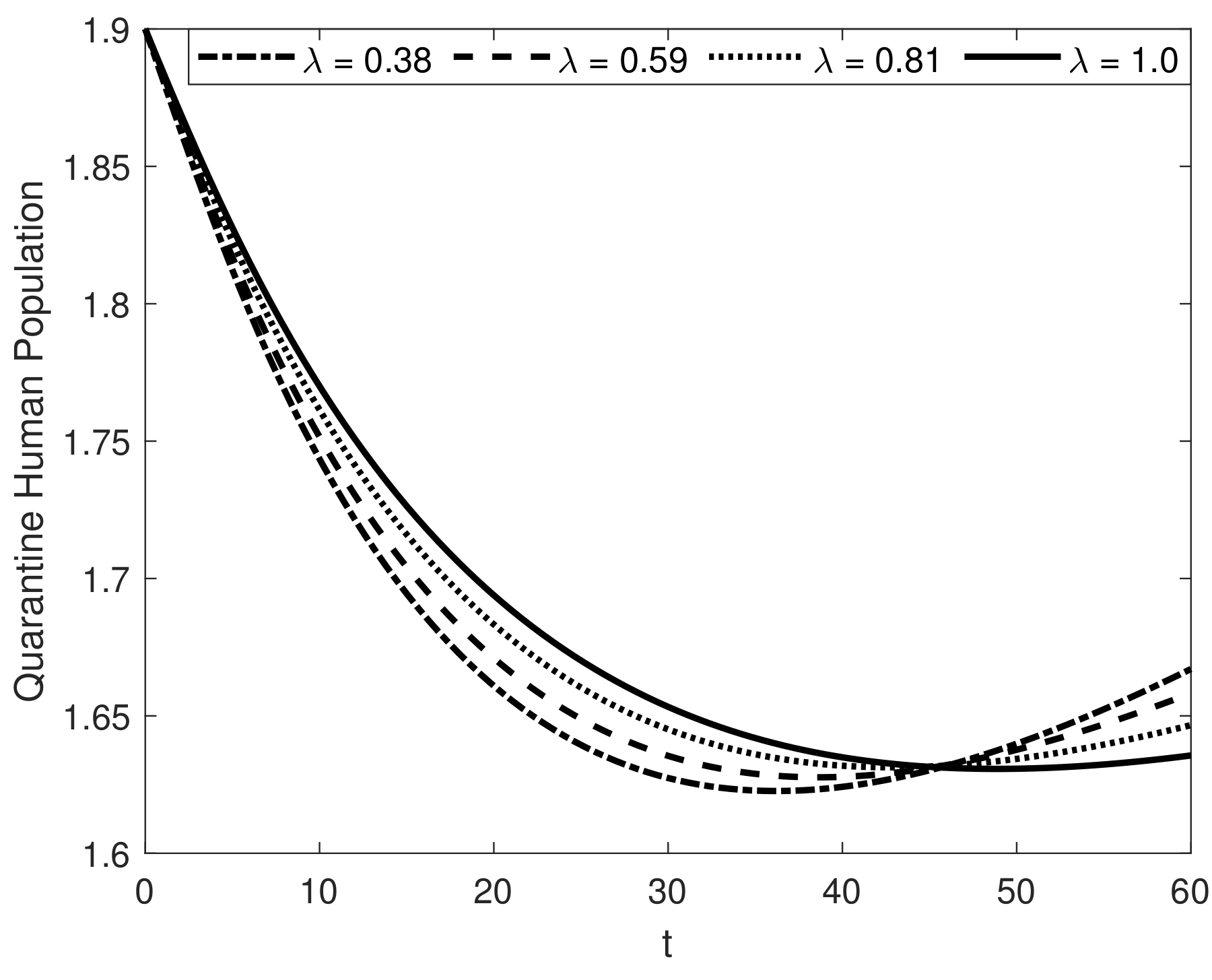
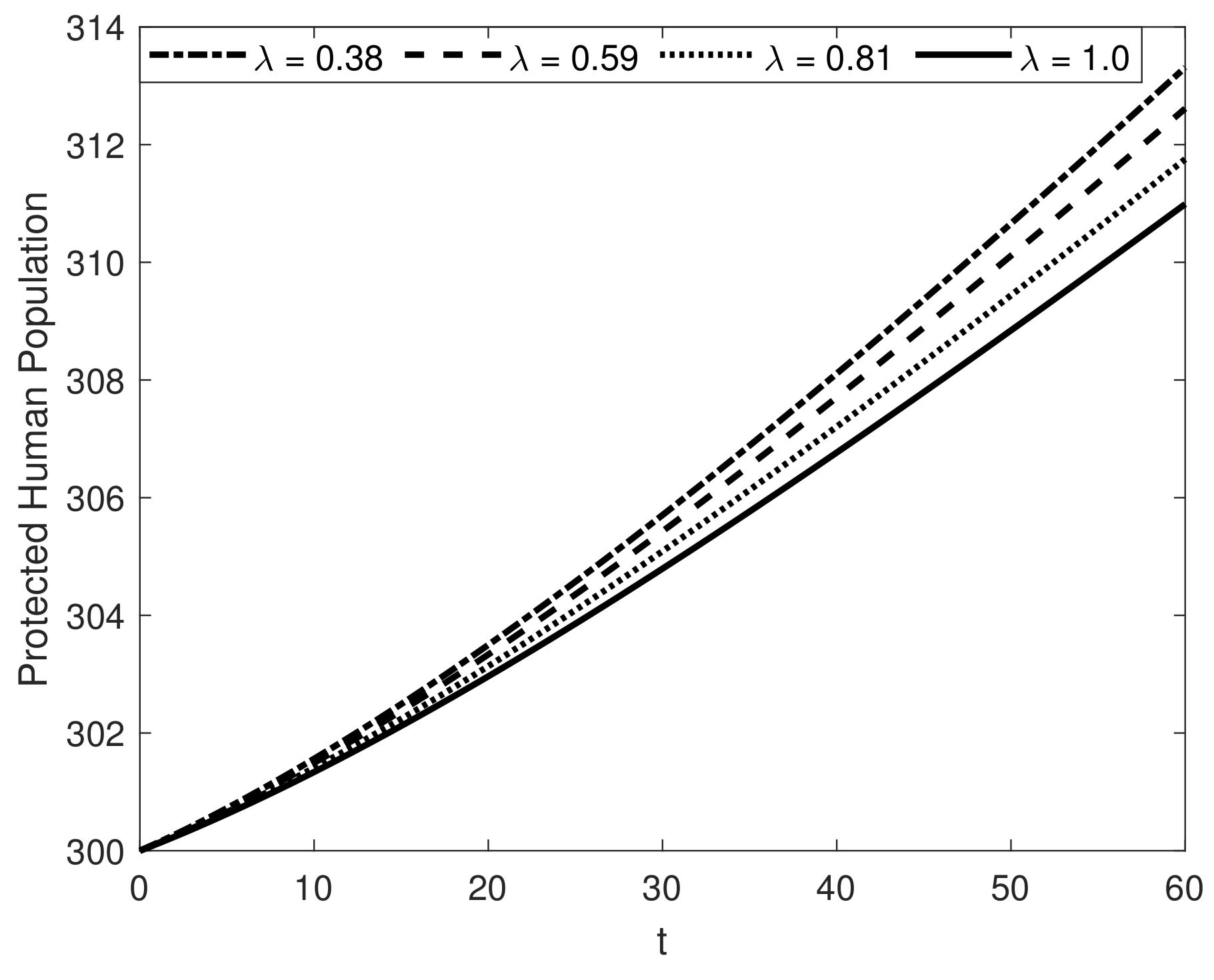
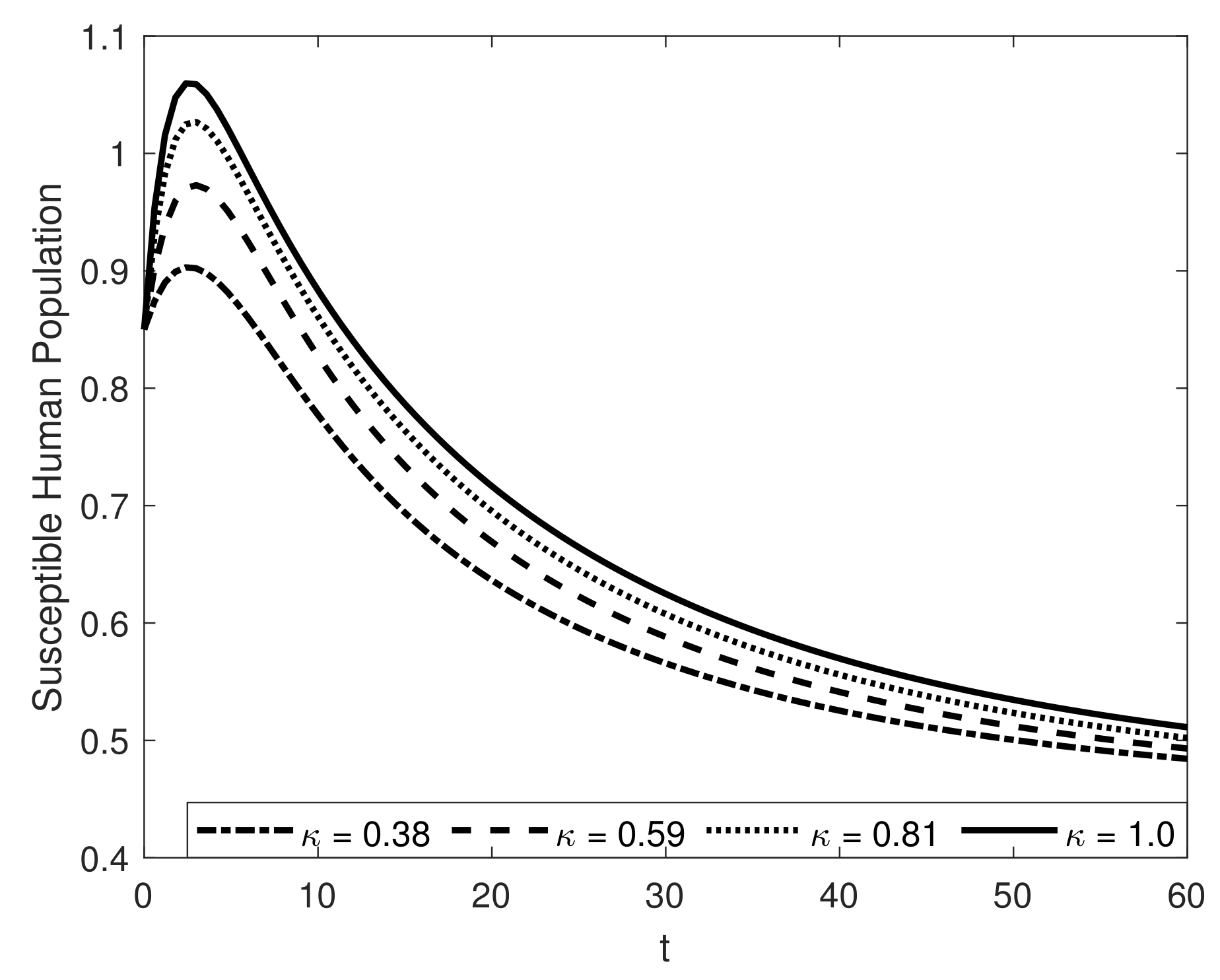
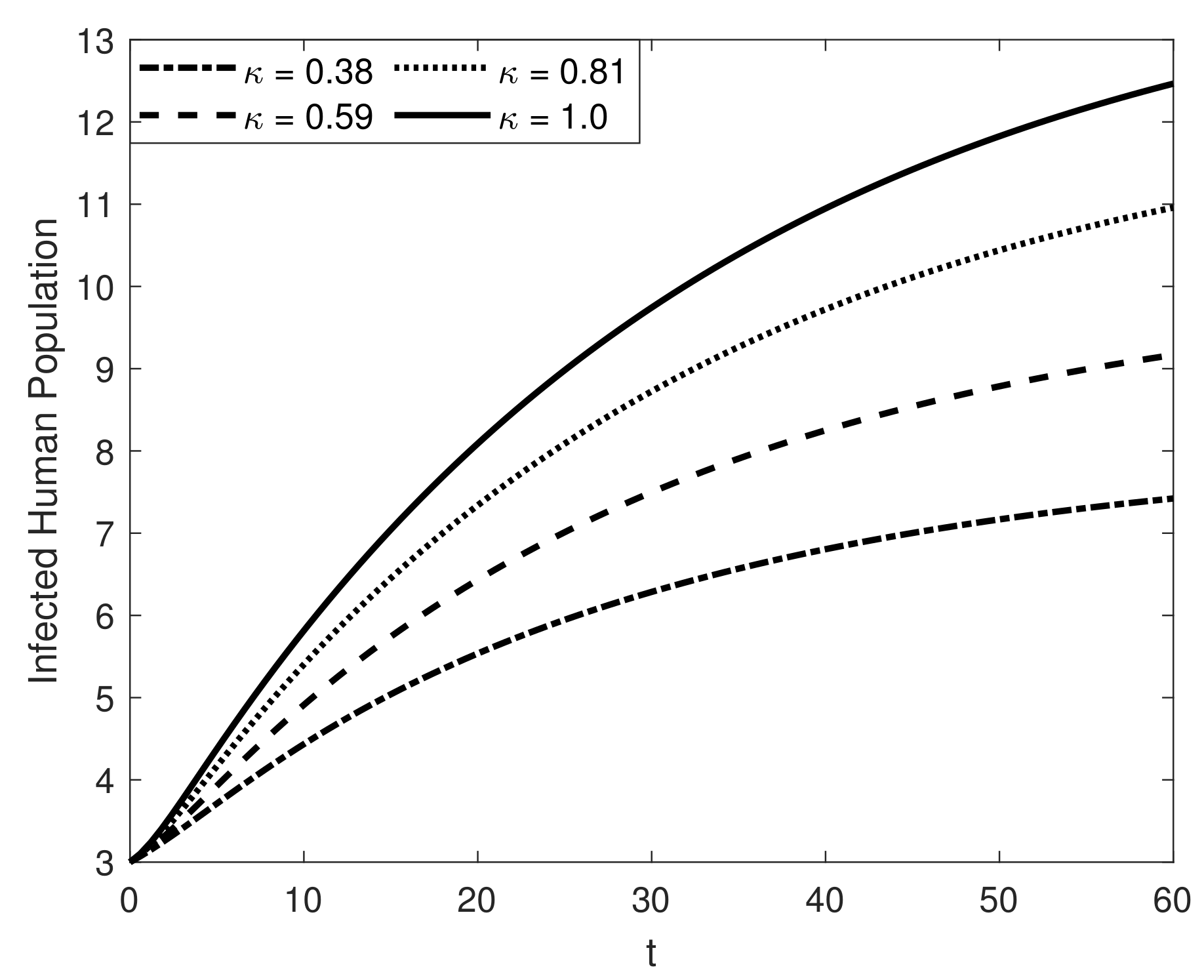
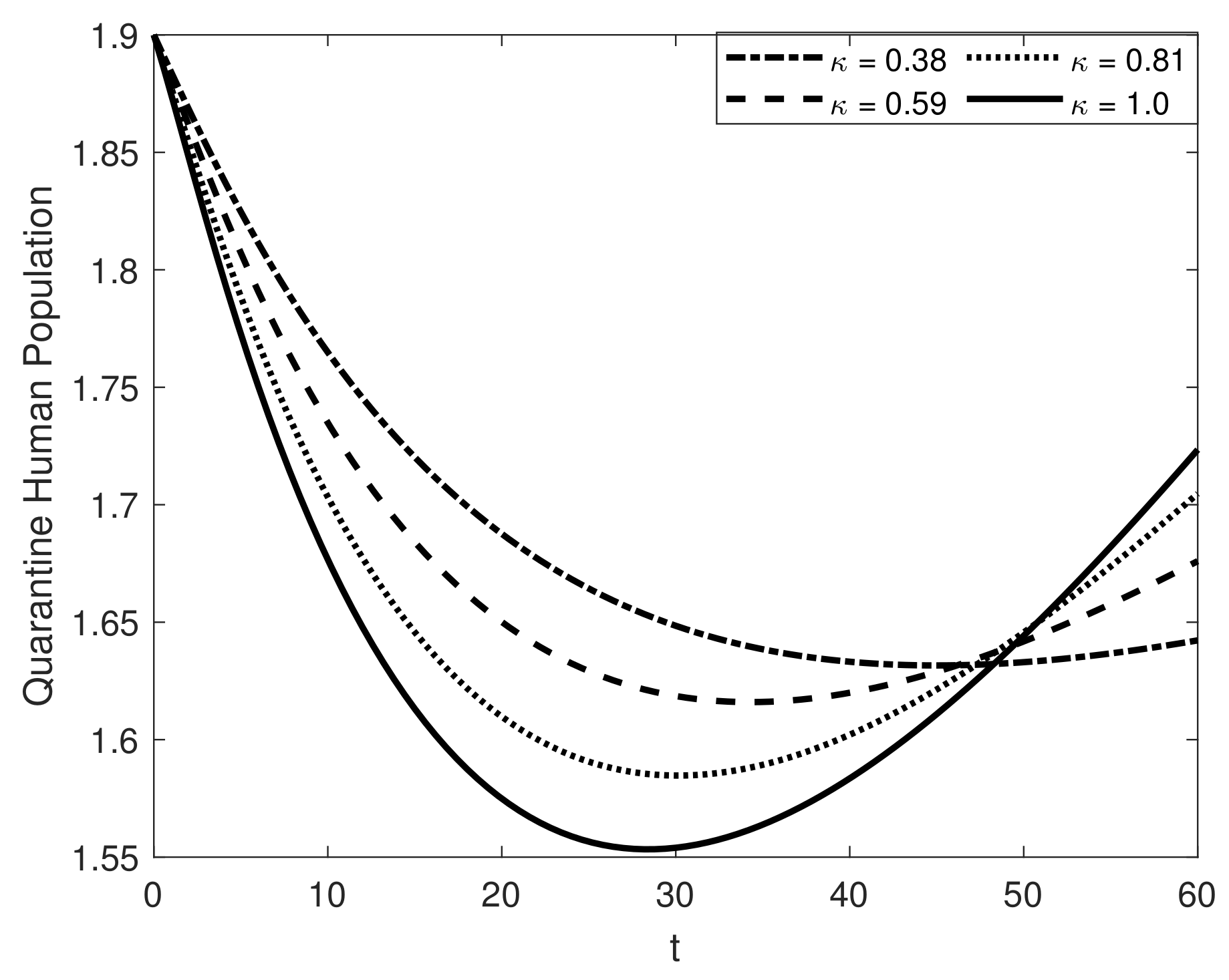
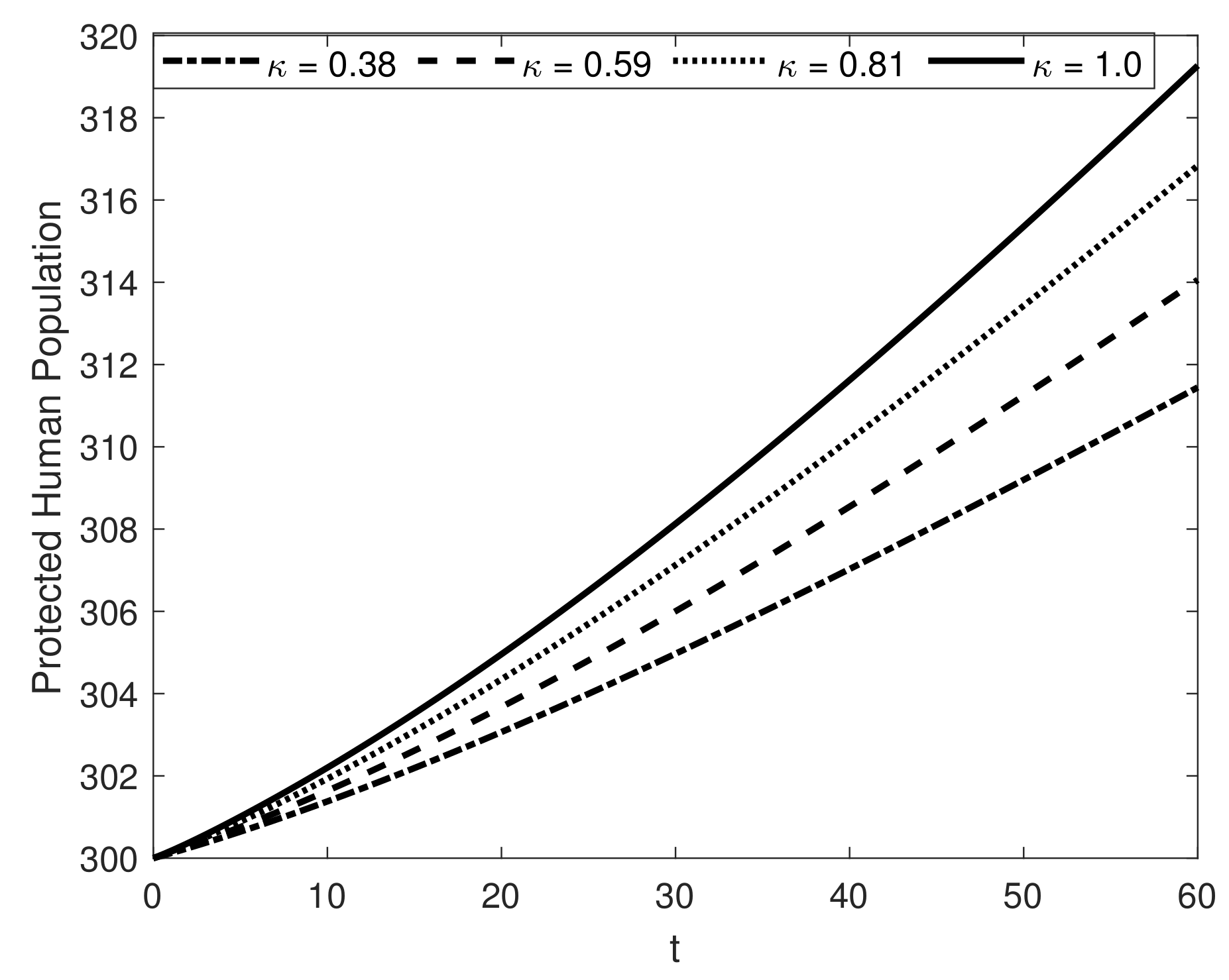
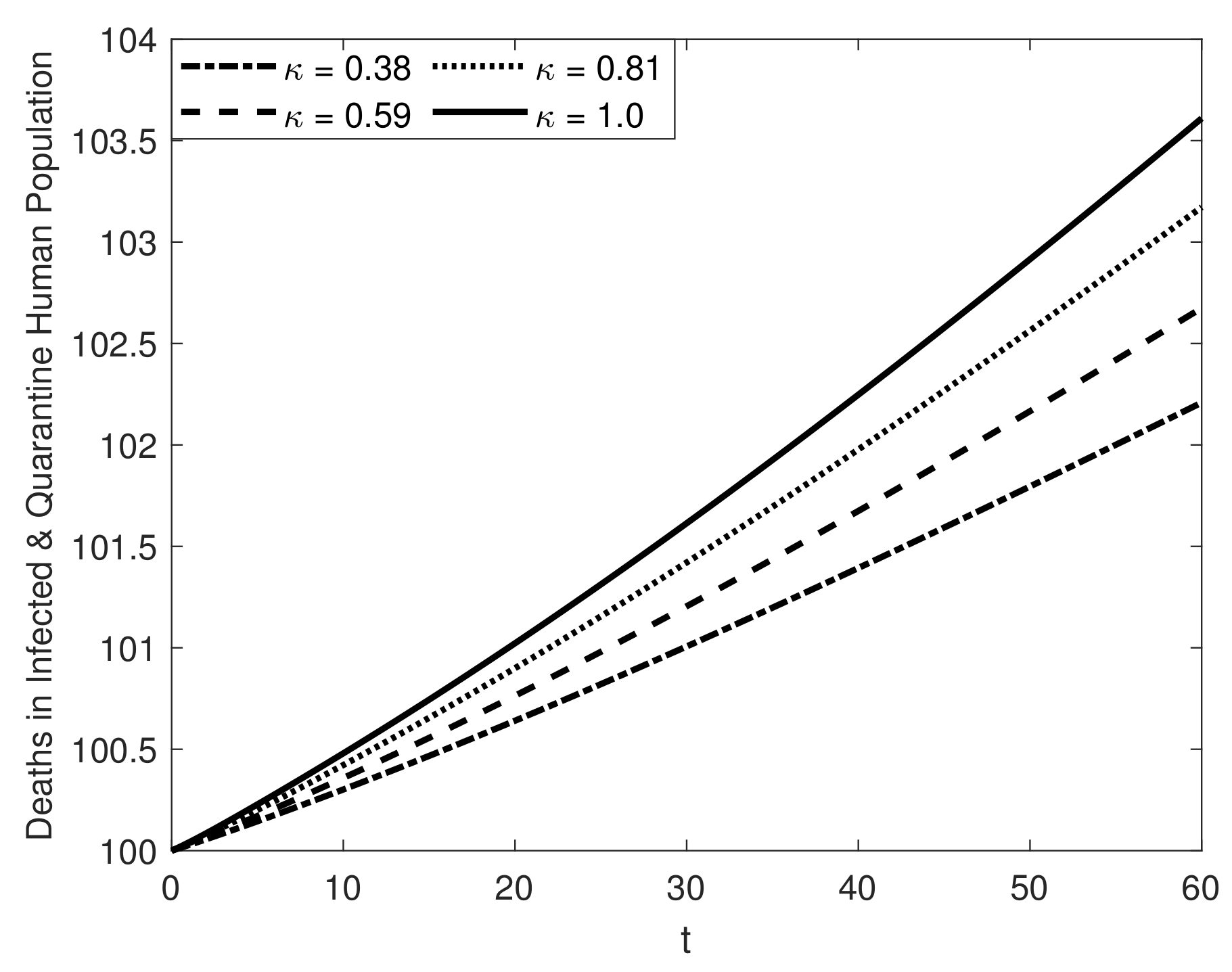
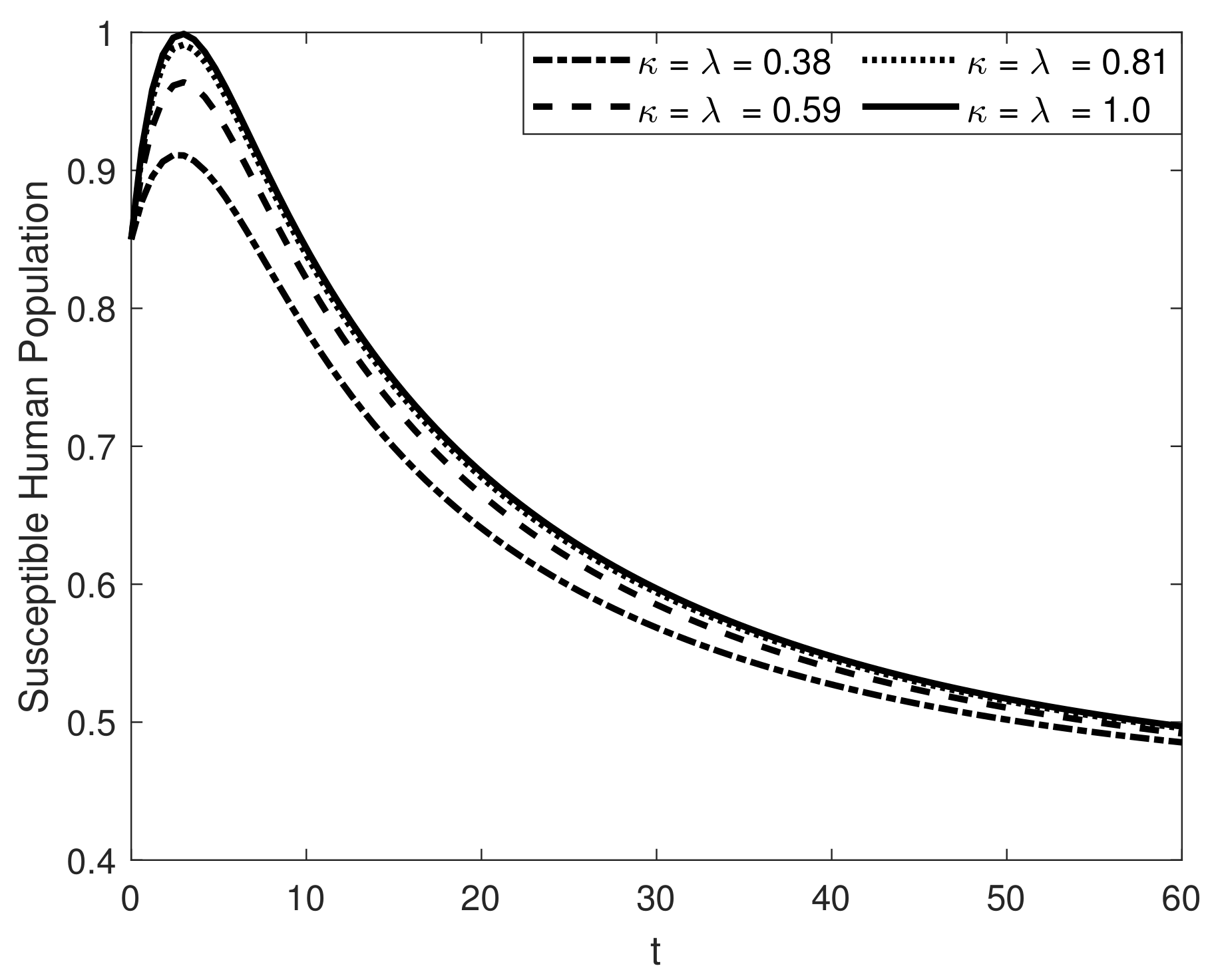
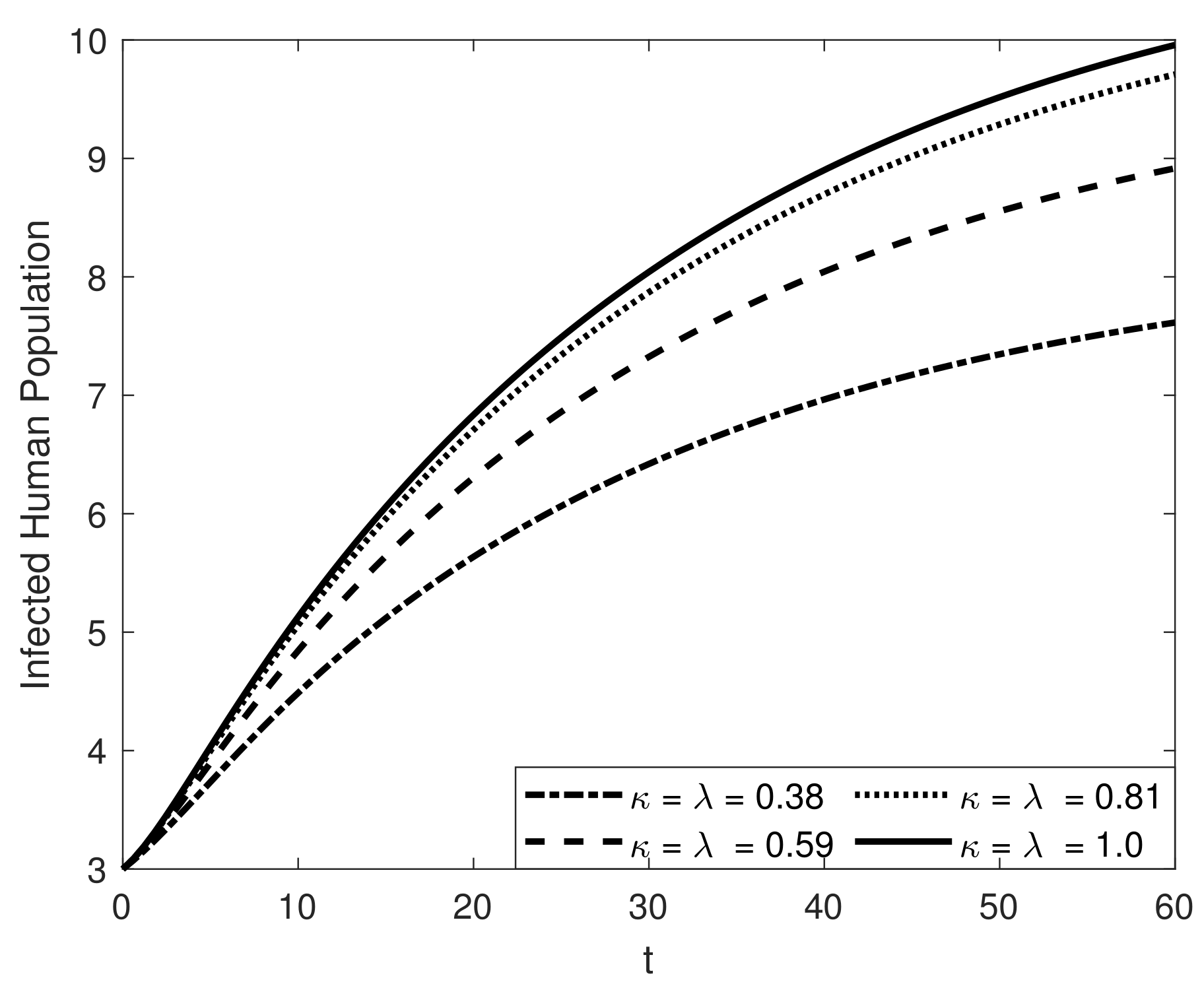
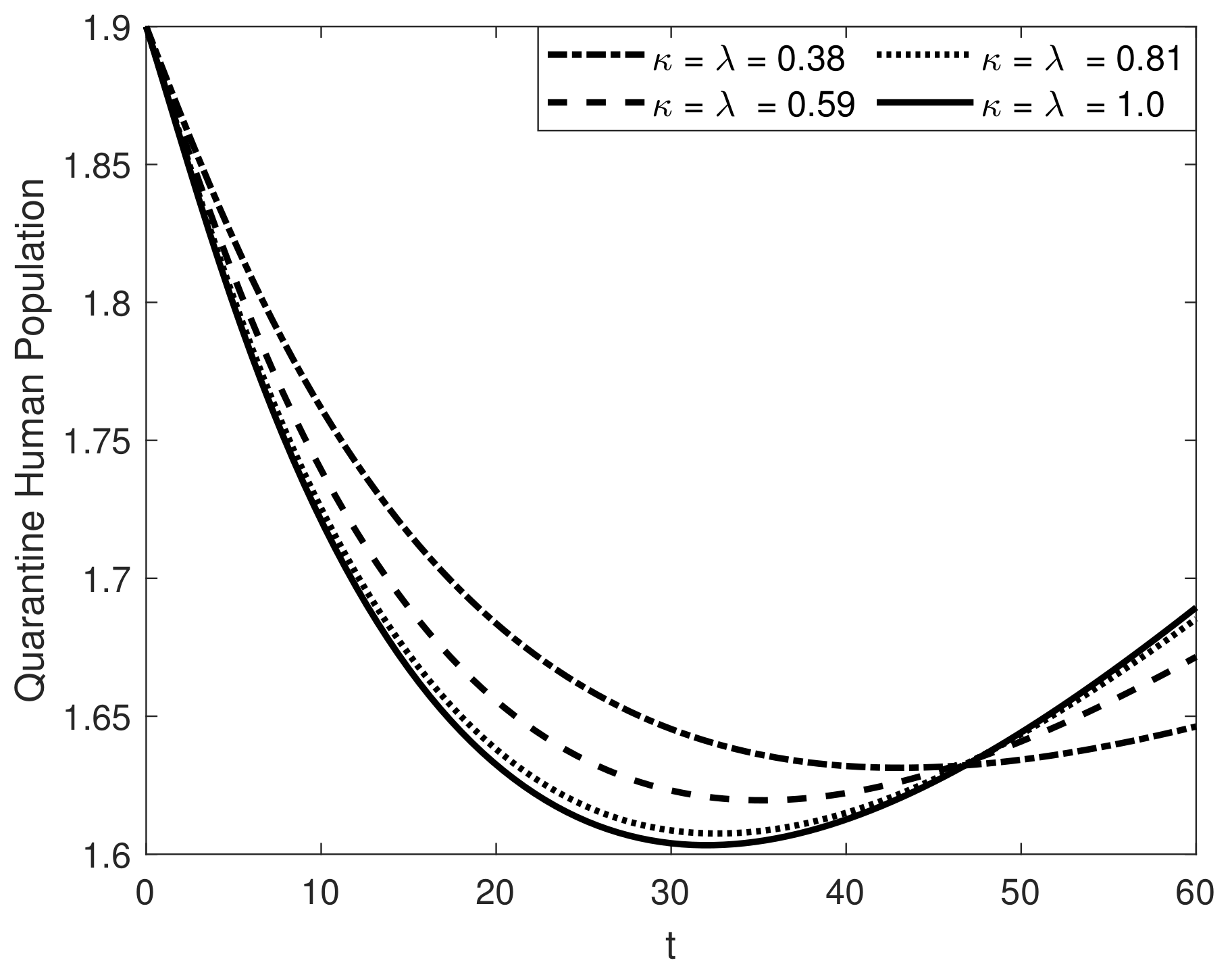
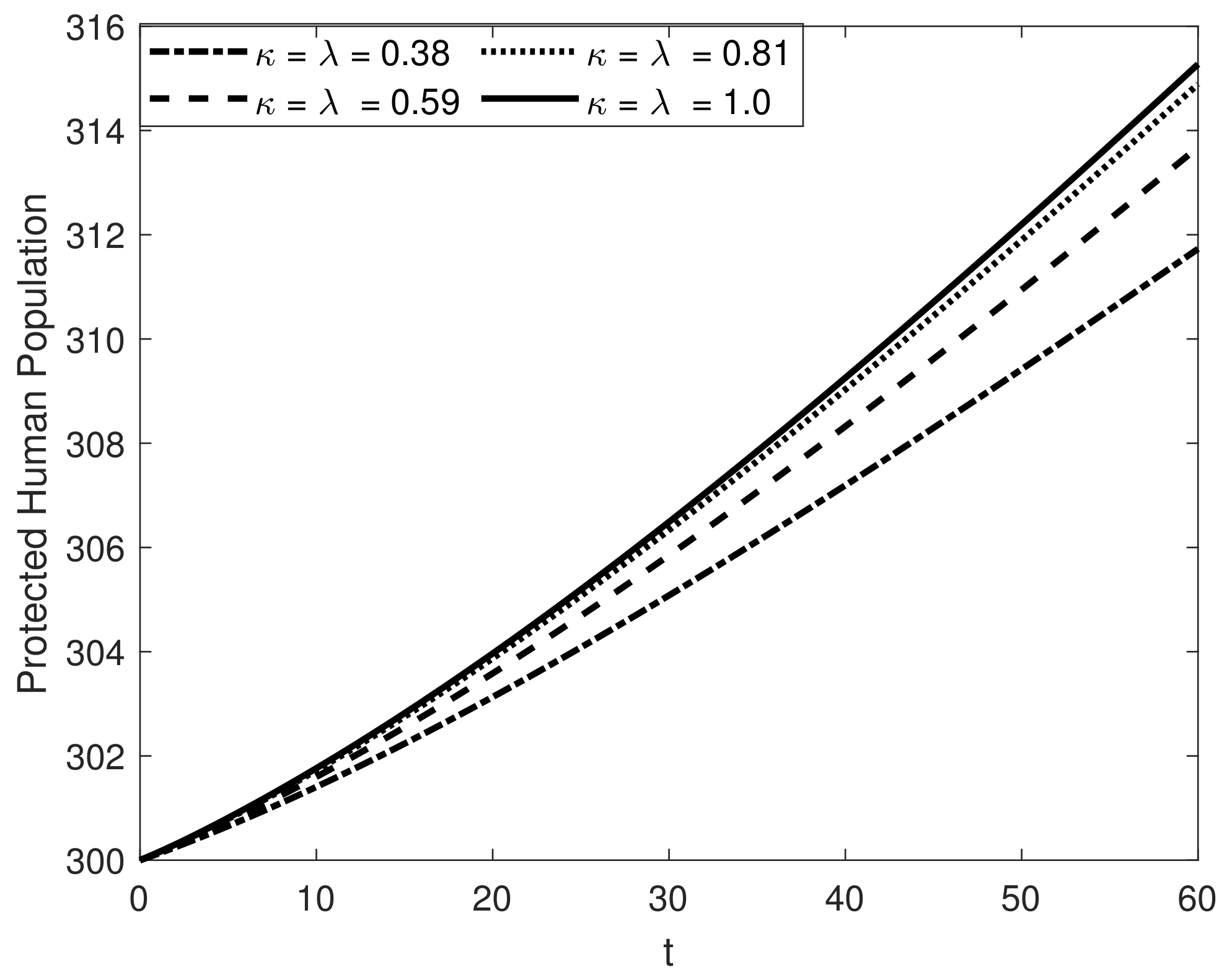
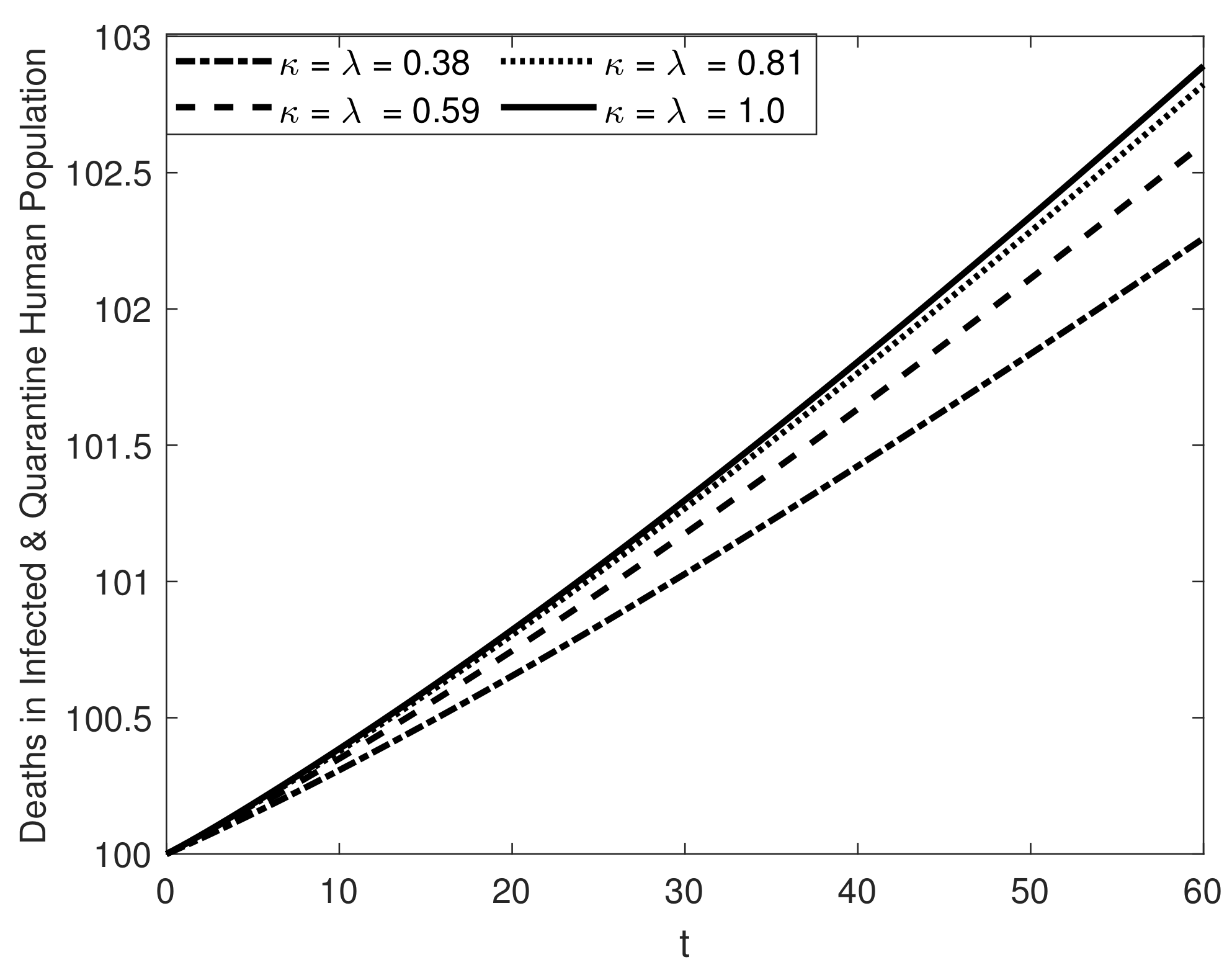
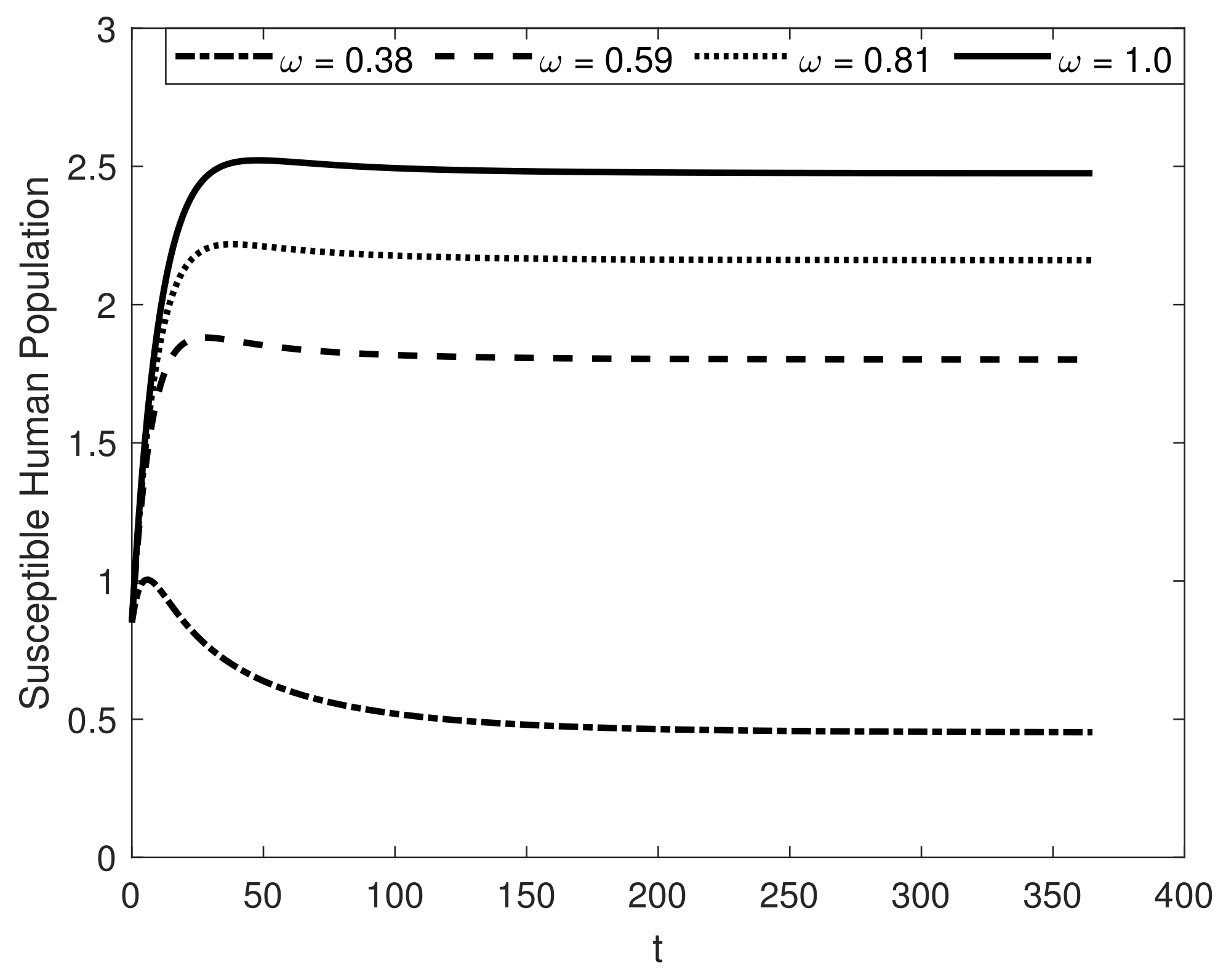
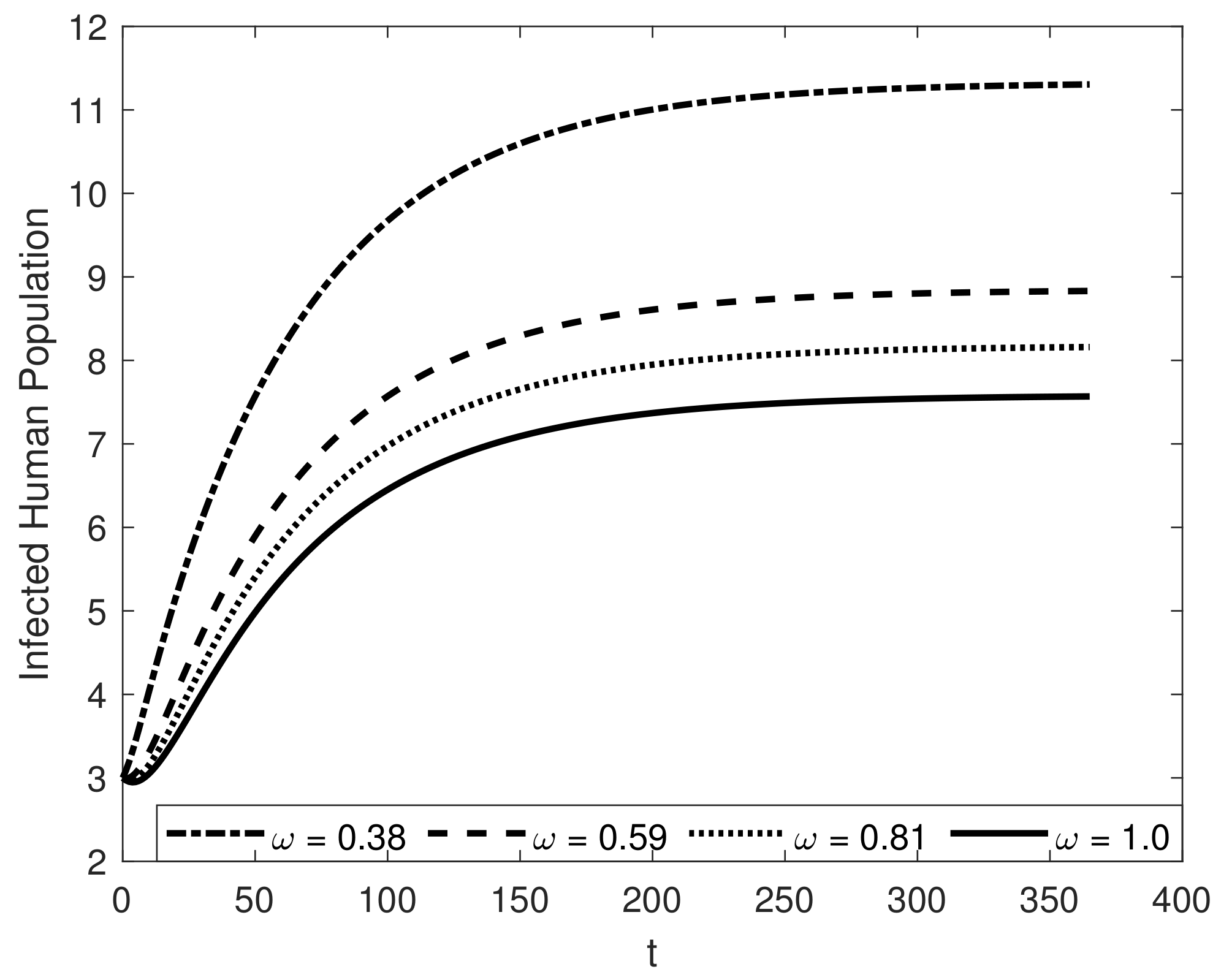
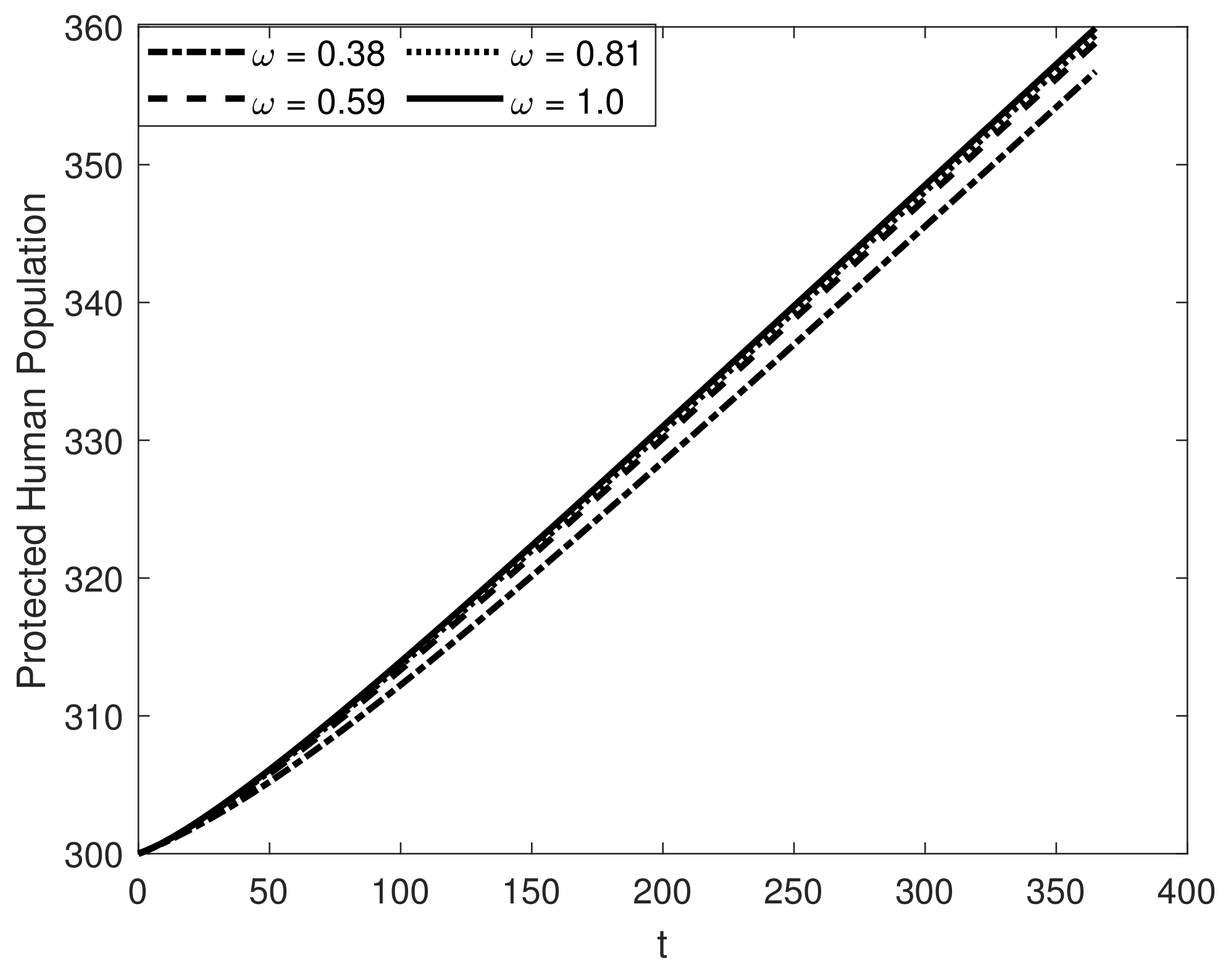
8. Results and Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, P.K.; Cunningham, A.A.; Patel, N.G.; Morales, F.J.; Epstein, P.R.; Daszak, P. Emerging infectious diseases of plants: Pathogen pollution, climate change and agrotechnology drivers. Trends Ecol. Evol. 2004, 19, 535–544. [Google Scholar] [CrossRef] [PubMed]
- Omame, A.; Isah, M.E.; Abbas, M. An optimal control model for COVID-19, zika, dengue, and chikungunya co-dynamics with reinfection. Optim. Control Appl. Methods 2023, 44, 170–204. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Biswas, S.K.; Biswas, M.H.A.; Ghosh, U. An SEQAIHR model to study COVID-19 transmission and optimal control strategies in Hong Kong, 2022. Nonlinear Dyn. 2023, 111, 6873–6893. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Khan, H.; Ahmad, F.; Tunç, O.; Idrees, M. On fractal-fractional COVID-19 mathematical model. Chaos Solitons Fractals 2022, 157, 111937. [Google Scholar] [CrossRef]
- Hamou, A.A.; Azroul, E.; Hammouch, Z.; Alaoui, A.L. A fractional multi-order model to predict the COVID-19 outbreak in Morocco. Appl. Comput. Math. 2020, 20, 177–203. [Google Scholar]
- Lu, Z.; Yu, Y.; Chen, Y.; Ren, G.; Xu, C.; Wang, S.; Yin, Z. A fractional-order SEIHDR model for COVID-19 with inter-city networked coupling effects. Nonlinear Dyn. 2020, 101, 1717–1730. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal–fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys. Stat. Mech. Its Appl. 2019, 526, 121127. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos Solitons Fractals 2020, 131, 109528. [Google Scholar] [CrossRef]
- Zhang, L.; ur Rahman, M.; Haidong, Q.; Arfan, M.; Adnan. Fractal-fractional Anthroponotic Cutaneous Leishmania model study in sense of Caputo derivative. Alex. Eng. J. 2021, 61, 4423–4433. [Google Scholar] [CrossRef]
- Shen, Z.H.; Chu, Y.M.; Khan, M.A.; Muhammad, S.; Al-Hartomy, O.A.; Higazy, M. Mathematical modeling and optimal control of the COVID-19 dynamics. Results Phys. 2021, 31, 105028. [Google Scholar] [CrossRef]
- Liu, S.; Pang, L.; Ruan, S.; Zhang, X. Global dynamics of avian influenza epidemic models with psychological effect. Comput. Math. Methods Med. 2015, 2015, 913726. [Google Scholar] [CrossRef]
- Gu, Y.; Khan, M.A.; Hamed, Y.; Felemban, B.F. A Comprehensive Mathematical Model for SARS-CoV-2 in Caputo Derivative. Fractal Fract. 2021, 5, 271. [Google Scholar] [CrossRef]
- Lu, H.; Ding, Y.; Gong, S.; Wang, S. Mathematical modeling and dynamic analysis of SIQR model with delay for pandemic COVID-19. Math. Biosci. Eng. 2021, 18, 3197–3214. [Google Scholar] [CrossRef]
- Bozdağ, F. The psychological effects of staying home due to the COVID-19 pandemic. J. Gen. Psychol. 2021, 148, 226–248. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361. [Google Scholar] [CrossRef]
- Buonomo, B.; Lacitignola, D. On the backward bifurcation of a vaccination model with nonlinear incidence. Nonlinear Anal. Model. Control 2011, 16, 30–46. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 1. [Google Scholar]
- Sinan, M.; Shah, K.; Kumam, P.; Mahariq, I.; Ansari, K.J.; Ahmad, Z.; Shah, Z. Fractional order mathematical modeling of typhoid fever disease. Results Phys. 2022, 32, 105044. [Google Scholar] [CrossRef]
- Mahmudov, E.N.; Mardanov, M.J. On duality in optimal control problems with second-order differential inclusions and initial-point constraints. Proc. Inst. Math. Mech. Nat. Acad. Sci. Azerb. 2020, 46, 115–128. [Google Scholar]
- Alekseev, V.M.; Tikhomirov, V.M.; Fomin, S.V. Optimal Control; Springer: New York, NY, USA, 2013. [Google Scholar]
- Shalsh, O.K.; Al-Nassir, S. Dynamics and optimal Harvesting strategy for biological models with Beverton-Holt growth. Iraqi. J. Sci. 2020, 223–232. [Google Scholar] [CrossRef]



| Symbol | Description of Compartment/Class | Initial Conditions |
|---|---|---|
| Susceptible Human Population | 0.85 | |
| Exposed Human Population | 3 | |
| Infected Human Population | 1.9 | |
| Recovered Human Population | 300 | |
| Susceptible Vector Population | 100 |
| Symbol | Description of Parameter | Value |
|---|---|---|
| Recruitment Rate [13]. | ||
| Natural Death Rate [13]. | ||
| Transmission rate. | 0.2784 | |
| Psychological Effect on Humans [14]. | [0,1] | |
| Recovery Rate of Infected Population [15]. | 0.1 | |
| Recovery Rate of Quarantine Population. | 0.020 | |
| Incubation Period. | 0.010 | |
| The mortality rate of the afflicted populace as a result of a pathological condition. | 0.015 | |
| Mortality rate among individuals subjected to quarantine as a result of disease. | 0.015 |
| Parameter | Sensitivity Index | Value | Parameter | Sensitivity Index | Value |
|---|---|---|---|---|---|
| −0.0799 | −1.0003 | ||||
| 1 | −0.7997 | ||||
| −0.1199 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinan, M.; Alharthi, N.H. Mathematical Analysis of Fractal-Fractional Mathematical Model of COVID-19. Fractal Fract. 2023, 7, 358. https://doi.org/10.3390/fractalfract7050358
Sinan M, Alharthi NH. Mathematical Analysis of Fractal-Fractional Mathematical Model of COVID-19. Fractal and Fractional. 2023; 7(5):358. https://doi.org/10.3390/fractalfract7050358
Chicago/Turabian StyleSinan, Muhammad, and Nadiyah Hussain Alharthi. 2023. "Mathematical Analysis of Fractal-Fractional Mathematical Model of COVID-19" Fractal and Fractional 7, no. 5: 358. https://doi.org/10.3390/fractalfract7050358
APA StyleSinan, M., & Alharthi, N. H. (2023). Mathematical Analysis of Fractal-Fractional Mathematical Model of COVID-19. Fractal and Fractional, 7(5), 358. https://doi.org/10.3390/fractalfract7050358







