Abstract
Fractals with different levels of self-similarity and magnification are defined as reduced fractals. It is shown that spectra of these reduced fractals can be constructed and used to describe levels of complexity of natural phenomena. Specific applications to biological systems, such as green algae, are performed, and it is suggested that the obtained spectra can be used to classify the considered algae by identifying spectra associated with them. The ranges of these spectra for green algae are determined and their extension to other biological as well as other natural systems is proposed.
1. Introduction
Mandelbrot [1] originally defined fractals as objects that are self-similar on all scales and whose dimensions are different than their topological dimensions. From a mathematical perspective, fractals are defined by listing their four basic characteristics [1,2,3], which are: self-similarity at all scales, fine structure at all magnifications, too irregular to be described by Euclidean geometry, and have non-topological (Hausdorff) dimension; mathematical objects that have these characteristics are called classical fractals [4]. To make fractals applicable to Nature, Mandelbrot [1] changed the definition to a more casual: “A fractal is a shape made of parts similar to the whole in some way”. Thus, the main difference between classical fractals and fractals that obey Mandelbrot’s casual definition is that their self-similarity is exact for the former and non-exact for the latter [3,4].
Fractals have been used in numerous research topics ranging from biology and biomedicine to physics, astronomy, geology, computer science, and in epidemiology, emerging diseases as well as in comparative studies [1,2,3,4,5,6]. In the previous applications of fractals to biology [7,8,9,10,11], the main emphasis was given to population biology [12], plant structures [13], gene expression [14], heart rates [15], cardiovascular system [16], kidney structure [17], cellular differentiation [18], neuron branching [19], and image rendering, image processing, mammography, images of human brains [20,21], as well as to the classification of strokes in brains [22]. Since fractals in Nature are directly related to some growth process, therefore, methods such as the Multiple Reduction Copy Machine (MRCM) and the L-systems have also been used to generate plants, trees and bushes [4].
Attempts have been made to introduce and use practical fractals [2], which basically refer to fractals with a limited range of self-similarity. On the other hand, multi-fractals are used to describe phenomena whose different components may have different scaling exponents, which may require a spectrum of exponents [2,3,4]. Moreover, it was also shown that a different family of fractals can also be defined by removing one fractal property from the list of fractal basic characteristics; for example, in intelligent processing systems, a fractal of limited scale range and partial symmetry is called semi-fractal [23]. Similar ideas were used in studies of images, structures and even sounds [24,25], but to the best of our knowledge, they have never been applied to biology and its systems.
Despite a broad range of applications of fractals to biology and bio medicine, we propose here to refine the idea of fractals by introducing the concept of reduced fractals with specific limited scale range and only partial self-similarity (see Section 2). Moreover, we demonstrate how to construct spectra of these reduced fractals and apply them to determine different levels of complexity of natural phenomena. Our specific application involves green algae [26,27], whose scales and self-similarities show significant variations. The main purpose of this paper is not to perform detailed studies of all known algae, but instead use selected green algae to justify the need for spectra of reduced fractals and demonstrate their advantage over the previous use of fractals in biology. We also suggest that the obtained spectra can be used to classify the considered algae by identifying spectra associated with them.
Our paper is organized as follows: in Section 2, reduced fractals are defined and applied to selected biological systems; fractal dimensions for the considered biological systems and the resulting spectra of reduced fractals for these systems are presented in Section 3; our conclusions are given in Section 4.
2. Reduced Fractals in Biology
As first pointed out by Mandelbrot [1], most natural structures do not show self-similarity at infinitely many stages, as classical fractals do, but instead their self-similarity occurs only at a finite number of stages. Moreover, there can be imperfections in self-similarity resulting from the fact that a smaller cluster is unlikely to be exactly the same as a larger cluster, in other words, self-similarity is only approximate [3,4,5,6]. If there are variations in miniature copies, then self-similarity is statistical [2,3]; however, if miniature copies are distorted (skewed), then self-similarity becomes self-affinity [2]. This shows that in natural structures the range of magnification is also finite [4].
The presence of these limitations leads us to believe that it is necessary to provide an integrated framework towards a definition of fractals applicable to natural structures, and such a framework is established in this paper by introducing the concepts of reduced fractals and their corresponding spectra, which for practical reasons must be discrete. The reduced fractals considered in this paper all have four basic characteristics described in Section 1, but two of them, namely, self-similarity and range of magnification, are finite; this makes our definition consistent with practical fractals introduced earlier [2], but different than the concept of semi-fractal [23]. Our definition also allows for wild fractal or fractals whose self-similarity is limited to 1 or 2 stages; nevertheless, some scaling properties of these fractals can still be identified [4]. In the following, we identify reduced fractals in selected biological systems.
3. Applications to Biology
3.1. Selected Biological Systems and Their Self-Similarity
Algae are very simple plants that can range from the microscopic, to large seaweeds. It’s very diverse and found everywhere, from being the ingredient used to thicken ice cream to producing 70% of the air we breathe. This diversity is reflected in the enormous variation exhibited by their morphological and physiological traits.There are several methods for algae identification such as genetic methods. However, such approach require time-consuming operations and becomes impractical for large-scale identification in fields such as food authentication. It becomes critically important to identify algae without compromising food safety and to meet the economic demands. With 37,000 algae species, using fractals makes it possible.
As examples of biological systems considered in his paper, we select green algae (Division: Charophyta and Chlorophyta), and consider two classes of Charophyta, namely, Charophyceae and Zygnematophyceae, and three classes of Chlorophyta, namely, Chlorophyceae, Ulvophyceae and Trebouxiophyceae [26,27]. In Figure 1, we present nine selected algae of the class Zygnematophyceae, and Figure 2 shows eight selected algae of Chlorophyceae; algae of other classes are used in the spectra of reduced fractals described in Section 3.3. As shown by the images presented in Figure 1 and Figure 2, we consider only green algae that mainly inhabit in freshwater, but five different classes, with each class containing algae of different sizes, shapes and nature. The considered sample of algae is diversified and rich in its structure, and thus it is sufficient to illustrate all the main concepts and objectives of this paper.

Figure 1.
DIC microscopy images of unicellular algae of the class Zygnematophyceae. (a) Euastrum bidentatum , (b) Euastrum oblongum , (c) Euastrum verrucosum , (d) Euastrum ansatum , (e) Euastrum humerosum , (f) Euastrum crassum , (g) Micrasterias americana , (h) Micrasterias truncata and (i) Micrasterias rotata .
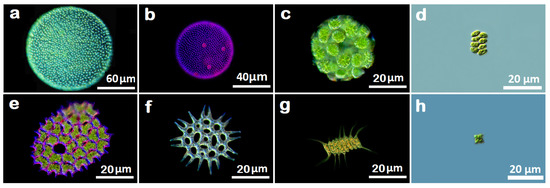
Figure 2.
DIC microscopy images of algae of class Chlorophyceae. (a) Volvox globator , (b) Volvox aureus , (c) Eudorina elegans , (d) Scenedesmus granlulatas , (e) Pediastrum clothratum , (f) Pediastrum angulosum , (g) Desmodesmus magnus and (h) Tetraedron minimum .
All considered algae of the class Zygnematophyceae are unicellular and they belong to the family Desmidiaceae; each one of them splits into two parts that have perfect symmetry; however, if we scale down, then they show no self-similarity. Nevertheless, these algae are examples of reduced fractals defined in Section 2. On the other hand, two selected algae of the class Chlorophyceae that are multicellular show more prominent self-similarity than the unicellular algae, but still their self-similarity is limited, and their range of magnification is finite, which means that these algae can also be represented by reduced fractals.
The limits on self-similarity and on the range of magnification in the class Chlorophyceae of colonial algae are presented in Table 1, which contains algae of different families, namely, Eudorina elegans belongs to the family Volvocaceae, the next two algae belong to the family Scenedesmaceae, and the remaining three algae are from the family Hydrodictyaceae. For the algae in Table 1, it is seen that the replication of colony (shown by magnification) is an indicator of limited self-similarity. Since both self-similarity and the range of magnification are finite, these algae can also be described by reduced fractals.

Table 1.
Fractal dimension of unicellular algae of the class Zygnematophyceae and its family Desmidiaceae.
The above description shows that the algae selected for this paper have self-similarities ranging from very limited, as is in the case of the unicellular algae of the class Zygnematophyceae, to more moderate, as observed in the multicellular algae of the same class and in the colonial algae of the class Chlorophyceae; similar limitations and variations are observed in the range of magnification. The observed self-similarity is limited, and it is not perfect, as there are variations in miniature copies, so self-similarity observed in the selected algae is limited and statistical. For these reasons, the algae considered in this paper are well represented by reduced fractals.
3.2. Fractal Dimension and Box-Counting Method
The sample of selected algae allowed us to identify reduced fractals as the best way to represent them and describe their physical properties; one such property is the irregularity, or complexity, of their surface and structure. According to Mandelbrot [1], the complexity can be measured by the so-called fractal dimension, FD, which is a bounded set in Euclidean n-space and is defined as
where represents a number of distinct copies of in the scale r [28]. Moreover, the union of copies must cover the set completely.
The can be calculated for deterministic fractals and if an object has deterministic self-similarity, its is the same as its box-counting dimension [28]. However, biological systems are not ideal deterministic fractals. Therefore, computed by the box-counting method is only an estimate of . Nevertheless, the box-counting method is one of the most commonly used techniques to calculate for images [28]. The method is also adapted in this paper to perform calculations of the fractal dimension for images of the selected green algae (see Section 3.1).
The images of the considered green algae are planes with the pixel position denoted by the coordinates , and with the third coordinate denoting pixel gray level. In the box-counting method, the plane is partitioned into separate blocks of size with being an integer and . As shown by Equation (1), the box-counting method requires , which is found in the following way [28]. Boxes of size , where is the height of each box associated with the gray level, are stuck on top of each other above each block. Then, the number of boxes, , covering each block is given by
where k and l represent the minimum and maximum gray levels in the th block that go in the kth and lth boxes, respectively [28]. Then, is calculated for different values of r by taking into account the contributions from all the blocks
which allows estimating the from the least squares linear fit of plotted versus . In the specific practical implementation of the box-counting method in this paper, we followed [29].
Now, in this approach, the slope of the line equals and it is defined as the amount of change along the -axis, divided by the amount of change along the -axis. The resulting slopes and fractal dimensions range between 1 and 2 for this kind of analysis, which corresponds to the range between a line that is straight with its dimension = 1 and a line that is so wiggly that it completely fills up a 2-dimensional plane. This means that when the slope becomes steeper, then the of such an image is larger because of its higher complexity. On the other hand, when the slope is flatter (closer to a straight-line), then the fractal dimension is smaller, as it reflects the image of lower complexity, which implies that the amount of detail grows slowly with increasing magnification.
Since in this paper, we consider some algae that show very limited self-similarity, all results presented below are obtained by performing calculations of by using the box-counting method. The computed fractal dimension by this method is a metric that characterizes algae complexity or space-filling characteristic. As already pointed out [4,30], most previous studies failed to evaluate the assumption of statistical self-similarity that underlies the validity of the method. Another source of error is arbitrary grid placement, which is strictly positive and varies as a function of scale, which may make the procedure’s slope estimation step non-unique [4]. In our calculations performed in this paper, both errors are eliminated by the box-counting method described above.
3.3. Fractal Dimension for Selected Algae
The results presented in Table 2 show that the unicellular algae of the the class Zygnematophyceae and the family Desmidiaceae have high fractal dimensions ranging approximately from to ; this narrow range of the implies that the level of complexity (or irregularity) of surfaces and structures is very similar for all these selected objects. The results are also consistent with the fact that the unicellular algae have very limited ranges of self-similarity and magnification that are observed in these objects as is already pointed out in Section 3.1. It must also be noted that the unicellular algae in Table 2 are separated into two groups called here Euastrum and Micrasterias, and that within each group, algae are ordered based on their increasing fractal dimension. Since all algae shown in Table 2 belong to the same family Desmidiaceae, similar ordering can be made for other families of green algae.

Table 2.
Fractal dimension of unicellular algae of the class Zygnematophyceae and its family Desmidiaceae.
The fractal dimension in Table 3 is computed for multicellular and colonial algae of three families (Volvocaceae, Scenedesmaceae and Hydrodictyaceae) of the class Chlorophyceae, and the results are presented for the selected members of each class, which are ordered based on their increasing fractal dimension. The presented results show that the of the two multicellular algae (Volvox globator and Volvox aureus) are the lowest, which means that the complexity of these two algae is the highest among the selected objects. Interestingly, the of Eudorina elegans is more similar to one member of the family Scenedesmaceae and one member of the family Hydrodictyaceae, which is caused by the fact that these algae are colonial despite being members of different families.

Table 3.
Fractal dimension of colonial and multicellular algae of the class Chlorophyceae and its three different families.
Similarly, fractal dimension of Tetraedron minimum, which belongs to the family Hydrodictyaceae, is closer to that of the members of the family Scenedesmaceae. The reason is likely caused by the fact that these algae are colonial, but also by similarities in their cell shapes. However, the two remaining members of the family Hydrodictyaceae have significantly higher fractal dimensions that may be caused by both different cell and colony shapes between Tetraedron minimum and these two members.
The results presented in Table 2 and Table 3 demonstrate that algae can be ordered within each family by using their . This may be useful in classification of algae and their studies, since typically algae within a given family are neither ordered nor organized [28]. The proposed order of decreasing complexity (see Table 2 and Table 3) can be replaced by increasing complexity, which would require us to reverse the orders in Table 2 and Table 3.
The validity of the computed fractal dimensions must be verified by comparing our results to those obtained before, specifically, for different algae. To the best of our knowledge, no FDs were calculated for the set of algae selected for this paper. However, for Cladophora rupestris of the class Chlorophyceae, was obtained [31], which is consistent with the values of Table 3 for the colonial forms. Independent calculations of FD for Cladophora rupestris done in [32] gave , which slightly differs from the results obtained in [31] and in Table 3; the main reasons for the difference are improvements in modern computations as compared to those preformed almost 25 years ago [32].
The calculations of FDs were also done for Laminaria digitata and Fucus serratus of the class Phaeophyceae, for which and were obtained, respectively [31]. These values are close to the FDs of Table 3 found by us for the multicellular forms. Moreover, the computations of FDs for 16 selected brown algae were also done [33], and the obtained results range between and , which is consistent with the results of Table 3. Thus, there is an agreement between the previously obtained results [31,32,33] and the results presented in this paper. However, it must be pointed out that direct comparisons cannot be done because there are no computations of FDs for green algae selected by us for our investigation.
3.4. Spectra of Reduced Fractals for Selected Green Algae
The fractal dimensions calculated for different green algae can now be used to obtain spectra of reduced fractals (SRFs). The spectra are generated by plotting the fractal dimensions versus selected characteristics of algae. Among different characteristics, we consider forms and shapes of algae described in Section 3.1. Moreover, we also demonstrate how to generate SRFs for algae of different classes and families. In the panels A, B, C and D of Figure 3, we show the SRFs for algae of different forms, classes, shapes and families. Let us now describe each panel of Figure 3 and discuss the biological implications of the presented SRFs.
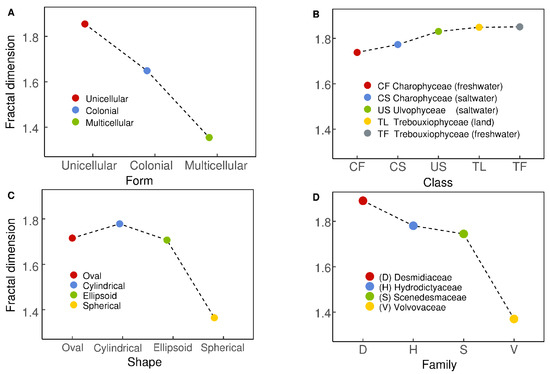
Figure 3.
Spectra of reduced fractals for algae of different form (panel (A)), class (panel (B)), shape (panel (C)), and family (panel (D)).
Panel A of Figure 3 shows the form of the SRF for one unicellular alga of the class Zygnematophyceae and the family Desmidiaceae, and one colonial and one multicellular algae of the class Chlorophyceae, whose families are Scenedesmaceae and Volvocaceae, respectively. As expected, the presented SRF demonstrates a rapid decrease of fractal dimension with increasing algae’s complexity. The observed almost linear spectrum allows us to establish the following criteria for classifying green algae: for unicellular, for colonial, and for multicellular.
The SRF presented in panel B of Figure 3 shows high fractal dimensions for all considered algae, which are two algae of the class Charophyceae, one alga of the class Ulvophyceae, and two algae of the class Trebouxiophyceae. The resulting spectrum shows that differences between freshwater and saltwater (or land) within the same class are practically negligible, which is shown by flat parts of the SRF. Moreover, the entire spectrum remains practically flat, which implies that differences in the fractal dimension (or complexity) between the considered three classes are small.
The fact that algae have different shapes is well-known [26,27]. Using several most commonly known shapes of green algae (see also Figure 1 and Figure 2, and Table 3), we obtained the RFS shown in panel C of Figure 3. The spectrum shows its maximum for cylindrical algae, and smaller values of the fractal dimension for oval and ellipsoid algae; both oval and ellipsoid algae have comparable fractal dimensions. An interesting result is that spherical algae have the lowest fractal dimensions, which implies that their complexity is the highest among algae considered for this spectrum.
The panel D of Figure 3 shows the SRF for different families. The presented results are consistent with the SRFs given in the previous panels, specifically, in panel A, as the SRF of panel D mainly reflects differences between algae being unicellular (Desmidiaceae), colonial (Hydrodictyaceae and Scenedesmaceae) or multicellular (Volvocaceae). The spectrum demonstrates (similar to the SRF of panel A) a rapid decrease in the fractal dimension, and related increase in algae complexity, for colonial algae as compared to unicellular ones. An even sharper decrease in the fractal dimension is observed for multicellular algae as compared to colonial. As expected, there is only a small difference in the fractal dimension between the families Hydrodictyaceae and Scenedesmaceae as members of these families are mainly colonial (see Table 3).
3.5. Discussion of the Obtained Results
The main results of this paper are fractal dimensions (FDs) given in Table 1 and Table 2, and the spectra of reduced fractals (SRFs) presented in Figure 3. The results were obtained for the selected green algae shown in Figure 1 and Figure 2, and our computations were performed using the box-counting method that is described in Section 3.2. A similar method was used in some previous studies to compute fractal dimensions for known images of different biological systems to determine their complexity, structure, function and organization [34,35,36], as well as for medical images [37]. This common use of the fractal dimension in the work cited above as well as in this work has been motivated by the fact that the FD captures and describes the complexity of an object by providing one unique number that corresponds to this object, and its value determines the change in complexity in detail with the change in scale.
We have also calculated the SRFs and demonstrated that they can be used as a new tool to investigate properties of green algae and also to classify them, based on the form of their SRF, within their families as currently algae of a given family are neither ordered nor organized [26,27]. Moreover, the SRFs can also be generated for other types of algae, namely, Macroalgae (red and brown) or Microalgae [26,27], as well as for many other diversified biological systems, such as the roots of plants [30] and their complexity [34], scaling time in biochemical networks [35], organization of ecosystems [36], human physiology and well-being [37], and microbial colonies [38]. We do hope that biologists working in different areas, and other natural scientists, find the SRFs useful in their work and apply them to different natural systems.
The main advantage of using SRFs is that the shapes of these spectra change from one biological system to another, which makes it easy to identify different systems by the characteristic shapes of their spectra. As a result, it is suggested that the spectra may be used as a tool to classify different systems, and also to make comparisons between different biological systems. In other words, the spectra uniquely show differences and similarities between diverse systems, which was not the case in the previous studies that were limited to one particular object of a certain class or family, and a certain shape or form. It must also be pointed out that the SRFs are an efficient and low-cost tool compared to other more advanced techniques, like machine learning or detailed digital analysis of images.
Finally, our suggestion that the SRFs can be used to classify different biological systems requires more studies. Specifically, a test analysis and a confusion matrix analysis are needed to formally demonstrate the validity of our suggestion; however, these topics are of the scope of this paper and they will be considered elsewhere.
4. Conclusions
The concept of reduced fractals, with a specific limited scale range and only partial self-similarity, is introduced and used to generate spectra of reduced fractals. To demonstrate the applicability of these spectra to biology, the spectra are generated for selected green algae, which include Charophyta and Chlorophyta algae, and their classes Charophyceae, Zygnematophyceae, Chlorophyceae, Ulvophyceae and Trebouxiophyceae. By showing how these spectra can be used to investigate physical properties of algae and to classify them within their families, we hope that the spectra will become a new tool to study algae, including also red and brown algae, as well as microalgae. It is also suggested that the spectra can be used for other biological systems, whose images are known, and that they may provide biologists with a tool to bridge over to physics, electro-sensory artificial life and synthetic biology. The spectra may also become a useful tool in other natural sciences.
Author Contributions
Conceptualization, D.T.P. and Z.E.M.; methodology, D.T.P. and Z.E.M.; validation, D.T.P. and Z.E.M.; formal analysis, D.T.P.; investigation, D.T.P. and Z.E.M.; writing—original draft preparation, D.T.P. and Z.E.M.; writing—review and editing, D.T.P. and Z.E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data used for this research is available in the paper.
Acknowledgments
We are indebted to three anonymous referees for their valuable suggestions that allow us to improve significantly the first version of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman & Company: San Francisco, CA, USA, 1982. [Google Scholar]
- Schroeder, M. Fractals, Chaos, Power Laws; W.H. Freeman & Company: New York, NY, USA, 1991. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. Chaos and Fractals; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gouyet, J.-F. Physics and Fractal Structures; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Bunde, A.; Havlin, S. (Eds.) Fractals in Science; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Buldyrev, S.V. Fractals in Biology. In Mathematics of Complexity and Dynamical Systems; Meyers, R., Ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Yates, E. Fractal Applications in Biology: Scaling Time in Biochemical Networks; Academic Press, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Crisan, D.; Mina, C.; Voinea, V. Fractal techniques for classifying biologic system. In Curran Associates, Inc. Proceedings; Curran Associates, Inc.: Red Hook, NY, USA, 2009. [Google Scholar]
- Havlin, S.; Buldyrev, S.; Goldberger, A.; Mantegna, R.N.; Ossadnik, S.M.; Peng, C.K.; Simons, M.; Stanley, H.E. Fractals in biology and medicine. Chaos Solitons Fractals 1995, 6, 172–201. [Google Scholar] [CrossRef] [PubMed]
- Losa, G. Fractals and Their Contribution to Biology and Medicine. Medicographia 2012, 34, 365–374. [Google Scholar]
- Newman, T.; Antonovics, J.; Wilbur, H. Population Dynamics with a Refuge: Fractal Basins and the Suppression of Chaos. Theor. Popul. Biol. 2002, 62, 121–128. [Google Scholar] [CrossRef]
- Alados, C.; Pueyo, Y.; Navas, D.; Cabezudo, B.; Gonzalez, A.; Freeman, D.C. Fractal analysis of plant spatial patterns: A monitoring tool for vegetation transition shifts. Biodivers. Conserv. 2005, 14, 1453–1468. [Google Scholar] [CrossRef]
- Aldrich, P.; Horsley, R.; Ahmed, Y.; Williamson, J.J.; Turcic, S.M. Fractal topology of gene promoter networks at phase transitions. Gene Regul. Syst. Biol. 2010, 4, 5389. [Google Scholar] [CrossRef]
- Guevara, M.; Glass, L.; Shrier, A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science 1981, 214, 1350–1353. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.; Amaral, L.; Goldberger, A.; Havlin, S.; Rosenblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef]
- Sernetz, M.; Wubbeke, J.; Wlczek, P. Three-dimensional image analysis and fractal characterization of kidney arterial vessels. Physica A 1992, 191, 13–16. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.; Liebovitch, L.; West, B. Fractal Physiology; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kniffki, K.; Pawlak, M.; Vahle-Hinz, C. Fractal dimensions and dendritic branching of neurons in the somatosensory thalamus. In Fractals in Biology and Medicine; Birkhauser: Basel, Switzerland, 1994; p. 221. [Google Scholar]
- Sztojanov, I.; Crisan; Mina, C.; Voinea, V. Image Processing in Biology Based on Fractal Analysis. In Image Processing; Chen, Y.-S., Ed.; INTECH: Zagreb, Croatia, 2009. [Google Scholar]
- Ieva, A.; Ebstan, F.; Grizzi, F.; Klonowski, W.; Martín-Landrove, M. Fractals in the neurosciences, part II: Clinical applications and future perspectives. Neuroscientist 2015, 21, 30–43. [Google Scholar] [CrossRef]
- Karaca, Y.; Moonis, M.; Baleanu, D. Fractal and multifractal-based predictive optimization model fro stroke subtypes’ classifications. Chaos Solitons Fractals 2020, 136, 199820. [Google Scholar] [CrossRef]
- Liao, S.; Shi, C. International Conference on Intelligent Processing; Beijing, China, 1997; p. 1419. [Google Scholar]
- Ogilvy, J. Theory of Wave Scattering from Random Rough Surfaces; Taylor and Francis: Philadelphia, PA, USA, 1991. [Google Scholar]
- Goff, J. The relationship between local-and global-scale scattering functions for fractal surfaces under a separation of scales hypothesis. J. Acoust. Soc. Am. 1995, 97, 1586–1595. [Google Scholar] [CrossRef]
- van der Hoek, C.; Mann, D.; Jahns, H. Algae An Introduction to Phycology; Cambridge Uni. Press: Cambridge, UK, 1995. [Google Scholar]
- Raven, P.; Evert, R.; Eichhorn, S. Biology of Plants; W.H. Freeman & Company: New York, NY, USA, 2015. [Google Scholar]
- Li, J.; Du, Q.; Sun, C. An improved box-counting method for image fractal dimension estimation. Pattern Recognit. 2009, 42, 2460–2469. [Google Scholar] [CrossRef]
- Gonzato, G. A practical implementation of the box counting algorithm. Comput. Geosci. 1998, 24, 95–100. [Google Scholar] [CrossRef]
- Bouda, M.; Caplan, J.; Saiers, J.E. Box-counting dimension revisited: Presenting an efficient method of minimizing quantization error and an assessment of the self-similarity of structural root systems. Front. Plant Sci. 2016, 7, 149. [Google Scholar] [CrossRef] [PubMed]
- Hooper, G.; Davenport, J. Epifaunal composition and fractal dimensions of intertidal marine macroalgae in relation to emersion. J. Mar. Biol. Assoc. UK 2006, 86, 1297–1304. [Google Scholar] [CrossRef]
- Corbit, J.; Garbary, D.J. Fractal dimension as a quantitative measure of complexity in plant development. Proc. R. Soc. Lond. B 1995, 262, 1–6. [Google Scholar]
- Gee, J.; Warwick, R.M. Metazoan community structure in relation to the fractal dimensions of marine macroalgae. Mar. Ecol. Prog. Ser. 1994, 103, 141–150. [Google Scholar] [CrossRef]
- Fielding, A. Applications of fractal geometry to biology. Bioinformatics 1992, 8, 359–366. [Google Scholar] [CrossRef]
- Yates, F.E. [30] fractal applications in biology: Scaling time in biochemical networks. Methods Enzymol. 1992, 210, 636–675. [Google Scholar]
- Kenkel, N.; Walker, D.J. Fractals in the biological sciences. Coenoses 1996, 11, 77–100. [Google Scholar]
- Kumar, D.; Arjunan, S.; Aliahmad, B. Fractals. Applications in Biological Signalling and Image Processing; CRS Publishing, Taylor and Francis Group: Boca Raton, FL, USA, 2021. [Google Scholar]
- Nai, G.A.; Martelli, C.A.T.; Medina, D.A.L.; de Oliveira, M.S.C.; Caldeira, I.D.; Henriques, B.C.; Marques, M.E.A. Fractal dimension analysis: A new tool for analyzing colony-forming units. MethodsX 2021, 8, 101228. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).