Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller
Abstract
1. Introduction
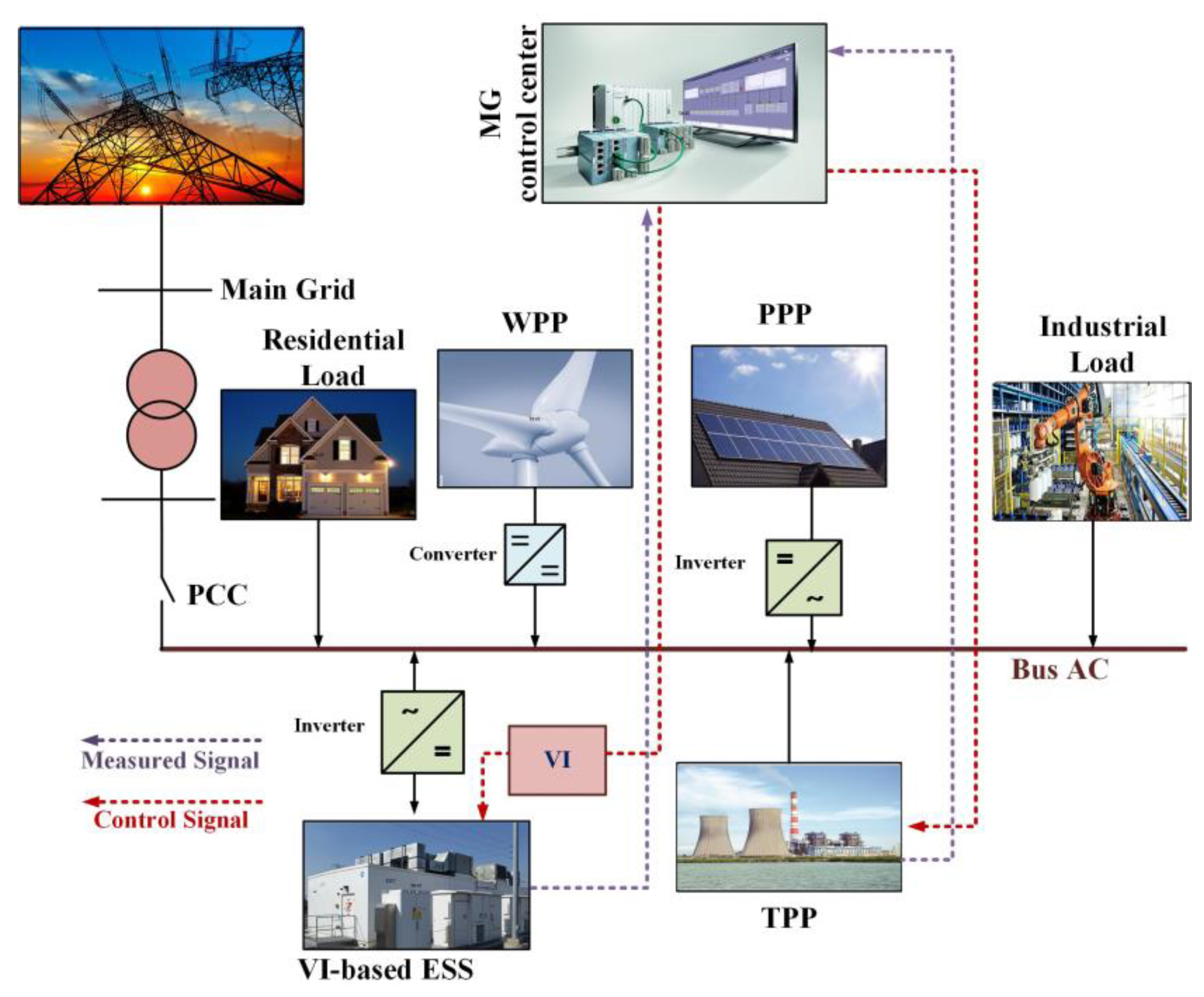
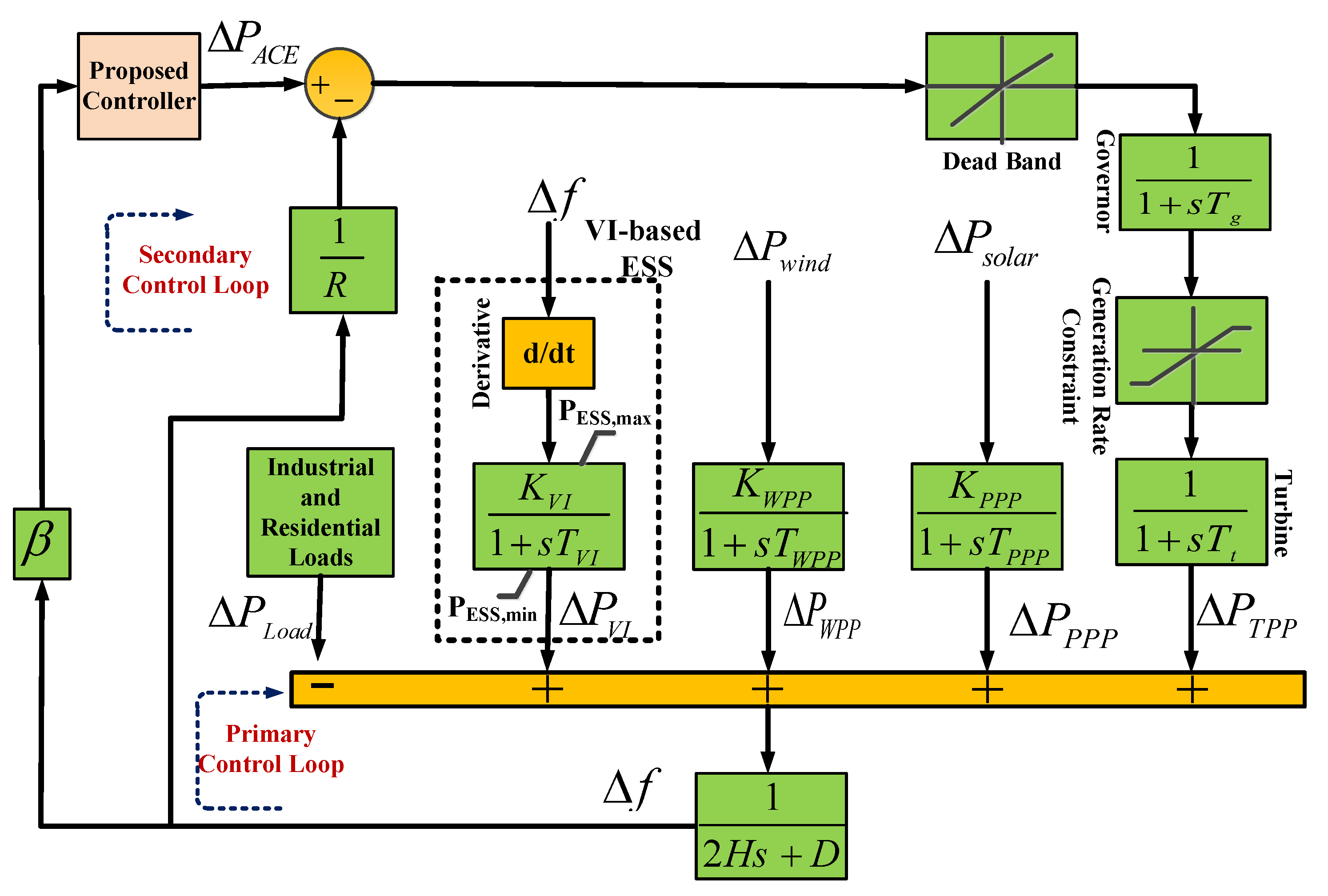
2. Microgrid Modeling
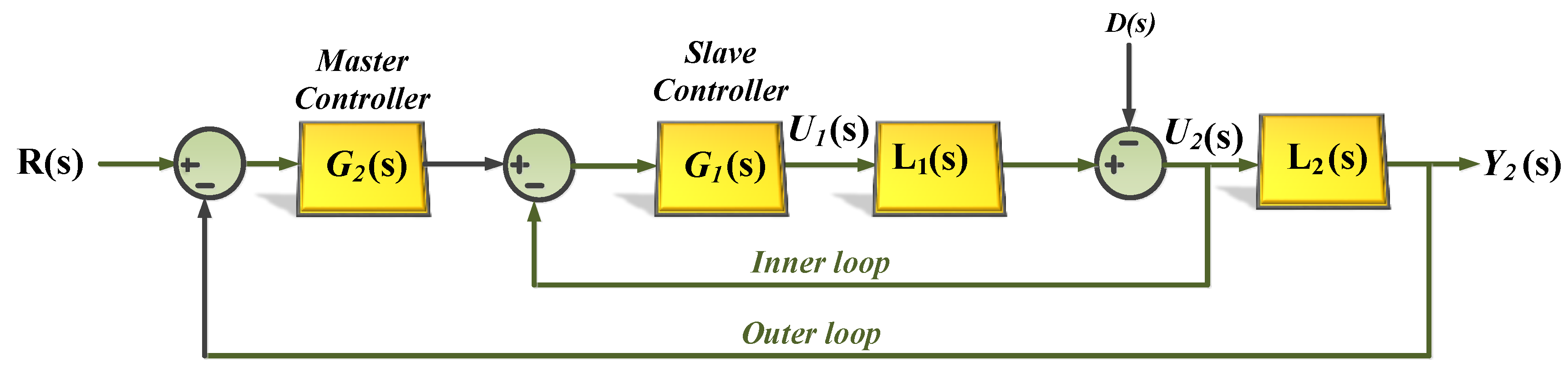
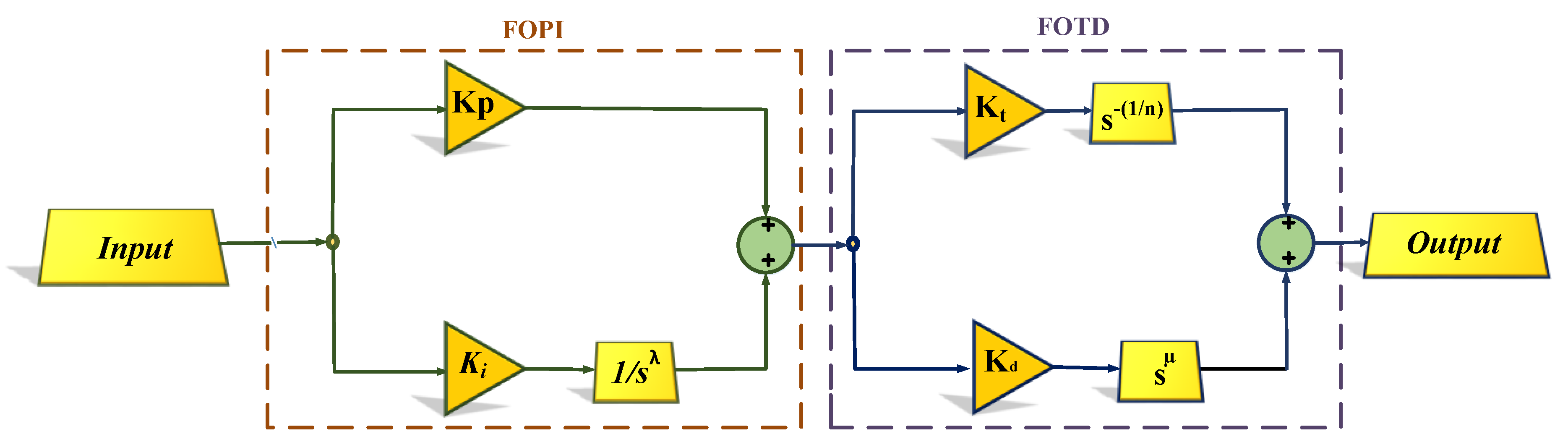
3. Design of the Proposed Fractional Order Cascade Controller
4. Optimization Algorithm to Tune the Controller’s Coefficients
| Algorithm 1. The pseudo-code of the KA algorithm |
| I: set the population II: evaluate the solute in the papulation III: set the best solute () IV: set filtration rate (FR, Equation (25)) V: set waste (W) VI: set filtered blood (FB) VII: set number of iteration (numofiter) VIII: while (iter < numofiter) do IX: for all X: generate new (Equation (24)) XI: check the using FR XII: if assigned to W XIV: apply reabsorption and generate (Equation (24)) XVI: if reabsorption is not satisfied ( cannot be a part of FB) XV: remove from W (excretion) XVII: insert a random S into W to replace XVIII: end if XIX: is reabsorbed XX: else XXI: if it is better than the in FB XXII: is secreted XXIII: else XXIV: is secreted XXV: end if XXIV: end if XXV: end for XXVI: rank the S from FB and update the XXVII: merge W and FB XXVIII: update filtration rate (Equation (25)) XXIX: end while XXX: return |
5. Simulation Results
5.1. Scenario 1
5.2. Scenario 2
5.3. Scenario 3
5.4. Scenario 4
5.5. Scenario 5
5.6. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khooban, M.H. An Optimal Non-Integer Model Predictive Virtual Inertia Control in Inverter-Based Modern AC Power Grids-Based V2G Technology. IEEE Trans. Energy Convers. 2021, 36, 1336–1346. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, J.; Luo, X.; Lai, C.S.; Yang, P.; Lai, L.L.; Li, P.; Guerrero, J.M.; Shahidehpour, M. Distributed Robust Model Predictive Control-Based Energy Management Strategy for Islanded Multi-Microgrids Considering Uncertainty. IEEE Trans. Smart Grid 2022, 13, 2107–2120. [Google Scholar] [CrossRef]
- Bera, A.; Chalamala, B.R.; Byrne, R.H.; Mitra, J. Sizing of Energy Storage for Grid Inertial Support in Presence of Renewable Energy. IEEE Trans. Power Syst. 2022, 37, 3769–3778. [Google Scholar] [CrossRef]
- Fathollahi, A.; Derakhshandeh, S.Y.; Ghiasian, A.; Khooban, M.H. Utilization of dynamic wireless power transfer technology in multi-depot, multi-product delivery supply chain. Sustain. Energy Grids Netw. 2022, 32, 100836. [Google Scholar] [CrossRef]
- Farsizadeh, H.; Gheisarnejad, M.; Mosayebi, M.; Rafiei, M.; Khooban, M.H. An Intelligent and Fast Controller for DC/DC Converter Feeding CPL in a DC Microgrid. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1104–1108. [Google Scholar] [CrossRef]
- Kang, W.; Li, Q.; Gao, M.; Li, X.; Wang, J.; Xu, R.; Chen, M. Distributed secondary control method for islanded microgrids with communication constraints. IEEE Access 2017, 6, 5812–5821. [Google Scholar] [CrossRef]
- Olabi, A.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Ranjan, M.; Shankar, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Zuo, Y.; Yuan, Z.; Sossan, F.; Zecchino, A.; Cherkaoui, R.; Paolone, M. Performance assessment of grid-forming and grid-following converter-interfaced battery energy storage systems on frequency regulation in low-inertia power grids. Sustain. Energy Grids Netw. 2021, 27, 100496. [Google Scholar] [CrossRef]
- Oshnoei, S.; Aghamohammadi, M.; Oshnoei, S. A Novel Fractional order controller based on Fuzzy Logic for Regulating the Frequency of an Islanded Microgrid. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 320–326. [Google Scholar]
- Oshnoei, A.; Kheradmandi, M.; Muyeen, S.M. Robust Control Scheme for Distributed Battery Energy Storage Systems in Load Frequency Control. IEEE Trans. Power Syst. 2020, 35, 4781–4791. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Turschner, D.; Beck, H.-P. Enhanced virtual inertia control based on derivative technique to emulate simultaneous inertia and damping properties for microgrid frequency regulation. IEEE Access 2019, 7, 14422–14433. [Google Scholar] [CrossRef]
- Shahgholian, G.; Mardani, E.; Fattollahi, A. Impact of PSS and STATCOM devices to the dynamic performance of a multi-machine power system. Eng. Technol. Appl. Sci. Res. 2017, 7, 2113–2117. [Google Scholar] [CrossRef]
- Habibi, M.; Oshnoei, A.; Vahidinasab, V.; Oshnoei, S. Allocation and sizing of energy storage system considering wind uncertainty: An approach based on stochastic SCUC. In Proceedings of the 2018 Smart Grid Conference (SGC), Sanandaj, Iran, 28–29 November 2018; pp. 1–6. [Google Scholar]
- Khezri, R.; Oshnoei, A.; Oshnoei, S.; Bevrani, H.; Muyeen, S. An intelligent coordinator design for GCSC and AGC in a two-area hybrid power system. Appl. Soft Comput. 2019, 76, 491–504. [Google Scholar] [CrossRef]
- Oshnoei, S.; Oshnoei, A.; Mosallanejad, A.; Haghjoo, F. Novel load frequency control scheme for an interconnected two-area power system including wind turbine generation and redox flow battery. Int. J. Electr. Power Energy Syst. 2021, 130, 107033. [Google Scholar] [CrossRef]
- Fathollahi, A.; Kargar, A.; Derakhshandeh, S.Y. Enhancement of power system transient stability and voltage regulation performance with decentralized synergetic TCSC controller. Int. J. Electr. Power Energy Syst. 2022, 135, 107533. [Google Scholar] [CrossRef]
- Abubakr, H.; Guerrero, J.M.; Vasquez, J.C.; Mohamed, T.H.; Mahmoud, K.; Darwish, M.M.F.; Dahab, Y.A. Adaptive LFC Incorporating Modified Virtual Rotor to Regulate Frequency and Tie-Line Power Flow in Multi-Area Microgrids. IEEE Access 2022, 10, 33248–33268. [Google Scholar] [CrossRef]
- Barbalho, P.I.N.; Lacerda, V.A.; Fernandes, R.A.S.; Coury, D.V. Deep reinforcement learning-based secondary control for microgrids in islanded mode. Electr. Power Syst. Res. 2022, 212, 108315. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Oshnoei, S.; Aghamohammadi, M.; Oshnoei, S.; Oshnoei, A.; Mohammadi-Ivatloo, B. Provision of Frequency Stability of an Islanded Microgrid Using a Novel Virtual Inertia Control and a Fractional Order Cascade Controller. Energies 2021, 14, 4152. [Google Scholar] [CrossRef]
- Kanellos, F.D. Real-time control based on multi-agent systems for the operation of large ports as prosumer microgrids. IEEE Access 2017, 5, 9439–9452. [Google Scholar] [CrossRef]
- Fathi, A.; Shafiee, Q.; Bevrani, H. Robust frequency control of microgrids using an extended virtual synchronous generator. IEEE Trans. Power Syst. 2018, 33, 6289–6297. [Google Scholar] [CrossRef]
- Fini, M.H.; Golshan, M.E.H. Determining optimal virtual inertia and frequency control parameters to preserve the frequency stability in islanded microgrids with high penetration of renewables. Electr. Power Syst. Res. 2018, 154, 13–22. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Watanabe, M.; Küfeoǧlu, S.K. Robust virtual inertia control of an islanded microgrid considering high penetration of renewable energy. IEEE Access 2017, 6, 625–636. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Robust virtual inertia control of a low inertia microgrid considering frequency measurement effects. IEEE Access 2019, 7, 57550–57560. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Fu, Y.; Shen, W. Multi-objective virtual inertia control of renewable power generator for transient stability improvement in interconnected power system. Int. J. Electr. Power Energy Syst. 2020, 117, 105641. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Li, B.; Shabib, G.; Elbaset, A.A.; Xu, D.; Mitani, Y. A new frequency control strategy in an islanded microgrid using virtual inertia control-based coefficient diagram method. IEEE Access 2019, 7, 16979–16990. [Google Scholar] [CrossRef]
- Abubakr, H.; Vasquez, J.C.; Hassan Mohamed, T.; Guerrero, J.M. The concept of direct adaptive control for improving voltage and frequency regulation loops in several power system applications. Int. J. Electr. Power Energy Syst. 2022, 140, 108068. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Muyeen, S.; Oshnoei, S.; Blaabjerg, F. Automatic generation control incorporating electric vehicles. Electr. Power Compon. Syst. 2019, 47, 720–732. [Google Scholar] [CrossRef]
- Oshnoei, S.; Oshnoei, A.; Mosallanejad, A.; Haghjoo, F. Contribution of GCSC to regulate the frequency in multi-area power systems considering time delays: A new control outline based on fractional order controllers. Int. J. Electr. Power Energy Syst. 2020, 123, 106197. [Google Scholar] [CrossRef]
- Peddakapu, K.; Srinivasarao, P.; Mohamed, M.R.; Arya, Y.; Krishna Kishore, D.J. Stabilization of frequency in Multi-Microgrid system using barnacle mating Optimizer-based cascade controllers. Sustain. Energy Technol. Assess. 2022, 54, 102823. [Google Scholar] [CrossRef]
- Singh, K.; Arya, Y. Tidal turbine support in microgrid frequency regulation through novel cascade Fuzzy-FOPID droop in de-loaded region. ISA Trans. 2022, 133, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Dash, P.; Saikia, L.C.; Sinha, N. Automatic generation control of multi area thermal system using Bat algorithm optimized PD–PID cascade controller. Int. J. Electr. Power Energy Syst. 2015, 68, 364–372. [Google Scholar] [CrossRef]
- Aziz, S.; Wang, H.; Liu, Y.; Peng, J.; Jiang, H. Variable universe fuzzy logic-based hybrid LFC control with real-time implementation. IEEE Access 2019, 7, 25535–25546. [Google Scholar] [CrossRef]
- Pothiya, S.; Ngamroo, I. Optimal fuzzy logic-based PID controller for load–frequency control including superconducting magnetic energy storage units. Energy Convers. Manag. 2008, 49, 2833–2838. [Google Scholar] [CrossRef]
- Tian, E.; Peng, C. Memory-based event-triggering H∞ load frequency control for power systems under deception attacks. IEEE Trans. Cybern. 2020, 50, 4610–4618. [Google Scholar] [CrossRef]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N.; Catalão, J.P. Frequency regulation in hybrid power systems using particle swarm optimization and linear matrix inequalities based robust controller design. Int. J. Electr. Power Energy Syst. 2014, 63, 887–900. [Google Scholar] [CrossRef]
- Sun, W.; Fang, Z.; Huang, L.; Li, Q.; Li, W.; Xu, X. Distributed robust secondary control of islanded microgrid with stochastic time-varying delays and external disturbances. Int. J. Electr. Power Energy Syst. 2022, 143, 108448. [Google Scholar] [CrossRef]
- Mohanty, B.; Hota, P.K. Comparative performance analysis of fruit fly optimisation algorithm for multi-area multi-source automatic generation control under deregulated environment. IET Gener. Transm. Distrib. 2015, 9, 1845–1855. [Google Scholar] [CrossRef]
- Khalili, J.; Dehkordi, N.M.; Hamzeh, M. Distributed event-triggered secondary frequency control of islanded AC microgrids under cyber attacks with input time delay. Int. J. Electr. Power Energy Syst. 2022, 143, 108506. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Riaño, I.; Gerndt, R.; Zelinka, I.; Gonzalez-Longatt, F.; Sood, V.K. Synthetic inertia control based on fuzzy adaptive differential evolution. Int. J. Electr. Power Energy Syst. 2019, 105, 803–813. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Ramachandran, R.; Othman, M.L.; Hizam, H.; Irudayaraj, A.X.R.; Guerrero, J.M.; Kumar, J.S. A Hankel matrix based reduced order model for stability analysis of hybrid power system using PSO-GSA optimized cascade PI-PD controller for automatic load frequency control. IEEE Access 2020, 8, 71422–71446. [Google Scholar] [CrossRef]
- Smith, E.J.; Robinson, D.A.; Agalgaonkar, A.P. A secondary strategy for unbalance consensus in an islanded voltage source converter-based microgrid using cooperative gain control. Electr. Power Syst. Res. 2022, 210, 108097. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Azar, A.T.; Aslam, S.; Alkhalifah, T.; Alturise, F. Optimized Fractional Order Integral-Tilt Derivative Controller for Frequency Regulation of Interconnected Diverse Renewable Energy Resources. IEEE Access 2022, 10, 43514–43527. [Google Scholar] [CrossRef]
- Tripathi, S.; Singh, V.P.; Kishor, N.; Pandey, A. Load frequency control of power system considering electric Vehicles’ aggregator with communication delay. Int. J. Electr. Power Energy Syst. 2023, 145, 108697. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Bahrampour, E.; Dehghani, M.; Asemani, M.H.; Abolpour, R. Load frequency fractional-order controller design for shipboard microgrids using direct search alghorithm. IET Renew. Power Gener. 2023, 17, 894–906. [Google Scholar] [CrossRef]
- Yin, L.; Cao, X.; Chen, L. High-dimensional Multiple Fractional Order Controller for Automatic Generation Control and Automatic Voltage Regulation. Int. J. Control Autom. Syst. 2022, 20, 3979–3995. [Google Scholar] [CrossRef]
- Sahoo, G.; Sahu, R.K.; Samal, N.R.; Panda, S. Analysis of type-2 fuzzy fractional-order PD-PI controller for frequency stabilisation of the micro-grid system with real-time simulation. Int. J. Sustain. Energy 2022, 41, 412–433. [Google Scholar] [CrossRef]
- Kumar, A.; Pan, S. Design of fractional order PID controller for load frequency control system with communication delay. ISA Trans. 2022, 129, 138–149. [Google Scholar] [CrossRef]
- Warrier, P.; Shah, P. Fractional order control of power electronic converters in industrial drives and renewable energy systems: A review. IEEE Access 2021, 9, 58982–59009. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.A.; Hosseinnia, S.H.; Petlenkov, E.; Ates, A.; Cech, M. Towards industrialization of FOPID controllers: A survey on milestones of fractional-order control and pathways for future developments. IEEE Access 2021, 9, 21016–21042. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; De Keyser, R. A review of recent developments in autotuning methods for fractional-order controllers. Fractal Fract. 2022, 6, 37. [Google Scholar] [CrossRef]
- Podlubny, I. Chapter 10—Survey of Applications of the Fractional Calculus; Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 1999; Volume 198. [Google Scholar]
- Aboelela, M.A.; Hennas, R.H.M. Development of a Fractional-Order PID Controller Using Adaptive Weighted PSO and Genetic Algorithms with Applications. In Fractional Order Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 511–551. [Google Scholar]
- Thakar, U.; Joshi, V.; Mehta, U.; Vyawahare, V.A. Fractional-order PI controller for permanent magnet synchronous motor: A design-based comparative study. In Fractional Order Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 553–578. [Google Scholar]
- Shahgholian, G.; Fattollahi, A. Improving power system stability using transfer function: A comparative analysis. Eng. Technol. Appl. Sci. Res. 2017, 7, 1946–1952. [Google Scholar] [CrossRef]
- Hall, J.E. Pocket Companion to Guyton & Hall Textbook of Medical Physiology E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Ekinci, S.; Demiroren, A.; Hekimoglu, B. Parameter optimization of power system stabilizers via kidney-inspired algorithm. Trans. Inst. Meas. Control 2019, 41, 1405–1417. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Alvankarian, J.; Abdullah, S. Kidney-inspired algorithm for optimization problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 358–369. [Google Scholar] [CrossRef]
- Idir, A.; Kidouche, M.; Bensafia, Y.; Khettab, K.; Tadjer, S.A. Speed control of DC motor using PID and FOPID controllers based on differential evolution and PSO. Int. J. Intell. Eng. Syst 2018, 20, 21. [Google Scholar] [CrossRef]
- Shabani, H.; Vahidi, B.; Ebrahimpour, M. A robust PID controller based on imperialist competitive algorithm for load-frequency control of power systems. ISA Trans. 2013, 52, 88–95. [Google Scholar] [CrossRef]
- Bruni, R.; Celani, F. Combining global and local strategies to optimize parameters in magnetic spacecraft control via attitude feedback. J. Optim. Theory Appl. 2019, 181, 997–1014. [Google Scholar] [CrossRef]


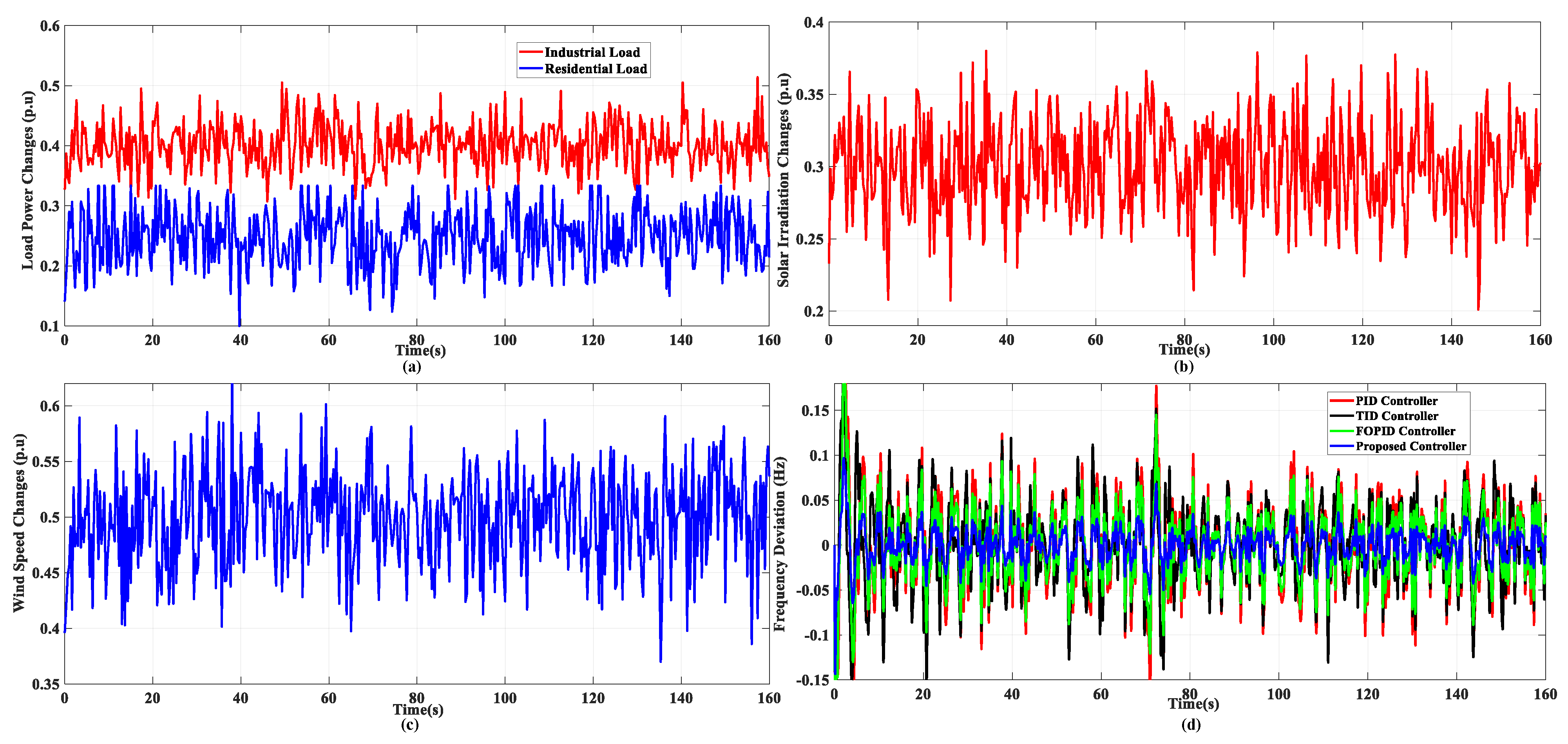
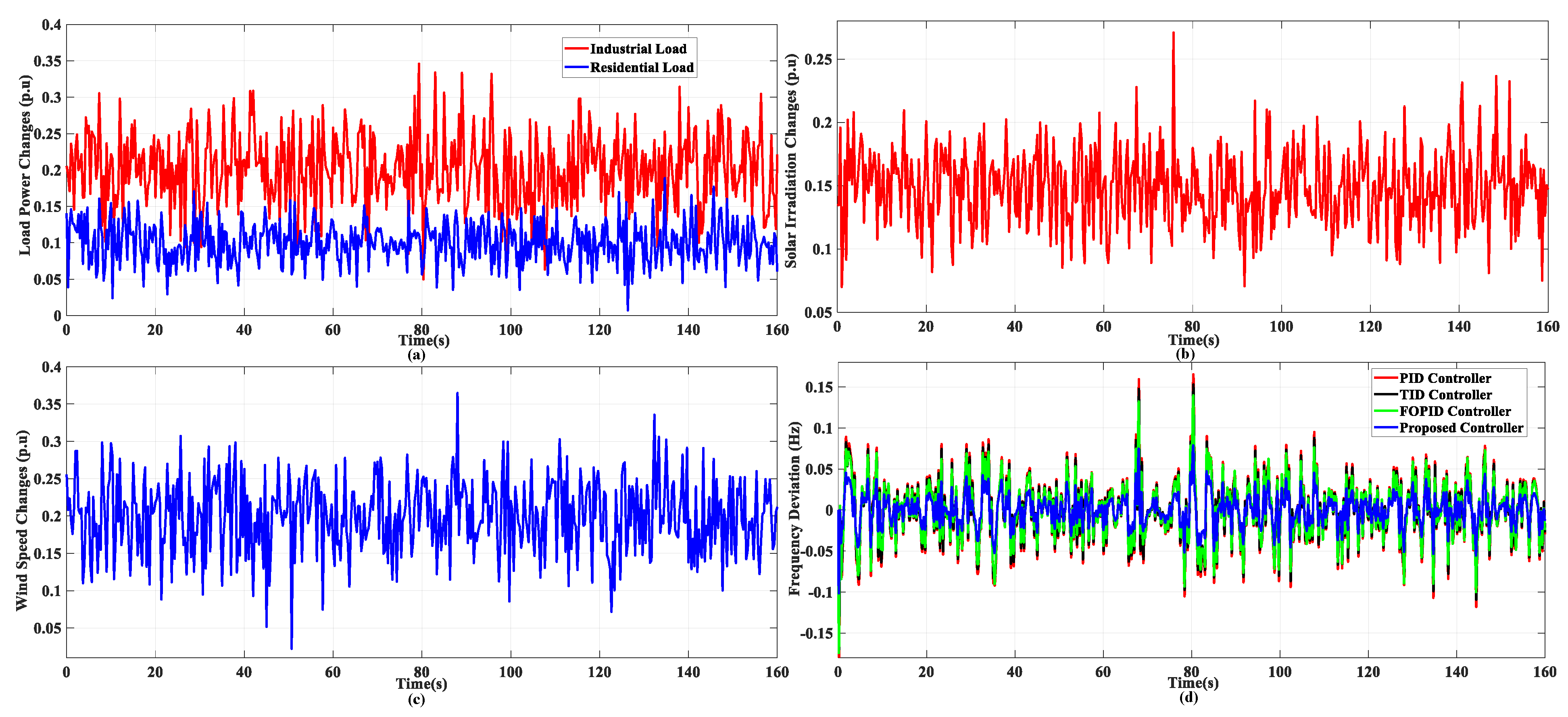
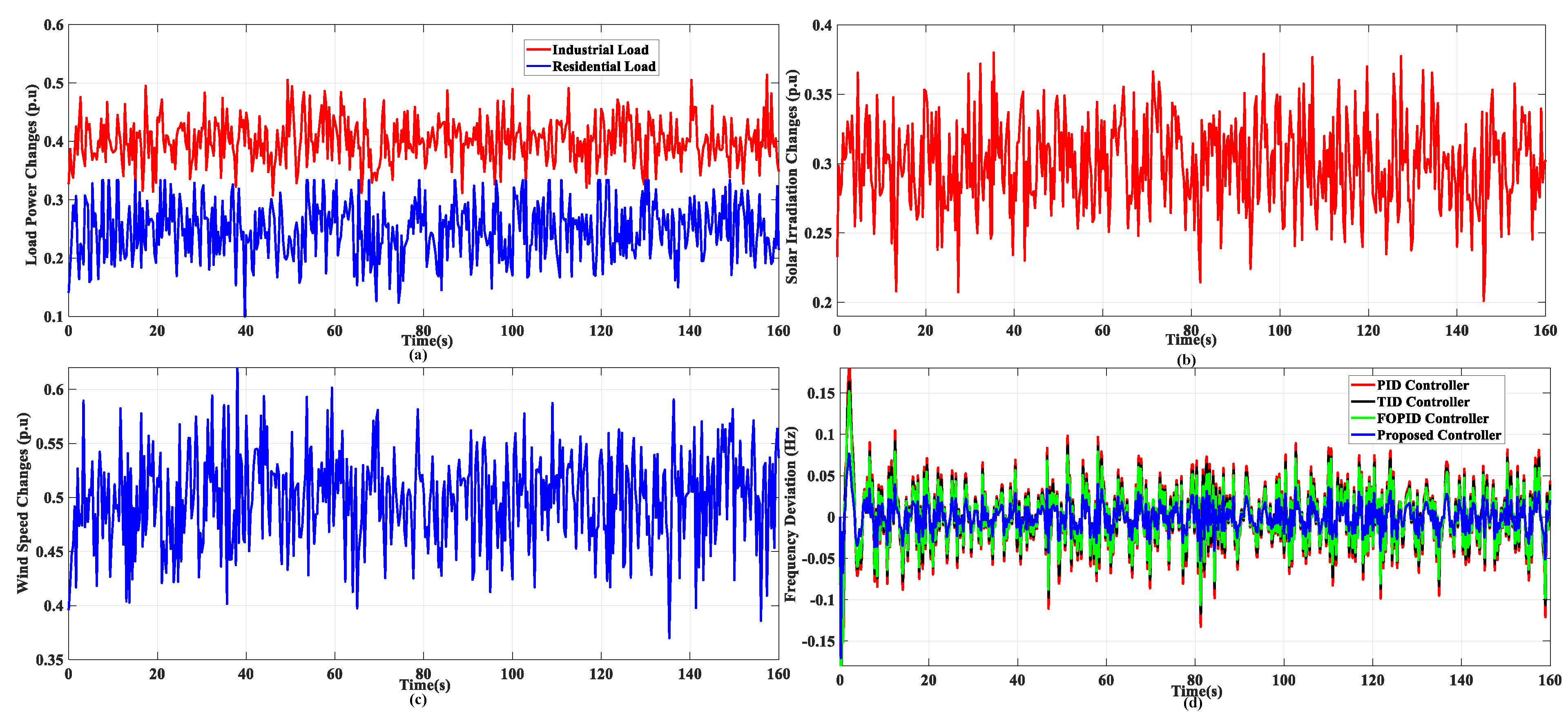

| Parameter | Description | Value |
|---|---|---|
| H | System inertia (p.u.MW/s) | 0.083 |
| D | Load damping coefficient (p.u.MW/Hz) | 0.015 |
| Tg | Governor time constant (s) | 0.1 |
| Tt | Turbine time constant (s) | 0.4 |
| R | Governor droop constant (Hz/p.u.MW) | 2.4 |
| B | Frequency bias factor (p.u.MW/Hz) | 1 |
| KESS | ESS gain | 0.8 |
| TESS | ESS time constant (s) | 10 |
| KWPP | WPP gain | 1 |
| TWPP | WPP time constant (s) | 1.5 |
| KPPP | PPP gain | 1 |
| TPPP | PPP time constant (s) | 1.85 |
| Controller | |||||||
|---|---|---|---|---|---|---|---|
| PID | 0.5 | −1.2 | 0.5 | - | - | - | - |
| TID | - | −1.34 | 0.67 | 0.74 | - | - | 3 |
| FOPID | 0.95 | −1.75 | 0.75 | - | 0.5 | 0.3 | - |
| Proposed FOCC | −9.5 | 5.8 | 0.9 | 0.5 | 0.1 | 0.4 | 3 |
| Index | PID | TID | FOPID | Proposed FOCC |
|---|---|---|---|---|
| ISE | 0.0464 | 0.0352 | 0.0285 | 0.0111 |
| ITAE | 0.597 | 0.472 | 0.349 | 0.194 |
| PID | TID | FOPID | Proposed FOCC | |
|---|---|---|---|---|
| Scenario 1 | 0.0103 | 0.0097 | 0.0081 | 0.005 |
| Scenario 2 | 0.0541 | 0.05 | 0.0425 | 0.0273 |
| Scenario 3 | 0.0421 | 0.038 | 0.0322 | 0.0207 |
| Scenario 4 | 0.0386 | 0.0348 | 0.0291 | 0.0183 |
| Scenario 5 | 0.0321 | 0.0283 | 0.025 | 0.0152 |
| Controller | Parameter | MAGFD | |
|---|---|---|---|
| Proposed FOCC | +30% | 0.0051 | |
| Tg | |||
| −30% | 0.0045 | ||
| +30% | 0.0055 | ||
| Tt | |||
| −30% | 0.0043 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oshnoei, S.; Fathollahi, A.; Oshnoei, A.; Khooban, M.H. Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller. Fractal Fract. 2023, 7, 343. https://doi.org/10.3390/fractalfract7040343
Oshnoei S, Fathollahi A, Oshnoei A, Khooban MH. Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller. Fractal and Fractional. 2023; 7(4):343. https://doi.org/10.3390/fractalfract7040343
Chicago/Turabian StyleOshnoei, Soroush, Arman Fathollahi, Arman Oshnoei, and Mohammad Hassan Khooban. 2023. "Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller" Fractal and Fractional 7, no. 4: 343. https://doi.org/10.3390/fractalfract7040343
APA StyleOshnoei, S., Fathollahi, A., Oshnoei, A., & Khooban, M. H. (2023). Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller. Fractal and Fractional, 7(4), 343. https://doi.org/10.3390/fractalfract7040343









