Input-Output Finite-Time Stability of Fractional-Order Switched Singular Systems with D-Perturbation
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
2.1. Fractional-Order Calculus
2.2. Fractional-Order Switched Singular Systems
3. Results
3.1. Input-output Finite-Time Stability
3.2. Input-Output Finite-Time Stabilization
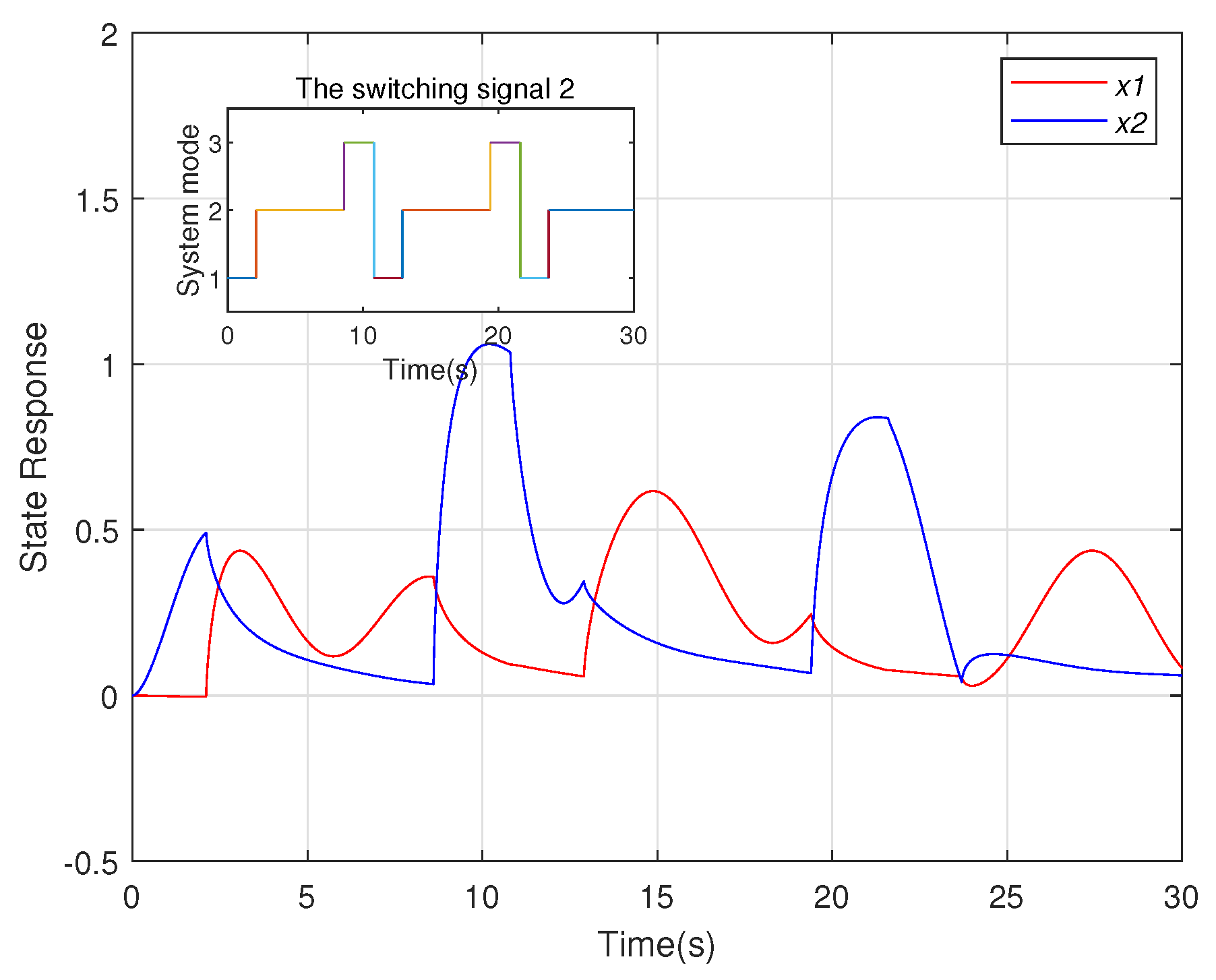
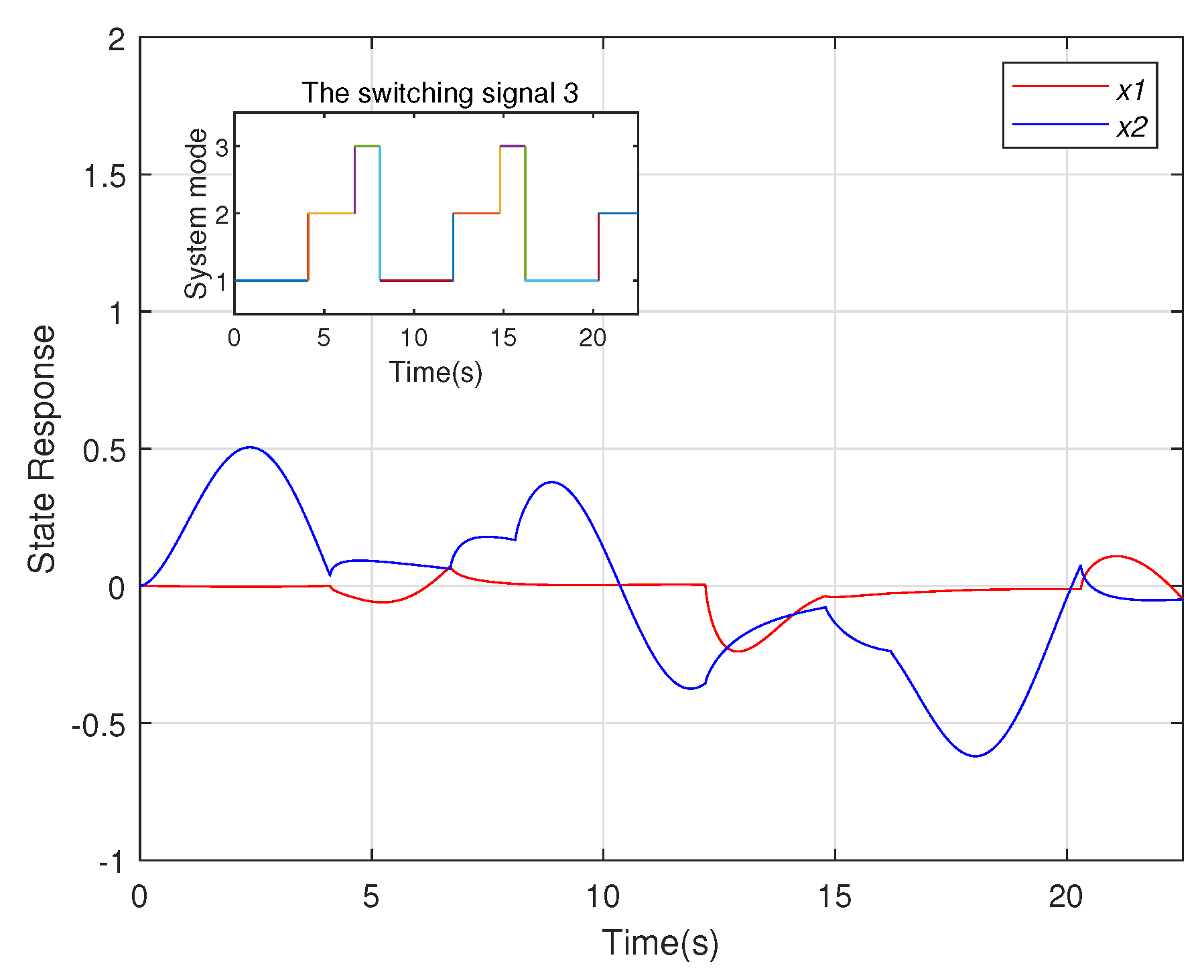
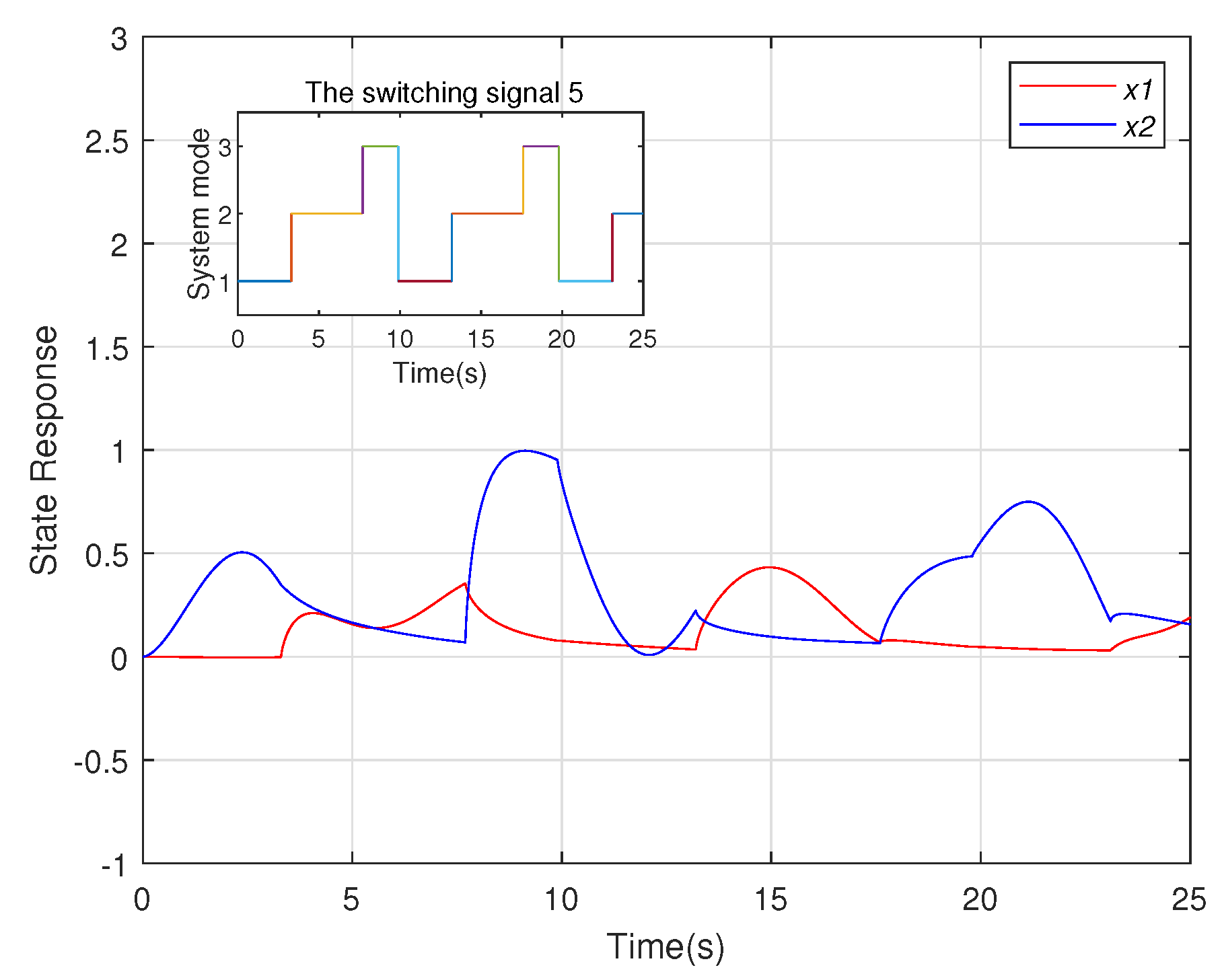
4. Numerical Example
Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ADT | average dwell time |
| MDADT | mode-dependent average dwell time |
| ΦDADT | Φ-dependent average dwell time |
| FOSSS | fractional-order switched singular systems |
| FOPSS | fractional-order positive switched systems |
| FOMS | fractional-order multiagent systems |
| LMIs | linear matrix inequalities |
| FTS | finite-time stability |
| FTB | finite-time boundedness |
| IO-FTS | input-output finite-time stability |
References
- Montseny, G.; Audounet, J.; Mbodje, B. Optimal models of fractional integrators and application to systems with fading memory. In Proceedings of the IEEE Systems Man and Cybernetics Conference—SMC, Le Touquet, France, 17–20 October 1993; Volume 5, pp. 65–70. [Google Scholar]
- Suki, B.; Barabasi, A.L.; Lutchen, K.R. Lung tissue viscoelasticity: A mathematical framework and its molecular basis. J. Appl. Physiol. 1994, 76, 2749–2759. [Google Scholar] [CrossRef] [PubMed]
- Heleschewitz, Z.; Matignon, D. Diffusive realisations of fractional integrodifferential operators: Structural analysis under approximation. IFAC Proceedings Volumes 1998, 31, 227–232. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D. Fractal heat conduction problem solved by local fractional variation iteration. Therm. Sci. 2013, 17, 625–628. [Google Scholar] [CrossRef]
- Yin, C.; Huang, X.; Chen, Y.; Dadras, S.; Zhong, S.-M.; Cheng, Y. Fractional-order exponential switching technique to enhance sliding mode control. Appl. Math. Model. 2017, 44, 705–726. [Google Scholar] [CrossRef]
- Yin, C.; Huang, X.; Dadras, S.; Cheng, Y.; Cao, J.; Malek, H.; Mei, J. Design of optimal lighting control strategy based on multi-variable fractional-order extremun seeking method. Inf. Sci. 2018, 465, 38–60. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Gómez-Aguilar, J.; Karaagac, B. Modelling analysis and simulations of some chaotic systems using derivative with Mittag-Leffler kernel. Chaos Solutions Fractals 2019, 125, 54–63. [Google Scholar] [CrossRef]
- Babiarz, A.; Legowski, A.; Niezabitowski, M. Controllability of positive discrete-time switched fractional order systems for fixed switching sequence. In Proceedings of the 8th International Conference, ICCCI 2016, Halkidiki, Greece, 28–30 September 2016. [Google Scholar]
- Zhao, X.D.; Yin, Y.F.; Zheng, X.L. State-dependent switching control of switched positive fractional-order systems. ISA Trans. 2016, 62, 103–108. [Google Scholar] [CrossRef]
- Dadras, S.; Malek, H.; Chen, Y. A note on the Lyapunov stability of fractional-order nonlinear systems. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Thuan, M.V.; Huong, D.C. New results on stabilization of fractional-order nonlinear systems via an LMI approach. Asian J. Control 2018, 20, 1541–1550. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhao, X.D.; Chen, Y. Finite-time stability and stabilization of fractional order positive switched systems. Circuits Syst. Singal Process. 2016, 35, 2450–2470. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, G. Finite-time stability of fractional order impulsive switched systems. Int. J. Robust Nonlinear Control. 2015, 25, 2207–2222. [Google Scholar] [CrossRef]
- Liu, L.P.; Cao, X.Y.; Fu, Z.M.; Song, S.Z.; Xing, H. Finite-time control of uncertain fractional-order positive impulsive switched systems with mode-dependent average dwell time. Circuits Syst. Signal Process. 2018, 37, 3739–3755. [Google Scholar] [CrossRef]
- Liu, L.P.; Cao, X.Y.; Fu, Z.M.; Song, S.Z.; Xing, H. Positive impulsive observer design of fractional-order positive switched systems with MDADT. Trans. Inst. Meas. Control 2019, 41, 1340–1347. [Google Scholar] [CrossRef]
- Liang, J.X.; Wu, B.W.; Liu, L.L.; Wang, Y.E.; Li, C.T. Finite-time stability and finite-time boundedness of fractional order switched systems. Trans. Inst. Meas. Control 2019, 41, 3364–3371. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, G.; Peng, Z.; Rahmani, A. Consensus of fractional-order multi-agent system via sampled-data event-triggered control. J. Frankl. Institue 2019, 356, 10241–10259. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X. Leader-following consensus of fractional-order multi-agent systems based on event-triggered control. Nonlinear Dyn. 2020, 99, 2219–2232. [Google Scholar] [CrossRef]
- Feng, T.; Guo, L.H.; Wu, B.W.; Chen, Y.Q. Stability analysis of switched fractional-order continuous-time systems. Nonlinear Dyn. 2020, 102, 2467–2478. [Google Scholar] [CrossRef]
- Zong, G.D.; Wang, X.H.; Zhao, H.J. Robust finite-time guaranteed cost control for impulsive switched systems with time-varying delay. Int. J. Control Autom. Syst. 2017, 15, 113–121. [Google Scholar] [CrossRef]
- Shang, Y.L.; Liu, L.P.; Di, Y.F.; Fu, Z.M.; Fan, B.O. Guaranteed cost and finite-time event-triggered control of fractional-order switched systems. Trans. Inst. Measrement Control 2021, 43, 2724–2733. [Google Scholar] [CrossRef]
- Liu, L.P.; Di, Y.F.; Shang, Y.L.; Fu, Z.M.; Fan, B. Guaranteed Cost and Finite-Time Non-fragile Control of Fractional-Order Positive Switched Systems with Asynchronous Switching and Impulsive Moments. Circuits Syst. Signal Process. 2021, 40, 3143–3160. [Google Scholar] [CrossRef]
- Yu, Q.; Zhai, G.S. Stability analysis of switched systems under Φ-dependent average dwell time. IEEE Access. 2020, 8, 30655–30663. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N. Switching law design for finite-time stability of singular fractional-order systems with delay. IET Control Theory Appl. 2018, 13, 1367–1373. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, Y.X.; Pan, F. Observer-based robust control for singular switched fractional order systems subject to actuator saturation. Appl. Math. Comput. 2021, 411, 126538. [Google Scholar] [CrossRef]
- Feng, T.; Wu, B.W.; Wang, Y.-E.; Liu, L.L. Input-output finite-time stability of fractional-order switched singular continuous-time systems. Asian J. Control. Affil. Acpa. Asian Control. Profr. Assoc. 2019, 23, 1052–1061. [Google Scholar] [CrossRef]
- Liu, J.; Lian, J.; Zhuang, Y. Robust stability for switched positive systems with D-perturbation and time-varying delay. Inf. Sci. 2016, 369, 522–531. [Google Scholar] [CrossRef]
- Xing, H.; Liu, L.P.; Cao, X.Y.; Fu, Z.M.; Song, S.Z. Guaranteed cost finite-time control of positive switched nonlinear systems with D-perturbation. Nephron Clin. Pract. 2017, 15, 1635–1648. [Google Scholar] [CrossRef]
- Liu, L.P.; Cao, X.Y.; Fu, Z.M.; Song, S.Z. Guaranteed cost finite-time control of fractional-order nonlinear positive switched systems with D-Perturbations via MDADT. J. Syst. Sci. Complex. 2019, 32, 857–874. [Google Scholar] [CrossRef]
- Delavari, H.; Baleavanu, D.; Sadati, J. Stability analysis of Caputo fractional-order nonlinear systems. Nonlinear Dyn. 2012, 67, 2433–2439. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.C. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]
- Zhou, L.; Ho, D.W.C.; Zhai, G. Stability analysis of switched linear singular systems. Automaica 2013, 49, 1481–1487. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems of Fractional Systems Theory; Springer: Berlin/Heidelberg, Germany, 2012; pp. 48–54. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Xue, N. Input-Output Finite-Time Stability of Fractional-Order Switched Singular Systems with D-Perturbation. Fractal Fract. 2023, 7, 341. https://doi.org/10.3390/fractalfract7040341
Yu Q, Xue N. Input-Output Finite-Time Stability of Fractional-Order Switched Singular Systems with D-Perturbation. Fractal and Fractional. 2023; 7(4):341. https://doi.org/10.3390/fractalfract7040341
Chicago/Turabian StyleYu, Qiang, and Na Xue. 2023. "Input-Output Finite-Time Stability of Fractional-Order Switched Singular Systems with D-Perturbation" Fractal and Fractional 7, no. 4: 341. https://doi.org/10.3390/fractalfract7040341
APA StyleYu, Q., & Xue, N. (2023). Input-Output Finite-Time Stability of Fractional-Order Switched Singular Systems with D-Perturbation. Fractal and Fractional, 7(4), 341. https://doi.org/10.3390/fractalfract7040341






