Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag
Abstract
1. Introduction
2. Methodology
2.1. Pore Structure Investigation of Water-Saturated Tight Sandstone Based on Fractal Analysis from NMR Spectra
2.2. Water Saturation Prediction Method of Gas-Bearing Tight Sandstone Based on Fractal Analysis from NMR Spectra
3. Model Validation
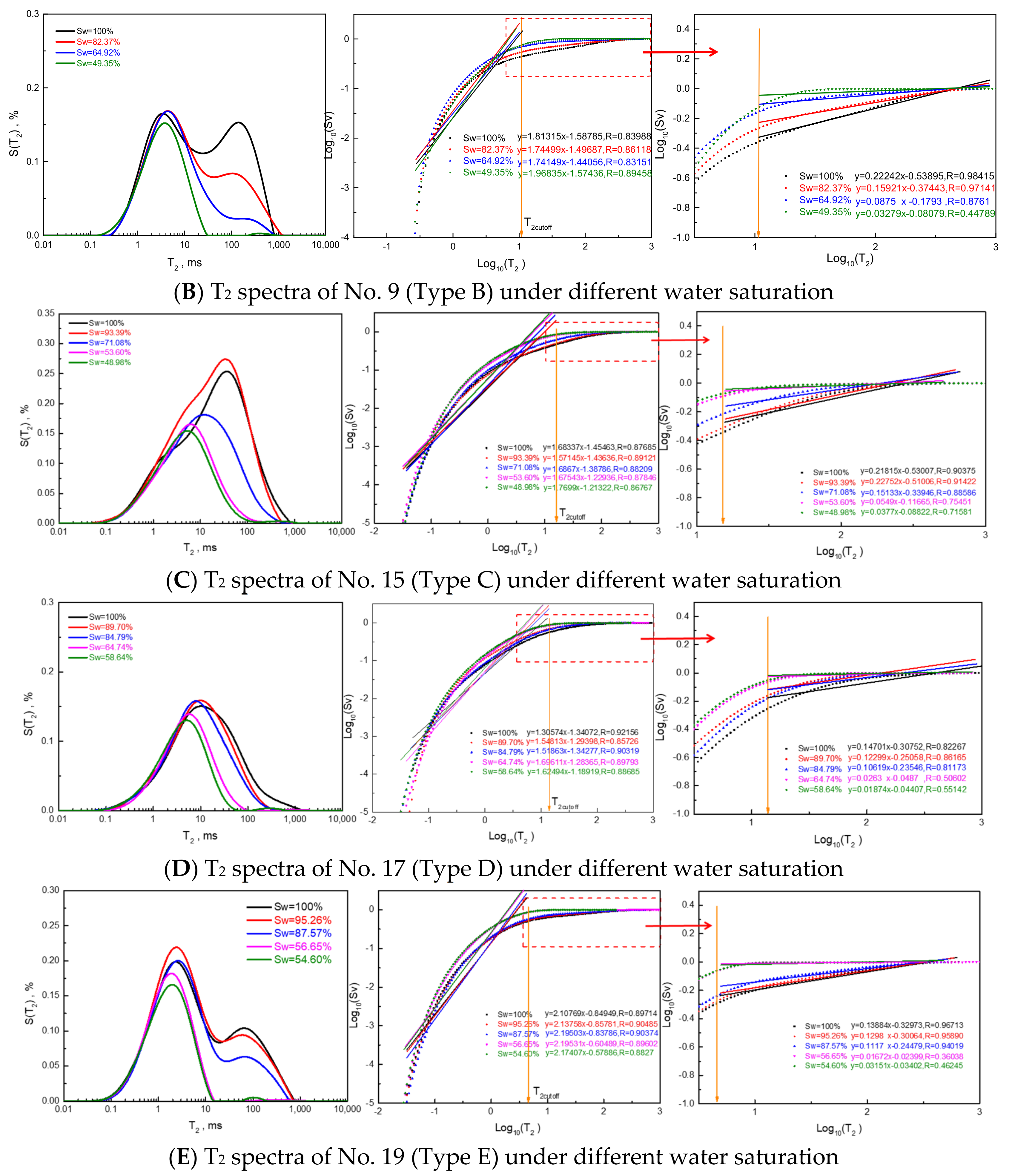
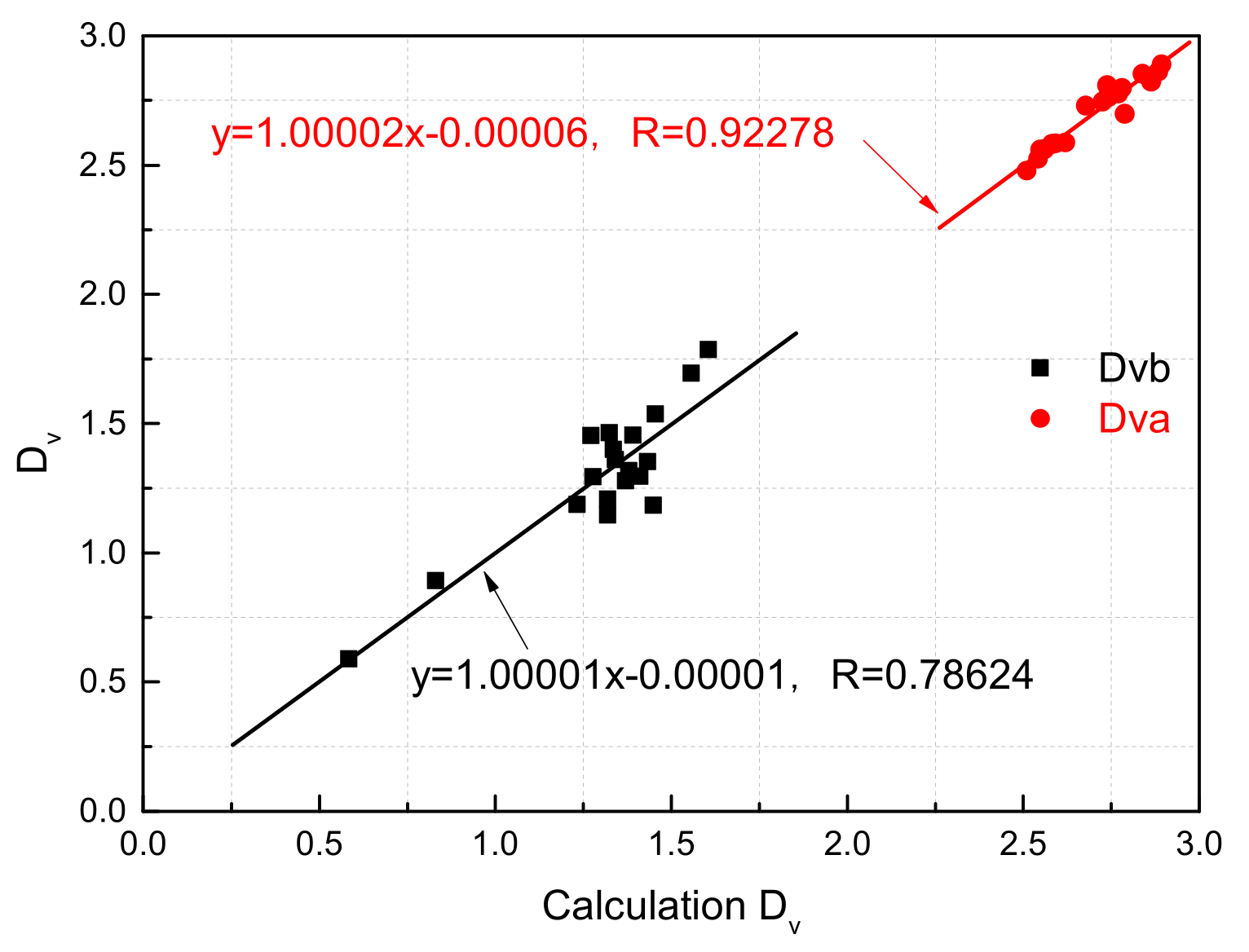
3.1. Pore Structure Characterization Method Based on Fractal Analysis from NMR Spectra
3.2. Water Saturation Prediction Method Based on Fractal Analysis from NMR Spectra
4. Application
5. Discussion and Future Work
5.1. Relationship of the Fractal Dimension from NMR with the Pore Size from the T2 Spectrum
5.2. Relationship of the Fractal Dimension from NMR with Swir and T2lm
5.3. Fractal-Based Water Saturation Prediction Model from NMR
5.4. Future Work
- The fractal dimension of tight sandstone is closely related to its pore structure [34]. The pore structures in the different study areas have their specific fractal features and may be characterized by double [35], triple, or multi-fractals. Launching research to figure out fractal characteristics in a specific study area is necessary;
- The double fractal theory is the basis of the water saturation prediction method based on the fractal dimension from NMR proposed in this paper. In order to improve the accuracy, multi-fractal theory can be introduced to establish the water saturation prediction model;
- At present, 2D NMR logging is widely used in reservoir evaluation, and the research on fractal characteristics of 2D NMR is a new hot spot;
- For T2, the relaxation characteristics of oil-bearing sandstone differ greatly from that of gas-bearing sandstone [36]. The water saturation prediction model for gas-bearing sandstone proposed in this paper cannot be applied in oil-bearing sandstone reservoirs, but it still has reference and guiding significance for deriving a water saturation prediction model for oil-bearing sandstone;
- The T2cut and T2lm are very important parameters for our research results, and lots of factors have significant affection on their values, such as pore size, clay content, pressure, and others. Previous studies have proved that factors leading to the decrease in the T2cut and T2lm include the compressed rock matrix, the growth of clay content, and hydrocarbon limiting in micro-pores. In the extending application of the new method in various types of hydrocarbon-bearing reservoirs, it is necessary to conduct experiments and analysis on the influence factors on the T2cut and T2lm.
6. Conclusions
- (1)
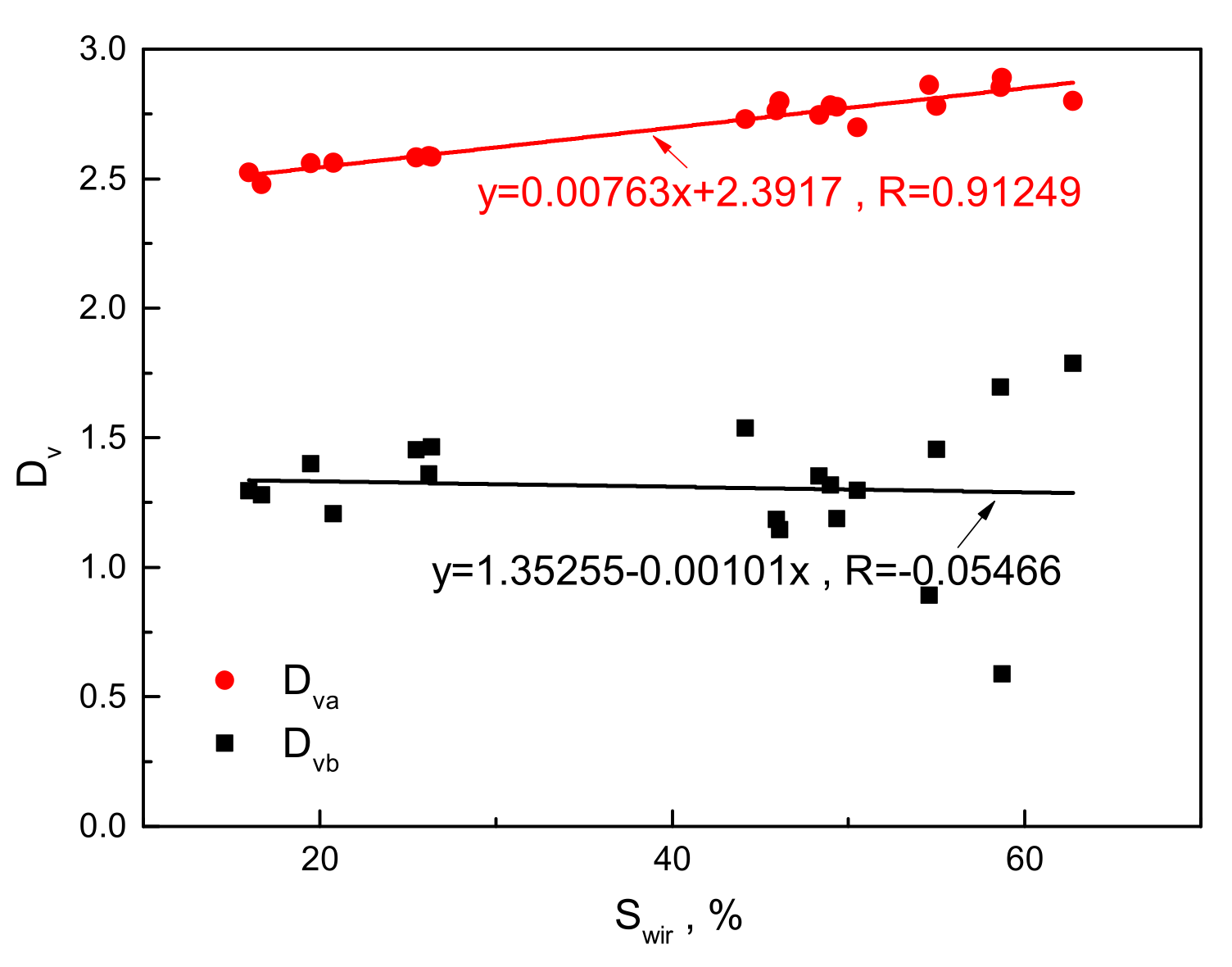
- Rock samples having similar pore structures have similar fractal features. The experimental data show that samples have a similar T2 curve monography, although the porosity differs, and and values are centrally distributed. This is the basis for pore structure characterization and classification method based on the fractal dimension from NMR. In addition, is in direct ratio to T2lm and Swir, but has no obvious correlation with these two parameters;
- (2)
- To analyze the relationship between pore size and the fractal dimension from NMR, pore size is divided into five types according to T2 spectra ranges, including (T2 range of 70–900 ms), (T2 range of 20–70 ms), (T2 range of 5–20 ms), (T2 range of 2–5 ms), and (T2 range of 0.1–2 ms). The fractal dimension is inversely proportional to and , increasing and which are occupied by the movable water, leading to decreasing bound water content and fractal dimension . The fractal dimension is in inverse ratio to and , while it is in direct ratio to , increasing and results in decreasing fractal dimension , but increasing leads to increasing fractal dimension ;
- (3)
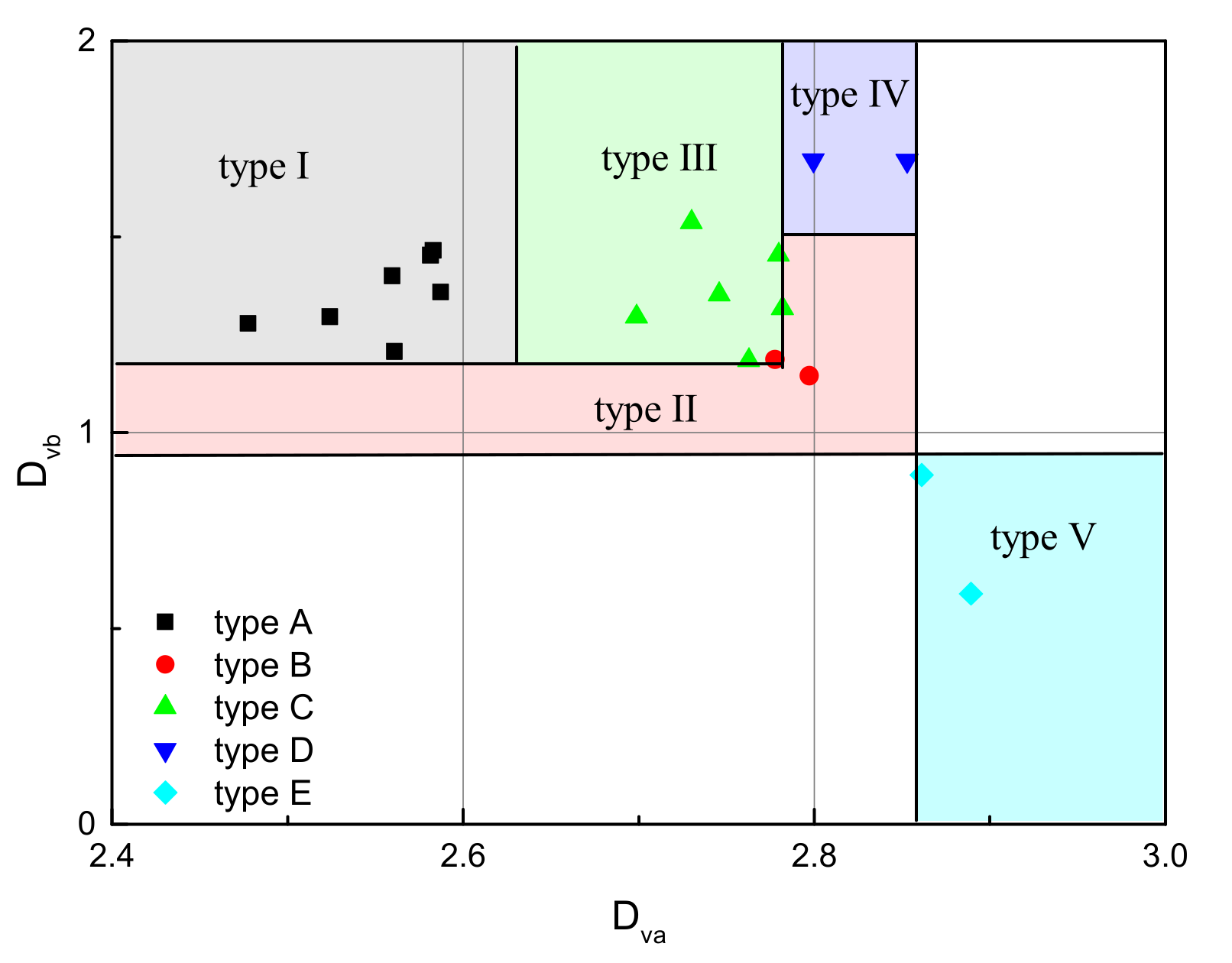
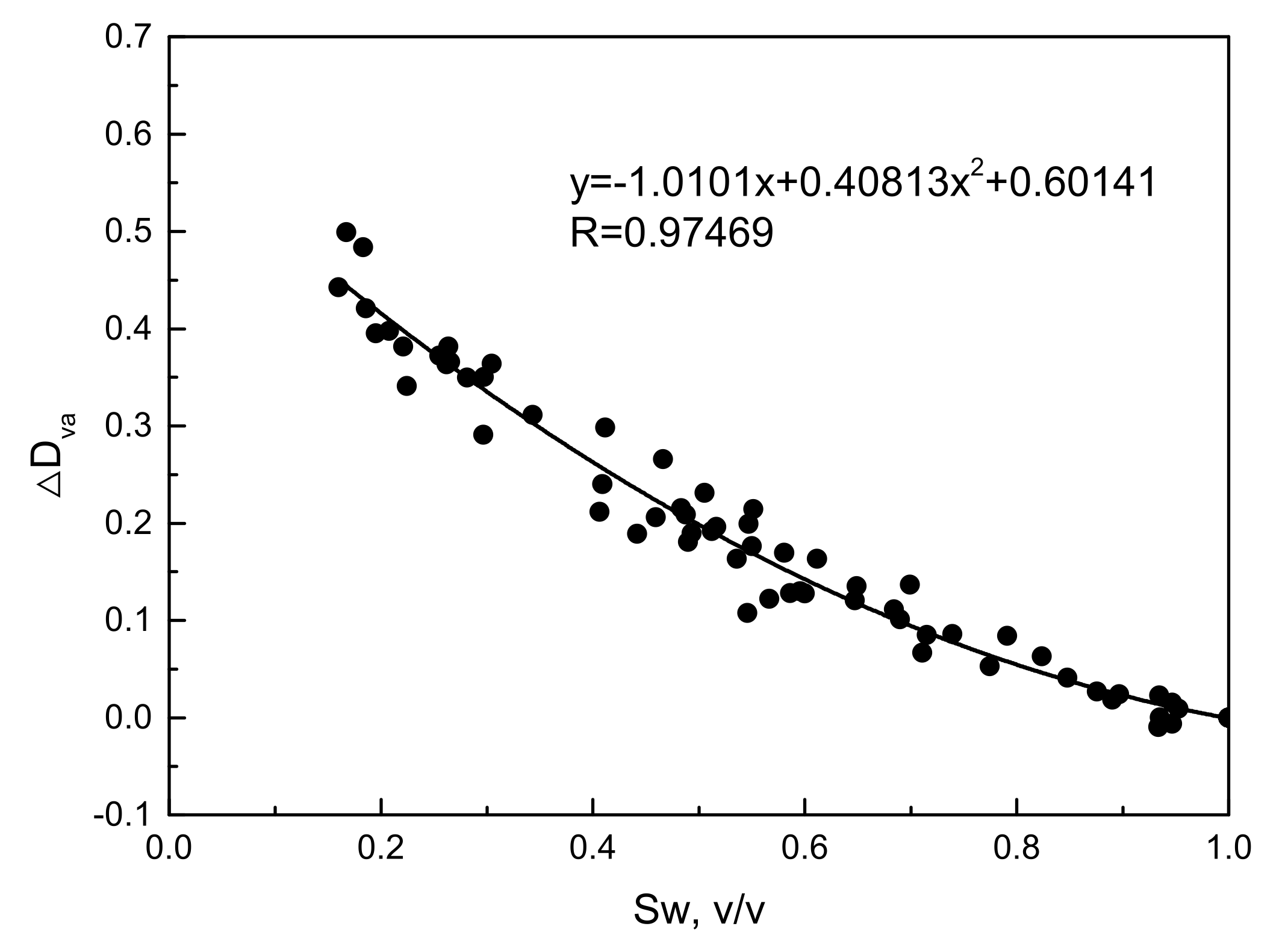
- In water-saturated rock, when macro-pores fill with gas, residual water-saturated pores are still satisfied with the fractal theory. As the NMR signal of the gas-filling pores is too small to be measured, the fractal dimension from NMR changes. As decreases, increases, but has little variation, and (the increment of ) is directly related to the water saturation of gas-bearing tight sandstone. When decreases to , approximately equals 3. As the pore structure transferred from Type A to Type E, the maximum value of (the difference between under state and that under 100% state) becomes smaller;
- (4)
- Experimental data and application result show that firstly, pore structure evaluation and classification can be achieved based on fractal analysis from NMR spectra; the method can be further applied in reservoir quality evaluation and favorable reservoir prediction. Secondly, the accuracy of calculated water saturation by the new method is higher than that calculated by the Archie model, and the fractal-based water saturation prediction method from NMR extends the application area of NMR logging and also provides a non-electrical idea for the qualitative identification and evaluation of gas-bearing tight sandstone reservoir, it has a reference for the gas-bearing recognition of tight sandstone and carbonate reservoirs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, S.O.N.G.; Zhuo, L.I.; Jiang, Z.; Qun, L.; Dongdong, L.; Zhiye, G. Progress and development trend of unconventional oil and gas geological research. Pet. Explor. Dev. 2017, 44, 675–685. [Google Scholar]
- Ren, J.; Zhang, L.; Ezekiel, J.; Ren, S.; Meng, S. Reservoir characteristics and productivity analysis of tight sand gas in Upper Paleozoic Ordos Basin China. J. Nat. Gas Sci. Eng. 2014, 19, 244–250. [Google Scholar] [CrossRef]
- Muther, T.; Nizamani, A.A.; Ismail, A.R. Analysis on the effect of different fracture geometries on the productivity of tight gas reservoirs Malays. J. Fundam. Appl. Sci. 2020, 16, 201–211. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Xiao, D.; Lu, S.; Lu, Z.; Huang, W.; Gu, M. Combining nuclear magnetic resonance and rate-controlled porosimetry to probe the pore-throat structure of tight sandstones. Pet. Explor. Dev. 2016, 43, 1049–1059. [Google Scholar] [CrossRef]
- Wang, R.; Shi, W.; Xie, X.; Zhang, W.; Qin, S.; Liu, K.; Busbey, A.B. Clay mineral content, type, and their effects on pore throat structure and reservoir properties: Insight from the Permian tight sandstones in the Hangjinqi area, north Ordos Basin, China. Mar. Pet. Geol. 2020, 115, 104281. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Wang, F.; Yang, K.; Cai, J. Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal statistical network properties. J. Pet. Sci. Eng. 2012, 92, 110–123. [Google Scholar] [CrossRef]
- Li, K. Analytical derivation of Brooks–Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Wang, X.; Zhu, Y.; Chang, M.; Uwamahoro, C. Pore structure heterogeneity of the Xiamaling Formation shale gas reservoir in the Yanshan area of China: Evaluation of geological controlling factors. Acta Geol. Sin.-Engl. Ed. 2019, 93, 588–603. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, Y.; Zhao, J.; Ren, L.; Zhao, C.; Zhao, J. Multiscale apparent permeability model of shale nanopores based on fractal theory. Energies 2019, 12, 3381. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Jiang, Y. A multiple fractal model for estimating permeability of dual-porosity media. J. Hydrol. 2016, 540, 659–669. [Google Scholar] [CrossRef]
- Song, Z.; Liu, G.; Yang, W.; Zou, H.; Sun, M.; Wang, X. Multi-fractal distribution analysis for pore structure characterization of tight sandstone—A case study of the Upper Paleozoic tight formations in the Longdong District, Ordos Basin. Mar. Pet. Geol. 2018, 92, 842–854. [Google Scholar] [CrossRef]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Rembert, F.; Jougnot, D.; Guarracino, L. A fractal model for the electrical conductivity of water-saturated porous media during mineral precipitation-dissolution processes. Adv. Water Resour. 2020, 145, 103742. [Google Scholar] [CrossRef]
- Feng, C.; Han, C.; Duan, W.; Wang, W.; Zhong, Y.; Feng, Z.; Zhang, N. Estimation of the Resistivity Index via Nuclear Magnetic Resonance Log Data Based on Fractal Theory. Geofluids 2020, 2020, 8871096. [Google Scholar] [CrossRef]
- Shi, Y.; Meng, H.; Liu, T.; Zhang, H.; Wang, C. Evaluation of Relative Permeability From Resistivity Data for Fractal Porous Media. Petrophys.-SPWLA J. Form. Eval. Reserv. Descr. 2020, 61, 303–317. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. 3D multi-fractal analysis of porous media using 3D digital images: Considerations for heterogeneity evaluation. Geophys. Prospect. 2019, 67, 1082–1093. [Google Scholar] [CrossRef]
- Zhao, P.; Luo, M.; Li, D.; Wu, Y.; Mao, Z.; Ostadhassan, M. Fractal Characterization and Petrophysical Analysis of 3D Dynamic Digital Rocks of Sandstone. Petrophys.-SPWLA J. Form. Eval. Reserv. Descr. 2021, 62, 500–515. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y. Fractal characterization of pore–fracture in low-rank coals using a low-field NMR relaxation method. Fuel 2016, 181, 218–226. [Google Scholar] [CrossRef]
- Liu, X.; Jin, Z.; Lai, J.; Fan, X.; Guan, M.; Shu, H.; Wang, G.; Liu, M.; Luo, Y. Fractal behaviors of NMR saturated and centrifugal T2 spectra in oil shale reservoirs: The Paleogene Funing formation in Subei basin, China. Mar. Pet. Geol. 2021, 129, 105069. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Z.; Lin, W.; Xiong, S.; Luo, Y.; Liu, X.; Xia, D. Fractal study on pore structure of tight sandstone based on full-scale map. Int. J. Oil Gas Coal Technol. 2019, 22, 123–139. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, F.; Zhang, C.; Song, Z.; Mo, W. Study on the Pore Structure and Fractal Dimension of Tight Sandstone in Coal Measures. Energy Fuels 2021, 35, 3887–3898. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Wang, G.; Yu, Z. Variable dimension fractal-based conversion method between the nuclear magnetic resonance T2 spectrum and capillary pressure curve. Energy Fuels 2020, 35, 351–357. [Google Scholar] [CrossRef]
- Wei, W.; Cai, J.; Hu, X.; Han, Q. An electrical conductivity model for fractal porous media. Geophys. Res. Lett. 2015, 42, 4833–4840. [Google Scholar] [CrossRef]
- Wang, F.; Cai, J. Characterization of petrophysical properties in tight sandstone reservoirs. In Petrophysical Characterization and Fluids Transport in Unconventional Reservoirs; Elsevier: Amsterdam, The Netherlands, 2019; pp. 37–59. [Google Scholar]
- Kashif, M.; Cao, Y.; Yuan, G.; Asif, M.; Javed, K.; Mendez, J.N.; Khan, D.; Miruo, L. Pore size distribution, their geometry and connectivity in deeply buried Paleogene Es1 sandstone reservoir, Nanpu Sag, East China. Pet. Sci. 2019, 16, 981–1000. [Google Scholar] [CrossRef]
- Zheng, H.J.; Dong, Y.X.; Zhu, G.Y.; Wang, X.D.; Xiong, Y. High-quality source rocks in Nanpu Sag. Pet. Explor. Dev. 2007, 34, 385. [Google Scholar]
- Guo, Y.; Pang, X.; Dong, Y.; Jiang, Z.; Chen, D.; Jiang, F. Hydrocarbon generation and migration in the Nanpu Sag, Bohai Bay Basin, eastern China: Insight from basin and petroleum system modeling. J. Asian Earth Sci. 2013, 77, 140–150. [Google Scholar] [CrossRef]
- Wang, E.; Liu, G.; Pang, X.; Wu, Z.; Li, C.; Bai, H.; Zhang, Z. Sedimentology, diagenetic evolution, and sweet spot prediction of tight sandstone reservoirs: A case study of the third member of the Upper Paleogene Shahejie Formation, Nanpu Sag, Bohai Bay Basin, China. J. Pet. Sci. Eng. 2020, 186, 106718. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Wang, G.; Guan, W.; Yu, Z. Modeling of gas saturation based on acoustic wave and pore structure classification and application in the low-porosity and low-permeability reservoir. Arab. J. Geosci. 2021, 14, 917. [Google Scholar] [CrossRef]
- Wu, B.; Xie, R.; Wang, X.; Wang, T.; Yue, W. Characterization of pore structure of tight sandstone reservoirs based on fractal analysis of NMR echo data. J. Nat. Gas Sci. Eng. 2020, 81, 103483. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.; Wang, Y.; Bai, L.; Li, W.; Li, S. A practical method to construct capillary pressure curves of reservoir using nmr logging date. Int. J. Oil Gas Coal Technol. 2019, 22, 433–446. [Google Scholar] [CrossRef]
- Winkler, M.; Freeman, J.J.; Appel, M. The limits of fluid property correlations used in NMR well logging: An experimental study of reservoir fluids at reservoir conditions. Petrophys.-SPWLA J. Form. Eval. Reserv. Descr. 2005, 46. [Google Scholar]
- Nie, R.S.; Zhou, J.; Chen, Z.; Liu, J.; Pan, Y. Pore structure characterization of tight sandstones via a novel integrated method: A case study of the Sulige gas field, Ordos Basin (Northern China). J. Asian Earth Sci. 2021, 213, 104739. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Zhu, X.; Chen, Y.; Li, R. Determination of nuclear magnetic resonance t2 cutoff value based on multifractal theory—An application in sandstone with complex pore structure. Geophysics 2015, 80, D11–D21. [Google Scholar] [CrossRef]
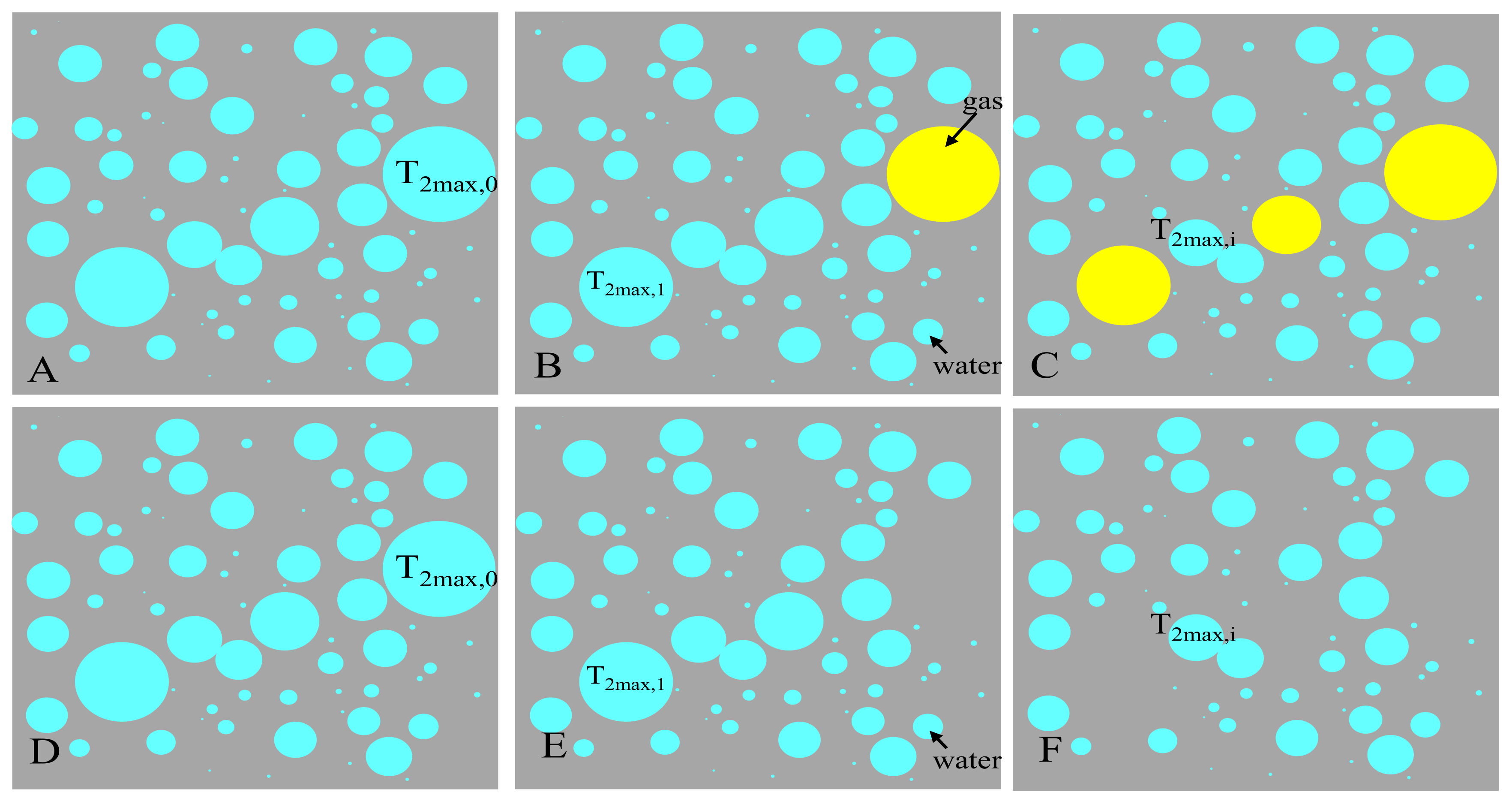
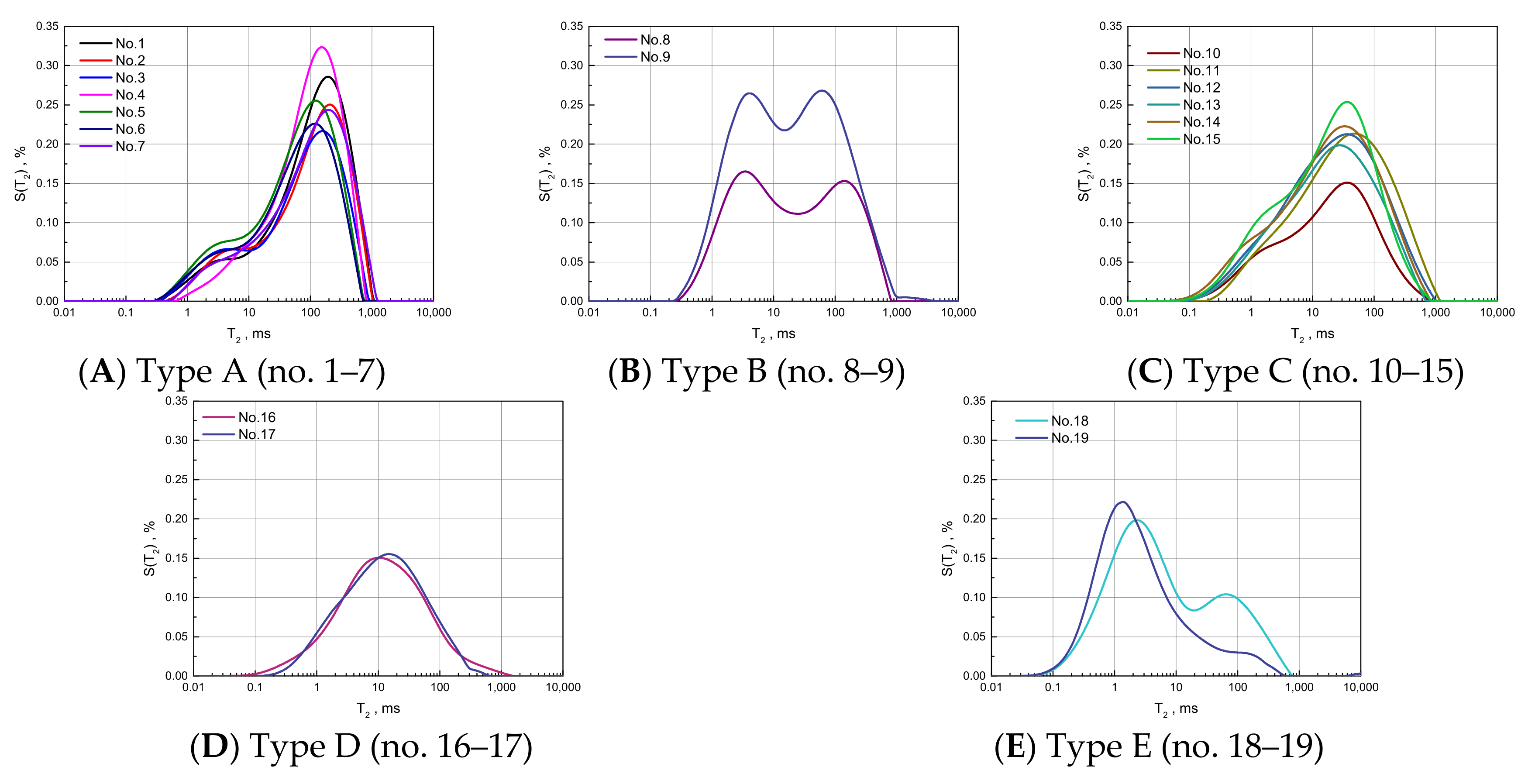
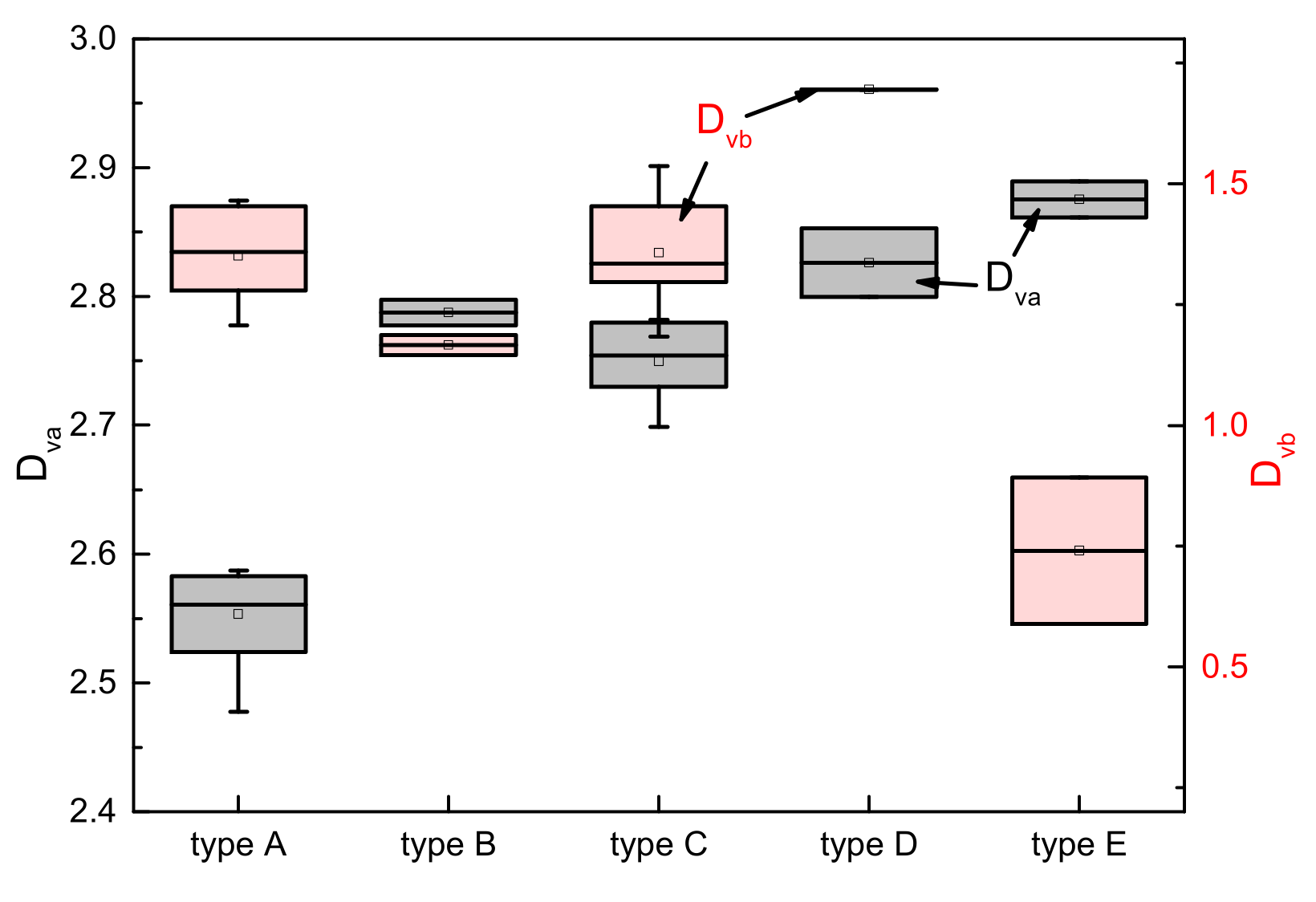


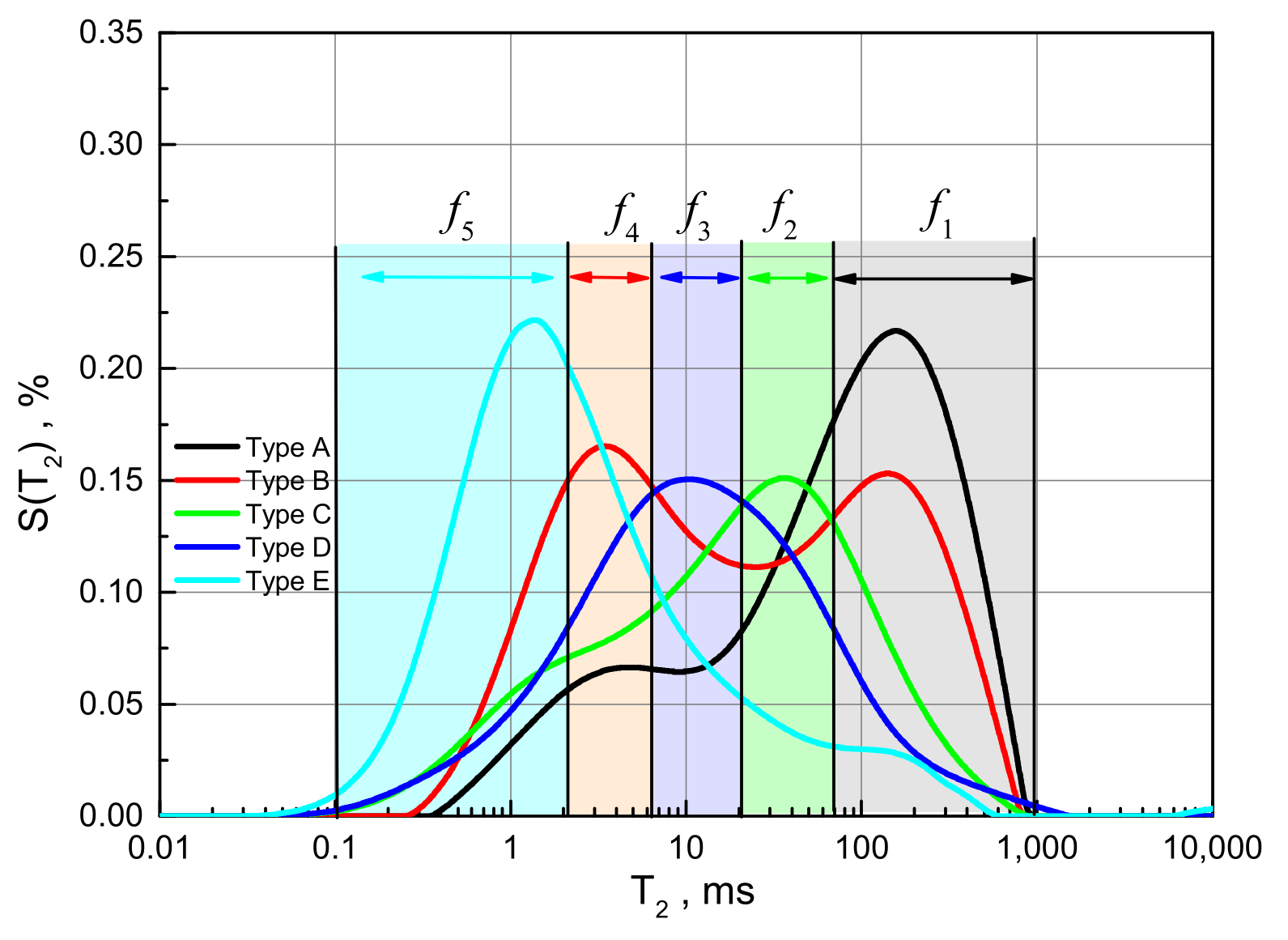

| No. | T2 Curves Morphology | Porosity v/v | Permeability md | Swir v/v | T2cut ms | T2lm ms | Dva | Dvb | f1 v/v | f2 v/v | f3 v/v | f4 v/v | f5 v/v |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | right unimodal pattern (T2 value of peak: 200 ms) | 12.51 | 23.21 | 16.00 | 14.70 | 74.67 | 2.52 | 1.30 | 0.61 | 0.19 | 0.10 | 0.05 | 0.05 |
| 2 | 11.30 | 8.74 | 20.78 | 22.59 | 70.64 | 2.56 | 1.21 | 0.60 | 0.18 | 0.12 | 0.06 | 0.04 | |
| 3 | 10.90 | 4.49 | 25.49 | 14.85 | 52.22 | 2.58 | 1.45 | 0.55 | 0.20 | 0.12 | 0.07 | 0.06 | |
| 4 | 13.90 | 31.13 | 16.72 | 19.71 | 77.62 | 2.48 | 1.28 | 0.64 | 0.21 | 0.11 | 0.03 | 0.01 | |
| 5 | 11.20 | 7.03 | 26.21 | 13.66 | 44.08 | 2.59 | 1.36 | 0.43 | 0.27 | 0.15 | 0.08 | 0.07 | |
| 6 | 11.30 | 6.81 | 26.37 | 17.43 | 43.63 | 2.58 | 1.46 | 0.49 | 0.24 | 0.14 | 0.07 | 0.06 | |
| 7 | 12.00 | 14.49 | 19.51 | 16.37 | 73.55 | 2.56 | 1.40 | 0.61 | 0.19 | 0.12 | 0.05 | 0.04 | |
| Range average value | 10.9–13.9 11.76 | 4.49–31.13 13.7 | 16–26.37 21.58 | 13.66–22.59 17.04 | 43.63–77.62 62.35 | 2.48–2.59 2.55 | 1.21–1.46 1.35 | 0.43–0.64 0.56 | 0.18–0.27 0.21 | 0.1–0.15 0.12 | 0.03–0.08 0.06 | 0.01–0.07 0.05 | |
| 8 | balanced bimodal pattern | 13.23 | 1.61 | 46.11 | 13.39 | 17.96 | 2.80 | 1.15 | 0.33 | 0.15 | 0.23 | 0.15 | 0.14 |
| 9 | 12.20 | 1.98 | 49.35 | 10.90 | 18.57 | 2.78 | 1.19 | 0.33 | 0.16 | 0.20 | 0.16 | 0.15 | |
| Range average value | 12.2–13.23 12.72 | 1.61–1.98 1.79 | 46.11–49.35 47.73 | 10.9–13.39 12.15 | 17.96–18.57 18.27 | 2.78–2.80 2.79 | 1.15–1.19 1.17 | 0.33–0.33 0.33 | 0.15–0.16 0.155 | 0.2–0.23 0.215 | 0.15–0.16 0.155 | 0.14–0.15 0.145 | |
| 10 | right unimodal pattern (T2 value of peak: 30 ms) | 8.06 | 0.49 | 50.52 | 17.48 | 15.40 | 2.70 | 1.30 | 0.15 | 0.31 | 0.26 | 0.12 | 0.17 |
| 11 | 14.10 | 2.49 | 44.17 | 23.98 | 27.89 | 2.73 | 1.54 | 0.36 | 0.25 | 0.21 | 0.09 | 0.09 | |
| 12 | 14.70 | 1.00 | 48.36 | 19.57 | 18.85 | 2.75 | 1.35 | 0.31 | 0.24 | 0.23 | 0.10 | 0.12 | |
| 13 | 13.10 | 0.69 | 45.92 | 14.31 | 16.97 | 2.76 | 1.18 | 0.28 | 0.25 | 0.24 | 0.11 | 0.13 | |
| 14 | 14.80 | 0.66 | 55.01 | 21.27 | 16.66 | 2.78 | 1.45 | 0.28 | 0.25 | 0.23 | 0.09 | 0.15 | |
| 15 | 15.30 | 1.09 | 48.98 | 16.22 | 15.40 | 2.78 | 1.32 | 0.25 | 0.27 | 0.23 | 0.10 | 0.15 | |
| Range average value | 8.6–15.3 13.34 | 0.49–2.49 1.07 | 44.17–55.01 48.83 | 14.31–23.98 18.81 | 15.4–27.89 18.52 | 2.70–2.78 2.75 | 1.18–1.54 1.36 | 0.15–0.36 0.27 | 0.24–0.31 0.26 | 0.21–0.26 0.23 | 0.09–0.12 0.1 | 0.09–0.17 0.13 | |
| 16 | balanced unimodal pattern (T2 value of peak: 10 ms) | 5.70 | 0.31 | 62.75 | 18.19 | 11.67 | 2.80 | 1.70 | 0.17 | 0.19 | 0.34 | 0.15 | 0.15 |
| 17 | 8.90 | 0.22 | 58.64 | 15.81 | 11.20 | 2.85 | 1.69 | 0.17 | 0.22 | 0.31 | 0.15 | 0.15 | |
| Range average value | 5.7–8.9 7.3 | 0.22–0.31 0.27 | 58.64–62.75 60.7 | 15.81–18.19 17 | 11.2–11.67 11.43 | 2.80–2.85 2.83 | 1.69–1.70 1.69 | 0.17–0.17 0.17 | 0.19–0.22 0.21 | 0.31–0.34 0.325 | 0.15–0.15 0.15 | 0.15–0.15 0.15 | |
| 18 | left bimodal pattern | 8.75 | 0.15 | 58.72 | 2.58 | 2.69 | 2.89 | 0.59 | 0.28 | 0.05 | 0.12 | 0.15 | 0.41 |
| 19 | 12.50 | 0.20 | 54.60 | 4.52 | 6.55 | 2.86 | 0.89 | 0.20 | 0.13 | 0.17 | 0.18 | 0.32 | |
| Range average value | 8.75–12.5 10.63 | 0.15–0.20 0.18 | 54.6–58.72 56.66 | 2.58–4.52 3.55 | 2.69–6.55 4.62 | 2.86–2.89 2.88 | 0.59–0.89 0.74 | 0.2–0.28 0.24 | 0.05–0.13 0.09 | 0.12–0.17 0.14 | 0.15–0.18 0.16 | 0.41–0.32 0.36 | |
| No | Sw | T2lm | Dva | Dvb | ΔDva | No | Sw | T2lm | Dva | Dvb | ΔDva |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 100.00 | 74.67 | 2.52 | 1.30 | 0.00 | 10 | 100.00 | 15.40 | 2.70 | 1.30 | 0.00 |
| 48.75 | 25.88 | 2.73 | 1.38 | 0.21 | 93.49 | 13.86 | 2.70 | 1.39 | 0.00 | ||
| 29.67 | 10.08 | 2.81 | 1.30 | 0.29 | 77.48 | 9.18 | 2.75 | 1.24 | 0.05 | ||
| 18.56 | 4.90 | 2.94 | 1.38 | 0.42 | 54.70 | 4.90 | 2.90 | 1.28 | 0.20 | ||
| 16.00 | 3.60 | 2.97 | 1.23 | 0.44 | 50.52 | 4.25 | 2.93 | 1.21 | 0.23 | ||
| 2 | 100.00 | 70.64 | 2.56 | 1.21 | 0.00 | 11 | 100.00 | 27.89 | 2.73 | 1.54 | 0.00 |
| 58.08 | 31.57 | 2.73 | 1.38 | 0.17 | 89.04 | 22.11 | 2.75 | 1.49 | 0.02 | ||
| 34.31 | 9.82 | 2.87 | 1.36 | 0.31 | 59.55 | 9.39 | 2.86 | 1.42 | 0.13 | ||
| 22.10 | 6.08 | 2.94 | 1.28 | 0.38 | 44.17 | 4.94 | 2.92 | 1.38 | 0.19 | ||
| 20.78 | 4.74 | 2.96 | 1.15 | 0.40 | 12 | 100.00 | 18.85 | 2.75 | 1.35 | 0.00 | |
| 3 | 100.00 | 52.22 | 2.58 | 1.45 | 0.00 | 93.46 | 17.33 | 2.77 | 1.46 | 0.02 | |
| 69.00 | 38.75 | 2.68 | 1.59 | 0.10 | 71.52 | 8.60 | 2.83 | 1.27 | 0.09 | ||
| 40.66 | 10.13 | 2.79 | 1.28 | 0.21 | 55.14 | 5.86 | 2.96 | 1.50 | 0.21 | ||
| 26.55 | 5.58 | 2.95 | 1.18 | 0.37 | 48.36 | 4.12 | 2.96 | 1.62 | 0.22 | ||
| 25.49 | 4.48 | 2.95 | 1.14 | 0.37 | 13 | 100.00 | 16.97 | 2.76 | 1.18 | 0.00 | |
| 4 | 100.00 | 77.62 | 2.48 | 1.28 | 0.00 | 94.66 | 15.28 | 2.78 | 1.52 | 0.02 | |
| 46.61 | 28.15 | 2.74 | 1.22 | 0.27 | 73.95 | 9.95 | 2.85 | 1.11 | 0.09 | ||
| 28.11 | 12.88 | 2.83 | 1.17 | 0.35 | 51.64 | 4.72 | 2.96 | 1.44 | 0.20 | ||
| 18.32 | 7.52 | 2.96 | 1.05 | 0.48 | 45.92 | 3.41 | 2.97 | 1.10 | 0.21 | ||
| 16.72 | 6.34 | 2.98 | 1.34 | 0.50 | 14 | 100.00 | 16.66 | 2.81 | 1.45 | 0.00 | |
| 5 | 100.00 | 44.08 | 2.59 | 1.36 | 0.00 | 94.67 | 16.12 | 2.81 | 1.62 | 0.00 | |
| 68.41 | 26.51 | 2.70 | 1.22 | 0.11 | 79.11 | 10.57 | 2.89 | 1.56 | 0.08 | ||
| 40.90 | 9.60 | 2.83 | 1.29 | 0.24 | 61.14 | 5.35 | 2.97 | 1.43 | 0.16 | ||
| 29.71 | 6.54 | 2.94 | 1.33 | 0.35 | 55.01 | 4.32 | 2.98 | 1.49 | 0.18 | ||
| 26.21 | 5.32 | 2.95 | 1.40 | 0.36 | 15 | 100.00 | 15.40 | 2.78 | 1.32 | 0.00 | |
| 6 | 100.00 | 43.63 | 2.58 | 1.46 | 0.00 | 93.39 | 13.86 | 2.78 | 1.43 | 0.00 | |
| 69.91 | 22.94 | 2.72 | 1.31 | 0.14 | 71.08 | 9.18 | 2.85 | 1.31 | 0.07 | ||
| 41.15 | 9.46 | 2.88 | 1.41 | 0.30 | 53.60 | 4.90 | 2.95 | 1.32 | 0.16 | ||
| 30.44 | 5.62 | 2.95 | 1.40 | 0.36 | 48.98 | 4.25 | 2.96 | 1.23 | 0.18 | ||
| 26.37 | 4.85 | 2.96 | 1.52 | 0.38 | 17 | 100.00 | 11.20 | 2.85 | 1.69 | 0.00 | |
| 7 | 100.00 | 73.55 | 2.56 | 1.40 | 0.00 | 89.70 | 8.79 | 2.88 | 1.45 | 0.02 | |
| 60.01 | 34.41 | 2.69 | 1.31 | 0.13 | 84.80 | 7.82 | 2.89 | 1.48 | 0.04 | ||
| 22.44 | 6.67 | 2.90 | 1.10 | 0.34 | 64.74 | 4.88 | 2.97 | 1.30 | 0.12 | ||
| 19.51 | 5.32 | 2.95 | 1.34 | 0.40 | 58.64 | 3.79 | 2.98 | 1.39 | 0.13 | ||
| 9 | 100.00 | 18.57 | 2.78 | 1.19 | 0.00 | 19 | 100.00 | 6.55 | 2.86 | 0.89 | 0.00 |
| 82.37 | 12.66 | 2.84 | 1.26 | 0.06 | 95.26 | 5.95 | 2.87 | 0.86 | 0.01 | ||
| 64.92 | 6.62 | 2.91 | 1.26 | 0.13 | 87.57 | 4.74 | 2.89 | 0.80 | 0.03 | ||
| 51.24 | 3.73 | 2.97 | 1.13 | 0.19 | 56.65 | 1.60 | 2.98 | 0.80 | 0.12 | ||
| 49.35 | 3.36 | 2.97 | 1.03 | 0.19 | 54.60 | 1.55 | 2.97 | 0.83 | 0.11 |
| Layer | RT (ohm.m) | POR (%) | PERM (md) | Sw_Archie (v/v) | Swir_nmr (v/v) | SW_T2 (v/v) | Dva0 | Dvb | Dva | Type | Production |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 38 | 10.1 | 0.34 | 0.65 | 0.64 | 0.89 | 2.649 | 1.254 | 2.663 | II | -- |
| 2 | 16 | 4.3 | 0.03 | 1 | 0.76 | 0.91 | 2.804 | 2.069 | 2.846 | III/IV | -- |
| 3 | 31 | 11.2 | 0.87 | 0.69 | 0.55 | 0.58 | 2.594 | 0.875 | 2.733 | I/III | -- |
| 4 | 30 | 13.2 | 1.6 | 0.6 | 0.37 | 0.48 | 2.429 | 0.954 | 2.638 | I/II | |
| 5 | 41 | 10.7 | 0.45 | 0.65 | 0.41 | 0.51 | 2.558 | 1.104 | 2.699 | I/II/IV | Gas 1.1 × 104 m3, no water |
| 6 | 31 | 10.2 | 0.22 | 0.64 | 0.5 | 0.53 | 2.646 | 2.288 | 2.702 | I/II | |
| 7 | 36 | 7.7 | 0.08 | 0.71 | 0.91 | 0.97 | 2.863 | 1.763 | 2.966 | IV/V | -- |
| 8 | 31 | 6.5 | 0.01 | 1 | 0.8 | 0.83 | 2.75 | 1.085 | 2.797 | IV/V | -- |
| 9 | 10 | 7.3 | 0.05 | 1 | 0.9 | 0.82 | 2.86 | 0.29 | 2.89 | V | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Yin, Q.; Zeng, J.; Wang, G.; Feng, C.; Zhang, P. Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal Fract. 2023, 7, 273. https://doi.org/10.3390/fractalfract7030273
Xie W, Yin Q, Zeng J, Wang G, Feng C, Zhang P. Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal and Fractional. 2023; 7(3):273. https://doi.org/10.3390/fractalfract7030273
Chicago/Turabian StyleXie, Weibiao, Qiuli Yin, Jingbo Zeng, Guiwen Wang, Cheng Feng, and Pan Zhang. 2023. "Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag" Fractal and Fractional 7, no. 3: 273. https://doi.org/10.3390/fractalfract7030273
APA StyleXie, W., Yin, Q., Zeng, J., Wang, G., Feng, C., & Zhang, P. (2023). Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal and Fractional, 7(3), 273. https://doi.org/10.3390/fractalfract7030273







