On Exact Solutions of Some Space–Time Fractional Differential Equations with M-truncated Derivative

Abstract

In this study, the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$ method is used to investigate the space–time fractional Burger-like equation and the space–time-coupled Boussinesq equation with M-truncated derivative, which have an important place in fluid dynamics. This method is efficient and produces soliton solutions. A symbolic computation program called Maple was used to implement the method in a dependable and effective way. There are also a few graphs provided for the solutions. Using the suggested method to solve these equations, we have provided many new exact solutions that are distinct from those previously found. By offering insightful explanations of many nonlinear systems, the study’s findings add to the body of literature. The results revealed that the suggested method is a valuable mathematical tool and that using a symbolic computation program makes these tasks simpler, more dependable, and quicker. It is worth noting that it may be used for a wide range of nonlinear evolution problems in mathematical physics. The study’s findings may have an influence on how different physical problems are interpreted.

1. Introduction

The use of nonlinear partial differential equations (NPDEs) is crucial in many disciplines, including physics, mathematics, fluid dynamics, and engineering sciences. Owing to NPDEs, numerous real-world problems have been modeled. To find exact solutions to NPDEs, a wide variety of effective mathematical techniques have been used [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Another new area that has gained interest during the past several decades is fractional calculus. Fractional differential equations (FDEs) have made many scientific phenomena, including viscoelasticity, plasma, solid mechanics, optical fibers, signal processing, electromagnetic waves, fluid dynamics, biomedical sciences, and diffusion processes, easily solvable. By employing a variety of methods to get exact solutions of FDE, researchers have improved the attractiveness of these equations. The ${\mathrm{G}}^{\prime }/{\mathrm{G}}^2$-expansion method [15,16], ansatz and Kudryashov method [17], the improved extended tanh-coth method [18], the first integral method [19], the exp-function method [20], the F-expansion method [21], the improved subequation method [22,23], and the functional variable method [24] are a few of these methods of note.

Burger’s equation has acoustic applications and has been implemented to model turbulence and some steady-state viscous flows. Moreover, it is also used in the mathematical modeling of fluid dynamics, nonlinear acoustic gas dynamics, traffic flow, shock wave theory, and turbulence problems. In the literature, Burger’s equation is presented in a number of different ways, including coupled Boussinesq Burger equations, Burger-like equations, viscous Burger equations, and inviscid Burger equations. The fractional coupled viscous Burgers equations have recently been the subject of a number of intriguing studies [25,26]. The tanh method was employed by Bulut et al. [27] to produce several solutions to this equation. Gencoglu [28] acquired complicated answers for it via a direct algebraic method. Eskandari and Taghizadeh discussed the exact solutions of the nonlinear space–time fractional Burger-like equation using the expfunction method [29].

The first model for nonlinear, dispersive wave propagation may be thought to be the Boussinesq type equations, which describe surface water waves with a horizontal scale significantly bigger than the water depth [30]. In mathematical physics, they might be considered a crucial class of fractional differential equations. To solve Boussinesq equations analytically and numerically, many methods have recently been employed. These include the exp-function method [31], the invariant subspace method [32], and the expansion method, a recently developed technique [33]. Equations of this type are also a crucial nonlinear model that may be found in physics, hydromechanics, and optics. Additionally, it is understood that it may be utilized to characterize the actual direction of wave propagation in plasma and nonlinear waves [34,35,36,37,38]. In shallow water waves for bilayer fluid flow, coupled Boussinesq equations appear. This occurs when a ship unintentionally spills oil, causing an oil slick to float above the water slide [39].

In this study, exact solutions of the space–time fractional Burger-like equation and the space–time coupled Boussinesq equation were investigated using the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$ method, which has never been discussed before. For this purpose, the recently studied M-truncated derivative in fractional derivative studies, which is different from other fractional derivatives, was used. In addition, the method mentioned has not been previously used in the solution of these equations. Therefore, we emphasize that these are novel results.

This work is broken into five sections. Section 1 outlines fractional calculations and includes a brief discussion of nonlinear partial and fractional differential equations. The Burger’s equation and the Boussinesq type equations, which form the basis of this work, are also discussed. Section 2 discusses the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$ method, which is an essential way for solving the problem, as well as M-truncated derivative theory. Section 3 analyzes the use of this method to obtain exact solutions to the space–time fractional Burger-Like equation and the space–time coupled Boussinesq equation. The explanations of the graphics of the solutions and the effect of the method on the results are given in Section 4. Section 5 provides an explanation of the results.

2. The Fundamental Concepts of the M-truncated Derivative and Algorithm of the Extended G${}^{\prime }$/G Method

2.1. The Basic Concepts of the M-Truncated Derivative

Some fundamental fractional calculus principles that have been employed in this study are presented in this section. These are M-truncated derivative and its features.

Definition 1. 

Assume $h:(0,\infty )\to \mathbb{R}$. For $0<\omega <1$, the truncated M-fractional derivative of $h\left(\theta \right)$ of order ω has been defined by [40] as follows:

$${}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{h\left(\theta \right)\right\}=\underset{\epsilon \to 0}{lim}\frac{h\left[\theta {}_j{\mathrm{E}}_{\delta }\left(ϵ{\theta }^{-\omega }\right)\right]-h\left(\theta \right)}{ϵ},\theta >0,$$

(1)

where ${}_j{\mathrm{E}}_{\delta }(.)$ is a truncated Mittag-Leffler function of one parameter, defined as follows:

$${}_j{\mathrm{E}}_{\delta }\left(v\right)=\sum _{i=0}^j\frac{v^i}{\mathsf{\Gamma }(\delta i+1)},\delta >0,v\in \mathbb{C}.$$

(2)

Theorem  1. 

Functions $f_1\left(\theta \right)$ and $f_2\left(\theta \right)$, which are ω-derivable with $0<\omega \le 1$ and $\delta >0$ at a point $\theta >0$, satisfy the following properties [40,41]:

• ${}_j{\mathcal{T}}_M^{\omega ,\delta }\{a_1{f}_1\left(\theta \right)+a_2{f}_2\left(\theta \right)\}=a_1{}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_1\left(\theta \right)\right\}+a_2{}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_2\left(\theta \right)\right\}$, $\forall a_1,a_2\in \mathbb{R}$,
• ${}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_1\left(\theta \right)f_2\left(\theta \right)\right\}=f_2{\left(\theta \right)}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_1\left(\theta \right)\right\}+f_1{\left(\theta \right)}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_2\left(\theta \right)\right\}$,
• ${}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{\frac{f_1\left(\theta \right)}{f_2\left(\theta \right)}\right\}=\frac{f_2{\left(\theta \right)}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_1\left(\theta \right)\right\}-f_1{\left(\theta \right)}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_2\left(\theta \right)\right\}}{{\left(f_2\left(\theta \right)\right)}^2}$,
• ${}_j{\mathcal{T}}_M^{\omega ,\delta }{\left(\theta \right)}^n=n{\left(\theta \right)}^{n-\omega }$, $n\in \mathbb{R}$,
• If $f_1$ is differentiable, then ${}_j{\mathcal{T}}_M^{\omega ,\delta }\left(f_1\right)\left(\theta \right)=\frac{{\theta }^{1-\omega }}{\mathsf{\Gamma }(\delta +1)}\frac{d{f}_1}{d\theta }$,
• ${}_j{\mathcal{T}}_M^{\omega ,\delta }(f_1\circ f_2)\left(\theta \right)=f_1^{\prime }{\left(f_2\left(\theta \right)\right)}_j{\mathcal{T}}_M^{\omega ,\delta }\left\{f_2\left(\theta \right)\right\}$.

2.2. Description of the Extended G${}^{\prime }$/G Method

In this section, the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$ method, which is applied in [42], is briefly defined. Assume that we have the nonlinear fractional differential equation as follows:

$$F(u,{\mathcal{T}}_{M,t}^{\omega ,\delta }u,{\mathcal{T}}_{M,x}^{\omega ,\delta }u,...)=0,$$

(3)

where ${\mathcal{T}}_{M,t}^{\omega ,\delta }$ and ${\mathcal{T}}_{M,x}^{\omega ,\delta }$ show M-truncated derivative, $u=u(x,t)$ is an unknown function, and F is a polynomial in $u(x,t)$.

• It is first required to transform (3) into an ordinary differential equation using the traveling wave transformation given as follows: [43,44]

  $$\begin{array}{cc}\hfill & u(x,t)=U\left(ϵ\right),\hfill \\ \hfill & ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left(m{x}^{\omega }+k{t}^{\omega }\right),\hfill \end{array}$$

  (4)

  where $\delta >0$, $m\ne 0$ and $k\ne 0$ are arbitrary constants. A nonlinear ordinary differential equation (ODE) as below is obtained, substituting (4) into (3) as follows:

  $$N(U,\frac{dU}{dϵ},\frac{d^{2}U}{d{ϵ}^2},..)=0.$$

  (5)
• It is presumed that the formal solution to (5) is the following:

  $$U\left(ϵ\right)=\sum _{i=-N}^N{a}_i{\left(\frac{G^{\prime }\left(ϵ\right)}{G\left(ϵ\right)}\right)}^i,$$

  (6)

  where $a_i$ is the real constant to be determined, and N is a positive integer that needs to be calculated. The following auxiliary linear ordinary differential equation has a similar solution as the $G\left(ϵ\right)$ function:

  $$G^{\prime \prime }\left(ϵ\right)+\lambda G^{\prime }\left(ϵ\right)+\mu G\left(ϵ\right)=0,$$

  (7)

  where $\lambda$ and $\mu$ are the real constants to be calculated.
• The system of algebraic equations is obtained by using (7) to substitute (6) into (5) and setting all of the coefficients for powers of $\frac{G^{\prime }\left(ϵ\right)}{G\left(ϵ\right)}$ to zero. Using Maple and similar software, this algebraic system can be solved in order to determine the values of the unknown constants $a_i$. Using (5), the value of N may be calculated in the following way, where $deg\left(U\right(ϵ\left)\right)=N$ is the degree of $U\left(ϵ\right)$:

  $$\begin{array}{cc}\hfill & deg\left[\frac{d^{q}U}{d{\epsilon }^q}\right]=N+q,\hfill \\ \hfill & deg\left[U^r{\left(\frac{d^{q}U}{d{\epsilon }^q}\right)}^s\right]=Nr+s(q+N).\hfill \end{array}$$
• The necessary exact solutions can be obtained in the following three cases using the general solution of (7).
  Case 1. If ${\lambda }^2-4\mu >0$, then

  $$\frac{G^{\prime }\left(ϵ\right)}{G\left(ϵ\right)}=-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right),$$

  (8)
  Case 2. If ${\lambda }^2-4\mu <0$, then

  $$\frac{G^{\prime }\left(ϵ\right)}{G\left(ϵ\right)}=-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right),$$

  (9)
  Case 3. If ${\lambda }^2-4\mu =0$, then

  $$\frac{G^{\prime }\left(ϵ\right)}{G\left(ϵ\right)}=-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}.$$

  (10)
  The exact solutions to (5) are obtained, where $A_1$ and $A_2$ are arbitrary constants.

3. Mathematical Analysis

In this section, we employ the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$- expansion method to obtain exact solutions to some nonlinear partial fractional differential equations, including the space–time fractional Burger-like equation and the space–time coupled Boussinesq equation. In fluid dynamics, such equations continue to garner a significant amount of interest.

3.1. The Space–Time Fractional Burger-Like Equation

We investigated the Burger-like equation in [29,45], which is a space–time fractional given below.

$${\mathcal{T}}_{M,t}^{\omega ,\delta }u+{\mathcal{T}}_{M,x}^{\omega ,\delta }u+u{\mathcal{T}}_{M,x}^{\omega ,\delta }u+\frac{1}{2}{\mathcal{T}}_{M,x}^{\omega ,\delta }{\mathcal{T}}_{M,x}^{\omega ,\delta }u=0,$$

(11)

where $\omega \in (0,1],0<\delta$. By applying the transformation Equation (4) to this equation, the following ordinary differential equation is gained:

$$(k+m)\frac{dU\left(ϵ\right)}{d\left(ϵ\right)}+\frac{m}{2}U\left(ϵ\right)\frac{dU\left(ϵ\right)}{d\left(ϵ\right)}+\frac{m^2}{2}\frac{d^{2}U\left(ϵ\right)}{d{\left(ϵ\right)}^2}=0.$$

(12)

By integrating Equation (12) once and taking constants of integration as zero, the following equation is found:

$$(k+m)U\left(ϵ\right)+\frac{m}{2}U{\left(ϵ\right)}^2+\frac{m^2}{2}\frac{dU\left(ϵ\right)}{d\left(ϵ\right)}=0.$$

(13)

By balancing the terms of $U^2$ and $\frac{dU\left(ϵ\right)}{d\epsilon }$ in Equation (13), we find $N=1$. For $N=1$, the solution arises through us of (6) as follows:

$$U\left(ϵ\right)=a_{-1}{\left(\frac{G^{\prime }}{G}\right)}^{-1}+a_0+a_1\left(\frac{G^{\prime }}{G}\right),$$

(14)

where $a_{-1},a_0$ and $a_1$ are unknown constants.

By substituting (14) using (7) into (13) and setting the coefficients of all powers of $\left(\frac{G^{\prime }}{G}\right)$ to be zero, nonlinear algebraic equations can be obtained. The occuring algebraic system is solved with Maple to find the values of unknown constants.

$$\begin{array}{cccc}\hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-2}\hfill & \hfill :& \frac{m}{2}{a}_{-1}^2+\frac{m^2}{2}\mu a_{-1}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-1}\hfill & \hfill :& (k+m)a_{-1}+m{a}_{-1}{a}_0+\frac{m^2}{2}\lambda a_{-1}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^0\hfill & \hfill :& (k+m)a_0+\frac{m}{2}{a}_0^2+m{a}_{-1}{a}_1+\frac{m^2}{2}{a}_{-1}-\frac{m^2}{2}\mu a_1=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^1\hfill & \hfill :& (k+m)a_1+m{a}_0{a}_1-\frac{m^2}{2}\lambda a_1=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^2\hfill & \hfill :& \frac{m}{2}{a}_1^2-\frac{m^2}{2}{a}_1=0.\hfill \end{array}$$

Solving this system of equations through Maple, we obtain the following results:

Result 1: $k=\frac{-m^2\lambda }{2}-m^2\left(\frac{-\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)-m,a_0=\left(\frac{-\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)m,a_1=0,a_{-1}=-m\mu$,

Result 2: $k=\frac{m^2\lambda }{2}-m^2\left(\frac{\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)-m,a_0=\left(\frac{\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)m,a_1=m,a_{-1}=0$.

The exact solutions to the space–time fractional Burger-Like equation can be obiatained by substituting these results into (14) and taking into account (8)–(10) as follows:

Solution 1:

If ${\lambda }^2-4\mu >0$, the hyperbolic solution is achieved

$$\begin{array}{cc}\hfill & u_1(x,t)=U_{11}\left(ϵ\right)=\left(\frac{-\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)m\hfill \\ \hfill & -m\mu {\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^{-1}.\hfill \end{array}$$

(15)

If ${\lambda }^2-4\mu =0$, then, the rational solution is found

$$\begin{array}{cc}\hfill & u_2(x,t)=U_{13}\left(ϵ\right)=-\frac{\lambda }{2}m-m\mu \left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right).\hfill \end{array}$$

(16)

In (15) and (16), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\frac{-m^2\lambda }{2}-m^2\left(\frac{-\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)-m\right)t^{\omega }\right]$.

Solution 2:

If ${\lambda }^2-4\mu >0$, the hyperbolic solution is obtained

$$\begin{array}{cc}\hfill & u_3(x,t)=U_{21}\left(ϵ\right)=\left(\frac{\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)m\hfill \\ \hfill & +m\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right).\hfill \end{array}$$

(17)

If ${\lambda }^2-4\mu =0$, then, the rational solution is found

$$\begin{array}{cc}\hfill & u_4(x,t)=U_{23}\left(ϵ\right)=m\left(\frac{A_2}{A_1+A_2ϵ}\right).\hfill \end{array}$$

(18)

In (17) and (18), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\frac{m^2\lambda }{2}-m^2\left(\frac{\lambda \mp \sqrt{{\lambda }^2-4\mu }}{2}\right)-m\right)t^{\omega }\right]$.

Figure 1 illustrates the exact solutions of $u(x,t)$ with some particular parameters.

3.2. The Space–Time Fractional Coupled Boussinesq Equation

We examine the space–time fractional coupled Boussinesq equation in [31], which is shown below.

$$\begin{array}{c}{\mathcal{T}}_{M,t}^{\omega ,\delta }u+{\mathcal{T}}_{M,x}^{\omega ,\delta }v=0,\hfill \\ \hfill & {\mathcal{T}}_{M,t}^{\omega ,\delta }v+\gamma {\mathcal{T}}_{M,x}^{\omega ,\delta }\left(u^2\right)-\beta {\mathcal{T}}_{M,x}^{\omega ,\delta }{\mathcal{T}}_{M,x}^{\omega ,\delta }{\mathcal{T}}_{M,x}^{\omega ,\delta }u=0,\hfill \end{array}$$

(19)

where $\omega \in (0,1],0<\delta$. The following ordinary differential equation system is obtained by applying the transformation Equation (4) to above equation for both $u(x,t)$ and $v(x,t)$:

$$\begin{array}{c}k\frac{dU\left(ϵ\right)}{d\left(ϵ\right)}+m\frac{dV\left(ϵ\right)}{d\left(ϵ\right)}=0,\hfill \\ k\frac{dV\left(ϵ\right)}{d\left(ϵ\right)}+\gamma m\frac{d}{d\left(ϵ\right)}\left(U^2\right)-\beta m^3\frac{d^{3}U\left(ϵ\right)}{d{\left(ϵ\right)}^3}=0.\hfill \end{array}$$

(20)

The following system is produced by once-integrating Equation (20) and setting the integration constants to zero:

$$\begin{array}{c}kU+mV=0,\hfill \\ kV+\gamma m{U}^2-\beta m^3\frac{d^{2}U\left(ϵ\right)}{d{\left(ϵ\right)}^2}=0.\hfill \end{array}$$

(21)

From the first equation of Equation (20), we can obtain the following:

$$V=-\frac{k}{m}U.$$

(22)

Substituting Equation (22) into the second equation of Equation (21), we obtain the following differential equation to find the solution of the system:

$$-\frac{k^2}{m}U\left(ϵ\right)+\gamma mU{\left(ϵ\right)}^2-\beta m^3\frac{d^{2}U\left(ϵ\right)}{d{\left(ϵ\right)}^2}=0.$$

(23)

Balancing the terms of $U^2$ and $\frac{d^{2}U\left(ϵ\right)}{d{\epsilon }^2}$ in Equation (21), we obtain $N=2$. For $N=2$, the solution arise with use of (6) as follows:

$$U\left(ϵ\right)=a_{-2}{\left(\frac{G^{\prime }}{G}\right)}^{-2}+a_{-1}{\left(\frac{G^{\prime }}{G}\right)}^{-1}+a_0+a_1\left(\frac{G^{\prime }}{G}\right)+a_2{\left(\frac{G^{\prime }}{G}\right)}^2,$$

(24)

where $a_{-2},a_{-1},a_0,a_1$ and $a_2$ are unknown constants.

Substituting (24) using (7) into (23), we produce nonlinear algebraic equations by setting the coefficients of all powers of $\left(\frac{G^{\prime }}{G}\right)$ to zero. The Maple program is used to solve the arising algebraic system and determine the values of the unidentified constants.

$$\begin{array}{cccc}\hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-4}\hfill & \hfill :& \gamma m^2{a}_{-2}^2-6\beta {\mu }^2{m}^4{a}_{-2}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-3}\hfill & \hfill :& 2\gamma m^2{a}_{-2}{a}_{-1}-10\beta \lambda \mu m^4{a}_{-2}-2\beta {\mu }^2{m}^4{a}_{-1}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-2}\hfill & \hfill :& -k^{2}m{a}_{-2}+\gamma m^2{a}_{-1}^2+2\gamma m^2{a}_{-2}{a}_0-\beta (4{\lambda }^2+8\mu )m^4{a}_{-2}-3\beta \lambda \mu m^4{a}_{-1}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^{-1}\hfill & \hfill :& -k^{2}m{a}_{-1}+2\gamma m^2{a}_{-2}{a}_{-1}+2\gamma m^2{a}_{-1}{a}_0-6\beta \lambda m^4{a}_{-2}-\beta ({\lambda }^2+2\mu )m^4{a}_{-1}=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^0\hfill & \hfill :& -k^{2}m{a}_0+\gamma m^2{a}_0^2+2\gamma m^2{a}_{-2}{a}_2+2\gamma m^2{a}_{-1}{a}_1-2\beta m^4{a}_{-2}-\beta \lambda m^4{a}_{-1}\hfill \\ \hfill & \hfill & & -\beta \lambda \mu m^4{a}_1-2\beta {\mu }^2{m}^4{a}_2=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^1\hfill & \hfill :& -k^{2}m{a}_1+2\gamma m^2{a}_0{a}_1+2\gamma m^2{a}_{-1}{a}_2-6\beta \lambda \mu m^4{a}_2-\beta ({\lambda }^2+2\mu )m^4{a}_1=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^2\hfill & \hfill :& -k^{2}m{a}_2+\gamma m^2{a}_1^2+2\gamma m^2{a}_0{a}_2-\beta (4{\lambda }^2+8\mu )m^4{a}_2-3\beta \lambda m^4{a}_1=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^3\hfill & \hfill :& 2\gamma m^2{a}_1{a}_2-10\beta \lambda m^4{a}_2-2\beta m^4{a}_1=0,\hfill \\ \hfill & {\left(\frac{G^{\prime }}{G}\right)}^4\hfill & \hfill :& \gamma m^2{a}_2^2-6\beta m^4{a}_2=0.\hfill \end{array}$$

The results of solving this system of equations using Maple are as follows:

Result 1: $k=\mp m\sqrt{\beta m(-{\lambda }^2+4\mu )},a_0=\frac{6\beta \mu m^2}{\gamma },a_1=\frac{6\beta \lambda m^2}{\gamma },a_2=\frac{6\beta m^2}{\gamma },a_{-1}=a_{-2}=0$,

Result 2: $k=\mp m\sqrt{\beta m({\lambda }^2-4\mu )},a_0=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma },a_1=\frac{6\beta \lambda m^2}{\gamma },a_2=\frac{6\beta m^2}{\gamma },a_{-1}=a_{-2}=0$,

Result 3: $k=\mp m\sqrt{\beta m(-{\lambda }^2+4\mu )},a_{-2}=\frac{6\beta {\mu }^2{m}^2}{\gamma },a_{-1}=\frac{6\beta \lambda \mu m^2}{\gamma },a_0=\frac{6\beta \mu m^2}{\gamma },a_1=a_2=0$,

Result 4: $k=\mp m\sqrt{\beta m({\lambda }^2-4\mu )},a_{-2}=\frac{6\beta {\mu }^2{m}^2}{\gamma },a_{-1}=\frac{6\beta \lambda \mu m^2}{\gamma },a_0=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma },a_1=a_2=0$

By entering these results into (24) and taking into consideration (8)–(10), we can obtain the space–time fractional coupled Boussinesq equation’s exact solutions as follows:

Solution 1:

If ${\lambda }^2-4\mu <0$, the trigonometric solution is acquired

$$\begin{array}{cc}\hfill & u_1(x,t)=U_{12}\left(ϵ\right)=\frac{6\beta \mu m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^2.\hfill \end{array}$$

(25)

From Equation (22),

$$\begin{array}{cc}\hfill & v_1(x,t)=-\frac{k}{m}[\frac{6\beta \mu m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^2].\hfill \end{array}$$

(26)

If ${\lambda }^2-4\mu =0$, then the rational solution is found

$$\begin{array}{cc}\hfill & u_2(x,t)=U_{13}\left(ϵ\right)=\frac{6\beta \mu m^2}{\gamma }+\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^2.\hfill \end{array}$$

(27)

From Equation (22),

$$\begin{array}{cc}\hfill & v_2(x,t)=-\frac{k}{m}[\frac{6\beta \mu m^2}{\gamma }+\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^2].\hfill \end{array}$$

(28)

In (25)–(28), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\mp m\sqrt{\beta m(-{\lambda }^2+4\mu )}\right)t^{\omega }\right]$.

Figure 2 and Figure 3 show the exact solutions of $u(x,t)$ and $v(x,t)$ with some particular parameters.

Solution 2:

If ${\lambda }^2-4\mu >0$, the hyperbolic solution is found

$$\begin{array}{cc}\hfill & u_3(x,t)=U_{21}\left(ϵ\right)=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^2.\hfill \end{array}$$

(29)

From Equation (22),

$$\begin{array}{cc}\hfill & v_3(x,t)=-\frac{k}{m}[\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^2].\hfill \end{array}$$

(30)

If ${\lambda }^2-4\mu =0$, then the rational solution is found

$$\begin{array}{cc}\hfill & u_4(x,t)=U_{23}\left(ϵ\right)=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }+\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^2.\hfill \end{array}$$

(31)

From Equation (22),

$$\begin{array}{cc}\hfill & v_4(x,t)=-\frac{k}{m}[\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }+\frac{6\beta \lambda m^2}{\gamma }\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)\hfill \\ \hfill & +\frac{6\beta m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^2].\hfill \end{array}$$

(32)

In (29)–(32), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\mp m\sqrt{\beta m({\lambda }^2-4\mu )}\right)t^{\omega }\right]$.

Solution 3:

If ${\lambda }^2-4\mu <0$, the trigonometric solution is acquired

$$\begin{array}{cc}\hfill & u_5(x,t)=U_{32}\left(ϵ\right)=\frac{6\beta \mu m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^{-2}.\hfill \end{array}$$

(33)

From Equation (22),

$$\begin{array}{cc}\hfill & v_5(x,t)=-\frac{k}{m}[\frac{6\beta \mu m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}ϵ\right)}\right)\right)}^{-2}].\hfill \end{array}$$

(34)

If ${\lambda }^2-4\mu =0$, then the rational solution is found

$$\begin{array}{cc}\hfill & u_6(x,t)=U_{33}\left(ϵ\right)=\frac{6\beta \mu m^2}{\gamma }+\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-2}.\hfill \end{array}$$

(35)

From Equation (22),

$$\begin{array}{cc}\hfill & v_6(x,t)=-\frac{k}{m}[\frac{6\beta \mu m^2}{\gamma }+\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-2}].\hfill \end{array}$$

(36)

In (33)–(36), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\mp m\sqrt{\beta m(-{\lambda }^2+4\mu )}\right)t^{\omega }\right]$.

Solution 4:

If ${\lambda }^2-4\mu >0$, the hyperbolic solution is achieved

$$\begin{array}{cc}\hfill & u_7(x,t)=U_{41}\left(ϵ\right)=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^{-2}.\hfill \end{array}$$

(37)

From Equation (22),

$$\begin{array}{cc}\hfill & v_7(x,t)=-\frac{k}{m}[\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }\hfill \\ \hfill & +\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}ϵ\right)}\right)\right)}^{-2}].\hfill \end{array}$$

(38)

If ${\lambda }^2-4\mu =0$, then the rational solution is found

$$\begin{array}{cc}\hfill & u_8(x,t)=U_{43}\left(ϵ\right)=\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }+\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-2}.\hfill \end{array}$$

(39)

From Equation (22),

$$\begin{array}{cc}\hfill & v_8(x,t)=-\frac{k}{m}[\frac{\beta ({\lambda }^2+2\mu )m^2}{\gamma }+\frac{6\beta \lambda \mu m^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-1}\hfill \\ \hfill & +\frac{6\beta {\mu }^2{m}^2}{\gamma }{\left(-\frac{\lambda }{2}+\frac{A_2}{A_1+A_2ϵ}\right)}^{-2}].\hfill \end{array}$$

(40)

In (37)–(40), $ϵ=\frac{\mathsf{\Gamma }(\delta +1)}{\omega }\left[m{x}^{\omega }+\left(\mp m\sqrt{\beta m({\lambda }^2-4\mu )}\right)t^{\omega }\right]$.

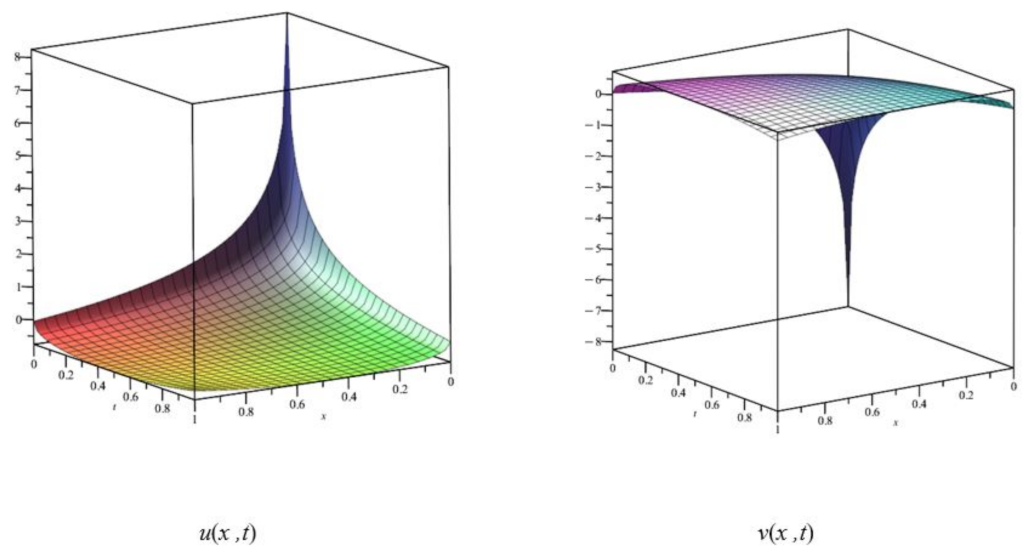
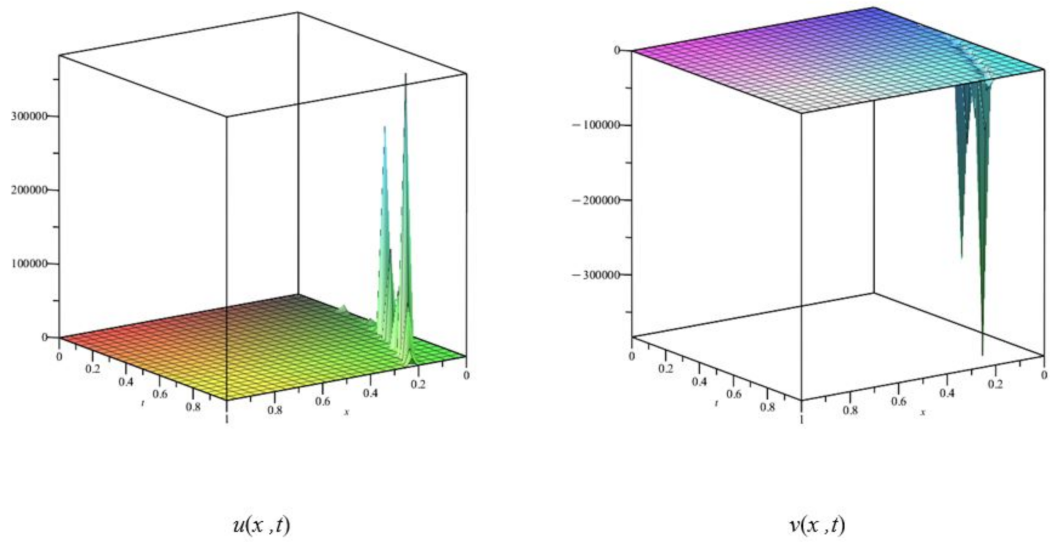
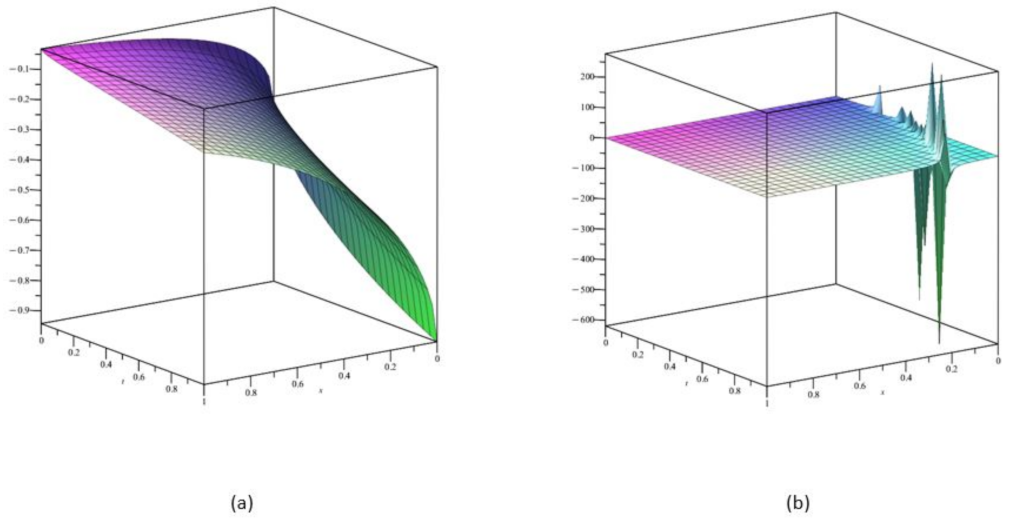
4. Results and Discussions

In this section, from a physical point of view, we discuss the obtained solutions to the space–time fractional Burger-like equation and the space–time coupled Boussinesq equation with the M-truncated time derivative, which are gained using the above-mentioned method. In order to verify the physical meaning of the mathematical models, we implemented several 3D plots and illustrations of the obtained solutions. Moreover, the effect of the fractional derivatives and the method on the solution of equations are mentioned.

Firstly, we plotted Equation (17), and as shown in Figure 1, we demonstrate the appropriate hyperbolic behavior of the obtained analytical solutions. In Figure 1a, the hyperbolic solution of (17) is plotted when $\lambda =2,\mu =0.5,A_1=2,A_2=m=1,\omega =0.5$. In Figure 1b, the real solutions of (17) are plotted when $\lambda =2,\mu =A_1=A_2=m=1,\omega =0.5$.

The plots for Equations (25) and (26) are presented in Figure 2. The trigonometric solution of (25) and (26) are plotted with $\lambda =1,\gamma =6,A_1=A_2=m=\beta =1,\mu =\omega =0.5$.

Finally, the plots for Equations (27) and (28) are presented in Figure 3. The real solution of (27) and (28) are plotted with $\lambda =1,\gamma =6,A_1=A_2=m=\beta =1,\mu =\omega =0.5$.

It has been proven that the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$-method is very useful and efficient and can be used in a wide variety of solutions. Hyperbolic, trigonometric, and rational solutions have clearly emerged with the distinctiveness and restrictive feature of the method. As a result, much newer and clearer solutions have been obtained. Fractional calculus is a new research field that has attracted many researchers, and although many studies have attempted to explain the physical meaning of fractional derivatives, it is still an open problem.

5. Conclusions

In this work, two nonlinear partial fractional differential equations were solved with M-truncated derivative using the extended ${\mathrm{G}}^{\prime }/\mathrm{G}$-method. Many novel exact solutions to the space–time fractional coupled Boussinesq equation and the space–time fractional coupled Burger-like equation were successfully found as applications. The extended ${\mathrm{G}}^{\prime }/\mathrm{G}$-method analysis of the aforementioned models was revealed using a thorough list of various solutions, including trigonometric, hyperbolic, and rational ones. It is important to note that the found solutions are novel since a new fractional derivative was used to explore the model’s new form. The fact that the solutions to the Equations (11) and (19) were obtained utilizing various derivatives and methods makes it clear that our results are original and have not previously been explored in the literature. The fact that the solutions to the equations in [29,31,45] were obtained using various derivatives methods demonstrates additionally attests to the novelty of our results.

The results of this study add to the corpus of literature by offering insightful explanations of several nonlinear systems. The solution described here, to our knowledge, have not been previously attempted. The outcomes also showed that Maple, a symbolic program computing system, simplifies, strengthens, and accelerates the suggested method as a helpful mathematical tool. It is worth considering that the recommended method may be used to solve a variety of nonlinear evolution issues in mathematical physics. The findings of the study may have an impact on how various physical issues are understood.