Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller
Abstract
:1. Introduction
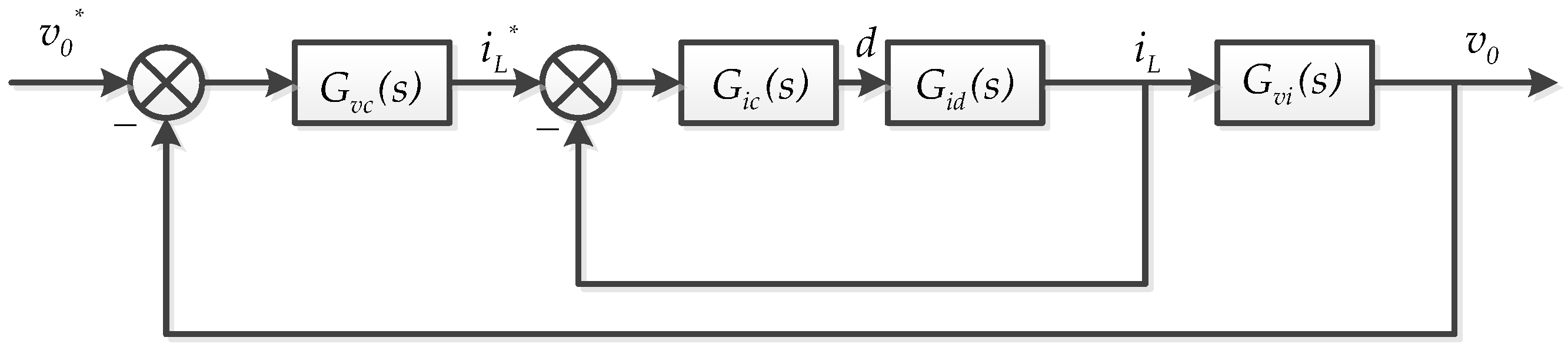
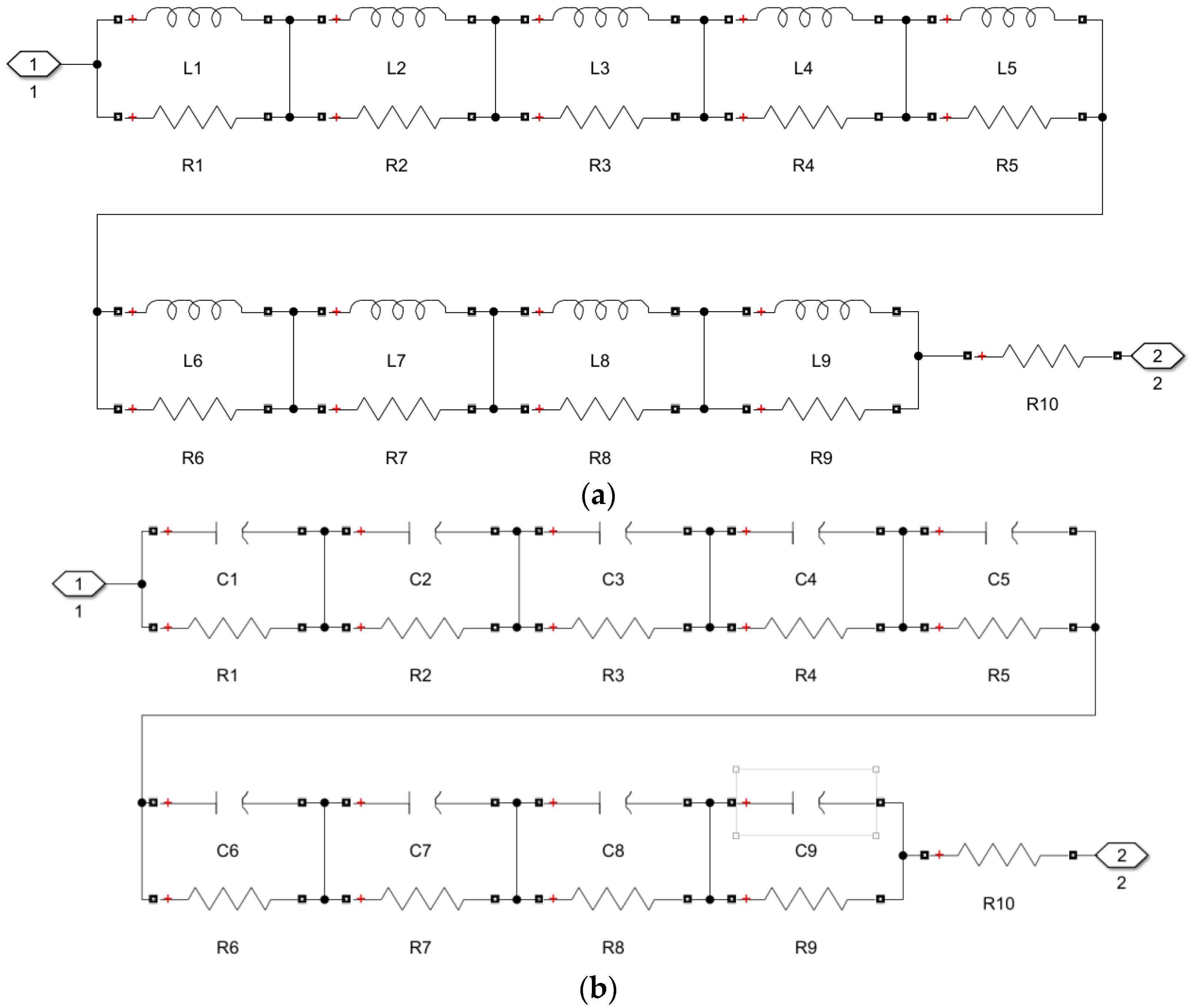
2. State Averaging Model for Fractional-Order Buck-Boost Converters
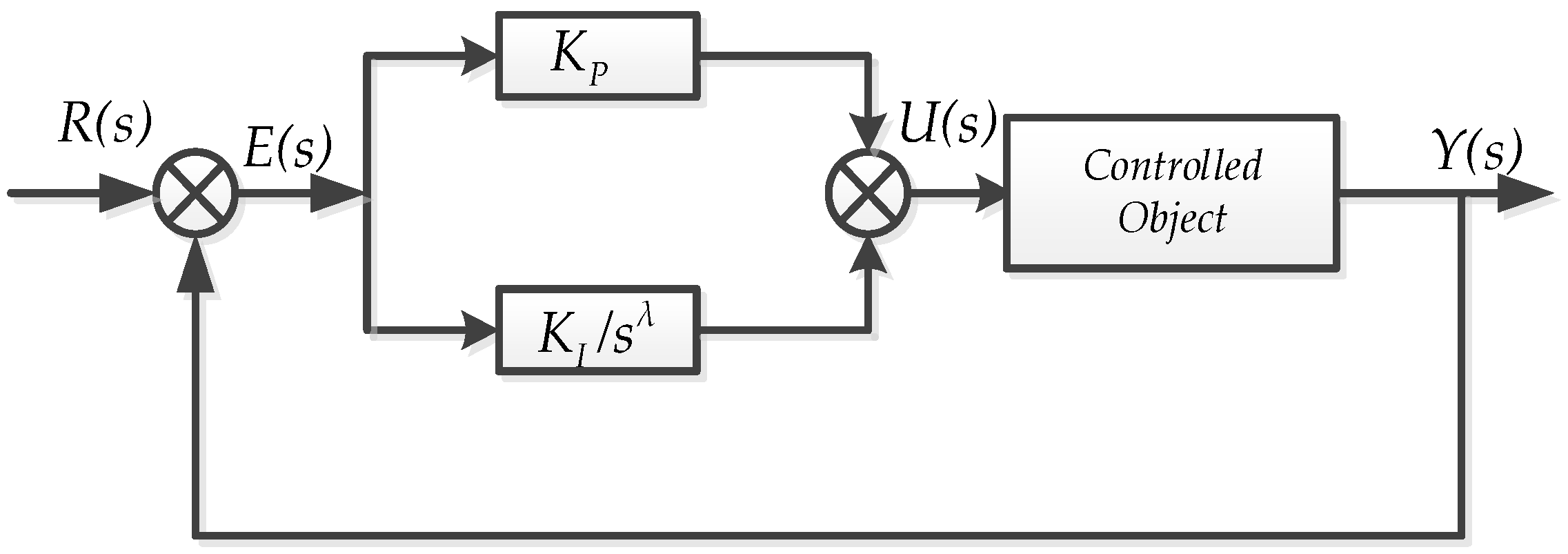
3. Design of Fractional-Order PIλ Controller
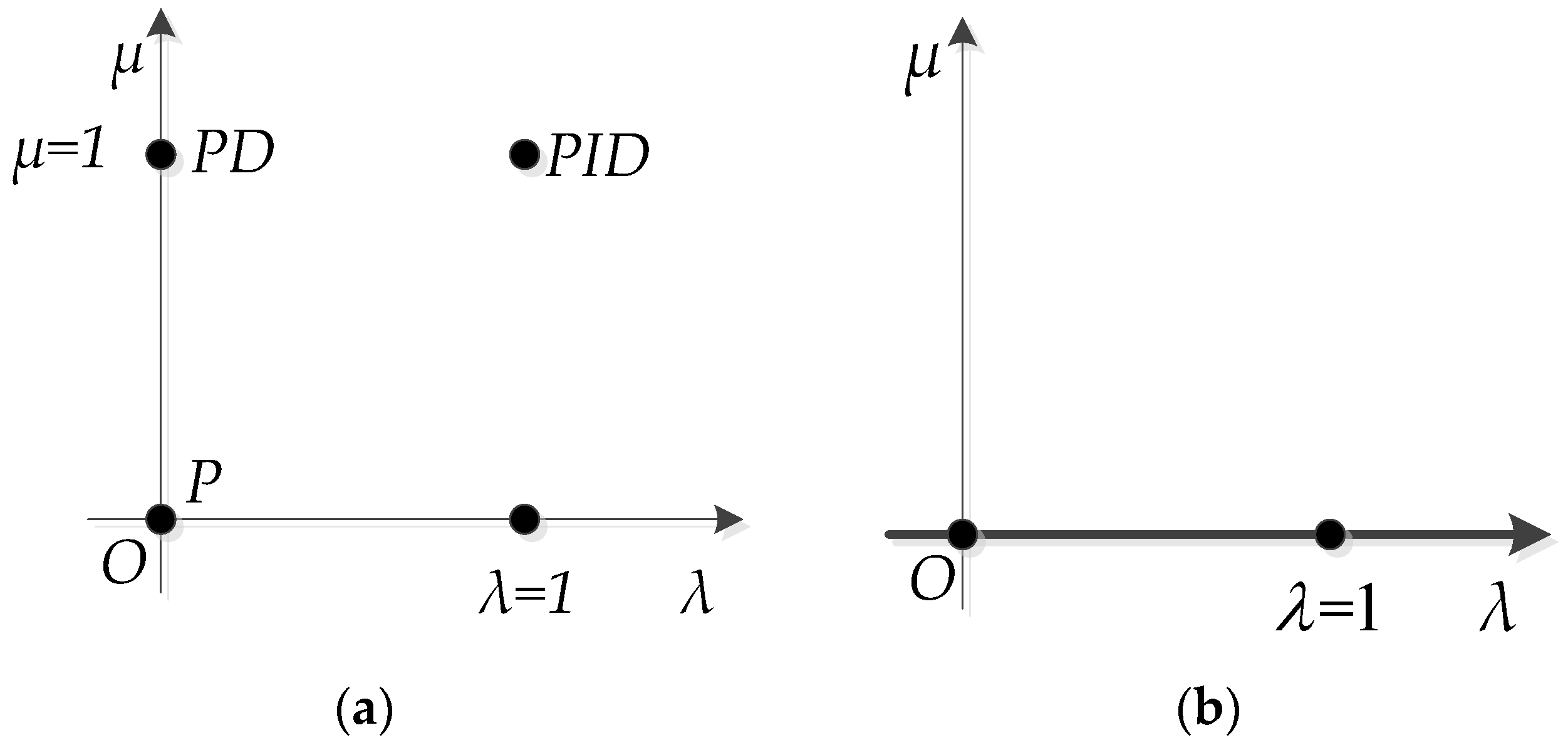
3.1. Introduction to Fractional-Order PIλ Controller
3.2. Design of Fractional-Order PIλ Controller
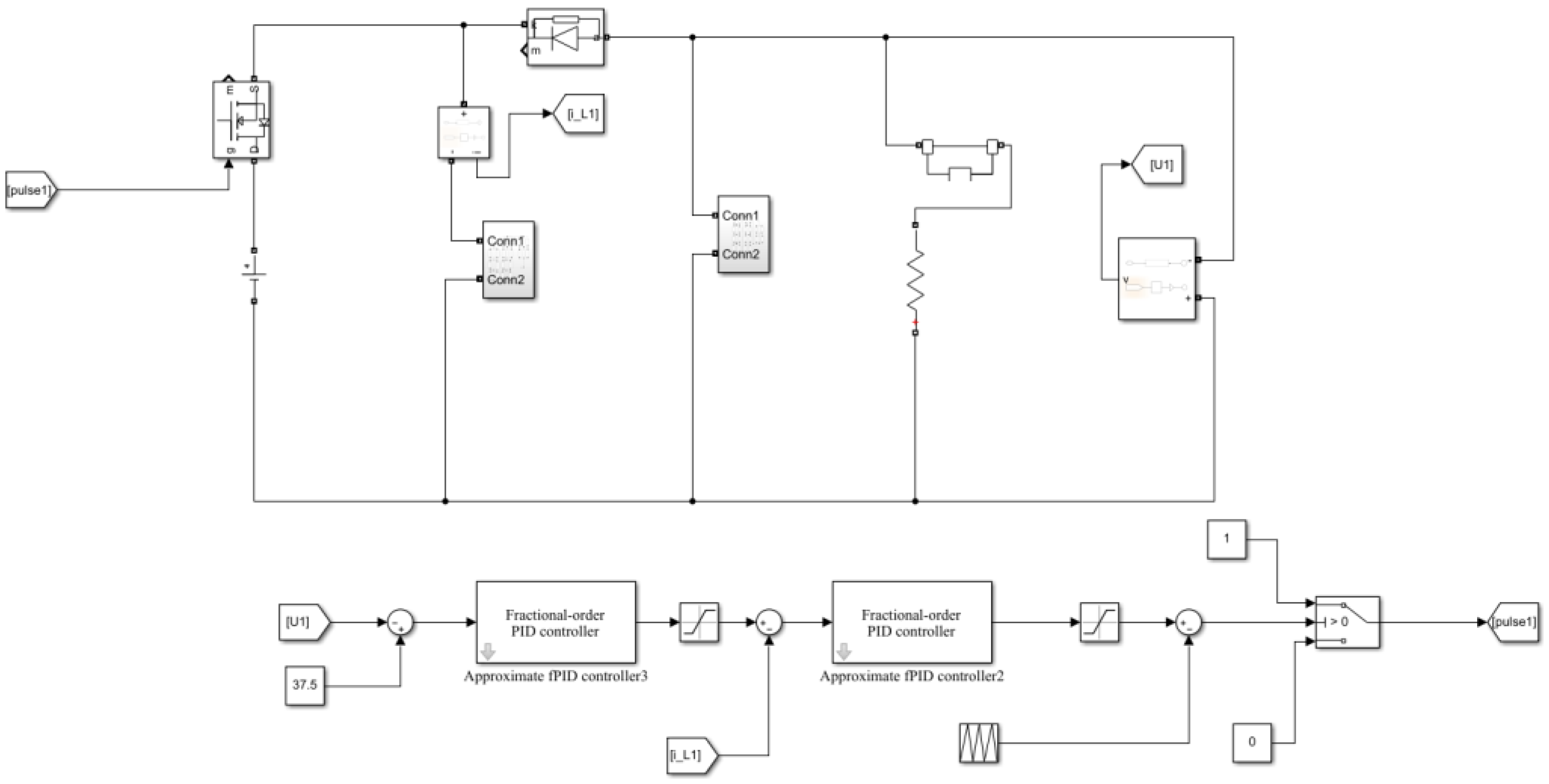
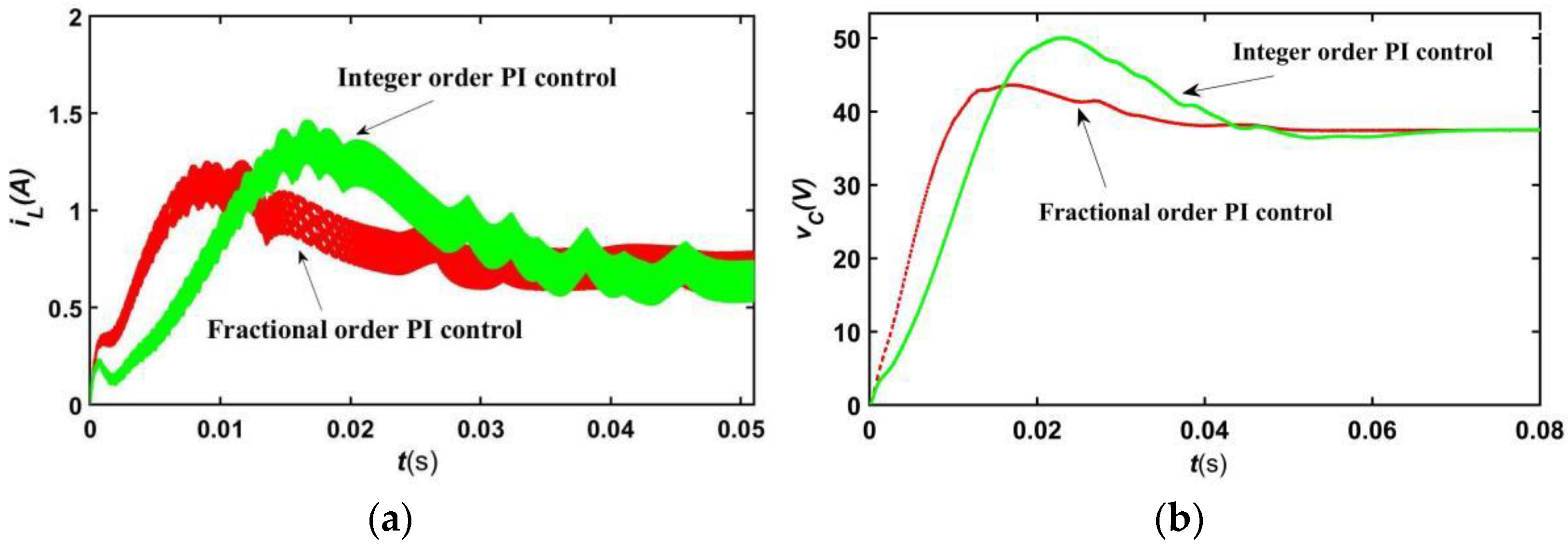
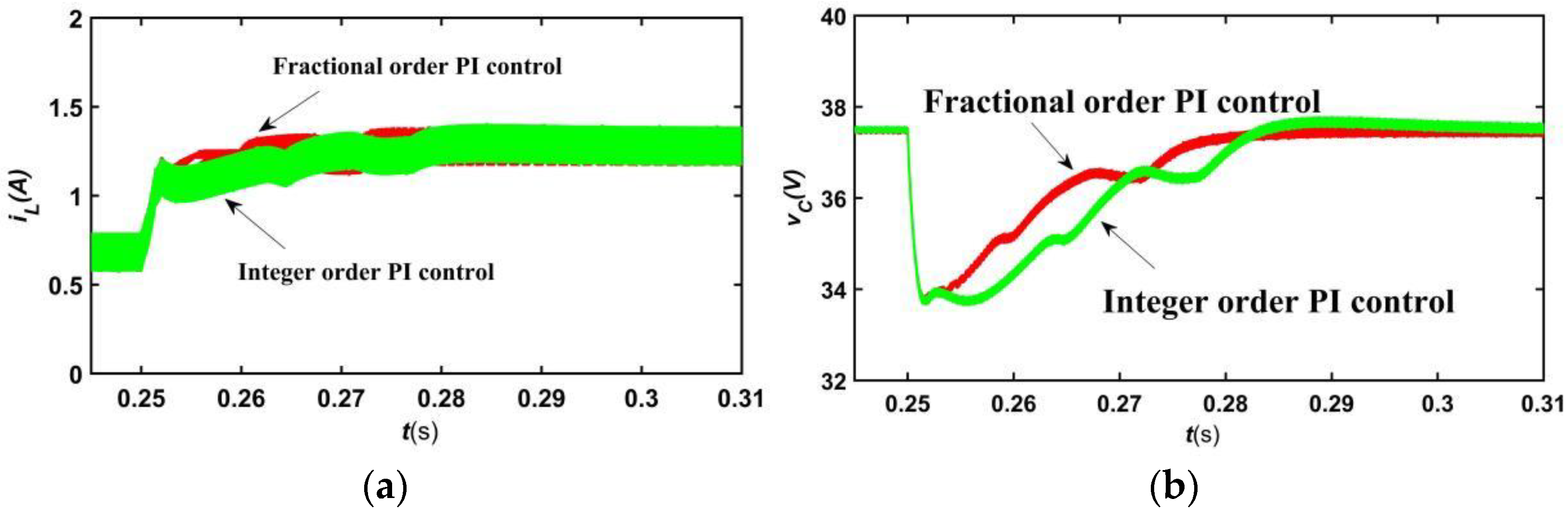
3.3. Control System Simulation and Analysis
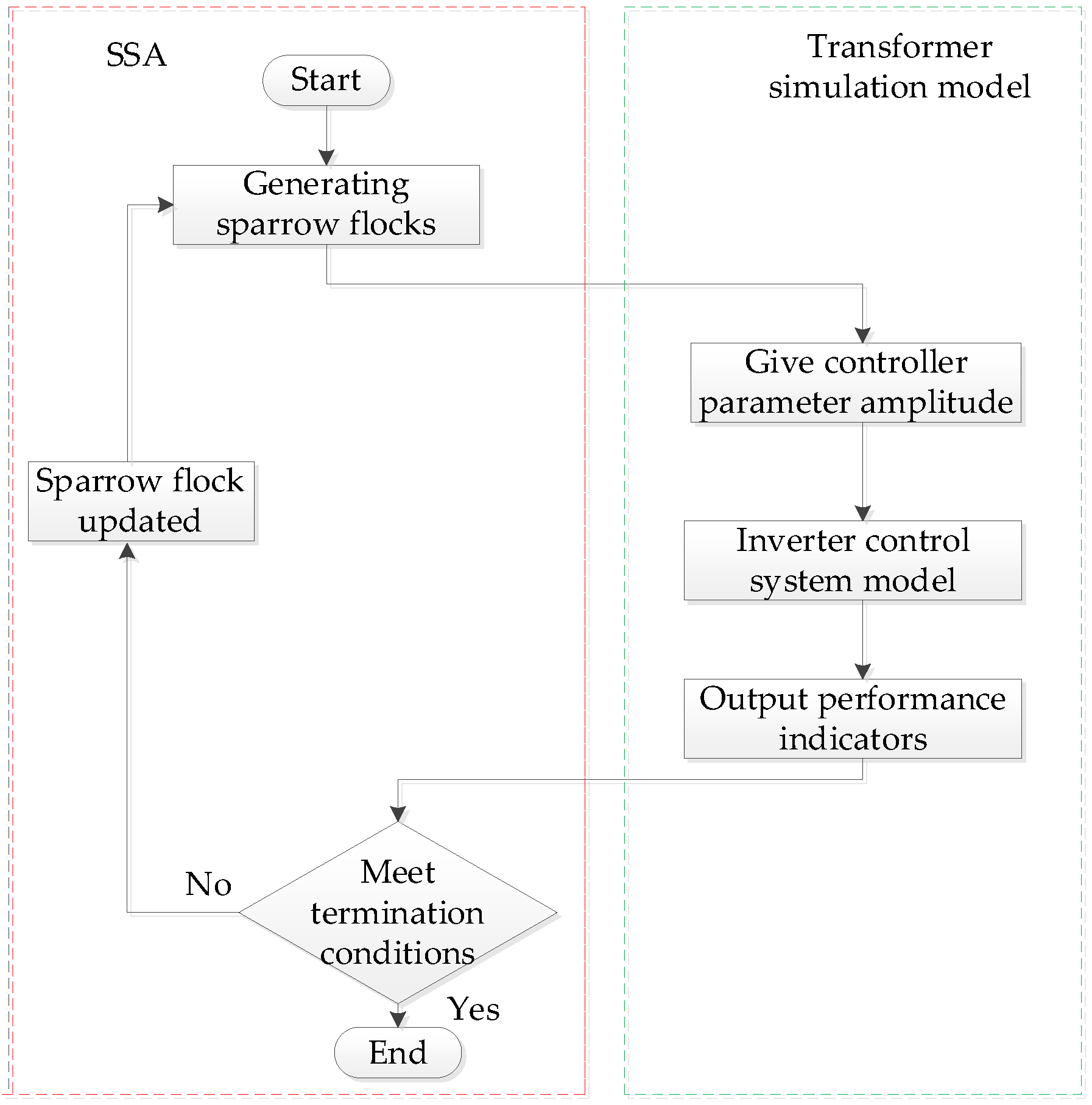
4. Design of Fractional-Order PIλ Control System Based on SSA
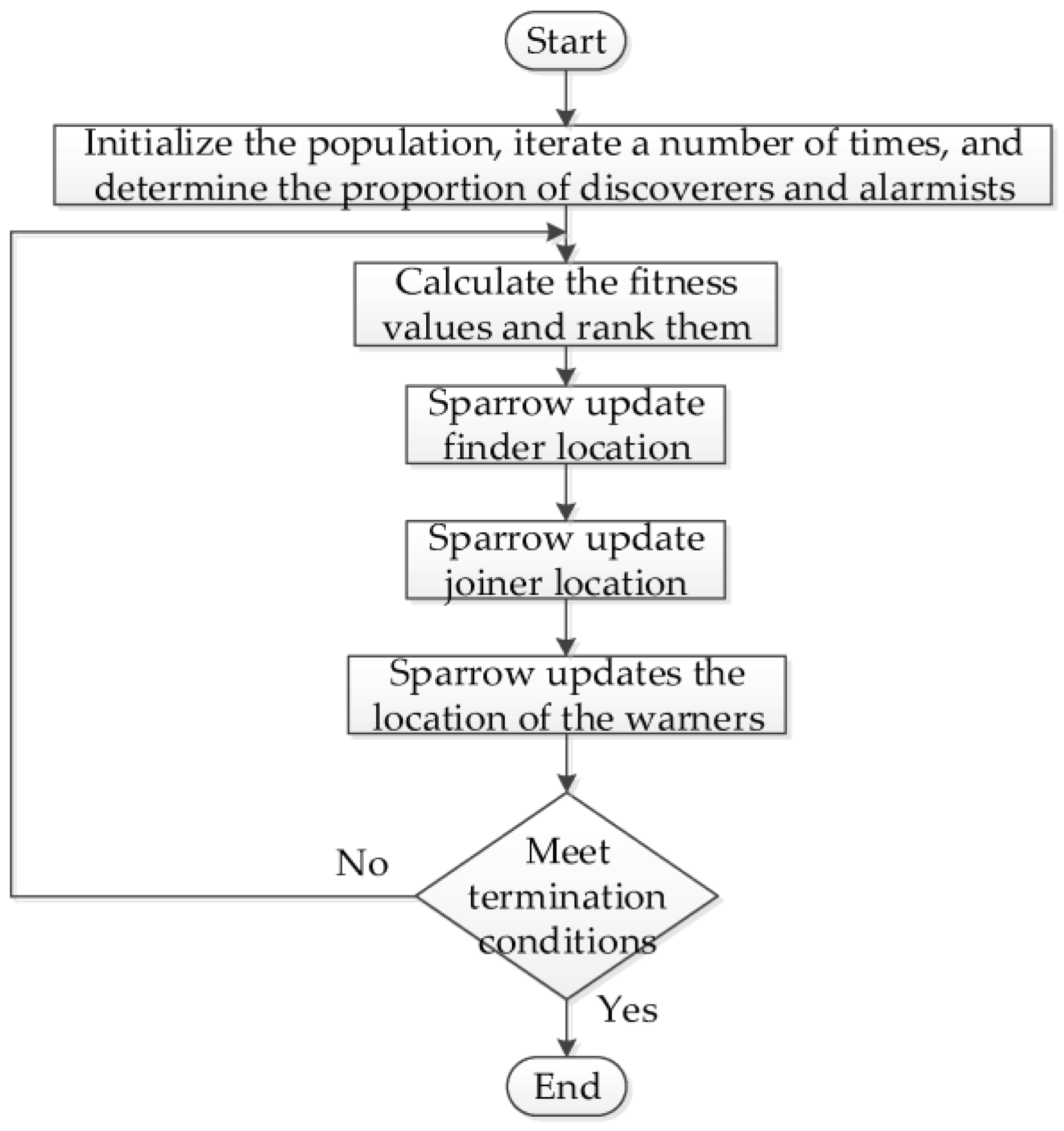
4.1. Sparrow Search Algorithm
4.2. Design of Fractional-Order PIλ Control System Based on SSA
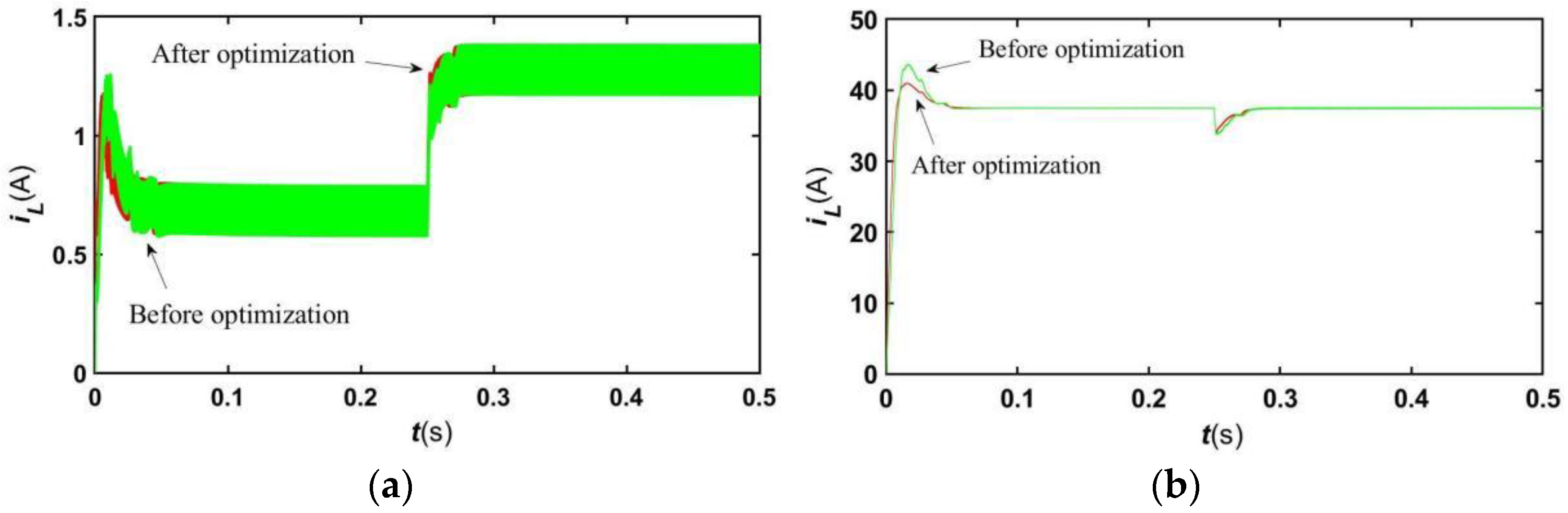
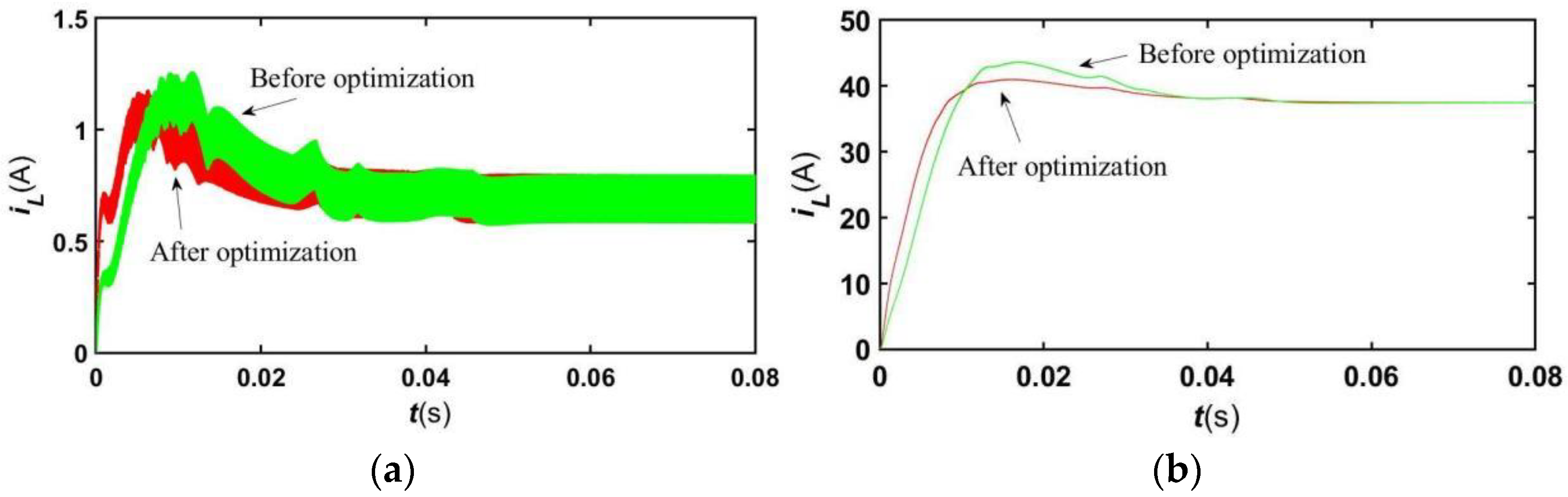
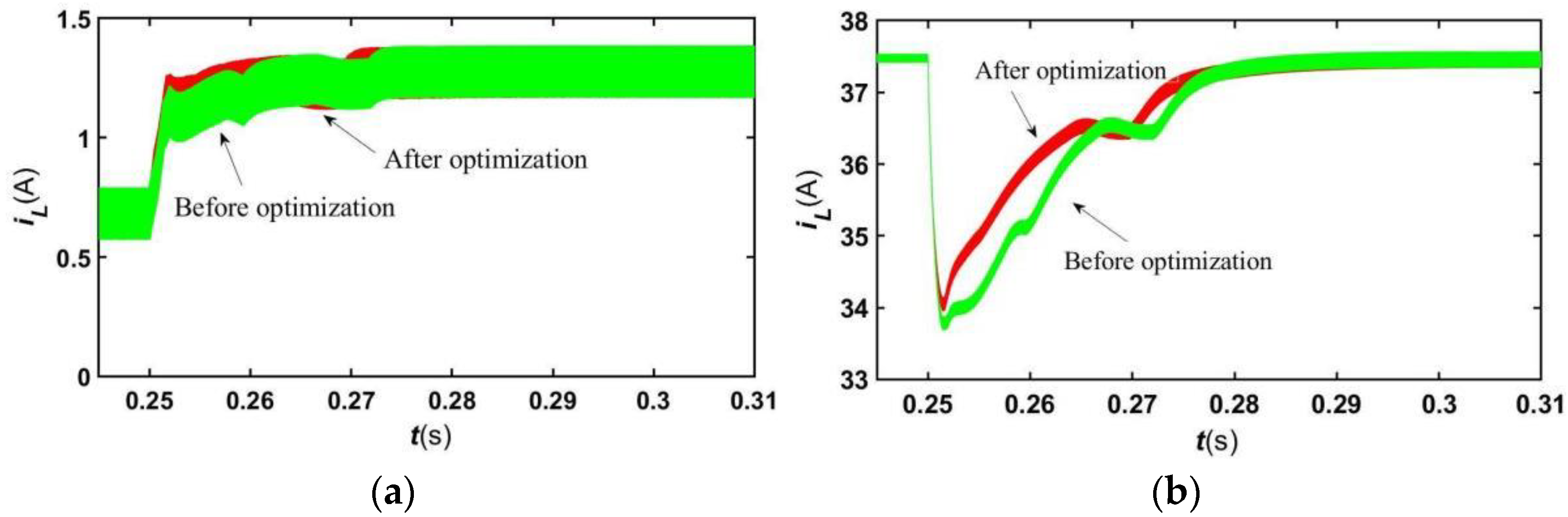
4.3. Simulation Analysis of the Optimized Control System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Radwan, A.G.; Emira, A.A. Modeling and analysis of fractional order DC-DC converter. ISA Trans. 2018, 82, 184–199. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.H.; Zhang, B.; Jiang, Y.W. Analysis and Modeling of Fractional-Order Buck Converter Based on Riemann-Liouville Derivative. IEEE Access 2019, 7, 162768–162777. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Zhang, B. High-Power Fractional-Order Capacitor With 1<α<2 Based on Power Converter. IEEE Trans. Ind. Electron. 2018, 65, 3157–3164. [Google Scholar] [CrossRef]
- Lalmalsawmi; Biswas, P.K. Full-Bridge DC-DC Converter and Boost DC-DC Converter with Resonant Circuit for Plug-in Hybrid Electric Vehicles. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ardi, H.; Ajami, A. Study on a High Voltage Gain SEPIC-Based DC–DC Converter with Continuous Input Current for Sustainable Energy Applications. IEEE Trans. Power Electron. 2018, 33, 10403–10409. [Google Scholar] [CrossRef]
- Magambo, J.S.N.T.; Bakri, R.; Margueron, X.; Le Moigne, P.; Mahe, A.; Guguen, S.; Bensalah, T. Planar Magnetic Components in More Electric Aircraft: Review of Technology and Key Parameters for DC–DC Power Electronic Converter. IEEE Trans. Transp. Electrif. 2017, 3, 831–842. [Google Scholar] [CrossRef]
- Aseem, K.; Selva Kumar, S. Closed loop control of DC-DC converters using PID and FOPID controllers. Int. J. Power Electron. Drive Syst. 2020, 11, 1323–1332. [Google Scholar]
- Mai, Y.F.; Tong, J.M. Design and simulation of hydraulic loading system based on fractional order control. J. Shanghai Univ. Technol. 2015, 37, 589–593. [Google Scholar]
- Qin, C.M. Research on Fractional-Order PID and Self-Anti-Disturbance Control for Hypersonic Vehicles; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Wu, G.Q.; Huang, H.J.; Ye, G.H. Semi-active control of automotive air suspension based on fractional order calculus. J. Agric. Mach. 2014, 45, 19–25. [Google Scholar]
- You, H.; Shen, Y.J.; Yang, S.P. Parameter optimization design of passive fractional-order automotive suspension based on particle swarm algorithm. Vib. Shock. 2017, 36, 224–234. [Google Scholar]
- Chai, X.H.; Cao, H.; Zhang, B. Boost converter full fractional order system analysis and control performance study. J. Power Supply 2019, 17, 27–33. [Google Scholar]
- Tan, C.; Liang, Z.S.; Zhang, J.Q. Nonlinear control of a fractional-order Boost converter in inductive current pseudo-continuous mode. J. Phys. 2014, 63, 89–94. [Google Scholar]
- Komathi, C.; Umamaheswari, M.G. Design of Gray Wolf Optimizer Algorithm-Based Fractional Order PI Controller for Power Factor Correction in SMPS Applications. IEEE Trans. Power Electron. 2020, 35, 2100–2118. [Google Scholar] [CrossRef]
- Zhang, X.C.; Li, H.; Su, W.Z. Study on fractional-order PIλ control and stability analysis of DC-DC converter. New Technol. Electr. Power 2019, 38, 21–31. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Westerlund, S. Dead Matter Has Memory; Causal Consulting: Kalmar, Sweden, 2002; Chapter 7. [Google Scholar]
- Petras, I. Fractional Order Nonlinear Systems—Modeling, Analysis and Simulation; Springer: New York, NY, USA, 2011. [Google Scholar]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Zhang, W.P. Modeling and Control of Switching Converters (Chapter 1); China Electric Power Publishing House: Beijing, China, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Feliu, V. Fractional-Order Systems and Controls, Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chen, H.; Xie, W.; Chen, X.; Han, J.; Aït-Ahmed, N.; Zhou, Z.; Tang, T.; Benbouzid, M. Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. J. Mar. Sci. Eng. 2020, 8, 309. [Google Scholar] [CrossRef]
- Xue, D.Y. Fractional Order Calculus and Fractional Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- Tan, C. Research on Modeling and Control of Quadratic and Pseudo-Continuous Boost Converters Based on Fractional Order Calculus Theory; China University of Petroleum: Beijing, China, 2016. [Google Scholar]
- Hamilton, W.D. Geometry for the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef] [PubMed]
- Pulliam, H.R. On the advantages of flocking. J. Theor. Biol. 1973, 38, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.K. Research and Application of a Novel Swarm Intelligence Optimization Technique; Donghua University: Shanghai, China, 2020. [Google Scholar]




| Controller | KIP | KII | λi |
|---|---|---|---|
| Integer order | 0.04 | 9.26 | 1 |
| Fractional order | 0.04 | 9.26 | 0.9 |
| Controller | KIP | KII | λi |
|---|---|---|---|
| Integer order | 0.04 | 9.26 | 1 |
| Fractional order | 0.04 | 9.26 | 0.9 |
| Status | Controller | Rise Time (s) | Reduction Ratio of Adjustment Time (%) | Maximum Fluctuation Amount (A) | Maximum Volatility Reduction Ratio (%) |
|---|---|---|---|---|---|
| Initial state | PI | 0.0041 | — | 0.663 | — |
| PIλ | 0.0087 | 21.3% | 0.461 | 30.46% | |
| Sudden load change | PI | 0.0291 | — | 0 | — |
| PIλ | 0.0234 | 19.6% | 0 | 0 |
| Status | Controller | Rise Time (s) | Reduction Ratio of Adjustment Time (%) | Maximum Fluctuation Amount (A) | Maximum Volatility Reduction Ratio (%) |
|---|---|---|---|---|---|
| Initial state | PI | 0.0136 | — | 12.62 | — |
| PIλ | 0.0095 | 25.4% | 6.13 | 51.43% | |
| Sudden load change | PI | 0.03 | — | 3.83 | — |
| PIλ | 0.0232 | 22.67% | 3.8 | 0.78% |
| KIP | KPV | KII | KIV | λi | λv |
|---|---|---|---|---|---|
| 0.063 | 0.081 | 10.12 | 19.54 | 0.88 | 0.89 |
| Status | Controller | Rise Time (s) | Reduction Ratio of Adjustment Time (%) | Maximum Fluctuation Amount (A) | Maximum Volatility Reduction Ratio (%) |
|---|---|---|---|---|---|
| Initial state | PI | 0.0041 | — | 0.461 | — |
| PIλ | 0.0025 | 39.34% | 0.381 | 17.35% | |
| Sudden load change | PI | 0.0234 | — | 0 | — |
| PIλ | 0.0219 | 6.4% | 0 | 0 |
| Status | Controller | Rise Time (s) | Reduction Ratio of Adjustment Time (%) | Maximum Fluctuation Amount (A) | Maximum Volatility Reduction Ratio (%) |
|---|---|---|---|---|---|
| Initial state | PI | 0.0095 | — | 6.13 | — |
| PIλ | 0.0084 | 11.58% | 3.54 | 42.25% | |
| Sudden load change | PI | 0.0232 | — | 3.8 | — |
| PIλ | 0.0208 | 10.34% | 3.52 | 7.37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Wan, D.; Qin, R. Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller. Fractal Fract. 2023, 7, 256. https://doi.org/10.3390/fractalfract7030256
Xie L, Wan D, Qin R. Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller. Fractal and Fractional. 2023; 7(3):256. https://doi.org/10.3390/fractalfract7030256
Chicago/Turabian StyleXie, Lingling, Di Wan, and Rui Qin. 2023. "Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller" Fractal and Fractional 7, no. 3: 256. https://doi.org/10.3390/fractalfract7030256
APA StyleXie, L., Wan, D., & Qin, R. (2023). Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller. Fractal and Fractional, 7(3), 256. https://doi.org/10.3390/fractalfract7030256





