A Study of Fractional-Order Memristive Ant Colony Algorithm: Take Fracmemristor into Swarm Intelligent Algorithm

Abstract

As the fourth fundamental circuit element, the memristor may execute computations while storing data. Fracmemristor takes advantage of the fractional calculate’s long-term memory, non-locality, weak singularity, and the memristor’s storage–computational integration. Since the physical structure of the fracmemristor is similar to the topology of the ant transfer probability flow in ACO, we propose the fractional-order memristive ant colony algorithm (FMAC), which uses the fracmemristor physical system to record the probabilistic transfer information of the nodes that the ant will crawl through in the future and pass it to the current node of the ant, so that the ant acquires the ability to predict the future transfer. After instigating the optimization capabilities with TSP, we discovered that FMAC is superior to PACO-3opt, the best integer-order ant colony algorithm currently available. FMAC operates substantially more quickly than the fractional-order memristor ant colony algorithm due to the transfer probability prediction module based on the physical fracmemristor system (FACA).

1. Introduction

Dorigo [1] introduced the first algorithm for the feeding behavior of an ant colony in 1992. This model was later perfected to become the meta-heuristic known as ant colony optimization (ACO) [2]. The first ant-based algorithm, namely the ant system [3], was subsequently transformed into an ant colony system [4] with other improvements. In contrast to the ant system [5], the ant colony system possesses four characteristics that set it apart from the former: a distinct transition rule, a variation in pheromone update rules, the implementation of local pheromone updates, and the presence of a unique node bias. To ensure that ants do not reach a state of early stagnation, Stützle and Hoos proposed max–min ant (MMAS) [6]. MMAS strictly regulates the total quantity of pheromones released within a specified period, which is a crucial difference from the ant system. Additionally, several improved algorithms, including algorithms for the optimization of ant nodes in ant colonies [7,8,9], ant colony parallel computing [10,11,12], ant colony initialization node selection [13,14,15], ant colony interaction system [16], etc. Each ant in a conventional integer-order ant colony algorithm (IACA) selects a neighboring edge based on a transition probability calculated from the value of the pheromone. This probability is determined by the present node and neighboring edges of the ant graph.

Based on the concept of combinatorial exhaustiveness of core circuit variables, Léon O. Chua [17,18] foretold the existence of a memristor in 1971. He referred to memristors as the fourth fundamental circuit element that humans have yet to find: Memristor—the missing circuit element [17]. By contrast, at that time, no physical component had been detected. When a research team of the HP company built a nanoscale $Ti{O}_2$ device in 2008 [19], they stunned the international electricity and electronics industry. An analysis revealed that the device was a physical memristor entity, which shook the sector internationally. Memristor research then began in several nations throughout the world. Chua [20,21,22] pushed for a more inclusive definition encompassing non-volatile memory devices with two terminals and a resistance-changing architecture. In the field of computer science, subjects such as neural networks [23,24], biological engineering [25], communication engineering, nonlinear circuits [26], as well as other domains, have a wide variety of application prospects, as well as people’s interests and studies.

For more than 200 years, the fractional calculation was a vital aspect of mathematical analysis. One area of investigation that needs to be explored is how fractional calculations can be used in modern signal analysis and processing. Non-integral order operation results in fractional computation with long-term memory, non-locality, and low singularity [27,28]. In addition, the extra freedom of movement of the system can be enhanced by increasing the fractional parameters. Fractional order calculus is extensively used in image processing [29,30,31,32] and signal processing [33,34,35]. Chen [36], in 2009, was the first to propose a fractional-order memristor. Chen came up with the idea for the present fractional-order memristor, which indicates that the stored charge $q$ is in the fractional order. Then, various fractional-order memristors [37,38,39,40] were presented as possible solutions. Long-term memory systems were found to be better described by the fractional order model. These assumptions can be derived from Chua’s axiomatic element system. The expanded fractional-order Chua’s periodic table was proposed by Pu [41,42]. After that, Pu [43,44] proposed the fractional-order memristors (fracmemristor), which are naturally transmitted from a fractor to a fracmemristor.

As a relatively new area of study, the use of fractional computation in swarm intelligence has attracted interest among some researchers. Some attempts have been made to use the fractional calculation in optimal control, fractional evolutionary equations [45], and ant colony algorithms that employ a fractional calculus to modify the pheromone update rates [46]. Because of its intrinsic qualities, such as long-term memory, non-locality, and weak singularity, fractional calculus has the potential to lead to widespread use in applications in intelligent signal processing. Pu [47] attempted to modify the transfer probability selection mechanism of IACA using a fractional-order calculus and proposed the fractional-order ant colony algorithm (FACA), thus enabling the ant colony algorithm to predict future transition probabilities and allowing FACA to converge more quickly. Building on this, we proposed a new fractional-order memristive ant colony algorithm (FMCA) that allows a single ant to update pheromones using the non-local nature of fractional-order calculus and using fractional-order memristors (fracmemristor) physical systems to quickly obtain the transfer probability of future nodes, allowing ants to be more accurate when choosing the following paths based on the transfer probability.

The text is structured as follows:

(a)

Section 2 gives some of the mathematical and physical knowledge needed for this paper. Section 2 concentrates on the mathematical principles of fractional memories and how to construct the capacitive scale of v-order chains. There are also several properties contained in the fractional-order memristor.

(b)

The formulation of the suggested fractional-order memristive ant colony algorithm (FMCA) is described in Section 3. By designing a fractional-order memristor for each ant to recall the future transfer probability information, a memristive physical system based on fracmemristor is conferred onto the ant. Based on the information placed by the fractional-order memristor (fracmemristor), the non-local characteristic of the fractional order is employed to enable the ant to forecast possibly better probability transfer pathways in the future. We also perform mathematical arguments to ensure that the FMAC converges.

(c)

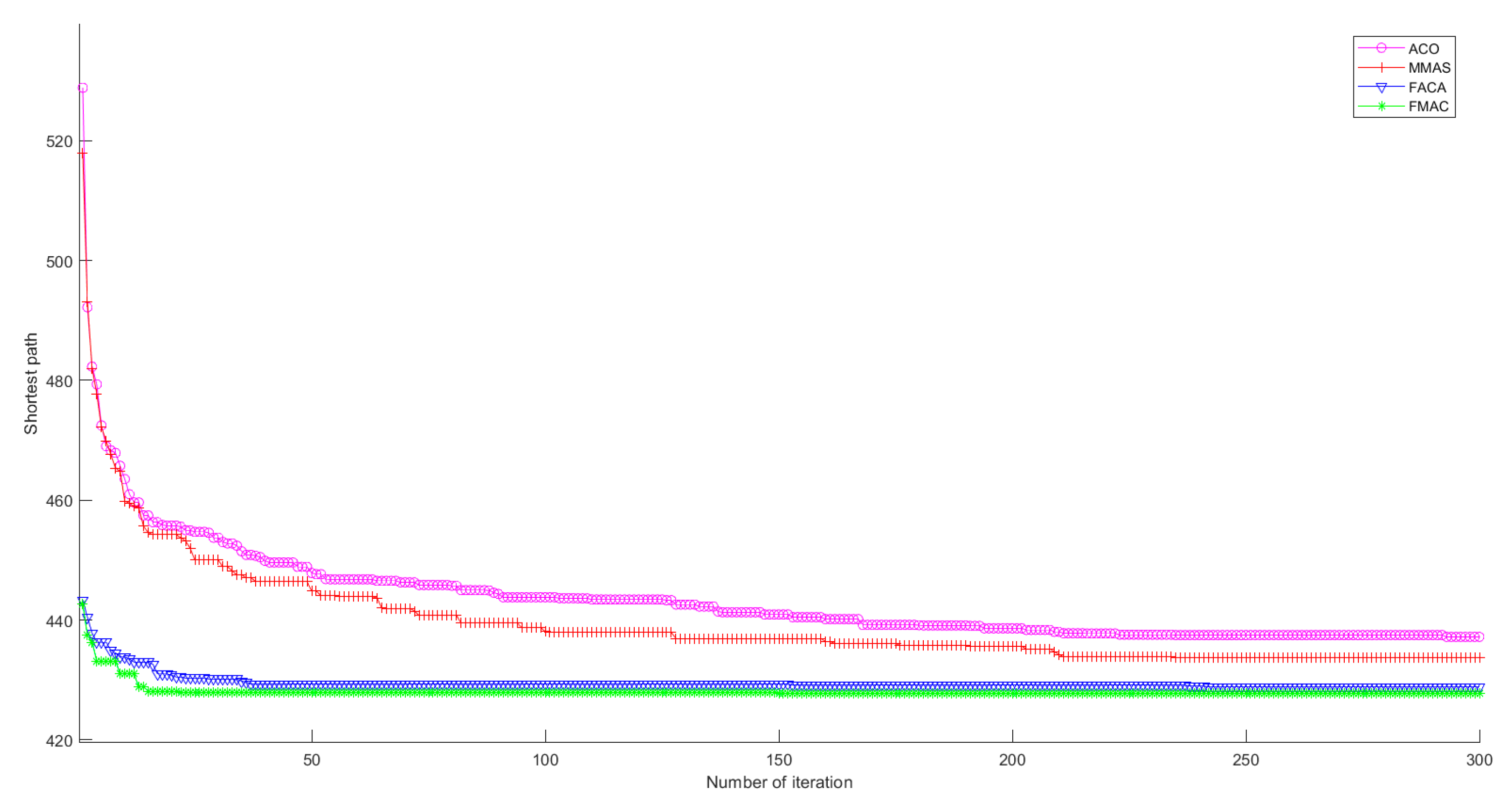
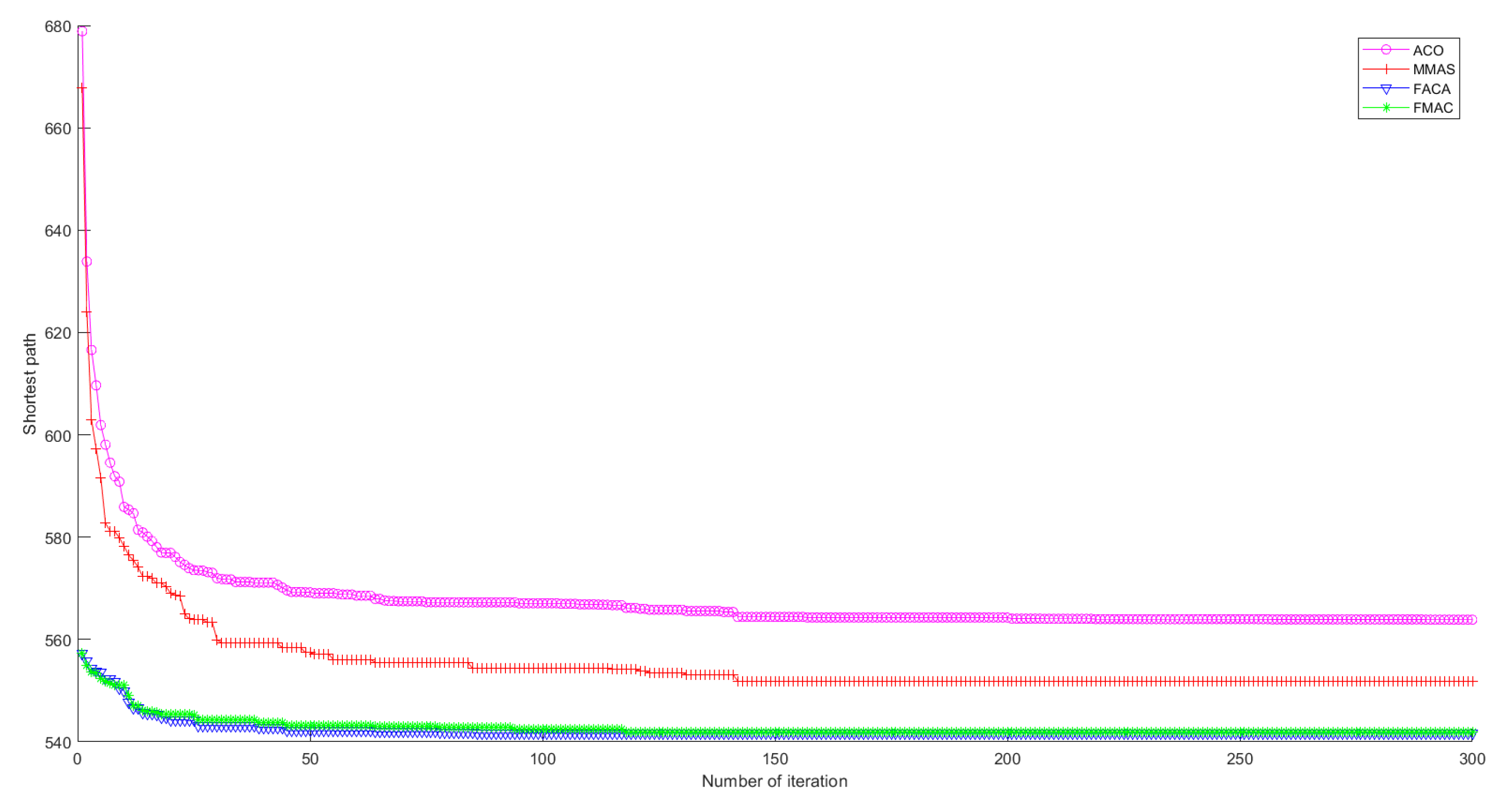
The experimental findings are presented in Section 4. First, we fixed the other parameters of the FMAC and experimentally determined the order range of the fracmemristor. Then, we compared the convergence speed of FMAC with those of ACO, MMAS, and FACA. Finally, we compared the optimal results of several algorithms for the different TSP problems.

2. Background

There are six relationships between the four circuit elements {$u$, $i$, $q$, $\phi$}, and it follows that

$$\{(u,\phi ),(i,q),(u,q),(i,\phi ),(q,\phi ),(i,u)\},$$

(1)

We are most familiar with $(i,q) and (u,\phi )$.

$$q(t)={\displaystyle {\int }_{-\infty }^{t}i(\tau )}d\tau ,$$

(2)

$$\phi (t)={\displaystyle {\int }_{-\infty }^{t}u(\tau )}d\tau ,$$

(3)

The pair (i, u) is Ohm’s law, which determines the resistor R in Equation (4). The couple (u, q) indicates the capacitator C in Equation (4), and the couple (i, φ) suggests the inductor L in Equation (4).

$$\begin{array}{l}u=Ri,\\ u=\frac{q}{C},\\ \phi =Li.\end{array}$$

(4)

Leon O. Chua could not identify a circuit item that directly represents the connection between $(q,\phi )$. Leon O. Chua argued that, from the point of view of axiomatic comprehensiveness, an electrical component exists to reflect their fundamental relationship in Equation (5). He designated the new component memory-resistor (memristor).

$$f(q,\phi )=0.$$

(5)

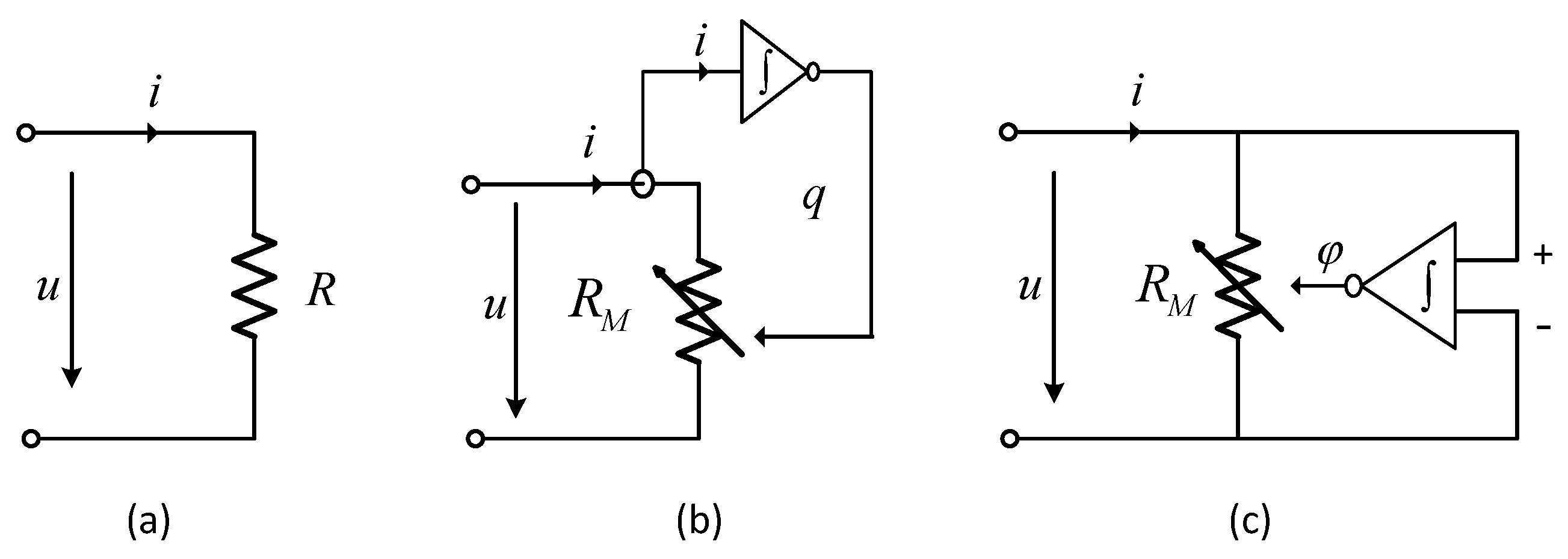
2.1. Memristor

If the φ is a unique value function of q, Equation (5) can be rewritten as follows,

$$\phi =\phi (q).$$

(6)

This calculates the differentiation between the two sides of time $t$

$$\frac{d\phi }{dt}=\frac{d\phi (q(t))}{dq}\cdot \frac{dq}{dt}=\frac{d\phi (q(t))}{dq}\cdot i(t),$$

(7)

The memristive characteristics are illustrated by rewriting Equation (7) as the volt–current Formula (8), which is mathematically symmetrical with the resistance formula: where $R_{\mathrm{M}}$ is the memristor’s resistance; and $R_{\mathrm{M}}$ is proportional to the current’s value passed through it over time. Therefore, it is referred to as a charge- or current-controlled memristor.

$$\begin{array}{l}u(t)=R_{\mathrm{M}}(q(t))i(t),\\ R_{\mathrm{M}}(q(t))\equiv \frac{d\phi (q)}{dq},\end{array}$$

(8)

If q is a unique value function of $\phi$, Equation (5) may be rewritten as follows:

$$q=q(\phi ),$$

(9)

$R_{\mathrm{M}}$ is the resistance of the memristor. Thus, $R_{\mathrm{M}}$ depends on how much voltage has been put on its terminals in the past. Therefore, the current-controlled memristors are also known as flux-controlled memristors.

$$\begin{array}{l}u(t)=R_{\mathrm{M}}(\phi (t))\cdot i(t),\\ R_{\mathrm{M}}(\phi )\equiv \frac{d\phi }{d(\phi )}.\end{array}$$

(10)

The expressions for the resistor, voltage-controlled memristor, and current-controlled memristor equations are mathematically equivalent. The resistor does not store any information, and its resistance remains the same throughout time. In the current-controlled memristor, $R_{\mathrm{M}}$ depends on charge $q$. The volt-controlled memristor $R_{\mathrm{M}}$ depends on flux $\phi$, and its resistance changes with flux $\phi$. Schematic diagrams of the circuit resistor, voltage-controlled memristor, and current-controlled memristor are shown in Figure 1.

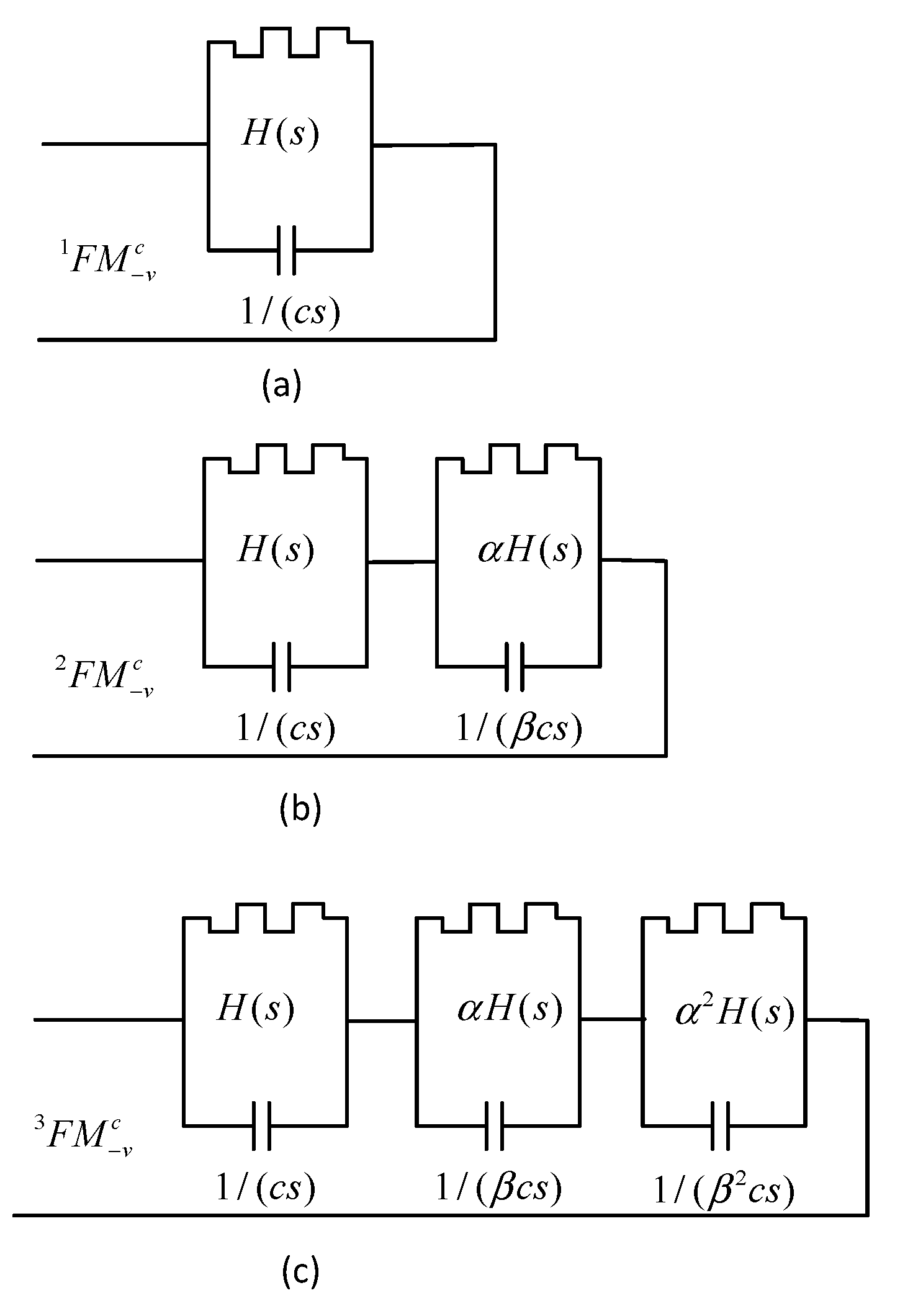
2.2. Fracmemristor

Using the Laplace transform on both sides of Equation (4), we obtain Equation (11).

$$L\{f(t)\}=F(s)=\frac{U(s)}{I(s)}=F{s}^u,$$

(11)

In Figure 2, Pu [37,38] determines that $S_1$ and $S_2$, respectively, represent the capacitive fractor and inductive fractor; whilst $S_3$ and $S_4$, respectively, represent the capacitive fracmemristor and inductive fracmemristor. The expression of the arbitrary-order capacitive fractor was obtained by Pu [37,38]. The derivation is given in Equation (12).

$$\begin{array}{l}{F}_{-v}^c =F_{-(m+p)}^c\\ \begin{array}{cc}& \hspace{1em}=\frac{V_i(s)}{I_i(s)}\end{array}\\ \begin{array}{cc}& \hspace{1em}=c^{-(m+p)}{r}^{1-p}{s}^{-(m+p)}.\end{array}\end{array}$$

(12)

In Equation (12), $m=[v]$ is the rounded-down integer part of $v$, and $p=v-m$. The driving function, capacitance, voltance, and resistance for a perfectly optimal v-order capacitive fractor are represented by the letters $F_{-v}^c$, $c$, $v$, $r$, respectively. Following the same procedure, we can determine the universal expression for the inductive fractor of the arbitrary order in Equation (13).

$$\begin{array}{l}{F}_v^l =F_{m+p}^l\\ \begin{array}{cc}& \begin{array}{l} =\frac{V_i(s)}{I_i(s)}\\ =l^{m+p}{r}^{1-p}{s}^{m+p}.\end{array}\end{array}\end{array}$$

(13)

Apply the signal and system analysis to the memristor in Equation (8). Equation (14) is derived by rewriting Equation (8).

$$\begin{array}{l} u(t) =\frac{d\phi (q)}{dq\cdot i(t)}\\ \begin{array}{cc}& \begin{array}{l}\hspace{1em}=[M(q)+\frac{qdM(q)}{dq}]i(t)\\ \hspace{1em}=H[q(t)]*i(t)\end{array}\end{array},\end{array}$$

(14)

The symbol * means convolution and the term $H[q(t)]$ refers to the transfer function of the memristor. We can obtain $u(s)=r[q(s)]i(s)$ by realizing the multiplication in the area of Laplace transforms. $r[q(s)]$ is the reactance of the memristor.

In Equation (13), we do the same thing for the inductive fractor,

$$F_{-v}^c=c^{-v}{r}^{1-p}{s}^{-v}.$$

(15)

We can replace $r$ with $r[q(s)]$. Because it depends on the $q$, we can obtain the current-controlled capacitive factor (CCFM) in Equation (16).

$$F_{-v}^{(C_{\mathrm{M}})}(s)=\frac{u(s)}{i(s)}=c^{-v}{\{r[q(s)]\}}^{1-p}{s}^{-v}.$$

(16)

$F_{-v}^{(C_{\mathrm{M}})}(s)$ represents the $v$-order CCFM and $c$ is the capacitance.

We can replace $r$ with $r[\phi (s)]$ in the inductive factor. Due to the fact that $r[\phi (s)]$ depends on the flux $\phi$, we can obtain the volt-controlled inductive factor in Equation (17). We name it VIFM for short.

$$F_{-v}^{(L_{\mathrm{M}})}(s)=\frac{u(s)}{i(s)}=l^{-v}{\{r[\phi (s)]\}}^{1-p}{s}^{-v}.$$

(17)

$F_v^{(L_{\mathrm{M}})}(s)$ represents the $v$-order VIFM and $l$ is the inductance.

The schematic diagrams of CCFM and VIFM are shown in Figure 3.

3. Algorithm

This section suggests a fractional-order memristive ant colony algorithm (FMAC) based on fracmemristor. To provide an estimate of the likelihood of transfer along potential future pathways, the fractional sequence memory system is provided. We can estimate the trend of future transfer probabilities based on the process of transfer probability change during the previous iteration using the transfer probabilities of the nodes along the ant’s route. The employment of fractional-order memristive capabilities in the transfer probability prediction model is primarily due to its inherent benefits in long-term memory and nonlocality. Fracmemristor can be used to calculate the probability transfer function in the ACO algorithm.

3.1. Physical Memristive System of Transition Probability Series in FMAC

In the traditional integer-order ant colony algorithm (IACA), each ant decides which edge to follow based on a transition probability. As an intriguing theoretical problem, we studied whether the forces inherent in the fractional calculation can be used to change the transition in IACAs by substituting the simple one-step probability with a more sophisticated expression that allows for some future information. In IACA, when arriving at a node, an ant evaluates the likelihood of its next move based on the transition probabilities $p_{ij}$ among the possible nodes of node $i$ and follows a predetermined path to get there. However, in FMCA, the ant obtains the transition probability $p_{ij}$ at node $i$, and selects the next node j by $p_{ij}$. At node j, we choose the next node k by the transition probability $p_{jk}$, and so on. In this manner, we obtain an ant’s future transition probability sequence in IACA. As shown in Figure 4, the memory computation mode of this ant in FMCA is almost identical to the working mode of the memristor, so we can construct a physical fracmemristor system to perform the prediction of ant transfer probabilities.

From the algorithm flowchart in Figure 4, we can construct a probabilistic transfer prediction system based on fracmemristor, the physical structure of which is shown in Figure 5. In this paper, we only discuss the low-pass filtering fracmemristor. The $v$-order low-pass filter capacitive-scale-chain fracmemristor (LCSF) [42] is shown in Figure 5a.

We perform a mathematical analysis of the LCSF. The $nth$ series circuit of $v\text{-}order$ LCSF can be rewritten as ${}^{n}NFM_{-v}^c(w)=\frac{1}{H(s)}{}^{n}FM_{-v}^c(s)=\frac{cs}{w}{}^{n}FM_{-v}^c(s)$ and $w=H(s)cs$. Thus, we obtain Equation (18),

$$\begin{array}{l}{}^1\mathrm{NFM}_{-v}^c(w)={\displaystyle \sum _{i=0}^{1-1}\frac{1}{{\alpha }^{-i}+{\beta }^{i}w}}=\frac{1}{1+w},\\ {}^2\mathrm{NFM}_{-v}^c(w)={\displaystyle \sum _{i=0}^{2-1}\frac{1}{{\alpha }^{-i}+{\beta }^{i}w}}=\frac{1}{1+w}+\alpha \left[{}^1\mathrm{NFM}_{-v}^c(\sigma w)\right],\\ {}^3\mathrm{NFM}_{-v}^c(w)={\displaystyle \sum _{i=0}^{3-1}\frac{1}{{\alpha }^{-i}+{\beta }^{i}w}}=\frac{1}{1+w}+\alpha \left[{}^2\mathrm{NFM}_{-v}^c(\sigma w)\right].\end{array}$$

(18)

Additionally, $\sigma =\alpha \beta$; similarly, $nth$ $v\text{-}order$ LCSF is

$$\begin{array}{cc}& {}^n\mathrm{NFM}_{-v}^c(w)={\displaystyle \sum _{i=0}^{n-1}\frac{1}{{\alpha }^{-i}+{\beta }^{i}w}}=\frac{1}{1+w}+\alpha \left[{}^{n-1}\mathrm{NFM}_{-v}^c(\sigma w)\right]\end{array},$$

(19)

Equation (19) is an irregular iterative scaling equation. In Figure 6, if $n\to \infty$, we obtain

$${}^n\mathrm{NFM}_{-v}^c(w)={}^{n-1}\mathrm{NFM}_{-v}^c(\sigma w),$$

(20)

Then,

$${}^n\mathrm{NFM}_{-v}^c(w)={\displaystyle \sum _{i=0}^{n-1}\frac{1}{{\beta }^{i}w+{\alpha }^{-i}}}=\frac{1}{w+1}+\alpha \left[{}^n\mathrm{NFM}_{-v}^c(\sigma w)\right],$$

(21)

By the general dynamical scaling law, which can be derived from Equation (15), the approximate solution to Equation (21) is

$$\begin{array}{l}{\mathrm{NFM}}_{-v}^c(w)=\frac{{[H(s)]}^{1-p}{c}^{-v}{s}^{-v}}{H(s)}\\ \begin{array}{cc}& \stackrel{\begin{array}{cc}when& \begin{array}{cc}p=w& \mathrm{and}0<v<1\end{array}\end{array}}{\to }\end{array}{[H(s)s]}^{-v}{c}^{-v},\\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& & \stackrel{\begin{array}{cc}\mathrm{if}& w=H(s)cs\end{array}}{\to }{\left[w\right]}^{-v}\end{array}\end{array}$$

(22)

Said another way, $c^{-v}H(s)$ is a scalar. Taking Equation (22) into Equation (21), we obtain Equation (23),

$${[w]}^{-v}=\frac{1}{w+1}+\alpha {[\sigma w]}^{-v}.$$

(23)

Because LCSF is a low-pass filter, when $s\to 0$, $w=H(s)cs\to 0$. Equation (23) is approximated as Equation (24),

$${[w]}^{-v}\stackrel{\begin{array}{cc}\mathrm{when}& w\to 0\end{array}}{\to }1+\alpha {[\alpha \beta w]}^{-v}$$

(24)

Given that the transition probability series in FMAC is similar in structure and function to the physical LCSF system, the circuit of LCSF is used to predict the transition probability flow $i_{in}$ in the future.

$$I_{in}(s)=V_{in}(s){[H(s)]}^{p-1}{c}^v{s}^v$$

(25)

The inverse Laplace transform of Equation (25) is as follows:

$$\begin{array}{l}{i}_{in}(t)=c^v{D}_t^v\left\{L^{-1}\left\{{[H(s)]}^{p-1}*v_{in}(t)\right\}\right\}\\ \begin{array}{cc}& \stackrel{k\to \infty }{\to }\end{array}{c}^v\left\{\begin{array}{c}{i}_{in}(t)(D_t^{-1}{i}_{in}(t))\\ +(-v)[i_{in}(t)(\alpha D_t^{-1}{i}_{in}(t)]\\ +\frac{(-v)(-v+1)}{2}[i_{in}(t)({\alpha }^2{D}_t^{-1}{i}_{in}(t)]\\ +\frac{(-v)(-v+1)(-v+2)}{6}[i_{in}(t)({\alpha }^3{D}_t^{-1}{i}_{in}(t)]\\ +\cdots \\ +\frac{\mathrm{\Gamma }(k-v-1)}{(k-1)!\mathrm{\Gamma }(-v)}[i_{in}(t)({\alpha }^{k-1}{D}_t^{-1}{i}_{in}(t)]\end{array}\right\}\end{array}$$

(26)

Substituting the results of Equation (26) into the FMCA probability transfer sequence model, we can obtain:

$$\begin{array}{l}{}^{m}p_{ij}^v\left(t\right)=p_{ij}\left(t\right)+(-v)p_{jk}(t)+\frac{(-v)(-v+1)}{2}{p}_{kl}(t)+\cdots +\frac{\mathrm{\Gamma }\left(m-v\right)}{\mathrm{\Gamma }\left(-v\right) \mathrm{\Gamma }\left(m+1\right)}{p}_{yz}\left(t\right)\\ \begin{array}{cc}& \end{array}\hspace{1em}=p_{ij}\left(t\right)+{\displaystyle \sum _{k=1}^{N_1-1}\left|\frac{\mathrm{\Gamma }\left(m-v\right)}{\mathrm{\Gamma }\left(-v\right) \mathrm{\Gamma }\left(m+1\right)}\right|p_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)}\end{array}$$

(27)

In Equation (27), the fracmemristor’s physical system conveys information on future transfer probabilities, combined with fractional order weights, to the current node.

3.2. Proposed Iterative Algorithm of the Fractional-Order Memristive Ant Colony Algorithm (FMCA)

In Section 3.1, we obtain the fracmemristor-based physical system, which is a transfer probability predictor of the ant colony algorithm. In Equation (27), $p_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)$ denotes the transfer probability of transferring to the $mth$ node at the $m-1th$ node after node $j$. Since the probability sums to 1, we normalize the probabilities. We obtain the transfer probability of FACA,

$${}^{m}p_{ij}^v\left(t\right)=\frac{1}{f}\{\begin{array}{l}{p}_{ij}\left(t\right)+{\displaystyle \sum _{m=1}^{N_1-1}\left|\frac{\mathrm{\Gamma }\left(m-v\right)}{\mathrm{\Gamma }\left(-v\right)\mathrm{\Gamma }\left(m+1\right)}\right|p_{\left(j+m-1\right)\left(j+k\right)}\left(t\right)}\hspace{1em}if j\in C_i^n\left(t\right) and \left(j+m\right)\in C_i^n\left(t\right)\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em} if j\notin C_i^n\left(t\right)\end{array} ,$$

(28)

$f={\displaystyle \sum _{k=0}^{N_1-1}\left|\frac{\mathrm{\Gamma }\left(m-v\right)}{\mathrm{\Gamma }\left(-v\right)\mathrm{\Gamma }\left(m+1\right)}\right|}$ is a normalization factor, and ${}^{m}p_{ij}^v\left(t\right)$ means the $v\text{-}order$ transition probability of an ant from the $i$ node to the $j$ node. $C_i^n\left(t\right)$ means the set of the following optional nodes; $\left(N_1-1\right)$ is the number of nodes connecting to the $j$ node. ${}^{m}p_{ij}^v\left(t\right)$ represents the $v\text{-}\mathrm{order}$ differential of $p_{ij}\left(t\right)$. $p_{i\mathrm{j}}\left(t\right)$ is the transition probability of IACA, so

$$p_{ij}\left(t\right)=\{\begin{array}{l}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{ \alpha }{[{\eta }_{ij}\left(t\right)]}^{ \beta }}{{\displaystyle \sum _{c\in C_i^m\left(t\right)}{\left[{\tau }_{ic}\left(t\right)\right]}^{ \alpha }{\left[{\eta }_{ic}\left(t\right)\right]}^{ \beta }}}\hspace{1em}if j\in C_i^n\left(t\right)\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if j\notin C_i^n\left(t\right) \end{array} ,$$

(29)

$$p_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)=\{\begin{array}{l}\frac{{\left[{\tau }_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)\right]}^{ \alpha }{\left[{\eta }_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)\right]}^{ \beta }}{{\displaystyle \sum _{c\in C_{\left(j+m-1\right)}^m\left(t\right)}{\left[{\tau }_{\left(j+m-1\right)C_{j+m-1}^n}\left(t\right)\right]}^{ \alpha }{\left[{\eta }_{\left(j+m-1\right)C_{j+m}^n}\left(t\right)\right]}^{ \beta }}}\hspace{1em}if \left(j+m\right)\in C_{\left(j+m-1\right)}^n\left(t\right)\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em} if \left(j+m\right)\notin C_{\left(j+m-1\right)}^n\left(t\right)\end{array} ,$$

(30)

$\alpha$ is the pheromone concentration and $\beta$ is the heuristic information. In Equations (29) and (30), ${\tau }_{\left(j+m\text{-}1\right)\left(j+m\right)}(t)$ is the pheromone concentration.

We obtained the pheromone concentration of the $tth$ iteration and performed an update of the pheromone concentration of FMAC.

$${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+{\displaystyle \sum _{m=1}^k\left|\frac{\mathrm{\Gamma }\left(m-v-1\right)}{\mathrm{\Gamma }\left(-v\right) \mathrm{\Gamma }\left(m\right)}\right|\Delta {\tau }_{ij}^{\mathrm{m}}\left(t\right)} ,$$

(31)

$\rho$ is the pheromone volatilization rate, and $0<\rho <1$, ${\tau }_{ij}\left(\mathrm{t}\right)\in \left[{\tau }_{min},{\tau }_{max}\right]$, where ${\tau }_{min}$ and ${\tau }_{max}$ are the lower-bound and upper-bound of the pheromone concentration. We obtained all the formulas and parameters needed for FMCA. Therefore, the algorithmic flow of the FMCA is as follows (Algorithm 1):

Algorithm 1: Proposed Iterative Algorithm of Fractional-Order Memristive Ant Colony Algorithm (FMCA)
1:	Initialization:
2:	Set the number of iterations $t=0$;
3:	Initialize ant colony algorithm (ACO) parameters,$v$, $\alpha$, $\beta$, $\rho$, $\xi$, $Q_G$, $Q_a$, $Q_P$, $\gamma$, ${\tau }_0$, ${\tau }_{min}$, and ${\tau }_{max}$;
4:	Place each ant in $G$ randomly, $m=1,\cdots ,Q_a$;
5:	for each edge $\left(i,j\right)$, do
6:	Set ${\tau }_{ij}\left(t\right)~U\left(0,{\tau }_0\right)$;
7:	Set ${\eta }_{ij}\left(t\right)=1/d_{ij}$;
8	End
9:	Initialize low-pass filtering fracmemristor (LCSF),
10:	Initialize the parameter of LCSF: $A,B,v_1$
11:	Repeat
12:	for each ant population, number the population from 1 to $\gamma$,
13:	for each ant, number the ant from 1 to $m=\mathrm{int} \left(Q_{\mathrm{a}}/\gamma \right)$, do
14:	Set $tab{u}_{\mathrm{t}}\left(m,\theta \right)=\Phi$;
15:	Repeat
16:	Take transfer probability series of ant $m$ into LCSF
17:	the $\mathrm{m}th$ ant travels from the $i$ node to the $j$ node;
18:	than set $tab{u}_{\mathrm{t}}\left(m,\theta \right)=tab{u}_{\mathrm{t}}\left(m,\theta \right)\cup \left\{\left(\mathrm{i},j\right)\right\}$;
19:	compute all transfer probability in $tab{u}_t\left(m,\theta \right)$
20:	Until completes travelling all nodes in $G$;
21:	compute and rank $L^{\mathrm{m}}\left(t\right)$,
22:	return the shortest path $L^1\left(t\right)$;
23:	end
24:	for the edge in graph,
25:	update pheromone concentration;
26	then update the transfer probability
27:	end
28:	end
29:	Compute the shortest way of $\gamma$ parts of ants;
30:	Update the pheromone concentration on the shortest visited way with ${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+1/L_{min}\left(t\right)$;
31:	Set $t=t+1$;
32:	until the maximum number of cycles is reached;
33:	Compute $\underset{m=1,2,\cdots ,Q_a}{\min }{\left[L^m\left(t\right)\right]}^{}$.

3.3. Convergence Analysis of FMCA from a Mathematical Point of View

The convergence of the FMAC is mathematically proven and analyzed in this section.

Lemma 1.

Concerning the concentration of pheromones at any given edge$(i,j)$of$G$,${\tau }_{ij}\left(\mathrm{t}\right)$, because of$0<\rho <1$, an upper bound${\tau }_{\max }$can be theoretically established, which is:

$$\underset{t\to \infty }{\lim }{\tau }_{ij}\left(t\right)\le {\tau }_{\max }=\Delta {\tau }_{\max }/\rho ,$$

(32)

where $\Delta {\tau }_{m\mathrm{ax}}=\max \left[ \Delta \tau \left(\mathrm{t}\right)\right]=\max \left[{\displaystyle \sum _{m=1}^{N_3}\left|\frac{\mathrm{\Gamma }\left(m-v-1\right)}{\mathrm{\Gamma }\left(-v\right)\mathrm{\Gamma }\left(m\right)}\right|\Delta {\tau }_{ij}^{\mathrm{m}}\left(t\right)}\right]={\displaystyle \sum _{m=1}^{N_3}\left|\frac{\mathrm{\Gamma }\left(m-v-1\right)}{\mathrm{\Gamma }\left(-v\right)\mathrm{\Gamma }\left(m\right)}\right|\frac{1}{L_{ts}}}\ge 0$, $\forall t\in \left(1,\infty \right)$, and $L_{t\mathrm{s}}$ is the theoretical shortest route.

Proof of Lemma 1.

From Equation (31), after the initial iteration, the maximum pheromone concentration ${\tau }_{ij}^{\max }$ along the edge $\left(\mathrm{i},j\right)$ in the graph can be calculated as:

$${\tau }_{ij}^{\max }\left(1\right)=\left(1-\rho \right){\tau }_{ij}\left(0\right)+\Delta {\tau }_{\max },$$

(33)

Thus, from Equations (31) and (33), after another iteration, we may obtain the following formula for the maximum pheromone concentration ${\tau }_{ij}^{\max }$ along each edge $\left(i,j\right)$:

$${\tau }_{ij}^{\max }\left(2\right)=\left(1-\rho \right){\tau }_{ij}\left(1\right)+\Delta {\tau }_{\max } ={\left(1-\rho \right)}^2{\tau }_{ij}\left(0\right)+\left(1-\rho \right)\Delta {\tau }_{\max }+\Delta {\tau }_{\max },$$

(34)

The maximum pheromone concentration ${\tau }_{ij}^{\max }$ of edge $\left(i,j\right)$ after the $tth$ iteration was similarly revised,

$${\tau }_{ij}^{\max }\left(\mathrm{t}\right)={\left(1-\rho \right)}^{ t}{\tau }_{ij}\left(0\right)+{\displaystyle \sum _{k=1}^t\left[{\left(1-\rho \right)}^{ t-k}\Delta {\tau }_{\max }\right]} .$$

(35)

Then, Equation (35) derives an inequality:

$${\tau }_{ij}\left(\mathrm{t}\right)\le {\tau }_{ij}^{\max }\left(\mathrm{t}\right)={\left(1-\rho \right)}^{ t}{\tau }_{ij}\left(0\right)+{\displaystyle \sum _{k=1}^t\left[{\left(1-\rho \right)}^{ t-k}\Delta {\tau }_{\max }\right]} ,$$

(36)

Because $0<\rho <1$, depending on the characteristics of the geometric progression sum, we obtain

$$\underset{t\to \infty }{\lim }{\tau }_{ij}\left(\mathrm{t}\right)\le \underset{t\to \infty }{\lim }\left\{{\left(1-\rho \right)}^{ t}{\tau }_{ij}\left(0\right)+ {\left\{\left[1-{\left(1-\rho \right)}^{ t}\right]/\rho \right\}}^{}\Delta {\tau }_{\max }\right\}=\Delta {\tau }_{\max }/\rho .$$

(37)

The proof ends. □

Lemma 2.

If$p_{id}^{\ast }\left(t\right)$is the lowest probability of finding the optimum travel route${\pi }^{\ast }$in the$tth$iteration, a random tiny integer$p_{sud}^t$and the upper bound$p_{up}^t$,$0<p_{up}^t<1$, a sufficient number of iterations$t$, we obtain that

$$p_{id}^{\ast }\left(t\right)\ge 1-p_{ub}^{\mathrm{t}},$$

(38)

$$\underset{t\to \infty }{\lim }{p}_{id}^{\ast }\left(t\right)=1.$$

(39)

Proof of Lemma 2.

Since the pheromone is bound: ${\tau }_{ij}\left(t\right)\in \left[{\tau }_{\min },{\tau }_{\max }\right]$, in Equations (28)–(30). We calculate the bottom bound $p_{min}^v$ of the minimum probability of an ant searching for the best trip path.

$$p_{\min }^v=\frac{1}{f}\left[p_{\min }+{\displaystyle \sum _{k=1}^{N_1-1}\left|\frac{\mathrm{\Gamma }\left(m-v\right)}{\mathrm{\Gamma }\left(-v\right)\mathrm{\Gamma }\left(m+1\right)}\right|p_{\min }}\right],$$

(40)

Taking the worst-case scenario into consideration, if the amount of pheromones is ${\tau }_{\min }$, and the pheromones of the others are ${\tau }_{\max }$, $p_{\min }=\frac{{\left(T_{\min }^{}\right)}^{ \alpha }{\left(N_{\min }^{}\right)}^{ \beta }}{{\left(T_{\min }^{}\right)}^{ \alpha }{\left(N_{\min }^{}\right)}^{ \beta }+{\displaystyle \sum _{\left(\mathrm{i}, \mathrm{u}\right) \in {\pi }^{\ast }} {\left[T_{iu}^{}\left(t\right)\right]}^{ \alpha }{\left[N_{iu}^{}\left(t\right)\right]}^{ \beta }}}=\frac{{\left(T_{\min }^{}\right)}^{ \alpha }{\left(N_{\min }^{}\right)}^{ \beta }}{{\left(T_{\min }^{}\right)}^{ \alpha }{\left(N_{\min }^{}\right)}^{ \beta }+\left(K_G-1\right){\left(T_{\max }^{}\right)}^{ \alpha }{\left(N_{\max }^{}\right)}^{ \beta }}$, $K_G$ is the interconnectedness of $G$,

$$\begin{array}{l}{T}_{\min }^{}=\underset{j\in C_i^{\mathrm{n}}\left(t\right) , \left(j+m\right)\in C_{\left(j+m-1\right)}^n\left(t\right)}{\min }\left[{\tau }_{ij}^{}\left(t\right), {\tau }_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)\right],\\ N_{\min }^{}=\underset{j\in C_i^n\left(t\right) ,\left(j+m\right)\in C_{\left(j+k-1\right)}^n\left(t\right)}{\min }\left[{\eta }_{ij}^{}\left(t\right), {\eta }_{\left(j+m-1\right)\left(j+m\right)}\left(t\right)\right].\\ \end{array}$$

Consequently, the $v\text{-}\mathrm{order}$ transition probability of the ant on a journey path $\pi$ in the $tth$ iteration

$$0<p_{\min }^v\left(t\right)\le {}^{m}p_{ij}^v\left(t\right)<1,$$

(41)

Because of $\left(i,j\right)\in \pi$ and ${\pi }^{\ast }\subset \pi$, any viable path developed satisfies the following conditions:

$$0<{\left[p_{\min }^v\left(t\right)\right]}^{Q_G}\le {\left[{}^{m}p_{ij}^v\left(t\right)\right]}^{Q_G}<1,$$

(42)

where $Q_G$ means the number of the nodes in the graph $G$, depending on the features of the complementary assembly, the upper bound $p_{ub}$ on the probability of not recognizing the best travel path $\pi$ is

$$p_{ub}=1-{\left[p_{\min }^v\left(t\right)\right]}^{Q_G} .$$

(43)

Then, from Equation (43), after the initial $t$ trials, the probability of covering any edge in the optimum travel route ${\pi }^{\ast }$ with the lowest upper bound $p_{up}^t$:

$$p_{up}^t={\left\{1-{\left[p_{\min }^v\left(t\right)\right]}^{Q_G} \right\}}^{ t}>0.$$

(44)

Therefore, the lowest bound $p_{id}^{\ast }$ of the probability of traversing the edge of the optimum travel path ${\pi }^{\ast }$ is that

$$p_{id}^{\ast }\ge 1-p_{up}^t=1-{\left\{1-{\left[p_{\min }^v\left(t\right)\right]}^{Q_G} \right\}}^{ t}.$$

(45)

From (42), we obtain the following:

$$\underset{t\to \infty }{\lim }{p}_{id}^{\ast }\ge \underset{t\to \infty }{\lim }\left\{ 1-{\left\{1-{\left[p_{\min }^v\left(t\right)\right]}^{Q_G} \right\}}^{ t}\right\}=1.$$

(46)

The proof ends. □

From above-mentioned proofs, as we have seen, FMAC can eventually find an optimal path.

4. Experiment of FMAC in TSP Problem

Ant colony algorithm (ACO) is a well-known method for solving discrete group optimization problems, such as the traveling salesman problem (TSP) and the vehicle routing issue, by emulating an ant colony seeking food. For the FMAC performance testing, we utilized a publicly accessible TSP problem benchmark library (TSPLIB [48]).

FMAC consists of two major components: the module of transfer probability prediction based on the fracmemristor (LCSF), whose series number is 8, and the FMAC module. Parameters of the FMAC in

Table 1. Parameters of FMAC.

Parameters	Value
$\alpha$	1
$\beta$	5
${\tau }_0$	0.1
$\rho$	0.2
$\xi$	1.7

: pheromone importance $\alpha$, heuristic factor importance $\beta$, pheromone evaporation coefficient $\rho$, constraint leniency $\xi$, fractional order $v$, the coefficient $v$ should be the same as the fractional order of LCSF.

4.1. Effect of Fractional-Order Coefficients V in FMAC

The fractional order is the most crucial parameter in FMAC, which controls the systematic properties of the physical memristive system LCSF and also plays a vital role in the fractional order ant colony algorithm module for pheromone concentration updating. In this section, we conducted experiments involving the TSP problem with the best known solution to determine the fractional order values.

In Equation (29), we selected the first eight look-forward transfer probability coefficients, and the value changes with $v$.

Table 2. The weighting coefficient changes with fractional-order $v$.

$v$	$w_0$	$w_1$	$w_2$	$w_3$	$w_4$	$w_5$	$w_6$	$w_7$
−1	1	1	1	1	1	1	1	1
−0.75	1	0.75	0.6563	0.6016	0.5640	0.5358	0.5134	0.4951
−0.5	1	0.5	0.375	0.3125	0.2734	0.2461	0.2256	0.2095
−0.25	1	0.25	0.1563	0.1172	0.0952	0.0809	0.0708	0.0632
0	1	0	0	0	0	0	0	0
0.25	1	0.25	0.0938	0.0547	0.0376	0.0282	0.0223	0.0183
0.5	1	0.5	0.125	0.0625	0.0391	0.0273	0.0205	0.0161
0.75	1	0.75	0.0938	0.0391	0.0220	0.0143	0.0101	0.0076
1	1	1	0	0	0	0	0	0

shows the result. When $-1<v<1$, $w_{n-1}>w_n$, the information regarding the future transfer probability is given to the current ant node, and the more away the node is, the less information is passed, corresponding with our intuitive perception.

We chose TSPLIB’s KroA100 to evaluate the performance of various fractional orders. The optimal theoretical global solution for kroA100 is 21282.

In

Table 3. Evaluation of FMCA in KroA100 with the change of fractional-order $v$.

$\mathit{v}$	Minimum Solution	Maximum Solution	Average Solution	Root Mean Square Error	Relative Error (%)
−0.75	21,282	22,064	21,673.7	450.83	1.85
−0.5	21,282	21,976	21,550.3	327.16	1.37
−0.25	21,282	21,518	21,483.7	136.19	0.39
0.0	21,282	21,926	21,582.4	373.54	1.48
0.25	21,282	21,926	21,571.6	346.77	1.23
0.5	21,282	21,873	21,490.4	201.86	0.51
0.75	21,282	21,508	21,301.5	54.12	0.13
1	21,282	21,703	21,432.7	97.16	0.32

, when $v=0.75$, the weighted coefficient makes sense, and FMAC achieves good optimization results. $v=0.75$ can only sometimes be the best fractional order of the FMCA for the TSP problem. As seen in Table 3, FMAC can accomplish a more desirable optimization when $0.5<v<1$. In this article, we set $v=0.75$ for all TSP problems.

4.2. FMAC Convergence Experiments

FMAC can communicate the future transfer probability information to the current node. From an application standpoint, FMAC should be able to converge more quickly than ICAC. In this part, we compare ACO, MMAS, and FACA with FMAC. The test cases were chosen from the TSPLIB: berlin52, eil51, eil76, eil101.

The hardware environment is 8.00 GB RAM and Intel (R) Core (TM) i5-4800 CPU 3.2 GHz; the software environment is Window10, MATLAB R2018a. The experiment is executed 20 times, and the maximum number of iterations is 300, and the ant’s number is 100.

As shown in Figure 7, Figure 8, Figure 9 and Figure 10, FMAC and FACA converge much faster than the traditional integer-order IACA in solving the TSP problems such as berlin52. As can be seen, for TSP problems with a small number of cities, FMAC gives better results in approximately 20 rounds, and converges almost to the optimal outcome at 50 iterations. In contrast, traditional IACAs such as ACO and MMAS converge much slower. Moreover, after 300 iterations, it is still possible to converge near the global optimum.

4.3. FMAC and Various Improved Ant Colony Algorithms for Comparison

For comparative purposes, the optimization capabilities of the FACA are evaluated by examining a large number of well-improved ACO algorithms, such as ACO [2], MMAS [6], PACO-3opt [49], and FACA [47]. We used the following TSPLIB test datasets: berlin52, eil51, eil76, eil101, rat99, and st70. The best solutions for berlin52, eil51, eil76, eil101, rat99, and st70 are 7542, 426, 538, 629, 1211, and 675, respectively.

The hardware environment is 8.00 GB RAM, and Intel (R) Core (TM) i5-4800 CPU 3.2 GHz; the software environment is Window10, MATLAB R2018a. The experiment is executed 20 times, the max iteration is 500, and the ant’s number is 100.

Table 4. Performance of experiment: (a) berlin52; (b) eil51; (c) eil76; (d) eil101; (e) rat99, and (f) st70 (NA in table means no data were obtained from the PACO-3opt paper).

Optimization Algorithms	Best Solution	Average Solution	Time Consumption
(a)
ACO [2]	7542	7657.2	43.24
MMAS [6]	7542	7596.3	56.48
PACO-3opt [49]	7542	7542	NA
FACA [47]	7542	7542	119.57
FMAC (ours)	7542	7542	75.17
(b)
ACO [2]	437	443.5	57.84
MMAS [6]	431	436.1	75.34
PACO-3opt [49]	426	426.3	NA
FACA [47]	426	427.4	156.77
FMAC (ours)	426	426.8	92.38
(c)
ACO [2]	544	563.6	129.04
MMAS [6]	537	552.9	167.58
PACO-3opt [49]	538	539.85	NA
FACA [47]	538	541.0	354.22
FMAC (ours)	538	541.3	186.18
(d)
ACO [2]	648	662.1	274.62
MMAS [6]	634	651.3	358.81
PACO-3opt [49]	629	630.5	NA
FACA [47]	629	630.6	758.10
FMAC (ours)	629	630.39	489.37
(e)
ACO [2]	1212	1216.7	300.71
MMAS [6]	1212	1214.5	383.83
PACO-3opt [49]	1213	1217.1	NA
FACA [47]	1211	1213.0	758.17
FMAC (ours)	1212	1214.1	512.09
(f)
ACO [2]	678	686.3	119.76
MMAS [6]	675	682.6	155.10
PACO-3opt [49]	676	677.85	NA
FACA [47]	675	680.1	323.82
FMAC (ours)	675	679.2	219.11

indicates that PACO-3opt, FACA, and FMAC are superior to ACO and MMAS. PACO-3opt [47] is now the best integer-order improved ant colony algorithm. FACA and FMAC obtain the shortest path of TSP in rat99 and st70, and are better than PACO-3opt. FMAC and FACA are almost the best algorithms for dealing with small-scale TSP problems among the ACO improvement algorithms. Applying LSCF to FACA, the physical equivalent circuit improves the efficiency of computing fractional order transfer probabilities, so FMAC should be faster than FACA operations. The experimental results verify our conjecture.

5. Discussion and Conclusions

5.1. Discusion

We conducted three experiments in Section 4. The fractional order of FMAC was determined in the first experiment, and FMAC produces the best performance in korA100 when v = 0.75. However, the optimal value of v varies for different TSP problems; in reality, FMAC has better results $0.5<v<1$. For the second and third experiments, we find that FMAC and FACA converge significantly faster than ACO and MMAS, and the optimal outcomes are superior to those obtained by ACO and MMAS. Nowadays, FMAC and FACA are nearly the optimum algorithms for small-scale TSP problems. Due to the fractional calculus being substituted into IACA to rewrite the transfer probabilities, FMAC and FACA need significantly more time than IACA. Thanks to the use of an equivalent physical circuit, the speed of FMAC is improved relative to FACA by approximately 30%.

5.2. Conclusions

The present research aimed to apply the fracmemristor to the fractional order ant colony algorithm. In our investigation of the analogous circuit of the fracmemristor, we discovered that the topology of the ant’s future transition probability sequence and the LCSF circuit are comparable. We continued to derive the LCSF formulation and found that it may be easily used for fractional order transfer probability calculations. This paper empirically demonstrates that hardware topological dimensions can be leveraged to accelerate the software algorithms with comparable topologies. However, the analysis is restricted to v-order LCSFs with the same topology and transition probability sequence for the ant’s future transitions. Then, can we artificially design fracmemristor systems with matching topologies to accelerate the processing of other algorithms? We will continue our research in this area—building fracmemristor physical systems to accelerate the algorithm.