Abstract
This paper first proposes a fractional prospect theory-based method for modeling the bidding strategy of a power retail company in the uniform pricing electricity market under price uncertainty. Different from the traditional methods which assume that the retail company always bids completely rationally to maximize its individual payoffs, this paper introduces the prospect theory (PT) into the bidding model to reflect the impacts of psychological factors and subjective perceptions. To address the partial uncertainties brought by the continuous probability distribution in the value function, this paper modifies the classical PT into the fractional prospect theory (FPT) and builds up the FPT-based bidding strategy model under 1-segment and 3-segment bidding rules. The simulation results show that the proposed method can effectively model the psychological factors in the bidding strategy of a power retail company in the uniform pricing electricity market under price uncertainty, which can help to further study the competition and equilibrium of the uniform pricing market considering the psychological factors of the participants.
1. Introduction
With the rise of worldwide reformulation of the electricity market, many power retail companies have been established and have begun to participate in the market competition [1]. These retail companies actively participate to bid and buy electricity in the wholesale market and sell it to the end-users in the retail market to earn the price difference. Consequently, research into the bidding strategies of retail companies in the electricity market has increased.
Generally, the relevant studies can be divided into three types: game theory methods, optimization-based method, and agent-based simulation methods. Game theory models and equilibrium analysis constitute the most widely employed methodological framework to study bidding strategies. For example, ref. [2] used the cooperative game of retail companies’ bidding in China’s spot market. To model the bidding model concerning the market clearing process, bi-level optimization with mathematical program with equilibrium constraints (MPEC) and Karush–Kuhn–Tucker (KKT) optimality conditions provide rigorous logic tools to study bidding strategies, which has been used to study the retailer’s bidding in the short-term electricity market [3]. In [4], the bi-level method was proposed for optimizing the retail company’s bidding in the block-bidding electricity market. Apart from game theory methods, optimization-based methods have been widely used for bidding strategy optimization. In [5], the bidding strategy of the retail company was optimized considering the price-sensitive loads. Ref. [6] studied the retail company’s bidding strategy with robust optimization under market price uncertainties. In [7], the retailer’s bidding strategy was optimized considering the price uncertainty, in which the demand price quota curve was applied to model the bidding impacts on the price uncertainties. In addition, agent-based methods are often applied with reinforcement learning to simulate a large-scale system with distributed bidders [8,9], in which Roth–Erev (RE) learning, Q-learning, and deep learning algorithms are often used. Ref. [10] studied the diverse bidding strategies of power retail company, in which different objective functions were proposed, and the power retail company was assumed to bid rationally following their objective functions.
To date, most of the above literature is founded on the presumption that retail companies always bid completely rationally to maximize their individual payoffs without considering psychological factors and subjective perceptions. Specifically, most work assumes that the retail company makes decisions according to the expected utility theory (EUT). In fact, real-world bidding decisions are significantly influenced by the bidder’s subjective perception during decision making, which often significantly deviates from the theoretical results [11]. If the psychological and subjective factors are neglected in the relevant studies and applications, the effectiveness and practicality of the corresponding conclusions will undoubtedly be limited. Considering that many bidding-relevant studies provide a theoretical basis and data support for policy making for the electricity market, it is necessary to include the real-world human-like bidding strategies into the relevant models.
A Nobel Prize-winning theory, Prospect Theory (PT) [11], provides a good approach to modeling human behaviors with psychological factors. PT is a theory of behavioral economics and behavioral finance that was developed by Daniel Kahneman and Amos Tversky in 1979, which explains the fact that people usually value gains and losses differently and place different weights on gains and losses in subjective perception. In the past decades, PT and its variants have been widely explored and applied for modeling individual and group decision making in various areas [12,13], e.g., supply chain designs [14] and stock investment [15]. In the field of power and energy systems, ref. [16] reviewed the economic decisions in the power system with the PT method. Moreover, PT has been applied in decisions for electric vehicle charging [17], power energy trading [18], renewable power investment [19], and electric consumer actions [20]. Focusing on the bidding studies in the power systems, PT has been applied to generation companies’ bidding [21,22] and prosumer’s bidding [23]. In other areas, PT has been used for bidding in the civil construction industry [24,25] and online auctions [26,27].
However, the above methods can hardly be directly used for a retail company’s bidding in the uniform pricing electricity market under price uncertainty. In the uniform pricing market, the retail company’s payoff is directly dependent on the market clearing price, and thus the payoff is uncertain due to the uncertain market price. As a result, the partial value function in the classical PT model becomes uncertain, making it further difficult to calculate the PT value using the classical PT method. In previous relevant studies, ref. [21] assumed that the market price can be forecasted perfectly and does not consider the price uncertainty in the PT model; refs. [22,23] studied the bidding strategy under the pay-as-bid pricing mechanism, in which the value function was only dependent on the bidding price. To the best of our knowledge, there are still no specific studies focusing on modeling PT-based bidding strategies concerning price uncertainty in the uniform pricing electricity market. However, compared to the pay-as-bid pricing mechanism, the uniform pricing mechanism has been more widely adopted. Nowadays, almost all the electricity wholesale markets around the world, e.g., in the U.S. [28] and China [29], apply uniform pricing mechanism. To make the PT model suitable for the uniform pricing electricity market under price uncertainty, we are motivated to modify the existing PT method to model a retail company’s bidding considering the psychological and subjective factors in the uniform pricing electricity market under price uncertainty. Compared to the existing work in [4,7,10], the prospect theory is introduced in this work to describe the psychological and subjective factors in the retail company’s biddings. Compared to our previous work in [23], the fractional prospect theory (FPT) is proposed for modeling the bidding strategy under a uniform pricing mechanism, in which the classical PT cannot directly deal with the uncertain terms brought by the continuous probability distribution in the value functions. The other differences are given in Table 1.

Table 1.
Literature review.
This paper first proposes a fractional prospect theory-based bidding strategy of a power retail company in the uniform pricing electricity market under price uncertainty, providing a mathematical model which is suitable for describing the psychological factors in uniform pricing market bidding. The main contributions of this paper are as follows.
- A fractional prospect theory (FPT)-based model to optimize the bidding strategy of a power retail company. The classical prospect theory is modified to the fractional prospect theory (FPT) to overcome the shortcoming that classical PT cannot directly deal with the partially uncertain terms brought by the continuous probability distribution in the value functions.
- A four-step method to calculate FPT value with partially uncertain value functions is proposed. Specifically, the deterministic and uncertain parts are calculated separately, and then they are added up with normalization. A genetic algorithm is provided to solve the FPT-based bidding model.
The remainder of this paper is organized as follows: Section 2 introduces the uniform pricing electricity market, including the market structure, bidding rules, and clearing mechanism. Section 3 presents the FPT method and FPT-based bidding strategy. Section 4 presents a genetic algorithm to solve the proposed model. In Section 5, a case study is conducted to verify the effectiveness of the proposed method, and Section 6 presents the conclusions.
2. Uniform Pricing Electricity Market
2.1. Market Structure
Generally, electricity markets include the wholesale market and the retail market from the viewpoint of the participants. Different products, e.g., power energy, regulation reserve, and spinning reserve, are traded in the market. In this paper, we focus on the bidding behaviors of the retail company in the wholesale market. The retail company buys electricity from the wholesale market and sells it to the end-users in the retail market to earn the price difference, as shown in Figure 1.
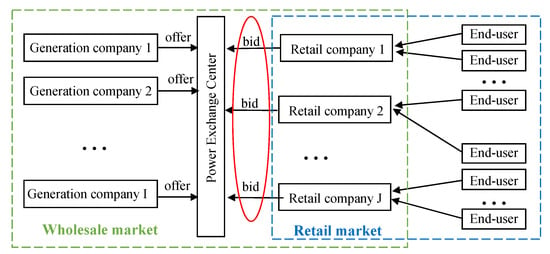
Figure 1.
Structure of the electricity market.
2.2. Bidding Rules and Uniform Pricing Mechanism
The retail company often has options to bid a single price and a demand quantity (under the 1-segment bidding rule) or a multi-segment price–quantity curve (under a multi-segment bidding rule) in the wholesale market. Bidding rules vary in different markets around the world, and the number of segments can be one (Jiangsu, China), three (Guangdong, China), six (Zhejiang, China), or ten (Australia [30] and PJM, U.S. [31]). Under a multi-segment bidding rule, the bidding quantity can be divided into several segments, and bidding prices are monotonically decreasing for each segment, as shown in Figure 2. The market operator will clean the market according to the bidding quantities and prices from all the participants, while the retail companies with higher bidding prices will have higher priorities to be cleared.
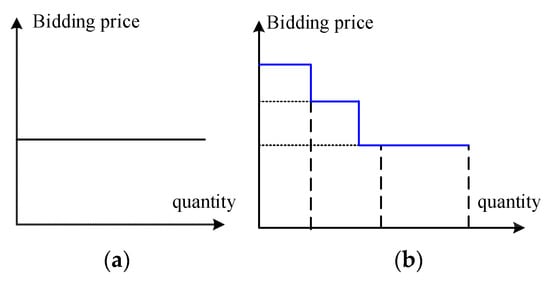
Figure 2.
Bidding rules (a) 1-segment bidding; (b) 3-segment bidding.
Currently, there are two main pricing mechanisms in the electricity market around the world: pay-as-bid and uniform pricing [32]. In the uniform pricing market, all winning participants are settled at the same market clearing price and purchase the same price to buy the electricity regardless of their bidding prices [33], while in the pay-as-bid market, winning participants buy the electricity at their individual bidding price. The choice between uniform and pay-as-bid pricing for electricity auctions has been one of the most important issues in newly deregulated electricity markets. Currently, compared to pay-as-bid, the uniform pricing mechanism is more widely applied in practice, and is currently used for all the wholesale electricity markets in the U.S. and most markets in China. Therefore, this paper studies the bidding strategy under the uniform pricing mechanism.
2.3. Uncertain Market Price
Market clearing price is uncertain due to the dynamic changing status of the market competition. Generally, the market clearing price is often assumed to satisfy the normal distribution. Considering that the market clearing price is not from negative infinite to positive infinite, the market clearing price is assumed to satisfy the normal distribution in the interval of , and the truncated normal distribution [34] is applied as shown by (1).
where is the probability distribution function (PDF) of the original normal distribution; is the cumulative distribution function (CDF) of the original normal distribution; and and are the expected value and the standard deviation of the truncated normal probability distribution, respectively.
3. Fractional Prospect Theory-Based Bidding Strategy
3.1. Different Conditions of Bidding Results
A power retail company can bid different prices in the electricity wholesale market, which can overall lead to two different conditions of the bidding results: win or fail, as shown in Figure 3. Under the 1-segment bidding rule, if the bidding price is higher or equal to the market clearing price (), it will win buying the electricity; if the bidding price is lower than the market clearing price (), it fails at bidding in the wholesale market and needs find other ways to meet the end-users’ demand. Some retail companies choose to buy electricity from other companies or utilities to meet the supply requirement of their end-users, and some may cancel the selling plan.
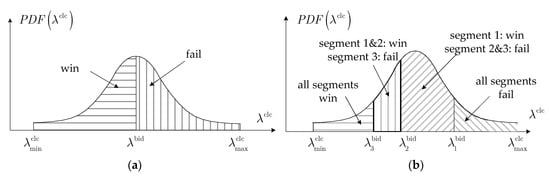
Figure 3.
Winning and losing conditions with uncertain price. (a) Two conditions under 1-segment bidding rule. (b) Four conditions under 3-segment bidding rule.
Note that the above analysis is based on the 1-segment bidding rule. If the market implements the N-segment bidding rule, the actual bidding result of the retail company will consist of N + 1 conditions. For example, Figure 3b presents the bidding results under the 3-segment bidding rule, and four conditions might occur. If the bidding prices of all segments are higher or equal to the market clearing price (), all segments win the bidding; if , the 1st and 2nd segments win and the 3rd one fails; if , the 1st segment wins and the 2nd and 3rd ones fail; and if , all segments fail.
3.2. Probability Model of Different Conditions
The probabilities of winning or failure are dependent on the probability of the market clearing price and can be calculated based on PDF. Under the 1-segment bidding rule, the winning probability is the integral value of the PDF from to , and the failure probability is the integral value of the PDF from to , as shown in (2).
3.3. Profit Model of Different Conditions
Assume that the electricity quantity needed to meet the demand is , and we assume that the retail company bids the quantity required without considering the demand uncertainty, i.e., . In the uniform pricing market, the trading will be settled by the uniform market clearing price. Here, we assume that the retail company sells the electricity to the end-user at the price of . If the retail company fails at bidding in the wholesale market, it needs to refund the end-users and the actual profit turns to zero. Then, the actual profit of the retail company under the 1-segment bidding rule is given as (3).
where is the bidding quantity under the 1-segment bidding rule, which in most cases is equal to the cleared amount of electricity unless it is the marginal participant in the market; is the sold price to the end-user.
3.4. Fractional Prospect Theory-Based Value Function Model
Traditionally, the expected utility theory (EUT) and classical prospect theory (PT) have been widely used to study the decision making of the participants in the electricity market. The EUT value is the expected profit of each condition, as shown in (4). As EUT assumes that the participants bid rationally but the actual decision-making behaviors are found to often deviate from the EUT under risk conditions, the classical prospect theory (PT) was proposed [12], as given in (5). Following the PT theory, people use their subjective values and probabilities rather than the actual ones to evaluate the possible outcomes, in which the summations of the productions of the subjective values and probabilities of all conditions is the PT value. The general formulas of the subjective probabilities and values are typically shown as (6) and (7), respectively [12], and the typical shapes of these two functions are illustrated in Figure 4.
where is the value function reflecting the subjective values, indicating how the retail company subjectively measures gains and losses with respect to a reference point; is the weighting function reflecting subjective probability; is the reference point, representing a turning point of gains and losses in the mind; and are risk attitude coefficients related to gains and losses, respectively; is the loss aversion parameter; and and are attitude coefficients of gains and losses probabilities, respectively.
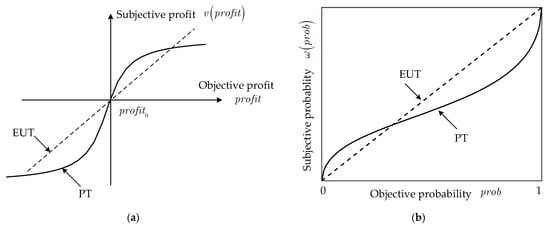
Figure 4.
Typical shapes of subjective (a) values and (b) probabilities.
However, the classical PT theory cannot be directly applied to the bidding problem in the uniform pricing market when considering price uncertainty. Firstly, it can be seen from (5) that classical PT is a form of the discrete distribution of the outcomes. The drawback is that it is not suitable for continuous distributions as has been pointed out in [35,36]. However, some segments of the profit functions (3) are dependent on the uncertain variable , and thus the value function is partially uncertain with a continuous probability distribution of . Secondly, note that the profit function is a segmented function, in which some segments consist of uncertain variables and others do not. In other words, only some segments of the profit functions (3) are uncertain and some others are deterministic. Therefore, the value function is partially uncertain, and it cannot directly apply some other PT-based method, e.g., cumulative PT [12].
A straightforward idea to solve the above problem is to discretize the continuous distribution into multiple outcomes and calculate the probability of each outcome, but this idea cannot work well because the discretized probabilities are usually very low, e.g., 0.001. In the classical PT method, these low probabilities will be transformed into subjective probabilities by the weighting function. Because the classical PT tends to overestimate the likelihood of small probability conditions, all these probabilities will likely be overestimated, and thus a distortion effect will be mistakenly imposed.
To address this issue, we modified the classical PT into a fractional PT to make it suitable for the piecewise function with partial uncertainties, while the basic idea is following the modified PT for continuous distributions [37,38]. Specifically, the overall function is divided into two parts: the uncertain part and the deterministic part. The uncertain part refers to the value function including uncertain variables, while the deterministic part refers to the totally deterministic part. The deterministic and uncertain parts are calculated separately and then added up with normalization. Finally, the proposed FPT method consists of four steps, as shown in Figure 5.

Figure 5.
The proposed FPT method.
Step 1. Derive the probability distribution of the uncertain parts in the profit function. The under the 1-segment bidding rule follows a similar truncated normal distribution as .
Step 2. Calculate the uncertain part via the continuous form of PT. For example, the in (5) under the 1-segment bidding rule is transformed into (8). Meanwhile, the probability weighting function is modified into (9) to reflect that the subjective evaluation distorts the objective probabilities.
Step 3. Add the deterministic and uncertain parts. This result under the 1-segment bidding rule is given as (10) and (11), respectively.
Step 4. Normalization. As the continuous form indeed consists of a large or infinite number of outcomes, the normalization with the sum of the weighted probabilities is essential [37]. Therefore, the final FPT value under the 1-segment bidding rule is normalized as (11).
Based on the same method, the final FPT value under the 3-segment bidding rule is given in (12).
3.5. Fractional Prospect Theory-Based Optimal Bidding Model
The FPT-based optimal bidding model of a retail company is to determine the optimal bidding prices and quantities for maximizing its FPT-based value, as shown by (13).
The constraints under the 1-segment rule are given as (14). Under the 3-segment bidding rule, the minimum percentage of the bidding quantity constraint of each segment is added, as shown in the last line in (15). For example, such a percentage is 20% in the Guangdong province monthly electricity market, which is one of the largest electricity markets in China.
where is the minimum percentage of the bidding quantity constraint.
4. Solving the Algorithm
In the FPT-based optimal bidding model, the objective function is a fractional function with integrals, and the integrand function includes probability distribution functions concerning the decision variables. Therefore, it is challenging to solve it analytically. To address this problem, we used a genetic algorithm (GA) [37] to solve this problem. The flow chart of the method for solving the proposed model is given in Figure 6, and the main parameters are given in Table 2.
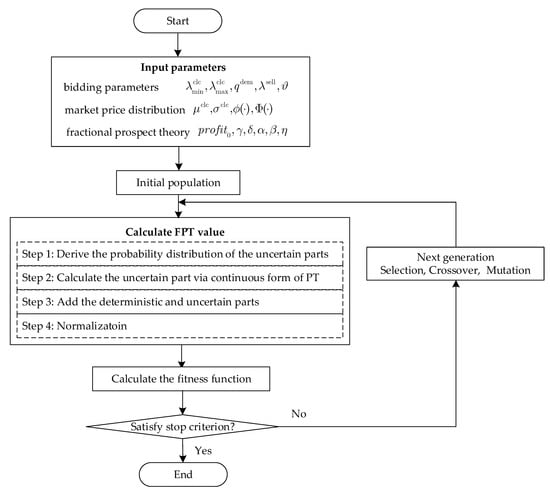
Figure 6.
Flowchart of GA for FPT-based optimal bidding problem.

Table 2.
GA parameters.
5. Case Study
5.1. Case Settings
This section conducts a case study of retail company biddings with the FPT-based method. In this work, we designed a virtual case, in which the market price data are set generally based on the monthly electricity market price of Guangdong province in China [38]. In detail, the relative parameters are given as follows: = CNY 439.8/MWh, = CNY 13/MWh, = 0, = = CNY 460/MWh, = 50 million kWh, and = 20%.
To compare the bidding strategies of the retail companies with different psychological prospects, three retail companies with the same bidding quantity but different FPT parameters were designed, representing the “real” bidder with conservative, neutral, and aggressive bidding strategies. In addition, the EUT-based bidder is also simulated, representing the rational bidding strategy.
The FPT-based parameters are given in Table 3. The average profit in China’s electricity market is about CNY 10–20/MWh. Therefore, the total profit of selling the electricity of 50 million kWh is around CNY 0.5–1.0 million. As a result, the reference point is set around CNY 0.5–1.0 million. The more aggressive bidder is set with a higher reference point of the profit () and a lower loss aversion , indicating that it has a higher profit goal and is less sensitive to loss. The parameters and represent the fact that people are more sensitive to the value changes closer to the reference point, which are usually set as 0.88 in most studies [12,16]. The parameters and are attitude coefficients of gain and loss probabilities, respectively. The more aggressive bidders are set with the lower and , representing that they are more likely to distort the objective probability, i.e., overestimating the events with low probability and underestimating the events with high probability.

Table 3.
FPT parameters.
5.2. Results under 1-Segment Bidding Rule
This section presents the optimized results with the EUT-based and FPT-based methods under the 1-segment bidding rule. Table 4 shows the optimal bidding price in the first line. The rational retail company bids at CNY 460.0/MWh with the EUT-based method, which is equal to the maximum available bidding price. Bidding at the highest price guarantees the probability of winning the bidding, which is the best bidding strategy for the perfectly rational bidder. Such a result is consistent with our common knowledge. In contrast, the prices of the “real” bidder with FPT-based methods deviate from the rational one. Because the “real” bidder has a reference point of the profit, it will bid a lower price to avoid a certain condition that it wins the bid to buy the electricity but the profit is lower than its reference point. If not considering the price uncertainty, we can easily calculate that the theoretical bidding prices for reaching the reference points (if the bid succeeds) as CNY 446.0 (conservative), 442.0 (neutral), and 438.0/MWh (aggressive). However, the prices of the “real” bidder also deviated from the above ones. The reason is that the decrease in the bidding price decreases the probability of winning the bid. Then, the optimized result is a comprehensive result of the subjective value and weighting functions caused by the price uncertainty and psychological factors, and the optimal FPT-based bidding prices are lower than the rational one but higher than the calculated theoretical ones. Comparing the results among the three FPT-based methods, the conservative bidder is more likely to avoid the risk of losing bids, and thus its bidding price (CNY 455.2/MWh) is the highest among them.

Table 4.
Optimized results under 1-segment bidding rule.
The second and third rows in Table 4 present the FPT and EUT values of each method. The FPT values reflect the subjective values in the bidder’s mind, while the increase of the reference points resulted in an overall decrease in the FPT values, and the FPT value gradually decreased from 106.03 thousand (conservative) to 84.37 thousand (neutral), and to 67.26 thousand (aggressive). As for the EUT value, it also decreased as the bidding strategy became more aggressive. Because the winning probability decreases as the bidding price decreases and the clearing price does not change in the uniform pricing market, the EUT is therefore decreasing. As a result, the EUT values of “real” bidders cannot reach the rational bidder, which is consistent with our common knowledge. Specifically, the EUT value of the “real” bidder decreased by 0.7% (conservative), 6.5% (neutral), and 19.6% (aggressive) compared to the rational bidder. However, it should be noted that the proposed method does not intend to show that the methods with higher EUT values overwhelm the lower ones. The main aim of the proposed method is to provide a model to mathematically describe the psychological factors for bidding in the uniform pricing market bidding. Moreover, it can be found that differences between FPT values of the three “real” bidders were much larger than their EUT value differences, indicating that the psychological factors enlarged the differences in their subjective minds.
5.3. Results under 3-Segment Bidding Rule
Table 5 presents the optimized results with the EUT-based and FPT-based methods under the 3-segment bidding rule. In the uniform pricing market, the optimal strategy for the rational bidder with the EUT-based method is to bid the same price (CNY 460.0/MWh) for all three segments, which is the same as the one under the 1-segment bidding rule. However, it is obvious that such a result significantly deviates from the realized data in the actual markets. For example, the Australian Energy Market (AEM) [32] and PJM (Pennsylvania–New Jersey–Maryland Interconnection) market in the U.S. [33] offer some historical bidding data to the public. From the actual data, it can be seen that most participants will not bid the same prices for different segments. Therefore, it is significantly necessary to consider the psychological factors in the bidding model. Meanwhile, because the bidding prices of the three segments are the same for the EUT-based method, the optimal solution of the bidding quantities is not unique.

Table 5.
Optimized results under 3-segment bidding rule.
As for the “real” bidder with the FPT-based method, the optimal prices are lower than the rational bidder to better reach the reference points to make a profit. For each bidder, the results show that it is likely to bid a relatively higher price in the first one or two segments with a large quantity. Such a strategy can help to ensure the first one or two segments have a larger probability to win. Comparing the results under the 3-segment bidding rule to the 1-segment one, most prices were lower than the corresponding prices under the 1-segment rule. Comparing the results of the three “real” bidders, the results show that as the bidder becomes more aggressive, the bidding prices decreased because the aggressive bidder has a higher reference point to pursue the profit, a lower to ignore the loss, and a smaller and to further underestimated the increasing probability of loss.
The FPT and EUT values of each method are presented in the last two rows in the Table 5. The results show that the FPT values decrease when the retail company becomes more aggressive, which is mainly caused by the increase in the reference point. Meanwhile, the “real” bidder had a lower EUT value than the rational bidder, which decreased by 5.3% (conservative), 15.4% (neutral), and 36.2% (aggressive) compared to the rational bidder.
Meanwhile, because the bidding prices of the three segments are the same for the EUT-based method, the optimal solution of the bidding quantities is not unique, which will be detailed discussed in Section 5.4.
5.4. Computation Performances
This section analyzes the computation performances of the proposed method. Figure 7 demonstrates the objective function values, bidding prices, and bidding quantities of different methods during GA iterations under the 3-segment rule. From the curves of the objective functions, it can be seen that all models converged quickly within 100 iterations. Meanwhile, the bidding prices also converged quickly and stayed stable. However, the bidding quantities showed considerable fluctuations. For the rational bidder with the EUT-based method, since the optimal bidding prices of the three segments are the same, the changes in each segment’s bidding quantities will not affect the objective value as long as the sum of the three segments’ bidding quantities stays the same. Similar results are found in the “real” bidder with FPT-based methods. When the bidding prices of some segments were the same or very close to each other, the changes in the corresponding segments’ bidding quantities did not affect the objective value, i.e., the optimal solution is not unique in such situations, which explains the volatility of the bidding quantities results.
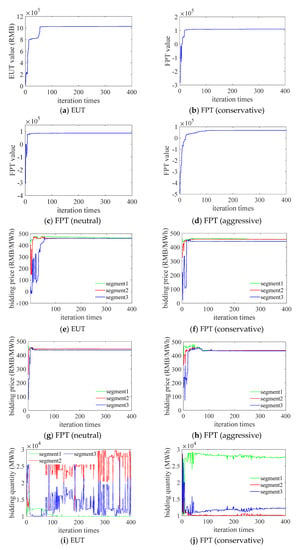
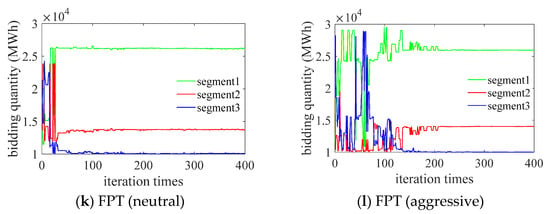
Figure 7.
Objective function values, bidding prices, and bidding quantities during GA iterations under the 3-segment rule: (a) objective function value of EUT; (b) objective function value of FPT (conservative); (c) objective function value of FPT (neutral); (d) objective function value of FPT (aggressive) (e) prices of EUT; (f) prices of FPT (conservative); (g) prices of FPT (neutral); (h) prices of FPT (aggressive); (i) quantities of EUT; (j) quantities of FPT (conservative); (k) quantities of FPT (neutral); (l) quantities of FPT (aggressive).
This work in carried on in MATLAB software on a personal computer with Intel(R) Core (TM) i7 1.80 GHz and 16 GB of memory. The optimality gap is 1 × 10−6. The average solution time is 1.78 s for 1-segment bidding and 8.34 s for 3-segment bidding for every iteration.
5.5. Sensitivity Analysis
This section conducts the sensitivity analysis of the FPT-based bidding results under the 1-segment bidding rule; the parameters are shown in Table 6.

Table 6.
FPT parameters for sensitivity analysis.
Figure 8 presents how the FPT value changed with the studied parameters. The results show that the FPT value decreased as the reference point increased and the loss aversion parameter increased. Specifically, with the increase of the reference point, it gets harder for the objective profit to reach the subjective profit aim (reference point). As a result, the distortion effect on the subjective value function, especially for the negative parts (), was more dominant in the FPT value function, and thus the FPT value continuously decreased. Comparing the results between the conservative, neutral, and aggressive strategies, it can be seen that when their reference points were the same, the conservative one had the lowest FPT value because its loss aversion parameter was the largest. As the reference point increased, the negative part occupies more of the FPT function, and thus the gaps between the three curves in Figure 8a also increased. Figure 8b shows that with the increase of the loss aversion parameter, the FPT value continuously decreased because the negative parts in the subjective value function decreased. Meanwhile, the gaps between the three curves increased as the loss aversion parameter increased in Figure 8b due to similar reasons as in Figure 8a.
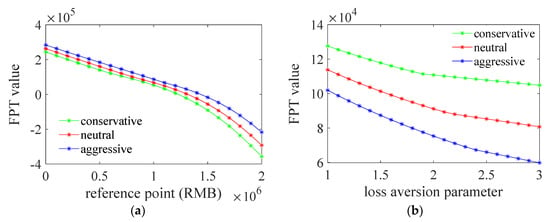
Figure 8.
FPT value with different (a) reference points; (b) loss aversion parameters.
6. Conclusions and Discussions
In the field of bidding strategy studies of retail companies in the electricity market, most of the existing research assumes that the retail company will always bid completely rationally to maximize its individual payoffs, which is not always the case in the real-world market. To incorporate the psychological factors and subjective perceptions into the bidding model, this paper first proposed a fractional prospect theory-based bidding strategy of power retail companies in the uniform pricing electricity market under price uncertainty. The main conclusions include:
- This paper proposed an FPT-based model to optimize the bidding strategy of a power retail company, which is suitable for describing the psychological and subjective factors in the bidding under the uniform pricing market with price uncertainty. Compared to the classical prospect theory, the proposed FPT method consists of four steps to calculate the deterministic and uncertain parts separately, and then add them up with normalization, which has advantages of dealing with the partially uncertain terms brought by the continuous probability distribution in the value functions.
- An FPT-based bidding strategy model was proposed to determine the optimal bidding strategy of the retail company regarding psychological factors. A genetic algorithm was presented to solve the proposed model. The objective function curves showed that all models converged quickly within 100 iterations.
- The results show that in the uniform pricing market, the optimal bidding price for a perfectly rational bidder is the selling price; meanwhile, for the “real” bidder, the optimal bid is at a lower price to avoid a certain condition that bidding is successful but the profit was lower than its reference point, and the result is a comprehensive result of the subjective value and weighting functions caused by the price uncertainty and psychological factors. The results under the 3-segment rule show that the “real” bidder tended to bid a relatively higher price in the first one or two segments with a large quantity for ensuring these segments have a larger probability to win. As the bidder becomes more aggressive, the bidding prices decreased. Meanwhile, when the bidding prices of some segments were the same or very close to each other, the optimal solution of the bidding quantities was not unique.
There are several open questions and research directions that we think are worth pursuing. When apply this method to a practical market, an important issue is how to determine the parameters of the FPT. Therefore, an interesting research direction is to extract these numbers from the real-world bidding data. Another interesting direction is to apply the FPT in the multi-agent simulation platform, which will help to simulate a more realistic electricity market.
Author Contributions
Conceptualization, Y.W.; Methodology, Y.W.; Software, J.J.; Validation, Z.C. and K.Z.; Writing, Y.W.; Funding acquisition, Z.C. and K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Grid Corporation of China under the project “Research on Multi-level Outage Planning Optimization and its Coordination Technology with Long-term Dispatching Decision” (No. 5108-202155042A-0-0-00).
Data Availability Statement
The simulation data is provided in the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xia, C.Y. Panorama of Big Data of Enterprises in China’s Electricity Sales Industry in 2022. Forward the Economist. 2022. Available online: https://ecoapp.qianzhan.com/detials/221021-58dac7cd.html (accessed on 1 December 2022).
- Peng, X.; Tao, X. Cooperative game of electricity retailers in China’s spot electricity market. Energy 2018, 145, 152–170. [Google Scholar] [CrossRef]
- Xiao, D.; do Prado, J.C.; Qiao, W. Optimal joint demand and virtual bidding for a strategic retailer in the short-term electricity market. Electr. Power Syst. Res. 2021, 190, 106855. [Google Scholar] [CrossRef]
- Guo, N.; Wang, Y.; Xu, Z.; Yan, G. Optimal pricing strategy of power-retailing companies considering demand response in block bidding markets. IET Gener. Transm. Distrib. 2020, 14, 1641–1652. [Google Scholar] [CrossRef]
- Hajati, M.; Seifi, H.; Sheikh-El-Eslami, M.K. Optimal retailer bidding in a DA market—A new method considering risk and demand elasticity. Energy 2011, 36, 1332–1339. [Google Scholar] [CrossRef]
- Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Optimal bidding strategy of electricity retailers using robust optimisation approach considering time-of-use rate demand response programs under market price uncertainties. IET Gener. Transm. Distrib. 2015, 9, 328–338. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Zhang, H.; Zhang, K. Optimal bidding of price-maker retailers with demand price quota curves under price uncertainty. IEEE Access 2020, 8, 120746–120756. [Google Scholar] [CrossRef]
- North, M.; Macal, C.; Conzelmann, G.; Koritarov, V.; Thimmapuram, P.; Veselka, T. Multi-Agent Electricity Market Modeling with EMCAS (No. ANL/DIS/CP-108599); Argonne National Laboratory: Lemont, IL, USA, 2002. Available online: https://www.osti.gov/servlets/purl/801575 (accessed on 1 December 2022).
- Jiang, Z.; Ai, Q. Agent-based simulation for symmetric electricity market considering price-based demand response. J. Mod. Power Syst. Clean Energy 2017, 5, 810–819. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Yuan, W.; Li, L. MRL-Based Model for Diverse Bidding Decision-Makings of Power Retail Company in the Wholesale Electricity Market of China. Axioms 2023, 12, 142. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory—Analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect-theory—Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, G.; Chen, X. SF-GRA method based on cumulative prospect theory for multiple attribute group decision making and its application to emergency supplies supplier selection. Eng. Appl. Artif. Intell. 2022, 110, 104679. [Google Scholar] [CrossRef]
- Li, W.; Zhao, J.-L.; Dong, L.; Wu, C. Coordination design of the coal-electricity supply chain contract for difference based on prospect theory. Kybernetes 2021, 50, 39–65. [Google Scholar] [CrossRef]
- Zhao, M.; Wei, G.; Wei, C.; Wu, J. Improved TODIM method for intuitionistic fuzzy MAGDM based on cumulative prospect theory and its application on stock investment selection. Int. J. Mach. Learn. Cybern. 2021, 12, 891–901. [Google Scholar] [CrossRef]
- Gan, L.; Hu, Y.; Chen, X.; Li, G.; Yu, K. Application and outlook of prospect theory applied to bounded rational power system economic decisions. IEEE Trans. Ind. Appl. 2022, 58, 3227–3237. [Google Scholar] [CrossRef]
- Li, Y.; Su, S.; Liu, B.; Yamashita, K.; Li, Y.; Du, L. Trajectory-driven planning of electric taxi charging stations based on cumulative prospect theory. Sustain. Cities Soc. 2022, 86, 104125. [Google Scholar] [CrossRef]
- Yao, Y.; Gao, C.; Chen, T.; Yang, J.; Chen, S. Distributed electric energy trading model and strategy analysis based on prospect theory. Int. J. Electr. Power Energy Syst. 2021, 131, 106865. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Xu, C.; Li, L. An integrated decision-making model for sustainable photovoltaic module supplier selection based on combined weight and cumulative prospect theory. Energy 2019, 181, 1235–1251. [Google Scholar] [CrossRef]
- Jhala, K.; Natarajan, B.; Pahwa, A. Prospect theory-based active consumer behavior under variable electricity pricing. IEEE Trans. Smart Grid 2019, 10, 2809–2819. [Google Scholar] [CrossRef]
- Vahid-Pakdel, M.J.; Ghaemi, S.; Mohammadi-ivatloo, B.; Salehi, J.; Siano, P. Modeling noncooperative game of GENCOS’ participation in electricity markets with prospect theory. IEEE Trans. Ind. Inform. 2019, 15, 5489–5496. [Google Scholar] [CrossRef]
- Lin, J.-k.; Hou, J.; Bao, T.; Luo, P.-p.; Lin, C.-n. Optimal bidding of generation companies based on prospect theory. Proc. Chin. Soc. Electr. Eng. 2009, 29, 97–101. [Google Scholar]
- Wang, Y.; Zhang, L.; Ding, Q.; Zhang, K. Prospect theory-based optimal bidding model of a prosumer in the power market. IEEE Access 2020, 8, 137063–137073. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Hsiang, C.-C. Bidding decision model based on prospect theory and game theory. In Proceedings of the 8th International Conference on Road and Airfield Pavement Technology (ICPT), Taipei, Taiwan, 14–18 July 2013. [Google Scholar]
- Cattell, D.W.; Bowen, P.A.; Kaka, A.P. Proposed framework for applying cumulative prospect theory to an unbalanced bidding model. J. Constr. Eng. Manag. ASCE 2011, 137, 1052–1059. [Google Scholar] [CrossRef]
- Brunner, T.; Reiner, J.; Natter, M.; Skierab, B. Prospect theory in a dynamic game: Theory and evidence from online pay-per-bid auctions. J. Econ. Behav. Organ. 2019, 164, 215–234. [Google Scholar] [CrossRef]
- Wang, S.; Qu, S.; Ma, G. Decision method of supplier selection for online multi-attribute procurement auction based on prospect theory and fuzzy theory. Control Decis. 2020, 35, 2637–2645. [Google Scholar]
- Independent System Operator New England. The Benefits of Uniform Clearing-Price Auctions for Pricing Electricity: Why Pay-as-Bid Auctions Do not Cost Less. ISONE Report. 2006. Available online: https://www.iso-ne.com/static-assets/documents/committees/comm_wkgrps/othr/clg/mtrls/2009/jul292009/uniform_clearing_price_auctions_whitepaper.pdf (accessed on 20 December 2022).
- Liu, T.; Xu, J. Equilibrium strategy based policy shifts towards the integration of wind power in spot electricity markets: A perspective from China. Energy Policy 2021, 157, 112482. [Google Scholar] [CrossRef]
- AEMO Energy Offers (Public). Available online: https://www.aemo.com.au/energy-systems/electricity/national-electricity-market-nem/data-nem/market-data-nemweb (accessed on 17 July 2022).
- PJM Manual 11: Energy & Ancillary Services Market Operations. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=200ce69f3ee2eea1f26897043555710ea30342cd (accessed on 16 July 2022).
- Son, Y.S.; Baldick, R.; Lee, K.H.; Siddiqi, S. Short-term electricity market auction game analysis: Uniform and pay-as-bid pricing. IEEE Trans. Power Syst. 2004, 19, 1990–1998. [Google Scholar] [CrossRef]
- Cramton, P.; Stoft, S. Why we need to stick with uniform-price auctions in electricity markets. Electr. J. 2007, 20, 26–37. [Google Scholar] [CrossRef]
- Burkardt, J. The Truncated Normal Distribution; Florida State University: Tallahassee, FL, USA, 2014; Volume 1, p. 35. [Google Scholar]
- Rieger, M.O.; Wang, M. Prospect theory for continuous distributions. J. Risk Uncertain. 2008, 36, 83–102. [Google Scholar] [CrossRef]
- Kothiyal, A.; Spinu, V.; Wakker, P.P. Prospect theory for continuous distributions: A preference foundation. J. Risk Uncertain. 2011, 42, 195–210. [Google Scholar] [CrossRef]
- Grefenstette, J.J. Genetic algorithms and machine learning. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993. [Google Scholar]
- Guangdong Power Exchange Center. Monthly Trading Data. 2022. Available online: https://pm.gd.csg.cn/views/page/market.html (accessed on 12 January 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).