Abstract
It is renowned that the immune reaction in the tumour micro environment is a complex cellular process that requires additional research. Therefore, it is important to interrogate the tracking path behaviour of tumor-immune dynamics to alert policy makers about critical factors of the system. Here, we use fractional derivative to structure tumor-immune interactions. Furthermore, in our research, we concentrated on the qualitative investigation and time series analysis of tumor-immune cell interactions. The solution routes are examined using a new numerical technique to emphasis the impact of the factors on tumor-immune system. We focused on the behaviour of the system with fluctuation of different values. The most crucial components of the proposed system are identified and policymakers are advised. The outcomes of the present study are the strong predictor of clinical success and the in-out of immune cells in a tumour is also critical to treatment efficacy. As a result, studying the behaviour of tumor-immune cell interactions is important to predict crucial factors for the prevention and management to the health officials.
1. Introduction
The human immune system, according to immunologists, comprises two key elements that collaborate to defend the organism of host body against diseases. The innate mechanism is the first element while the adaptive mechanism is the second. In the first one, pathogens are met with a more widespread and quicker defence mechanism. Natural killer cells, neutrophil leukocytes and macrophages are among the cells involved in this process. Neutrophils travel with the help of tissue and flow in the host blood to destroy infections and germs in the body of the host. Monocytes move in a host’s bloodstream and have the ability to look for infected areas. The second reaction, on the other hand, is directed at a specific pathogen and takes longer to establish a defence than the innate response. T lymphocytes, B lymphocytes and dendritic cells are the cells of the second reaction mechanism. Dendritic cells initiate the adaptation process in this protective system, and then pathogens activate naive T cells. B lymphocytes create unique antibodies to a specific pathogen, whereas T lymphocytes make specialized cells including T regulatory, Cytotoxic T Lymphocytes, T memory cells and T helper cells to resist or fight an infection. Cytotoxic T Lymphocytes, commonly known as killer cells are the most effective cells which are also named CD8+ T-Cells. These cells destroy all the other cells not from the body of host and expresses T-cell receptors. It is reported that numerous substances from the outside and pathogens including viruses, bacteria and other microbes enter into the human body but the immune system attempt to block their reproduction in order to lessen the chances of infections.
It is reported that the most common cause of death is cancer in the world. The American Cancer Society estimates the current cancer burden by projecting the number of cases and deaths per year. In the United States, approximately 16 lakh new cases would be diagnosed in 2014, with roughly 5 lakh cancer fatalities [1]. Its formation and destruction processes are poorly understood. After cardiovascular illnesses, the second leading cause of death is cancer [2]. It is one of the three largest hazards to the global economy, according to the World Economic Forum (WEF), because of the rising cost of treatment, threats to productivity, and the consequences of expenditures on household deprivation [3]. The human body is made up of a variety of cell kinds. The division and enpension of these cells produces new cells in the body, however, sometimes new cells are created even when they are not required and tumor may be produced as a result of this. Tumors may be cancerous or noncancerous, a noncancerous tumour is a tumour cell mass that does not fragment or expand outside of its initial growing location. In general, noncancerous effects on the body are not dangerous and are simple to cure. When a benign tumour becomes large enough to interfere with regular physiological functioning, it becomes hazardous. Malignant tumours are hazardous non encapsulated tumour cell growths. Cancer cells, through lymph or blood channels, interfere with the normal functioning of organs over time. The term secondary tumour describes this stage. The growth of malignant cells is a complicated process that involves the interaction of many different cells. When tumour cells are detected as non-self in host body, the system of immune stimulated to seek out and eliminate them [4,5,6,7].
It has been acknowledged that mathematical models are a significant tool for visualising complicated biological processes and recommending efficient infection control approaches [8,9,10]. Different models in term of mathematics for cancer have been proposed in the literature to explain the complicated biological events of cancer using discrete, continuous, or hybrid assumptions [11,12,13,14]. The research presented in [15] gives a thorough summary of the many methodologies employed in modelling the tumor-immune system interaction dynamics. The authors in [16,17,18,19] used ODE’s to explore the interaction between tumour cells and several types of immune cells. The researchers in [5] investigate the nonlinear dynamics of immunogenic tumours, which include immunostimulation of tumour development, tumour sneaking through, and the establishment of a dormant tumour. In [18], the tumour was found to be dormant in a simple model, but there was tumour recurrence in the presence of immune cells in the time delay model. The notion of pray predictor [20,21,22], which showed single cell interactions, has been used to efficiently simulate a variety of biological events. For interactions between tumour cells and natural killer cells, the cell-by-cell method is effective. To depict the dynamics of tumour malignancy, the interactions of tumor-immune are portrayed on various scales with numerous hypothesize [23,24,25]. To depict the influence of immunotherapy on tumor-immune dynamics, a more accurate mathematical model is required. Our major goal in this work is to better understand the complicated non-linear processes of tumor-immune interactions with therapy by formulating it.
The theory of fractional-calculus is extremely important and has a wide range of applications in science and engineering [26,27]. It is reported that the framework of fractional-calculus gives a more flexible framework for formulating biological processes in mathematical biology [28]. In the literature, several fractional operators are developed to visualize the dynamics of different phenomena, however, some of these operators have limitations and cannot represent the crossover behaviour and singularity of a system. Recently, Caputo and Fabrizio [29] suggested a fractional derivative operator with a nonsingular and exponential kernel to get over these limitations. This operator has the benefit of a nonlocal and nonsingular kernel, making it ideal for describing and analysing the dynamics of biological events [30]. As tumor is a major issue for public health and more research is required to investigate the biology of tumor-immune interactions. Therefore, we use CF fractional framework to conceptualize the complex tumor-immune system in order to obtain more accurate results and examine tumor biology more accurately.
The article is structured as: A mathematical model of tumor-immune cells interactions is constructed through fractional derivatives in Section 2. The rudimentary results and theory of the fractional-calculus has been given in Section 3. In Section 4, of the paper, we introduced a novel numerical approach to study the tracking path of the system. We examined the tumor-immune dynamics with the variation of several input factors in Section 5. In Section 6, we offered the conclusion of the overall work.
2. Tumor-Immune Cells Dynamics
Resting cells and hunting cells are the main source to eradicate tumour cells in the body. Here, we assume that hunting cells can kill tumour while resting cells cannot. It is because of the tumour cells which create antigens on its outer surface, the cellular immune reaction recognises and removes them from the host. The antigenicity of the tumour determines the intensity of the immune response. T-cells carry out the immune system’s cellular response. T-cell’s surfaces have specific receptors like antibody that detect antigen fragments on the surface of tumour cells during maturation. The MHC molecule is a protein that distinguishes in non-self and self within resting T lymphocytes. Resting T cells engulf tumour cells and create a variety of growth factors known as cytokines, but they are unable to destroy tumour cells. The cytotoxic T lymphocytes are activated by cytokines, which are chemical messenger switches (hunting cells). Unlike resting T lymphocytes, cytotoxic T lymphocytes not only release a variety of cytokines but also kill tumour cells by producing a cytotoxic response which paralyses their prey.
We created a model of tumour formation in immune reaction based on the above biological process. The model is predicated on the following assumptions with resting cells R, hunting cells H and tumor cells T: The Michaelis Menten function considers that resting cells were also activated by the presence of malignant cells; A transformed hunting T cell will not move to the stage of resting; In the absence of tumour cells, logistic growth are followed by resting cells; through contact or direct touch, resting predator cells are transformed to hunting cells; According to the law of mass action, tumour cells and hunting predator cells are wiped off at a pace proportionate to their densities; A logistic growth function is anticipated for tumour cell proliferation without the presence of hunting CTL cells. In formulation of the model, the rate at which normal cells convert into tumor cells is indicated by ℏ while the tumor growth rate is denoted by and the carrying capacity is symbolized by . The parameters and represent the killing rate of T by H and H by T, respectively. The apoptosis rate of H and R are indicated by and while the carrying capacity and growth rate of R are represented by and . These assumptions lead to the below dynamics
with the condition
where the resting cells proliferation rate is indicated by and proliferation for half saturation is indicated by . In addition to this, the rate at which the resting cells convert into hunting cells is indicated by .
Non-integer or fractional operators, which have memory qualities and are useful for illustrating numerous natural phenomena, scientific truths, and facts with nonlocal dynamics, hereditary property and crossover behavior. It is well-known that the nature of mostly biological processes nonlocal, crossover and possess memory effects which can be effectively modelled through fractional operators. Hence, we modelled the intricate phenomena of tumor through fractional-calculus to represents its dynamical behavior more accurately. Thus, our tumour model (1) in fractional framework is given by
in which indicates Caputo-Fabrizio derivative. In the upcoming section, we will present basic idea of fractional theory for the investigation of our tumor model.
3. Fractional Theory
In this part of research work, we will list basic knowledge of Caputo-Fabrizio(CF) derivative to investigate our tumour-immune dynamics. The rudimentary theory is given as:
Definition 1.
Let us suppose , then the CF derivative [29] is given by the below
in which ℑ is the order derivative with . If , then the below mentioned is obtained
Remark 1.
Definition 2.
For a given function k, the following represents fractional integral
in which indicates fractional integral in CF sense of order ℑ.
Remark 2.
After the simplification of Definition 2, we have
with , . Thus, the below new definition is obtained in [31] by utilizing Equation (8) in the form
4. Novel Numerical Technique for The System
In this section, the main purpose is to demonstrate the dynamical behaviour of the recommended fractional model (2) of tumor-immune interaction. Several numerical techniques for Caputo-Fabrizio fractional systems have been proposed in the literature to emphasise their dynamics [32,33,34]. We will use the [34] scheme to depict the dynamics of our fractional system (2) of tumor, since it is more trustworthy, simple to implement, and stable. To proceed further, we take the first equation of our suggested model of tumor-immune interaction as follows
Here, take we have
and
The difference terms are as
In addition to this, the function is approximated on as follows
where representing the time. The following integral is determined with the help of , given by
Putting (15) in (13), we have
which is a numerical technique for the solution of system (2) of tumour-immune interaction. Proceeding in the same way, we get
and
This approach is a two-step Adams-Bashforth strategy for the Caputo-Fabrizio operator that takes into consideration the kernel’s nonlinearity as well as the exponential decay rule. The suggested scheme’s stability and convergence are discussed in depth in [34].
5. Results and Discussion
To simulate the suggested model, we employed the numerical approach described above in Section 4. Our main aim is to perform numerical simulations to illustrate the influence of the input components on the solution paths of the system. We shall propose the most crucial aspects of the tumor-immune cell system based on our experimental findings. The oscillatory and chaotic nature of the system is investigated through different input parameters. It is well-known that the chaos of system leads to unexpected results and it is the name given to unexpected and irregular behaviour of the system. It discusses the traits of the change from order to chaos or from stability to instability. Here, our main concern is to visualize the dynamical behaviour of tumor-immune system and point out the most sensitive parameters responsible for the chaos of the system.
We presented the dynamical behaviour of the recommended system of tumor-immune with different values of fractional parameter in the first simulation shown in Figure 1, Figure 2 and Figure 3 to emphasise the influence of fractional order on the system’s solution paths. The influence of the fractional order on the system’s dynamical behaviour was seen, demonstrating the parameter’s efficacy and predicting that it may be employed as a system control parameter. In the second simulation illustrated in Figure 4, Figure 5, Figure 6 and Figure 7, we take different values of the input parameter to show the contribution of this parameter in the dynamics of tumor-immune. The tracking path behaviour and the chaos of the system has been visualized in Figure 6 by taking . In this simulation, we observed the effect of on the system of tumor-immune. In the last simulation, we take the input value to show the impact of a1 on the dynamics. The chaotic behaviour of the system illustrates how little disturbances may result in significant changes in the system. These chaotic plots show how unstable the system is and how susceptible it is to initial conditions, making it unpredictable. Our research showed that the nonlinearity of the system significantly increases oscillation and chaos, and that these two behaviours are closely related. The results of this numerical study anticipate the complex interactions between tumour and immune cells, suggesting that more suitable values of parameter and state-variables are needed to lesson the chaotic nature of the dynamics.
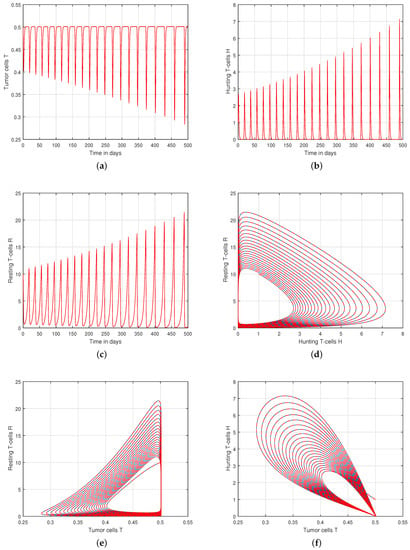
Figure 1.
Tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with fractional order .
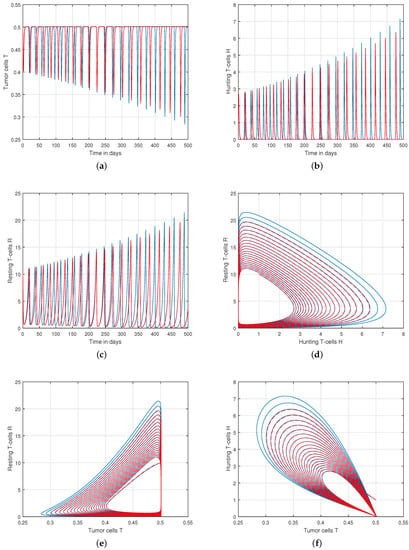
Figure 2.
Tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with fractional order .
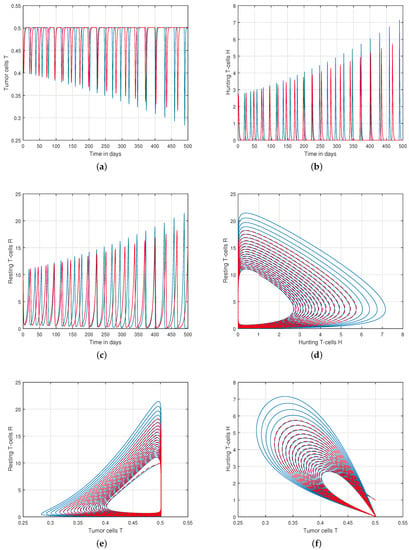
Figure 3.
Tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with fractional order .
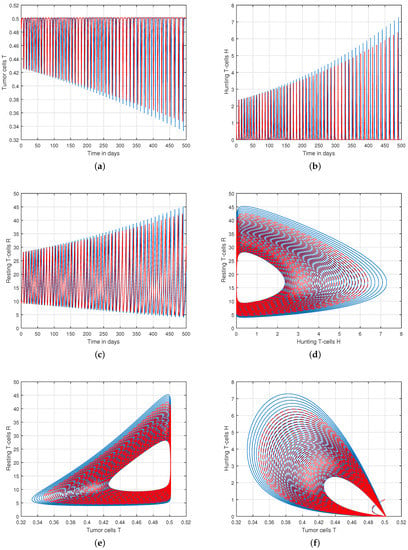
Figure 4.
Analysis of tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with input parameter .
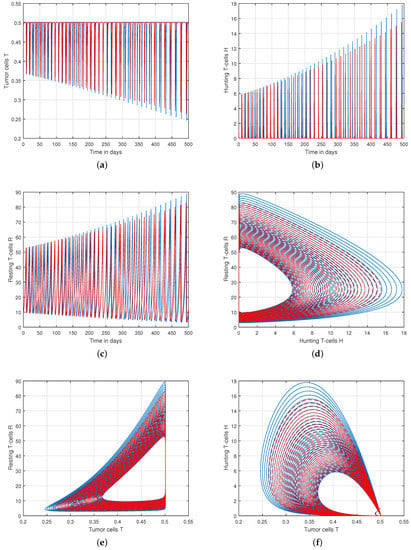
Figure 5.
Analysis of tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with input parameter .
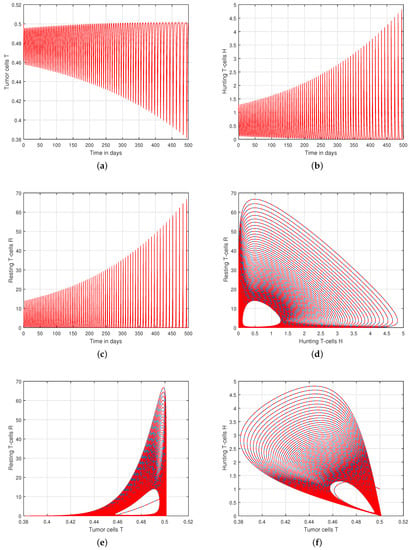
Figure 6.
Graphical view analysis of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with input parameter .
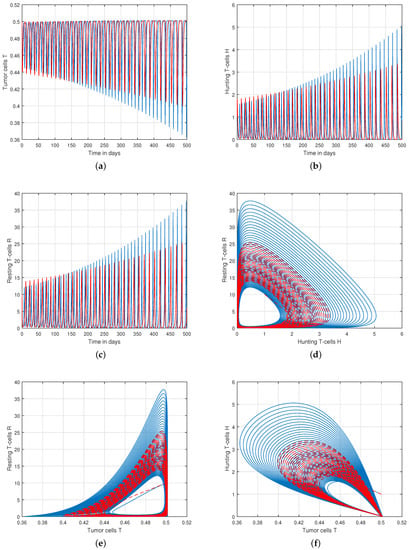
Figure 7.
Analysis of tracking path behaviour of (a) tumor cells T, (b) hunting T-cells H, (c) resting T-cells R and chaotic phenomena of (d) hunting T-cells H vs. resting T-cells R, (e) tumor cells T vs. resting T-cells R, (f) tumor cells T vs. hunting T-cells H with and .
The relationship of tumour cells as prey and the immune system as predator, which comprises of hunting and resting cells, has been investigated. A greater knowledge of the immune system’s role in dormancy might lead to the development of immunological therapeutics to inhibit the advancement of the tumor and the subsequent switch from dormancy to tumor growth. Our research might lead to new clinical detection approaches and therapy alternatives for preventing lethal tumor recurrence and spread. The outcome of this dynamic is a strong predictor of clinical success, and immune cell penetration into, or exclusion from, a tumour is also critical to immunotherapy efficacy. The numerical findings and quantitative analysis alerts policy makers and health officials to the system’s most important aspects for control and prevention.
6. Concluding Remarks
In this work, we constructed a mathematical model for the interactions of tumor-immune cells in the framework of the fractional derivative to obtain more accurate results. The basic results of fractional-calculus are presented for the analysis of the system. The outcomes showed that mathematical modelling can provide unique insights into these interactions. We investigated the dynamical behaviour of the tumor-immune interactions numerically. A novel numerical technique is provided to illustrate the influence of the different input factors on the output of the system. We have shown the impact of input parameters of the system to conceptualize the role of these parameters. The chaotic phenomena and oscillation of the system have been illustrated to identify the most sensitive parameter which disturbs the stability of the system. The most essential factors of tumor-immune cell dynamics are identified and recommended for future investigation to public health professionals. Our finding suggested that more suitable values of state-variables and parameters are needed to reduce the chaos of the system. We predicted that the oscillatory and chaotic nature of the system is interlinked and is due to the strong nonlinearity of the system.
Author Contributions
Conceptualization, R.J. and S.B.; methodology, H.A. and M.J.; software, S.Z. and M.A.; validation, S.Z. and M.J.; formal analysis, S.B. and R.J.; investigation, R.J. and S.B.; resources, S.B., S.Z. and R.J.; writing—original draft preparation, R.J., S.B. and M.J.; writing—review and editing, M.J. and S.Z.; visualization, S.B., H.A. and R.J.; supervision, S.Z. and S.B; project administration, M.J., S.Z. and H.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Research Groups Program [grant number R.G.P.2/25/44].
Data Availability Statement
No data associated in the manuscript.
Conflicts of Interest
We declare that there is no conflict of interest in this manuscript.
References
- Siegel, R.L.; Jemal, A. Cancer Facts & Figures; American Cancer Society, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- Rihan, F.A.; Safan, M.; Abdeen, M.A.; Abdel Rahman, D. Qualitative and computational analysis of a mathematical model fo tumor-immune interactions. J. Appl. Math. 2012, 2012, 475720. [Google Scholar] [CrossRef]
- Abbas, A. Cellular and Molecular Immunology; Abbas, A.K., Lichtman, A.H., Pober, J.S., Eds.; University of Michigan: Ann Arbor, MI, USA, 1997. [Google Scholar]
- Nani, F.; Freedman, H.I. A mathematical model of cancer treatment by immunotherapy. Math. Biosci. 2000, 163, 159–199. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
- Robertson-Tessi, M.; El-Kareh, A.; Goriely, A. A mathematical model of tumorimmune interactions. J. Theor. Biol. 2012, 294, 56–73. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Bramson, J.L.; Earn, D.J. Interactions between the immune system and cancer: A brief review of non-spatial mathematical models. Bull. Math. Biol. 2011, 73, 2–32. [Google Scholar] [CrossRef] [PubMed]
- Jan, R.; Shah, Z.; Deebani, W.; Alzahrani, E. Analysis and dynamical behavior of a novel dengue model via fractional calculus. Int. J. Biomath. 2022, 15, 2250036. [Google Scholar] [CrossRef]
- Jan, R.; Xiao, Y. Effect of partial immunity on transmission dynamics of dengue disease with optimal control. Math. Method. Appl. Sci. 2019, 42, 1967–1983. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, Z. Analysis of an influenza A (H1N1) epidemic model with vaccination. Arab. J. Math. 2012, 1, 267–282. [Google Scholar] [CrossRef]
- Das, P.; Upadhyay, R.K.; Das, P.; Ghosh, D. Exploring dynamical complexity in a time-delayed tumor-immune model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 123118. [Google Scholar] [CrossRef]
- Chaplain, M.A. Multiscale mathematical modelling in biology and medicine. IMA J. Appl. Math. 2011, 76, 371–388. [Google Scholar] [CrossRef]
- Martin, R.B.; Fisher, M.E.; Minchin, R.F.; Teo, K.L. A mathematical model of cancer chemotherapy with an optimal selection of parameters. Math. Biosci. 1990, 99, 205–230. [Google Scholar] [CrossRef] [PubMed]
- Deisboeck, T.S.; Wang, Z.; Macklin, P.; Cristini, V. Multiscale cancer modeling. Annu. Rev. Biomed. Eng. 2011, 13, 127–155. [Google Scholar] [CrossRef] [PubMed]
- Woelke, A.L.; Murgueitio, M.S.; Preissner, R. Theoretical modeling techniques and their impact on tumor immunology. Clin. Dev. Immunol. 2010, 2010, 271794. [Google Scholar] [CrossRef] [PubMed]
- Saleem, M.; Agrawal, T. Chaos in a tumor growth model with delayed responses of the immune system. J. Appl. Math. 2012, 2012, 891095. [Google Scholar] [CrossRef]
- Zhivkov, P.; Waniewski, J. Modelling tumour-immunity interactions with different stimulation functions. Int. J. Appl. Math. Comput. Sci. 2003, 13, 307–315. [Google Scholar]
- Galach, M. Dynamics of the tumor-immune system competition-the effect of time delay. Int. J. Appl. Math. Comput. Sci. 2003, 13, 395–406. [Google Scholar]
- Babbs, C.F. Predicting success or failure of immunotherapy for cancer: Insights from a clinically applicable mathematical model. Am. J. Cancer Res. 2012, 2, 204–213. [Google Scholar]
- d’Onofrio, A.; Gatti, F.; Cerrai, P.; Freschi, L. Delay-induced oscillatory dynamics of tumour-immune system interaction. Math. Comput. Model. 2010, 51, 572–591. [Google Scholar] [CrossRef]
- Letellier, C.; Denis, F.; Aguirre, L.A. What can be learned from a chaotic cancer model. J. Theor. Biol. 2013, 322, 7–16. [Google Scholar] [CrossRef]
- Rocha, A.M.A.; Costa, M.F.P.; Fernandes, E.M. On a multiobjective optimal control of a tumor growth model with immune response and drug therapies. Int. Trans. Oper. Res. 2018, 25, 269–294. [Google Scholar] [CrossRef]
- Tripathi, C.; Tewari, B.N.; Kanchan, R.K.; Baghel, K.S.; Nautiyal, N.; Shrivastava, R.; Kaur, H.; Bhatt, M.L.B.; Bhadauria, S. Macrophages are recruited to hypoxic tumor areas and acquire a pro-angiogenic M2-polarized phenotype via hypoxic cancer cell derived cytokines Oncostatin M and Eotaxin. Oncotarget 2014, 5, 5350. [Google Scholar] [CrossRef] [PubMed]
- Italiani, P.; Boraschi, D. From monocytes to M1/M2 macrophages: Phenotypical vs. functional differentiation. Front. Immunol. 2014, 5, 514. [Google Scholar] [CrossRef] [PubMed]
- Laoui, D.; Movahedi, K.; Van Overmeire, E.; Van den Bossche, J.; Schouppe, E.; Mommer, C.; Nikolaou, A.; Morias, Y.; De Baetselier, P.; Van Ginderachter, J.A. Tumorassociated macrophages in breast cancer: Distinct subsets, distinct functions. Int. J. Dev. Biol. 2011, 55, 861–867. [Google Scholar] [CrossRef]
- Boulaaras, S.; Jan, R.; Khan, A.; Ahsan, M. Dynamical analysis of the transmission of dengue fever via Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals X 2022, 8, 100072. [Google Scholar] [CrossRef]
- Jan, R.; Khan, A.; Boulaaras, S.; Ahmed Zubair, S. Dynamical Behaviour and Chaotic Phenomena of HIV Infection through Fractional Calculus. Discret. Dyn. Nat. Soc. 2022, 2022, 5937420. [Google Scholar] [CrossRef]
- Jan, R.; Boulaaras, S. Analysis of fractional-order dynamics of dengue infection with non-linear incidence functions. Trans. Inst. Meas. Control 2022. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Mandal, M.; Jana, S.; Nandi, S.K.; Kar, T.K. Modelling and control of a fractionalorder epidemic model with fear effect. Energy Ecol. Environ. 2020, 5, 421–432. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Liu, Y.; Fan, E.; Yin, B.; Li, H. Fast algorithm based on the novel approximation formula for the Caputo-Fabrizio fractional derivative. Aims Math. 2020, 5, 1729–1744. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, A.; Li, X. A second-order finite difference scheme for quasilinear time fractional parabolic equation based on new fractional derivative. Int. J. Comput. Math. 2018, 95, 396–411. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).