New Fractional Cancer Mathematical Model via IL-10 Cytokine and Anti-PD-L1 Inhibitor
Abstract
1. Introduction
2. Basic Tools
3. Model in Caputo Sense
3.1. Stability Analysis of the Model in Caputo Fractional Derivative
3.2. The Existence and Uniqueness of Solution in Caputo Fractional Derivative
- where × ; are positive constants.
- Y(t) is satisfied in Equation (17).
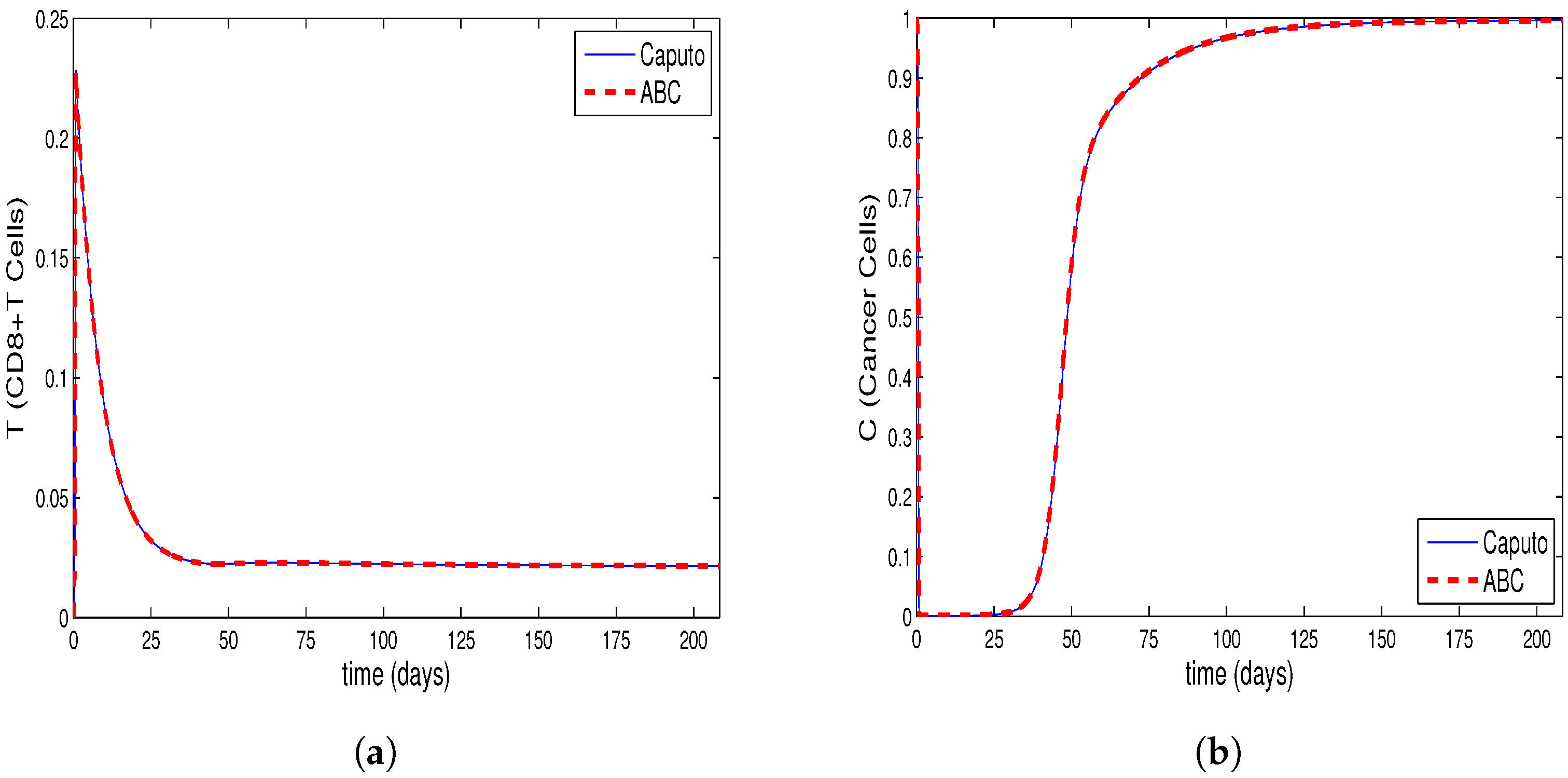
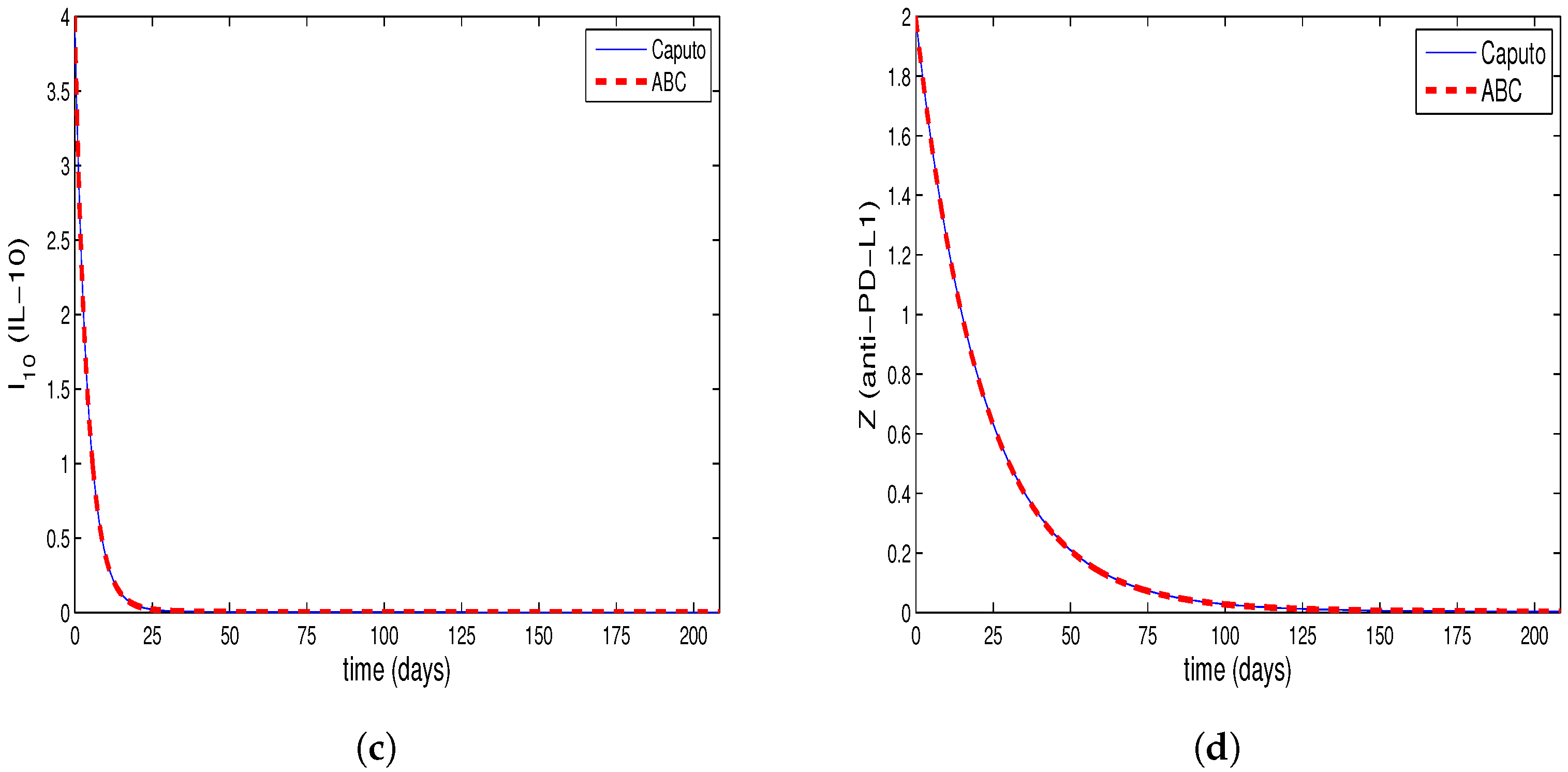
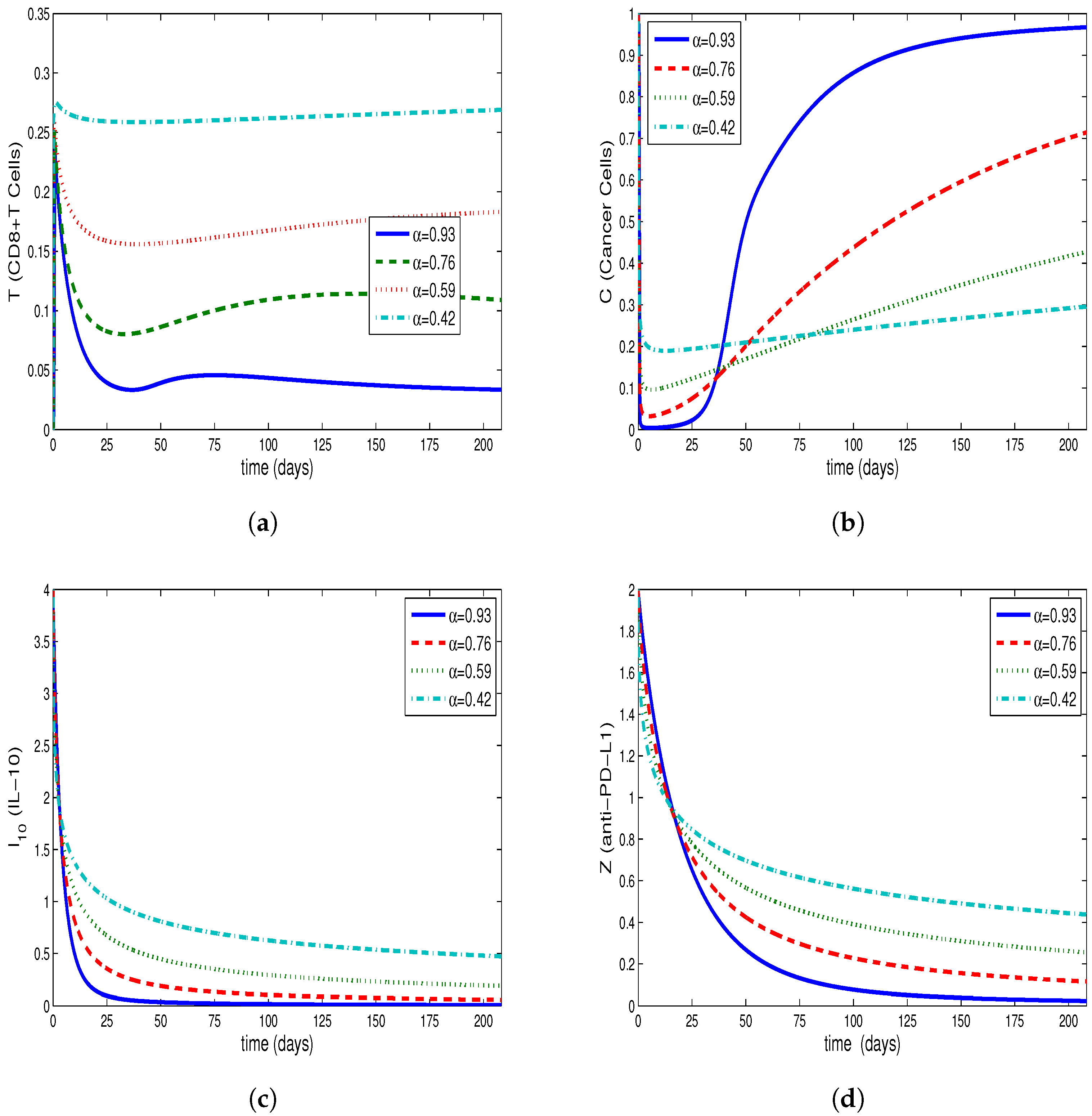
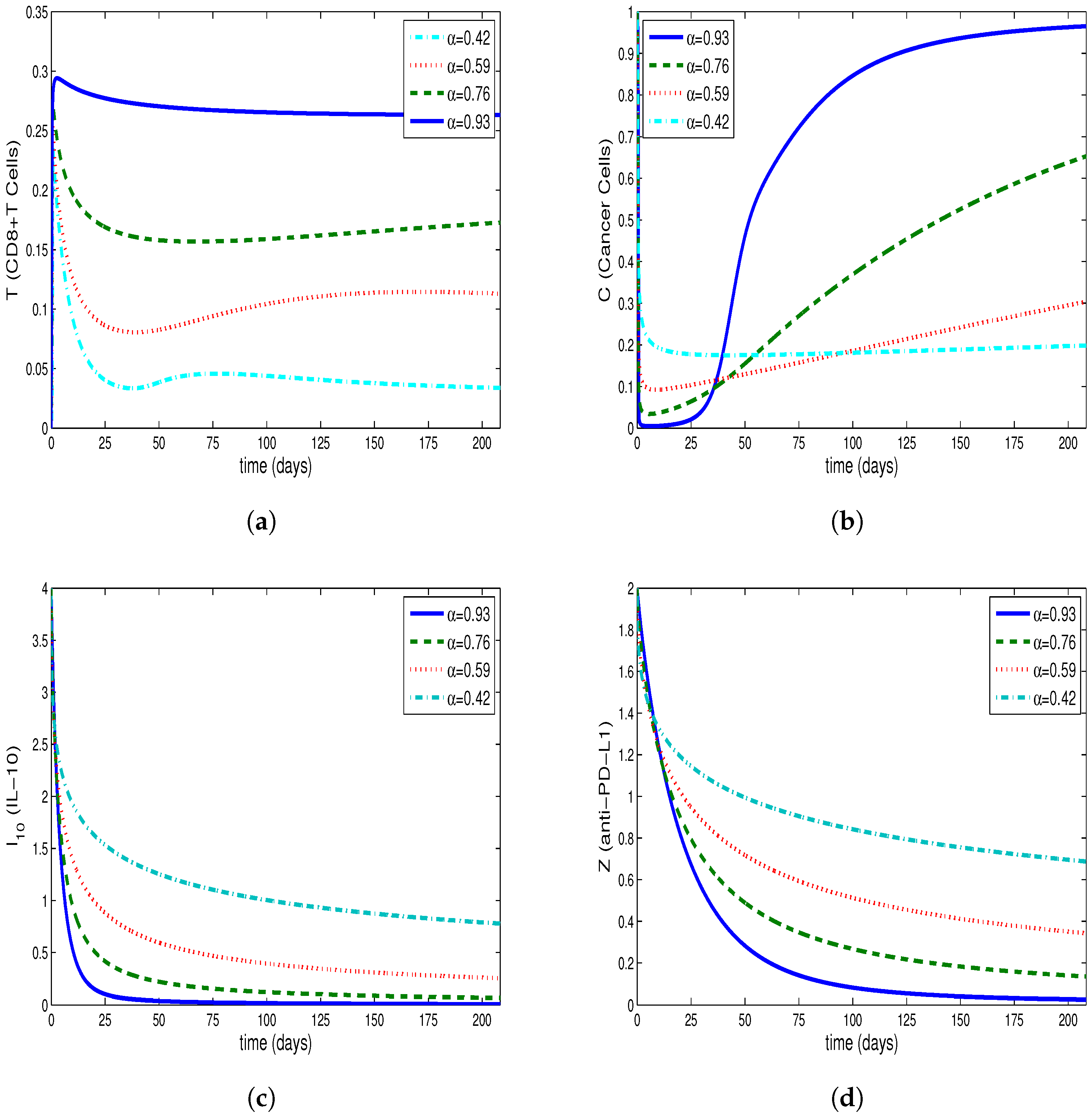
4. Comparing Numerical Results of Model with Caputo Derivate and ABC Derivative
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fife, B.T.; Pauken, K.E.; Eagar, T.N.; Obu, T.; Wu, J.; Tang, Q.; Bluestone, J.A. Interactions between PD-1 and PD-L1 promote tolerance by blocking the TCR-induced stop signal. Nat. Immunol. 2009, 10, 1185–1192. [Google Scholar] [CrossRef]
- Francisco, L.M.; Salinas, V.H.; Brown, K.E.; Vanguri, V.K.; Freeman, G.J.; Kuchroo, V.K.; Sharpe, A.H. PD-L1 regulates the development, maintenance, and function of induced regulatory T cells. J. Exp. Med. 2009, 206, 3015–3029. [Google Scholar] [CrossRef] [PubMed]
- Latchman, Y.; Wood, C.R.; Chernova, T.; Chaudhary, D.; Borde, M.; Chernova, I.; Iwai, Y.; Long, A.J.; Brown, J.A.; Nunes, R.; et al. PD-L2 is a second ligand for PD-1 and inhibits T cell activation. Nat. Immunol. 2001, 2, 261–268. [Google Scholar] [CrossRef]
- Bertucci, F.; Finetti, P.; Birnbaum, D.; Mamessier, E. The PD1/PDL1 axis, a promising therapeutic target in aggressive breast cancers. OncoImmunology 2016, 5, e1085148. [Google Scholar] [CrossRef]
- Muenst, S.; Schaerli, A.R.; Gao, F.; Daster, S.; Trella, E.; Droeser, R.A.; Muraro, M.G.; Zajac, P.; Zanetti, R.; Gillanders, W.E.; et al. Expression of programmed death ligand 1 (PD-L1) is associated with poor prognosis in human breast cancer. Breast Cancer Res. Treat. 2014, 146, 5–24. [Google Scholar] [CrossRef] [PubMed]
- Chan, I.H.; Wu, V.; Bilardello, M.; Mar, E.; Oft, M.; Van Vlasselaer, P.; Mumm, J.B. The potentiation of IFN-γ and induction of cytotoxic proteins by pegylated IL-10 in human CD8 T cells. J. Interferon Cytokine Res. 2015, 35, 948–955. [Google Scholar] [CrossRef]
- Naing, A.; Papadopoulos, K.P.; Autio, K.A.; Ott, P.A.; Patel, M.R.; Wong, D.J.; Falchook, G.S.; Pant, S.; Whiteside, M.; Rasco, D.R.; et al. Safety, antitumor activity, and immune activation of pegylated recombinant human interleukin-10 (AM0010) in patients with advanced solid tumors. J. Clin. Oncol. 2016, 34, 3562–3569. [Google Scholar] [CrossRef]
- Sun, H.; Gutierrez, P.; Jackson, M.J.; Kundu, N.; Fulton, A.M. Essential role of nitric oxide and interferon-gamma for tumor immunotherapy with interleukin-10. J. Immunother. 2010, 23, 208–214. [Google Scholar] [CrossRef]
- Podlunby, I. Fractional Differantial Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and applications to heat transfer model. Therm. Sci. 2016, 370, 763–769. [Google Scholar] [CrossRef]
- Piccoli, B.; Castiglione, F. Optimal vaccine scheduling in cancer immunotherapy. Phys. A 2006, 370, 672–680. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. Equilibrium points, stability and numerical solutions of fractional-order predator-pey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Bozkurt, F. Stability Analysis of a Fractional-Order Differential Equation System of a GBM-IS Interaction Depending on the Density. Appl. Math. Inf. Sci. 2014, 8, 1021–1028. [Google Scholar] [CrossRef]
- El-Sayeda, A.M.A.; El-Mesiryb, A.E.M.; El-Sakab, H.A.A. On the fractional-order logistic equation. Appl. Math. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Iqbal, S.A.; Hafez, G.; Chu, Y.M.; Park, C. Dynamical analysis of nonautonomous RLC circuit with the absence and presence of Atangana-Baleanu fractional derivative. JAAC 2022, 12, 770–789. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.M.; Yassen, M.F.; Ahmad, I.; Pongsakorn, S.; Khan, M.A. A fractional Sars-Cov-2 model with Atangana-Baleanu derivative: Application to fourth wave. Fractals 2022, 30, 2240210. [Google Scholar] [CrossRef]
- Khan, D.; Ali, G.; Khan, A.; Khan, I.; Chu, Y.M.; Nisar, K.S. A New Idea of Fractal-Fractional Derivative with Power Law Kernel for Free Convection Heat Transfer in a Channel Flow between Two Static Upright Parallel Plates. Comput. Mater. Contin. 2020, 65, 1237–1251. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Baleanu, D. Is it possible to derive Newtonian equations of motion with memory? Int. J. Theor. Phys. 2010, 49, 701–708. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Machado, J.A.T. Fractional model for malaria transmission under control strategies. Comput. Math. Appl. 2013, 66, 908–916. [Google Scholar] [CrossRef]
- Baleanu, D. About fractional quantization and fractional variational principles. Commun. Nonlin. Sci. 2009, 14, 2520–2523. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Machado, J.A.T. Complex order van der Pol oscillator. Nonlinear Dyn. 2010, 65, 247–254. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Ozdemir, N.; Baleanu, D. Mathematical Modelling and Optimization of Engineering Problems; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Hristov, J. Magnetic field diffusion in ferromagnetic materials: Fractional calculus approaches. Int. J. Optim. Control Theor. Appl. 2021, 11, 1–5. [Google Scholar] [CrossRef]
- Uçar, S. Analysis of hepatitis B disease with fractal–fractional Caputo derivative using real data from Turkey. J. Comput. Appl. Math. 2023, 419, 114692. [Google Scholar] [CrossRef]
- Uçar, S. Existence and Uniqueness Results for a Smoking Model with Determination and Education in the Frame of Non-Singular Derivatives. Discrete Contin. Dyn. Syst. Ser. S 2021, 14, 2571–2589. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Yusuf, A.; Ali, A.I. Caputo Type Fractional Operator Applied to Hepatitis B System. Fractals 2021, 10, 2240023. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S. A study on fractional predator-prey-pathogen model with Mittag-Leffler kernel-based operators. Numer. Methods Partial. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Joshi, H.; Jha, B.K. Chaos of calcium diffusion in Parkinson’s infectious disease model and treatment mechanism via Hilfer fractional derivative. Math. Model. Numer. Simul. Appl. 2021, 1, 84–94. [Google Scholar]
- Naik, P.A.; Eskandari, Z.; Yavuz, M.; Zu, J. Complex dynamics of a discrete-time Bazykin–Berezovskaya prey-predator model with a strong Allee effect. J. Comput. Appl. Math. 2022, 413, 114401. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Evirgen, F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J. Comput. Appl. Math. 2023, 418, 114654. [Google Scholar] [CrossRef]
- Shafik, M.; Abbas, M.; Abdullah, M.A.; Majeed, A.; Abdeljawad, T.; Alqudah, M. Numerical solutions of time fractional Burgers’ equation involving Atangana–Baleanu derivative via cubic B-spline functions. Results Phys. 2022, 34, 105244. [Google Scholar] [CrossRef]
- Koca, I. Analysis of rubella disease model with non-local and non-singular fractional derivatives. Int. J. Optim. Control Theor. Appl. 2018, 8, 17–25. [Google Scholar] [CrossRef]
- Hamou, A.A.; Rasul, R.R.; Hammouch, Z.; Ozdemir, N. Analysis of rubella disease model with non-local and non-singular fractional derivatives. Comput. Appl. Math. 2022, 41, 1–33. [Google Scholar]
- Özdemir, N.; Uçar, E. Investigating of an immune system-cancer mathematical model with Mittag-Leffler kernel. AIMS Math. 2020, 5, 1519–1531. [Google Scholar] [CrossRef]
- Dokuyucu, M.A.; Celik, E.; Bulut, H.; Baskonus, H.M. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur. Phys. J. Plus 2018, 133, 1–6. [Google Scholar] [CrossRef]
- Uçar, E.; Özdemir, N.; Altun, E. Fractional order model of immune cells influenced by cancer cells. Math. Model. Nat. Phenom. 2019, 14, 308. [Google Scholar] [CrossRef]
- Uçar, E.; Özdemir, N. A fractional model of cancer-immune system with Caputo and Caputo-Fabrizio derivatives. Eur. Phys. J. Plus 2021, 136, 1–17. [Google Scholar] [CrossRef]
- Naim, M.; Yassine, S.; Nwar, Z. Stability characterization of a fractional-order viral system with the non-cytolytic immune assumption. Math. Model. Numer. Simul. Appl. 2022, 2, 164–176. [Google Scholar] [CrossRef]
- Farayola, M.F.; Shafie, S.; Siam, F.M.; Khan, I. Mathematical modeling of radiotherapy cancer treatment using Caputo fractional derivative. Comput. Methods Programs Biomed. 2020, 188, 105306. [Google Scholar] [CrossRef]
- Sheergojri, A.R.; Iqbal, P.; Agarwal, P.; Ozdemir, N. Uncertainty-based Gompertz growth model for tumor population and its numerical analysis. Int. J. Optim. Control Theor. Appl. 2022, 12, 137–150. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Balzotti, C.; D’Ovidio, M.; Loret, P. Fractional SIS epidemic models. Fractal Fract. 2020, 4, 44. [Google Scholar] [CrossRef]
- Traver, J.E.; Nuevo-Gallardo, C.; Tejado, I.; Fernández-Portales, J.; Ortega-Morán, J.F.; Pagador, J.B.; Vinagre, B.M. Cardiovascular Circulatory System and Left Carotid Model: A Fractional Approach to Disease Modeling. Fractal Fract. 2022, 6, 64. [Google Scholar] [CrossRef]
- Lai, X.; Friedman, A. Combination therapy of cancer with cancer vaccine and immune checkpoint inhibitors: A mathematical model. PLoS ONE 2017, 12, e0178479. [Google Scholar] [CrossRef]
- Lai, X.; Friedman, A. Mathematical modeling of cancer treatment with radiation and PD-L1 inhibitor. Sci. China Math. 2020, 63, 465–484. [Google Scholar] [CrossRef]
- Bonyah, E.; Zarin, R.; Wati, F. Mathematical modeling of cancer and hepatitis co-dynamics with non-local and non-singular kernel. Commun. Math. Biol. Neurosci. 2020, 2020, 91. [Google Scholar]
- Ucar, E.; Ozdemir, N.; Altun, E. Qualitative analysis and numerical simulations of new model describing cancer. J. Comput. Appl. 2023, 422, 114899. [Google Scholar] [CrossRef]
| Parameter | Meaning | Value (Unit) |
|---|---|---|
| a | the initial density of CD8+T cells | |
| b | the reproduction rate of CD8+T | |
| c | the death ratio of CD8+T cells | () |
| p | the carrying capacity of CD8+T cells | 1 |
| d | the tumor growth ratio | |
| q | the carrying capacity of cancer cells | 1 |
| e | the death ratio of cancer cells under the effect of IL-10 | |
| z | the death ratio of cancer cells under the effect of anti-PD-L1 | 1 |
| f | the decay rates of IL-10 | |
| the decay rates of anti-PD-L1 | () |
| CD8+T Cells | Tumor Cells | IL-10 | Anti-PD-L1 | |
|---|---|---|---|---|
| 1 | ||||
| CD8+T Cells | Tumor Cells | IL-10 | Anti-PD-L1 | |
|---|---|---|---|---|
| 1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uçar, E.; Özdemir, N. New Fractional Cancer Mathematical Model via IL-10 Cytokine and Anti-PD-L1 Inhibitor. Fractal Fract. 2023, 7, 151. https://doi.org/10.3390/fractalfract7020151
Uçar E, Özdemir N. New Fractional Cancer Mathematical Model via IL-10 Cytokine and Anti-PD-L1 Inhibitor. Fractal and Fractional. 2023; 7(2):151. https://doi.org/10.3390/fractalfract7020151
Chicago/Turabian StyleUçar, Esmehan, and Necati Özdemir. 2023. "New Fractional Cancer Mathematical Model via IL-10 Cytokine and Anti-PD-L1 Inhibitor" Fractal and Fractional 7, no. 2: 151. https://doi.org/10.3390/fractalfract7020151
APA StyleUçar, E., & Özdemir, N. (2023). New Fractional Cancer Mathematical Model via IL-10 Cytokine and Anti-PD-L1 Inhibitor. Fractal and Fractional, 7(2), 151. https://doi.org/10.3390/fractalfract7020151






