Models for Simulation of Fractal-like Particle Clusters with Prescribed Fractal Dimension
Abstract
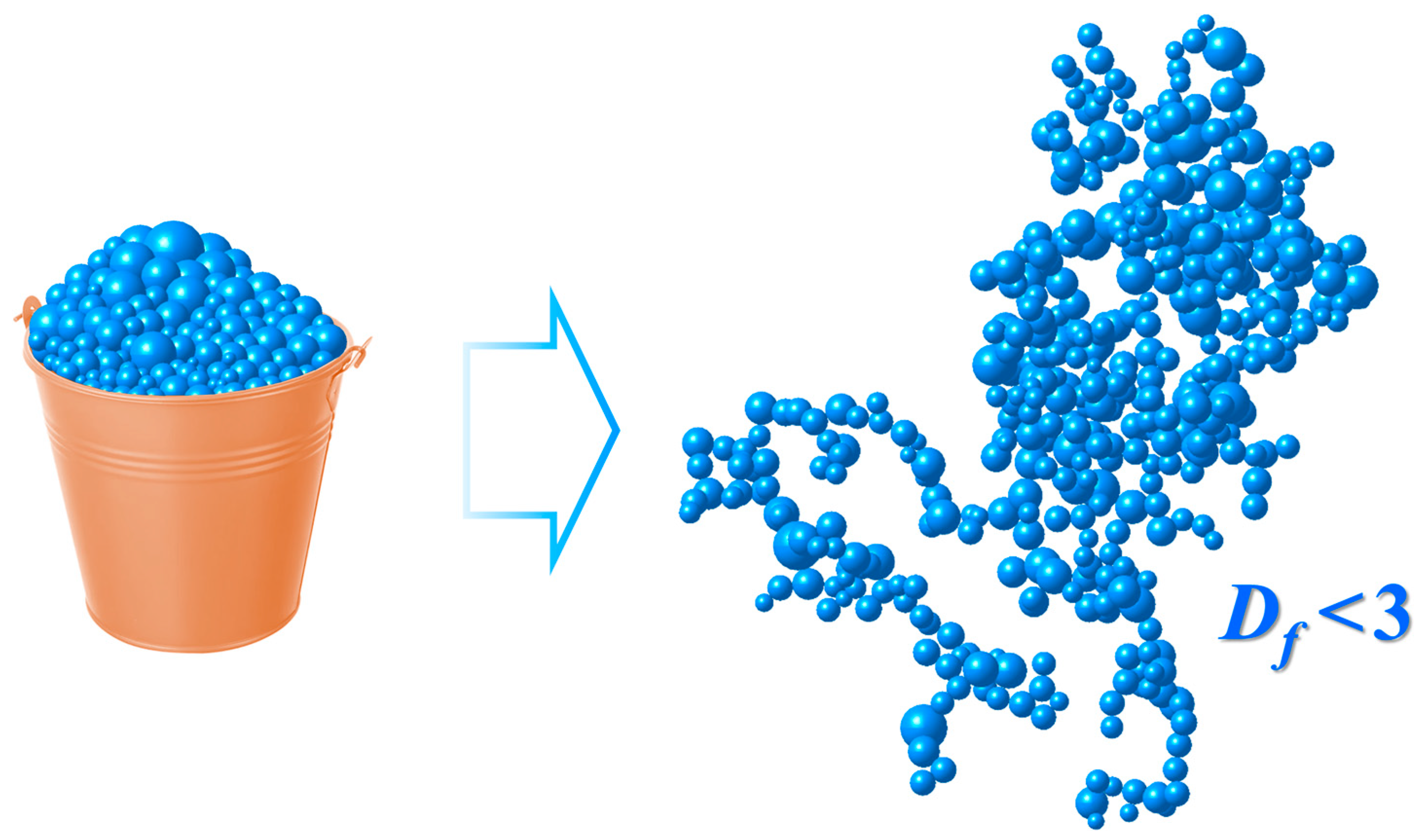
:1. Introduction
2. Fractal Cluster Models
2.1. Population Balance Equations
2.2. Langevin Dynamics and Its Derivatives
2.3. Monte Carlo Techniques
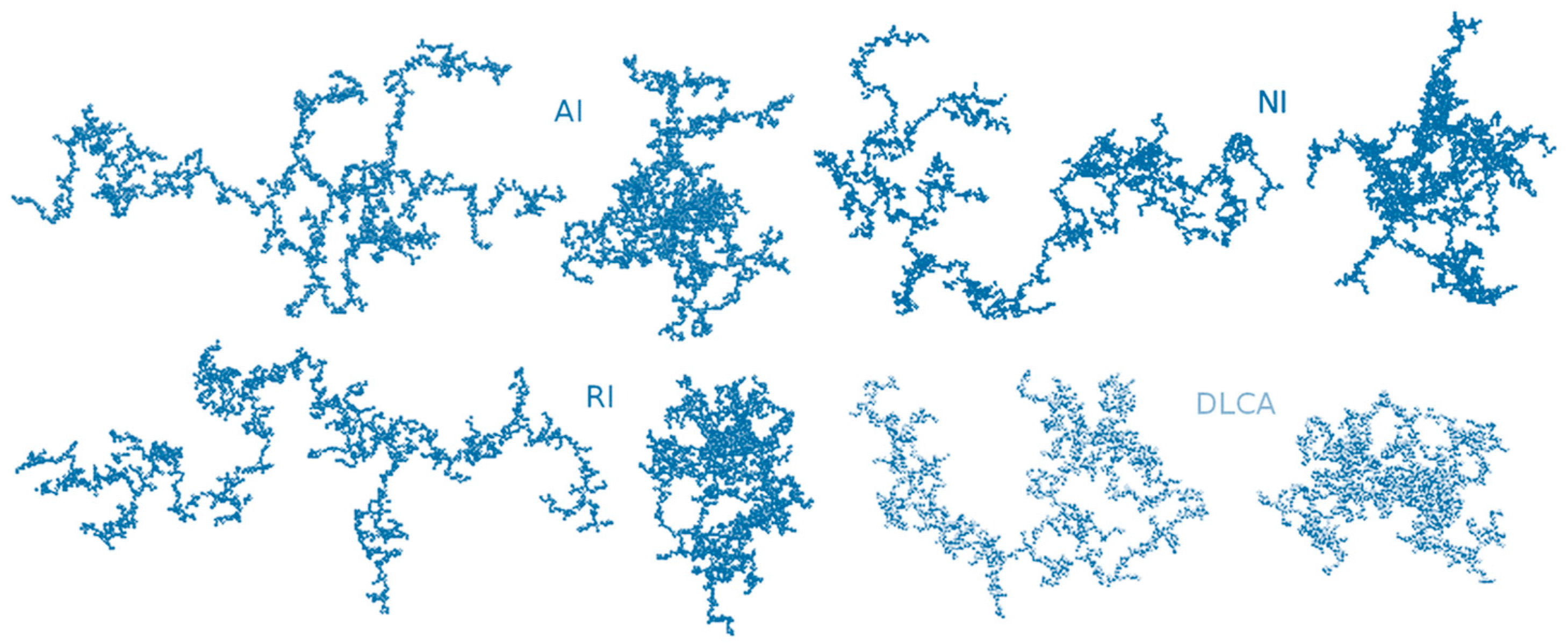
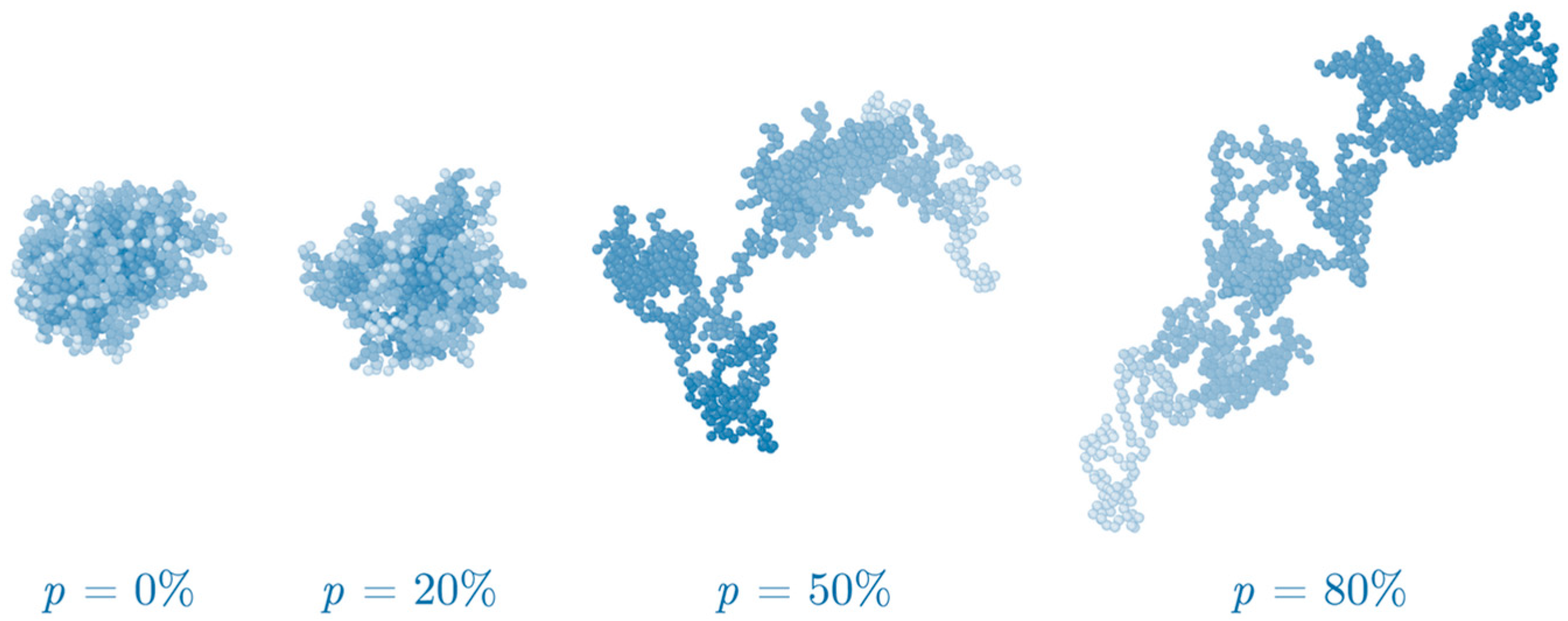
2.3.1. Modifications of DL(C)A
2.3.2. Eden Model and Its Derivatives
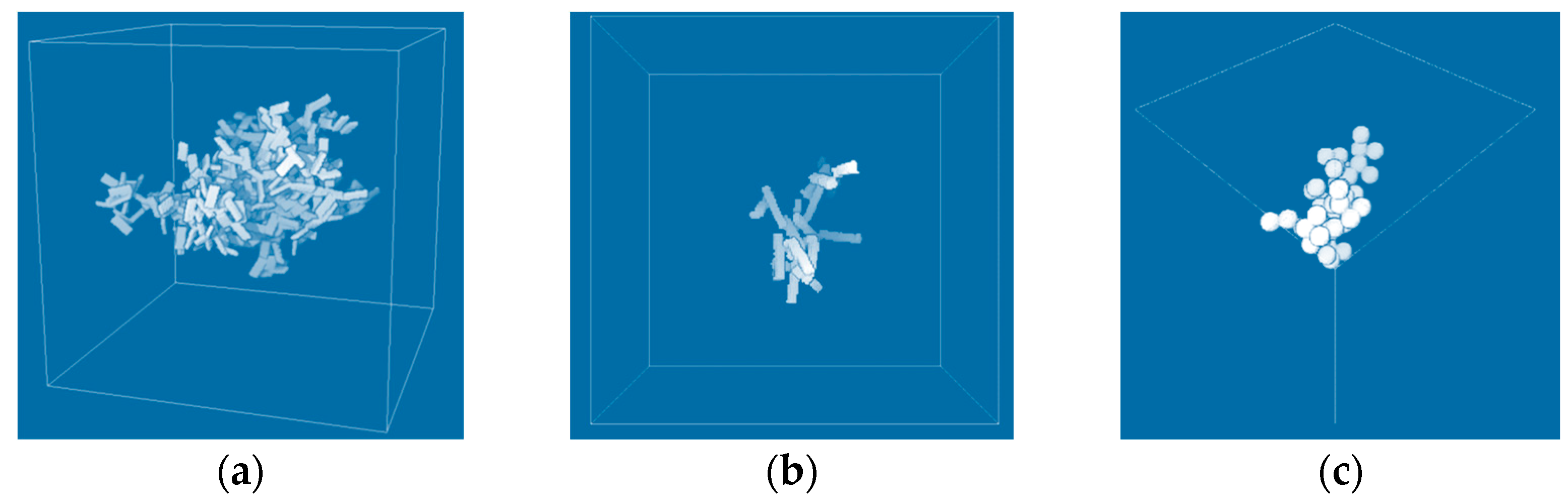
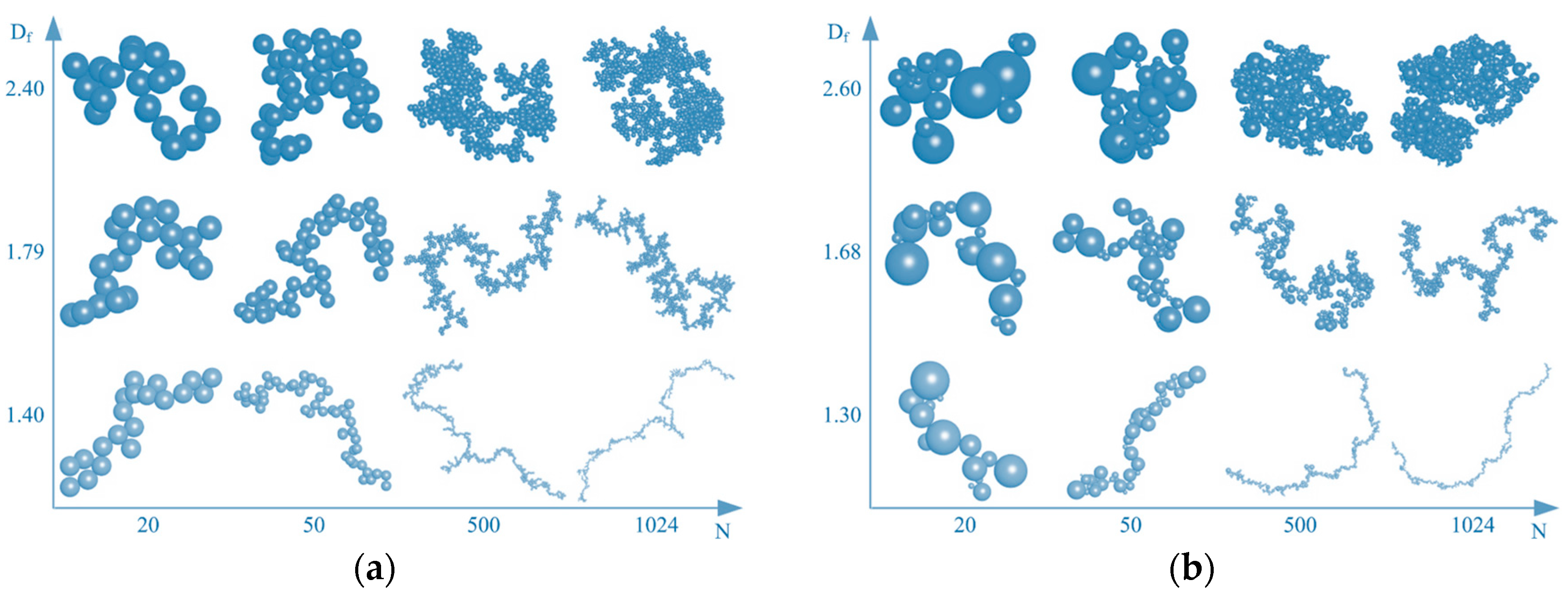
2.4. Hierarchical Assembly According to Mass–Radius Ratio
2.4.1. Monodisperse Particle–Cluster Models
2.4.2. Polydisperse Particle–Cluster Models
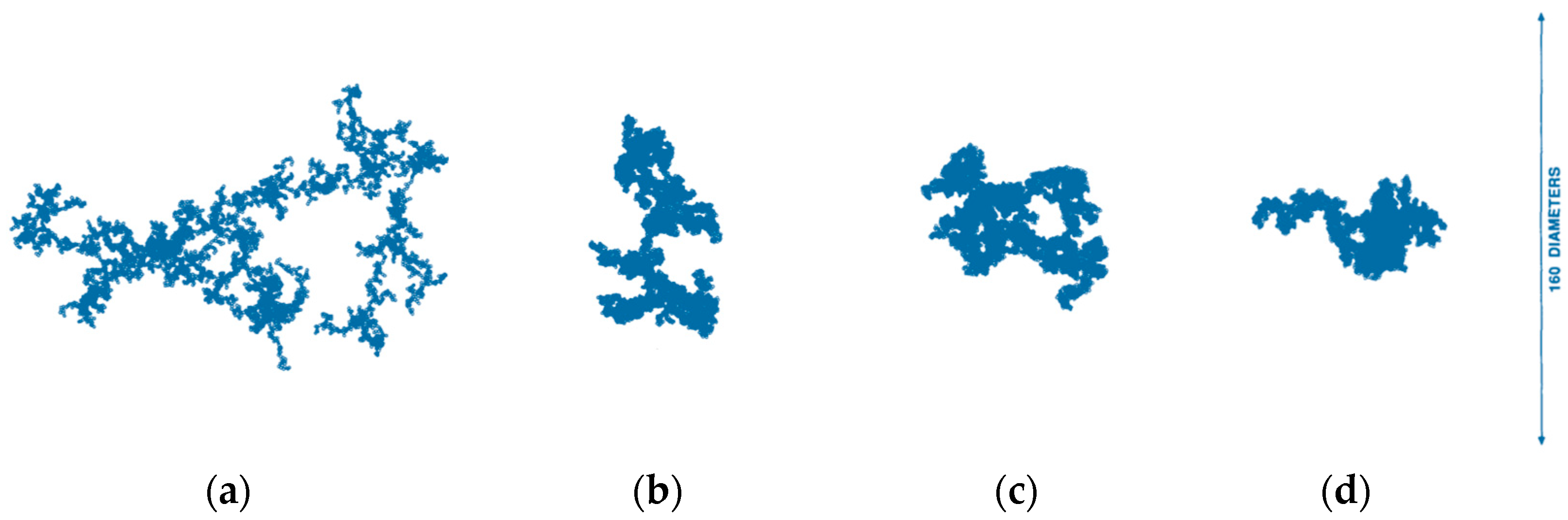
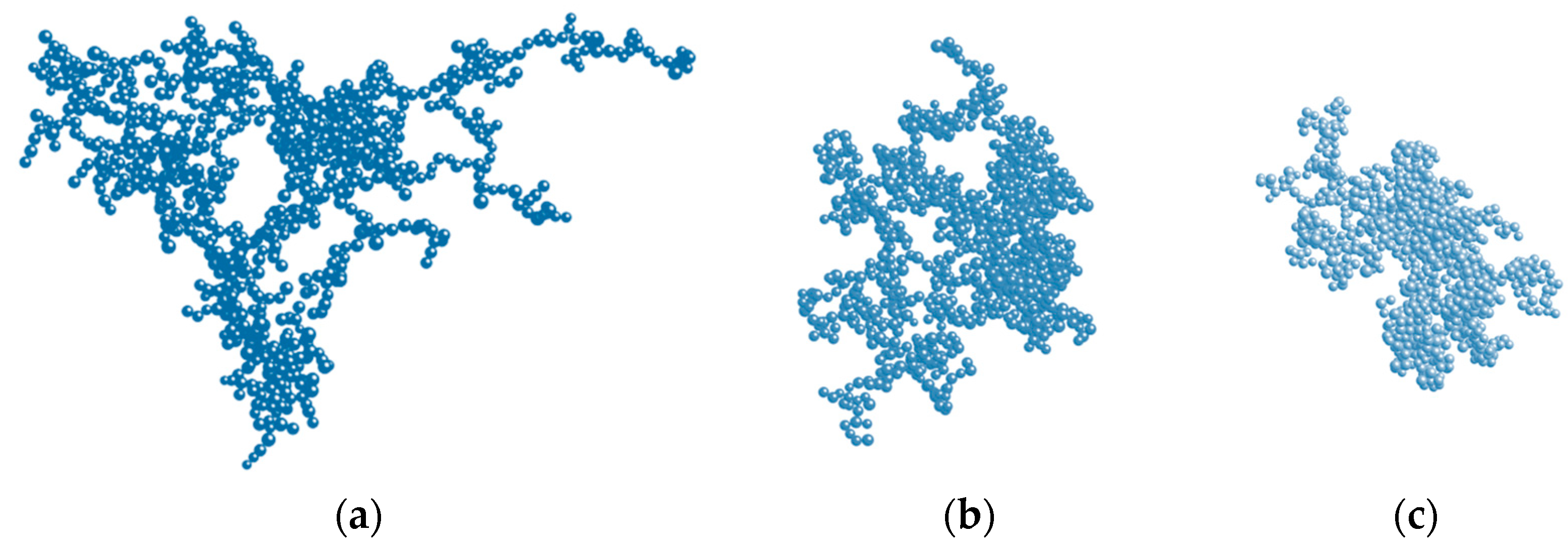
2.4.3. Cluster–Cluster Models of Monodisperse Particles
2.4.4. Cluster-Cluster Models of Polydisperse Particles
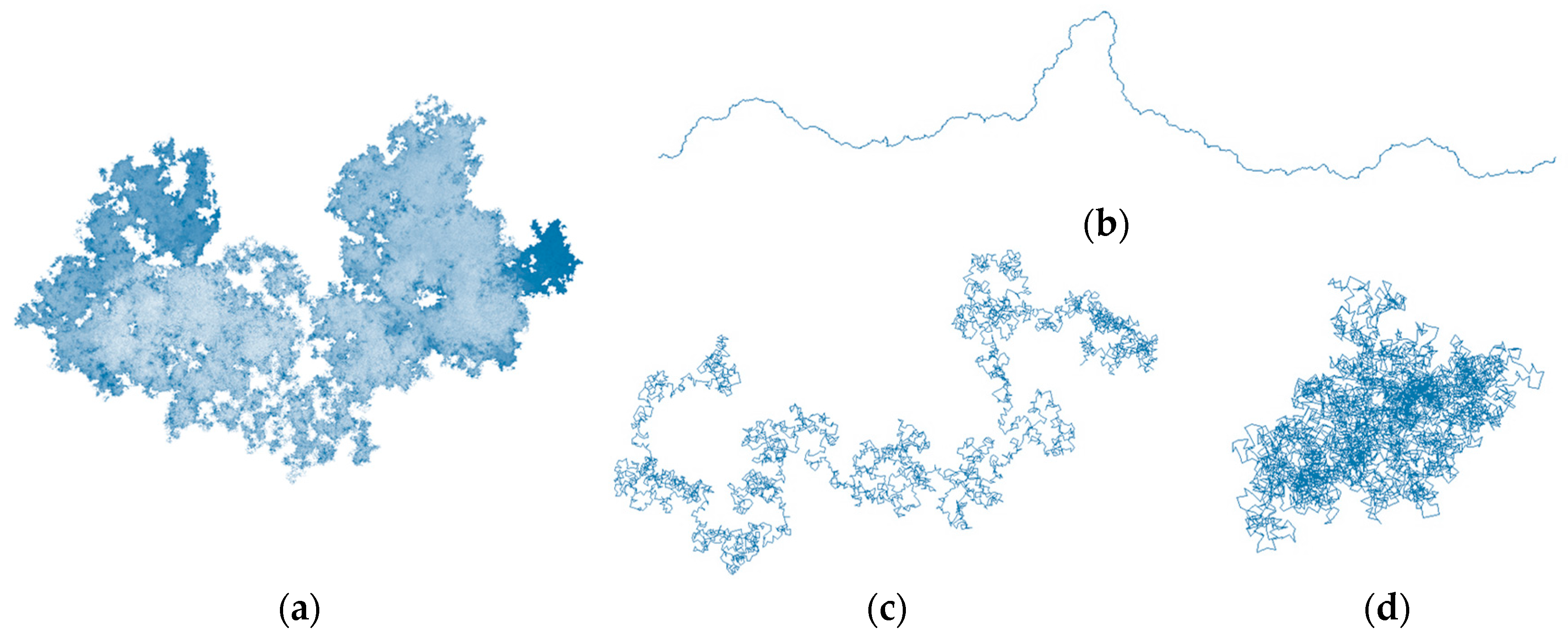
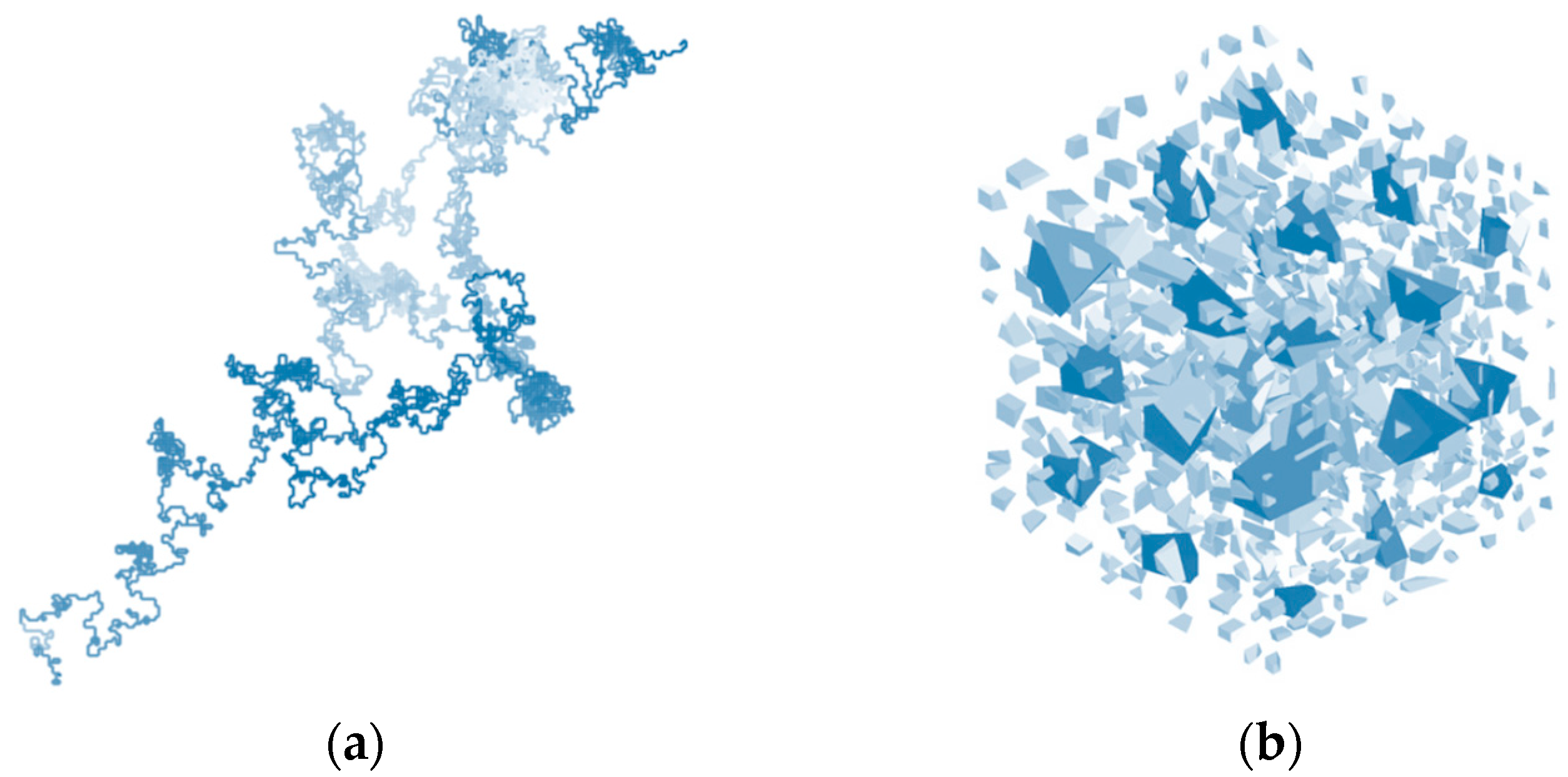
2.5. Fractal Chains
2.6. Some Exotic Examples in One Line
2.6.1. Möbius Fractal
2.6.2. Modeling Method Based on the Menger Sponge
2.6.3. Dynamic Lattice Liquid Model
3. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Co.: San Francisco, CA, USA, 1982; 460p. [Google Scholar]
- Sander, L.M. Fractal growth processes. Nature 1986, 322, 789–793. [Google Scholar] [CrossRef]
- Pfeifer, P. Fractal dimension as working tool for surface-roughness problems. Appl. Surf. Sci. 1984, 18, 146–164. [Google Scholar] [CrossRef]
- Timmons, J.; Falzone, G.; Balonis, M.; Bauchy, M.; Sant, G. Anomalous variations in the viscous activation energy of suspensions induced by fractal structuring. J. Colloid Interface Sci. 2018, 530, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Lesin, V.I.; Koksharov, Y.A.; Khomutov, G.B. Viscosity of liquid suspensions with fractal aggregates: Magnetic nanoparticles in petroleum colloidal structures. Colloids Surf. A Physicochem. Eng. Asp. 2011, 392, 88–94. [Google Scholar] [CrossRef]
- Meakin, P. Fractal aggregates in geophysics. Rev. Geophys. 1991, 29, 317–354. [Google Scholar] [CrossRef]
- Gmachowski, L. Fractal aggregate model of chain with mixed statistics. Polymer 2007, 48, 4316–4321. [Google Scholar] [CrossRef]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988; 284p. [Google Scholar]
- Maximova, N.; Dahl, O. Environmental implications of aggregation phenomena: Current understanding. Curr. Opin. Colloid Interface Sci. 2006, 11, 246–266. [Google Scholar] [CrossRef]
- Xu, P.; Mujumdar, A.S.; Yu, B. Fractal theory on drying: A review. Dry. Technol. 2008, 26, 640–650. [Google Scholar] [CrossRef]
- Pratsinis, S.E. Flame aerosol synthesis of ceramic powders. Prog. Energy Combust. Sci. 1998, 24, 197–219. [Google Scholar] [CrossRef]
- Kim, M.Y.; Park, S.H. A numerical aerosol model Fractal Aggregate Moment Model (FAMM) to simulate simultaneous nucleation, coagulation, surface growth, and sintering of fractal aggregates. Aerosol Sci. Technol. 2019, 53, 493–507. [Google Scholar] [CrossRef]
- Weisenstein, D.K.; Keith, D.W.; Dykema, J.A. Solar geoengineering using solid aerosol in the stratosphere. Atmos. Chem. Phys. 2015, 15, 11835–11859. [Google Scholar] [CrossRef]
- Yang, X.; Wang, F.; Yang, X.; Zhou, Q. Fractal dimension in concrete and implementation for meso-simulation. Constr. Build. Mater. 2017, 143, 464–472. [Google Scholar] [CrossRef]
- Smith, T.G., Jr.; Lange, G.D.; Marks, W.B. Fractal methods and results in cellular morphology—Dimensions, lacunarity and multifractals. J. Neurosci. Methods 1996, 69, 123–136. [Google Scholar] [CrossRef] [PubMed]
- Sosnowski, T.R. Nanosized and nanostructured particles in pulmonary drug delivery. J. Nanosci. Nanotechnol. 2015, 15, 3476–3487. [Google Scholar] [CrossRef] [PubMed]
- Oświȩcimka, P.; Kwapień, J.; Drozdz, S. Multifractality in the stock market: Price increments versus waiting times. Phys. A 2005, 347, 626–638. [Google Scholar] [CrossRef]
- Schaefer, D.W.; Martin, J.E.; Wiltzius, P.; Cannell, D.S. Fractal geometry of colloidal aggregates. Phys. Rev. Lett. 1984, 52, 2371–2374. [Google Scholar] [CrossRef]
- Lazzari, S.; Nicoud, L.; Jaquet, B.; Lattuada, M.; Morbidelli, M. Fractal-like structures in colloid science. Adv. Colloid Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef]
- Dickinson, E. Structure and rheology of colloidal particle gels: Insight from computer simulation. Adv. Colloid Interface Sci. 2013, 199–200, 114–127. [Google Scholar] [CrossRef]
- Eggersdorfer, M.L.; Pratsinis, S.E. The structure of agglomerates consisting of polydisperse particles. Aerosol Sci. Technol. 2012, 46, 347–353. [Google Scholar] [CrossRef]
- Morán, J.; Yon, J.; Poux, A. Monte Carlo Aggregation Code (MCAC) Part 1: Fundamentals. J. Colloid Interface Sci. 2020, 569, 184–194. [Google Scholar] [CrossRef]
- Beeckmans, J.M. The density of aggregated solid aerosol particles. Ann. Occup. Hyg. 1964, 7, 299–305. [Google Scholar] [CrossRef]
- Meakin, P. Fractal Aggregates. Adv. Colloid Interface Sci. 1987, 28, 249–331. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. Measures of fractal lacunarity: Minkowski content and alternatives. In Fractal Geometry and Stochastics. Progress in Probability; Bandt, C., Graf, S., Zähle, M., Eds.; Birkhäuser: Basel, Switzerland, 1995; Volume 37, pp. 15–42. [Google Scholar]
- Tomchuk, O.V.; Bulavin, L.A.; Pipich, V.; Ryukhtin, V.; Ivankov, O.I.; Aksenov, V.L.; Avdeev, M.V. Fractal aggregation in silica sols in basic tetraethoxysilane/ethanol/water solutions by small-angle neutron scattering. J. Mol. Liq. 2020, 304, 112736. [Google Scholar] [CrossRef]
- Bushell, G.C.; Yan, Y.D.; Woodfield, D.; Raper, J.; Amal, R. On techniques for the measurement of the mass fractal dimension of aggregates. Adv. Colloid Interface Sci. 2002, 95, 1–50. [Google Scholar] [CrossRef] [PubMed]
- Anitas, E.M. Small-Angle Scattering (Neutrons, X-rays, Light) from Complex Systems. Fractal and Multifractal Models for Interpretation of Experimental Data; Springer: Cham, Switzerland, 2019; 116p. [Google Scholar] [CrossRef]
- Beaucage, G. Determination of branch fraction and minimum dimension of mass-fractal aggregates. Phys. Rev. E 2004, 70, 031401. [Google Scholar] [CrossRef] [PubMed]
- Besselink, R.; Stawski, T.M.; Van Driessche, A.E.S.; Benning, L.G. Not just fractal surfaces, but surface fractal aggregates: Derivation of the expression for the structure factor and its applications. J. Chem. Phys. 2016, 145, 211908. [Google Scholar] [CrossRef]
- Tence, M.; Chevalier, J.P.; Jullien, R. On the measurement of the fractal dimension of aggregated particles by electron microscopy: Experimental method, corrections and comparison with numerical models. J. Phys. 1986, 47, 1989–1998. [Google Scholar] [CrossRef]
- Dastanpour, R.; Boone, J.M.; Rogak, S.N. Automated primary particle sizing of nanoparticle aggregates by TEM image analysis. Powder Technol. 2016, 295, 218–224. [Google Scholar] [CrossRef]
- Kütz, S.; Schmidt-Ott, A. Use of a low-pressure impactor for fractal analysis of submicron particles. J. Aerosol Sci. 1990, 21, S47–S50. [Google Scholar] [CrossRef]
- Schmidt-Ott, A.; Baltensperger, U.; Gaggeler, H.W.; Jost, D.T. Scaling behaviour of physical parameters describing agglomerates. J. Aerosol Sci. 1990, 21, 711–717. [Google Scholar] [CrossRef]
- Magill, J. Fractal dimension and aerosol particle dynamics. J. Aerosol Sci. 1991, 22, S165–S168. [Google Scholar] [CrossRef]
- Wu, H.; Morbidelli, M. A model relating structure of colloidal gels to their elastic properties. Langmuir 2001, 17, 1030–1036. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three. I. Fractal theory of heterogeneous surfaces. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Avnir, D.; Farin, D.; Pfeifer, P. Chemistry in noninteger dimensions between two and three. II. Fractal surfaces of adsorbents. J. Chem. Phys. 1983, 79, 3566–3571. [Google Scholar] [CrossRef]
- Heinson, W.R.; Sorensen, C.M.; Chakrabarti, A. A three parameter description of the structure of diffusion limited cluster fractal aggregates. J. Colloid Interface Sci. 2012, 375, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Yon, J.; Morán, J.; Ouf, F.-X.; Mazur, M.; Mitchell, J.B. From monomers to agglomerates: A generalized model for characterizing the morphology of fractal-like clusters. J. Aerosol Sci. 2021, 151, 105628. [Google Scholar] [CrossRef]
- Morán, J.; Henry, C.; Poux, A.; Yon, J. Impact of the maturation process on soot particle aggregation kinetics and morphology. Carbon 2021, 182, 837–846. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B. 1983, 27, 5686–5697. [Google Scholar] [CrossRef]
- Meakin, P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation. Phys. Rev. Lett. 1983, 51, 1119–1122. [Google Scholar] [CrossRef]
- Meakin, P. Off lattice simulations of cluster-cluster aggregation in dimensions 2–6. Phys. Lett. A 1985, 107, 269–272. [Google Scholar] [CrossRef]
- Brasil, A.M.; Farias, T.L.; Carvalho, M.G. Evaluation of the fractal properties of cluster–cluster aggregates. Aerosol Sci. Technol. 2000, 33, 440–454. [Google Scholar] [CrossRef]
- Kolb, M.; Botet, R.; Jullien, R. Scaling of kinetically growing clusters. Phys. Rev. Lett. 1983, 51, 1123–1126. [Google Scholar] [CrossRef]
- Brown, W.D.; Ball, R.C. Computer simulation of chemically limited aggregation. J. Phys. A Math. Gen. 1985, 18, L517–L521. [Google Scholar] [CrossRef]
- Jullien, R.; Kolb, M. Hierarchical model for chemically limited clustercluster aggregation. J. Phys. A Math. Gen. 1984, 17, L639–L643. [Google Scholar] [CrossRef]
- Kolb, M.; Jullien, R. Chemically limited versus diffusion limited aggregation. J. Phys. Lett. 1984, 45, L977–L981. [Google Scholar] [CrossRef]
- Ball, R.C.; Jullien, R. Finite size effects in cluster-cluster aggregation. J. Phys. Lett. 1984, 45, 1031–1035. [Google Scholar] [CrossRef]
- Meakin, P.; Jullien, R. The effects of restructuring on the geometry of clusters formed by diffusion-limited, ballistic, and reaction-limited cluster-cluster aggregation. J. Chem. Phys. 1988, 89, 246–250. [Google Scholar] [CrossRef]
- Viglis, T.A. Flory theory of polymeric fractals—Intersection, saturation and condensation. Phys. A 1988, 153, 341–354. [Google Scholar] [CrossRef]
- Malcai, O.; Lidar, D.A.; Biham, O. Scaling range and cutoffs in empirical fractals. Phys. Rev. E 1997, 56, 2817–2828. [Google Scholar] [CrossRef]
- Tomchuk, O.V. Fractal concept in structural analysis of nanosystems: A retrospective look and prospects. Ukr. J. Phys. 2020, 65, 709–728. [Google Scholar] [CrossRef]
- Voss, R.F. Multiparticle fractal aggregation. J. Stat. Phys. 1984, 36, 861–872. [Google Scholar] [CrossRef]
- Jullien, R.; Botet, R.; Mors, P.M. Computer simulations of cluster-cluster aggregation. Faraday Discuss. Chem. Soc. 1987, 83, 125–137. [Google Scholar] [CrossRef]
- Botet, R.; Jullien, R. Fractal aggregates of particles. Ph. Transit. 1990, 24–26, 691–736. [Google Scholar] [CrossRef]
- Jullien, R. The application of fractals to colloidal aggregation. Croat. Chem. Acta 1992, 65, 215–235. [Google Scholar]
- Meakin, P. A Historical introduction to computer models for fractal aggregates. J. Sol-Gel Sci. Technol. 1999, 15, 97–117. [Google Scholar] [CrossRef]
- Meakin, P. Effects of cluster trajectories on cluster-cluster aggregation: A comparison of linear and Brownian trajectories in two- and three-dimensional simulations. Phys. Rev. A 1984, 29, 997–999. [Google Scholar] [CrossRef]
- Avdeev, M.V.; Aksenov, V.L.; Rosta, L. Pressure induced changes in fractal structure of detonation nanodiamond powder by small-angle neutron scattering. Diam. Relat. Mater. 2007, 16, 2050–2053. [Google Scholar] [CrossRef]
- Tomchuk, O.V.; Avdeev, M.V.; Aksenov, V.L.; Shulenina, A.V.; Ivankov, O.I.; Ryukhtin, V.; Vékás, L.; Bulavin, L.A. Temperature-dependent fractal structure of particle clusters in aqueous ferrofluids by small-angle scattering. Colloids Surf. A Physicochem. Eng. Asp. 2021, 613, 126090. [Google Scholar] [CrossRef]
- Chakraborti, R.K.; Gardner, K.H.; Atkinson, J.F.; van Benschoten, J.E. Changes in fractal dimension during aggregation. Water Res. 2003, 37, 873–883. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.-T.; Ou-Yang, Z.-C. Diffusion-limited aggregation with polygon particles. Commun. Theor. Phys. 2012, 58, 895–901. [Google Scholar] [CrossRef]
- Farias, T.L.; Köylü, Ü.Ö.; Carvalho, M.G. Effects of polydispersity of aggregates and primary particles on radiative properties of simulated soot. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 357–371. [Google Scholar] [CrossRef]
- Hasmy, A.; Vacher, R.; Jullien, R. Small-angle scattering by fractal aggregates: A numerical investigation of the crossover between the fractal regime and the Porod regime. Phys. Rev. B 1994, 50, 1305–1308. [Google Scholar] [CrossRef]
- Goudeli, E.; Eggersdorfer, M.L.; Pratsinis, S.E. Coagulation of agglomerates consisting of polydisperse primary particles. Langmuir 2016, 32, 9276–9285. [Google Scholar] [CrossRef] [PubMed]
- Tenti, J.M.; Hernández Guiance, S.N.; Irurzun, I.M. Fractal dimension of diffusion-limited aggregation clusters grown on spherical surfaces. Phys. Rev. E 2021, 103, 012138. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Singh, A.K.; Kolan, S.R.; Tsotsas, E. Fractal analysis of aggregates: Correlation between the 2D and 3D box-counting fractal dimension and power law fractal dimension. Chaos Solitons Fractals 2022, 160, 112246. [Google Scholar] [CrossRef]
- Schmidt, P.W. Small-angle scattering studies of disordered, porous and fractal systems. J. Appl. Cryst. 1991, 24, 414–435. [Google Scholar] [CrossRef]
- Cherny, A.Y.; Anitas, E.M.; Kuklin, A.I.; Balasoiu, M.; Osipov, V.A. Scattering from generalized Cantor fractals. J. Appl. Cryst. 2010, 43, 790–797. [Google Scholar] [CrossRef]
- Cherny, A.Y.; Anitas, E.M.; Osipov, V.A.; Kuklin, A.I. Deterministic fractals: Extracting additional information from small-angle scattering data. Phys. Rev. E 2011, 84, 036203. [Google Scholar] [CrossRef]
- Kryven, I.; Lazzari, S.; Storti, G. Population balance modeling of aggregation and coalescence in colloidal systems. Macromol. Theory Simul. 2014, 23, 170–181. [Google Scholar] [CrossRef]
- Rigopoulos, S. Population balance modelling of polydispersed particles in reactive flows. Prog. Energy Combust. Sci. 2010, 36, 412–443. [Google Scholar] [CrossRef]
- Kim, J.; Kramer, T.A. Improved orthokinetic coagulation model for fractal colloids: Aggregation and breakup. Chem. Eng. Sci. 2006, 61, 45–53. [Google Scholar] [CrossRef]
- Kostoglou, M.; Konstandopoulos, A.G.; Friedlander, S.K. Bivariate population dynamics simulation of fractal aerosol aggregate coagulation and restructuring. J. Aerosol Sci. 2006, 37, 1102–1115. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Ansell, G.C.; Dickinson, E. Short-range structure of simulated colloidal aggregates. Phys. Rev. A 1987, 35, 2349–2352. [Google Scholar] [CrossRef] [PubMed]
- Phung, T.N.; Brady, J.F.; Bossis, G. Stokesian Dynamics simulation of Brownian suspensions. J. Fluid Mech. 1996, 313, 181–207. [Google Scholar] [CrossRef]
- Sierou, A.; Brady, J.F. Accelerated Stokesian Dynamics simulations. J. Fluid Mech. 2001, 448, 115–146. [Google Scholar] [CrossRef]
- Whittle, M.; Dickinson, E. Brownian dynamics simulation of gelation in soft sphere systems with irreversible bond formation. Mol. Phys. 1997, 90, 739–757. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Heyes, D.M.; Mitchell, P.J. Mean-field hydrodynamics brownian dynamics simulations of stabilized colloidal liquids under shear. J. Non-Newton. Fluid. Mech. 1997, 68, 101–124. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Statistical mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Ferri, G.; Humbert, S.; Digne, M.; Schweitzer, J.-M.; Moreaud, M. Simulation of large aggregate particles system with a new morphological model. Image Anal. Stereol. 2021, 40, 71–84. [Google Scholar] [CrossRef]
- Mountain, R.D.; Mulholland, G.W.; Baum, H. Simulation of aerosol agglomeration in the free molecular and continuum flow regimes. J. Colloid Interface Sci. 1986, 114, 67–81. [Google Scholar] [CrossRef]
- Meakin, P. Cluster-particle aggregation with fractal (Levy flight) particle trajectories. Phys. Rev. B 1984, 29, 3722–3725. [Google Scholar] [CrossRef]
- Jungblut, S.; Joswig, J.-O.; Eychmüller, A. Diffusion- and reaction-limited cluster aggregation revisited. Phys. Chem. Chem. Phys. 2019, 21, 5723–5729. [Google Scholar] [CrossRef] [PubMed]
- Meakin, P. Structural readjustment effects in cluster-cluster aggregation. J. Phys. 1985, 46, 1543–1552. [Google Scholar] [CrossRef]
- Jullien, R.; Hasmy, A. Fluctuating bond aggregation: A model for chemical gel formation. Phys. Rev. Lett. 1995, 74, 4003–4006. [Google Scholar] [CrossRef]
- Jullien, R. A new model of cluster aggregation. J. Phys. A Math. Gen. 1986, 19, 2129–2136. [Google Scholar] [CrossRef]
- Mors, P.M.; Botet, R.; Jullien, R. Cluster-cluster aggregation with dipolar interactions. J. Phys. A Math. Gen. 1987, 20, L975–L980. [Google Scholar] [CrossRef]
- Jullien, R.; Meakin, P. Simple models for the restructuring of three-dimensional ballistic aggregates. J. Colloid Interface Sci. 1989, 127, 265–272. [Google Scholar] [CrossRef]
- Oh, C.; Sorensen, C.M. The effect of overlap between monomers on the determination of fractal cluster morphology. J. Colloid Interface Sci. 1997, 193, 17–25. [Google Scholar] [CrossRef]
- Meakin, P. The effects of rotational diffusion on the fractal dimensionality of structures formed by cluster–cluster aggregation. J. Chem. Phys. 1984, 81, 4637–4639. [Google Scholar] [CrossRef]
- Loskutov, A.; Andrievsky, D.; Ivanov, V.; Vasiliev, K.; Ryabov, A. Fractal growth of rotating DLA-clusters. Macromol. Symp. 2000, 160, 239–248. [Google Scholar] [CrossRef]
- Kim, S.; Lee, K.-S.; Zachariah, M.R.; Lee, D. Three-dimensional off-lattice Monte Carlo simulations on a direct relation between experimental process parameters and fractal dimension of colloidal aggregates. J. Colloid Interface Sci. 2010, 344, 353–361. [Google Scholar] [CrossRef]
- Heinson, W.R.; Pierce, F.; Sorensen, C.M.; Chakrabarti, A. Crossover from ballistic to epstein diffusion in the free-molecular regime. Aerosol Sci. Technol. 2014, 48, 738–746. [Google Scholar] [CrossRef]
- Goudeli, E.; Eggersdorfer, M.L.; Pratsinis, S.E. Coagulation−agglomeration of fractal-like particles: Structure and self-preserving size distribution. Langmuir 2015, 31, 1320–1327. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, S.; Hisaeda, Y.; Asakuma, Y.; Aoki, H.; Miura, T.; Yano, H.; Sawa, Y. Simulation of soot aggregates formed by benzene pyrolysis. Combust. Flame 1999, 117, 851–860. [Google Scholar] [CrossRef]
- Camejo, M.D.; Espeso, D.R.; Bonilla, L.L. Influence of primary-particle density in the morphology of agglomerates. Phys. Rev. E 2014, 90, 012306. [Google Scholar] [CrossRef] [PubMed]
- Morán, J.; Yon, J.; Poux, A.; Corbin, F.; Ouf, F.-X.; Siméon, A. Monte Carlo Aggregation Code (MCAC) Part 2: Application to soot agglomeration, highlighting the importance of primary particles. J. Colloid Interface Sci. 2020, 575, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Paoluzzi, M.; Leoni, M.; Marchetti, M.C. Fractal aggregation of active particles. Phys. Rev. E 2018, 98, 052603. [Google Scholar] [CrossRef]
- Nicolás-Carlock, J.R.; Carrillo-Estrada, J.L.; Dossetti, V. Fractality à la carte: A general particle aggregation model. Sci. Rep. 2016, 6, 19505. [Google Scholar] [CrossRef] [PubMed]
- Hurd, A.J.; Schaeffer, D.W. Diffusion-limited aggregation in two dimensions. Phys. Rev. Lett. 1985, 54, 1043–1046. [Google Scholar] [CrossRef] [PubMed]
- Jullien, R. Transparency effects in cluster-cluster aggregation with linear trajectories. J. Phys. A Math. Gen. 1984, 17, L771–L776. [Google Scholar] [CrossRef]
- Eden, M. A two-dimensional growth process. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Neyman, J., Ed.; University of California Press: Berkeley, LA, USA, 1961; Volume IV, pp. 223–239. [Google Scholar]
- Takeuchi, K.A. Statistics of circular interface fluctuations in an off-lattice Eden model. J. Stat. Mech. 2012, 5, P05007. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liu, P.L.; Bassingthwaighte, J.B. Off-lattice Eden-C cluster growth model. J. Phys. A Math. Gen. 1995, 28, 2141–2147. [Google Scholar] [CrossRef]
- Guesnet, E.; Dendievel, R.; Jauffrès, D.; Martin, C.L.; Yrieix, B. A growth model for the generation of particle aggregates with tunable fractal dimension. Phys. A 2019, 513, 63–73. [Google Scholar] [CrossRef]
- Filippov, A.V.; Zurita, M.; Rosner, D.E. Fractal-like aggregates: Relation between morphology and physical properties. J. Colloid Interface Sci. 2000, 229, 261–273. [Google Scholar] [CrossRef]
- Mackowski, D.W. Calculation of total cross sections of multiple-sphere clusters. J. Opt. Soc. Am. A 1994, 11, 2851–2861. [Google Scholar] [CrossRef]
- Mackowski, D.W. Electrostatics analysis of radiative absorption by sphere clusters in the Rayleigh limit: Application to soot particles. Appl. Opt. 1995, 34, 3535–3545. [Google Scholar] [CrossRef]
- Singh, A.K.; Tsotsas, E. A tunable aggregation model incorporated in Monte Carlo simulations of spray fluidized bed agglomeration. Powder Technol. 2020, 364, 417–428. [Google Scholar] [CrossRef]
- Dolotov, S.V.; Roldughin, V.I. Simulation of ESR spectra of metal nanoparticle aggregates. Colloid J. 2007, 69, 9–12. [Google Scholar] [CrossRef]
- Tomchuk, O.V.; Volkov, D.S.; Bulavin, L.A.; Rogachev, A.V.; Proskurnin, M.A.; Korobov, M.V.; Avdeev, M.V. Structural characteristics of aqueous dispersions of detonation nanodiamond and their aggregate fractions by small-angle neutron scattering. J. Phys. Chem. C 2015, 119, 794–802. [Google Scholar] [CrossRef]
- Singh, A.K.; Tsotsas, E. A Fast and improved tunable aggregation model for stochastic simulation of spray fluidized bed agglomeration. Energies 2021, 14, 7221. [Google Scholar] [CrossRef]
- Sorensen, C.M.; Roberts, G.C. The prefactor of fractal aggregates. J. Colloid Interface Sci. 1997, 186, 447–452. [Google Scholar] [CrossRef]
- Tomchuk, O.V.; Avdeev, M.V.; Bulavin, L.A. Modeling fractal aggregates of polydisperse particles with tunable dimension. Colloids Surf. A Physicochem. Eng. Asp. 2020, 605, 125331. [Google Scholar] [CrossRef]
- Ehrl, L.; Soos, M.; Lattuada, M. Generation and geometrical analysis of dense clusters with variable fractal dimension. J. Phys. Chem. B 2009, 113, 10587–10599. [Google Scholar] [CrossRef]
- Gmachowski, L. Calculation of the fractal dimension of aggregates. Colloids Surf. A Physicochem. Eng. Asp. 2002, 211, 197–203. [Google Scholar] [CrossRef]
- Singh, A.K.; Tsotsas, E. Stochastic model to simulate spray fluidized bed agglomeration: A morphological approach. Powder Technol. 2019, 355, 449–460. [Google Scholar] [CrossRef]
- Bushell, G.; Amal, R. Fractal aggregates of polydisperse particles. J. Colloid Interface Sci. 1998, 205, 459–469. [Google Scholar] [CrossRef]
- Bushell, G.; Amal, R.; Raper, J. The effect of polydispersity in primary particle size on measurement of the fractal dimension of aggregates. Part. Part. Syst. Charact. 1998, 15, 3–8. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Piña-Salazar, E.-Z.; Kirkensgaard, J.J.K.; Terzyk, A.P.; Futamura, R.; Hayashi, T.; Ōsawa, E.; Kaneko, K.; Ciach, A. Reconstructing the fractal clusters of detonation nanodiamonds from small-angle X-ray scattering. Carbon 2020, 169, 349–356. [Google Scholar] [CrossRef]
- Tan, Z.-J.; Zou, X.-W.; Zhang, W.-B.; Jin, Z.-Z. Influence of particle size on diffusion-limited aggregation. Phys. Rev. E 1999, 60, 6202–6205. [Google Scholar] [CrossRef] [PubMed]
- Braga, F.L.; Mattos, O.A.; Amorina, V.S.; Souza, A.B. Diffusion limited aggregation of particles with different sizes: Fractal dimension change by anisotropic growth. Phys. A 2015, 429, 28–34. [Google Scholar] [CrossRef]
- Kätzel, U.; Bedrich, R.; Stintz, M.; Ketzmerick, R.; Gottschalk-Gaudig, T.; Barthel, H. Dynamic light scattering for the characterization of polydisperse fractal systems: I. Simulation of the diffusional behavior. Part. Part. Syst. Charact. 2008, 25, 9–18. [Google Scholar] [CrossRef]
- Kätzel, U.; Vorbau, M.; Stintz, M.; Gottschalk-Gaudig, T.; Barthel, H. Dynamic light scattering for the characterization of polydisperse fractal systems: II. Relation between structure and DLS results. Part. Part. Syst. Charact. 2008, 25, 19–30. [Google Scholar] [CrossRef]
- Wang, Y.; Maurel, G.; Couty, M.; Detcheverry, F.; Merabia, S. Implicit medium model for fractal aggregate polymer nanocomposites: Linear viscoelastic properties. Macromolecules 2019, 52, 2021–2032. [Google Scholar] [CrossRef]
- Karagiannakis, N.P.; Skouras, E.D.; Burganos, V.N. Modelling thermal conduction in polydispersed and sintered nanoparticle aggregates. Nanomaterials 2022, 12, 25. [Google Scholar] [CrossRef]
- Singh, A.K.; Tsotsas, E. Influence of polydispersity and breakage on stochastic simulations of spray fluidized bed agglomeration. Chem. Eng. Sci. 2022, 247, 117022. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Plane DLA is not self-similar; is it a fractal that becomes increasingly compact as it grows? Phys. A 1992, 191, 95–107. [Google Scholar] [CrossRef]
- Oh, C.; Sorensen, C.M. Structure factor of diffusion-limited aggregation clusters: Local structure and non-self-similarity. Phys. Rev. E 1998, 57, 784–790. [Google Scholar] [CrossRef]
- Skorupski, K.; Mroczka, J.; Wriedt, T.; Riefler, N. A fast and accurate implementation of tunable algorithms used for generation of fractal-like aggregate models. Phys. A 2014, 404, 106–117. [Google Scholar] [CrossRef]
- Thouy, R.; Jullien, R. A cluster-cluster aggregation model with tunable fractal dimension. J. Phys. A Math. Gen. 1994, 27, 2953–2963. [Google Scholar] [CrossRef]
- Thouy, R.; Jullien, R.; Benoit, C. Density of vibrational states of fractal aggregates: Scalar interactions. J. Non-Cryst. Solids 1998, 232–234, 674–681. [Google Scholar] [CrossRef]
- Vormoor, O. Large scale fractal aggregates using the tunable dimension cluster–cluster aggregation. Comput. Phys. Commun. 2002, 144, 121–129. [Google Scholar] [CrossRef]
- Morán, J.; Fuentes, A.; Liu, F.; Yon, J. FracVAL: An improved tunable algorithm of cluster–cluster aggregation for generation of fractal structures formed by polydisperse primary particles. Comput. Phys. Commun. 2019, 239, 225–237. [Google Scholar] [CrossRef]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987; 335p. [Google Scholar]
- Ilatovskiy, A.V.; Lebedev, D.V.; Filatov, M.V.; Petukhov, M.G.; Isaev-Ivanov, V.V. SANS spectra of the fractal supernucleosomal chromatin structure models. J. Phys. Conf. Ser. 2012, 351, 012007. [Google Scholar] [CrossRef]
- Tomchuk, O.V. Some aspects of small-angle scattering by fractal chains. AIP Conf. Proceed. 2019, 2163, 020006. [Google Scholar] [CrossRef]
- von Koch, H. On a continuous curve without a tangent, obtained by an elementary geometrical construction (Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire). Ark. Mat. Astron. Fys. 1904, 1, 681–702. [Google Scholar]
- Tomchuk, O.V. Stochastic fractal by deterministic algorithm: Introducing the Möbius fractal. AIP Conf. Proceed. 2021, 2377, 020002. [Google Scholar] [CrossRef]
- Möbius, A.F. About a special kind of reversal of the series (Über eine besondere art von umkehrung der reihen). J. Reine Angew. Math. 1832, 9, 105–123. [Google Scholar]
- Yang, X.; Wang, F. Random-fractal-method-based generation of meso-model for concrete aggregates. Powder Technol. 2015, 284, 63–77. [Google Scholar] [CrossRef]
- Menger, K. Dimensionstheorie; B. G. Teubner: Leipzig, Germany; Berlin, Germany, 1928; 319p. [Google Scholar]
- Polanowski, P. Parallel simulation of random fractal growth using dynamic lattice liquid (DLL) model. J. Non-Cryst. Solids 2007, 353, 4575–4580. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomchuk, O. Models for Simulation of Fractal-like Particle Clusters with Prescribed Fractal Dimension. Fractal Fract. 2023, 7, 866. https://doi.org/10.3390/fractalfract7120866
Tomchuk O. Models for Simulation of Fractal-like Particle Clusters with Prescribed Fractal Dimension. Fractal and Fractional. 2023; 7(12):866. https://doi.org/10.3390/fractalfract7120866
Chicago/Turabian StyleTomchuk, Oleksandr. 2023. "Models for Simulation of Fractal-like Particle Clusters with Prescribed Fractal Dimension" Fractal and Fractional 7, no. 12: 866. https://doi.org/10.3390/fractalfract7120866
APA StyleTomchuk, O. (2023). Models for Simulation of Fractal-like Particle Clusters with Prescribed Fractal Dimension. Fractal and Fractional, 7(12), 866. https://doi.org/10.3390/fractalfract7120866





