A New Fractional-Order Virtual Inertia Support Based on Battery Energy Storage for Enhancing Microgrid Frequency Stability
Abstract
:1. Introduction
- Propose a FO derivative control that is applied to the suggested, developed virtual inertia model. The FOVIC has the benefit of reducing system order, which can considerably suppress frequency fluctuation and output power oscillation.
- Including FOVIC boosts the system’s degree of freedom, thus strengthening system stability and further enhancing dynamic performance in the presence of numerous operational circumstances and high RES penetration rates.
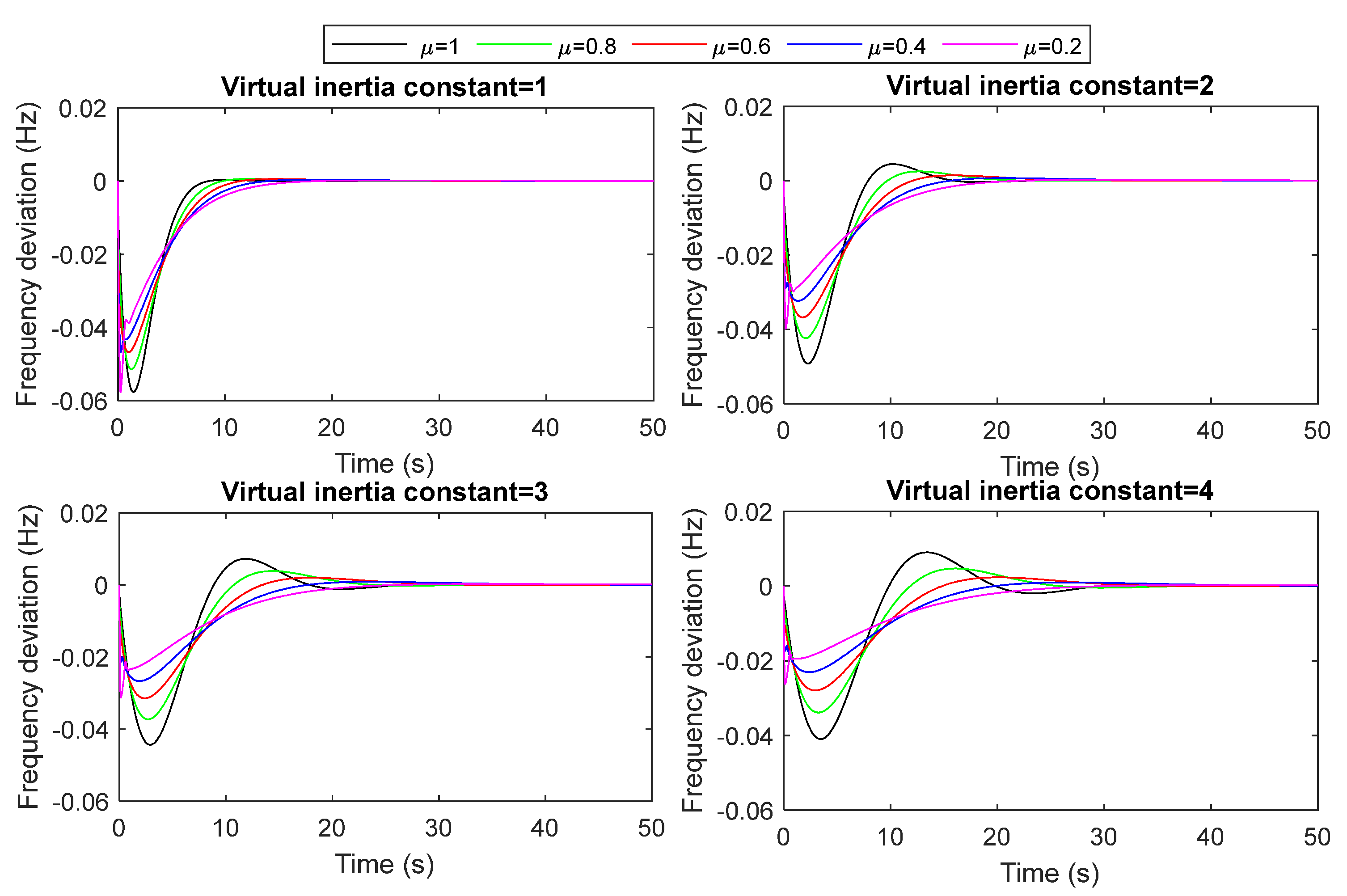
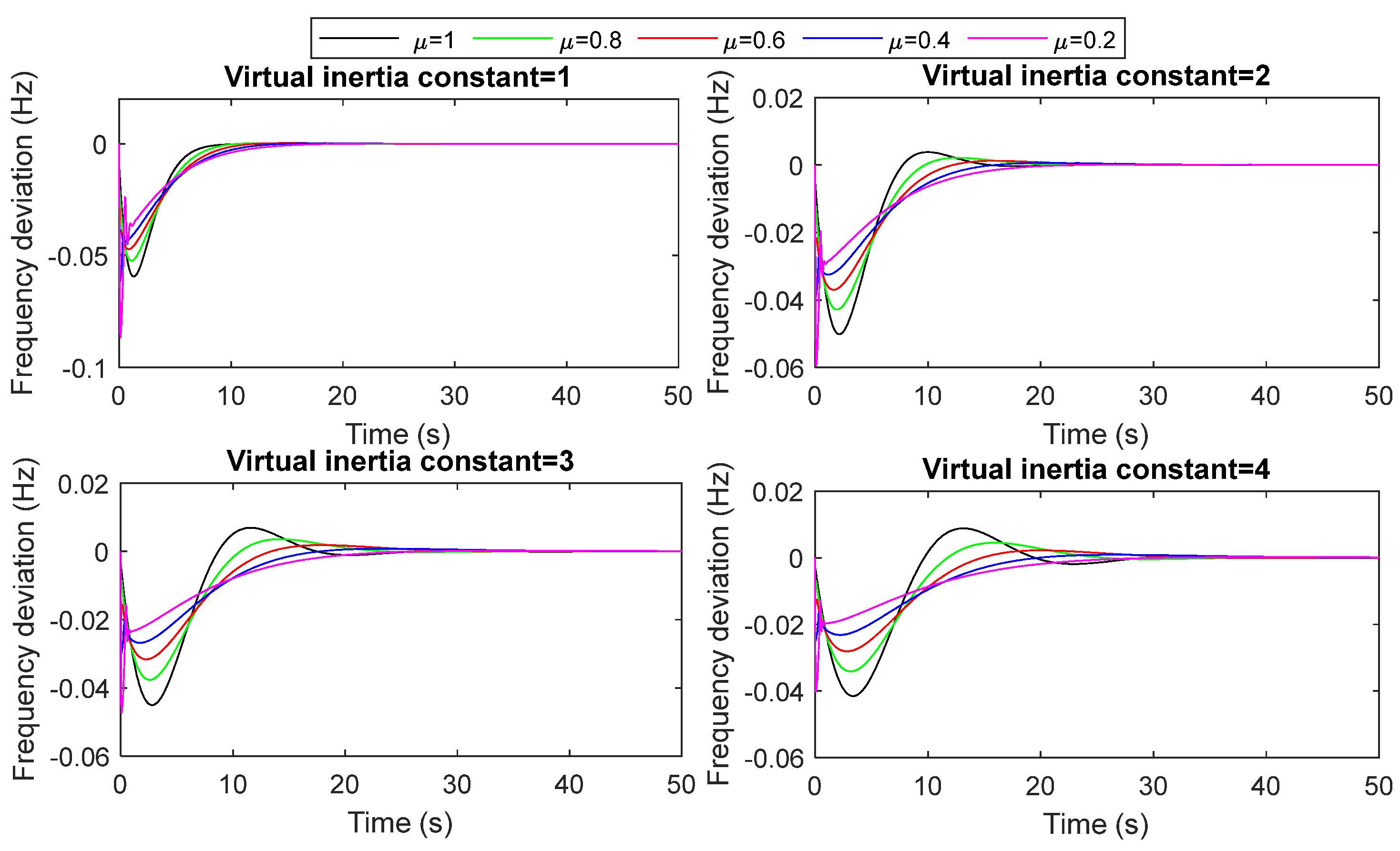
- The considered islanded MG with the proposed FOVIC scheme is examined under different values of the virtual inertia constant and different values of FO operators, highlighting the best operating values for varied case studies.
- Graphical and numerical outcomes from simulation indicate how competent the suggested control strategy is, where it can significantly reduce frequency deviations compared to the conventional controllers in the literature.
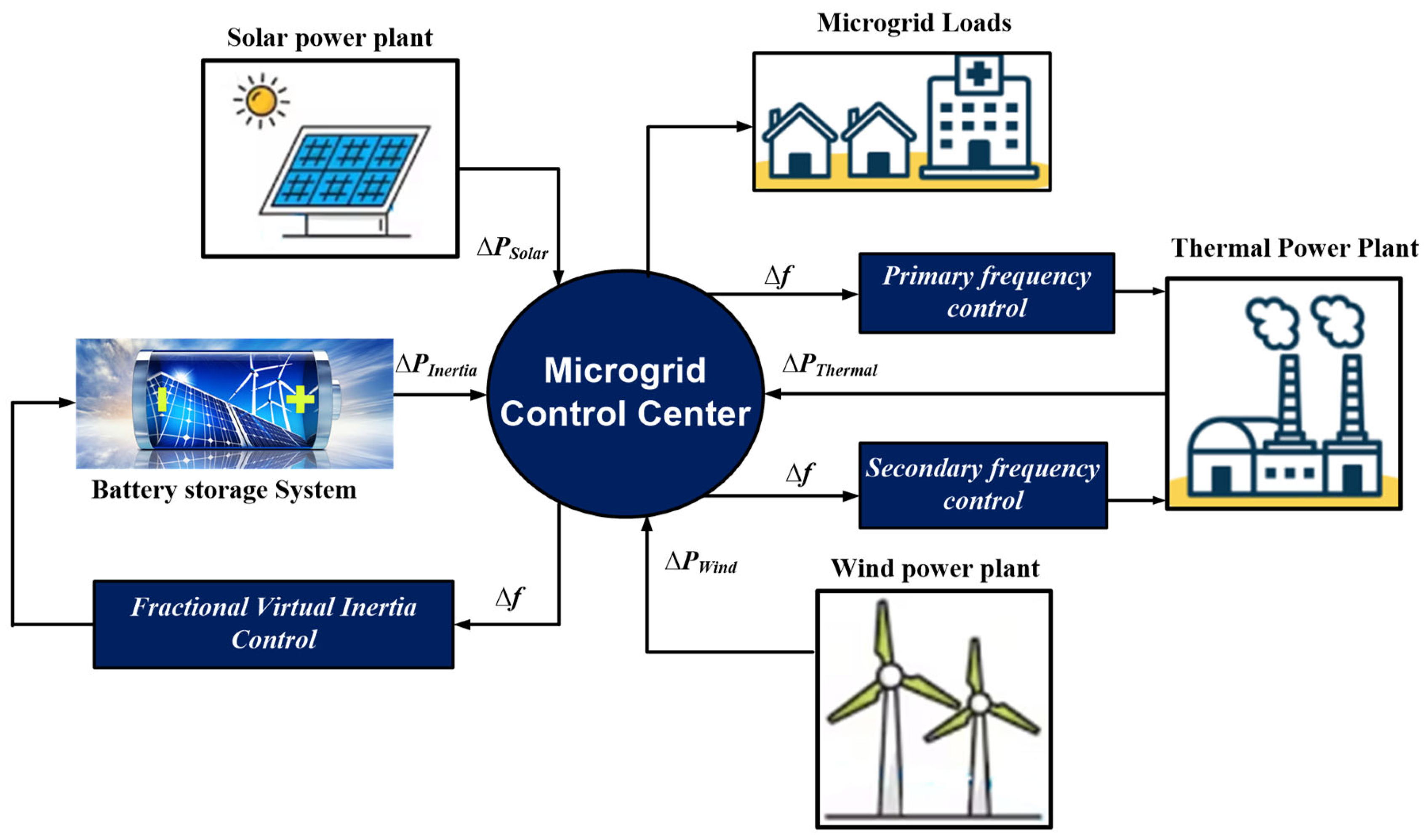
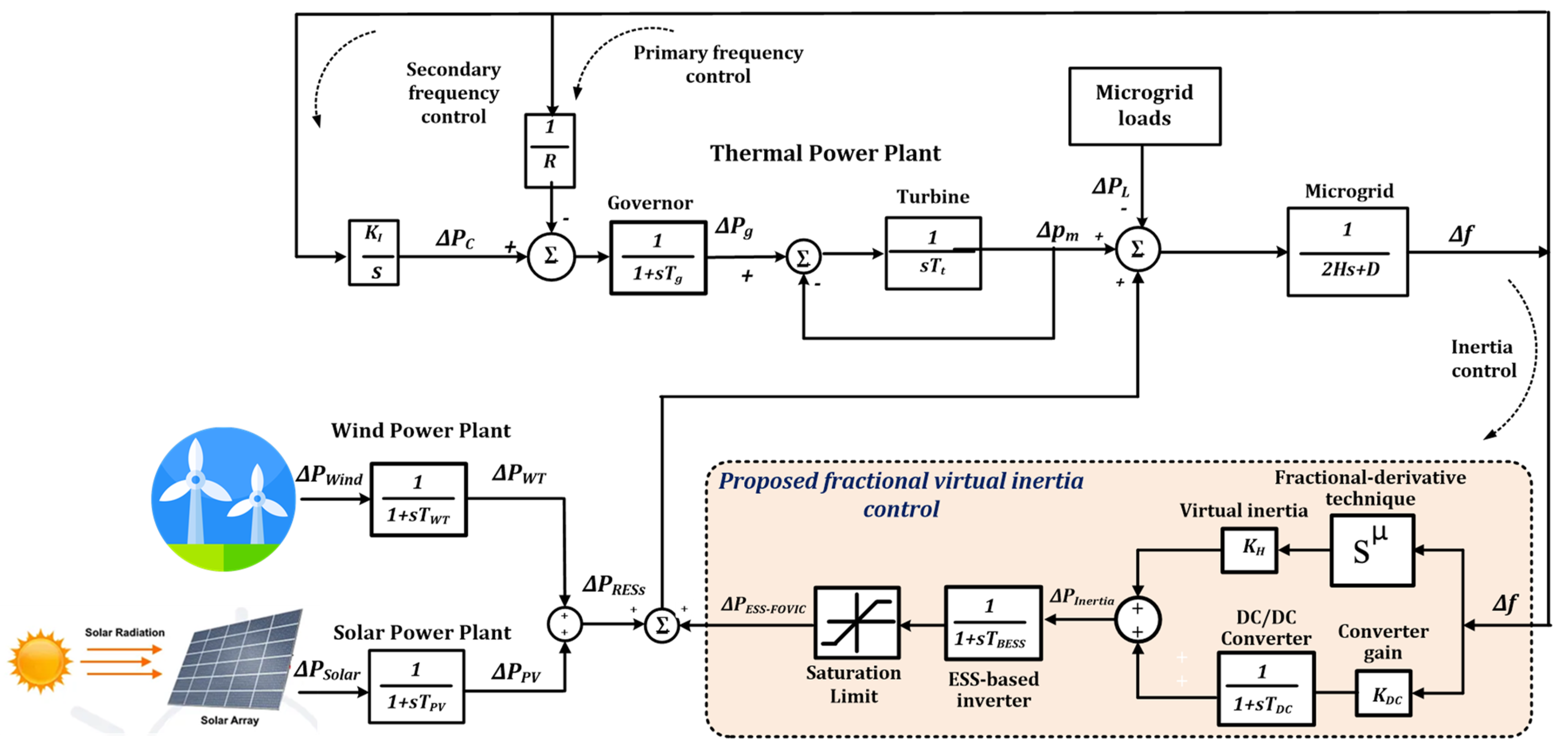
2. System Modelling and Configuration
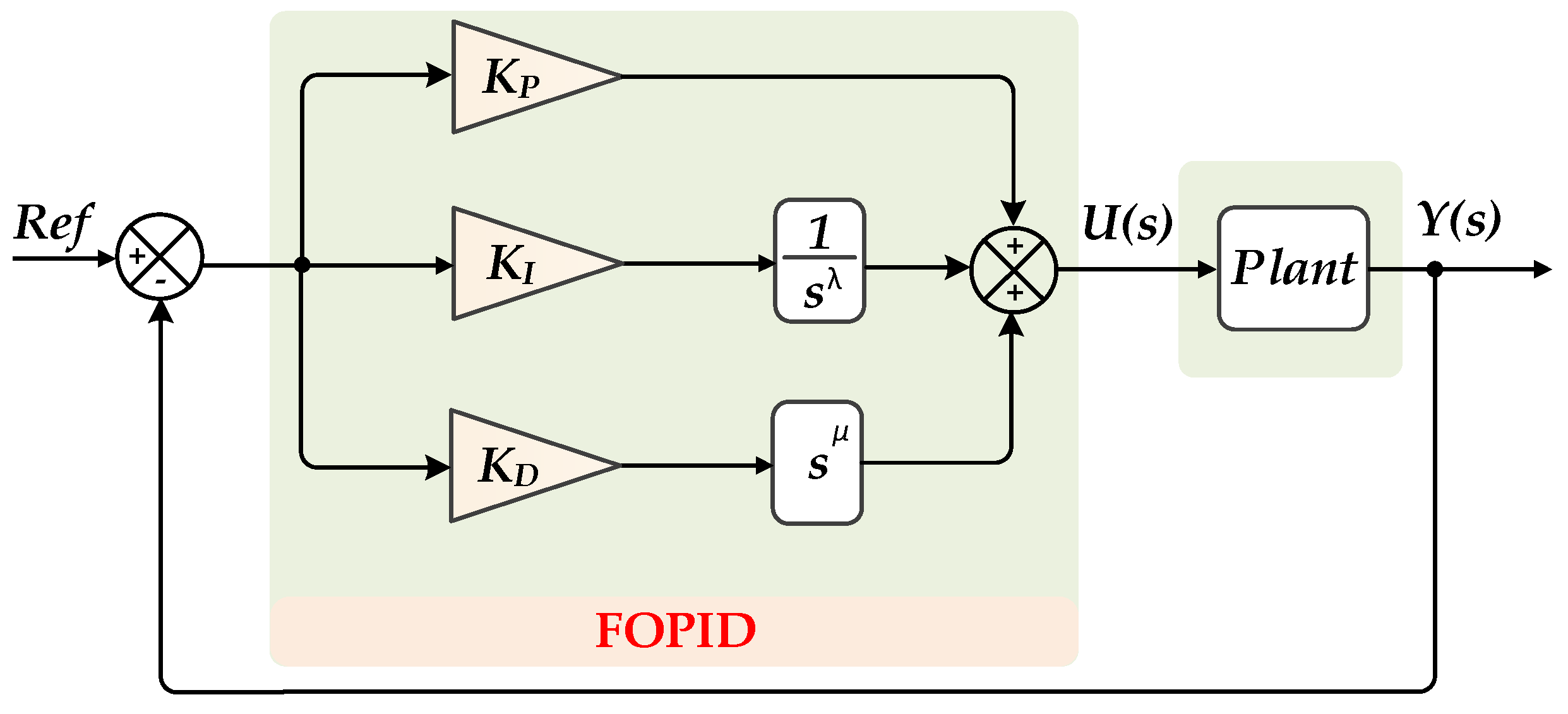
3. Proposed Fractional-Order VIC (FOVIC)
3.1. Description of the Fractional-Order Calculus
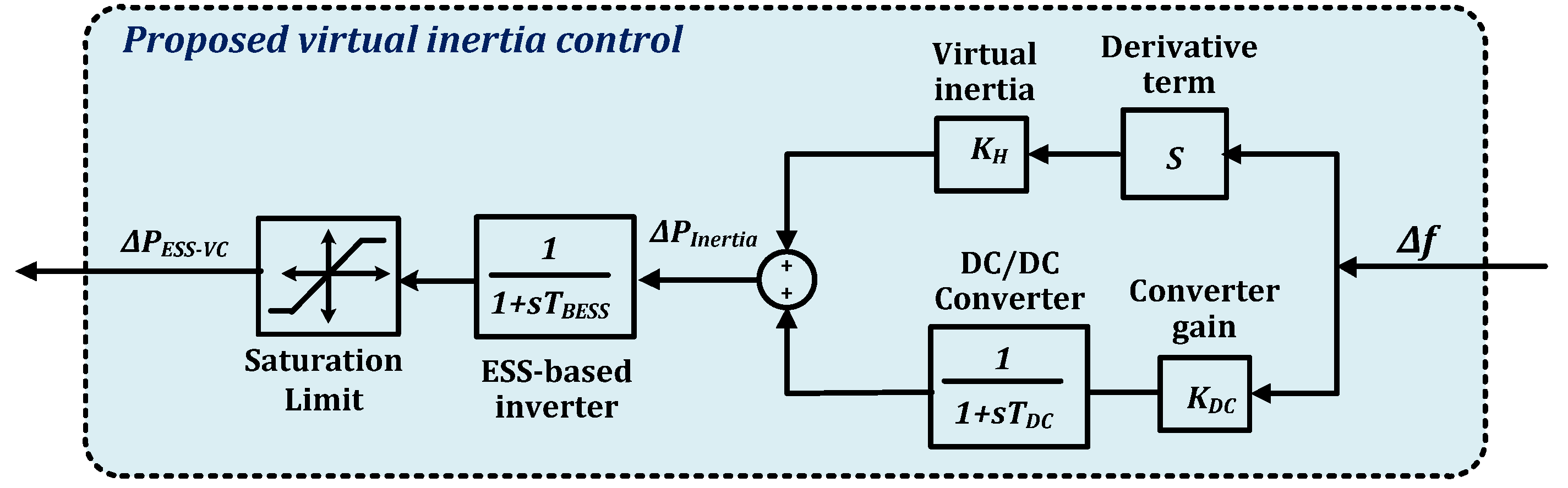
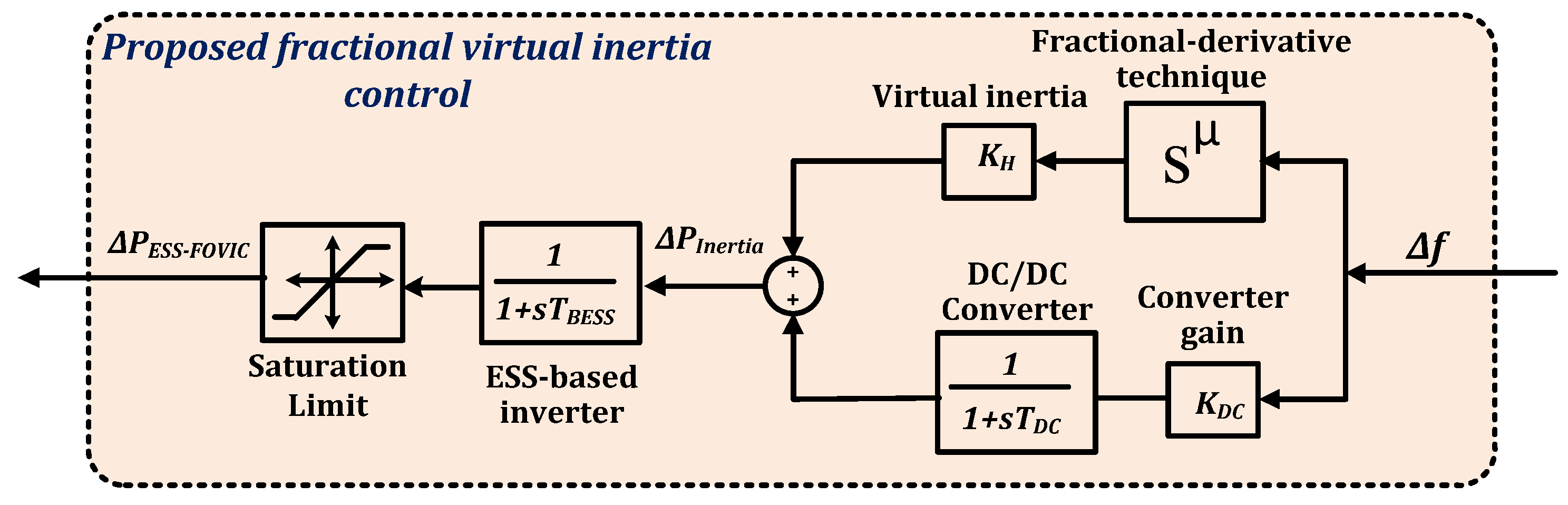
3.2. Description of the Proposed Fractional-Order Virtual Inertia Control
4. Simulation Results
- A.
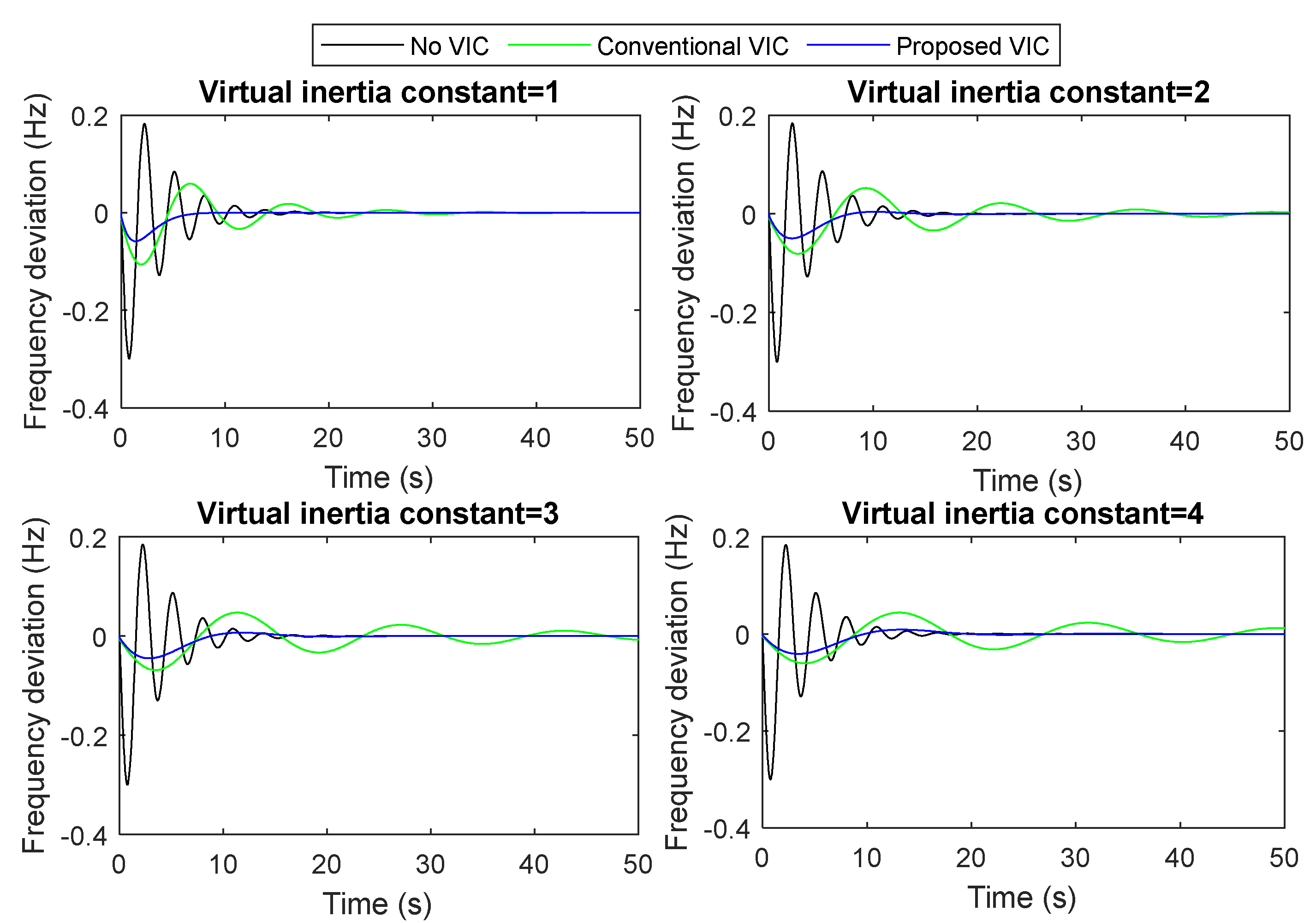
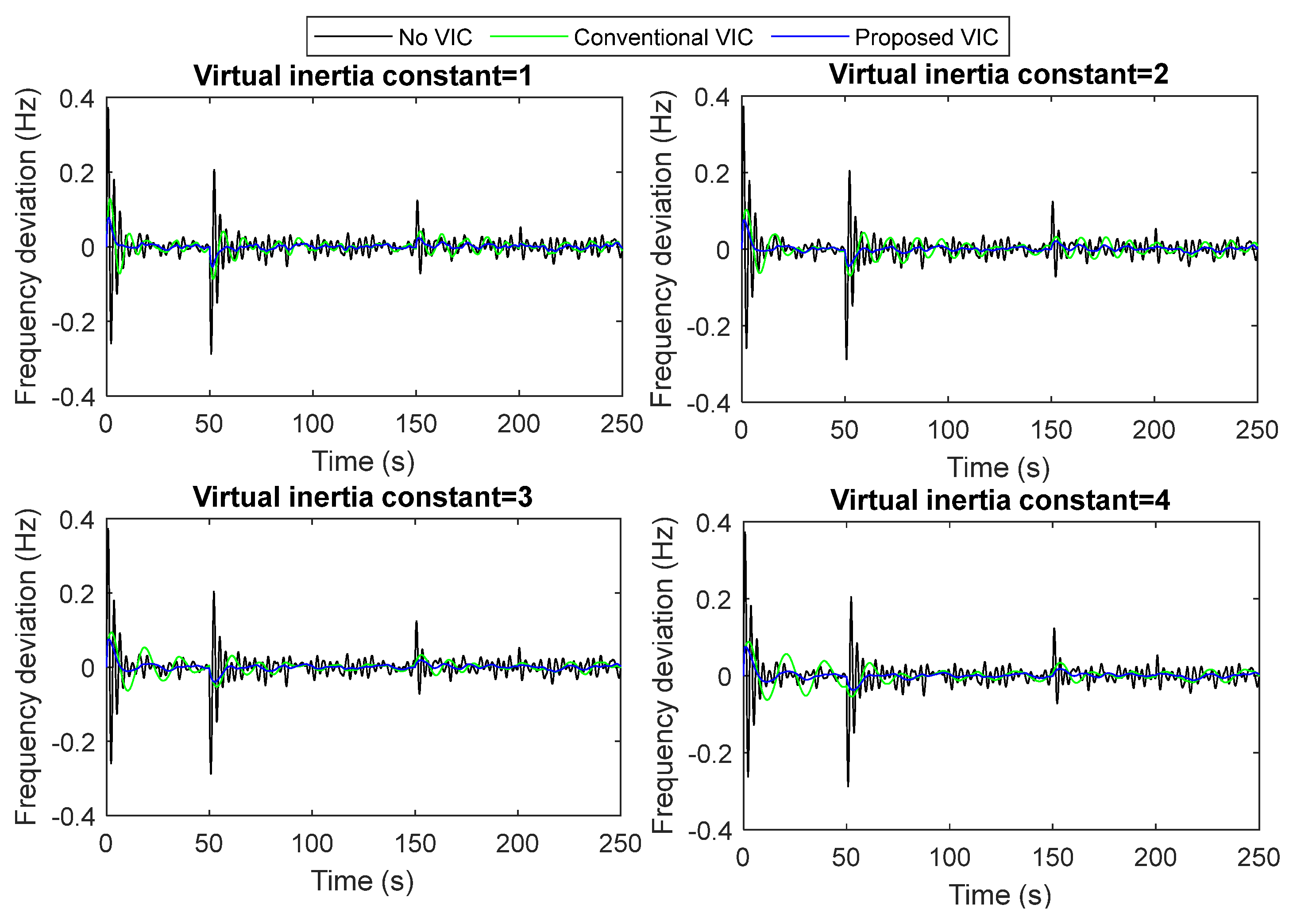
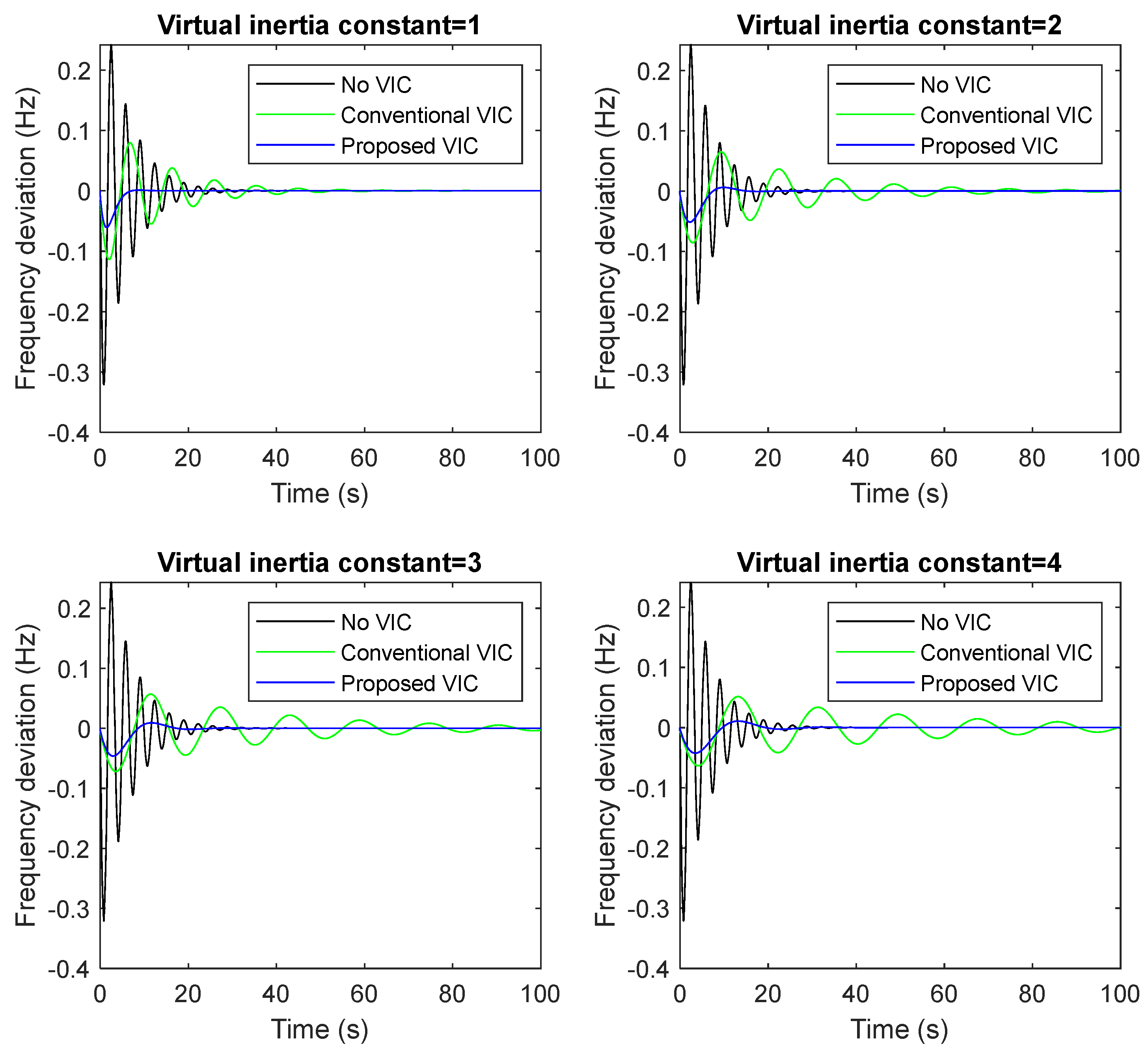
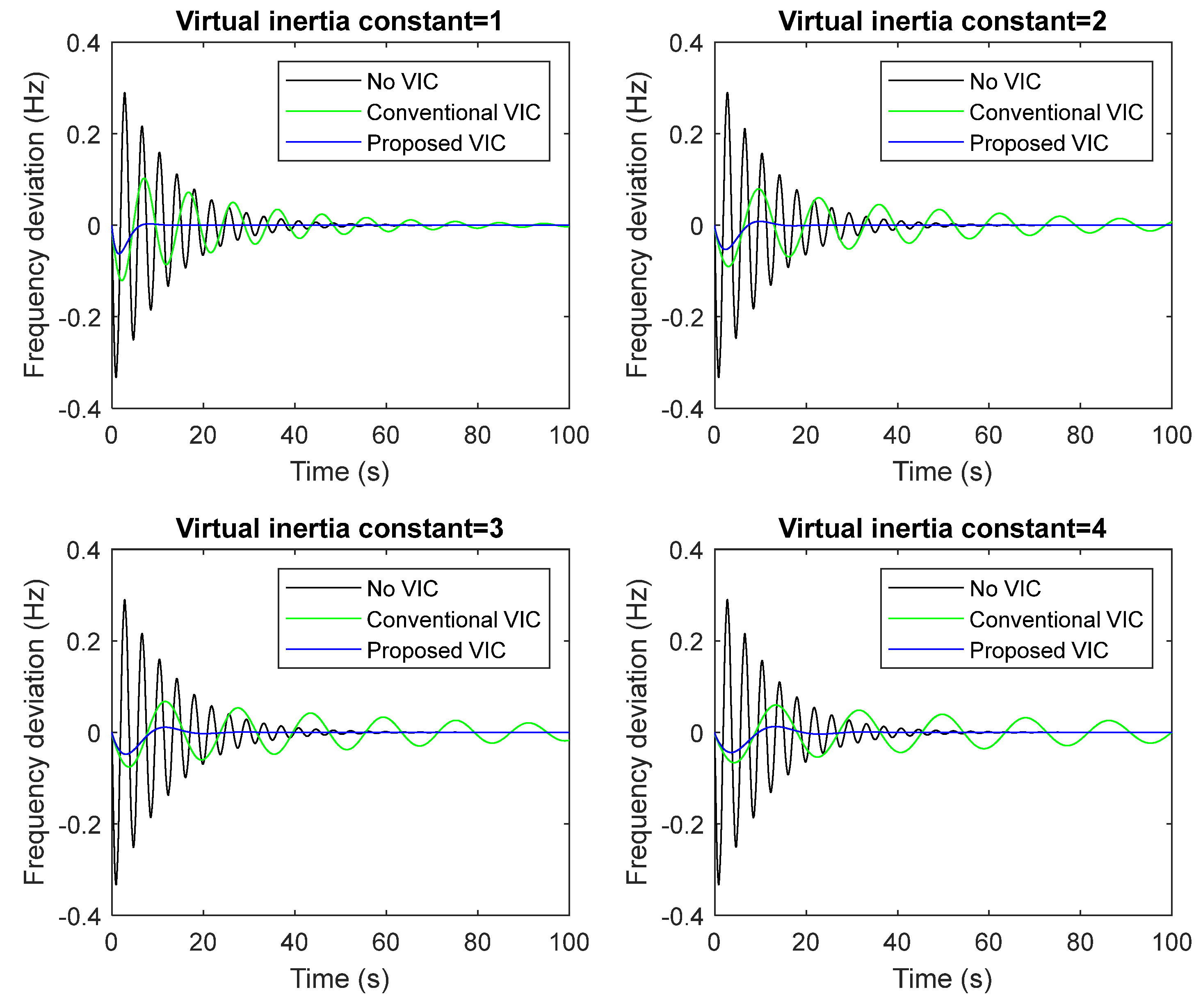
- A1. Evaluation of the developed VIC model’s performance under sudden load changes and different values of the virtual inertia constant
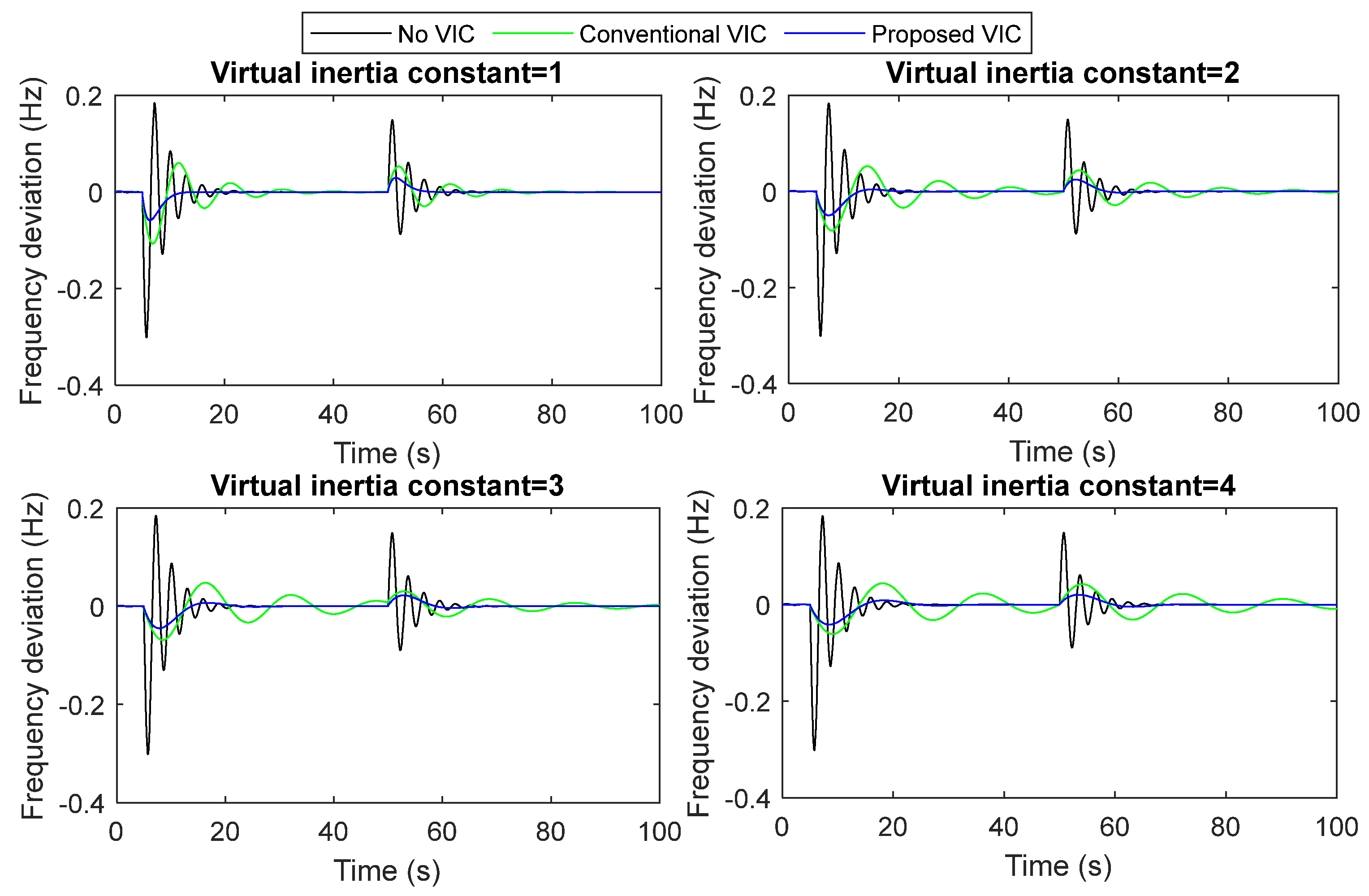
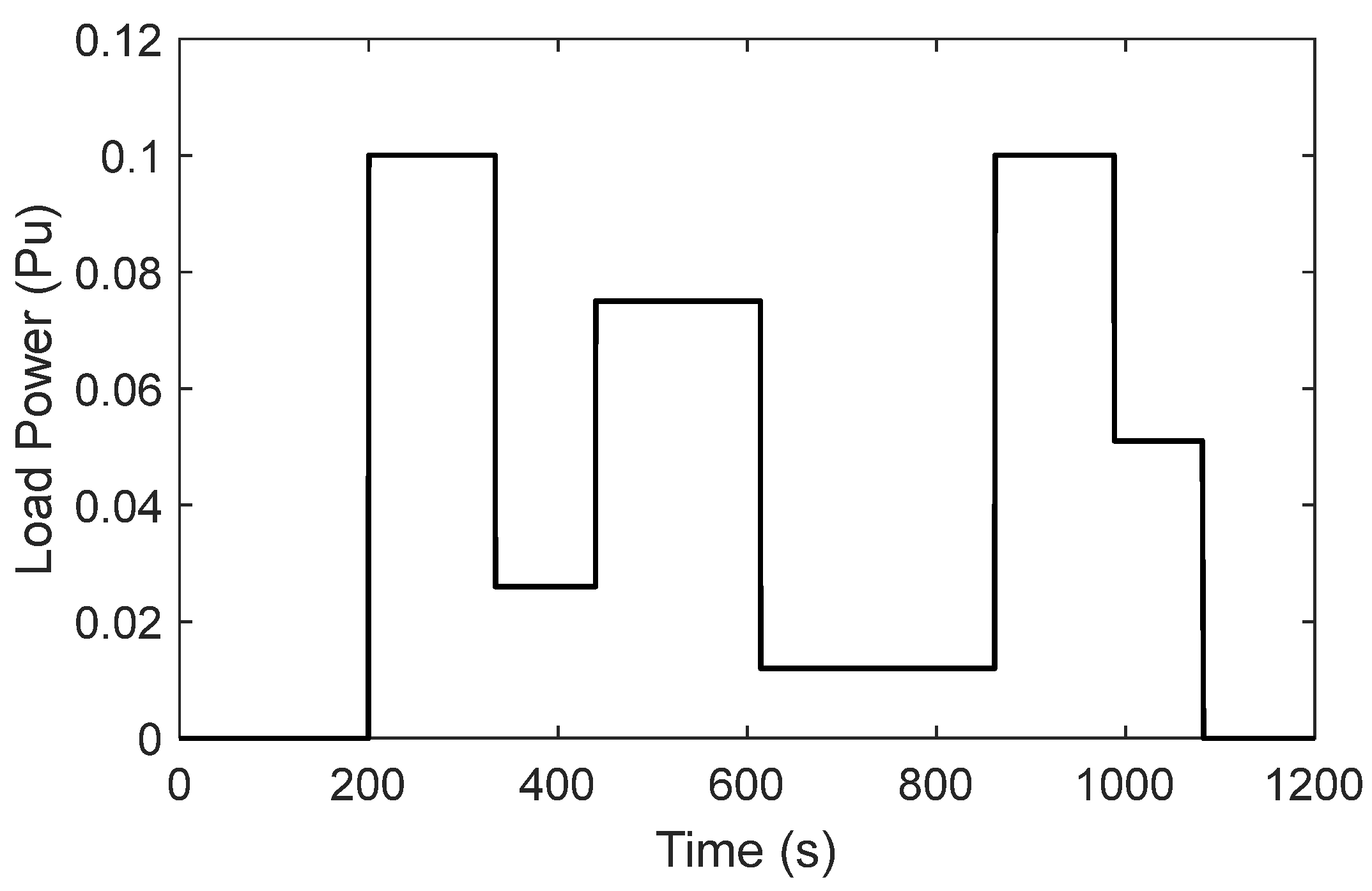
- A2. Evaluation of the developed VIC model’s performance under several load step changes
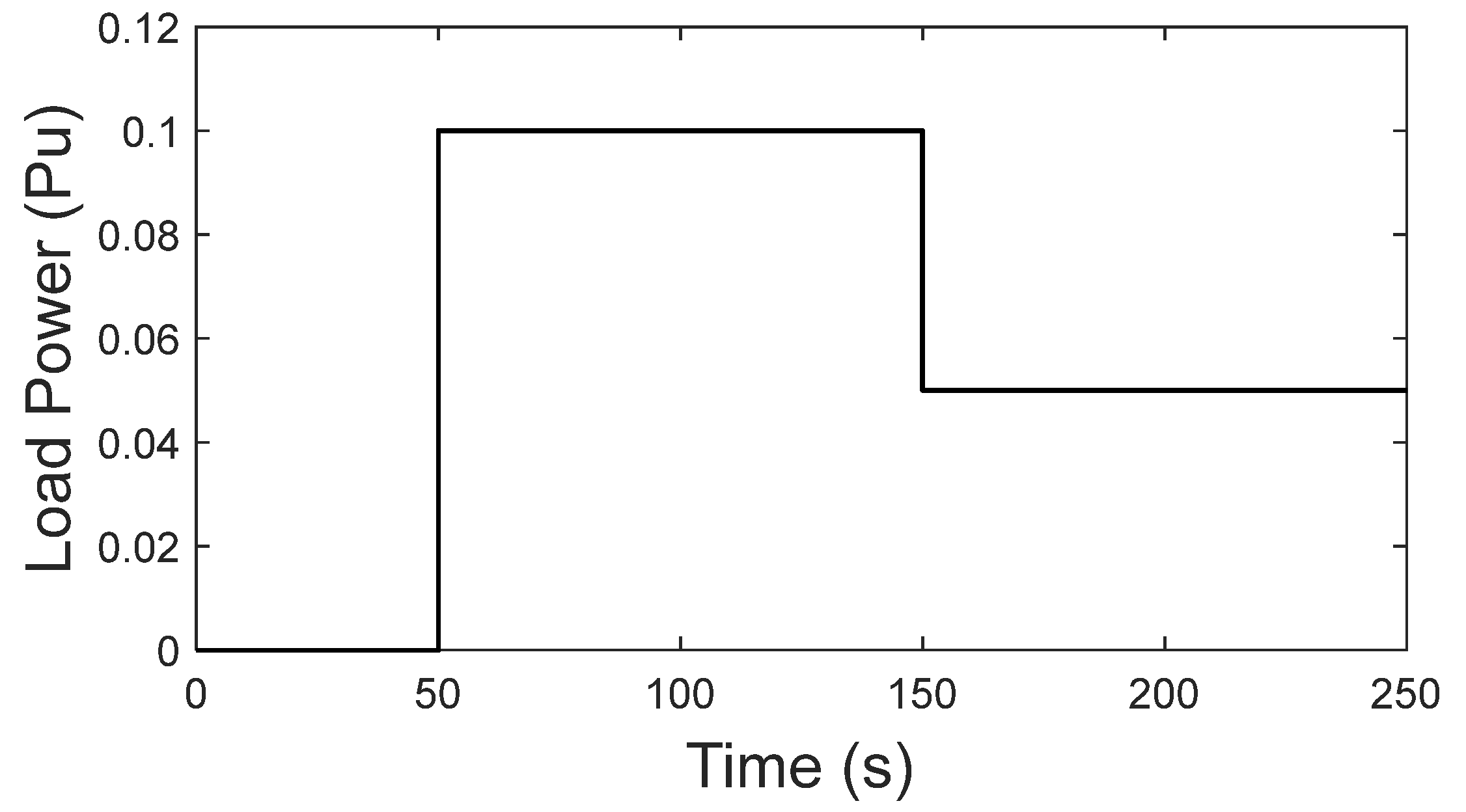
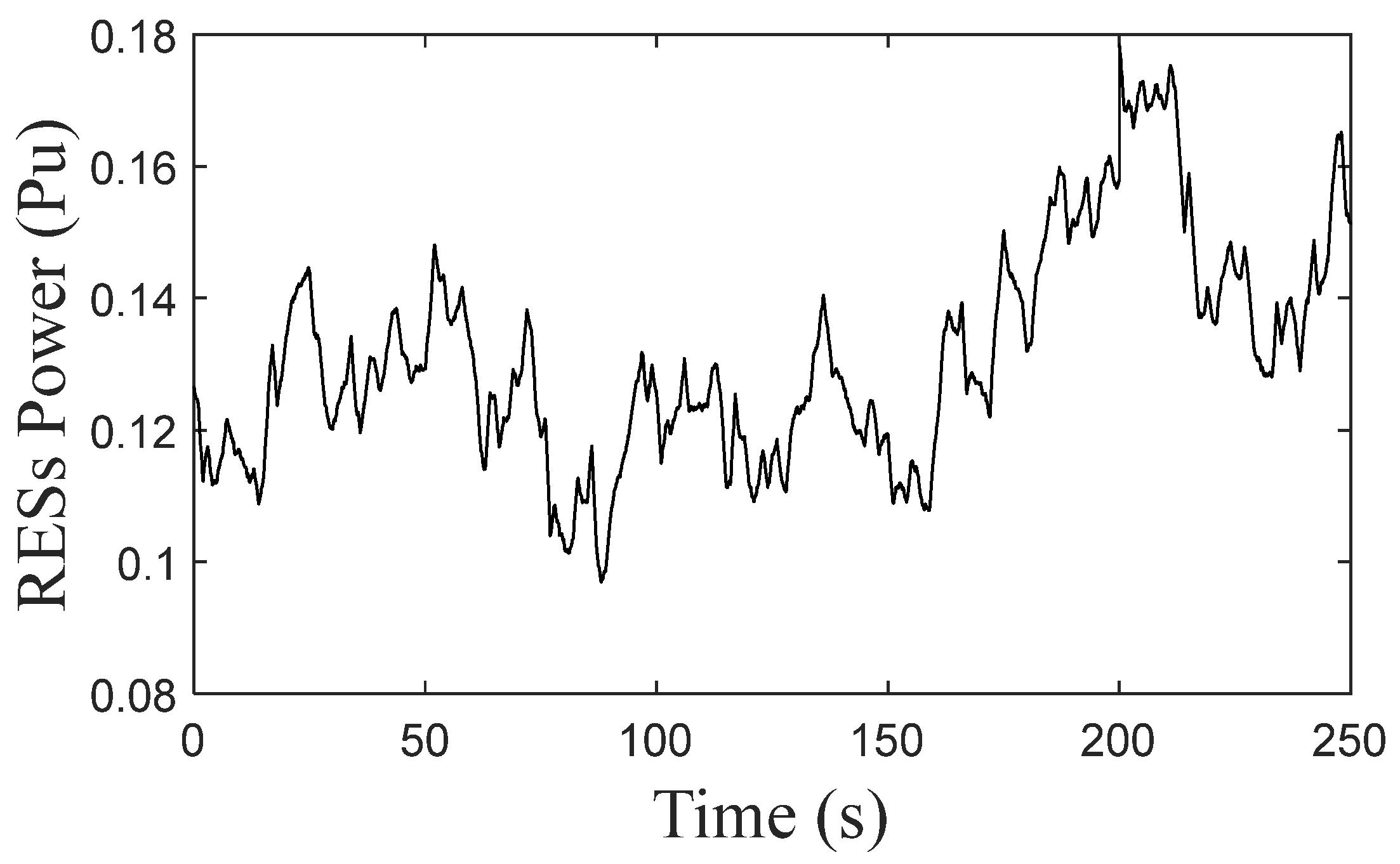
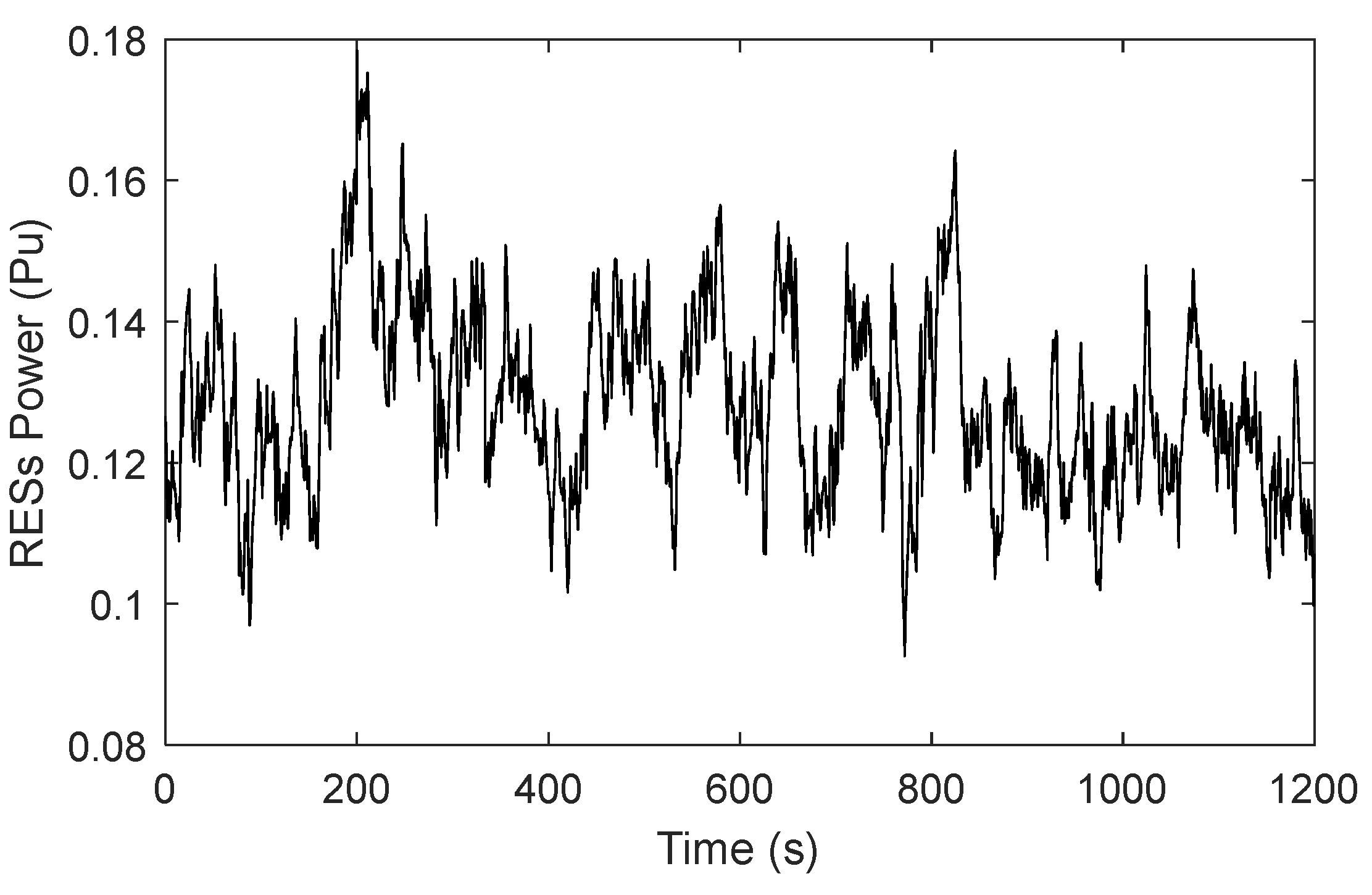
- A3. Evaluation of the developed VIC model’s performance under step load change and RES presence
- A4. Evaluation of the developed VIC model’s performance considering communication delay.
- B1. Evaluation of the proposed FOVIC model’s performance under sudden load change
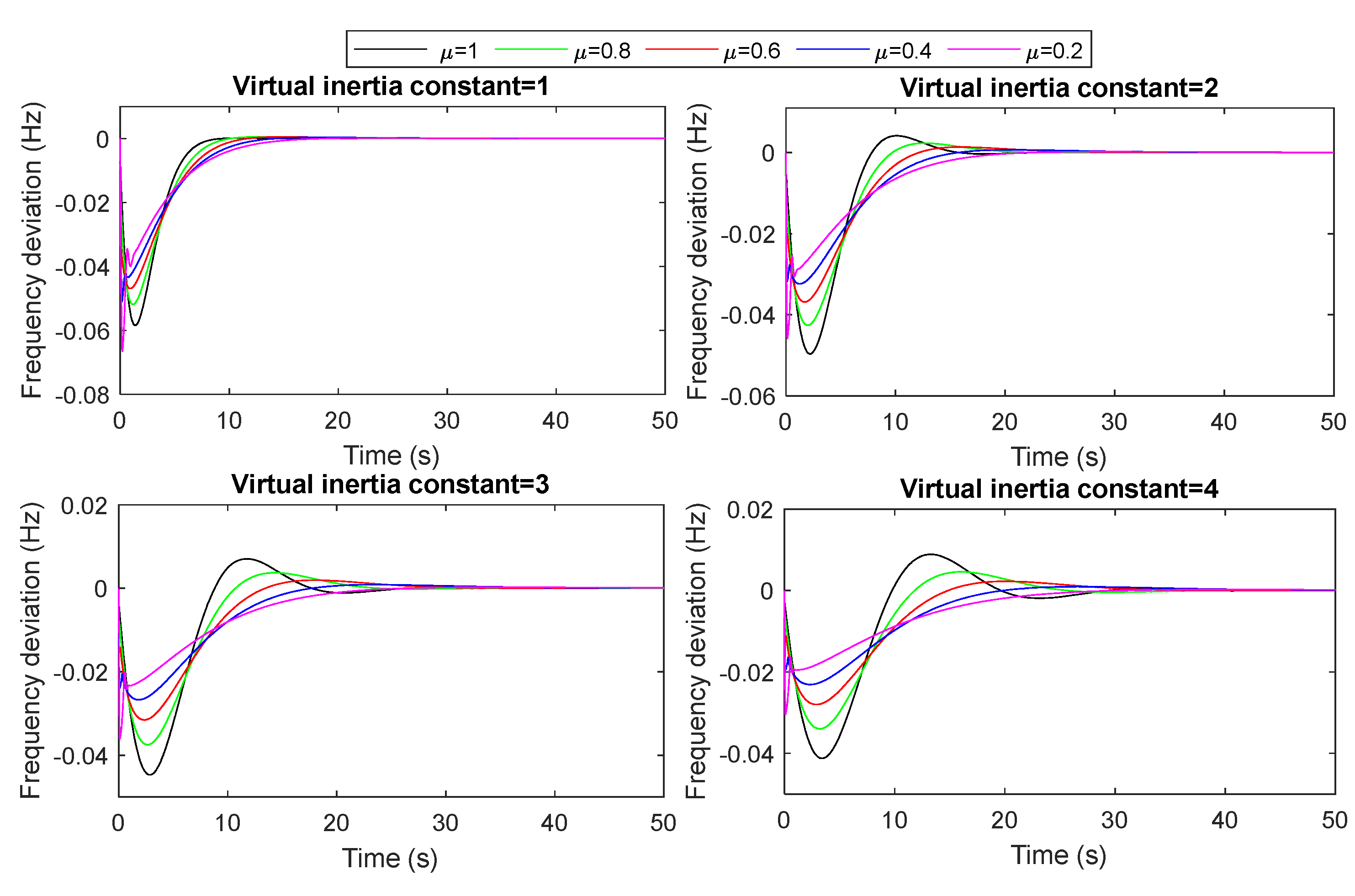
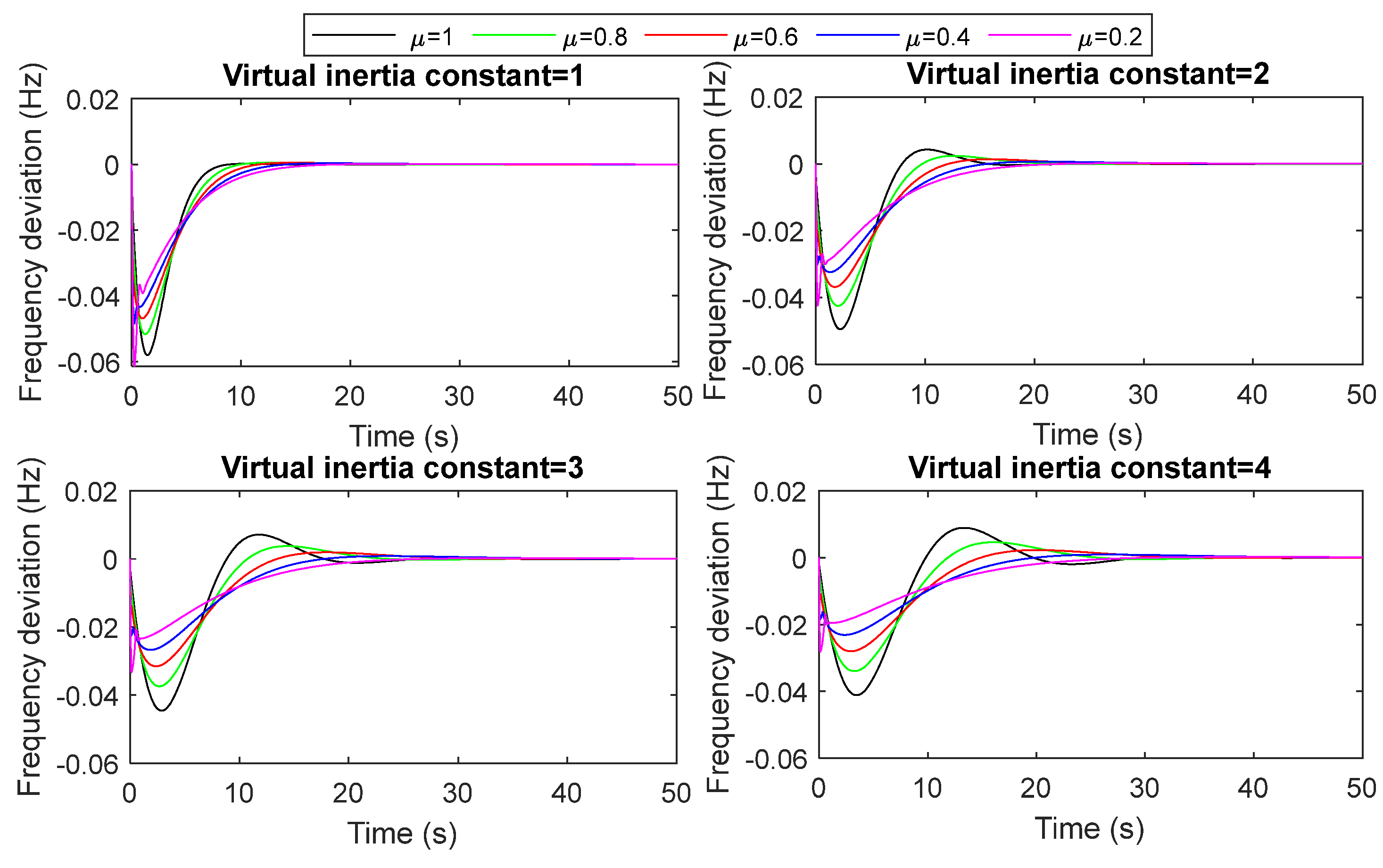
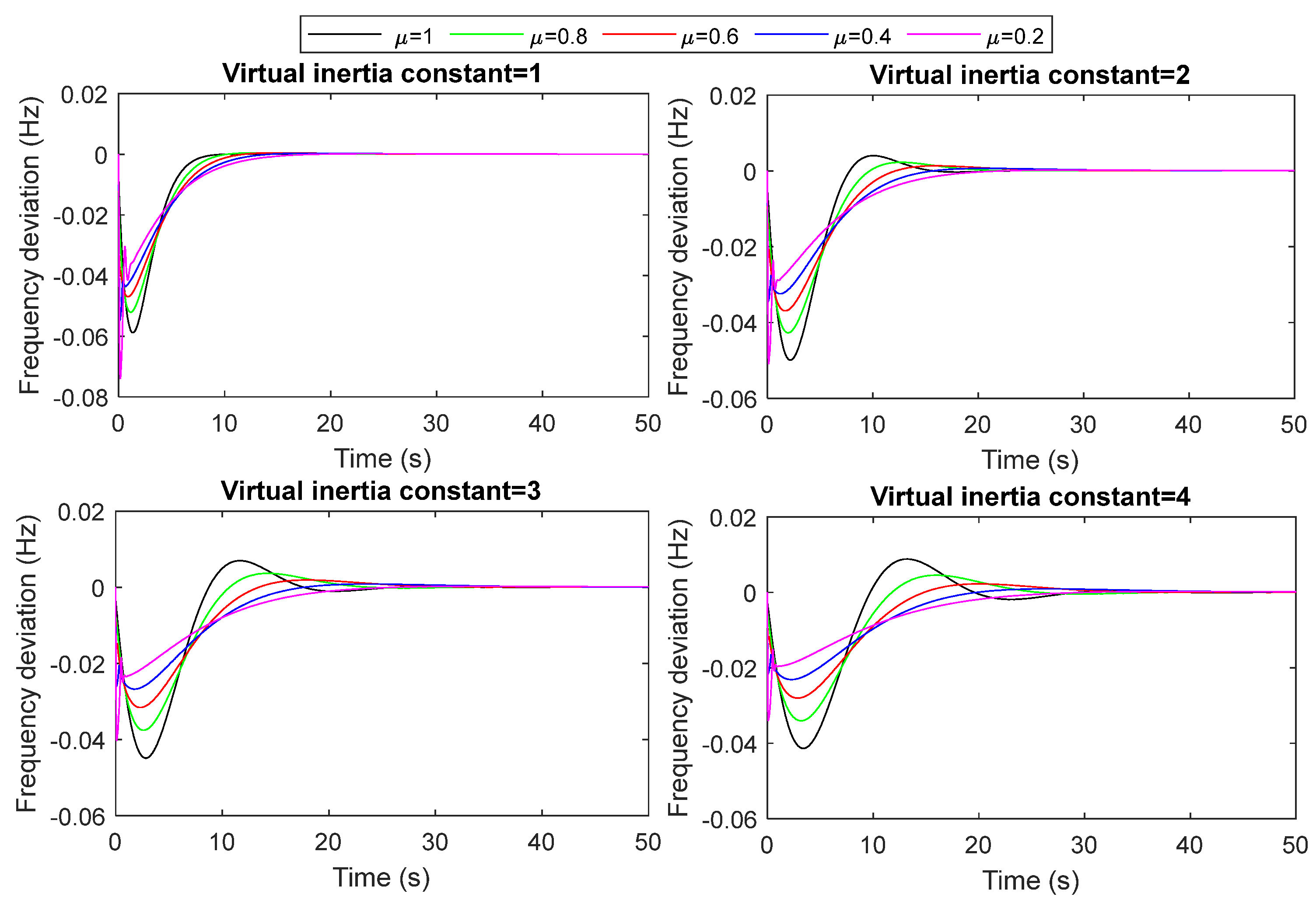
- B2. Evaluation of the proposed FOVIC model’s performance under system inertia changes
- B3. Evaluation of the proposed FOVIC model’s performance under step load change and RESs
5. Discussion
- The proposed VIC model handles the sudden change in load demand better than the conventional VIC system by about 45% and the secondary frequency control (i.e., without VIC) system by about 80%. As a result, the proposed VIC model’s developed structure has been chosen over alternative solutions for microgrid stabilization during sudden/series load changes.
- The performance of the three control systems used—the proposed VIC model, the conventional VIC model, and the secondary load frequency control, i.e., without VIC—is evaluated under high RESs penetration as well as varying values of the system inertia constant. The system with secondary frequency control (i.e., without the VIC model) gives high oscillations that threaten the system’s stability. Nonetheless, the proposed VIC and conventional VIC models are both able to stabilize the system frequency within an acceptable range. Among these two, the proposed VIC system exhibits the best frequency response under different values of the virtual inertia constant, with a maximum frequency deviation of ±0.059 Hz (in comparison with ±0.11 Hz by the conventional VIC system).
- Communication time delay: With the proposed VIC model, the best frequency nadir (about 0.06 Hz) was recorded. In comparison, the conventional VIC model exhibits a frequency drop of about 0.12 Hz, whereas the load frequency control displays about 0.33 Hz. Because of this, the proposed VIC model works best in situations where there is a varying random time delay within the range of (0, 0.2), as in the case of the practical system.
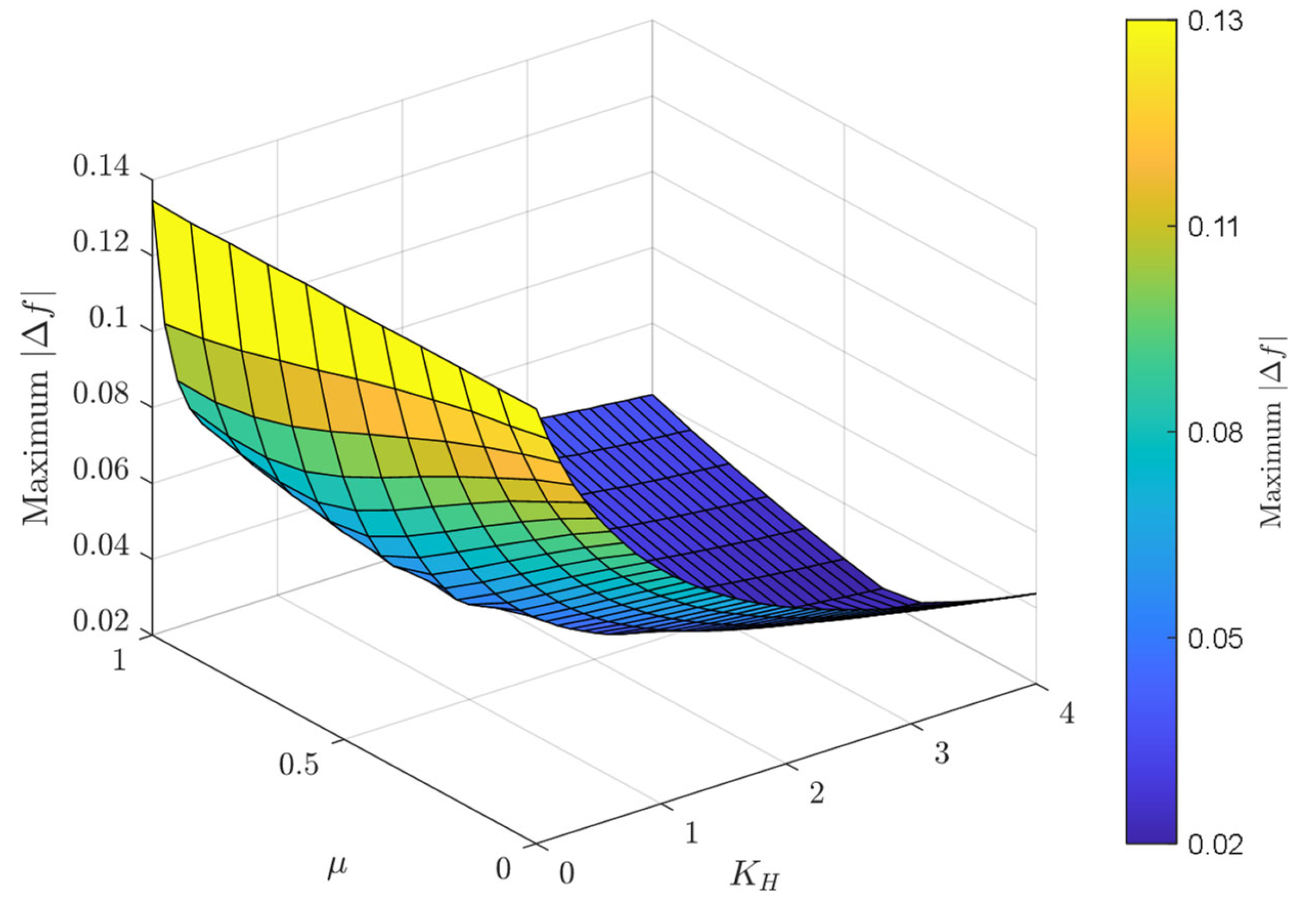
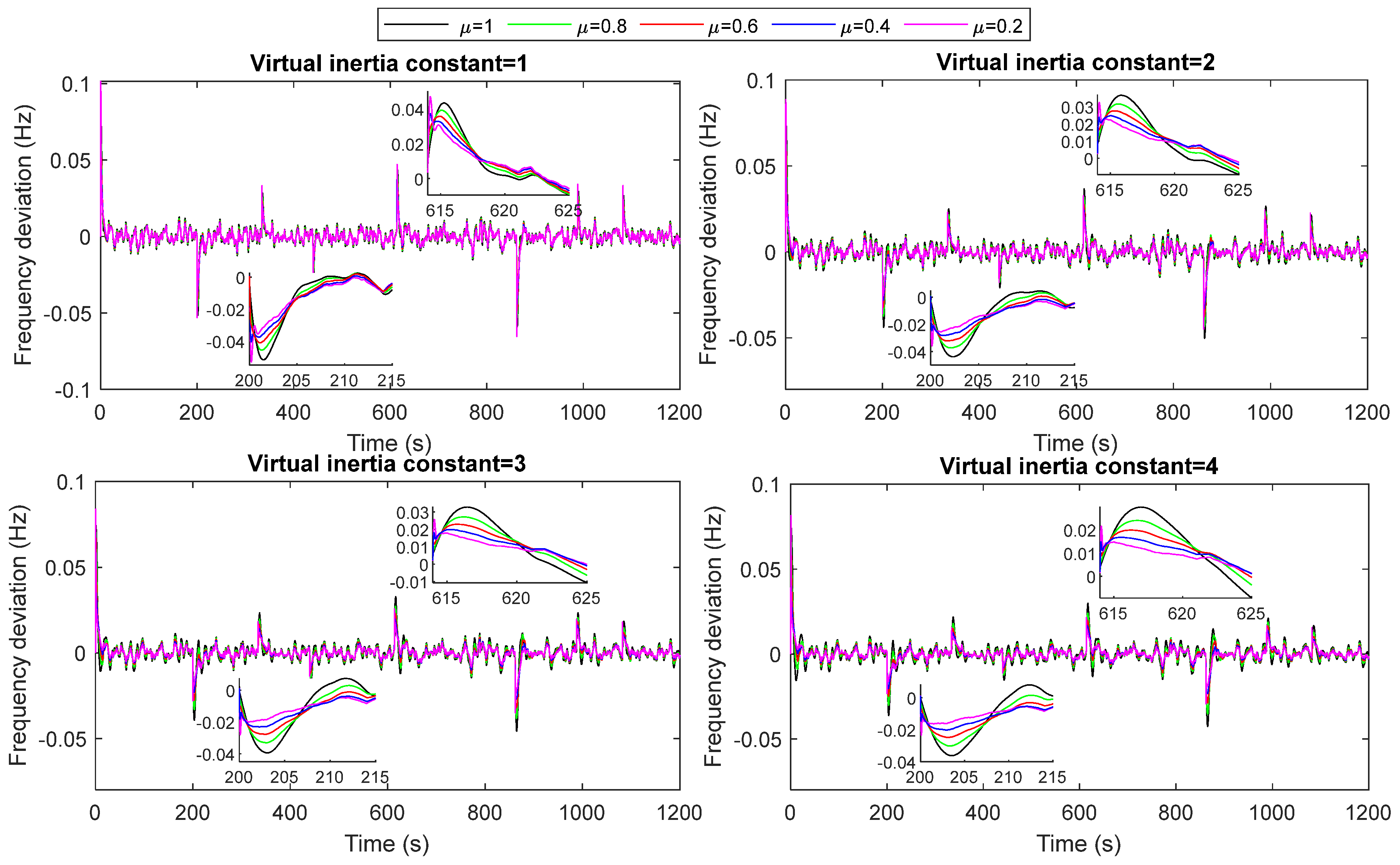
- The performance of the proposed VIC based on fractional-order derivative control has been evaluated under load/RESs fluctuations, system uncertainties (i.e., increasing/decreasing the system inertia by ±25% and ±50%), and different values in the virtual inertia constant and FO operators. The results show that the microgrid with the proposed FOVIC scheme at the fractional operator equal to 0.4 is significantly more stable and faster than that designed with other fractional operator values. Furthermore, it is clear that this value falls within the range of values that were previously mentioned in the section on theoretical analysis.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Renewable Energy Agency (IRENA). Global Energy Transformation: A Roadmap to 2050; IRENA: Masdar City, United Arab Emirates, 2019.
- Magdy, G.; Nour, M.; Shabib, G.; Elbaset, A.A.; Mitani, Y. Supplementary Frequency Control in a High-Penetration Real Power System by Renewables Using SMES Application Electrical Systems. J. Electr. Syst. 2019, 15, 526–538. [Google Scholar]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Fathi, A.; Shafiee, Q.; Bevrani, H. Robust Frequency Control of Microgrids Using an Extended Virtual Synchronous Generator. IEEE Trans. Power Syst. 2018, 33, 6289–6297. [Google Scholar] [CrossRef]
- Peng, Q.; Jiang, Q.; Yang, Y.; Liu, T.; Wang, H.; Blaabjerg, F. On the Stability of Power Electronics-Dominated Systems: Challenges and Potential Solutions. IEEE Trans. Ind. Appl. 2019, 55, 7657–7670. [Google Scholar] [CrossRef]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. Vol. 2014, 19, 7290–7297. [Google Scholar] [CrossRef]
- Santurino, P.; Sigrist, L.; Ortega, Á.; Renedo, J.; Lobato, E. Optimal coordinated design of under-frequency load shedding and energy storage systems. Electr. Power Syst. Res. 2022, 211, 108423. [Google Scholar] [CrossRef]
- Ranjan, M.; Shankar, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Makolo, P.; Zamora, R.; Lie, T.-T. The role of inertia for grid flexibility under high penetration of variable renewables—A review of challenges and solutions. Renew. Sustain. Energy Rev. 2021, 147, 111223. [Google Scholar] [CrossRef]
- Mohanty, B.; Hota, P.K. Comparative performance analysis of fruit fly optimisation algorithm for multi-area multi-source automatic generation control under deregulated environment. IET Gener. Transm. Distrib. 2015, 9, 1845–1855. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Aly, M.; Alqahtani, M.H.; Aljumah, A.S.; Almutairi, S.Z.; Mohamed, E.A. New Cascaded 1+PII2D/FOPID Load Frequency Controller for Modern Power Grids including Superconducting Magnetic Energy Storage and Renewable Energy. Fractal Fract. 2023, 7, 672. [Google Scholar] [CrossRef]
- Shayeghi, H.; Rahnama, A.; Bizon, N. TFODn-FOPI multi-stage controller design to maintain an islanded microgrid load-frequency balance considering responsive loads support. IET Gener. Transm. Distrib. 2023, 17, 3266–3285. [Google Scholar] [CrossRef]
- Peddakapu, K.; Srinivasarao, P.; Mohamed, M.; Arya, Y.; Kishore, D.K. Stabilization of frequency in Multi-Microgrid system using barnacle mating Optimizer-based cascade controllers. Energy Technol. Assess. 2022, 54, 102823. [Google Scholar] [CrossRef]
- Sahu, P.C.; Jena, S.; Mohapatra, S.; Debdas, S. Impact of energy storage devices on microgrid frequency performance: A robust DQN based grade-2 fuzzy cascaded controller. e-Prime 2023, 6, 100288. [Google Scholar] [CrossRef]
- Ali, H.; Li, B.; Xu, Z.; Liu, H.; Xu, D. Virtual Synchronous Generator Design Based Modular Multilevel Converter for Microgrid Frequency Regulation. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; Volume 1, pp. 1–6. [Google Scholar]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Nour, M.; Magdy, G.; Chaves-Ávila, J.P.; Sánchez-Miralles, A.; Jurado, F. A new two-stage controller design for frequency regulation of low-inertia power system with virtual synchronous generator. J. Energy Storage 2023, 62, 106952. [Google Scholar] [CrossRef]
- Mohammadi-ivatloo, B. Provision of Frequency Stability of an Islanded Microgrid Cascade Controller. Energies 2021, 14, 4152. [Google Scholar]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. A Novel Coordination Scheme of Virtual Inertia Control and Digital Protection for Microgrid Dynamic Security Considering High Renewable Energy Penetration. IET Renew. Power Gener. 2019, 13, 462–474. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Chikuni, E.; Rashayi, E. Effects of the Synthetic Inertia from wind power on the total system inertia after a frequency disturbance. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 826–832. [Google Scholar]
- Hu, Y.; Wei, W.; Peng, Y.; Lei, J. Fuzzy virtual inertia control for virtual synchronous generator. Chinese Control Conf. CCC 2016, 2016, 8523–8527. [Google Scholar]
- Magnus, D.M.; Scharlau, C.C.; Pfitscher, L.L.; Costa, G.C.; Silva, G.M. A novel approach for robust control design of hidden synthetic inertia for variable speed wind turbines. Electr. Power Syst. Res. 2021, 196, 107267. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Li, B.; Shabib, G.; Elbaset, A.A.; Xu, D.; Mitani, Y. A New Frequency Control Strategy in an Islanded Microgrid Using Virtual Inertia Control-Based Coefficient Diagram Method. IEEE Access 2019, 7, 16979–16990. [Google Scholar] [CrossRef]
- Sockeel, N.; Gafford, J.; Papari, B.; Mazzola, M. Virtual Inertia Emulator-Based Model Predictive Control for Grid Frequency Regulation Considering High Penetration of Inverter-Based Energy Storage System. IEEE Trans. Sustain. Energy 2020, 11, 2932–2939. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Fawzy, A.; Bakeer, A.; Magdy, G.; Atawi, I.E.; Roshdy, M. Adaptive Virtual Inertia-Damping System Based on Model Predictive Control for Low-Inertia Microgrids. IEEE Access 2021, 9, 109718–109731. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability Assessment and Optimization Methods for Microgrid with Multiple VSG Units. IEEE Trans. Smart Grid 2016, 9, 1462–1471. [Google Scholar] [CrossRef]
- Padhy, S.; Panda, S. Simplified grey wolf optimisation algorithm tuned adaptive fuzzy PID controller for frequency regulation of interconnected power systems. Int. J. Ambient. Energy 2022, 43, 4089–4101. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Xu, D. A new optimal robust controller for frequency stability of interconnected hybrid microgrids considering non-inertia sources and uncertainties. Int. J. Electr. Power Energy Syst. 2021, 128, 106651. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Z.; Yu, J.; Huang, J.; Li, W. Coordinated control parameter setting of DFIG wind farms with virtual inertia control. Int. J. Electr. Power Energy Syst. 2020, 122, 106167. [Google Scholar] [CrossRef]
- Fini, M.H.; Golshan, M.E.H. Determining optimal virtual inertia and frequency control parameters to preserve the frequency stability in islanded microgrids with high penetration of renewables. Electr. Power Syst. Res. 2018, 154, 13–22. [Google Scholar] [CrossRef]
- Mohamed Mostafa Elsaied, H.M.H.; Hameed, W.H.A. Frequency stabilization of a hybrid three-area power system equipped with energy. IET Renew. Power Gener. 2022, 16, 3267–3286. [Google Scholar] [CrossRef]
- Alilou, M.; Azami, H.; Oshnoei, A.; Mohammadi-Ivatloo, B.; Teodorescu, R. Fractional-Order Control Techniques for Renewable Energy and Energy-Storage-Integrated Power Systems: A Review. Fractal Fract. 2023, 7, 391. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Kriging Based Surrogate Modeling for Fractional Order Control of Microgrids. IEEE Trans. Smart Grid 2015, 6, 36–44. [Google Scholar] [CrossRef]
- Monje, A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional Order Systems and Controls; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Debbarma, S.; Saikia, L.C.; Sinha, N. AGC of a multi-area thermal system under deregulated environment using a non-integer controller. Electr. Power Syst. Res. 2013, 95, 175–183. [Google Scholar] [CrossRef]
- Saxena, S. Load frequency control strategy via fractional-order controller and reduced-order modeling. Int. J. Electr. Power Energy Syst. 2019, 104, 603–614. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional Order AGC for Distributed Energy Resources Using Robust Optimization. IEEE Trans. Smart Grid 2015, 7, 2175–2186. [Google Scholar] [CrossRef]
- Nour, M.; Magdy, G.; Chaves-Avila, J.P.; Sanchez-Miralles, A.; Petlenkov, E. Automatic Generation Control of a Future Multisource Power System Considering High Renewables Penetration and Electric Vehicles: Egyptian Power System in 2035. IEEE Access 2022, 10, 51662–51681. [Google Scholar] [CrossRef]
- Yu, Y.; Guan, Y.; Kang, W.; Chaudhary, S.K.; Vasquez, J.C.; Guerrero, J.M. Fractional-Order Virtual Synchronous Generator. IEEE Trans. Power Electron. 2023, 38, 6874–6879. [Google Scholar] [CrossRef]
- Long, B.; Li, X.; Rodriguez, J.; Guerrero, J.M.; Chong, K.T. Frequency stability enhancement of an islanded microgrid: A fractional-order virtual synchronous generator. Int. J. Electr. Power Energy Syst. 2023, 147. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Applying fractional order PID to design TCSC-based damping controller in coordination with automatic generation control of interconnected multi-source power system. Eng. Sci. Technol. Int. J. 2017, 20, 1–17. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Moschos, I.; Parisses, C. A novel optimal PIλDND2N2 controller using coyote optimization algorithm for an AVR system. Eng. Sci. Technol. Int. J. 2022, 26, 100991. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Virtual Inertia Synthesis and Control; Springer: Dordrecht, The Netherlands, 2021. [Google Scholar]


| Parameter | Value |
|---|---|
| Equivalent inertia constant, H (p.u. MWs) | 0.082 |
| Microgrid frequency, f (Hz) | 50.000 |
| Microgrid damping coefficient, D (p.u.MW/Hz) | 0.015 |
| Turbine time constant, Tt (s) | 0.400 |
| Governor time constant, Tg (s) | 0.100 |
| Speed droop characteristic, R (Hz/p.u.MW) | 2.400 |
| Integral control variable gain, KI | -0.50 |
| Wind turbine time constant, TWT (s) | 1.500 |
| Solar system time constant, TPV (s) | 1.800 |
| Inverter time constant for conventional VIC, TBESS (s) | 0.200 |
| Inverter time constant for proposed VIC, TBESS (s) | 0.100 |
| DC/DC converter time constant, TDC (s) | 0.100 |
| DC/DC converter gain, KDC | 1.000 |
| Control Approach | Δf (KH = 1) | Δf (KH = 2) | Δf (KH = 3) | Δf (KH = 4) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MUS (Hz) | MOS (Hz) | TS (s) | MUS (Hz) | MOS (Hz) | TS (s) | MUS (pu) | MOS (pu) | TS (s) | MUS (pu) | MOS (pu) | TS (s) | |
| No VIC | 2.99 × 10−1 | 1.82 × 10−1 | 28.72 | 2.99 × 10−1 | 1.82 × 10−1 | 28.72 | 2.99 × 10−1 | 1.82 × 10−1 | 28.72 | 2.99 × 10−1 | 1.82 × 10−1 | 28.72 |
| Con. VIC | 1.06 × 10−1 | 5.96 × 10−2 | 63.74 | 8.08 × 10−2 | 5.24 × 10−2 | 108.37 | 6.84 × 10−2 | 4.75 × 10−2 | 155.06 | 6.06 × 10−2 | 4.40 × 10−2 | 204.26 |
| Pro. VIC | 5.85 × 10−2 | 1.05 × 10−4 | 13.09 | 4.97 × 10−2 | 4.15 × 10−3 | 22.41 | 4.47 × 10−2 | 7.06 × 10−3 | 33.81 | 4.13 × 10−2 | 8.87 × 10−3 | 46.07 |
| FO Operator | Δf (KH = 1) | Δf (KH = 2) | Δf (KH = 3) | Δf (KH = 4) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MUS (Hz) | MOS (Hz) | TS (s) | MUS (Hz) | MOS (Hz) | TS (s) | MUS (pu) | MOS (pu) | TS (s) | MUS (pu) | MOS (pu) | TS (s) | |
| μ =1 | 5.85 × 10−2 | 1.05 × 10−4 | 13.09 | 4.97 × 10−2 | 4.15 × 10−3 | 22.41 | 4.47 × 10−2 | 7.06 × 10−3 | 33.81 | 4.13 × 10−2 | 8.87 × 10−3 | 46.07 |
| μ =0.8 | 5.19 × 10−2 | 4.78 × 10−4 | 22.44 | 4.26 × 10−2 | 2.32 × 10−3 | 22.11 | 3.75 × 10−2 | 3.71 × 10−3 | 33.87 | 3.40 × 10−2 | 4.58 × 10−3 | 46.38 |
| μ =0.6 | 4.69 × 10−2 | 4.94 × 10−4 | 29.27 | 3.69 × 10−2 | 1.35 × 10−3 | 32.56 | 3.16 × 10−2 | 1.92 × 10−3 | 33.34 | 2.80 × 10−2 | 2.26 × 10−3 | 35.51 |
| μ =0.4 | 5.10 × 10−2 | 3.36 × 10−4 | 35.45 | 3.24 × 10−2 | 6.63 × 10−4 | 44.32 | 2.67 × 10−2 | 8.35 × 10−4 | 49.97 | 2.31 × 10−2 | 9.20 × 10−4 | 54.41 |
| μ =0.2 | 6.65 × 10−2 | 1.31 × 10−4 | 38.67 | 4.59 × 10−2 | 1.99 × 10−4 | 51.41 | 3.61 × 10−2 | 2.23 × 10−4 | 61.93 | 3.04× 10−2 | 2.28 × 10−4 | 70.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nour, M.; Magdy, G.; Bakeer, A.; Telba, A.A.; Beroual, A.; Khaled, U.; Ali, H. A New Fractional-Order Virtual Inertia Support Based on Battery Energy Storage for Enhancing Microgrid Frequency Stability. Fractal Fract. 2023, 7, 855. https://doi.org/10.3390/fractalfract7120855
Nour M, Magdy G, Bakeer A, Telba AA, Beroual A, Khaled U, Ali H. A New Fractional-Order Virtual Inertia Support Based on Battery Energy Storage for Enhancing Microgrid Frequency Stability. Fractal and Fractional. 2023; 7(12):855. https://doi.org/10.3390/fractalfract7120855
Chicago/Turabian StyleNour, Morsy, Gaber Magdy, Abualkasim Bakeer, Ahmad A. Telba, Abderrahmane Beroual, Usama Khaled, and Hossam Ali. 2023. "A New Fractional-Order Virtual Inertia Support Based on Battery Energy Storage for Enhancing Microgrid Frequency Stability" Fractal and Fractional 7, no. 12: 855. https://doi.org/10.3390/fractalfract7120855
APA StyleNour, M., Magdy, G., Bakeer, A., Telba, A. A., Beroual, A., Khaled, U., & Ali, H. (2023). A New Fractional-Order Virtual Inertia Support Based on Battery Energy Storage for Enhancing Microgrid Frequency Stability. Fractal and Fractional, 7(12), 855. https://doi.org/10.3390/fractalfract7120855











