Dilatancy Equation Based on the Property-Dependent Plastic Potential Theory for Geomaterials

Abstract

The dilatancy equation ignores the noncoaxiality of granular soil for the coaxial assumption of the direction of the stress and strain rate in conventional plastic potential theory, which is inconsistent with extensive laboratory tests. To reasonably describe the noncoaxial effects on dilatancy, the energy dissipation of plastic flow is derived based on the property-dependent plastic potential theory for geomaterials and integrates the noncoaxiality, the potential theory links the plastic strain of granular materials with its fabric, and the noncoaxiality is naturally related to the mesoscopic properties of materials. When the fabric is isotropic, the dilatancy equation degenerates into the form of the critical state theory, and when the fabric is anisotropic, it naturally describes the effects of noncoaxiality. In the plane stress state, a comparison between a simple shear test and prediction of the dilatancy equation shows that the equation can reasonably describe the effect of noncoaxiality on dilatancy with the introduction of microscopic fabric parameters, and its physical significance is clear. This paper can provide a reference for the theoretical description of the macro and micro mechanical properties of geomaterials.

1. Introduction

Dilatancy is the variation of soil porosity due to the particle rearrangement under shear stress and is an essential mechanical property to distinguish geomaterial from other nongranular materials and to establish the constitutive model. Based on the energy principle, studying dilatancy is reasonable, and energy function at the critical state is usually used to describe dilatancy, such as Rowe’s dilatancy equation in previous research [1]. Researchers gradually realized that the dilatancy of granular soil is also related to the material state in a later study [2]. Although Rowe also pointed out that the influence of material state should be considered in the dilatancy theory [1], after many scholars performed similar research, the stress dilatancy theory was successfully applied to the constitutive model of granular materials [3,4,5], and many scholars studied the particle breakage of rockfill from the perspective of energy [6,7,8]. Stress-dilatancy theory is widely used in the study of mechanical properties and the constitutive model of soil.

With the deepening of research, noncoaxiality has gradually attracted attention, which was first found by De Josselin de Jong [9] and has a significant effect on the mechanics and deformation of geomaterials. Therefore, based on the conventional plastic potential theory to derive dilatancy equations, there are some limitations in describing noncoaxiality due to the theory implying the coaxial assumption of direction between the stress and plastic strain rate. Researchers have conducted deeper research on noncoaxiality in subsequent theoretical and experimental studies [10,11]. Several scholars conducted simple shear tests to investigate noncoaxiality, such as the simple shear test of sand [12] and aluminum rod accumulation [13]. Lade [14] also found noncoaxial phenomena on the deviatoric plane in the true triaxial test of sand, where the direction of the stress and strain rate is coaxially under triaxial compression and tension tests and noncoaxial under other stress paths. Li [15] designed a similar true triaxial test, and although ideal spherical glass beads with a single particle size were used, obvious noncoaxiality was still observed. Xiong [16] found that noncoaxiality would cause the dilatancy curve to deviate from Rowe’s line, which has a significant effect on sand dilatancy. Ignoring the noncoaxiality to deduce the dilatancy equation is unreasonable. Therefore, some scholars have integrated noncoaxiality into the research on dilatancy. Gutierrez [17] introduced the noncoaxial constant into the plastic theory and further analyzed plastic work and dilatancy. However, the noncoaxial angle seems to always exist in the whole stress space after the noncoaxial constant is set, which is inconsistent with the test results of Lade and Ducan [14]. Rudnicki [18] proposed a noncoaxial model for calculating the plastic deformation of the fractured rock mass. Xiong [16] modified Rowe’s dilatancy equation by introducing Gutierrez’s noncoaxial coefficient. Lashkari [19] proposed a dilatancy equation in the noncoaxiality constitutive model, and the noncoaxial coefficient is consistent with Gutierrez’s previous research [20]. Tsegaye [21] established noncoaxial stress-dilatancy frames for axisymmetric, plane-strain, and general stress states, and presented a mechanism for establishing noncoaxial angular development in axisymmetric and plane-strain states. Pouragha [22] explored dilatancy aspects. The above research introduces corresponding parameters to improve the dilatancy equation based on the noncoaxial test phenomenon. At the microscopic level, noncoaxiality is a result of anisotropy [23] from the perspective of fabric properties described as a reasonable method.

To reasonably describe the stress–strain of granular materials, several researchers turned their theoretical studies to microscopic soil mechanics. Oda [24] used fabric tensors to describe the microscopic structure of granular materials and explored the connection between the initial fabric and the mechanical properties. Experiments by Wong [25] confirmed the connection between fabric anisotropy and the noncoaxiality of granular materials. Li and Dafalias [26] studied the anisotropy of sand from a microscopic perspective. In a study on microscopic soil mechanics, some researchers used fractal theory to describe the microstructure of granular materials [27]. The fractal dimension is used to characterize the particle breakage, and the fractal dimension before and after shearing is introduced into the constitutive model to simulate the influence of the change in the microscopic morphology of the particles on the stress–strain relationship [28,29]. Based on consideration of the microscopic characteristics of materials, Li [30] carried out relevant research work, established the anisotropic failure criterion of sand from the perspective of the combination of macro and micro, analyzed the noncoaxial characteristics of the simple shear test [31], and proposed the property-dependent plastic potential theory for geomaterials (potential theory for short) [32]. The theory connects the plastic deformation of materials with its microscopic fabric and describes the plastic strain rate related to material properties.

Dilatancy equations are usually derived according to the plastic flow rule and energy relation of materials. Therefore, from the perspective of the macro–micro combination, based on the potential theory, the dilatancy equation will be modeled combined with the idea of the energy transformation relation and the critical state of the soil. In the dilatancy equation, the microstructure of particles will be described by the long axis of particles and employed to define the noncoaxial coefficients. The noncoaxial coefficients will be introduced into the dilatancy equation to describe the effect of noncoaxiality on the geomaterials’ dilatancy from a microscale perspective. Finally, the results of a simple shear test will be used to verify the rationality of the dilatancy equation.

2. Dilatancy Equation Based on the Potential Theory

2.1. Establishment Method

The dilatancy equation is established according to the energy transformation relation in plastic deformation and the critical state of the soil. In the potential theory, the plastic strain rate is shown in Equation (1), where g represents the plastic potential function to describe the direction of plastic flow, dλ represents the plastic scalar factor, the derivation process can be referred to in reference [32], ${\overline{F}}_{lj}$ is the direction tensor of the fabric tensor $F_{lj}$, $P_F$ is the size of the fabric tensor, and $P_F{=1/(3+a}_1{+a}_2{+a}_3)$. According to the characteristics of the direction tensor, ${\overline{F}}_{il}$ can be decomposed into two parts, such as Equation (2) and Equation (3). ${\delta }_{lj}$ in the equation is the Kronecker tensor, and when $i=j$, ${\delta }_{11}={\delta }_{22}={\delta }_{33}=1$, it represents isotropy. ${\tilde{s}}_{lj}$ represents the anisotropic part, and $a_{i_{(i=1,2,3)}}$ represents anisotropy in the main direction of the fabric. When the material is isotropic, $a_1=a_2=a_3=0$ and ${\overline{F}}_{lj}={\delta }_{lj}$, the expression of plastic strain increment is consistent with the conventional plastic potential theory. When the material is anisotropic, the anisotropic parameter $a_{i_{(i=1,2,3)}}$ is nonzero, and the plastic strain rate is naturally decomposed into two parts, isotropic and anisotropic, as shown in Equation (4).

$${\mathrm{d}\epsilon }_{lj}^p=\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_{il}}{\overline{F}}_{il}$$

(1)

$$F_{lj}=P_F\left({\delta }_{lj}+{\tilde{s}}_{lj}\right)=P_F\left({\overline{F}}_{lj}\right)$$

(2)

$${\delta }_{ij}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right], {\tilde{s}}_{ij}=\left[\begin{array}{ccc}{a}_1& 0& 0\\ 0& a_2& 0\\ 0& 0& a_3\end{array}\right]$$

(3)

$${\mathrm{d}\epsilon }_{lj}^p=\mathrm{d}\lambda (\frac{\partial g}{\partial {\sigma }_{ij}}+\frac{\partial g}{\partial {\sigma }_{il}}{\tilde{s}}_{il})$$

(4)

According to Equations (1)–(4), the plastic dissipated work can be written in the form of Equation (5):

$${\mathrm{d}W}^p{=\sigma }_{lj}{\mathrm{d}\epsilon }_{lj}^p{=\sigma }_{lj}\left(\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_{ij}}+\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_{il}}{\tilde{s}}_{il}\right)$$

(5)

where ${\mathrm{d}W}^p$ is the plastic dissipated work, $\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_{ij}}$ is the isotropic part of the plastic strain rate, and $\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_{il}}{\tilde{s}}_{il}$ is the anisotropic part of the plastic strain rate. The plastic dissipated work can be written as Equation (6) in the principal stress space, and stress ${\sigma }_{lj}$ and strain increments ${\mathrm{d}\epsilon }_{lj}^p$ are ${\sigma }_k$ and ${\mathrm{d}\epsilon }_k^p$ instead, respectively. ${\sigma }_k$ is the principal stress expressed by stress invariants, which can be written as Equation (7).

$${\mathrm{d}W}^p{=\sigma }_{lj}{ \mathrm{d}\epsilon }_{lj}^p={\sigma }_k{ \mathrm{d}\epsilon }_k^p={\sigma }_k\left(\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_k}+\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_k}{s}_k\right)$$

(6)

$${\sigma }_k=p+\frac{2}{3}{q \sin [\theta }_{\sigma }+\frac{2\pi (2-k)}{3}]$$

(7)

According to Equation (1), the principal plastic strain increment ${\mathrm{d}\epsilon }_k^p$ can be written by strain rate invariants as shown in Equation (8), where ${\mathrm{d}\gamma }^p$ is the plastic shear strain rate. The stress invariants in Equation (7) and strain increment invariants in Equation (8) are substituted into Equation (6) to obtain the energy relation based on the potential theory, as shown in Equation (9). In Equation (7), $p=\left({\sigma }_1+{\sigma }_2+{\sigma }_3\right)/3$ represents the average principal stress, $q=\frac{1}{\sqrt{2}}\sqrt{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_1-{\sigma }_3)}^2}$ is the generalized shear stress, and the stress lode angle ${\theta }_{\sigma }$ represents the stress direction, which is defined on the deviatoric plane; the calculation formula is shown in Equation (12). ${\mathrm{d}\epsilon }_v^p$ and ${\mathrm{d}\gamma }^p$ are the increments of the plastic volumetric strain and shear strain, respectively, and the angle ${\theta }_{\mathrm{d}\epsilon }$ represent the direction of the strain rate, ${\theta }_{\mathrm{d}\epsilon }=arctan\left[\frac{1}{\sqrt{3}}\left(2\frac{{\mathrm{d}\epsilon }_2{-\mathrm{d}\epsilon }_3}{{ \mathrm{d}\epsilon }_1{-\mathrm{d}\epsilon }_3}-1\right)\right]$.

$${\mathrm{d}\epsilon }_k^p=\frac{1}{3}{\mathrm{d}\epsilon }_v^p{+\mathrm{d}\gamma }^p\sin \left[{\theta }_{\mathrm{d}\epsilon }+\frac{2(2-k)\pi }{3}\right]$$

(8)

$$\begin{array}{cc}& {\mathrm{d}W}^p{=p \mathrm{d}\epsilon }_v^p+\frac{{2q \mathrm{d}\gamma }^p}{3}{\displaystyle \sum }_{\mathrm{k}=1}^3\sin \left[{\theta }_{\sigma }+\frac{2\pi (2-k)}{3}\right]\sin \left[{\theta }_{\mathrm{d}\epsilon }+\frac{2\pi (2-k)}{3}\right]\hfill \\ & {=p \mathrm{d}\epsilon }_v^p{+q \mathrm{d}\gamma }^p\cos \left({\theta }_{\sigma }-{\theta }_{\mathrm{d}\epsilon }\right)\hfill \end{array}$$

(9)

According to the critical state theory, when the soil reaches the critical state, the stress and volumetric strain rate hold. Under the action of shear stress, shear deformation occurs continuously, and the stress ratio reaches the critical stress ratio ${\eta }_c$. At this point, the energy relation based on the potential theory can be simplified to Equation (10) in the critical state, and the three-dimensional dilatancy equation shown in Equation (11) based on the potential theory can be obtained.

$${ \mathrm{d}W}^p{=p \mathrm{d}\epsilon }_v^p{+q \mathrm{d}\gamma }^p\cos \left({\theta }_{\sigma }-{\theta }_{\mathrm{d}\epsilon }\right)={\eta }_c{ p \mathrm{d}\gamma }^p$$

(10)

$$\frac{{\mathrm{d}\epsilon }_v^p}{{\mathrm{d}\gamma }^p}={\eta }_c-\cos \left({\theta }_{\sigma }-{\theta }_{\mathrm{d}\epsilon }\right)\frac{q}{p}$$

(11)

where the stress lode angle is shown in Equation (12), which is consistent with Equation (7). The strain increments lode angle can be redefined in Equation (13) according to the potential theory and a detailed analysis process can be found in reference [32].

$${\theta }_{\sigma }=\arctan \left[\frac{1}{\sqrt{3}}\left(2\frac{{\sigma }_2-{\sigma }_3}{{\sigma }_1-{\sigma }_3}-1\right)\right]$$

(12)

$${\theta }_{\mathrm{d}\epsilon }=\arctan \left[\frac{1}{\sqrt{3}}\left(2\frac{{\mathrm{d}\epsilon }_2-{\mathrm{d}\epsilon }_3}{{ \mathrm{d}\epsilon }_1-{\mathrm{d}\epsilon }_3}-1\right)\right]=\arctan \left[\frac{1}{\sqrt{3}}\left(2\frac{\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_2}{\overline{F}}_2-\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_3}{\overline{F}}_3}{ \mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_1}{\overline{F}}_1-\mathrm{d}\lambda \frac{\partial g}{\partial {\sigma }_3}{\overline{F}}_3}-1\right)\right]$$

(13)

According to Equation (10), when the stress lode angle is equal to the strain lode angle, it is coaxial. The analysis combined with Figure 1 and Equation (13) shows that when the material with the transversely isotropic fabric, $F_2=F_3$, and under triaxial compression, ${\sigma }_1 > {\sigma }_2 = {\sigma }_3$, the principal stress acts in the three directions of F₁, F_2, and F₃, respectively, ${\theta }_{\sigma } = {\theta }_{\mathrm{d}\epsilon }$, and the stress and strain increments are coaxial. In the triaxial tensile state, ${\sigma }_1={\sigma }_2{ > \sigma }_3$, the principal stress acts on F₂, F₃, and F₁, respectively, the stress lode angle is equal to the strain lode angle, and the stress and strain increment are coaxial. In other stress states of the deviatoric plane, ${\theta }_{\sigma }\ne {\theta }_{\mathrm{d}\epsilon }$. Accordingly, the description of noncoaxiality under different stress states is associated with the meso-fabric properties of materials, which is different from the noncoaxial coefficients commonly used in previous research, has clearer physical significance, and is consistent with the experimental phenomenon in reference [14].

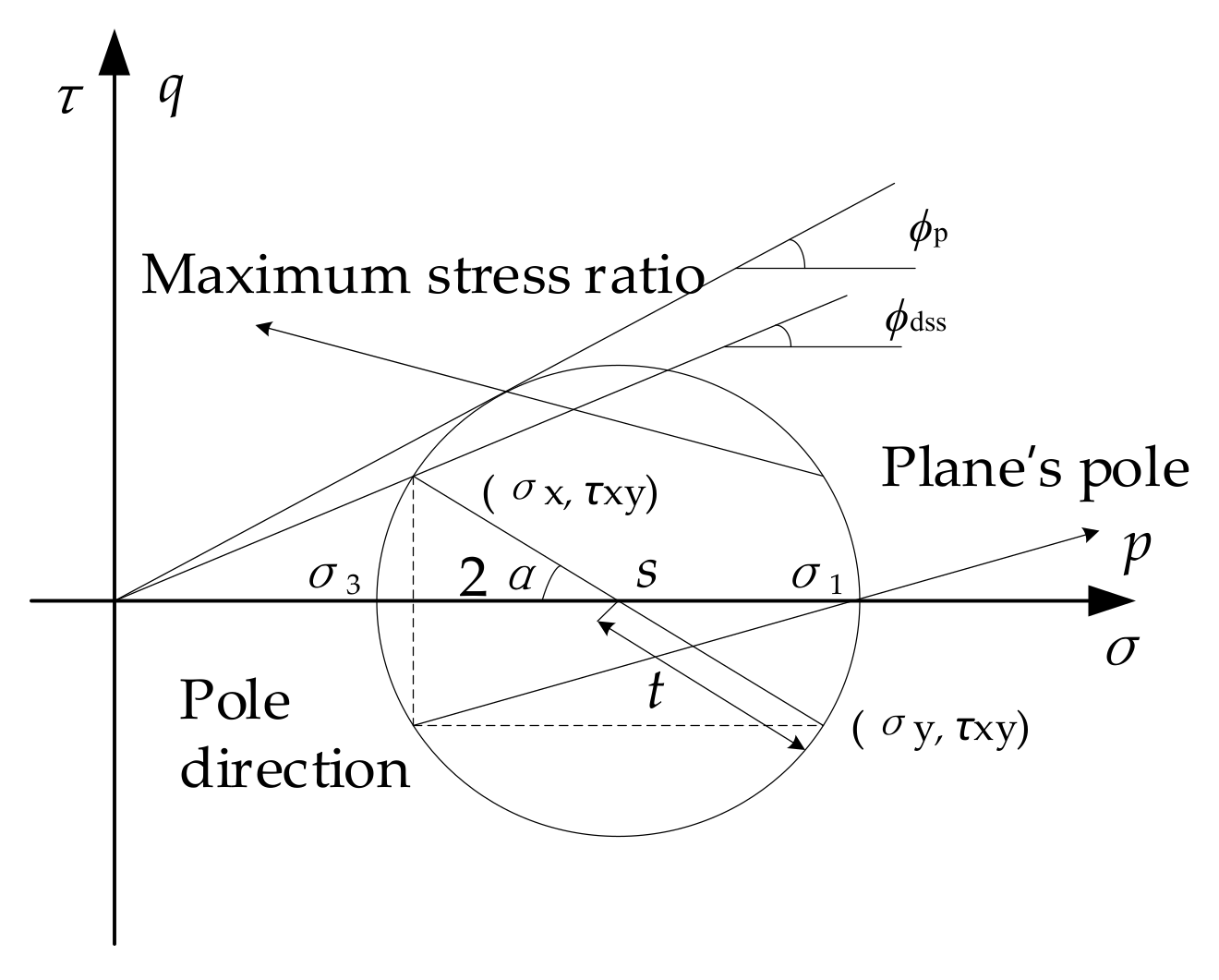
2.2. Description of Dilatancy under Plane Stress State

To verify the rationality of the dilatancy equation in this paper, we first derived the dilatancy equation under the plane stress state. Mohr’s circle under plane stress is shown in Figure 2, where ϕ_dss and ϕ_p are the friction angle and the peak friction angle, respectively. The relation between stress components σ_x, σ_y, σ_z, normal stress s, and shear stress t is shown in Equation (14). Similarly, the relation between the strain component increments dε_x, dε_y, and dε_z, volumetric strain, and shear strain in the strain Mohr’s circle can be written as Equation (15).

$${\sigma }_x=s-t\cos \left(2\alpha \right), {\sigma }_y=s+t\cos \left(2\alpha \right), {\tau }_{xy}=t\sin \left(2\alpha \right)$$

(14)

$$\left.\begin{array}{c}{\mathrm{d}\epsilon }_x^p=\frac{1}{2}{\mathrm{d}\epsilon }_{\nu }^p-\frac{1}{2}{\mathrm{d}\gamma }^p\cos \left(2\beta \right)\\ {\mathrm{d}\epsilon }_y^p=\frac{1}{2}{\mathrm{d}\epsilon }_{\nu }^p+\frac{1}{2}{\mathrm{d}\gamma }^p\cos \left(2\beta \right)\\ {\mathrm{d}\epsilon }_{xy}^p=\frac{1}{2}{\mathrm{d}\gamma }^p\sin \left(2\beta \right)\end{array}\right\}$$

(15)

where α is the stress direction angle (as shown in Figure 2) and β is the strain increment direction angle in the strain space. Assuming the elastic strain is negligible, stress invariants and strain invariants can be written as:

$$\begin{gathered} s=\frac{{\sigma }_x{+\sigma }_y}{2}=\frac{{\sigma }_1{+\sigma }_3}{2}, t=\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2}=\frac{{\sigma }_1-{\sigma }_3}{2}, \\ {\mathrm{d}\epsilon }_{\nu }^p{=\mathrm{d}\epsilon }_1^p{+\mathrm{d}\epsilon }_2^p, {\mathrm{d}\gamma }^p{=\mathrm{d}\epsilon }_1^p-{\mathrm{d}\epsilon }_2^p \end{gathered}$$

(16)

In the plane stress state, the plastic dissipation work can be written as Equation (17). The stress component and strain component of Equation (14) and Equation (15) are substituted into Equation (17), respectively, and the incremental expression of the plastic dissipation work shown in Equation (18) is further determined. According to critical state soil mechanics, the volumetric strain increment of soil reaches zero and the stress ratio reaches the critical stress ratio ${\eta }_c$ under the plane stress state, and the plastic dissipation work increment described in Equation (18) can be written the form of Equation (19) while the dilatancy equation under plane stress can be obtained through further modifications as Equation (20). Here, ${\mathrm{d}\epsilon }_v^p$ and ${\mathrm{d}\gamma }^p$ are the volume strain and shear strain increments, and s and t are the average principal stress and shear stress, respectively.

$${\mathrm{d}W}^p{=\sigma }_{lj}{\mathrm{d}\epsilon }_{lj}^p={\sigma }_x{\mathrm{d}\epsilon }_x^p{+\sigma }_y{\mathrm{d}\epsilon }_y^p+2{\tau }_{xy}{\mathrm{d}\epsilon }_{xy}^p$$

(17)

$${\mathrm{d}W}^p{=s \mathrm{d}\epsilon }_v^p{+t \mathrm{d}\gamma }^p\cos (2\Delta )$$

(18)

$${\mathrm{d}W}^p{=s \mathrm{d}\epsilon }_v^p{+t \mathrm{d}\gamma }^p\cos (2\Delta )=s {\eta }_c{\mathrm{d}\gamma }^p$$

(19)

$$\frac{{\mathrm{d}\epsilon }_v^p}{{\mathrm{d}\gamma }^p}={\eta }_c-c\frac{t}{s}$$

(20)

In Equation (17), $c=\cos (2\Delta )=\cos (2\alpha -2\beta )$, as shown in Figure 2, α can be written as Equation (21) according to the geometric relation, and β can also be written as Equation (22) in the strain space. ${\eta }_c$ can be regarded as different parameters for sand with different densities.

$$\alpha =\frac{1}{2}\arctan \frac{2{\tau }_{xy}}{{\sigma }_y-{\sigma }_x}$$

(21)

$$\beta =\frac{1}{2}\arctan \frac{2\mathrm{d}{\gamma }^p}{{\mathrm{d}\epsilon }_y^p-{\mathrm{d}\epsilon }_x^p}$$

(22)

In the strain space, according to the idea of strain distribution in the potential theory, the strain increment in Equation (22) is expressed by Equation (1) and resubstituted into Equation (22), and the expression of strain rate direction angle Equation (23) based on the potential theory is obtained. It should be noted that in most cases, geomaterials are transversely isotropic, so the transversely isotropic fabric is adopted in the strain distribution by Equation (1). The specific components of the fabric are shown in Equation (24), and two components of the fabric direction tensor in Equation (4) can be written as Equation (25) where g represents the plastic potential function and a represents the anisotropic parameter of transversely isotropic fabric. The value of a is measured by the method proposed by Li [33], where $a_{i_{(i=1,2,3)}}$ represents the amplitude parameter of the orthorhombic anisotropy as shown in Equation (26) and the physical meanings of θ^(K) and α^(K) are shown in Figure 3. When ${\alpha }^{\left(K\right)}=\pi /4$, ${\sin (\alpha }^{\left(K\right)}{)=\cos (\alpha }^{\left(K\right)})$, $a_2=a_3$, which is transversely isotropic, and the value of a is shown in Equation (27). In Equations (26) and (27), N is the particle number of the sample, and it represents the number of contact fabrics when F_ij is employed to describe the contact of particles.

$$\beta =\frac{1}{2}arctan\frac{2\frac{\partial g}{\partial {\tau }_{xy}}(1+a)}{\frac{\partial g}{\partial {\sigma }_y}(1-a)-\frac{\partial g}{\partial {\sigma }_x}(1+a)}$$

(23)

$$F_{lj}=\frac{1}{3+a}\left[\begin{array}{ccc}1-a& 0& 0\\ 0& 1+a& 0\\ 0& 0& 1+a\end{array}\right]$$

(24)

$${\delta }_{ij}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right], {\tilde{s}}_{ij}=\left[\begin{array}{ccc}-a& 0& 0\\ 0& a& 0\\ 0& 0& a\end{array}\right]$$

(25)

$$\begin{array}{cc}& a_1=\frac{1}{2N}{\left\{{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}{(\cos }^2\left({\theta }_1^{\left(K\right)}\right)-{\sin }^2\left({\theta }_1^{\left(K\right)}\right){\cos }^2\left({\alpha }^{\left(K\right)}\right))\right]}^2+{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}\sin \left({2\theta }_1^{\left(K\right)}\right)\cos \left({\alpha }^{\left(K\right)}\right)\right]}^2\right\}}^{\frac{1}{2}}\hfill \\ & a_2=\frac{1}{2N}{\left\{{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}{(\cos }^2\left({\theta }_1^{\left(K\right)}\right)-{\sin }^2\left({\theta }_1^{\left(K\right)}\right){\sin }^2\left({\alpha }^{\left(K\right)}\right))\right]}^2+{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}\sin \left({2\theta }_1^{\left(K\right)}\right)\sin \left({\alpha }^{\left(K\right)}\right)\right]}^2\right\}}^{\frac{1}{2}}\hfill \\ & a_3=\frac{1}{2N}{\left\{{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}{\sin }^2\left({\theta }_1^{\left(K\right)}\right)\cos \left({2\alpha }^{\left(K\right)}\right)\right]}^2+{\left[{\displaystyle {\displaystyle \sum }_{K=1}^{2N}}{\sin }^2\left({2\theta }_1^{\left(K\right)}\right)\sin \left(2{\alpha }^{\left(K\right)}\right)\right]}^2\right\}}^{\frac{1}{2}}\hfill \end{array}$$

(26)

$$a=\frac{1}{2N}{\left\{{\left[{\displaystyle \sum }_{K=1}^{2N}{(\cos }^2\left({\theta }_1^{\left(K\right)}\right)-\frac{{\sin }^2\left({\theta }_1^{\left(K\right)}\right)}{2})\right]}^2+\frac{1}{2}{\left[{\displaystyle \sum }_{K=1}^{2N}\sin \left({2\theta }_1^{\left(K\right)}\right)\right]}^2\right\}}^{\frac{1}{2}}$$

(27)

We then introduce two directional angles of Equations (21) and (23) into Equation (20), and the expression form of the dilatancy equation based on the potential theory under plane stress can be obtained. The plastic potential g can be obtained by integrating the equation $D=-\mathrm{dt}/\mathrm{ds}$; in the critical state, the plastic volumetric strain increment and shear stress are constant, which means $\mathrm{d}p{\mathrm{d}\epsilon }_v^p+\mathrm{d}q\mathrm{d}{\gamma }^p=0$. We let $D=\frac{{\mathrm{d}\epsilon }_v^p}{{\mathrm{d}\gamma }^p}=-\frac{\mathrm{d}q}{\mathrm{d}p }=-\frac{\mathrm{d}t}{\mathrm{d}s}$, and introducing the dilatancy equation (Equation (28)) into the expression of the critical state obtains the plastic potential g by the integral as shown in Equation (29).

$$D=\frac{{\mathrm{d}\epsilon }_v^p}{{\mathrm{d}\gamma }^p}={\mathrm{d}}_0({\eta }_c-c\frac{t}{s})$$

(28)

$$g=t+\frac{{\mathrm{d}}_0{\eta }_{c}s}{{\mathrm{d}}_{0}c-1}\left[{\left(\frac{s}{s_0}\right)}^{{\mathrm{d}}_{0}c-1}-1\right]$$

(29)

where s₀ represents the initial average principal stress. It can be seen that the dilatancy equation can reflect the noncoaxiality of stress and plastic strain increments in the plane stress state and also reflect the coaxiality when a = 0. According to Equation (23), the more obvious the anisotropy is, the more significant the noncoaxiality is. The dilatancy and stress ratio under plane stress are shown in Figure 4, which is drawn by setting different model parameters, in which d₀ was defined by Li [2] and anisotropic parameter a was under the same stress condition. With the gradual increase in the stress ratio, dilatancy presents as shear contraction followed by dilatancy. With the increase in the fabric parameter a, the difference in dilatancy is more significant with different anisotropy. With the decrease in material coefficient d₀, the volume contraction is lower, and the difference in dilatancy is lower.

3. Model Verification

To verify the dilatancy equation, Equation (20) is compared with the results of the simple shear test [34]. First, the simple shear test is introduced. The principal stress rotation in the loading process is the noticeable feature of the simple shear test, and the position of the failure plane is uncertain, as shown in Figure 5. The black line is the initial stress unit, and the blue line is the stress unit after deformation. In the laboratory test, Cambridge University’s Mark 5 DSS apparatus was used to shear the sample prepared by Leighton–Buzzard sand. The consolidation of the sample is loaded under the normal stress σ_y = 400 kPa. After the loading starts, shear is carried out at a constant shear rate until the peak value is reached. The test can reflect the rotation of principal stress and the noncoaxiality between the stress direction and strain increment direction, which is consistent with the research goal of this paper.

3.1. Noncoaxiality Verification

The predicted and tested values of principal stress rotation are shown in Figure 6a. In this paper, the critical stress ratio ${\sin \phi }_c$ of loose sand, medium dense sand, and dense sand in relevant tests are extracted from [17], which was performed by Cole [34]. The experimental results show an extremely small difference in the principal stress rotation angle among the samples, the simulation results are close to the experimental values, and the model’s principal stress rotation angle is consistent with the experiment. Figure 6b–d shows the variation in noncoaxial angles, which decrease with the increase in the stress ratio (${\tau }_{xy}/{\sigma }_y$) under different densities, gradually close to the coaxial state. When the stress ratio of loose and medium-dense sand is close to 0.6, the noncoaxial angle is close to zero. When the stress ratio of dense sand reaches 0.8, the noncoaxial angle is approximately 5°. The dilatancy equation can aptly predict this law, which shows that the dilatancy equation in this paper is reasonable.

3.2. Verification of Dilatancy

Noncoaxiality has a significant effect on the dilatancy of sand [35] and the critical stress ratio with three densities is set to a fixed value in this section ($\sin {\phi }_c=0.5$), the dilatancy coefficient D is calculated by different anisotropic parameters a, the effect of noncoaxiality on dilatancy is analyzed, and the predicted and experimental values(−dv/dγ) are shown in Figure 7. When the fabric parameter a in the dilatancy equation takes different values, the dilatancy of prediction shows the same law with three densities, and the law of first contraction and then dilatancy is consistent with the experiment. The loose sand test results show significant volume contraction, which is closer to the predicted value and is consistent with the findings that noncoaxiality can lead to more significant volume contraction than in reference [16], indicating that the noncoaxial coefficient modified by the dilatancy equation from the mesoscopic perspective can reasonably reflect the influence of noncoaxiality on dilatancy. Meanwhile, under the low-stress ratio, the deformation is greatly affected by the material properties [36,37,38], and the different noncoaxiality values with different a values lead to the curves of dilatancy not coinciding. When reaching the high-stress ratio, the effect of material properties is weak, the stress–strain tends to be coaxial, and the dilatancy curves of different a values are less affected by noncoaxial and gradually coincide, which is consistent with the existing consensus.

4. Conclusions

To integrate the effect of noncoaxiality and describe the dilatancy of geomaterials reasonably, the strain increment lode angle ${\theta }_{\mathrm{d}\epsilon }$ defined in the potential theory by macro-micro combination is used to define the noncoaxial coefficient, introducing noncoaxiality to the dilatancy equation. It can reflect the influence of noncoaxiality on dilatancy and comprehensively considers the material properties. Finally, the rationality of the dilatancy equation is verified by a simple shear test, and the following conclusions are drawn:

(1)

For noncoaxial conditions, calculation using stress invariants and strain increment invariants will overestimate the energy dissipated during loading. The energy transformation relation based on the potential theory introduces a new noncoaxial coefficient with values of 0–1, which can reasonably correct the influence of noncoaxiality on energy dissipation. Meanwhile, the influence of material microscopic properties on energy dissipation is introduced, which is closer to the actual condition.

(2)

The new noncoaxial coefficient is different from previous research, which is not only related to the stress level and stress direction but also related to the material microscopic fabric characteristics. The potential theory can be used to calculate the newly defined noncoaxial coefficient to provide a dilatancy equation considering noncoaxiality. When the microscopic fabric is isotropic, the noncoaxial coefficient is naturally 1, and the dilatancy equation can be reduced to the form of the critical state theory. When the fabric is anisotropic, the noncoaxial angle is related to the material anisotropy, the geometric relation between the fabric and the stress direction. The dilatancy equations can naturally describe noncoaxial effects, and the physical meaning is clearer.

(3)

Under the simple shear stress state, after introducing the noncoaxial coefficient, the dilatancy equation can naturally reflect the influence of noncoaxiality on the dilatancy under the condition of principal stress rotation. At the low-stress ratio, the generation of noncoaxiality depends on the material properties and has a significant effect on dilatancy. When the stress ratio is high, the influence of material properties on stress and strain is not obvious, the stress and strain naturally tend to be coaxial, and the influence on dilatancy is weakened. The experimental results verify the effectiveness of the proposed dilatancy equation.